A Novel Voltage Sag Detection Method Based on a Selective Harmonic Extraction Algorithm for Nonideal Grid Conditions
Abstract
:1. Introduction
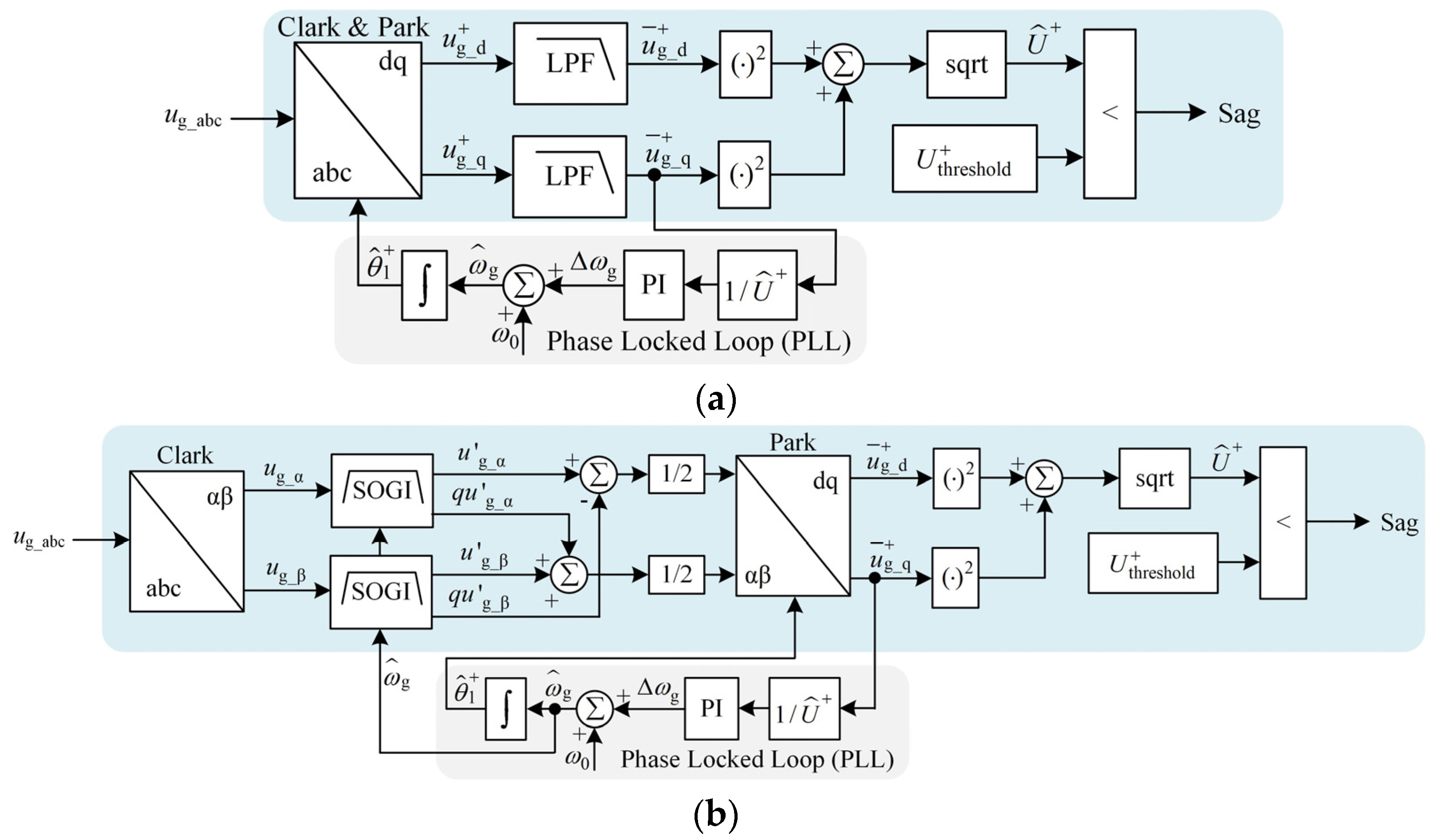
2. Voltage Sag and Traditional Detection Methods Based on SRF
3. SHEA Principle and Performance Analysis
3.1. Mathematical Modelling of SHEA
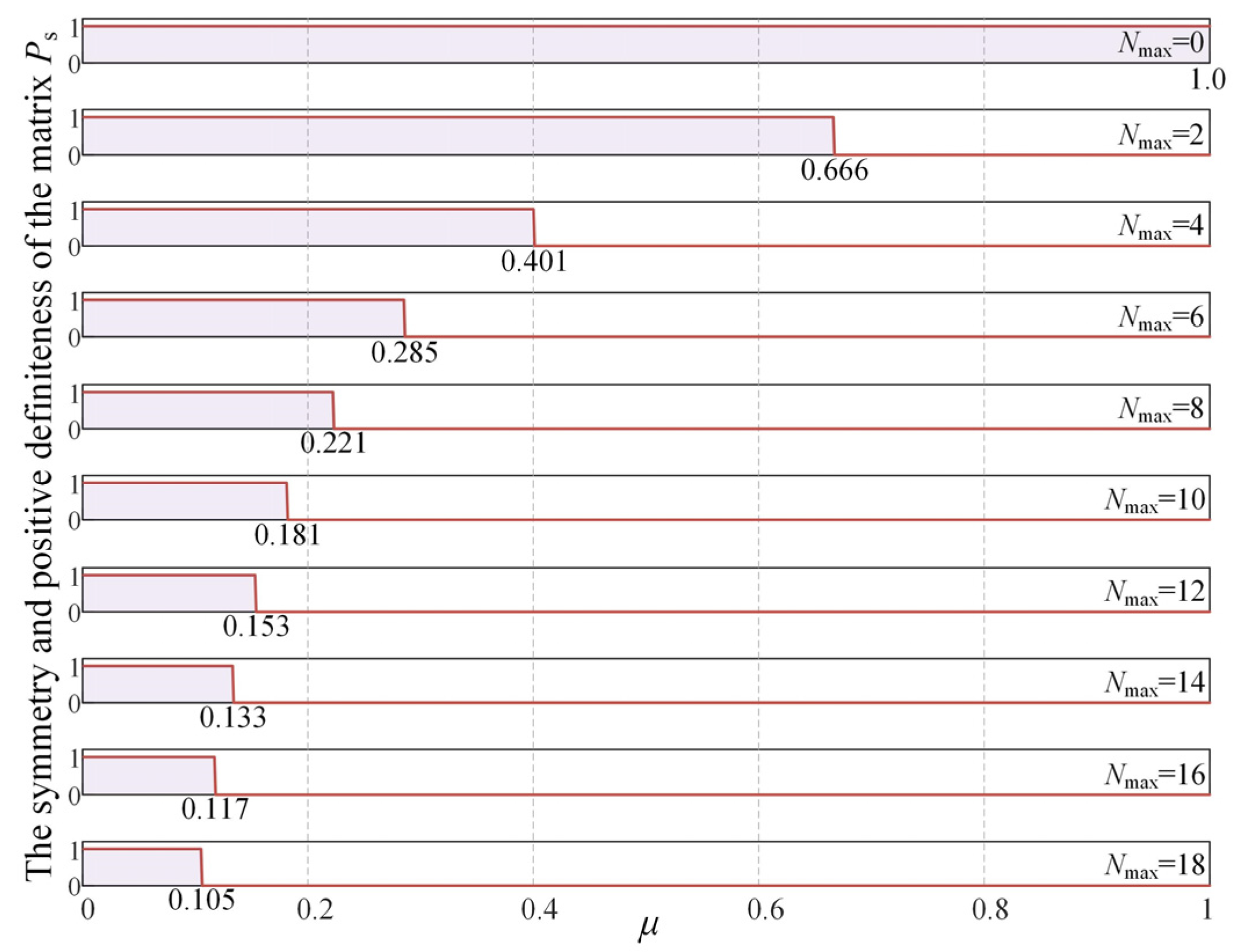
3.2. Controllability and Stability Analysis of SHEA
3.2.1. Controllability Analysis
3.2.2. Stability Analysis
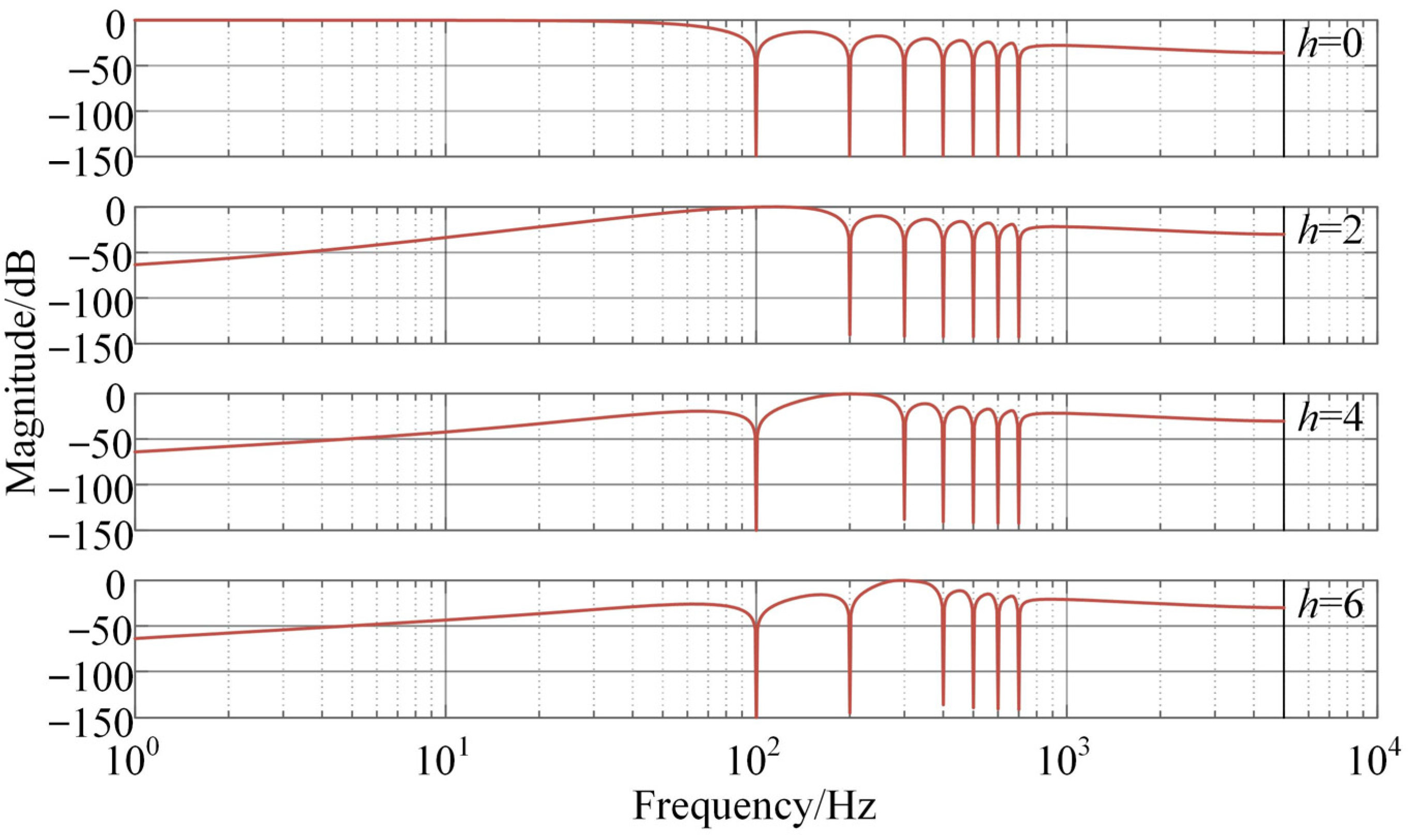
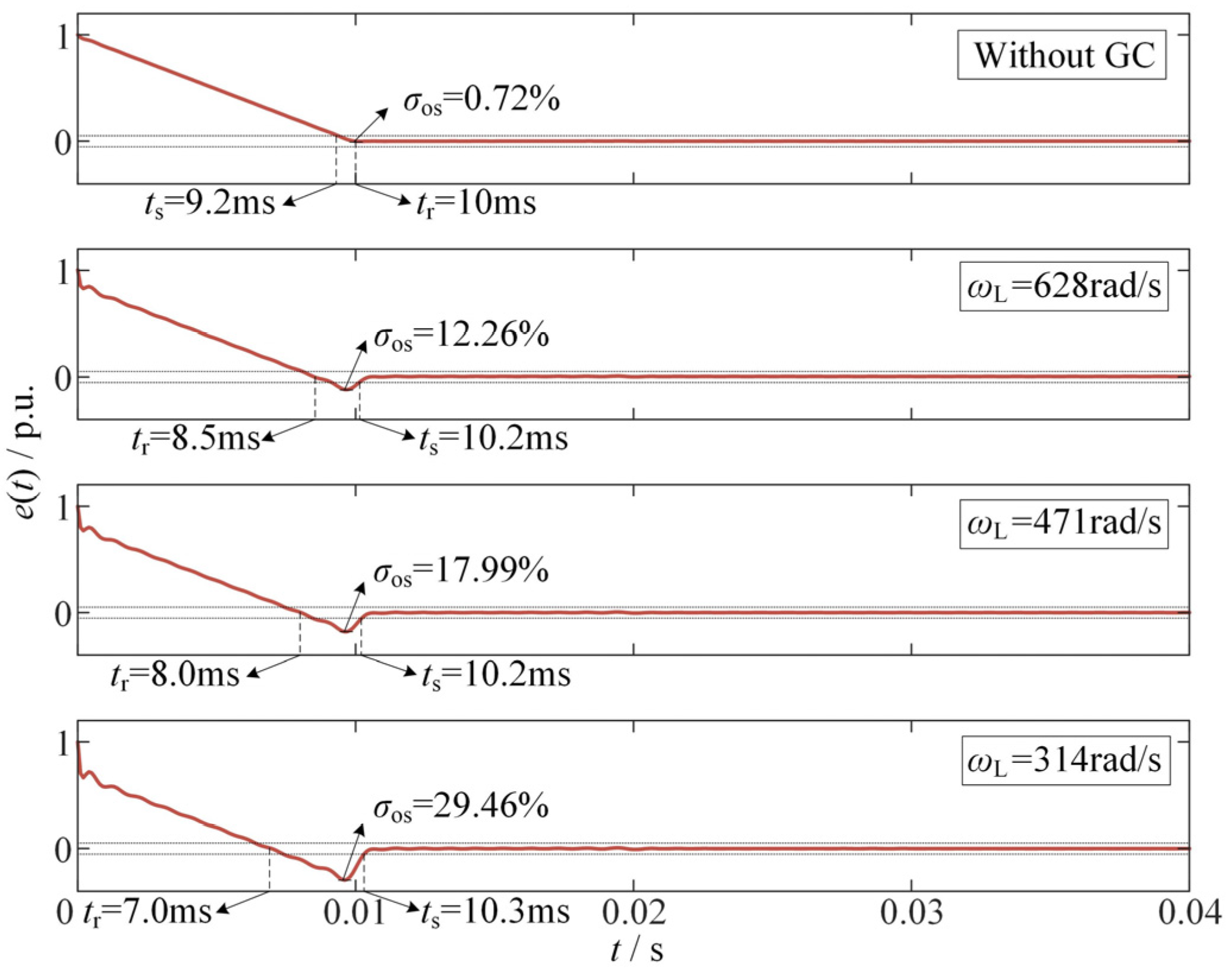
3.3. Performance Evaluation of SHEA
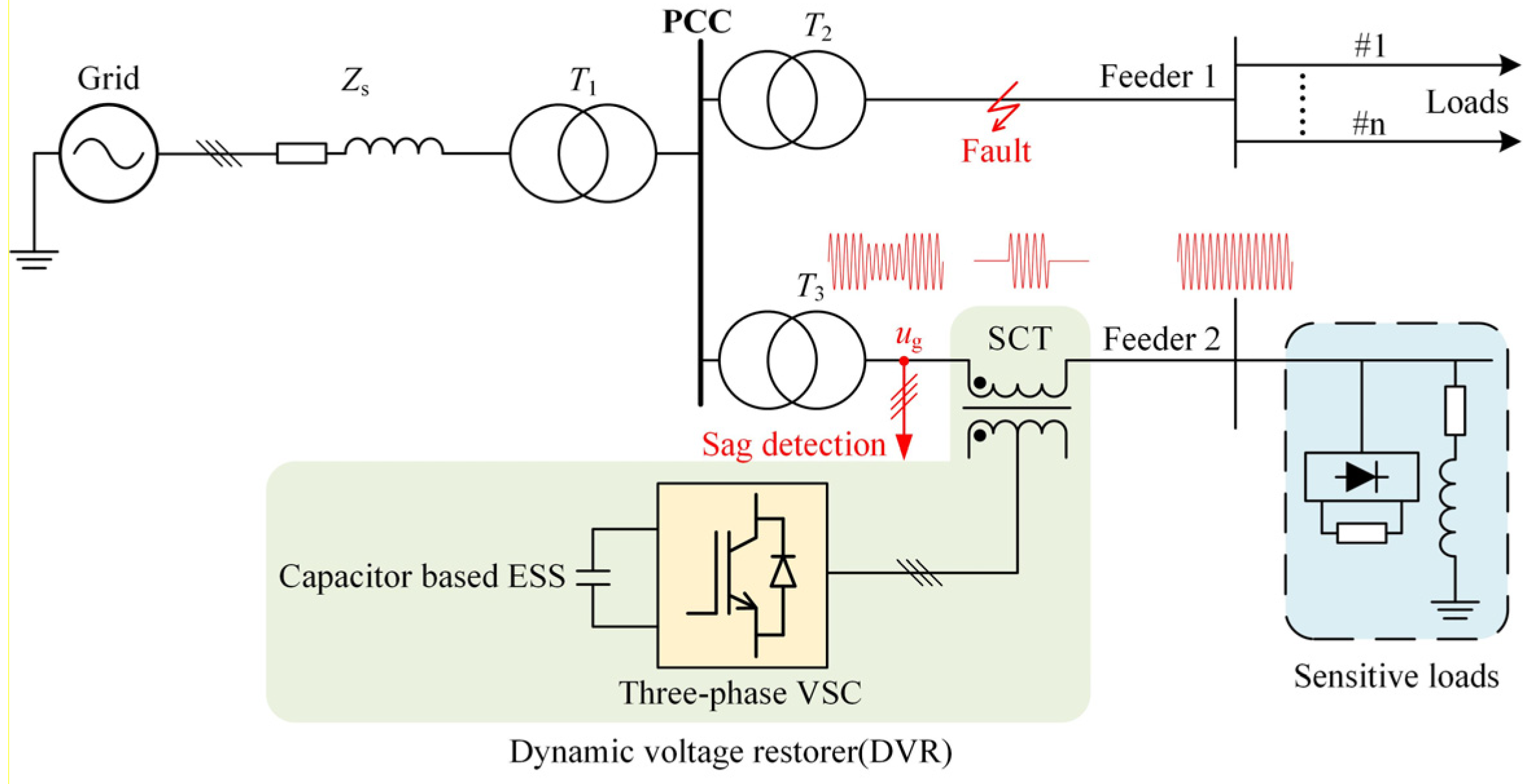
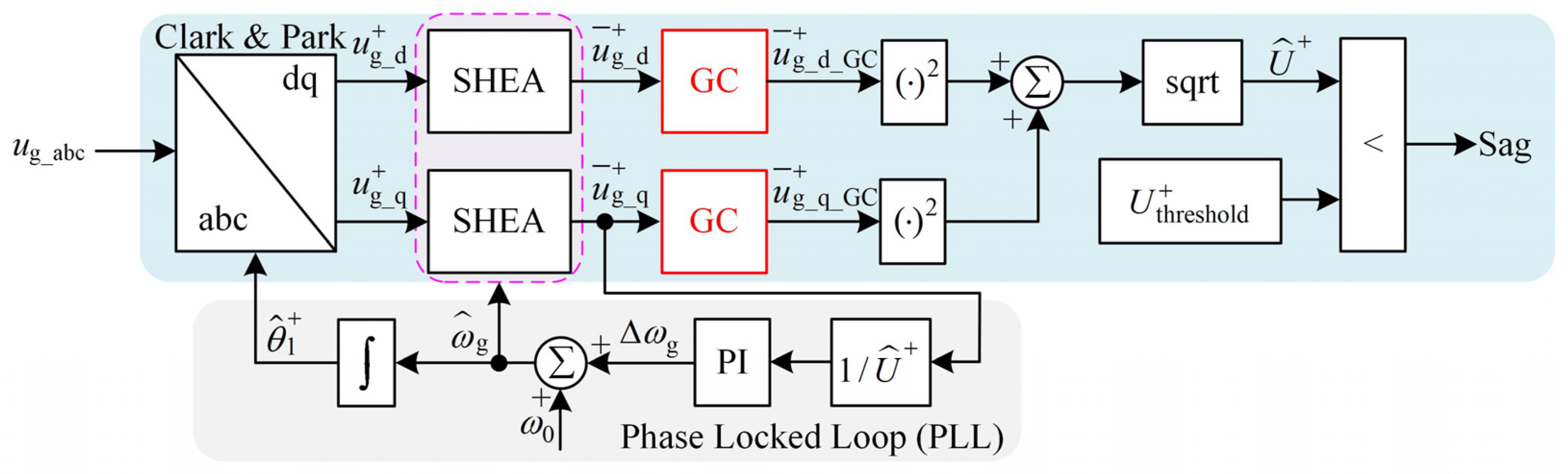
4. A Novel Voltage Sag Detection Method Based on SHEA and Its Optimization
5. Simulation Results
- (1)
- Symmetrical voltage sag with Udepth1 happens in a three-phase power grid.
- (2)
- The three-phase power grid undergoes an asymmetrical sag of type C (as shown in Figure 2) with Udepth2.
- (3)
- Symmetrical voltage sag with Udepth1 occurs accompanied by phase variation θvariation.
- (4)
- Symmetrical voltage sag with Udepth1 occurs accompanied by frequency drift of fvariation.
- (5)
- Symmetrical voltage sag with Udepth1 occurs injected with harmonic disturbance, which is given in Table 1.
- (6)
- The three-phase power grid experiences an asymmetrical sag of type C accompanied by phase variation of θvariation, frequency drift of fvariation and harmonic disturbance.
5.1. Comparison with SRF-LPF and DSOGI-SRF
5.2. Comparison with Other Methods
5.3. Reliability Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CS | Computer system |
| ASD | Adjustable speed driver |
| PLC | Programmable logic controller |
| DVR | Dynamic voltage restorer |
| APF | Active power filter |
| SHEA | Selective harmonic extraction algorithm |
| GC | Gain compensator |
| ESS | Energy storage system |
| SCT | Series-coupled transformer |
| VSC | Voltage source converter |
| RMS | Root mean square |
| FFT | Fast Fourier transform |
| DFT | Discrete Fourier transform |
| GDFT | Generalized Discrete Fourier transform |
| GDSC | Generalized delayed signal cancellation |
| WT | Wavelet transform |
| RNN | Recurrent neural network |
| LES | Least error squares |
| FIR | Finite impulse response |
| PLL | Phase-locked loop |
| LPF | Low-pass filter |
| DSOGI | Dual second order generalized integrator |
| MSOGI | Multi second order generalized integrator |
| LTI | Linear time invariant |
| SRF | Synchronously Rotating Frame |
| 3ph-3w | Three-phase and three-wire |
| ug_a, ug_b, ug_c | Instantaneous grid voltage |
| Uh+, Uh− | Amplitude of the hth harmonic component of the positive-sequence (negative-sequence) of the grid voltage |
| φh+, φh− | Phase angle of the hth harmonic component of the positive-sequence (negative-sequence) of the grid voltage |
| ωg | Actual angular frequency of fundamental voltage of power grid |
| Estimated angular frequency of fundamental voltage of power grid | |
| ω0 | Rated angular frequency of fundamental component of u(k) |
| f0 | Rated frequency of power grid |
| ωL | Transition angle frequency of the zero |
| ωH | Transition angle frequency of the pole |
| Ts | Sampling period |
| fs | Sampling frequency |
| Estimated fundamental positive-sequence phase angle | |
| Positive-sequence amplitude of fundamental voltage of power grid | |
| U+threshold | Threshold for sag judgment |
| u(k) | Instantaneous measured voltage |
| uh(k) | hth harmonic of u(k) |
| N | Number of harmonic components of u(k) |
| Nmax | Highest harmonic number of SHEA |
| xh(k) | Discrete state variable of the hth harmonic component of u(k) in SHEA |
| Uh | AC RMS of the hth harmonic |
| φh | Phase angle of the hth harmonic |
| µ | Controllability factor for SHEA |
| Sh | Second-order rotating transformation matrix of the hth harmonic |
| S | 2N-order square matrix |
| E1×2N | Matrix of dimension (1 × 2N) with all elements of 1 |
| Pc | Controllability matrix for SHEA |
| Q | Positive definite symmetric matrix in Lyapunov’s analysis |
| Ps | Stability related matrix |
| e(t) | Response error |
| ess | Steady-state error after convergence |
| σos | Percentage of overshoot peak value |
| tr | Rise time of error curve |
| ts | Convergence time within ±2% |
| tj | Judge time of sag detection related to threshold (0.9 p.u.) |
| Ug_line | Rated grid line voltage |
| Udepth1 | Symmetrical sag depth |
| Udepth2 | Asymmetrical sag depth |
| fvariation | Variation of frequency |
| θvariation | Variation of phase angle |
References
- Khergade, A.V.; Satputaley, R.J.; Borghate, V.B.; Raghava, B. Harmonics Reduction of Adjustable Speed Drive Using Transistor Clamped H-Bridge Inverter Based DVR With Enhanced Capacitor Voltage Balancing. IEEE Trans. Ind. Appl. 2020, 56, 6744–6755. [Google Scholar] [CrossRef]
- Emerging Power Quality Problems and State-of-the-Art Solutions. IEEE Trans. Ind. Electron. 2017, 64, 761–763. [CrossRef] [Green Version]
- Moghassemi, A.; Padmanaban, S. Dynamic Voltage Restorer (DVR): A Comprehensive Review of Topologies, Power Converters, Control Methods, and Modified Configurations. Energies 2020, 13, 4152. [Google Scholar] [CrossRef]
- Ghodsi, M.; Barakati, S.M.; Guerrero, J.M.; Vasquez, J.C. Dynamic Voltage Restore Based on Switched-Capacitor Multilevel Inverter with Ability to Compensate for Voltage Drop, Harmonics, and Unbalancing Simultaneously. Electr. Power Syst. Res. 2022, 207, 107826. [Google Scholar] [CrossRef]
- Abas, N.; Dilshad, S.; Khalid, A.; Saleem, M.S.; Khan, N. Power Quality Improvement Using Dynamic Voltage Restorer. IEEE Access 2020, 8, 164325–164339. [Google Scholar] [CrossRef]
- Khergade, A.; Satputaley, R.; Patro, S.K. Investigation of Voltage Sags Effects on ASD and Mitigation Using ESRF Theory-Based DVR. IEEE Trans. Power Deliv. 2021, 36, 3752–3764. [Google Scholar] [CrossRef]
- Tu, C.; Guo, Q.; Jiang, F.; Wang, H.; Shuai, Z. A Comprehensive Study to Mitigate Voltage Sags and Phase Jumps Using a Dynamic Voltage Restorer. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1490–1502. [Google Scholar] [CrossRef]
- Zhang, H.; Xiao, G.; Lu, Z.; Chai, Y. Reduce Response Time of Single-Phase Dynamic Voltage Restorer (DVR) in a Wide Range of Operating Conditions for Practical Application. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2101–2113. [Google Scholar] [CrossRef]
- Li, Z.; Guo, X.; Wang, Z.; Yang, R.; Zhao, J.; Chen, G. An Optimal Zero-Sequence Voltage Injection Strategy for DVR Under Asymmetric Sag. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2595–2607. [Google Scholar] [CrossRef]
- Koroglu, T.; Tan, A.; Savrun, M.M.; Cuma, M.U.; Bayindir, K.C.; Tumay, M. Implementation of a Novel Hybrid UPQC Topology Endowed With an Isolated Bidirectional DC–DC Converter at DC Link. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2733–2746. [Google Scholar] [CrossRef]
- Soomro, A.H.; Larik, A.S.; Mahar, M.A.; Sahito, A.A.; Soomro, A.M.; Kaloi, G.S. Dynamic Voltage Restorer—A Comprehensive Review. Energy Rep. 2021, 7, 6786–6805. [Google Scholar] [CrossRef]
- Chawda, G.S.; Shaik, A.G.; Mahela, O.P.; Padmanaban, S.; Holm-Nielsen, J.B. Comprehensive Review of Distributed FACTS Control Algorithms for Power Quality Enhancement in Utility Grid With Renewable Energy Penetration. IEEE Access 2020, 8, 107614–107634. [Google Scholar] [CrossRef]
- Pal, R.; Gupta, S. Topologies and Control Strategies Implicated in Dynamic Voltage Restorer (DVR) for Power Quality Improvement. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 581–603. [Google Scholar] [CrossRef]
- Molla, E.M.; Kuo, C.-C. Voltage Quality Enhancement of Grid-Integrated PV System Using Battery-Based Dynamic Voltage Restorer. Energies 2020, 13, 5742. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, L.; Wang, R.; Zhang, L.; Cai, X. A Novel SPLL and Voltage Sag Detection Based on LES Filters and Improved Instantaneous Symmetrical Components Method. IEEE Trans. Power Electron. 2015, 30, 1177–1188. [Google Scholar] [CrossRef]
- Fitzer, C.; Barnes, M.; Green, P. Voltage Sag Detection Technique for a Dynamic Voltage Restorer. IEEE Trans. Ind. Appl. 2004, 40, 203–212. [Google Scholar] [CrossRef]
- Florio, A.; Mariscotti, A.; Mazzucchelli, M. Voltage Sag Detection Based on Rectified Voltage Processing. IEEE Trans. Power Deliv. 2004, 19, 1962–1967. [Google Scholar] [CrossRef]
- Chen, C.-I.; Chen, Y.-C.; Chen, C.-H.; Chang, Y.-R. Voltage Regulation Using Recurrent Wavelet Fuzzy Neural Network-Based Dynamic Voltage Restorer. Energies 2020, 13, 6242. [Google Scholar] [CrossRef]
- Chang, G.W.; Chen, C.-I. Performance Evaluation of Voltage Sag Detection Methods. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–6. [Google Scholar]
- Gupta, N.; Seethalekshmi, K. Artificial Neural Network and Synchrosqueezing Wavelet Transform Based Control of Power Quality Events in Distributed System Integrated with Distributed Generation Sources. Int. Trans. Electr. Energy Syst. 2021, 31, e12824. [Google Scholar] [CrossRef]
- Katić, V.A.; Stanisavljević, A.M. Smart Detection of Voltage Dips Using Voltage Harmonics Footprint. IEEE Trans. Ind. Appl. 2018, 54, 5331–5342. [Google Scholar] [CrossRef]
- Stanisavljević, A.M.; Katić, V.A. Magnitude of Voltage Sags Prediction Based on the Harmonic Footprint for Application in DG Control System. IEEE Trans. Ind. Electron. 2019, 66, 8902–8912. [Google Scholar] [CrossRef]
- Bagheri, A.; Mardaneh, M.; Rajaei, A.; Rahideh, A. Detection of Grid Voltage Fundamental and Harmonic Components Using Kalman Filter and Generalized Averaging Method. IEEE Trans. Power Electron. 2016, 31, 1064–1073. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Lin, H.; Teng, Z.; Zhang, F.; Xu, Y. A Voltage Sag Detection Method Based on Modified S Transform With Digital Prolate Spheroidal Window. IEEE Trans. Power Deliv. 2021, 36, 997–1006. [Google Scholar] [CrossRef]
- Liu, H.; Hu, H.; Chen, H.; Zhang, L.; Xing, Y. Fast and Flexible Selective Harmonic Extraction Methods Based on the Generalized Discrete Fourier Transform. IEEE Trans. Power Electron. 2018, 33, 3484–3496. [Google Scholar] [CrossRef]
- Sridharan, K.; Babu, B.C. Accurate Phase Detection System Using Modified SGDFT-Based PLL for Three-Phase Grid-Interactive Power Converter During Interharmonic Conditions. IEEE Trans. Instrum. Meas. 2022, 71, 9000311. [Google Scholar] [CrossRef]
- Neves, F.A.S.; de Souza, H.E.P.; Bradaschia, F.; Cavalcanti, M.C.; Rizo, M.; Rodriguez, F.J. A Space-Vector Discrete Fourier Transform for Unbalanced and Distorted Three-Phase Signals. IEEE Trans. Ind. Electron. 2010, 57, 2858–2867. [Google Scholar] [CrossRef]
- Wang, Y.F.; Li, Y.W. Three-Phase Cascaded Delayed Signal Cancellation PLL for Fast Selective Harmonic Detection. IEEE Trans. Ind. Electron. 2013, 60, 1452–1463. [Google Scholar] [CrossRef]
- Golestan, S.; Ramezani, M.; Guerrero, J.M.; Freijedo, F.D.; Monfared, M. Moving Average Filter Based Phase-Locked Loops: Performance Analysis and Design Guidelines. IEEE Trans. Power Electron. 2014, 29, 2750–2763. [Google Scholar] [CrossRef] [Green Version]
- Taiwo, O.P.; Tiako, R.; Davidson, I.E. Voltage Unbalance Mitigation and Voltage Profile Enhancement in Secondary Distribution System Using Dynamic Voltage Restorer. Int. J. Eng. Res. Afr. 2018, 34, 81–101. [Google Scholar] [CrossRef]
- Golestan, S.; Monfared, M.; Freijedo, F.D. Design-Oriented Study of Advanced Synchronous Reference Frame Phase-Locked Loops. IEEE Trans. Power Electron. 2013, 28, 765–778. [Google Scholar] [CrossRef]
- Sillapawicharn, Y.; Kumsuwan, Y. Dual Low Pass Filter-Based Voltage Sag Detection for Voltage Sag Compensator under Distorted Grid Voltages. In Proceedings of the 2014 International Electrical Engineering Congress (iEECON), Chonburi, Thailand, 19–21 March 2014; pp. 1–4. [Google Scholar]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. A Robust and Fast Synchronization Technique for Adverse Grid Conditions. IEEE Trans. Ind. Electron. 2017, 64, 3188–3194. [Google Scholar] [CrossRef]
- Kumsuwan, Y.; Sillapawicharn, Y. A Fast Synchronously Rotating Reference Frame-Based Voltage Sag Detection under Practical Grid Voltages for Voltage Sag Compensation Systems. In Proceedings of the 6th IET International Conference on Power Electronics, Machines and Drives (PEMD 2012), Bristol, UK, 27–29 March 2012; pp. 1–5. [Google Scholar]
- Khoshkbar Sadigh, A.; Smedley, K.M. Fast and Precise Voltage Sag Detection Method for Dynamic Voltage Restorer (DVR) Application. Electr. Power Syst. Res. 2016, 130, 192–207. [Google Scholar] [CrossRef]
- Xu, J.; Qian, H.; Hu, Y.; Bian, S.; Xie, S. Overview of SOGI-Based Single-Phase Phase-Locked Loops for Grid Synchronization Under Complex Grid Conditions. IEEE Access 2021, 9, 39275–39291. [Google Scholar] [CrossRef]
- Dehghani Arani, Z.; Taher, S.A.; Ghasemi, A.; Shahidehpour, M. Application of Multi-Resonator Notch Frequency Control for Tracking the Frequency in Low Inertia Microgrids Under Distorted Grid Conditions. IEEE Trans. Smart Grid 2019, 10, 337–349. [Google Scholar] [CrossRef]
- Rodríguez, P.; Luna, A.; Candela, I.; Mujal, R.; Teodorescu, R.; Blaabjerg, F. Multiresonant Frequency-Locked Loop for Grid Synchronization of Power Converters Under Distorted Grid Conditions. IEEE Trans. Ind. Electron. 2011, 58, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Wei, D. A Frequency-Adaptive Improved Moving-Average-Filter-Based Quasi-Type-1 PLL for Adverse Grid Conditions. IEEE Access 2020, 8, 54145–54153. [Google Scholar] [CrossRef]
- Roldán-Pérez, J.; García-Cerrada, A.; Ochoa-Giménez, M.; Zamora-Macho, J.L. Delayed-Signal-Cancellation-Based Sag Detector for a Dynamic Voltage Restorer in Distorted Grids. IEEE Trans. Sustain. Energy 2019, 10, 2015–2027. [Google Scholar] [CrossRef]
- Alam, M.R.; Muttaqi, K.M.; Bouzerdoum, A. Characterizing Voltage Sags and Swells Using Three-Phase Voltage Ellipse Parameters. IEEE Trans. Ind. Appl. 2015, 51, 2780–2790. [Google Scholar] [CrossRef]
- Bollen, M.H.J. Voltage Recovery after Unbalanced and Balanced Voltage Dips in Three-Phase Systems. IEEE Trans. Power Deliv. 2003, 18, 1376–1381. [Google Scholar] [CrossRef]
- Ignatova, V.; Granjon, P.; Bacha, S. Space Vector Method for Voltage Dips and Swells Analysis. IEEE Trans. Power Deliv. 2009, 24, 2054–2061. [Google Scholar] [CrossRef] [Green Version]
- Zou, Y.; Zhang, L.; Xing, Y.; Zhang, Z.; Zhao, H.; Ge, H. Generalized Clarke Transformation and Enhanced Dual-Loop Control Scheme for Three-Phase PWM Converters Under the Unbalanced Utility Grid. IEEE Trans. Power Electron. 2022, 37, 8935–8947. [Google Scholar] [CrossRef]
- Islam, M.Z.; Reza, M.S.; Hossain, M.M.; Ciobotaru, M. Three-Phase PLL Based on Adaptive Clarke Transform Under Unbalanced Condition. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 382–387. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, B.; Deng, W. Feasibility Study on One Cycle Control for PWM Switched Converters. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; Volume 5, pp. 3359–3365. [Google Scholar]
- Li, X.; Qu, L.; Ren, W.; Zhang, C.; Liu, S. Controllability of the Three-Phase Inverters Based on Switched Linear System Model. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 287–292. [Google Scholar]
- Yu, J.; Cheng, M.; Gao, D.; Gu, Y.; Yu, J. A Lyapunov Stability Theory-Based Control Method for Three-Level Shunt Active Power Filter. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 8683–8687. [Google Scholar]
- Li, L.; Yang, H.; Guo, W.; Liu, Y. Analysis and Application of Lyapunov-Based Stable Control of the Single-Phase Shunt Active Power Filter. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–4. [Google Scholar]







| Parameter | Value |
|---|---|
| Rated grid line voltage (Ug_line) | 380 V (1.0 p.u.) |
| Rated frequency (f0) | 50 Hz |
| Symmetrical sag depth (Udepth1) | 0.4 p.u. |
| Asymmetrical sag depth (Udepth2) | 0.2 p.u. |
| Variation of frequency (fvariation) | +5 Hz |
| Variation of phase angle (θvariation) | −20° |
| Background harmonic distortion | 0.05 p.u. 5th positive-sequence harmonic 0.05 p.u. 7th negative-sequence harmonic |
| Injected harmonic disturbance | 0.10 p.u. 3rd positive-sequence harmonic 0.05 p.u. 5th positive-sequence harmonic 0.01 p.u. 5 kHz noise |
| Sampling frequency (fs) | 10 kHz |
| Threshold for sag judgment (U+threshold) | 0.9 p.u. |
| Grid Conditions | Performance Metrics | SRF-LPF [32] | DSOGI-SRF [36] | Numerical Matrix [16] | SRF-RMS [35] | GDFT [25] | Proposed Method |
|---|---|---|---|---|---|---|---|
| Symmetrical sag | Judge time tj (0.9 p.u.) | 2.9 ms | 1.9 ms | 1.1 ms | 2.6 ms | 2.2 ms | 1.0 ms |
| Convergence time ts (2%) | 9.3 ms | 12.0 ms | 3.7 ms | 9.6 ms | 6.9 ms | 10.4 ms | |
| Asymmetrical sag | Judge time tj (0.9 p.u.) | 5.4 ms | 4.5 ms | 1.2 ms | 5.2 ms | 3.5 ms | 3.8 ms |
| Convergence time ts (2%) | 10% Vp-p ripple | 7.4 ms | 3.0 ms | 7.5 ms | 9.3 ms | 5.5 ms | |
| Symmetrical sag with phase variation | Judge time tj (0.9 p.u.) | 2.8 ms | 1.6 ms | 1.1 ms | 2.3 ms | 1.7 ms | 1.0 ms |
| Convergence time ts (2%) | 9.2 ms | 28.6 ms | 3.8 ms | 9.5 ms | 15.2 ms | 13.3 ms | |
| Symmetrical sag with frequency drift | Judge time tj (0.9 p.u.) | 2.9 ms | 1.5 ms | 1.1 ms | 2.5 ms | 1.9 ms | 0.8 ms |
| Convergence time ts (2%) | 9.3 ms | 24.4 ms | 25% Vp-p ripple | 9.4 ms | 11.9 ms | 10.2 ms | |
| Symmetrical sag with harmonic interference | Judge time tj (0.9 p.u.) | 3.3 ms | 2.3 ms | missing | 3.0 ms | 2.6 ms | 1.3 ms |
| Convergence time ts (2%) | 5% Vp-p ripple | 7% Vp-p ripple | — | 9.3 ms | 6.5 ms | 10.2 ms | |
| Asymmetrical sag with comprehensive disturbance | Judge time tj (0.9 p.u.) | 6.3 ms | 6.7 ms | missing | 5.8 ms | 2.2 ms | 4.5 ms |
| Convergence time ts (2%) | 7% Vp-p ripple | 7% Vp-p ripple | — | 3.2% Vp-p ripple | 14.2 ms | 12.3 ms | |
| Shallow symmetrical sag | False margin (relative to 0.9 p.u.) | 0.04 p.u. | false | false | 0.038 p.u. | false | 0.015 p.u. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Yang, R.; Guo, X.; Wang, Z.; Chen, G. A Novel Voltage Sag Detection Method Based on a Selective Harmonic Extraction Algorithm for Nonideal Grid Conditions. Energies 2022, 15, 5560. https://doi.org/10.3390/en15155560
Li Z, Yang R, Guo X, Wang Z, Chen G. A Novel Voltage Sag Detection Method Based on a Selective Harmonic Extraction Algorithm for Nonideal Grid Conditions. Energies. 2022; 15(15):5560. https://doi.org/10.3390/en15155560
Chicago/Turabian StyleLi, Zhenyu, Ranchen Yang, Xiao Guo, Ziming Wang, and Guozhu Chen. 2022. "A Novel Voltage Sag Detection Method Based on a Selective Harmonic Extraction Algorithm for Nonideal Grid Conditions" Energies 15, no. 15: 5560. https://doi.org/10.3390/en15155560
APA StyleLi, Z., Yang, R., Guo, X., Wang, Z., & Chen, G. (2022). A Novel Voltage Sag Detection Method Based on a Selective Harmonic Extraction Algorithm for Nonideal Grid Conditions. Energies, 15(15), 5560. https://doi.org/10.3390/en15155560








