2D Combustion Modeling of Cell Venting Gas in a Lithium-Ion Battery Pack

Abstract

With the rapid development of lithium-ion battery technology, powertrain electrification has been widely applied in vehicles. However, if thermal runaway occurs in a lithium-ion battery pack, the venting gas in the cells will spread and burn rapidly, which poses a great threat to safety. In this study, a 2D CFD simulation of the combustion characteristics of cell venting gas in a lithium-ion battery pack is performed, and the possibility of detonation of the battery pack is explored. First, a numerical model for the premixed combustion of venting gas is established using a two-step combustion mechanism. The combustion characteristics are then simulated in a 2D channel for the stoichiometric combustible mixture, and the variations in the flame velocity and pressure increment in the flow channel are analyzed. Next, the effects of the initial conditions inside the battery pack, including the pressure, temperature, and excess air coefficient, on the flame propagation process and pressure variation are evaluated. The results indicate that the flame velocity increases with the increase in the initial pressure or temperature and that the influence of the initial temperature is more acute. The maximum flame speed is achieved with a slightly rich mixture, about 450 mm·s⁻¹. When the excess air coefficient is around 0.9, the flame propagation changes from a slow deflagration to a fast deflagration, which causes a high risk of explosion for the battery pack.

1. Introduction

Lithium-ion batteries have a higher power density relative to conventional energy storage devices such as lead acid batteries and nickel-chromium batteries. They also have the advantages of long-lifetime and no memory effect, which are suitable for electric energy storage. Meanwhile, electric vehicles powered by lithium-ion batteries will not emit any pollutant emissions such as HC, CO, and NO_x during the working process, which is more environmentally friendly compared with traditional vehicles using internal combustion engines. However, the safety issues caused by lithium-ion batteries are serious and occur more frequently with the wide deployment of electric vehicles. Most fire accidents are the spontaneous combustion of lithium-ion batteries [1]. The severe consequences of these accidents make the safety of lithium-ion batteries the focus of many investigations.

Combustion of lithium-ion batteries may be triggered by the thermal runaway process due to the mechanical, thermal, and electrical abuse of batteries. Thermal runaway normally refers to the uncontrollable temperature rise of a lithium-ion battery caused by internal exothermic reactions. Thermal abuse is one of the main reasons for the thermal runaway of lithium-ion batteries [2]. If thermal runaway occurs, the internal reactions of the battery release a large amount of heat. The heat release rate might be as high as 8.3 kW for one 18650 lithium-ion cell [3]. Thermal runaway also leads to the instability of the separator, electrode, and electrolyte under a high temperature such that a large amount of combustible gas is produced. Furthermore, a quick increase in the internal pressure will open the exhaust valve, which is likely to form a jet fire. A large number of electrolyte droplets, combustible gases, and solid particles are sprayed from the cell. The positive electrode oxides may decompose and oxygen can be generated, which will accelerate the reaction process in the cell [4,5]. These materials spread out and mix with the air in the battery pack, making it flammable due to the generation of partially oxidized species such as CO. Additionally, high-temperature cell walls and solid particles, or sometimes an electric arc, can provide the required ignition energy [6,7,8]. Therefore, a fast flame propagation follows which can even cause an explosion.

The species of the venting gas are associated with the materials of the positive electrode, the liquid electrolyte, and the state of charge (SOC) of the cell. Sometimes, over 80% of them are H₂, CO, CO₂, CH₄, and C₂H₄ [9,10]. The detailed mass fractions are sensitive to the SOC. Essl et al. [11] found that the content of CO was increased at 100% SOC compared with 0% SOC. Ethyl carbonate (EC), propylene carbonate (PC), ethyl methyl carbonate (EMC), dimethyl carbonate (DMC), and diethyl carbonate (DEC) are the main components of the liquid electrolyte. Henriksen et al. [12] measured the laminar flame speed of DMC under various equivalence ratios. A maximum flame speed of 300 mm·s⁻¹ was recorded when the equivalence ratio was 1.04, which was much less than that of hydrogen [13]. Qiao et al. [14] analyzed the fire parameters for the electrolyte EC/PC/EMC (25/25/50). The heat release rate of this pool fire decreased as the pressure decreased.

Current investigations into the combustion characteristics of lithium-ion batteries were mainly focused on the heat release rate, accumulated heat release, flame height, and temperature. Chen et al. [15] tested the combustion process of a module consisting of 32 cells of an 18650 battery. The peak heat release rate occurred at 442.6 kW. The effect of environmental pressure was also evaluated [16]. The combustion characteristics of a 78 Ah soft pack battery (NCM811) were studied by Zou et al. [17]. The heat release rate increased as the SOC rose, and a maximum of 154.32 kW was measured under 100% SOC.

The explosion of a lithium-ion battery is reflected by the maximum pressure, the pressure rising rate, and the explosion limit. According to the working conditions, explosions can be divided into constant-pressure explosions in open space [18], limited explosions in semi-open space [19], and constant-volume explosions in confined space [20]. Chen et al. [21] studied the pressure of an NCM 111 battery during the thermal runaway process and a maximum of 107.2 kPa was measured with a pressure rising rate of 697.4 kPa·s⁻¹. Baird et al. [13] investigated the laminar flame speeds and maximum pressures of four typical venting gases. Henriksen et al. [22] simulated the venting gas with a mixture of H₂, CO, CO₂, CH₄, C₂H₄, and C₂H₆. Chen et al. [23] studied the explosion lower limit of the venting gas and found that the limit first increased and then decreased as the SOC ascended.

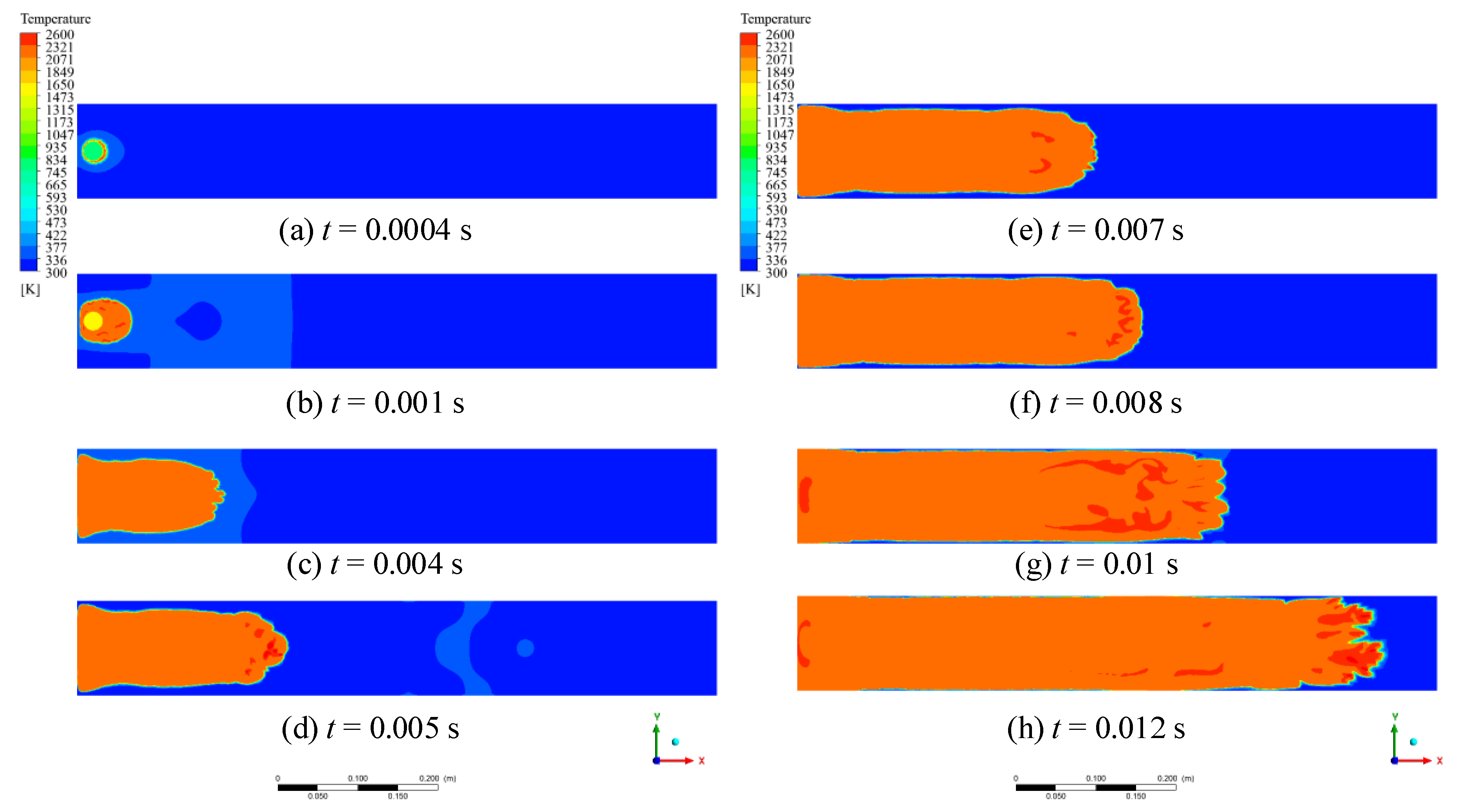
Current investigations concentrated on jet fires in an open space and deflagration in a closed constant-volume bomb, which could reflect the disastrous consequences of thermal runaway. However, practical combustion accidents occurring in electric vehicles are more likely in semi-confined spaces. A combustible mixture forms in a semi-confined space. If these venting gases are ignited, it is likely to have harmful consequences on external personnel or devices. At present, little research has discussed this kind of combustion of lithium-ion batteries. Pressure wave propagation and the interaction with the combustion flame are rarely studied. Therefore, in this study, the combustion characteristics of the venting gases in a semi-confined space are explored. The processes of pressure wave propagation and flame front spread are simulated. The possibility of detonation is discussed. First, based on the finite volume method and a finite rate model, a 2D channel is used to simulate the semi-confined space in a battery pack. The combustion characteristics of the stoichiometric mixture formed by the venting gases and the air are analyzed in the 2D channel. Subsequently, the effects of the initial pressure, temperature, and excess air coefficient on the flame speed and pressure variation are discussed. The possibility of deflagration is estimated. The results can provide some insights into the design of lithium-ion battery packs.

2. Mathematical Model

2.1. Governing Equations

The reaction flow is governed by the conservation equations. The mass equation is expressed as:

$$\frac{\partial \rho }{\partial t}+\nabla \cdot \left(\rho \overrightarrow{v}\right)=0$$

(1)

The momentum equation is denoted by:

$$\frac{\partial }{\partial t}\left(\rho \overrightarrow{v}\right)+\nabla \cdot \left(\rho \overrightarrow{v}\overrightarrow{v}\right)=-\nabla p+\nabla \cdot \left(\stackrel{\overline{¯}}{\tau }\right)+\rho \overrightarrow{g}$$

(2)

The energy equation is:

$$\frac{\partial }{\partial t}\left(\rho \left(e+\frac{v^2}{2}\right)\right)+\nabla \cdot \left(\rho v\left(h+\frac{v^2}{2}\right)\right)=\nabla \cdot \left(k_{eff}\nabla T-{\displaystyle \sum _j{h}_j{\overrightarrow{J}}_j+{\stackrel{\overline{¯}}{\tau }}_{eff}\overrightarrow{v}}\right)+S_h$$

(3)

where S_h is the energy source term and can be denoted by:

$$S_{h,reaction}=-{\displaystyle \sum _j\frac{h_j^0}{M_j}}{R}_j$$

(4)

2.2. Turbulence Model

The RANS model is often used in flow simulation. k-ε and k-ω are two typical turbulence models. The precision of the standard k-ε model in the boundary layer is not satisfied, which may lead to low robustness and a delay in flow separation. The prediction of the standard k-ω model in the boundary layer is improved while it is sensitive to the free flow in the proximity of the boundary layer. The SST k-ω model combines the advantages of these two models. The k-ω model is used for the flow in the boundary layer and the k-ε model is used for the free flow. Therefore, the SST k-ω model is employed in this study. Compared with direct numerical simulation, the accuracy of the SST k-ω model may be lower. However, the computation load is reduced evidently, and the important detailed flow characteristics can be obtained.

The turbulent kinetic energy is expressed as:

$$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_i}\left(\rho k{u}_i\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k-Y_k+S_k+G_b$$

(5)

The dissipation rate is denoted by:

$$\frac{\partial }{\partial t}\left(\rho \omega \right)+\frac{\partial }{\partial x_i}\left(\rho \omega u_i\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\omega }}\right)\frac{\partial \omega }{\partial x_j}\right]+G_{\omega }-Y_{\omega }+S_{\omega }+G_{\omega b}$$

(6)

The turbulent viscosity is described by μ_t. To prevent the overestimation of the turbulent stress under an inverse pressure gradient, the constraint function F is introduced to give a more accurate prediction of the flow separation.

$${\mu }_t=\frac{\rho k}{\omega }\times F$$

(7)

2.3. Species Transport

In a small finite volume, the mass change rate of a species is equal to the sum of the diffusion flux, the generation rate due to the chemical reactions, and the source term.

$$\frac{\partial }{\partial t}\left(\rho Y_i\right)+\nabla \cdot \left(\rho \overrightarrow{v}{Y}_i\right)=-\nabla \cdot {\overrightarrow{J}}_i+R_i+S_i$$

(8)

The diffusion flux of the i-th species ${\overrightarrow{J}}_i$ is caused by the concentration gradient or the temperature variation, which can be determined by Fick’s law.

$${\overrightarrow{J}}_i=-\left(\rho D_{i,m}+\frac{{\mu }_t}{S{c}_t}\right)\nabla Y_i-D_{T,i}\frac{\nabla T}{T}$$

(9)

2.4. Chemical Reaction

The finite rate model is used to describe the complicated chemical reactions of the combustion process. The rate coefficient of a reaction is expressed by the Arrhenius law.

$$k=A{e}^{-E_a/RT}{C}_A{}^{\mathrm{a}}{C}_B{}^{\mathrm{b}}$$

(10)

A two-step mechanism is used for the combustion of the venting gas. First, CO is produced following the oxidation of hydrocarbons, and then CO continues to react with oxygen and CO₂ is obtained. This two-step mechanism has a fast calculation speed with an acceptable precision [24]. The venting gas mainly consists of H₂, CO, CH₄, and C₂H₄. The oxidations of CH₄ and C₂H₄ are simulated by the two-step mechanism, which has a prediction capability of the temperature field for the jet flame simulation of the lithium-ion battery [25]. The detailed chemical reactions are listed in

Table 1. Chemical reaction mechanism of the venting gas.

Reaction	Rate Coefficient
H2 + 0.5O2 → H2O	$1\times {10}^{11}\exp \left(-\frac{8.314\times {10}^7}{RT}\right){\left[{\mathrm{H}}_2\right]}^1{\left[{\mathrm{O}}_2\right]}^{0.5}$
CH4 + 1.5O2 → CO + 2H2O	$5.012\times {10}^{11}\exp \left(-\frac{2.0\times {10}^8}{RT}\right){\left[{\mathrm{CH}}_4\right]}^{0.7}{\left[{\mathrm{O}}_2\right]}^{0.8}$
C2H4 + 2O2 → 2CO + 2H2O	$1.125\times {10}^{10}\exp \left(-\frac{1.256\times {10}^8}{RT}\right){\left[{\mathrm{C}}_2{\mathrm{H}}_4\right]}^{0.1}{\left[{\mathrm{O}}_2\right]}^{1.65}$
CO + 0.5O2 → CO2	$2.239\times {10}^{12}\exp \left(-\frac{1.7\times {10}^8}{RT}\right){\left[\mathrm{CO}\right]}^1{\left[{\mathrm{O}}_2\right]}^{0.25}{\left[{\mathrm{H}}_2\mathrm{O}\right]}^{0.5}$
CO2 → CO + 0.5O2	$5\times {10}^8\exp \left(-\frac{1.7\times {10}^8}{RT}\right){\left[{\mathrm{CO}}_2\right]}^1$

.

3. Combustion Simulation

3.1. Geometry

Figure 1 shows the 2D channel used in this study. The length is 800 mm and the height is 120 mm. The left end is closed while the right end is open. A homogeneous combustible mixture is assumed in the channel. An ignition spot is set at the center line with a distance of 20 mm to the left end. The parameters for the ignition model are given in

Table 2. Parameters for the ignition model.

Parameter	Value
Ignition spot (mm)	(20, 0)
Ignition timing (s)	0
Ignition duration (s)	0.001
Initial spark radius (mm)	2
Ignition energy (J)	0.005

. In practice, the combustible gaseous mixture is normally ignited by the jet flame or sprayed with hot solid particles [26] immediately. Here, the propagation processes of the pressure wave and flame front are of main concern. Therefore, an artificial ignition spot is employed to simulate the ignition process of the premixed combustion.

3.2. Boundary Conditions

To estimate the pressure variation in the channel, a compressible flow with an ideal gas assumption is used to determine the density. The boundary conditions of the model are listed in

Table 3. Configurations of the 2D model.

Item	Configuration
Turbulence model	SST k-ω
Velocity-pressure couple	Yes
Discretion	Second-order upwind
Chemical reaction	Species transport/finite rate model
Time step	1 × 10−5 s
Grid adaption	Two time-steps

. The turbulence model is set as SST k-ω. The finite rate model is used to model the combustion and species transportation is also considered. The second-order upwind algorithm is used to discretize the partial equations with regard to time and space. A velocity-pressure coupled method is used to obtain the solution. The grid adaption is performed every two time-steps to give a more precise modeling of the flame front. If the temperature or vorticity gradient exceeds 5%, a refinement is activated. If the gradient is less than 2%, a mesh reduction is performed. The convergence residual is 10-5 for mass, species, and energy equations.

The wall is assumed to be adiabatic. A pressure outlet is set at the right end with a pressure the same with the initial value in the channel. Initially, the air (298 K, 101 kPa) in the channel is mixed with the venting gas and a homogeneous combustible mixture is obtained with a temperature of 329 K and a pressure of 154.2 kPa. The initial conditions are determined according to the energy equation and assuming both the venting gas and the air are ideal gases. The mole fractions of venting gases are the measured data from an NCM622 lithium-ion battery under 100% SOC [27]. The species with a mole fraction of less than 4% are neglected. The amount of venting gas is determined assuming a stoichiometric mixture is formed after mixing. The detailed mole fractions are listed in

Table 4. Mole fractions of the species before combustion.

Species	Stoichiometric Mixture
H2	0.0915
CO	0.0822
CO2	0.0775
C2H4	0.0138
CH4	0.0117
O2	0.1519
N2	0.5714

.

3.3. Model Validation

To validate the grid independence, three different grids are designed. The height of the first layer in the proximity of the wall is set to 0.5 mm for the normal grid.An increased rate of 1.2 is then applied. An overall number of 220 cells along the length direction and 52 cells along the height direction are obtained. The increase rates are 1.0 and 1.4 for the coarse and fine grids, respectively.

Table 5. Configuration of the grids.

Grid	Total Cells	Max. Cell Size (mm)
Coarse	7175	4.79
Normal	11,169	3.77
Fine	16,306	3.11

shows the results of the grids.

The temperature profiles along the flame thickness direction for the three grids are shown in Figure 2a when the flame front arrives at a fixed point where x = 0.4 m. The x-axis is along the centerline in the x-direction shown in Figure 1 and is normalized to the overall length of the channel. It can be seen that the temperature in the burnt zone is around 2200 K while it is much lower (close to 400 K) in the unburnt region. Because violent chemical reactions occur in the flame front region, the temperature decreases rapidly. Although there are some deviations in this flame front region due to the limit of the computational steps, the profile of the normal grid approximates to that of the fine grid. Figure 2b shows the positions of the flame front as a function of time. The flame velocity of the coarse grid is much faster than the others. Although certain deviations between the normal and fine grids occur in the middle of the curves, the overall flame velocities show a high consistency.

The flame thickness is estimated according to the temperature gradient [28] and expressed as:

$${\delta }_l=\frac{T_b-T_u}{{\left(dT/dx\right)}_{max}}$$

(11)

The results for the flame thickness of the coarse, normal, and fine grids are 2.87 mm, 2.56 mm, and 2.52 mm, respectively. The deviation between the coarse and normal grid is 12.4%. However, this deviation decreases to 1.63 between the normal and fine grids. Therefore, the normal grid is used for the following analysis after a trade-off of the precision and computation load.

To validate the accuracy of the model, the results of the simulated flame speed are compared with that measured in a constant-volume bomb. The positions of the flame front at different moments were measured by a high-speed camera. The experimental results are shown in Figure 3a. The time interval is 1 ms between two adjacent fronts. Figure 3b shows the simulated results using the same conditions.The flame velocity is then estimated according to the average distance between the adjacent profiles and the results are displayed in Figure 3c. The simulated average flame velocity manifests a slightly decreasing trend while the experimental profile shows an opposite tendency. Nevertheless, the measured average flame velocity is about 7.37 m·s⁻¹. The simulated average velocity is 6.28 m·s⁻¹ with a deviation of 14.8%. Generally, the established simulation model has an acceptable precision and can be used to predict the flame propagation process.

4. Results of Stoichiometric Mixture

4.1. Flame Propagation

The flame propagation process of the stoichiometric mixture is simulated, and the results are shown in Figure 4. The ignition energy is added as the energy source term into the energy equation at first. The mixture is ignited at 0.0004 s with a flame kernel radius of 2 mm. The temperature inside the kernel is increased to 823 K. Subsequently, a laminar flame is propagated outwards on a sphere surface. The smooth flame front becomes wrinkled as the combustion continues. Large cracks even appear on the surface. The temperature of the burnt gas is increased to about 2270 K.

The flame propagation process is treated as the spread of a combustion wave from the viewpoint of laminar premixed combustion theory. The flame front spreads outwards at a laminar velocity from the burnt zone to the unburnt zone. A smooth surface occurs due to a laminar reaction. In contrast, a turbulent flame can be treated as the flow of laminar reaction in a turbulent field. Local temperature, velocity, and species concentration fluctuate in a turbulent combustion. The flame front is wrinkled because of the turbulence field. Thus, the reaction area is increased significantly, leading to an apparent increase in the flame velocity. For turbulent combustion, the average flame velocity S_flame is determined by the differential of the flame front position X_flame.

$$S_{flame}=\frac{d{X}_{flame}}{dt}$$

(12)

The estimated average flame velocity inside the channel is displayed in Figure 5. Once the combustible mixture is ignited, the average flame velocity is maintained at around 40 m·s⁻¹ for a while. After 0.0036 s, the flame kernel gets enough energy, and the flame velocity rises rapidly and approaches 100 m·s⁻¹. Then, because a turbulent flow is formed gradually, the flame velocity fluctuates several times until 0.01 s. After that, a second rapid increase in the flame velocity occurs and a maximum flame velocity of 144 m·s⁻¹ is achieved.

The instability of turbulent flame propagation leads to multiple velocity peaks in the channel. The factors affecting flame instability are usually thermal-mass diffusion instability and hydrodynamic instability, which can be distinguished according to the shape of the combustion wave and the form of the flame surface. Thermal-mass diffusion refers to the change of flame surface structure caused by uneven heat conduction and species mass transport on the flame surface. The Lewis number (Le) is usually used to reflect the relative ratio of thermal diffusion to mass diffusion. When Le < 1, the mass diffusion on the flame surface is greater than the thermal diffusion, which leads to the instability of the flame; otherwise, the flame tends to be stable. Hydrodynamic instability is due to the existence of a certain curvature on the flame surface, which makes the velocity vector converge or diverge in the flow process, resulting in an increase or decrease in the velocity. Before the flame surface acceleration and the velocity peaks, the flame surface structure has some wrinkles, and the velocity vector tends to converge towards the center of the nearly spherical flame surface. Wrinkles increase the surface area of the flame front, and the heat release rate rises. Accordingly, the pressure behind the flame front increases. Hence, the flow divergence trend increases the flame propagation velocity further. At 0.01 s, large-scale folds and flow divergence caused by the variation of flame surface curvature can be clearly observed in the flame surface, which can also explain the rapid increase of flame front propagation velocity.

4.2. Pressure Variation

The peak pressure is an important parameter in evaluating the possibility of explosion during the combustion process of a lithium-ion battery. The mechanical stress of the packing material should be able to bear the pressure increase. Therefore, four different locations are selected to measure the pressure variations in the channel. The distances from the left end are 0.1 m, 0.3 m, 0.5 m, and 0.7 m, respectively. The overpressure ΔP is defined as the measured pressure minus the initial pressure in the channel and it is used to label the pressure variation during the flame propagation process. Figure 6 shows the results of the measured overpressures at the four locations. There are two apparent peaks of the overpressure for the stoichiometric combustion process with an initial pressure of 154.2 kPa.

Figure 7 shows the distribution of the density gradient during flame propagation, which can be used to reflect the propagation of pressure waves in the channel. The first pressure peak appears during the ignition process and propagates in the channel as a pressure wave, which is shown in Figure 7a,b. The first rapid change of overpressure occurs at each measuring location, and an obvious pressure peak can be observed at x = 0.7 m. The maximum overpressure generated by the ignition is about 22.9 kPa, and the absolute pressure is 177.1 kPa. At the initial stage of combustion, the pressure wave generated during ignition is helpful for the flame to propagate in the unburned zone and the temperature rises, resulting in a period of high pressure at x = 0.1 m, as shown in Figure 7c. When the combustion wave propagates, it will cause a negative pressure zone behind the wave. The maximum negative pressure is about −13.5 kPa and the absolute pressure is 140.7 kPa. The second pressure peak occurs when the high-temperature burnt gas expands and is compressed on the wall surface, resulting in a large combustion overpressure. The results are shown in Figure 7d. This overpressure is caused by the combustion wave. The maximum overpressure is 15.6 kPa and the absolute pressure is 169.8 kPa. Generally, the pressure variation in the channel is caused by the ignition at the beginning and then gradually changes to the mode propelled by the combustion wave.

5. Effects of Initial Conditions

When the combustible mixture is formed in the channel by the venting gas of a lithium-ion battery, its combustion and explosion characteristics will be affected by the initial state of the mixture. In the above section, a stoichiometric mixture with an equivalence ratio of 1 is assumed. Herein, the effects of the initial pressure, initial temperature, and initial equivalence ratio of the mixture are estimated during the flame propagation process in the channel.

5.1. Initial Pressure

The combustion characteristics are analyzed with an initial pressure of 81 kPa, 101 kPa, 154 kPa, and 174 kPa. The initial temperature is set to 329 K and the equivalence ratio is 1. Figure 8a shows the results of the flame front position as a function of time under different initial pressures. The times that the flame front propagates to the right end are 0.0176 s, 0.0154 s, 0.0126 s, and 0.0114 s when the initial pressure is 81 kPa, 101 kPa, 154 kPa, and 174 kPa, respectively. As the initial pressure increases, the required propagation time decreases, and the flame velocity increases. Figure 8b shows the results of the average flame velocity under different initial pressures. The maximum average flame velocities are 93.5 m·s⁻¹, 100 m·s⁻¹, 138.2 m·s⁻¹, and 151.5 m·s⁻¹, corresponding to an initial pressure of 81 kPa, 101 kPa, 154 kPa, and 174 kPa. A similar trend is displayed with the propagation time. However, no deflagration appears, and the combustion mode is not changed. According to the laminar premixed combustion theory, the laminar flame velocity S_L is proportional to the initial pressure P₀, which can be expressed as:

$$S_L\propto {\mathrm{P}}_0{}^{\mathrm{n}/2-1}$$

(13)

where n is the reaction order. For the combustion mechanism of the venting gas of a lithium-ion battery, the reaction order is greater than two. Therefore, the laminar flame velocity increases as the initial pressure rises. On the other hand, when the initial temperature and the equivalence ratio of the mixture remain unchanged, the increase in the initial pressure will increase the species mass in the fixed volume channel, and the corresponding chemical reaction rate will increase. The increase in the initial pressure will reduce the stability of the flame front. Under a high initial pressure, the wrinkles will occur earlier and more frequently on the flame front surface, and the roughness of the flame surface will increase, leading to an increase in the reaction surface area that accelerates the propagation of the flame front, as shown in Figure 8c.

The results of the combustion pressure in the channel at x = 0.7 m are shown in Figure 9. A similar trend is obtained for different initial pressures. One peak pressure occurs due to the ignition and the other appears because of the combustion wave. With regard to the considered initial pressures (81 kPa, 101 kPa, 154 kPa, and 174 kPa), the maximum overpressures are 10 kPa, 13.8 kPa, 23.1 kPa, and 25.6 kPa for the first peak while they are slightly reduced to 5 kPa, 8.2 kPa, 13.1 kPa, and 16.6 kPa for the second peak. As the initial pressure increases, the overpressures caused by the ignition and the combustion wave are all increased, indicating a more violent combustion.

5.2. Initial Temperature

The combustion characteristics of the venting gas with an initial temperature of 300 K, 329 K, 360 K, and 400 K are investigated subsequently. 329 K is close to the temperature of the stoichiometric mixture of the venting gas with the air in the pack at 300 K. 360 K approaches the boiling point of DMC (363 K) and 400 K is slightly less than the boiling point of DEC (401 K). Generally, the vent valve will open readily after the liquid electrolyte starts to boil. Therefore, these values are specified as the initial temperature, respectively. The initial pressure is set to 154 kPa with an equivalence ratio of 1. The results of the flame front position as a function of time are shown in Figure 10a. The required times for the flame propagating to the right end are 0.0134 s, 0.0126 s, 0.008 s, and 0.00528 s for the four initial temperatures. As the initial temperature increases, the required time reduces and the average flame velocity increases. Compared with the result of an initial temperature of 300 K, the propagation time of an initial temperature of 329 K decreases by about 6%. Furthermore, the times for the cases with an initial temperature of 360 K and 400 K are decreased significantly by 40.3% and 60.6%, respectively. A large increase in the flame velocity indicates that such a great increase in the initial temperature may result in the variation of the combustion mode. Figure 10b shows the profiles of the average flame velocity as a function of time under different initial temperatures. At the initial temperature of 300 K, 329 K, 360 K, and 400 K, the maximum average flame velocity is 109.2 m·s⁻¹, 138.2 m·s⁻¹, 264.7 m·s⁻¹, and 402.5 m·s⁻¹, respectively. The results imply a high sensitivity of the initial temperature to the flame velocity of the venting gas. Normally, the laminar flame velocity S_L has an Arrhenius relation with the initial temperature T₀ as:

$$S_L\propto e^{-E_a/R{T}_0}$$

(14)

The reaction rate increases exponentially with the increase in the initial temperature because the activation energy normally is not influenced by the temperature. The average flame velocity at an initial temperature of 329 K is close to that of 300 K. When the initial temperature continues to increase, the average flame velocity increases significantly.

When the initial temperature is 400 K, the flame propagation shows a different variation compared with the other three initial temperatures. The flame velocity exceeds the local sonic speed, and the deflagration mode occurs for the combustion of the venting gas mixture. Normally, the pressure wave propagates in the unburned gas at the local sound speed. The pressure wave originally generated during the ignition should decay rapidly and will not have an evident acceleration impact on the front unburned gas. However, when the initial temperature is 400 K, the shock wave and its reflected wave generated by the flame combustion spread forward in a more obvious cell shape, as shown in Figure 11. The pressure wave continuously imposes on the unburned gas, making its pressure and temperature rise evidently. The flame propagates and accelerates in the channel. When the flame reaches the local sound velocity of the unburned gas, the flame front will catch up with the forward propagation speed of the pressure wave, forming a deflagration wave structure where the precursor shock wave is superimposed on the subsequent rapid chemical reaction surface. Accordingly, the temperature and pressure of the unburned gas mixture in front of the flame surface are further increased. The combustion mode changes from slow deflagration (less than the local sonic speed) to fast deflagration (greater than the local sonic speed). Therefore, if the venting gas of a lithium-ion battery mixes with the air and the temperature is higher than 400 K, there is a high risk of fast deflagration and even the explosion of the battery pack.

The results of the pressure variation as a function of time are shown in Figure 12 under different initial temperatures. The pressure is measured at the location X = 0.7 m. When the initial temperature is 300 K, 329 K, 360 K, and 400 K, the maximum overpressure caused by the ignition is 17 kPa, 23 kPa, 17 kPa, and 48 kPa, respectively. The corresponding maximum overpressure caused by the combustion wave is 13 kPa, 13 kPa, 22 kPa, and 42 kPa, respectively. At the initial temperature of 400 K, the maximum overpressure when reaching the fast deflagration state is significantly greater than the cases of the other initial temperatures.

5.3. Excess Air Coefficient

Finally, the effects of the equivalence ratio of the gas mixture on the flame propagation are evaluated. Assuming that the initial amount of air in the channel before mixing with the venting gas remains constant, the quantity of venting gas erupted from the battery determines the initial equivalence ratio of the mixture. In this study, the excess air coefficient α is used to assess the effects of the initial concentration of the venting gas. α is defined as the ratio of the actual air quantity in the channel to the air mass required to completely burn the venting gas. Before mixing, the temperature and pressure of the air in the channel are 298 K and 1 bar. Combustible mixtures with different excess air coefficients are determined by changing the molar value of the venting gas. The detailed initial states under different excess air coefficients are shown in

Table 6. Initial states and mole fractions of the combustible mixture for the 2D model.

State	α = 0.7	α = 0.8	α = 0.9	α = 1	α = 1.1	α = 1.2
T0 (K)	336.2	333.5	331.3	329.4	327.7	326.2
P0 (kPa)	176.0	167.0	160.0	154.1	149.5	145.6
H2	0.1169	0.1070	0.0987	0.0915	0.0800	0.0854
CO	0.1050	0.0961	0.0886	0.0822	0.0718	0.0766
CO2	0.0990	0.0906	0.0836	0.0775	0.0677	0.0723
C2H4	0.0177	0.0162	0.0149	0.0138	0.0121	0.0129
CH4	0.0150	0.0137	0.0127	0.0117	0.0103	0.0109
O2	0.1358	0.1420	0.1473	0.1519	0.1592	0.1558
N2	0.5107	0.5343	0.5543	0.5714	0.5989	0.5861

. The α value is specified to cover the typical range for premixed combustion, from stochiometric to power mixtures with slightly rich concentrations and economic mixtures with slightly lean concentrations, respectively. In this range, the flame propagation process is the most dramatic.

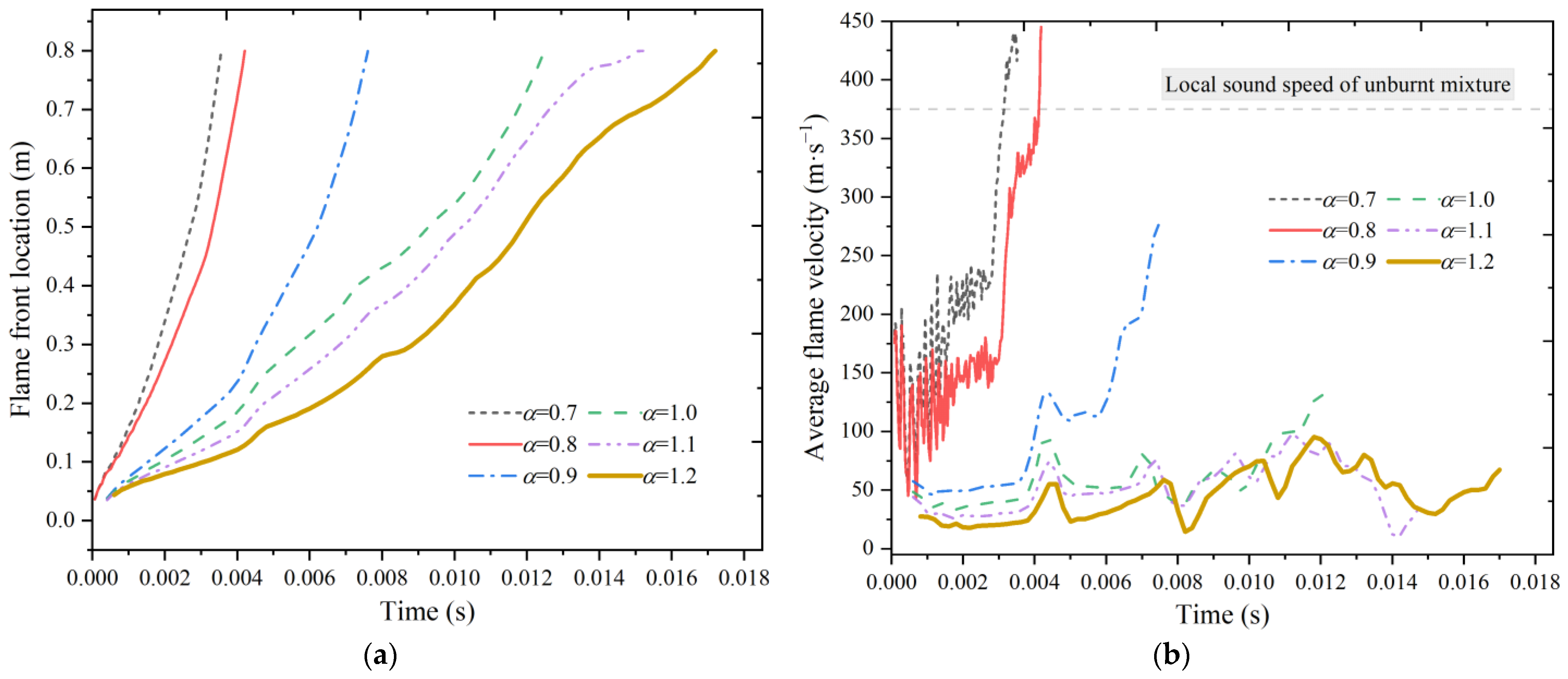
Figure 13a shows the results of the flame front position as a function of time under different excess air coefficients. When the excess air coefficient decreases from 1.2 to 0.7, the time required for the flame front to propagate to the right end is 0.0172 s, 0.0152 s, 0.0126 s, 0.0076 s, 0.00418 s, and 0.00354 s, respectively. With the decrease in the excess air coefficient, the molar amount of the venting gas in the channel increases, the time required for flame propagation decreases, and the average propagation velocity increases. Figure 13b shows the profile of the average flame velocity under different excess air coefficients. When the excess air coefficient decreases from 1.2 to 0.7, the maximum average flame velocity increases from 95.25 m·s⁻¹ to 437.5 m·s⁻¹. The average flame velocity is larger in a slightly fuel-rich mixture. The maximum velocity arrives at 445 m·s⁻¹ when the excess air coefficient is 0.8.

When the excess air coefficient is around 0.9, the combustion mode changes. When the excess air coefficient is decreased to 0.8, the average flame velocity has exceeded the local sonic speed, and the combustion mode has changed from slow deflagration to fast deflagration, which significantly increases the risk of a combustion accident. The local sonic velocity is a criterion to distinguish the combustion mode. Once the flame propagation velocity reaches the sound velocity, the pressure disturbance generated by the combustion wave will be behind the flame front surface and will no longer affect the flame surface. The flame continues to be accelerated during the propagation, forming shock waves at the flame front. The unburned gases will become directly combusted under the action of shock waves and energy is released to maintain the flame propagation speed. In such circumstances, deflagration waves will turn into detonation waves. Obviously, it is difficult to produce detonation in a channel with an open end. However, the detonation may still occur under fuel-rich conditions.

The results of combustion pressure measured at the location X = 0.7 m under different excess air coefficients are shown in Figure 14. The maximum overpressure caused by the ignition pressure wave is 10.9 kPa, 20.3 kPa, 22.9 kPa, 22 kPa, 61.7 kPa, and 91.14 kPa while the maximum overpressure caused by the combustion wave is 11.8 kPa, 12.8 kPa, 13 kPa, 53 kPa, 91.3 kPa, and 94.9 kPa, respectively.

6. Conclusions

In this study, the combustion characteristics of the venting gas from a lithium-ion battery are simulated and analyzed in a 2D channel with an open end. The flame propagation velocity and pressure variation are estimated for a stoichiometric mixture at first. The effects of the initial states, including the initial pressure, temperature, and equivalence ratio, are then assessed.

The pressure variation in the channel is mainly caused by the ignition pressure wave and the following combustion wave. For the combustion process with a stoichiometric mixture, the peak overpressure from the ignition pressure wave is 22.9 kPa, which is greater than the peak overpressure produced by the combustion wave at 15.6 kPa at the initial stage of ignition. Increasing the initial pressure in the channel will reduce the stability of the flame front, and more wrinkles will appear earlier, leading to an increase in the flame surface area. The maximum flame velocity will increase accordingly in the channel. Under an initial pressure of 175 kPa, the maximum flame velocity is 151 m·s⁻¹, and the maximum overpressure is 25.6 kPa. The maximum overpressure increases with the increase in the initial pressure.

The combustion of the mixture in the channel is sensitive to the initial temperature. Increasing the initial temperature will increase the flame propagation velocity. When the initial temperature is 400 K, the maximum flame velocity is 400 m·s⁻¹, which is greater than the local sound velocity of the unburned gas, and the combustion mode changes to fast deflagration. The maximum overpressure of the ignition pressure wave at the initial temperature of 400 K is 48 kPa, and the maximum overpressure of the combustion wave is 42 kPa, which is twice the overpressure at the initial temperature of 360 K. When the initial temperature is above 400 K, the explosion risk is high.

With the increase in the amount of venting gas, the excess air coefficient in the channel decreases, and the maximum flame velocity increases first and then decreases. When the excess air coefficient is 0.8, the maximum flame speed is achieved with a slightly rich mixture, which is about 445 m·s⁻¹. When the excess air coefficient is below 0.9, the combustion mode changes from slow deflagration to fast deflagration, which has a high risk of explosion. When the excess air coefficient is 0.8, the peak overpressure caused by the ignition pressure wave is 61.7 kPa, which is less than that caused by the combustion wave of 91.3 kPa. The maximum combustion overpressure increases with the decrease in excess air coefficient, and a high risk of explosion exists when the venting gas mixture is rich.

In practice, to avoid dramatic explosions when thermal runaway occurs, some control methods can be employed. First, a relief valve can be used to control the pressure in the battery pack. If the pressure exceeds a certain value over the ambient pressure, the relief valve opens automatically to limit the combustion pressure. Second, nonflammable phase-change materials can be inserted into the pack to reduce the combustion temperature. Third, fire retardants can be released if the venting gas is detected in the pack. The amount of venting gas, the equivalence ratio, and the ignition point are three key factors. Because high-temperature solid particles are sprayed together with the venting gas and sometimes even an electric arc occurs in the venting gas due to charged particles, it is difficult to control the ignition point, and more investigation is required.

This study only considers the propagation process in a 2D channel. In the future, a more precise 3D simulation needs to be performed to give a more precise evaluation. Meanwhile, it is difficult to measure the pressure variation in such a high-temperature environment. Further experimental facility needs to be developed and experimental validation is also required.