Distributed ESS Capacity Decision for Home Appliances and Economic Analysis

Abstract

The imbalance between the supply and demand of electricity is becoming expansive due to the increase in renewable energy penetration. Consequently, the time-varying electricity price is proposed as a tool to manage the mismatch. To cope with the electricity price difference across time and to extract the benefit to the limit, an energy storage system (ESS) can be a good tool to smooth out electricity usage. Nevertheless, ESS can be expensive due to the high installation cost and centrally managed system. In this paper, we propose a distributed ESS installed in each home appliance. Separately installed batteries can avoid sizeable initial investment costs. We calculated the benefit of the system that mainly stemmed from the electricity price difference and compared the benefits across various sizes of the battery system. In addition, the charging/discharging schedule depends on the power consumption profile and electricity price distribution. Decreasing battery prices and rising electricity price volatility can increase the system’s potential benefit.

1. Introduction

Demand-side energy management is one essential part of efficient energy use, as studied in many papers [1,2,3,4,5,6]. As consumers are sensitive to electricity price, the time-varying electricity pricing model is used as a tool for demand-side management by reducing the energy usage when the excess demand is high [1,7,8].

Aside from the demand-side management motive, varying electricity price also reflects high renewable energy penetration in power systems [9,10,11]. The levels of renewable penetration often result in various price schemes [12]. Figure 1 shows three different time-varying electric price schemes; time of use pricing (TOU) with a 23.5 ¢/kWh peak and off-peak price difference found in the state of Texas [13]; TOU with a 4.9 ¢/kWh peak and off-peak price difference found in South Korea [14]; real-time pricing (RTP) found in the city of Chicago [15]. The energy price difference increases as the supply and demand mismatch worsen. For example, the Texas case shown in Figure 1c includes a zero price period during the nighttime resulting from the deepening penetration of renewable energy sources, especially wind power generators. The energy storage system (ESS), which can charge and discharge energy, becomes a solution to supply and demand mismatching problems. As a result, ESS can benefit the energy provider and consumer, improving economic benefit, reliability, and power quality.

A Battery Pack, Power Conditioning System (PCS) [16], and the energy management system (EMS) [3,17,18] are the key components of ESS. In Figure 2a, smart meters are attached to EMS, and it monitors the electricity price and controls the electricity usage. Schedulers decide when to charge and discharge the energy. PCS converts electrical energy into a usable form. In this study, we assumed plug-and-play EMS and PCS are available. The energy storage size of the battery ESS is decided by battery capacity.

The cost of battery ESS is mainly determined by the battery price, which has rapidly declined due to the increase in production scale and improvement of manufacturing techniques [19,20]. The rapid growth of the electric vehicle (EV) industry is pushing more investment toward Lithium-Ion (Li-Ion) battery techniques [6,21,22] as EV consumes a large amount of Li-Ion battery. With the increase in investment, EV batteries can also be recycled in home appliances [22,23]. If EV batteries are reused, the price is expected to be below 100 $/kWh after 2025 [20,24].

The economic benefits of using battery ESS will be realistic in the near future with the increasing time-varying electricity price gap with lowered battery price. In this study, we focused on optimizing the economic benefit from the perspective of households by exploiting the electricity price difference between the peak and off-peak hours [25,26]. Introducing the ESS in households creates some challenges, e.g., calculation of expected return, initial investment cost, and charging/discharging decision. All of them are directly linked to the financial benefit and payback period of the ESS. Oftentimes, the calculation of the optimal economic benefit and payback period is ambiguous for individual households.

Several studies have analyzed the concept of distributed ESS. Many papers discussed energy storage system design in renewable energy generation such as wind energy storage projects [27] or microgrids [28]. Our paper uses the same arbitrage scheme of [27] but applying the idea to the distributed energy appliances as in [28]. Park et al. applied distributed ESS to smart LED streetlight systems to avoid high installation costs and low management efficiencies. The contribution of our paper is that we applied the idea of arbitrage to the distributed ESS system that is applied on various home appliances with different electricity usage levels. The idea can be beneficial for households, since it can benefit the user by efficiently managing the energy usage and avoiding the cost of unexpected power outages. For example, Texas suffered a major power crisis in 2021 due to the severe winter storm. Many people had a hard time due to the spiked price resulting from the failure of the power system. Distributed energy storage installed in essential home appliances can be one solution to avoid the unwanted cost of unexpected weather environments or power outages due to uncontrollable factors.

Additionally, our way of figuring out the charging and recharging schedule is much simpler than what has been utilized in the ESS design as in [27]. Instead of solving a complicated linear programming problem with many constraints, we use a simple iterative process to find a price threshold to calculate the ESS running cost.

This paper discusses the distributed ESS at the home appliance level focusing on the economic benefit from the electricity price difference. Figure 2a shows the typical form of ESS, which is noted as the central ESS [4]. On the other hand, the distributed ESS shown in Figure 2b has distributed ESS for individual home appliances. The placement of distributed ESS can be prioritized to the home appliance that results in the biggest benefit. On the other hand, central ESS has single storage that covers all the home appliances. Placing a central ESS requires a large amount of initial investment cost and space, which prevents households from adopting ESS. In the case of distributed ESS, households can split the initial investment cost and fault range, as shown in

Table 1. Comparison between central and distributed ESS.

ESS Type	Placement Priority	Initial Investment Cost	Fault Range
Central	Cannot be split	Large	Large
Distributed	Prioritizable	Small	Small

. Distributed ESS needs a more precise methodology to prioritize ESS placement and calculate the optimal battery capacity for each home appliance.

In this study, charging/discharging schedules to maximize potential benefits of the distributed ESS for home appliances are investigated, given the power consumption profile for each home appliance and time-varying electricity price [29]. Optimal battery capacity and economic benefits with an expected payback period are calculated for both distributed and central ESS. We used the well-known golden search method to find the best price threshold that determines the battery recharging schedule [30]. Using the model, ESS payback period analysis has been performed based on the electricity price gap and storage price. Furthermore, the economic benefit comparison between the central and the distributed ESS has been made with installing priority decisions using the cost–benefit rule.

In Section 2, the charging/discharging ESS model is introduced. In Section 3, simulations are performed based on the three different time-varying electricity price plans adopted in South Korea, the state of Texas, and the city of Chicago. Power consumption profiles of three different major home appliances, i.e., TV, refrigerator, and washing machine, are targeted to find the optimal battery capacity for maximum profit. In Section 4, discussions including ESS-type comparison, payback period, and price gap are included to assure the economic benefit of distributed ESS. In the final section, conclusions are presented.

2. Charging/Discharging Model of Battery ESS

The ESS model uses both energies stored in the battery and the wall power. The charging and discharging rule can be written as (2) and (3). Essentially, the rule is determined by the electricity price. If the market electricity price is lower than a certain threshold, then the battery system recharges. If it is above the threshold, the battery discharges the energy.

To introduce the notation, $\underline{p}$ is the threshold price, $h_t$ is the decision of recharging and $z_t$ is the use of wall power. If $h_t=1$, then the battery recharges and $h_t=-1$ is the state of discharging. $h_t=0$ is the case when the battery does not recharge or discharge. $z_t$ is whether the system uses wall power in addition to the battery. If $z_t=1$, then wall power is used. Each state of charging and discharging can be written using the notation.

First, if the electricity price is less than the threshold, then the decision of recharging $h_t$ is determined by the state of charge, $b_t$. If the battery is not full, or $0\le b_t<K$, then the system recharges ($h_t=1$) while wall power is used for that appliance ($z_t=1$).

On the other hand, if the electricity price is higher than the threshold ($p_t>\underline{p}$), then the choice of discharge is determined by the state of charge ($b_t$) and the amount of electricity used ($y_t$). If the battery has more than the amount of electricity needed ($y_t\le b_t\le K$), then the battery discharges energy ($h_t=-1)$, and no wall power is used ($z_t=0$). If it does not have enough energy ($0<b_t<y_t$), then the wall power is used in addition to the battery system. If there is no electricity charged in the battery ($b_t=0$), only wall power is used ($z_t=1$). Equations (2) and (3) summarize the battery charging and discharging schedule that depends on the electricity price ($p_t$) and the battery state ($b_t$).

$$\left\{\begin{array}{c}\mathrm{Battery}\mathrm{charges}:h_t=1\hfill \\ \mathrm{Battery}\mathrm{discharges}:h_t=-1\hfill \\ \mathrm{Wall}\mathrm{power}\mathrm{use}:z_t=1\hfill \end{array}\right.$$

(1)

$$\begin{array}{cc}\hfill p_t& \le \underline{p}\left\{\begin{array}{c}{h}_t=1,z_t=1\mathrm{if}0\le b_t<K\hfill \\ h_t=0,z_t=1\mathrm{if}{b}_t=K\hfill \end{array}\right.\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill p_t& >\underline{p}\left\{\begin{array}{c}{h}_t=-1,z_t=0\mathrm{if}{y}_t\le b_t\le K\hfill \\ h_t=-1,z_t=1\mathrm{if}0<b_t<y_t\hfill \\ h_t=0,z_t=1\mathrm{if}{b}_t=0\hfill \end{array}\right.\hfill \end{array}$$

(3)

The amount of electricity used by the appliance is from two sources: the battery and the wall power. If the total amount of electricity that an appliance needs is $y_t$, then a part of it comes from the battery ($y_t^1$), and the other part is from the wall power ($y_t^2$). So, $y_t=y_t^1+y_t^2$. The state of charge of a battery is affected by $y_t^1$ while $y_t^2$ only affects the total cost of electricity. The battery state of charge ($b_t$) is changed discretely. First, the recharging decision ($h_t=1$) adds energy with size x to the battery system ($b_t$). Second, the amount of electricity the battery uses, $y_t^1$, is subtracted if the battery discharges energy ($h_t=-1$). Since the energy conversion processes result in loss, the charging and discharging efficiency is modeled as ${\delta }_1,0<{\delta }_1<1$ and ${\delta }_2,0<{\delta }_2<1$. When electricity is charged to the battery, there is lost energy during the process of recharging. Therefore, even though x amount of electricity is charged, only ${\delta }_{1}x<x$ amount is charged. In addition, the extra electricity during the process due to the system’s inefficiency is captured by $\frac{1}{{\delta }_2}$. ${\delta }_2$ is the efficiency loss when energy is discharged from the battery.

$$b_t=b_{t-1}+1(h_t=1){\delta }_{1}x-1(h_t=-1)\frac{1}{{\delta }_2}{y}_t^1$$

(4)

The battery system is designed to minimize the total electricity cost, which is (5). The amount of electricity usage is from the battery recharging ($h_t$) and the wall power ($z_t$) with the amount of electricity used, $y_t^2$, needed to be added. Using the objective function (5), threshold price $\underline{p}$ is chosen.

$$\underset{\underline{p}}{\min }\underset{t=0}{\sum ^{24}}\left[1(h_t=1)x+1(z_t=1)y_t^2\right]p_t$$

(5)

Price Threshold

Under the real-time pricing system where the electricity price changes over the hours, Equation (5) is the objective function to derive the optimal threshold of the battery ESS. In order to minimize the objective function as in (5), the charging and discharging schedule depends on the threshold price. There could be two potential ways of finding the threshold price. First, we can find an optimal threshold price by conducting an iterative process by plugging in the various sizes of the electricity price threshold in between the minimum and maximum price of the data in electricity cost function calculation as in (5).

Another way of doing so is to use intuition behind the cost function calculation. This method can be explained as follows. Assume the battery capacity is K. Then, to minimize potential cost, it is optimal to charge K amount of energy during the off-peak hours and use it during peak hours. If it is a time-of-use price schedule, then the gap between peak and off-peak prices is obvious because there are only two prices. On the other hand, in the fully dynamic price, the real-time price scheme, the off-peak price is the average electricity price below the threshold, while the peak price is the average price above the threshold. The average cost of a battery ESS, which is used as a baseline for threshold price calculation, can be written as (8) and (9).

Specifically, the required electricity can be written as the sum of hourly usage, ${\displaystyle \underset{t=1}{\sum ^{24}}}{y}_t$. t is the notation of the hour when the appliance is working, and $y_t$ is the hourly usage. So, $t=\{1,2,\cdots 24\}$. Among the total energy usage, $y_{\mathrm{on}}$ would be the energy used in the peak hours, while $y_{\mathrm{off}}$ is the off-peak usage.

The amount of electricity used in the off-peak hours is multiplied by the electricity price lower than the price threshold ($p_l=E\left(p_{t}1(p_t\le \underline{p})\right))=E\left(p_t\right|p_t\le \underline{p})$, and the rest is multiplied by the price above the threshold ($p_u=E\left(p_{t}1(p_t\ge \underline{p})\right)=E\left(p_t\right|p_t\ge \underline{p})$). The cost of the system without the battery can be easily written as Equation (6).

$$E\left(\cos \mathrm{t}\right|\mathrm{no}\mathrm{ESS})=y_{\mathrm{on}}{p}_u+y_{\mathrm{off}}{p}_l$$

(6)

The battery system covers the part of the required electricity, and the rest uses the wall power. Then, the expected cost of the battery system would be written as (7).

$$E\left(\cos \mathrm{t}\right|\mathrm{with}\mathrm{ESS})=(y_{\mathrm{on}}-K)p_u+(y_{\mathrm{off}}+K)p_l$$

(7)

The optimization is to find the threshold price $\underline{p}$ that minimizes (8), and the optimal capacity K depends on the threshold price $\underline{p}$.

$$\begin{array}{cc}\hfill \min E\left(\cos \mathrm{t}\right|y)& =\left(y_{\mathrm{on}}-K\left(\underline{p}\right)\right)E\left(p\right|p\ge \underline{p})+\left(K\left(\underline{p}\right)+y_{\mathrm{off}}\right)E\left(p\right|p\le \underline{p})\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill =\underset{\underline{p}}{\min }\underset{K\left(\underline{p}\right)}{\min }& y_{\mathrm{on}}{p}_u+y_{\mathrm{off}}{p}_l-K\left(\underline{p}\right)\left(p_u-p_l\right)\hfill \end{array}$$

(9)

This threshold calculation is where we depart from the literature. Many papers in the literature use many optimization techniques such as dynamic programming [26,31] or genetic algorithm [25]. However, the optimization process often needs calculation which is impossible for the small, portable appliance design. We are focusing on the daily electronics that do not have a sophisticated system. Therefore, we are approaching the problem by assuming the daily usage profile is deterministic and known. Additionally, the price threshold can be updated as time goes by. However, the calculation itself should depend on the historical price. Therefore, the system memory size or the amount of electricity price history saved on the system determines the frequency of threshold price updates.

3. Simulation and Result

This section presents the benefit and costs of installing ESS by implementing the model above and the data. Three different cases that use two types of time-varying prices are used in this section. The electricity price plans used in the simulation are from the user price plan in South Korea, the state of Texas, and the city of Chicago. The first case is based on South Korea’s regulated market with less renewable penetration and has relatively small differences between off-peak and peak hours. The second case is the real-time pricing rule with more extensive penetration of renewables than the first case, which is based on American Illinois and ComEd. They offer a real-time pricing plan in the Chicago area, and the price is pegged with PJM’s marginal rates. The third case is a large renewable energy penetration case such as Texas. It resembles time-of-use pricing as in the first case, but the electricity price is zero during the off-peak hours. Often, a negative electricity price is observed, which shows great intermittency and demand/supply imbalance.

Here, we applied the previous method to a hypothetical profile that is built on the data. There are two main components: price profile and power consumption profile. First, we discussed how the electricity price is constructed based on the statistics of the data. Second, the power consumption profile of the three appliances is presented.

The proposed optimization algorithm can be performed for any battery type. Depending on the battery types, the life cycle, Depth of Discharge (DoD), C-rate, and related control and battery management strategies would differ [32]. Nevertheless, the optimization process to select the battery capacity is the same regardless of the battery types. For the following simulation, Li-Ion is used.

3.1. Home Appliance Power Usage

The electricity consumption profile is constructed on the power consumption specs publicized by the Energy Labeling & Standard regulation of the Korea Energy Agency (KEA). In order to mimic the household electricity usage, we used the common specs of appliances that are used by a household with four people. The profile is in

Table 2. Home appliances energy consumption profile.

	Washing Machine	TV	Refrigerator
Unit	18 kg	49 inch	270 L
Usage profile	1 h/day	8 h/day 1	N (33.3, 4) 2
Power consumption	600 W	70 W	33.3 W

¹ TV is on during 7–9 am and 6 pm–12 am. ² Normal with mean 33.4 and standard deviation 4.

. The size of the refrigerator is 270 L, and it is assumed to be used at all hours. The amount of electricity used is simulated as a normal distribution with a mean of 33.3, and a washing machine variance of 4.18 kg and 49-inch TV are also used in the simulation. The number of usage of the appliances throughout the day is also incorporated in the simulation. Figure 3 shows the three major home appliances’ hourly energy usage throughout a day, i.e., washing machine, TV, and refrigerator.

3.2. Time-Varying Electricity Prices and Battery

The three different time-varying electricity prices shown in Figure 1 are investigated. Case 1 in Section 3 is the case in Figure 1a, which is the time-varying price scheme found in the state of Texas [13]. With the help of the high penetration of wind energy, the price gap between the peak and the off-peak period is high. Case 2 in Section 3 is the case in Figure 1b, which is the case of South Korea [14], the Korean government regulates the electricity price. Compared to Case 1, the price gap is marginal, since the power system is not highly dependant on renewable energy. Finally, case 3 in Section 3 is the case in Figure 1c, the time-varying price scheme found in the city of Chicago [15], where the electricity price varies continuously over a day.

We conducted a simulation based on the optimization algorithm in the previous section. In the simulation, the typical C-rate for the Li-ion battery is higher than 0.7, whereas we used 0.3 for the C-rate. The dynamics of electricity price variation in Figure 1 is slower than the household ESS charging/discharging current rate. Therefore, the proposed optimization method is not limited by power but depends on the energy capacity. Ranges of C-rate can be used for constraining the optimization process. Given the parameters, the daily electricity costs $C\left(\underline{p}\right)$ for various K values are calculated and compared. Finally, we also plotted the SoC ($b_t$) profile at the optimal capacity level. When finalizing battery capacity, State-of-Health (SoH) can be considered by dividing the battery capacity by SoH. The typical SoH for the ESS is 80%. Battery degradation dynamics over a time period are not considered to avoid the complication of the optimization algorithm.

3.2.1. Case 1: Reliant, State of Texas

Figure 1a shows that the price scheme used in the simulation is from the Texas Reliant Energy company’s electricity plan, which is advertised as the ‘Truly Free Nights Plan’. It charges zero price during the off-peak hours and 23.5 ¢/kWh during the daytime (6 a.m.–8 p.m.), including delivery charges.

To find a battery size that offers the most benefits, we compared the net economic benefits of batteries of various sizes. The economic benefit of a household is the total electricity cost reduction that a user can achieve. The benefits unit is calculated yearly (10) by multiplying 365 by the daily benefits. Finally, the payback period, the number of break-even years, is calculated by dividing the battery cost by the yearly benefits.

$$\begin{array}{cc}\hfill \mathrm{Benefit}[\$/\mathrm{years}]& =365(\mathrm{Elec}.\mathrm{Price}@K=0-\mathrm{Elec}.\mathrm{Price})\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \mathrm{Payback}\left[\mathrm{years}\right]& =\frac{\mathrm{Battery}\mathrm{Cos}\mathrm{t}}{\mathrm{Yearly}\mathrm{Benefit}}\hfill \end{array}$$

(11)

Table 3. Capacity Decision: Refrigerator, TOU, Case 1.

Elec. Cost	Benefit	Battery Size	Battery Cost	Payback
($/day)	($/year)	(Wh)	($)	(years)
0.111		0
0.092	6.784	91	9.1	1.34
0.072	13.940	182	18.2	1.31
0.054	20.753	273	27.3	1.32
0.034	28.021	364	36.4	1.30
0.015	34.898	456	45.6	1.31
0.000	40.381	547	54.7	1.35
0.000	40.381	638	63.8	1.58
0.000	40.381	729	72.9	1.81
0.000	40.381	820	82.0	2.03

The battery cost is assumed to be 100 $/kWh. ${\delta }_1$ = 0.9, ${\delta }_2$ = 0.9.

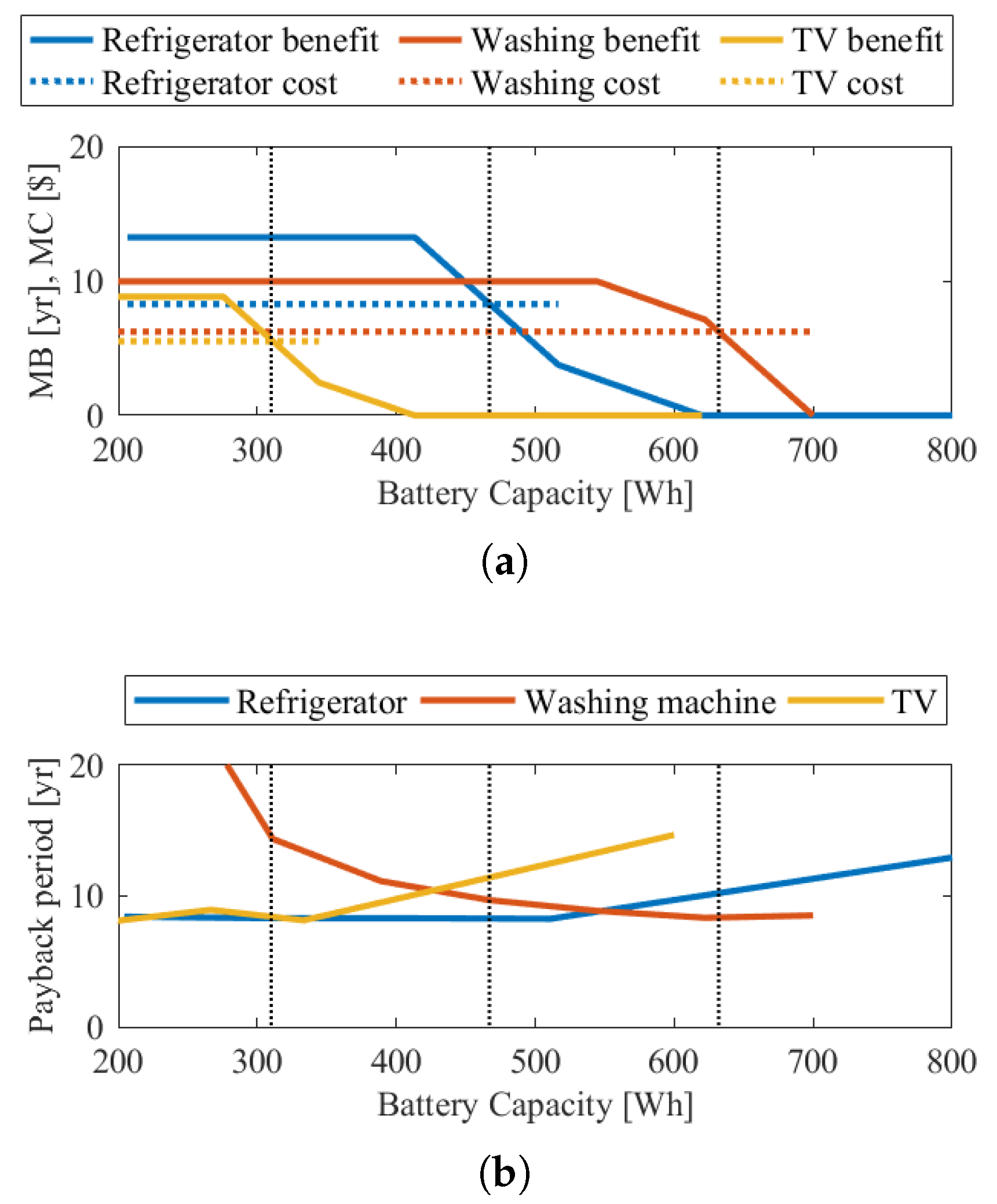
summarizes the results from the simulation. We calculated the ESS’s daily electricity cost in the first column. The battery with the size of 540 Wh offers the largest benefit, while the battery with the size of 360 Wh provides the shortest payback period. The choice of battery size would depend on the objectives, such as obtaining the shortest return period or maximizing the financial benefits of using the system. The optimal battery capacity determined by the TV and washing machine payback period is 160 Wh and 600 Wh, respectively. The number of payback periods was 1.3 years at their optimal battery capacity.

Figure 4a shows the daily electricity cost to run each home appliance as a function of battery capacity. When the battery capacity in the distributed ESS increases, the daily electricity cost decreases to 0 $/day. The optimal battery capacity is selected to assure a minimum payback period. Figure 4b shows the SoC of home appliances with optimal battery capacity. It is observed that the electricity is charged during the zero price period and discharged at the peak cost period.

3.2.2. Case 2: KEPCO, South Korea

The price gap between the off-peak and peak hours of KEPCO plan shown in Figure 1b is smaller than Case 1 in Figure 1a. As a result, the economic benefit from the distributed ESS is smaller than in Case 1.

The economic benefit in the South Korea case is smaller than Texas case as in

Table 4. Capacity Decision: Refrigerator, TOU, Case 2.

Elec. Cost	Benefit	Battery Size	Battery Cost	Payback
($/day)	($/year)	(Wh)	($)	(years)
0.066		0
0.064	0.807	91	9.1	11.3
0.061	1.754	182	18.2	10.4
0.059	2.619	273	27.3	10.4
0.056	3.585	364	36.4	10.2
0.054	4.421	456	45.6	10.3
0.052	4.949	547	54.7	11.0
0.052	4.949	638	63.8	12.9
0.052	4.949	729	72.9	14.7
0.052	4.949	820	82.0	16.6

The battery cost: 100 $/kWh. ${\delta }_1$ = 0.9, ${\delta }_2$ = 0.9.

due to the smaller electricity price difference. The payback period is 10.2 years. Compared to the payback period of 1.3 years in Case 1, the Case 2 payback period is much longer.

Figure 5a plots the daily electricity cost with different sizes of batteries. If we compare the daily electricity cost without any battery and with the battery that gives the shortest payback period, the cost dropped to 85.1%, 74.8%, and 78.6% for refrigerators, washing machines, and TV. The optimal battery sizes based on the payback periods are 360 Wh, 600 Wh, and 330 Wh, respectively. The battery capacity compared to the sum of daily use of energy, $d_u$, was 46.7% 100%, and 67.9%.

Intuitively, the ESS stores the energy during off-peak hours, and the optimal amount of stored energy should be used in peak hours. We are considering a linear system where the installation cost of the battery is proportional to the capacity size, and the marginal benefit for increasing 1 unit of the battery capacity (Wh) is the constant, the gap between the off-peak and peak electricity price. Therefore, installing the battery to the size of peak energy usage is always the best option when the marginal benefit is positive.

3.2.3. Case 3: ComEd, City of Chicago

Case 3 is the real-time pricing case, which is the most radical of the three. The pricing schedule from ComEd is used since the price varies every hour, and there is no evident fixed peak and off-peak price. We used the data of ComEd from June to August 2020. We applied the intuitive rule described in the price threshold section and compared the results with the brute-force method that plugs in every different price threshold schedule.

In

Table 5. Price Threshold Comparison.

Difference ($)	Refrigerator	Washing Machine	TV
K (1)	0.228	0.179	0.204
K (2)	0.010	0.082	0.000
K (3)	0.009	0.045	0.005
K (4)	0.003	0.027	0.006
K (5)	0.000	0.000	0.004
K (6)	0.000	0.015	0.012
K (7)	0.000	0.000	0.003
K (8)	0.002	0.000	0.002
K (9)	0.003	0.000	0.002
K (10)	0.004	0.001	0.001

, we compared the price thresholds results from the two methods ((5) and (9)), which is in the unit of US dollars ($). Each row that is written in (K(1) and K(10)) is the group of battery capacity that is sliced by ten deciles. The maximum battery capacity is the amount of electricity needed for one day’s usage, and we sliced it into ten groups. There is some difference in the small battery groups, while the difference disappears for the large battery capacity groups.

Figure 6a shows that the daily electricity cost varies by the size of battery capacity. It shows the optimal sizes of battery capacity are around 90 Wh, 600 Wh, and 330 Wh for the refrigerator, washing machine, and TV, respectively. Unlike the time-of-use pricing case, the daily cost changes smoothly. In Figure 6b, the SoC changes are similar to other cases: charge during off-peak hours and discharge during the peak hours. In

Table 6. Battery capacity analysis: refrigerator, Case 3.

Elec. Cost	Benefit	Battery Size	Battery Cost	Payback
($/day)	($/year)	(Wh)	($)	(years)
0.066		0
0.064	0.807	91	9.1	11.3
0.061	1.754	182	18.2	10.4
0.059	2.619	273	27.3	10.4
0.056	3.585	364	36.4	10.2
0.054	4.421	456	45.6	10.3
0.052	4.949	547	54.7	11.0
0.052	4.949	638	63.8	12.9
0.052	4.949	729	72.9	14.7
0.052	4.949	820	82.0	16.6

Battery cost and efficiency used: 100 $/kWh. ${\delta }_1$ = 0.9, ${\delta }_2$ = 0.9.

, the payback period is longer than the TOU price case. The benefit from ESS is marginal for the real-time compared to the TOU.

The electricity price is stable, and the economic benefit is small. The benefit of the TOU price plan is greater than that of the real-time price cases. The imbalance between demand and supply in urban areas results in price variation.

4. Economic Benefit Analysis

This section analyzes the economic benefit of using the ESS system in the sense of a payback period. The reason why we focus on the payback period is as follows. First, running the ESS system is always better than not running it, since it creates daily benefits due to the electricity price difference. It is always beneficial to install the ESS system if we do not consider the system installation cost, mainly the battery cost. Second, the payback period calculation is similar to the break-even analysis commonly used in project profitability projection. It is an effective measure to compare various options with different fixed cost levels. Therefore, instead of using total benefits from the ESS system, we chose the payback period to compare the net benefits of installing the system.

The price gap between the off-peak and peak hours determines the benefit of the system and the payback period. Therefore, the electricity price distributed matters for the calculation. We analyzed various cases with different scenarios of electricity prices. In addition, the distributed and the central ESS are analyzed for the operating condition that ensures a minimum payback period.

4.1. Payback Period Analysis

Figure 7a is the payback period of ESS for the refrigerator with an increasing price gap between the peak and off-peak hours $(p_p-p_{op})$. The cost and capacity of the battery were fixed to 100 $/kWh and 500 Wh. For the price gap in Case 1 (Texas), the payback period is around one year as in Table 3, while the Case 2, the payback period is around 10 years, as shown in Table 4. The difference in payback years indicates that the distributed ESS is more suitable for the TOU price scheme in Texas with a larger price gap than in South Korea. As the price gap increases, the payback period quickly reduced. The payback periods fewer than 2 years need a price gap larger than 10 ¢/kWh. Figure 7b shows the Case 1 (Texas) payback period over battery prices. The payback period decreases while the battery cost decreases.

4.2. Comparison between Distributed and Central ESS

The economic benefit comparison analysis has been performed. The central ESS energy usage profile becomes a summation of each distributed ESS in the household. Payback periods are compared regarding optimal ESS capacity calculated based on Section 2. The analysis is conducted using the TOU pricing scheme in Case 1 with a unit battery price of 80 $/kWh.

The results in

Table 7. Economic benefit and payback period of distributed and central ESS.

	Opt. Capacity	Payback Period	Benefit/Battery
	(Wh)	(year)	($/Wh)
Refrigerator	455.56	1.038	0.074
Washing Machine	600.00	1.049	0.076
TV	166.67	1.040	0.077
Central	1273.33	1.039	0.076

Simulation used the TOU price scheme in case 1. 80 $/kWh is used for the battery price.

are based on hourly level calculations that can create some numerical errors due to the limitation of the calculation unit. We are considering the electricity cost in the unit of hours, so there could be some amount of energy that is not fully covered by the battery system. In other words, the optimal capacity derived in an hour unit can be smaller than the amount of energy used in the peak hours, resulting in some residuals similar to rounding errors. The optimal capacity of the central and some of the distributed battery capacity should be equal in principle, and it should be the same if the calculation is performed in the continuous domain.

Table 7 summarizes the economic benefit and payback periods. The optimal capacity which gives the shortest payback period is calculated in column 2. The payback period, the duration of usage that can compensate for the cost for the battery, is in column 3. The three appliances give a similar payback period and economic benefit. That is due to the innate structure of the ESS; the benefit solely comes from the price gap, which is the same across different appliances. The unit battery capacity benefit in a year is calculated as $\frac{\min (K,y_{on})(p_{\mathrm{on}}-p_{\mathrm{off}})\times 365}{K}$ where $y_{\mathrm{on}}$ is the amount of electricity usage during peak hours, while $p_{\mathrm{on}},p_{\mathrm{off}}$ are the electricity price during peak and off-peak hours, respectively. If $K\le y_{\mathrm{on}}$, then the K in both the denominator and numerator disappear, leaving only the benefit from the price gap. After multiplying it with the efficiency, the benefit for each unit of the battery becomes the same across different appliances. The payback period can be calculated in a similar fashion, $\frac{cK}{365\times 0.81\times \min (y_{\mathrm{on}},K)(p_{\mathrm{on}}-p_{\mathrm{off}})}$.

These results indicate that placing distributed ESS will result in the same economic benefit but with the additional benefit of a smaller initial investment cost and fault range, as shown in Table 1.

4.3. Installing Priority Decision

The cost–benefit rule can prioritize the installment order of distributed ESS for home appliances. The total net benefit for installing the ESS is (12) where $B_1$, $B_2$, and $B_3$ are the benefit of three different home appliances. The cost for ESS is $c{K}_n$ for the battery with $K_n$ size. The order of installation should follow the marginal rule. The appliance that gives a higher benefit for each unit of the battery should have priority. The order of installation is 1 for the first and 2, 3, subsequently in (13).

$$\underset{K_1,K_2,K_3}{\max }{B}_1\left(K_1\right)+B_2\left(K_2\right)+B_3\left(K_3\right)-c(K_1+K_2+K_3)$$

(12)

$$\frac{\partial B_1\left(K_1\right)}{\partial K_1}>\frac{\partial B_2\left(K_2\right)}{\partial K_2}>\frac{\partial B_3\left(K_3\right)}{\partial K_3}$$

(13)

This rule also holds for the three different appliances in our example. Figure 8a shows the marginal benefit (MB) for operating ESS for 8 years and the cost for increasing the battery size. The refrigerator resulted in the highest benefit compared to the TV and washing machine, which was due to the frequent use during the peak hours. The optimal size of the battery would be the point at which the benefit is the same as the cost. The point would be the capacity that returns the shortest payback period for the appliances as in Figure 8b. The appliances which are frequently used during the peak hours would achieve higher benefit from ESS. If the marginal benefit (MB) of expanding the ESS exceeds the cost (MC), then it is optimal to enlarge the battery size. If it is smaller than the cost, then it is better to reduce the battery size. If the order of installation is implemented, then the refrigerator should be installed first, then the washing machine and TV.

5. Conclusions

Despite many reasons to introduce ESS to households, the introduction is slow. One of the difficulties associated with introducing ESS is the benefit calculation justifying the installation. For the homeowner, the benefit calculation, including initial investment cost and the payback period calculation, is essential. Many researchers have been developing exact methodologies for benefit calculations. However, these methodologies are difficult to be used for an individual, e.g., a homeowner. The electricity price plan and the load profile of the home appliances are different and difficult to be collected except for the householder. This paper proposes a straightforward methodology to calculate the benefit of distributed ESS for households given the electricity price variation and load profile of home appliances. Instead of solving a complicated optimization problem, we approach the problem by focusing on the threshold price and the average price. The methodology may be used as design guidance to the homeowner willing to introduce ESS.

ESS results in economic benefit under time-varying electricity price schemes. To calculate the optimal charging/discharging schedule and battery size, time-varying electrical pricing, battery cost, and power consumption profiles are used. The method calculates the optimal battery capacity to result in a minimum payback period for three different time-varying price schemes and home appliances.

Further analysis on the economic benefit is performed to justify the feasibility of the distributed ESS. Distributed ESS assures a smaller initial investment cost and fault range compared to the central ESS. The distributed ESS needs to be installed primarily for the load which consumes the largest energy in peak hours to return maximum benefits. Finally, due to the innate structure of ESS, both distributed and central systems resulted in the same payback period for the optimal battery capacity.

The relationship between the payback period and the time-varying electricity price gap is investigated to ensure distributed ESS’s practical use. The minimum payback period of ESS is determined by the electricity price gap and battery price. The Texas case showed a payback period of 1.3 years with a price gap is 23 ¢/kWh, where the price gap is large for high renewable energy penetration. The trend of increasing electricity price volatility and decreasing battery price would make ESS possible and profitable in the near future. Our methodology of calculating battery capacity and charging/discharging scheme suggests a portable and effective way of managing electricity demand that can be applied to diverse appliances.