Analysis and Mitigation of Harmonic Resonances in Multi–Parallel Grid–Connected Inverters: A Review
Abstract
1. Introduction
2. Stability of the Grid Connected VSI
- = ∞, i.e., = 0.
- The ratio of satisfies the Nyquist stability criterion.
- The intersection points of the magnitude curves for the inverter output admittance and the grid admittance , which represent the zero–dB crossing points of their ratio.
- The phase margin at the intersection point of and , which can be calculated as:where and are the phase angle of the inverter output admittance and the grid admittance, respectively. A positive phase margin angle ensures the VSI–grid system’s stability [25].
- The admittance itself has no right half-plane poles, which implies that the VSI is internally stable at the point of common coupling (PCC), i.e., stable when connected to an ideal zero impedance grid.
- The admittance has a real part which is nonnegative, i.e., , }, which indicates that the phase of is within [−90°, 90°].
- A smaller total time delay (computation-plus–PWM, time delay) associated with sampling and PWM can improve the passivity of the output admittance.
- A lower bandwidth of the outer loops, such as the dc link/power control loop and the PLL.
- Using the stationary reference frame ( frame) in the current controller helps restrict the PLL influence because the negative–real–part region due to the PLL effect extends if the current controller employs a -frame.
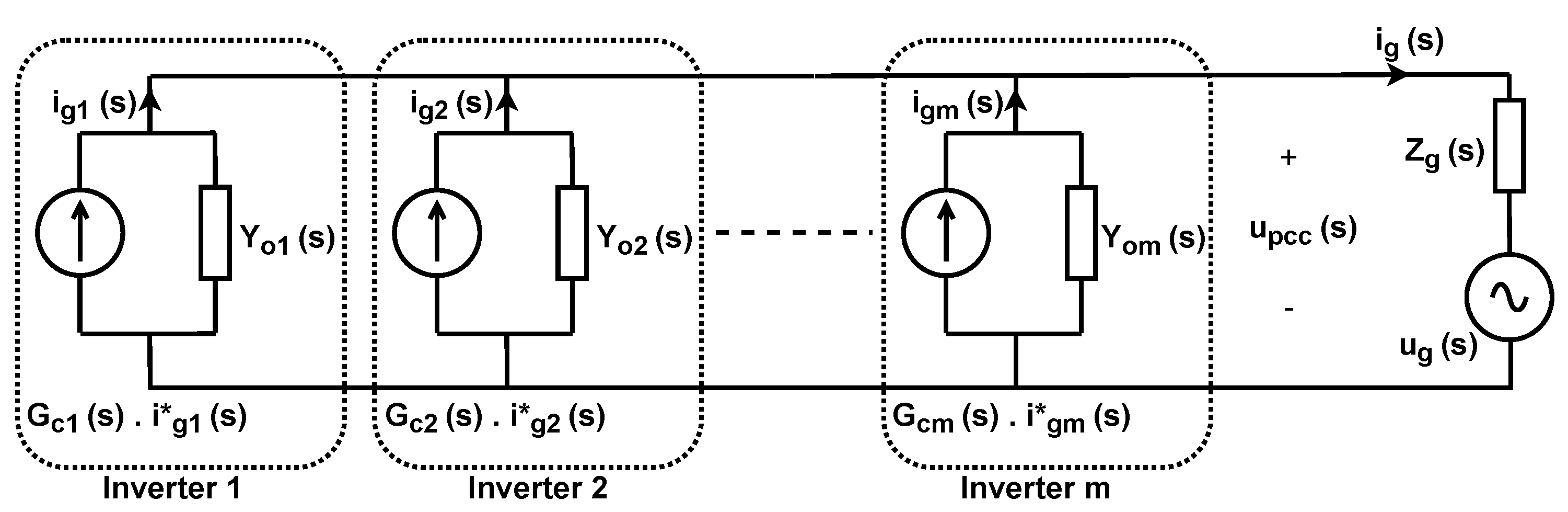
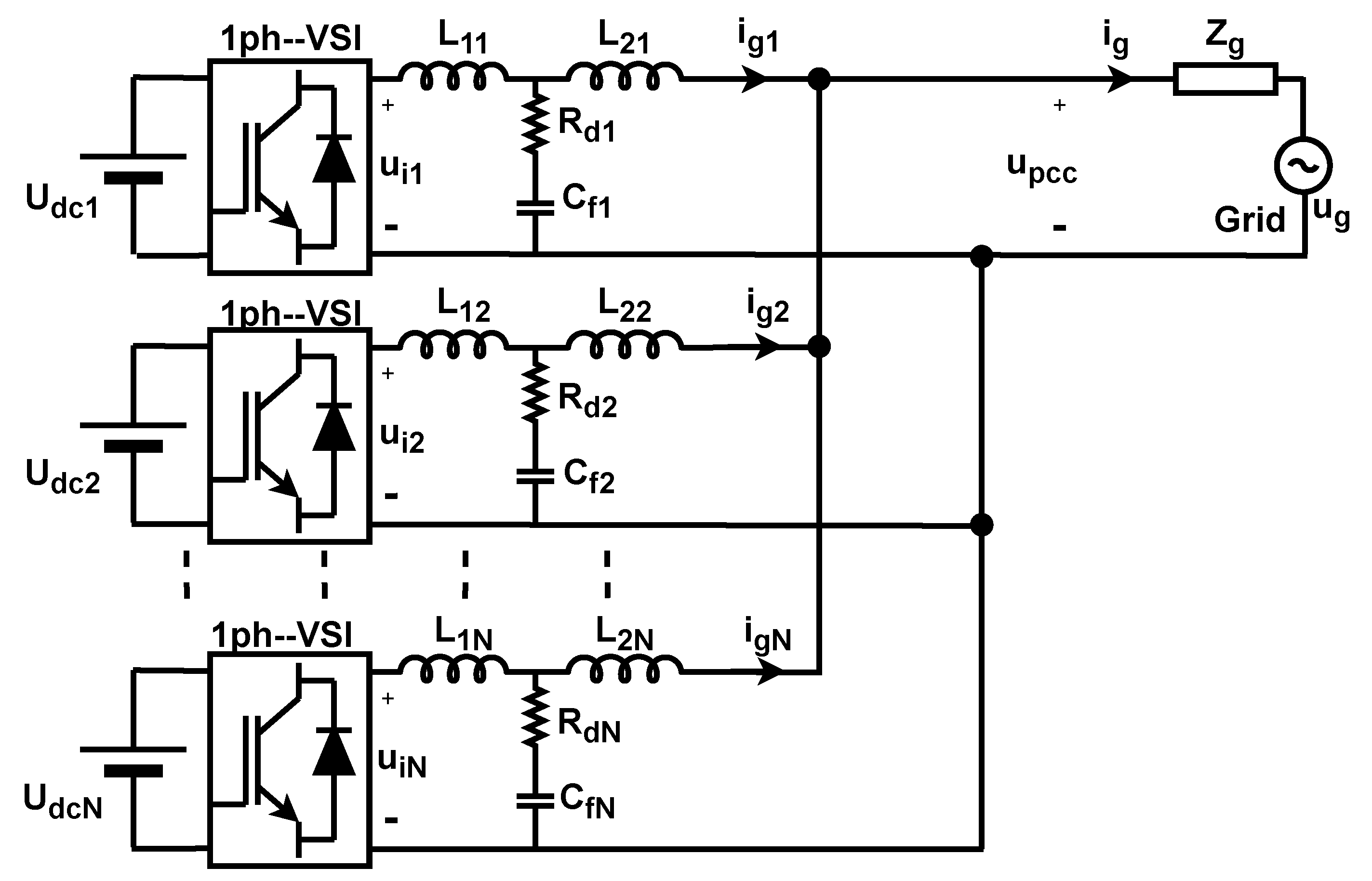
2.1. Multi–Parallel Inverter–Grid System
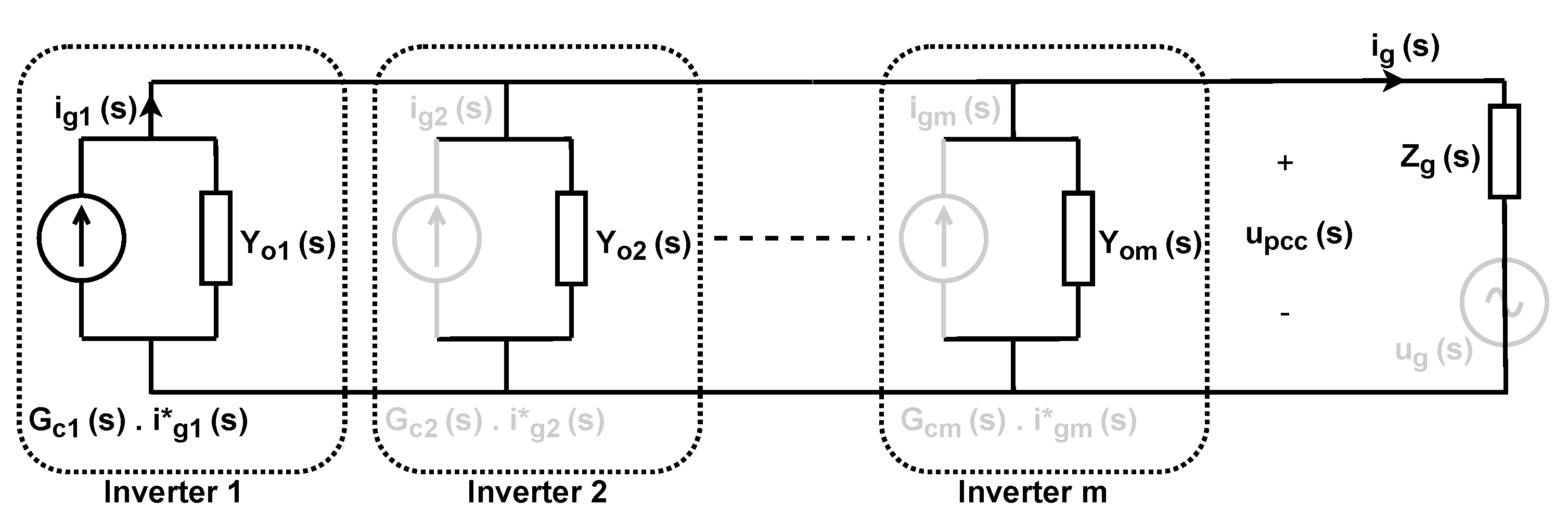
2.2. Main Current
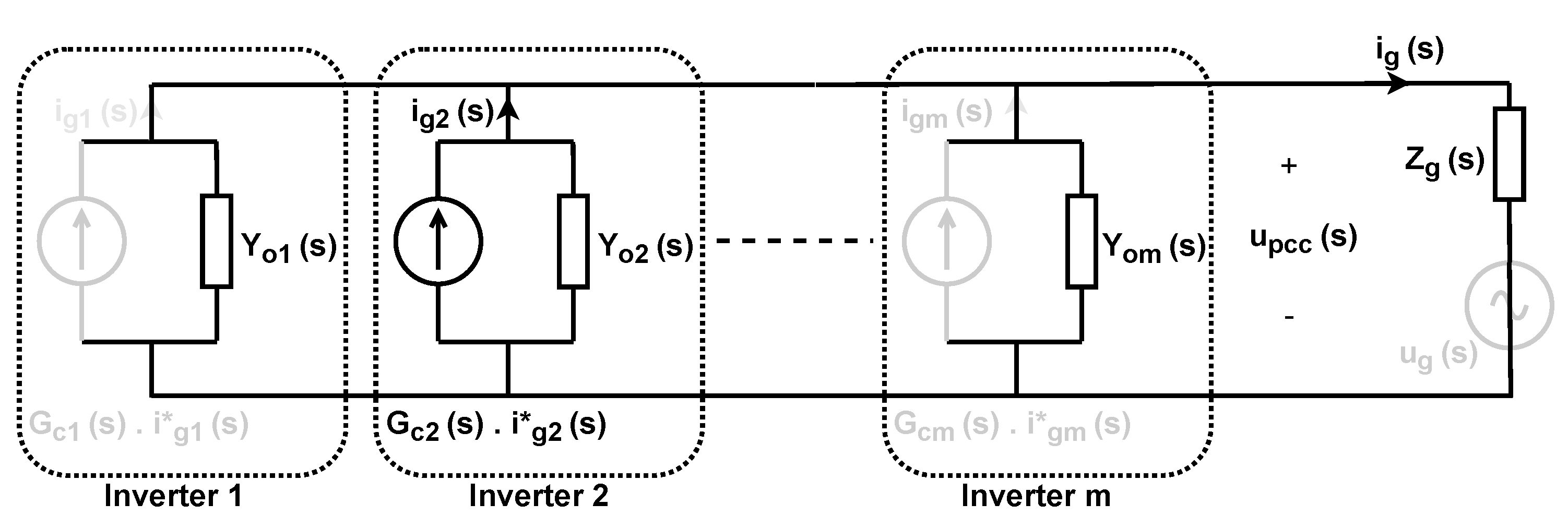
2.3. Interactive Current
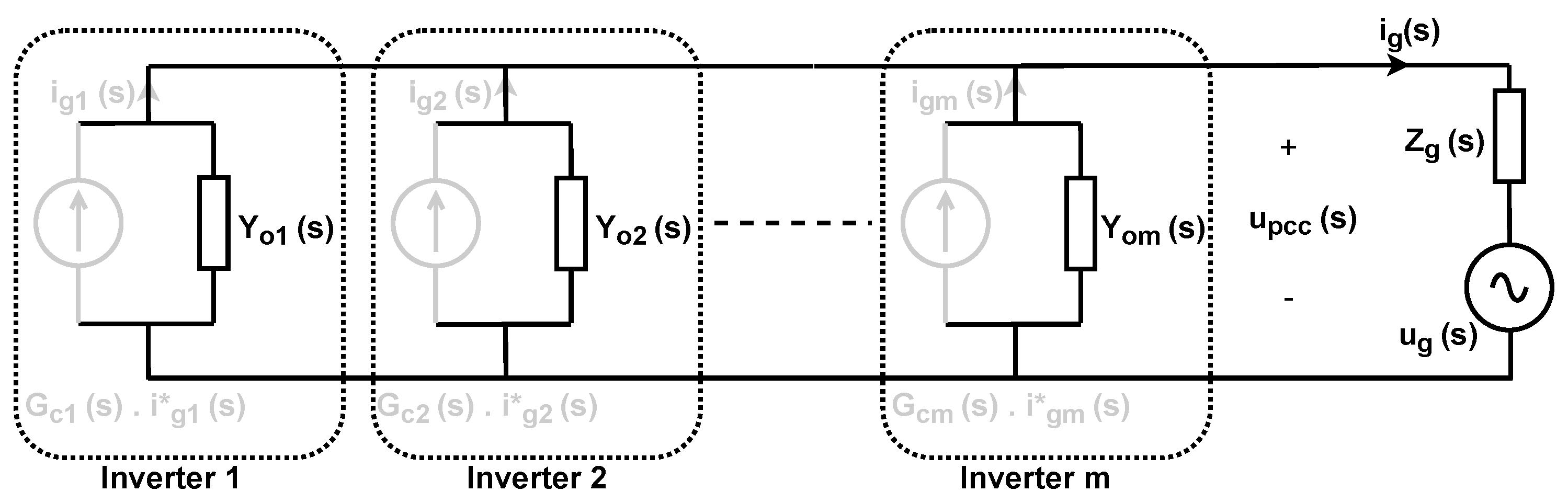
2.4. Common Current
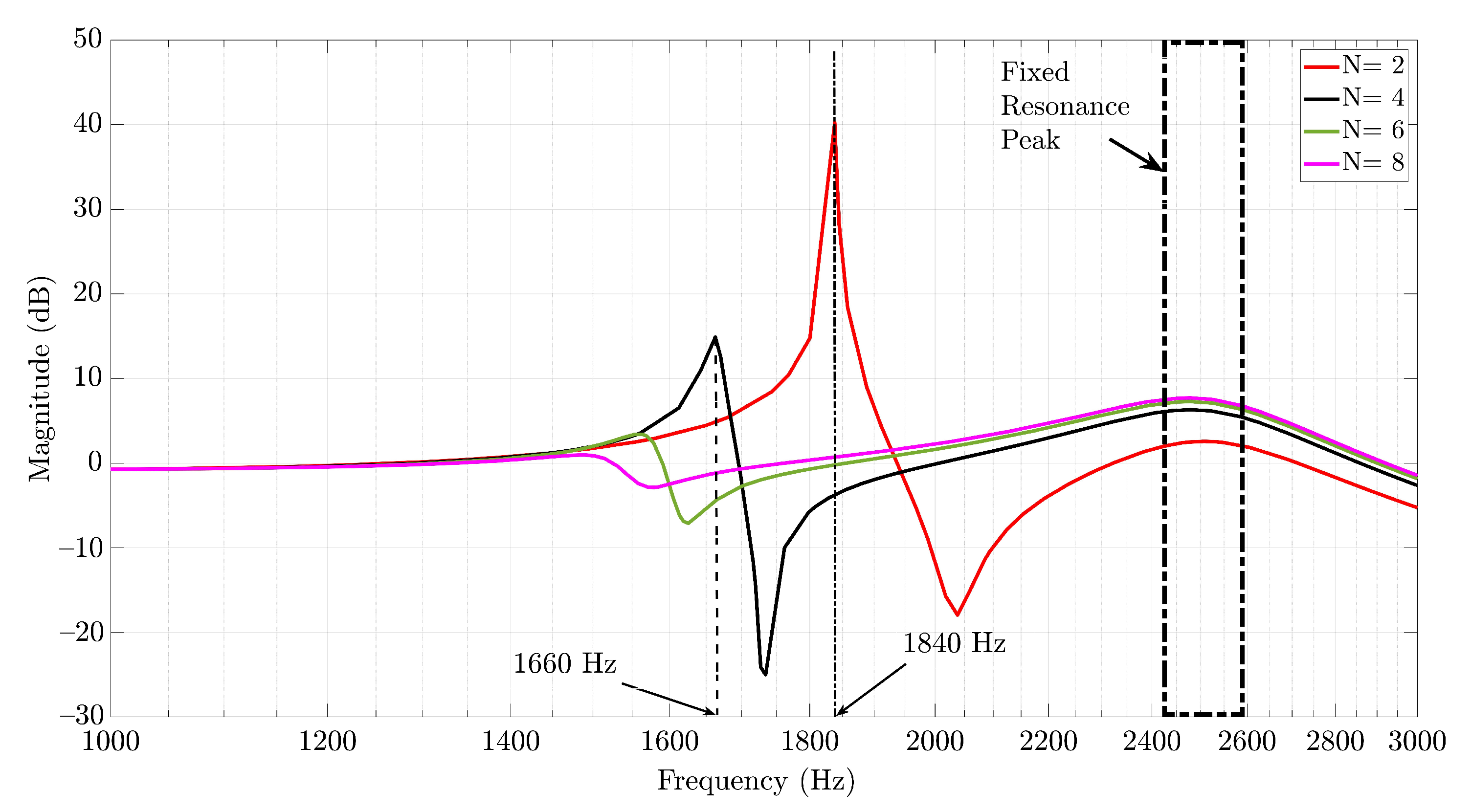
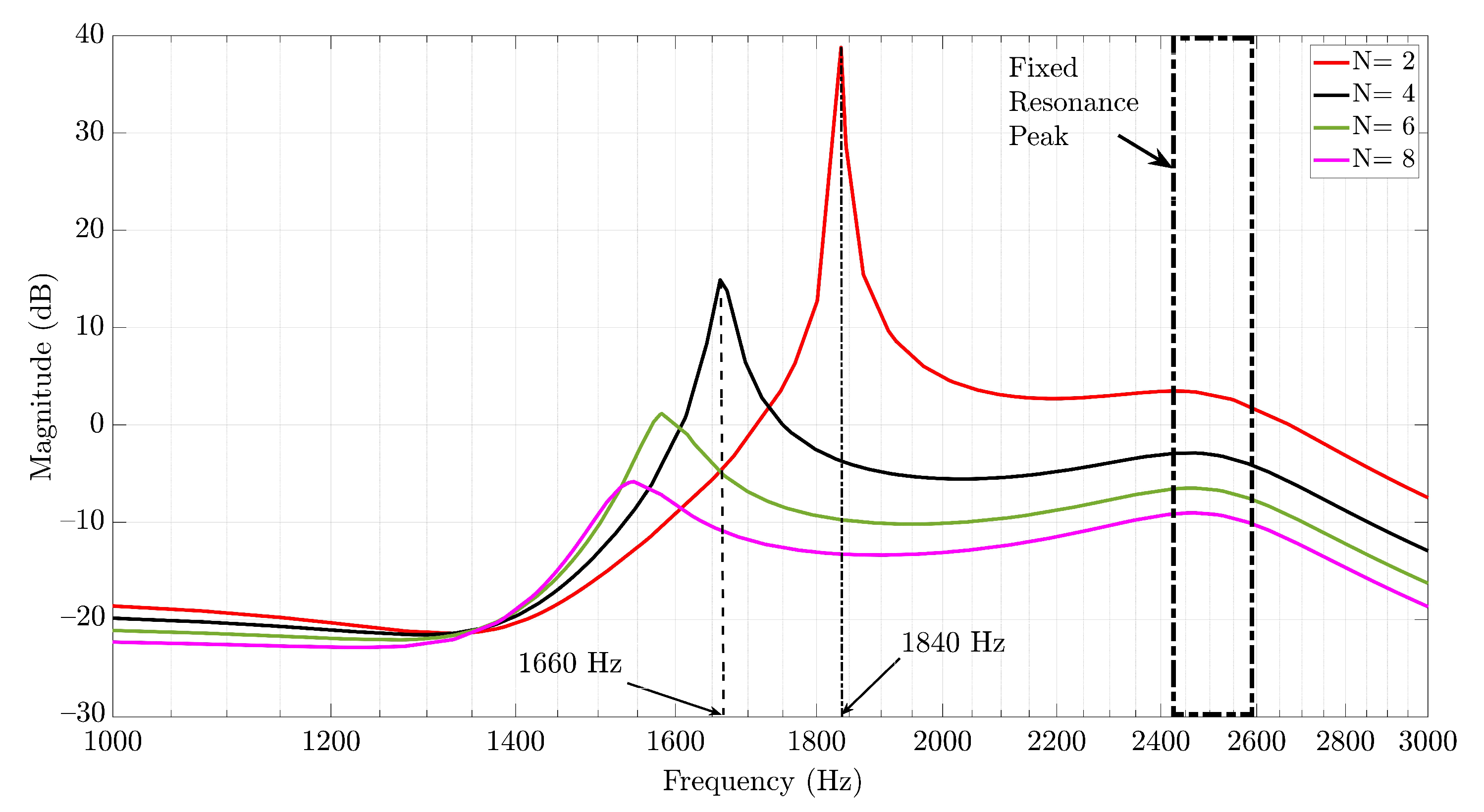
3. Example of Resonances in a Multi–Parallel Grid–Connected Inverter System
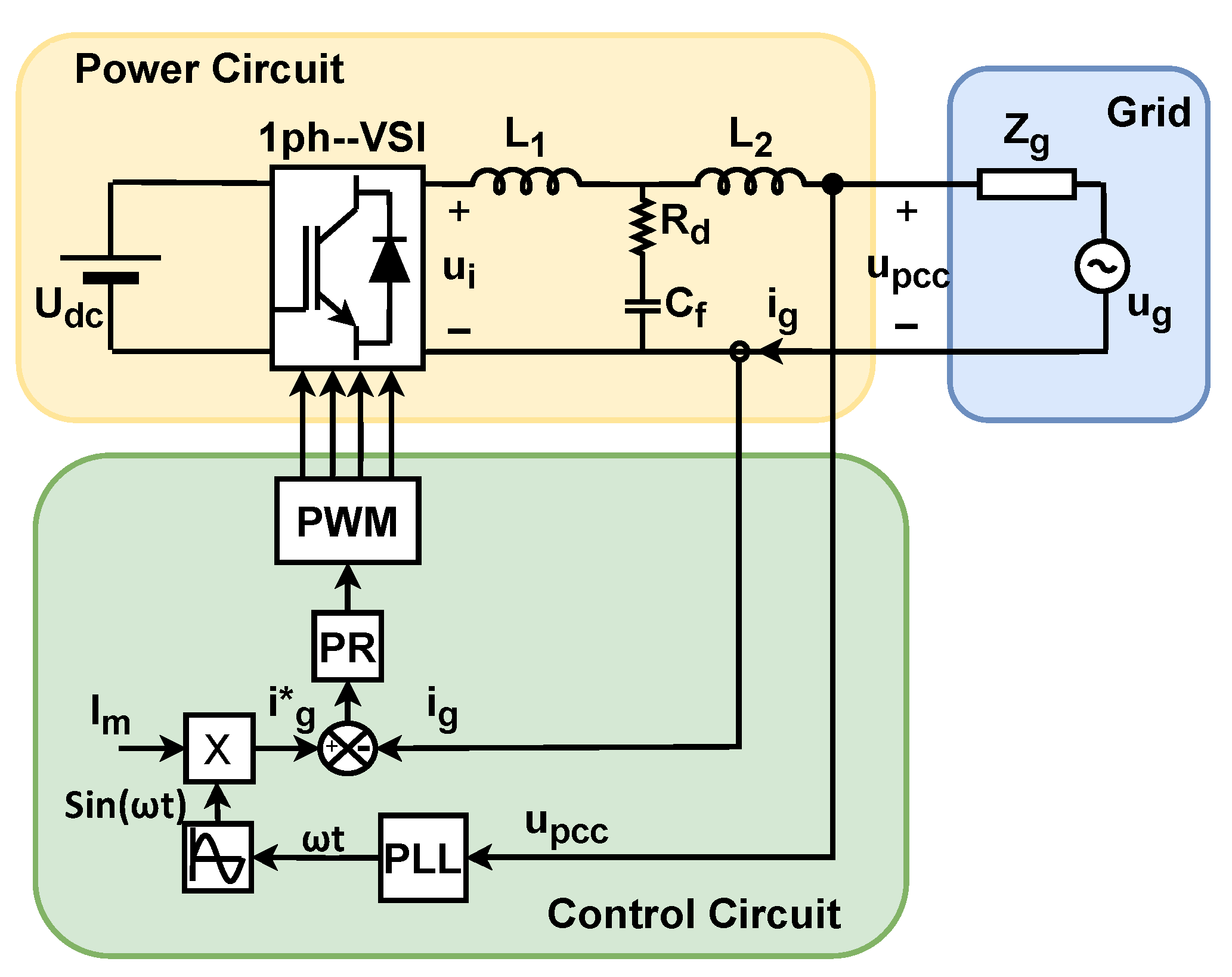
3.1. Model of Single VSI
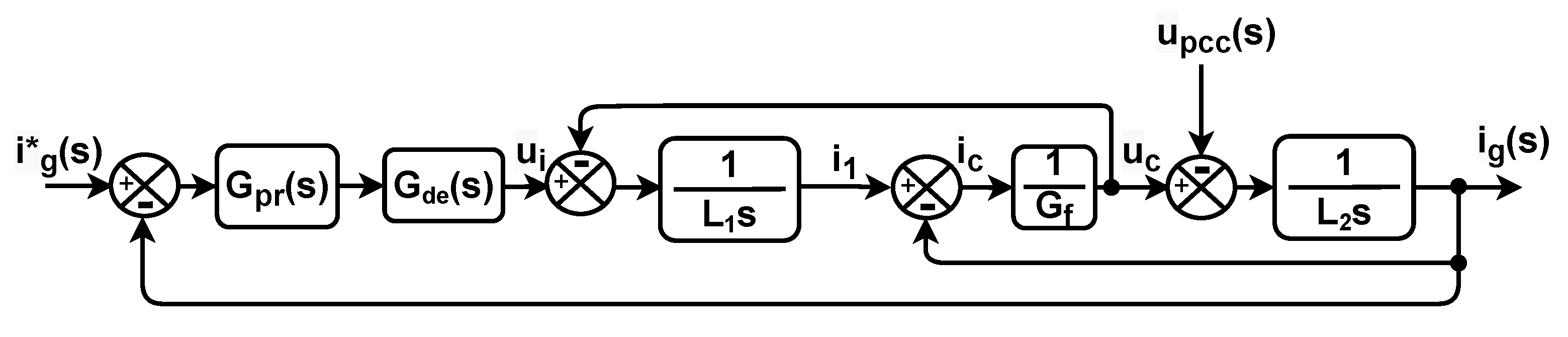
3.2. Small-Signal Model
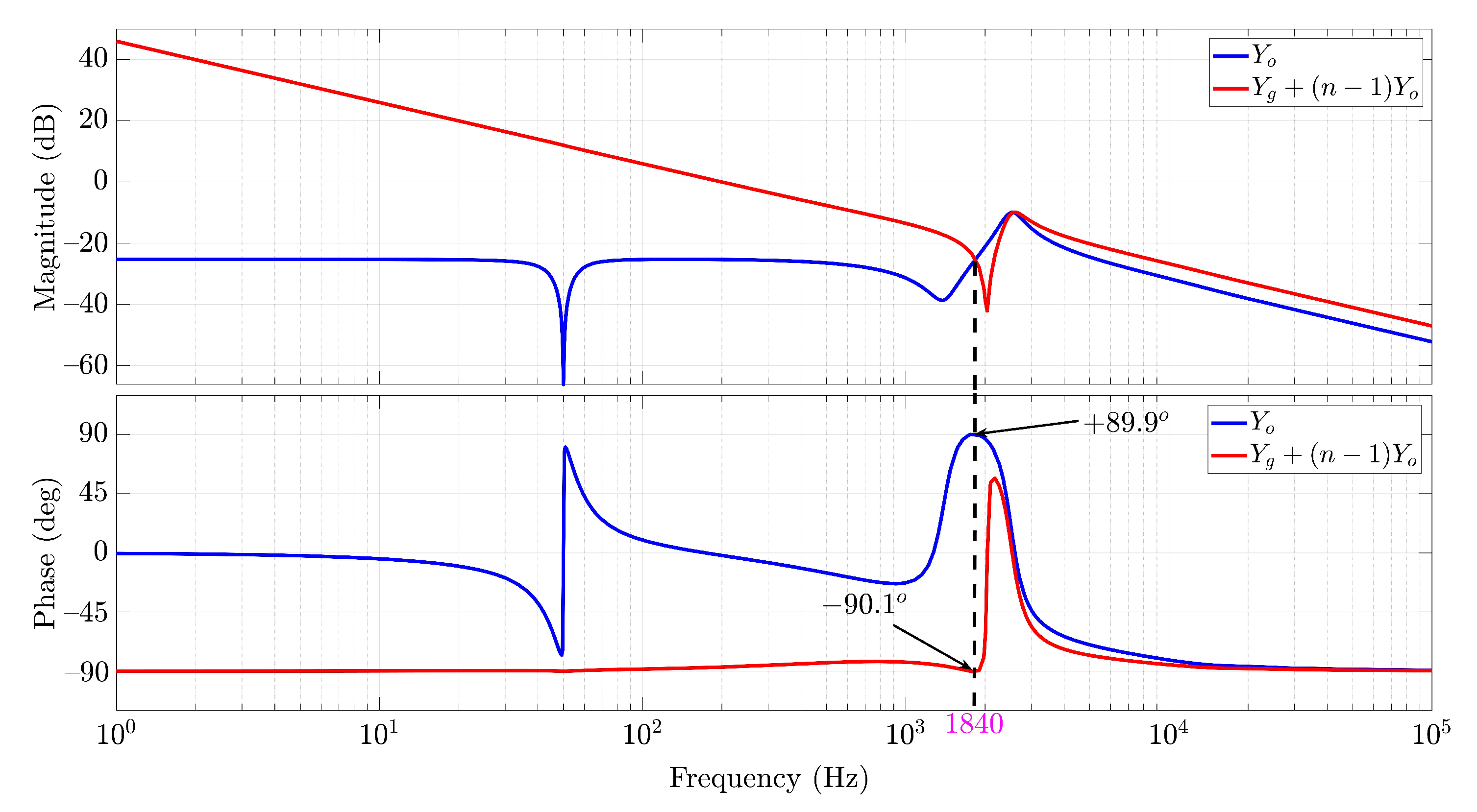
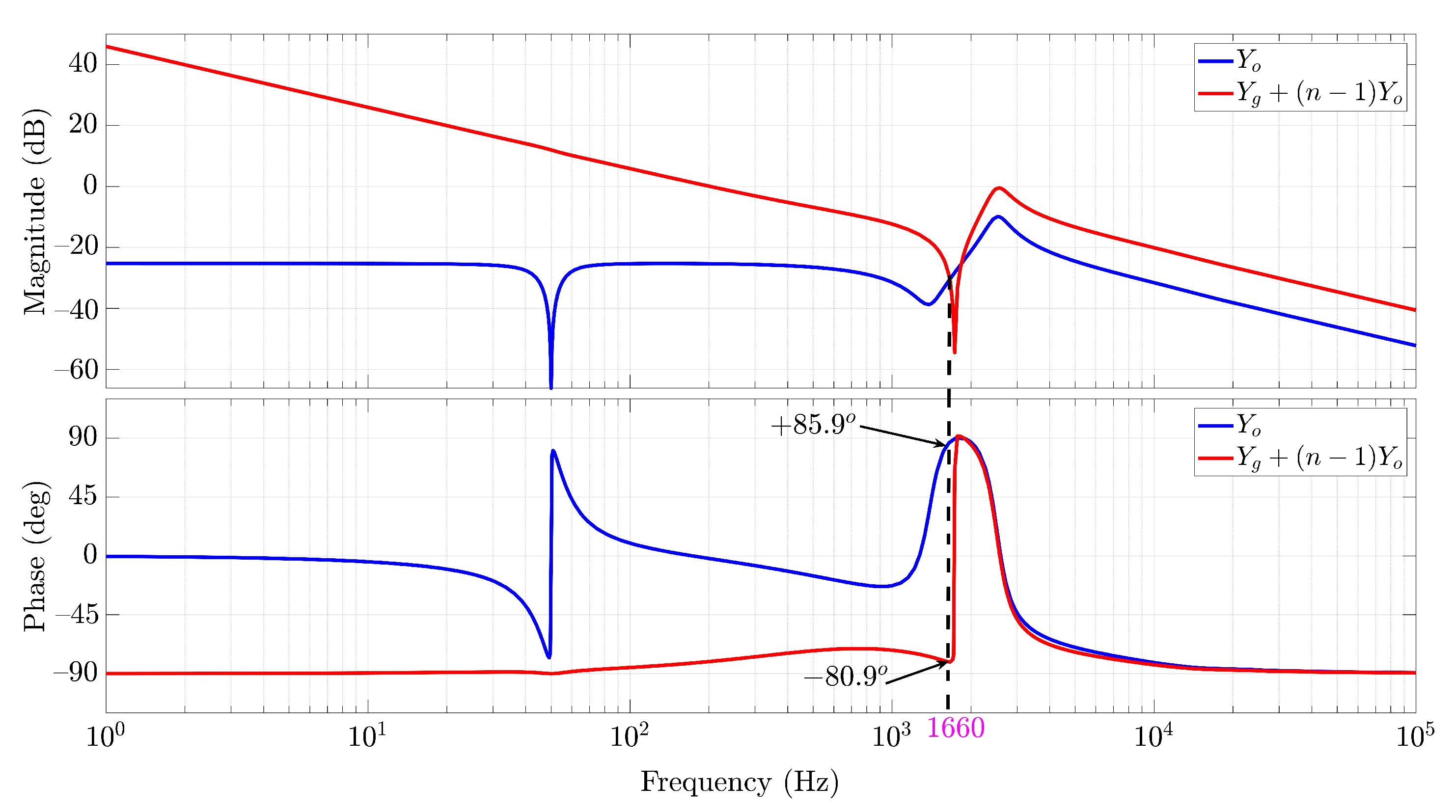
3.3. Single Inverter Grid Interaction
3.4. Main Current Resonance of the Inverter Itself
3.5. Interactive Current Resonance
3.6. Common Current Resonance
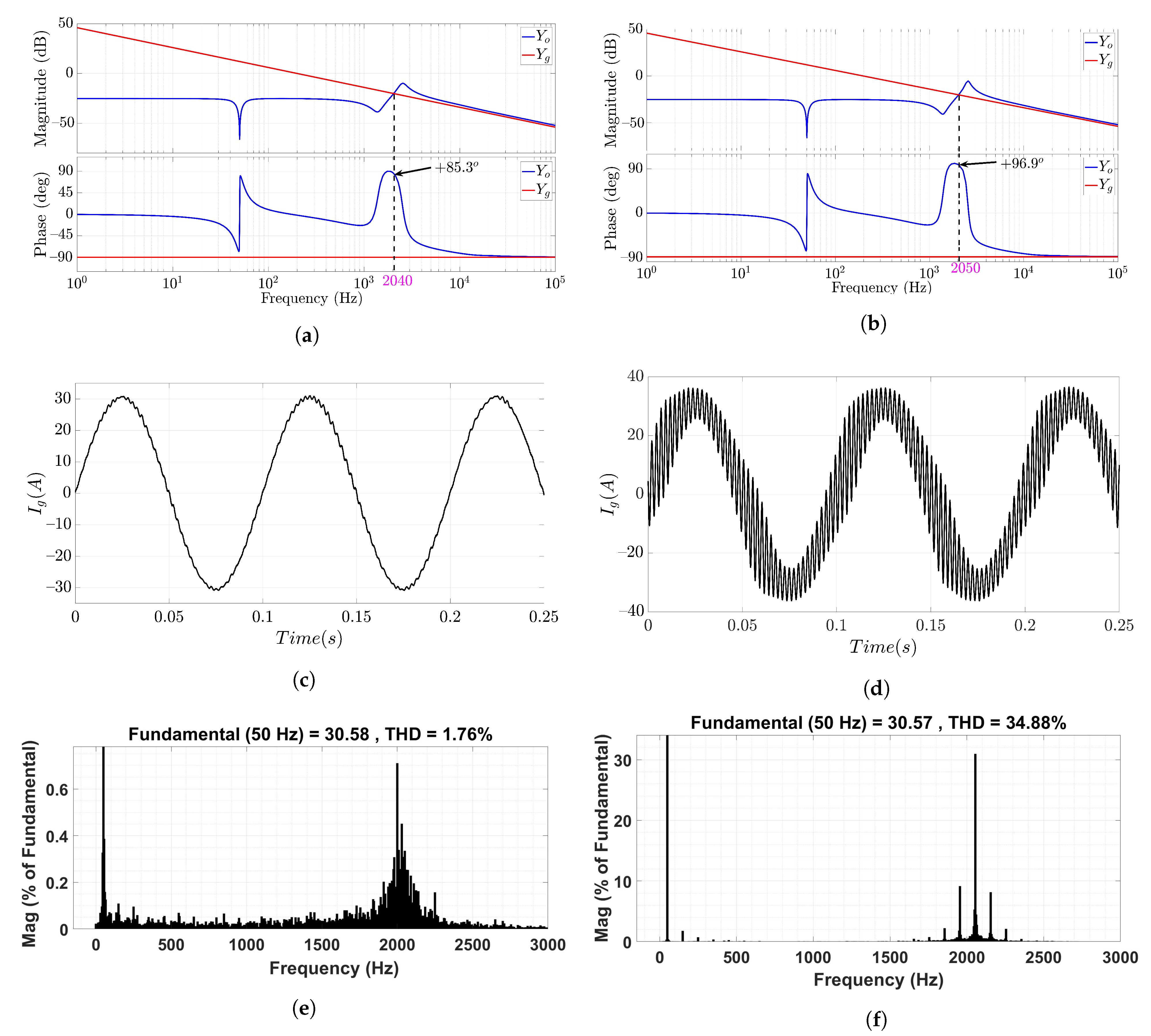
3.7. Interactions in a Multi–Parallel VSI–Grid System
3.8. Some Practical Considerations
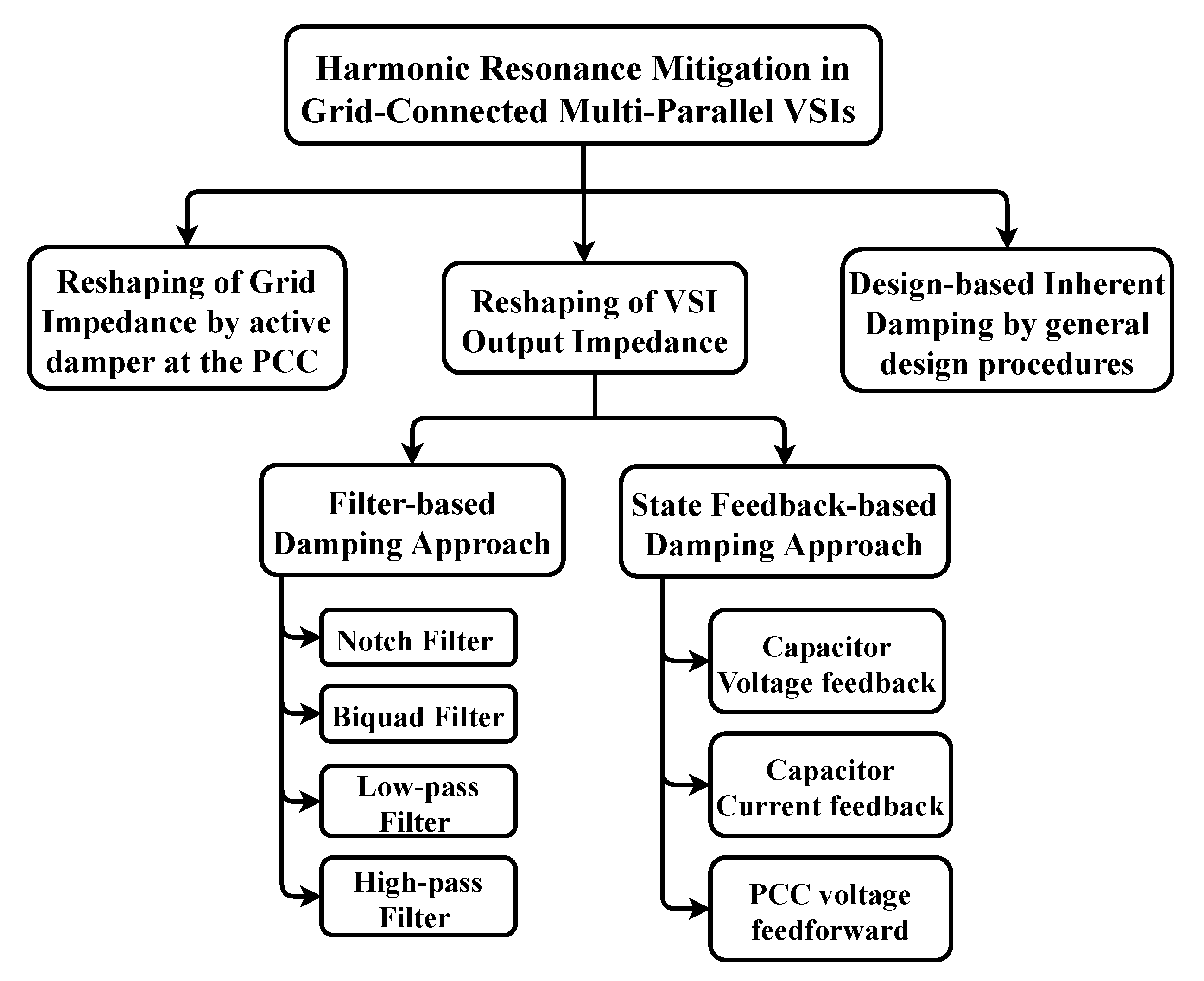
4. Suppression of Different Resonances in Multi–Parallel Grid–Connected Inverters
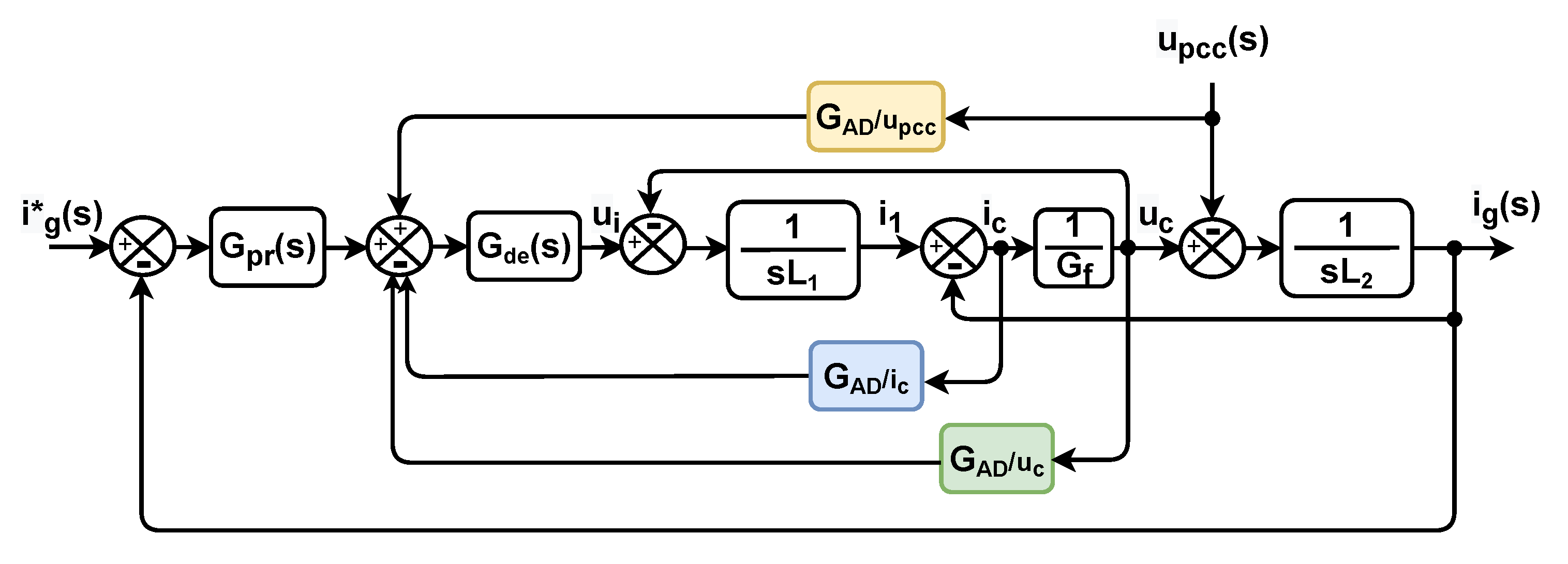
4.1. Reshaping of Inverter Output Impedance–Based Damping
4.1.1. State–Feedback–Based Damping Approach
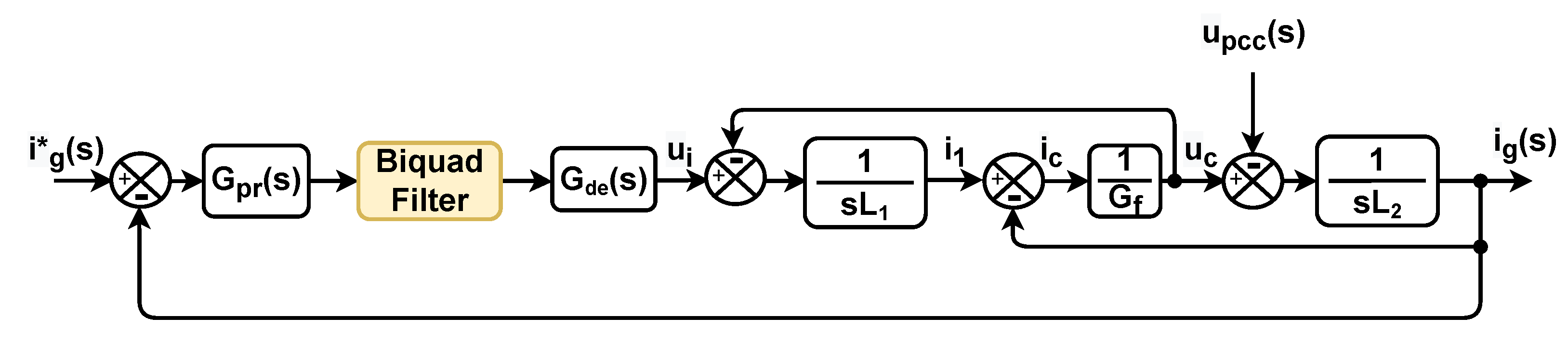
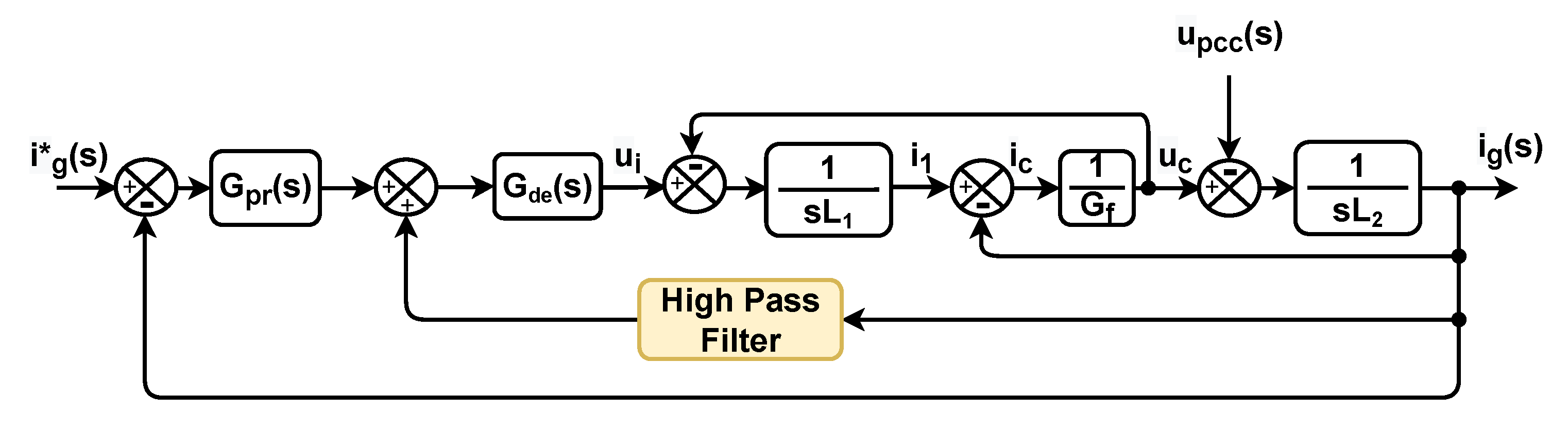
4.1.2. Filter–Based Damping Approach
4.2. Resonance Damping Based on the Reshaping of Grid Impedance
4.3. Design-Based Inherent Damping
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cook, J.; Oreskes, N.; Doran, P.T.; Anderegg, W.R.; Verheggen, B.; Maibach, E.W.; Carlton, J.S.; Lewandowsky, S.; Skuce, A.G.; Green, S.A.; et al. Consensus on consensus: A synthesis of consensus estimates on human-caused global warming. Environ. Res. Lett. 2016, 11, 048002. [Google Scholar] [CrossRef]
- United Nations Treaty Collection. Chapter XXBII. In 7.d Paris Agreement; United Nations Treaty Collection: New York, NY, USA, 2015; p. 12. [Google Scholar]
- Murdock, H.E.; Gibb, D.; Andre, T.; Sawin, J.L.; Brown, A.; Ranalder, L.; Collier, U.; Dent, C.; Epp, B.; Hareesh Kumar, C.; et al. Renewables 2021—Global Status Report. 2021. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2021_Full_Report.pdf (accessed on 22 July 2022).
- Blaabjerg, F.; Yang, Y.; Ma, K.; Wang, X. Power electronics-the key technology for renewable energy system integration. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 1618–1626. [Google Scholar]
- Agorreta, J.L.; Borrega, M.; López, J.; Marroyo, L. Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants. IEEE Trans. Power Electron. 2010, 26, 770–785. [Google Scholar] [CrossRef]
- Enslin, J.H.; Heskes, P.J. Harmonic interaction between a large number of distributed power inverters and the distribution network. IEEE Trans. Power Electron. 2004, 19, 1586–1593. [Google Scholar] [CrossRef]
- Li, C. Unstable operation of photovoltaic inverter from field experiences. IEEE Trans. Power Deliv. 2017, 33, 1013–1015. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, F.; Zou, R.; Li, Y. Harmonic Resonance Characteristic of Large-scale PV Plant: Modelling, Analysis and Engineering Case. IEEE Trans. Power Deliv. 2022, 37, 2359–2368. [Google Scholar] [CrossRef]
- Gomes, C.C.; Cupertino, A.F.; Pereira, H.A. Damping techniques for grid-connected voltage source converters based on LCL filter: An overview. Renew. Sustain. Energy Rev. 2018, 81, 116–135. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y.; He, Y.; Chung, H.S.H.; Liserre, M.; Blaabjerg, F. Damping methods for resonances caused by LCL-filter-based current-controlled grid-tied power inverters: An overview. IEEE Trans. Ind. Electron. 2017, 64, 7402–7413. [Google Scholar] [CrossRef]
- Beres, R.N.; Wang, X.; Liserre, M.; Blaabjerg, F.; Bak, C.L. A review of passive power filters for three-phase grid-connected voltage-source converters. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 4, 54–69. [Google Scholar] [CrossRef]
- Zhang, C.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Resonance damping techniques for grid-connected voltage source converters with LCL filters—A review. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Dubrovnik, Croatia, 13–16 May 2014; pp. 169–176. [Google Scholar]
- Han, Y.; Yang, M.; Li, H.; Yang, P.; Xu, L.; Coelho, E.A.A.; Guerrero, J.M. Modeling and stability analysis of LCL-type grid-connected inverters: A comprehensive overview. IEEE Access 2019, 7, 114975–115001. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Bosnjak, D.; Harris, B. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid. IEEE Trans. Power Electron. 2012, 28, 234–246. [Google Scholar] [CrossRef]
- Sun, J. Small-signal methods for AC distributed power systems—A review. IEEE Trans. Power Electron. 2009, 24, 2545–2554. [Google Scholar]
- Wang, Y.; Wang, X.; Chen, Z.; Blaabjerg, F. Small-signal stability analysis of inverter-fed power systems using component connection method. IEEE Trans. Smart Grid 2017, 9, 5301–5310. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Small-signal stability assessment of power electronics based power systems: A discussion of impedance-and eigenvalue-based methods. IEEE Trans. Ind. Appl. 2017, 53, 5014–5030. [Google Scholar] [CrossRef]
- Wang, F.; Duarte, J.L.; Hendrix, M.A.; Ribeiro, P.F. Modeling and analysis of grid harmonic distortion impact of aggregated DG inverters. IEEE Trans. Power Electron. 2010, 26, 786–797. [Google Scholar] [CrossRef]
- He, Y.; Wang, X.; Pan, D.; Ruan, X.; Su, G. An Ignored Culprit of Harmonic Oscillation in LCL-Type Grid-Connected Inverter: Resonant Pole Cancelation. IEEE Trans. Power Electron. 2021, 36, 14282–14294. [Google Scholar] [CrossRef]
- Chen, H.c.; Cheng, P.t.; Wang, X.; Blaabjerg, F. A passivity-based stability analysis of the active damping technique in the offshore wind farm applications. IEEE Trans. Ind. Appl. 2018, 54, 5074–5082. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Ali, R.; O’Donnell, T. Parameters Influencing Harmonic Stability for Single-phase Inverter in the Low Voltage Distribution Network. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Espoo, Finland, 18–21 October 2021; pp. 1–5. [Google Scholar]
- Yu, Y.; Li, H.; Li, Z.; Zhao, Z. Modeling and analysis of resonance in LCL-type grid-connected inverters under different control schemes. Energies 2017, 10, 104. [Google Scholar] [CrossRef]
- Sowa, I.; Domínguez-García, J.L.; Gomis-Bellmunt, O. Impedance-based analysis of harmonic resonances in HVDC connected offshore wind power plants. Electr. Power Syst. Res. 2019, 166, 61–72. [Google Scholar] [CrossRef]
- Jia, L.; Ruan, X.; Zhao, W.; Lin, Z.; Wang, X. An adaptive active damper for improving the stability of grid-connected inverters under weak grid. IEEE Trans. Power Electron. 2018, 33, 9561–9574. [Google Scholar] [CrossRef]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-admittance calculation and shaping for controlled voltage-source converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Loh, P.C. Passivity-based stability analysis and damping injection for multi–paralleled VSCs with LCL filters. IEEE Trans. Power Electron. 2017, 32, 8922–8935. [Google Scholar] [CrossRef]
- Hans, F.; Schumacher, W.; Chou, S.F.; Wang, X. Passivation of current-controlled grid-connected VSCs using passivity indices. IEEE Trans. Ind. Electron. 2018, 66, 8971–8980. [Google Scholar] [CrossRef]
- Harnefors, L.; Wang, X.; Yepes, A.G.; Blaabjerg, F. Passivity-based stability assessment of grid-connected VSCs—An overview. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 4, 116–125. [Google Scholar] [CrossRef]
- Han, Y.; Yang, M.; Yang, P.; Xu, L.; Blaabjerg, F. Passivity-based stability analysis of parallel single-phase inverters with hybrid reference frame control considering PLL effect. Int. J. Electr. Power Energy Syst. 2022, 135, 107473. [Google Scholar] [CrossRef]
- Ma, J.; Wang, X.; Blaabjerg, F.; Song, W.; Wang, S.; Liu, T. Multisampling method for single-phase grid-connected cascaded H-bridge inverters. IEEE Trans. Ind. Electron. 2019, 67, 8322–8334. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, P.; Yu, C.; Li, F.; Do, H.T.; Cao, R. Study of a current control strategy based on multisampling for high-power grid-connected inverters with an LCL filter. IEEE Trans. Power Electron. 2016, 32, 5023–5034. [Google Scholar] [CrossRef]
- Roy, T.K.; Mahmud, M.A.; Islam, S.; Oo, A.M. Power quality improvements in single-phase grid-connected photovoltaic systems using a nonlinear adaptive controller. In Proceedings of the 2018 Australasian Universities Power Engineering Conference (AUPEC), Auckland, New Zealand, 27–30 November 2018; pp. 1–6. [Google Scholar]
- Gui, Y.; Wang, X.; Wu, H.; Blaabjerg, F. Voltage-modulated direct power control for a weak grid-connected voltage source inverters. IEEE Trans. Power Electron. 2019, 34, 11383–11395. [Google Scholar] [CrossRef]
- Sun, J.; Wang, G.; Du, X.; Wang, H. A theory for harmonics created by resonance in converter-grid systems. IEEE Trans. Power Electron. 2018, 34, 3025–3029. [Google Scholar] [CrossRef]
- Lu, M.; Wang, X.; Blaabjerg, F.; Loh, P.C. An analysis method for harmonic resonance and stability of multi-paralleled LCL-filtered inverters. In Proceedings of the 2015 IEEE 6th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Aachen, Germany, 22–25 June 2015; pp. 1–6. [Google Scholar]
- Lu, M.; Wang, X.; Loh, P.C.; Blaabjerg, F. Resonance interaction of multiparallel grid-connected inverters with LCL filter. IEEE Trans. Power Electron. 2016, 32, 894–899. [Google Scholar] [CrossRef]
- Tan, S.; Yang, G.; Geng, H.; Ma, S.; Wu, W. A resonance suppression method for a multiple grid-connected-converter system with LCL filter. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014; pp. 1104–1109. [Google Scholar]
- Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. A new single-phase PLL structure based on second order generalized integrator. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–6. [Google Scholar]
- Yang, Z.; Shah, C.; Chen, T.; Yu, L.; Joebges, P.; De Doncker, R.W. Stability investigation of three-phase grid-tied pv inverter systems using impedance models. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2672–2684. [Google Scholar] [CrossRef]
- Teodorescu, R.; Blaabjerg, F.; Liserre, M.; Loh, P.C. Proportional-resonant controllers and filters for grid-connected voltage-source converters. IEE Proc.-Electr. Power Appl. 2006, 153, 750–762. [Google Scholar] [CrossRef]
- Zhou, S.; Zou, X.; Zhu, D.; Tong, L.; Zhao, Y.; Kang, Y.; Yuan, X. An improved design of current controller for LCL-type grid-connected converter to reduce negative effect of PLL in weak grid. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 648–663. [Google Scholar] [CrossRef]
- Khajeh, K.G.; Solatialkaran, D.; Zare, F.; Mithulananthan, N. Harmonic analysis of multi-parallel grid-connected inverters in distribution networks: Emission and immunity issues in the frequency range of 0–150 kHz. IEEE Access 2020, 8, 56379–56402. [Google Scholar] [CrossRef]
- Barsali, S. Benchmark Systems for Network Integration of Renewable and Distributed Energy Resources; International Council on Large Electric Systems: Paris, France, 2014. [Google Scholar]
- Wang, X.; Blaabjerg, F.; Liserre, M.; Chen, Z.; He, J.; Li, Y. An active damper for stabilizing power-electronics-based AC systems. IEEE Trans. Power Electron. 2013, 29, 3318–3329. [Google Scholar] [CrossRef]
- Qian, Q.; Xie, S.; Huang, L.; Xu, J.; Zhang, Z.; Zhang, B. Harmonic suppression and stability enhancement for parallel multiple grid-connected inverters based on passive inverter output impedance. IEEE Trans. Ind. Electron. 2017, 64, 7587–7598. [Google Scholar] [CrossRef]
- Bai, H.; Wang, X.; Blaabjerg, F. Passivity enhancement in renewable energy source based power plant with paralleled grid-connected VSIs. IEEE Trans. Ind. Appl. 2017, 53, 3793–3802. [Google Scholar] [CrossRef]
- Guo, Y.; Lu, X.; Chen, L.; Zheng, T.; Wang, J.; Mei, S. Functional-rotation-based active dampers in AC microgrids with multiple parallel interface inverters. IEEE Trans. Ind. Appl. 2018, 54, 5206–5215. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, L.; Lu, X.; Wang, J.; Zheng, T.; Mei, S. Region Based Stability Analysis of Active Dampers in AC Microgrids with Multiple Parallel Interface Inverters. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1098–1101. [Google Scholar]
- Yamashita, K.; Villanueva, S.M.; Cutsem, T.V.; Martins, J.C.; Song, Z.; Zhu, L.; Renner, H.; Aristidou, P.; Green, I.; Lammert, G.; et al. Modelling of Inverter-Based Generation for Power System Dynamic Studies; CIGRE: Paris, France, 2018. [Google Scholar]
- Qiu, Q.; Huang, Y.; Ma, R.; Kurths, J.; Zhan, M. Black-Box Impedance Prediction of Grid-Tied VSCs Under Variable Operating Conditions. IEEE Access 2021, 10, 1289–1304. [Google Scholar] [CrossRef]
- Cifuentes, N.; Sun, M.; Gupta, R.; Pal, B.C. Black-Box Impedance-Based Stability Assessment of Dynamic Interactions Between Converters and Grid. IEEE Trans. Power Syst. 2021, 37, 2976–2987. [Google Scholar] [CrossRef]
- De Meerendre, M.K.; Prieto-Araujo, E.; Ahmed, K.H.; Gomis-Bellmunt, O.; Xu, L.; Egea-Àlvarez, A. Review of local network impedance estimation techniques. IEEE Access 2020, 8, 213647–213661. [Google Scholar] [CrossRef]
- Ahmed, S.; Shen, Z.; Mattavelli, P.; Boroyevich, D.; Karimi, K.J. Small-signal model of voltage source inverter (VSI) and voltage source converter (VSC) considering the deadtime effect and space vector modulation types. IEEE Trans. Power Electron. 2016, 32, 4145–4156. [Google Scholar] [CrossRef]
- Shi, H.; Zhuo, F.; Zhang, D.; Geng, Z.; Wang, F. Modeling, analysis, and measurement of impedance for three-phase AC distributed power system. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 4635–4639. [Google Scholar]
- Capponi, L.; Fernández, I.; Roggo, D.; Arrinda, A.; Angulo, I.; De La Vega, D. Comparison of measurement methods of grid impedance for narrow band-PLC up to 500 kHz. In Proceedings of the 2018 IEEE 9th International Workshop on Applied Measurements for Power Systems (AMPS), Bologna, Italy, 26–28 September 2018; pp. 1–6. [Google Scholar]
- Rhode, J.P.; Kelley, A.W.; Baran, M.E. Complete characterization of utilization-voltage power system impedance using wideband measurement. IEEE Trans. Ind. Appl. 1997, 33, 1472–1479. [Google Scholar] [CrossRef]
- Shah, S.; Koralewicz, P.; Gevorgian, V.; Liu, H.; Fu, J. Impedance methods for analyzing stability impacts of inverter-based resources: Stability analysis tools for modern power systems. IEEE Electrif. Mag. 2021, 9, 53–65. [Google Scholar] [CrossRef]
- Xueguang, Z.; Li, W.; Xiao, Y.; Wang, G.; Xu, D. Analysis and suppression of circulating current caused by carrier phase difference in parallel voltage source inverters with SVPWM. IEEE Trans. Power Electron. 2018, 33, 11007–11020. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. Impedance shaping of the grid-connected inverter with LCL filter to improve its adaptability to the weak grid condition. IEEE Trans. Power Electron. 2014, 29, 5795–5805. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Y.; Wang, S.; Chen, J.; Gong, C. Impedance-phased dynamic control method for grid-connected inverters in a weak grid. IEEE Trans. Power Electron. 2016, 32, 274–283. [Google Scholar] [CrossRef]
- Chen, T.; Lee, C.K.; Hui, S.R. A general design procedure for multi-parallel modular grid-tied inverters system to prevent common and interactive instability. IEEE Trans. Power Electron. 2019, 34, 6025–6030. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Y.; Guerrero, J.M.; Kuang, H.; Huang, Y.; Zhou, L.; Luo, A. Generalized coupling resonance modeling, analysis, and active damping of multi-parallel inverters in microgrid operating in grid-connected mode. J. Mod. Power Syst. Clean Energy 2016, 4, 63–75. [Google Scholar] [CrossRef]
- Chen, Z.; Luo, A.; Chen, Y.; Li, M. Resonance features of multi-paralleled grid-connected inverters and its damping method. In Proceedings of the 2014 International Power Electronics and Application Conference and Exposition, Shanghai, China, 5–8 November 2014; pp. 120–125. [Google Scholar]
- Tan, S.; Geng, H.; Yang, G. Impedance matching based control for the resonance damping of microgrids with multiple grid connected converters. J. Power Electron. 2016, 16, 2338–2349. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Wang, H.; Luo, A.; Huai, K. Oscillation suppression method by two notch filters for parallel inverters under weak grid conditions. Energies 2018, 11, 3441. [Google Scholar] [CrossRef]
- Gharanikhajeh, K.; Solatialkaran, D.; Zare, F.; Faradjizadeh, F.; Yaghoobi, J.; Nadarajah, M. A Harmonic Mitigation Technique for Multi-Parallel Grid-Connected Inverters in Distribution Networks. IEEE Trans. Power Deliv. 2022, 37, 2843–2856. [Google Scholar]
- Khajeh, K.G.; Farajizadeh, F.; Solatialkaran, D.; Zare, F.; Yaghoobi, J.; Nadarajah, M. A Full-Feedforward Technique to Mitigate the Grid Distortion Effect on Parallel Grid-Tied Inverters. IEEE Trans. Power Electron. 2022, 37, 8404–8419. [Google Scholar] [CrossRef]
- Yang, Q.X.; Li, K.; Zhao, C.M.; Wang, H. The resonance suppression for parallel photovoltaic grid-connected inverters in weak grid. Int. J. Autom. Comput. 2018, 15, 716–727. [Google Scholar] [CrossRef]
- Tao, H.; Zhou, Y.; Zhang, G.; Zheng, Z. Parallel Resonance Mechanism Analysis and Suppression of Inductance-Capacitance-Inductance Grid-Connected Inverters. Energies 2019, 12, 1656. [Google Scholar] [CrossRef]
- Lu, X.; Sun, K.; Huang, L.; Liserre, M.; Blaabjerg, F. An active damping method based on biquad digital filter for parallel grid-interfacing inverters with LCL filters. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC 2014, Fort Worth, TX, USA, 16–20 March 2014; pp. 392–397. [Google Scholar]
- Pena-Alzola, R.; Roldán-Pérez, J.; Bueno, E.; Huerta, F.; Campos-Gaona, D.; Liserre, M.; Burt, G. Robust active damping in LCL-filter-based medium-voltage parallel grid inverters for wind turbines. IEEE Trans. Power Electron. 2018, 33, 10846–10857. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Luo, A.; Huai, K. Stability enhancement for parallel grid-connected inverters by improved notch filter. IEEE Access 2019, 7, 65667–65678. [Google Scholar] [CrossRef]
- Samanes, J.; Gubía, E. Sensorless active damping strategy for parallel interleaved voltage source power converters with LCL filter. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 3632–3639. [Google Scholar]
- Qian, Q.; Zhang, B.; Ni, Z.; Xie, S.; Xu, J.; Xu, K. Circulating resonant current suppression for current-controlled inverters based on output impedance shaping. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 4794–4798. [Google Scholar]
- Liang, J.; Jiang, J.; Ojo, O.; Haruna, J. Damping for Multi-Paralleled Grid Tied Inverters with LCL Filters. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 5879–5886. [Google Scholar]
- Zheng, F.; Lin, X.; Zhang, Y.; Deng, C. Design of a novel hybrid control strategy for multi-inverter parallel system for resonance suppression. Energy Sci. Eng. 2020, 8, 2878–2893. [Google Scholar] [CrossRef]
- Li, D.; Chen, M.; Yang, W.; Lin, X. A Novel Hybrid Control Algorithm for Suppressing the Resonance of Multiple Inverters in Parallel. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I& CPS Asia), Weihai, China, 13–16 July 2020; pp. 1186–1191. [Google Scholar]
- Awal, M.; Yu, W.; Husain, I. Passivity-based predictive-resonant current control for resonance damping in LCL-equipped VSCs. IEEE Trans. Ind. Appl. 2019, 56, 1702–1713. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, S. A novel inverter-side current control method of LCL-filtered inverters based on high-pass-filtered capacitor voltage feedforward. IEEE Access 2020, 8, 16528–16538. [Google Scholar] [CrossRef]
- Wang, X.; Pang, Y.; Loh, P.C.; Blaabjerg, F. A series-LC-filtered active damper with grid disturbance rejection for AC power-electronics-based power systems. IEEE Trans. Power Electron. 2014, 30, 4037–4041. [Google Scholar] [CrossRef]
- Zheng, C.; Zhou, L.; Xie, B.; Zhang, Q.; Li, H. A stabilizer for suppressing harmonic resonance in multi-parallel inverter system. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017; pp. 1–6. [Google Scholar]
- Wan, Q.; Zhang, H. Research on resonance mechanism and suppression technology of photovoltaic cluster inverter. Energies 2018, 11, 938. [Google Scholar] [CrossRef]
- Peng, Y.; He, Y.; Hang, L. Active Compensator for Multi-Paralleled Grid-Tied Inverters under variable Grid Conditions. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 2629–2636. [Google Scholar]
- Sun, J.j.; Hu, W.; Zhou, H.; Jiang, Y.M.; Zha, X.M. A resonant characteristics analysis and suppression strategy for multiple parallel grid-connected inverters with LCL filter. J. Power Electron. 2016, 16, 1483–1493. [Google Scholar] [CrossRef][Green Version]
- Yuan, C.; Shi, D.; Hu, Q.; Liao, Y.; Yu, J.; Zhou, P. Active Damping Resonance Suppression and Optimization of Photovoltaic Cluster Grid Connected System. J. Electr. Eng. Technol. 2021, 16, 2509–2521. [Google Scholar] [CrossRef]



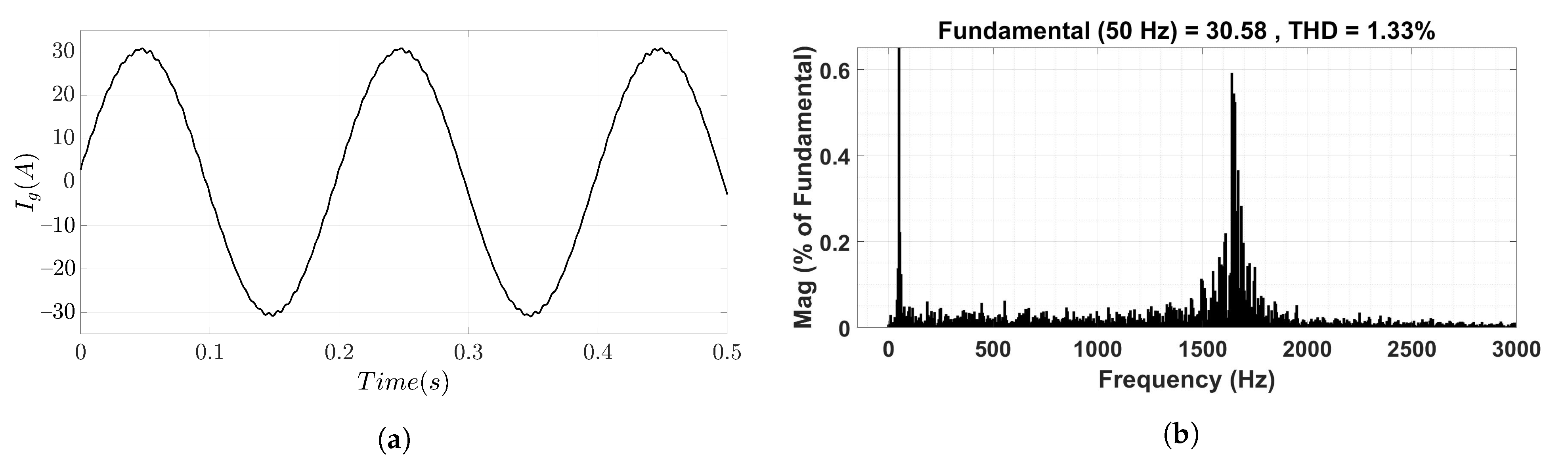
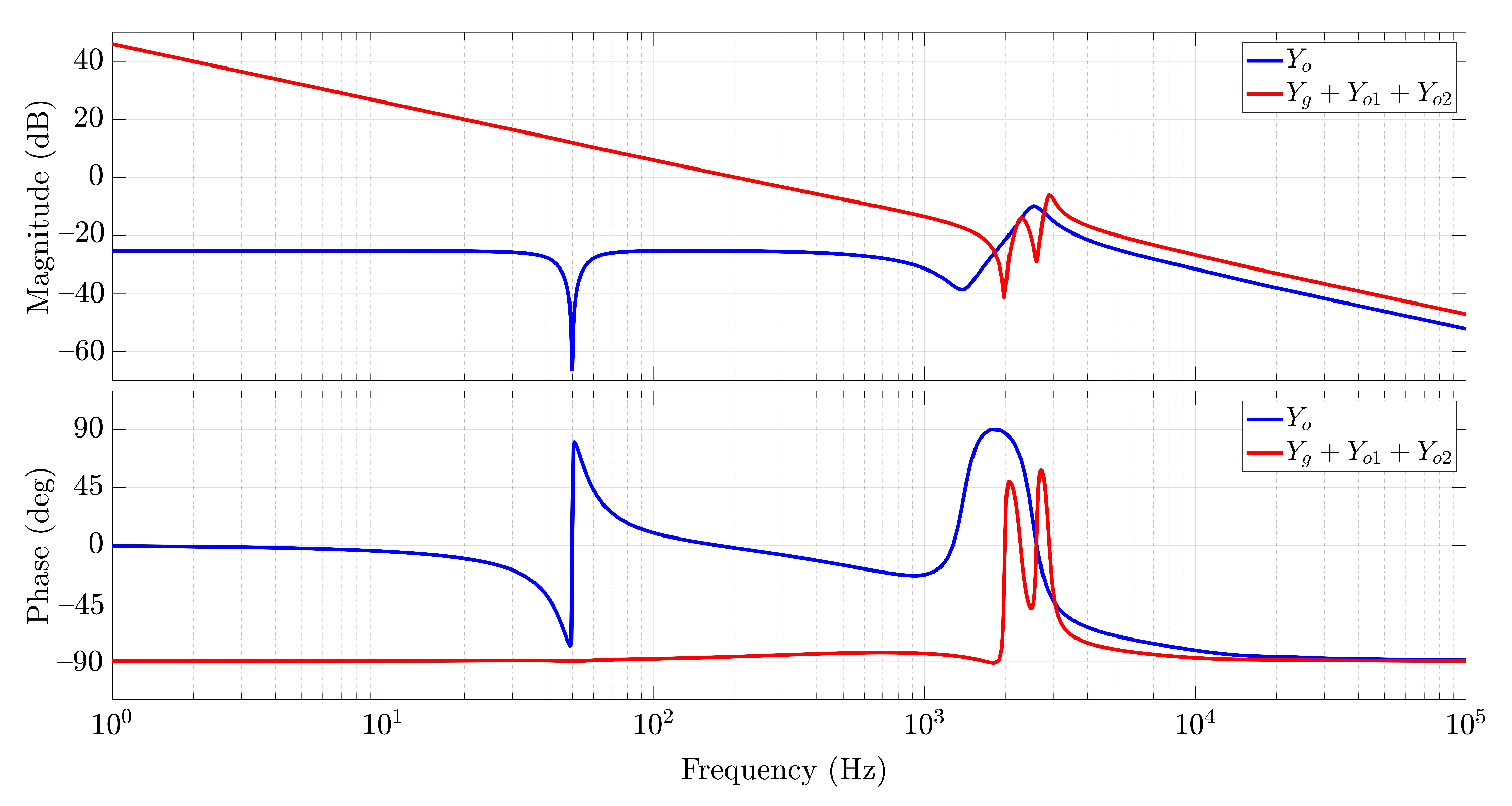
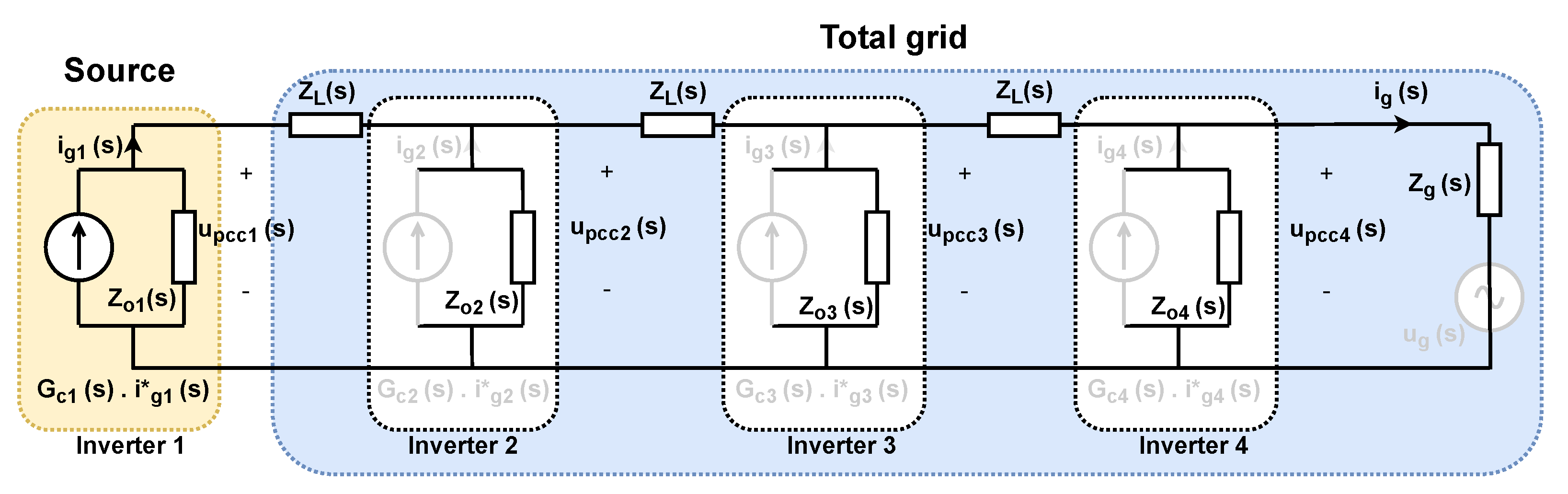
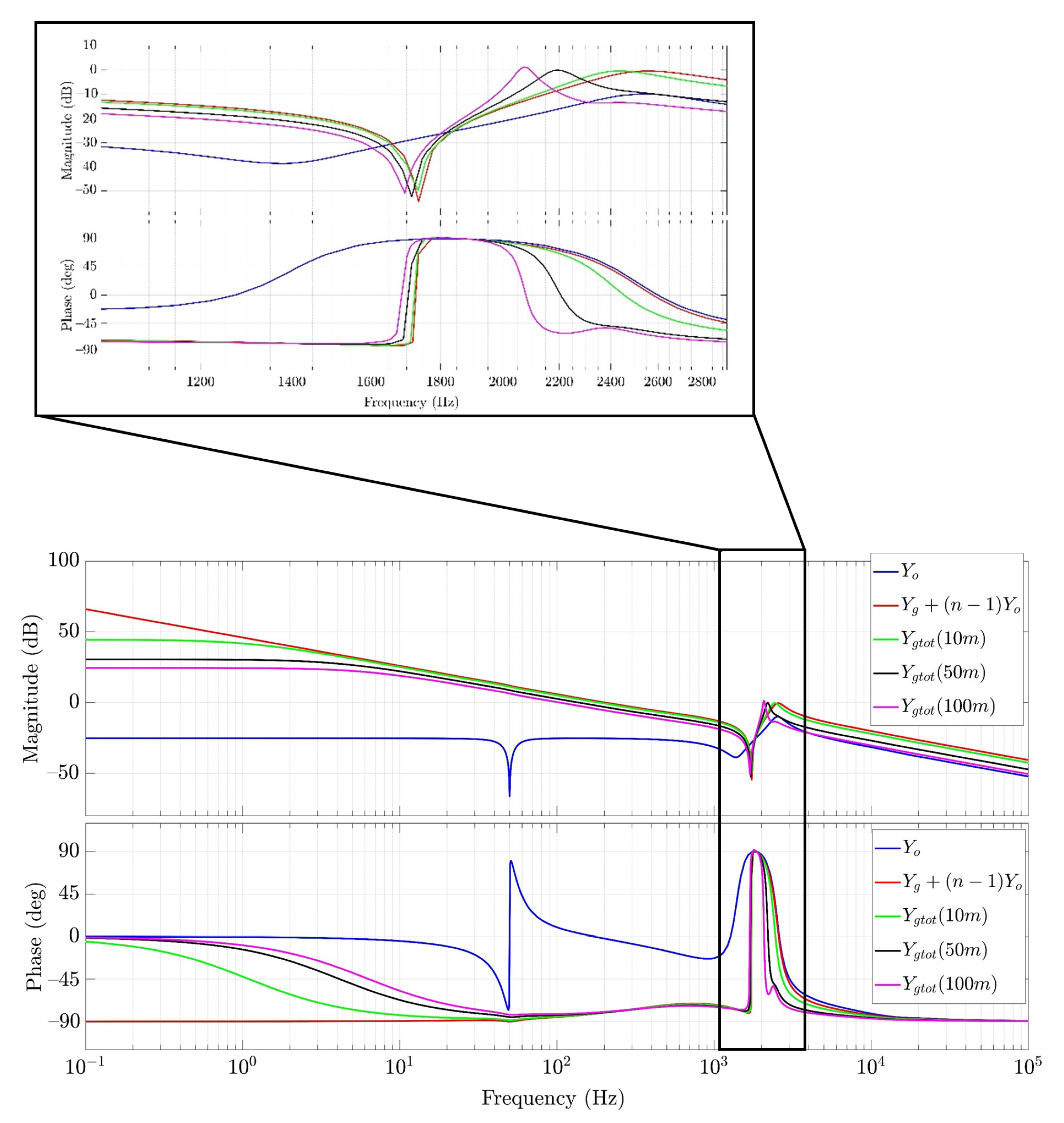
| Parameter | Symbol | Value |
|---|---|---|
| Rated Power | 5 kW | |
| DC link Voltage | 400 V | |
| Grid voltage | 230 V | |
| Grid frequency | 50 Hz | |
| Switching frequency | 10 kHz | |
| Sampling frequency | 20 kHz | |
| Inverter–side Inductor | 2.6 mH | |
| Grid–side Inductor | 0.65 mH | |
| Filter Capacitor | 5 µf | |
| Damping resistor | 4.8 | |
| PR controller gains | , | 18.35, 2017, 0.5 |
| Grid impedance | 0.8 mH |
| Damping Strategy | Concept | Approach | Pros | Cons |
|---|---|---|---|---|
| Reshaping the inverter output impedance | State variable feedback–based damping (Virtual impedance–based damping) [49,63,64,65,66,67,68] |
|
|
|
| Filter–based damping [70,71,72,74,75] |
|
|
| |
| Reshaping the grid impedance | Active damper [45,81,82,83,84] | Adding an additional converter at the PCC |
|
|
| Inherent damping–based system [47,62] | General design procedure for multi–parallel inverter systems | Developing the control and filter parameters methodically |
| Valid only for a resistive–inductive grid impedance |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, R.; O’Donnell, T. Analysis and Mitigation of Harmonic Resonances in Multi–Parallel Grid–Connected Inverters: A Review. Energies 2022, 15, 5438. https://doi.org/10.3390/en15155438
Ali R, O’Donnell T. Analysis and Mitigation of Harmonic Resonances in Multi–Parallel Grid–Connected Inverters: A Review. Energies. 2022; 15(15):5438. https://doi.org/10.3390/en15155438
Chicago/Turabian StyleAli, Ramy, and Terence O’Donnell. 2022. "Analysis and Mitigation of Harmonic Resonances in Multi–Parallel Grid–Connected Inverters: A Review" Energies 15, no. 15: 5438. https://doi.org/10.3390/en15155438
APA StyleAli, R., & O’Donnell, T. (2022). Analysis and Mitigation of Harmonic Resonances in Multi–Parallel Grid–Connected Inverters: A Review. Energies, 15(15), 5438. https://doi.org/10.3390/en15155438






