Real-Time Locational Detection of Stealthy False Data Injection Attack in Smart Grid: Using Multivariate-Based Multi-Label Classification Approach
Abstract
:1. Introduction
- Using the multivariate-based LSTM-TCN increased the performance of the architecture and can better distinguish the FDIA multi-label classes. Furthermore, the proposed model is very fast, stable, and efficient in terms of training and testing time.
- The suggested approach is universal, i.e., it is not dependent on the statistical assumption of the attack model.
- Our design is robust and scalable since it can adapt to detect slight and high -norms of FDIAs and varying topology models.
- Extensive investigations are conducted to evaluate and verify the proposed architecture. A parameter sensitivity test is also carried out to assess the suggested frameworks’ performance and applicability capabilities. Extensive results in the IEEE 118-bus system reveal that the proposed architecture achieves a locational detection accuracy of 98.6% and a presence detection accuracy of 99.8%, on average using only two layers of the FCN and one layer of LSTM. We can conclude that the proposed framework is a scalable, robust, accurate technique and outperforms the state-of-the-art benchmarks [20,21].
2. Related Work
3. Preliminaries
3.1. Power System Model
3.2. False Data Injection Attack (FDIA)
- Stealthy FDIAs: They are structured attacks that are not detected by typical methods of bad data detection.
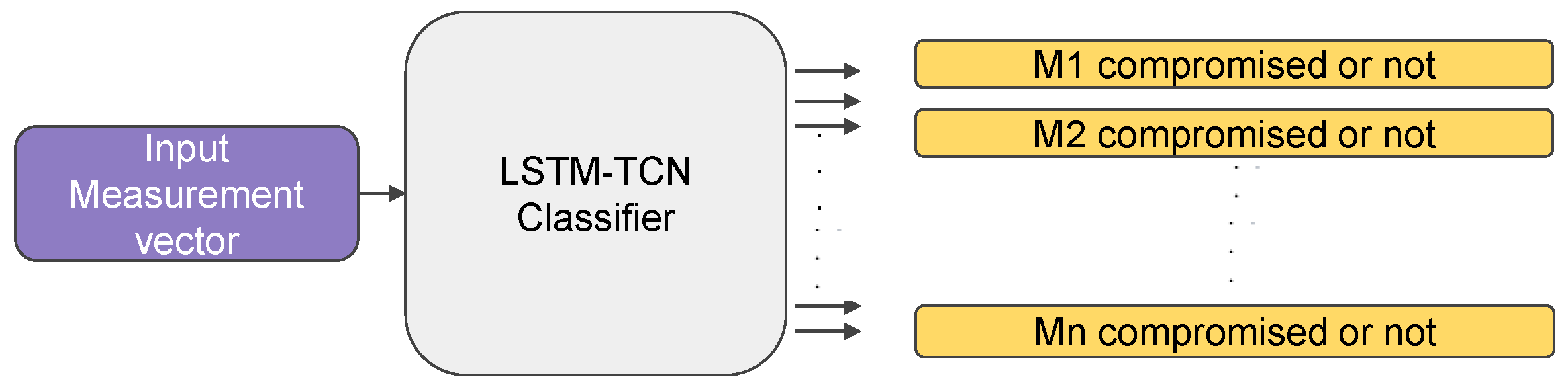
4. FDIA Location-Based Detection Scheme as a Multivariate Multi-Label Classification Approach
4.1. Detection of FDIA Location
4.2. FDIA Proposed Detection Mechanism
4.2.1. Input
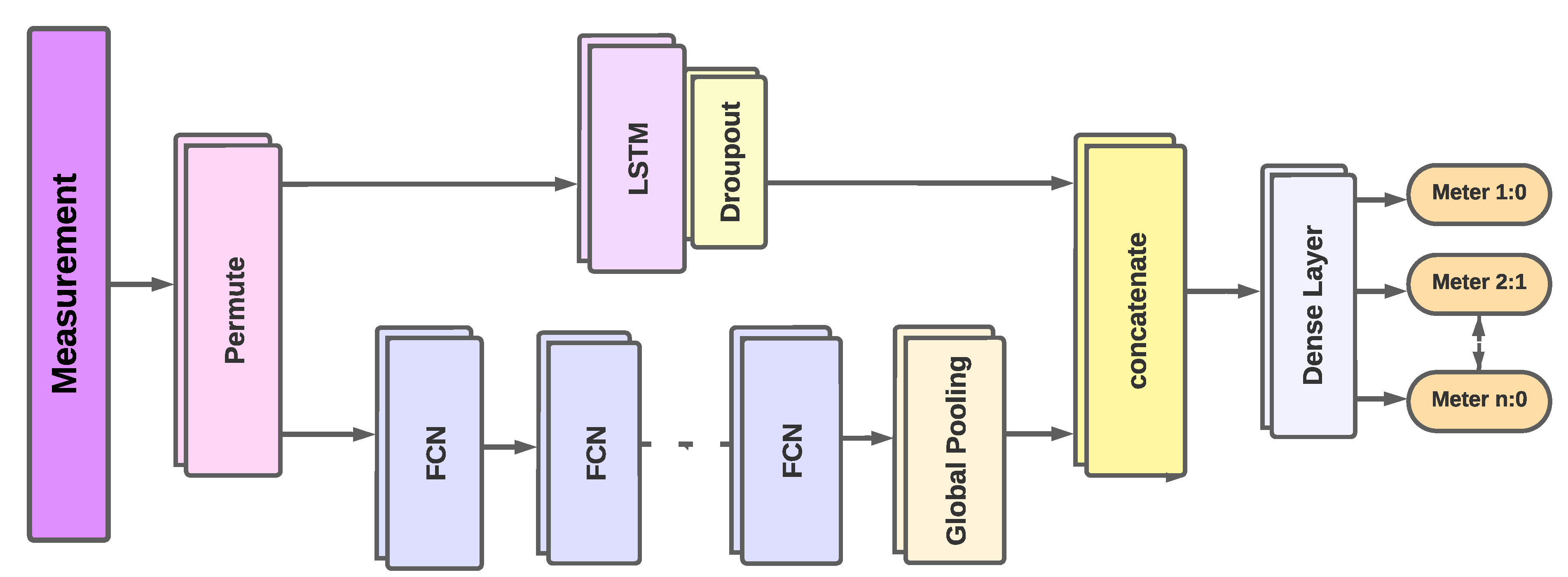
4.2.2. Proposed Architecture
Fully Convolutions Blocks
LSTM RNNs Block
LSTM Concatenated with FCNs Block
Fully Connected Layer
Dimension Shuffle
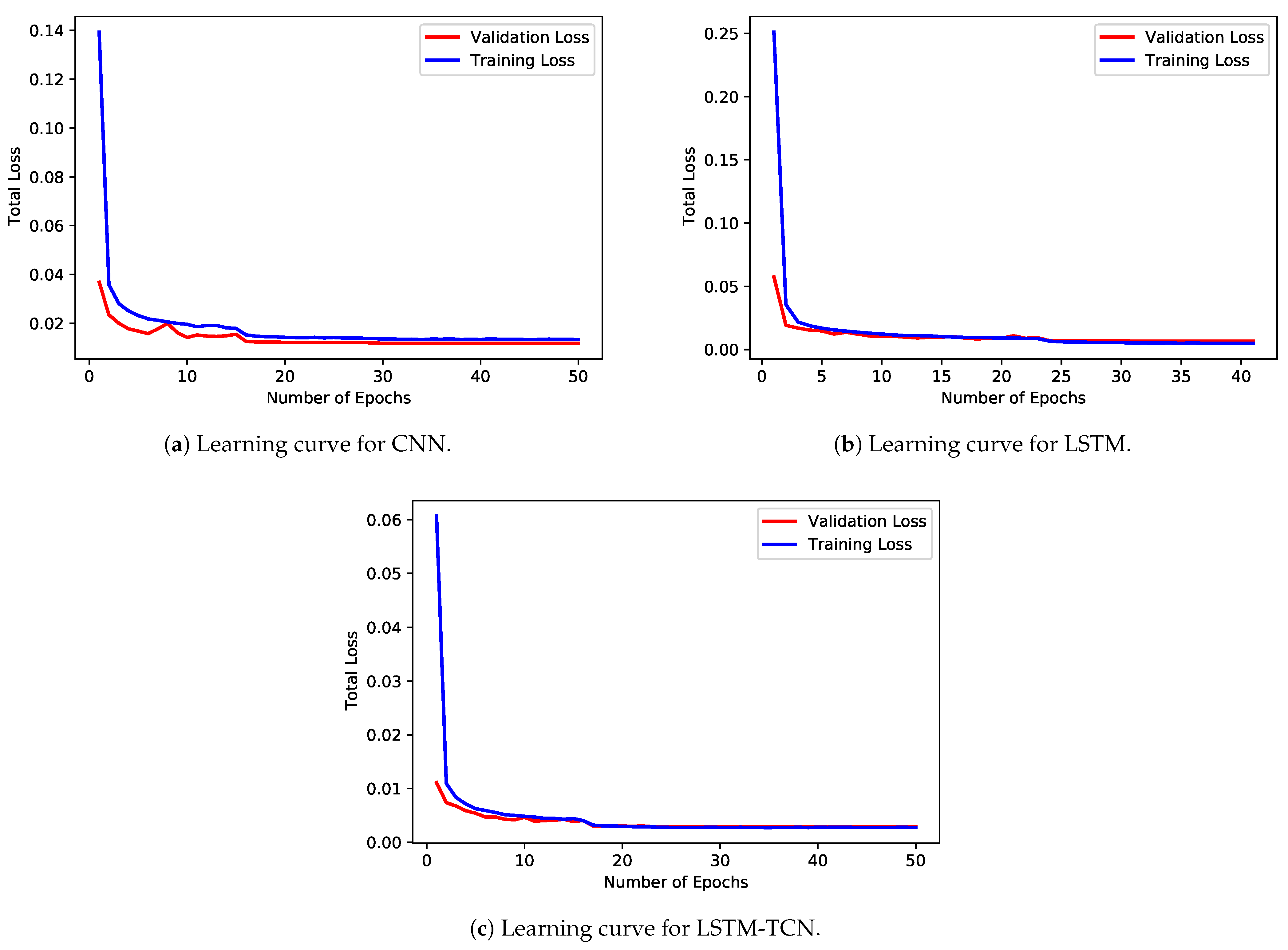
4.3. Training Procedure
4.3.1. Mini-Batch, Cross-Validation, and Early Stopping Technique
4.3.2. Loss Function
5. Experimental Results
5.1. Dataset Generation
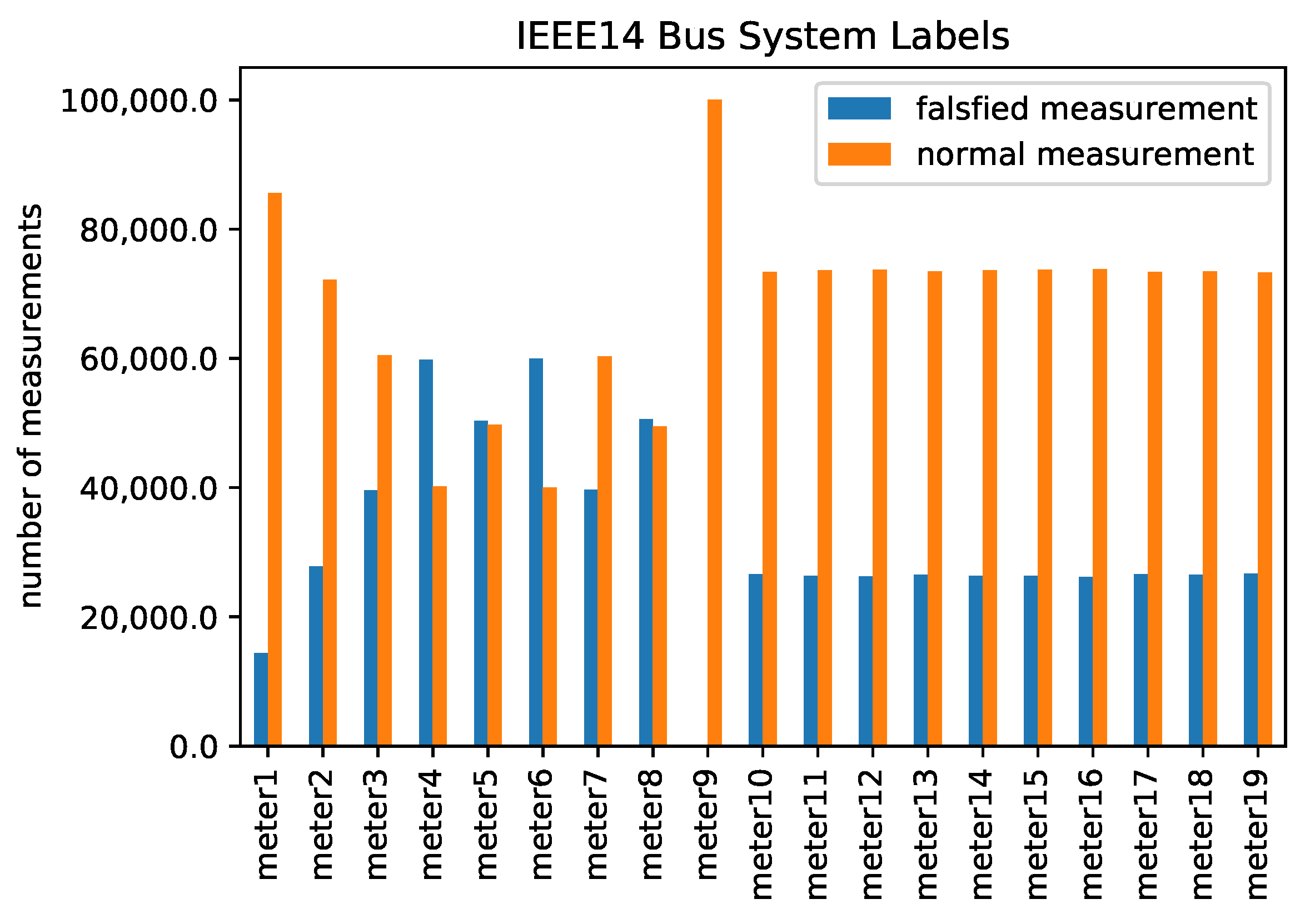
- IEEE14-bus system:
- –
- Number of transmission lines and buses are 20 lines and 14 buses, respectively.
- –
- Number of total meter measurements are 19, of which 11 are flow measurements and 9 are injected measurements.
- IEEE118-bus system:
- –
- Number of transmission lines and buses are 186 lines and 118 buses, respectively.
- –
- Number of total meter measurements are 180, of which 110 are flow measurements and 70 are injected measurements.
- Meter measurements are indexed based on the network topology. first, the line flow meters are indexed from as follows:
- The unindexed meters connecting bus k are indexed and set as ;
- If k > 14 (118), the indexing process is terminated; otherwise, the policy returns back to first step. Then, the index is continued from line meters, and the injection meters are labeled based on ascending order of the bus index. An indexed measurement placement of the IEEE 14-bus system is depicted in [20];
- Ten thousand sets of loads are randomly chosen to implement the FDIA:
- For each attack, a set of target state variables to compromise is randomly selected. In the 14-bus power system, the target state variables have a discrete uniform (2, 5) distribution, whereas the 118-bus power system has a discrete uniform (2, 10) distribution.
- Transmission line impedance is set according to [18], and the -norm of the injected data (expected value of the Euclidean norm of the attack vector) varies from 1 to 5. A noise standard deviation of 0.2 was added in both compromised and uncompromised data.
- For each set of load and its particular target state variables, a stealthy FDIA is generated according to the min-cut algorithm in [18].
- Finally, to take into consideration the noise in measurement, a random Gaussian noise with a standard deviation of 0.2 was added in both compromised and uncompromised data.
- After the training data are generated, the above process is repeated 10 times to generate 10 independent sets of testing data, which naturally introduces validation variations.
Training and Testing Datasets
- For training, input measurements and training labels are generated with a dimension of 110,000 × B. The training data are composed of samples with no attack vector and 10,000 instances under attack.
- For testing, a testing set is generated with a dimension of 10,000 × B for measurements and labels. Input measurements are composed of 5000 uncompromised samples and 5000 compromised samples [18]. Over all of the test datasets, the results of all trials have been averaged.
5.2. Evaluation Metrics
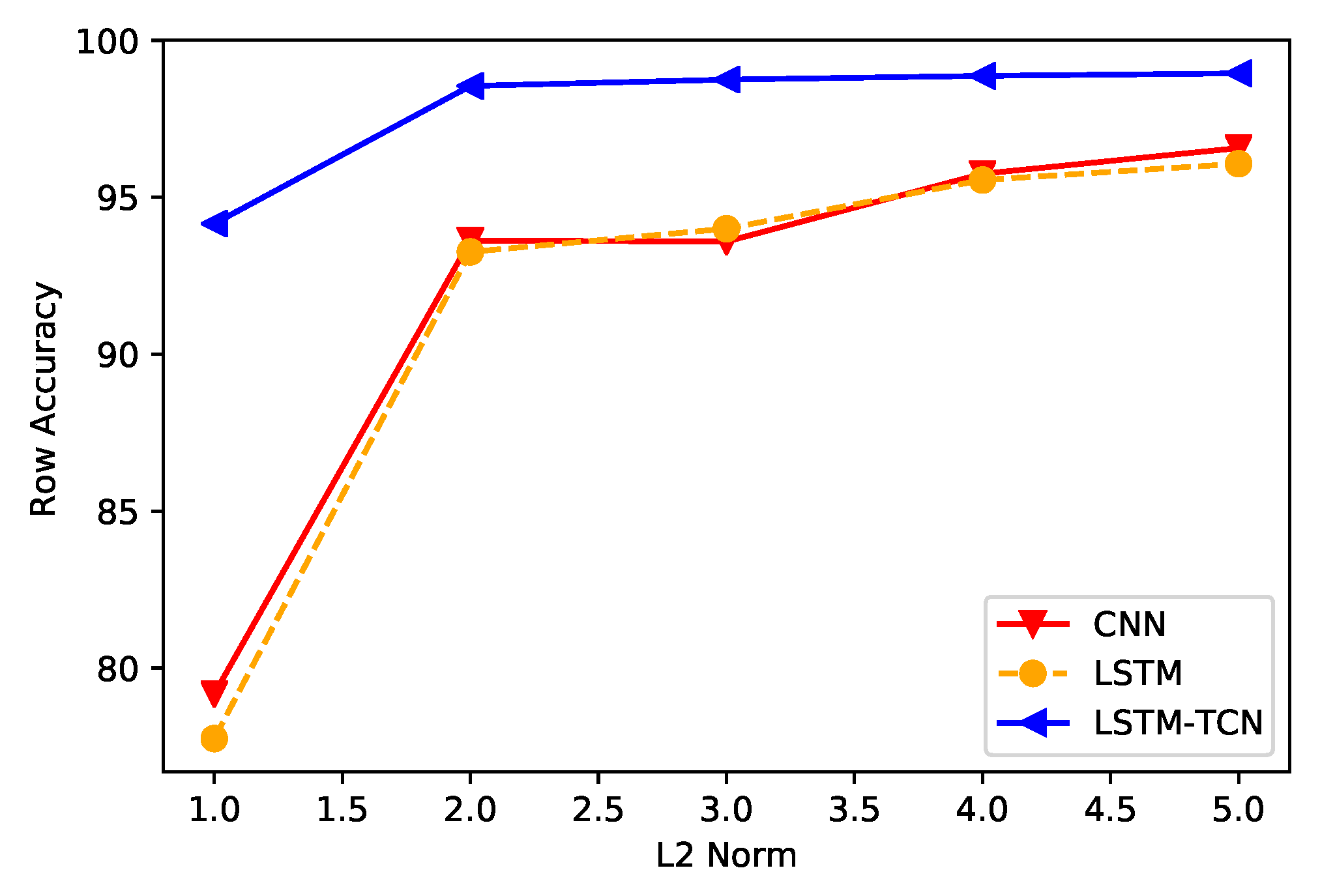
5.2.1. IEEE 14-Bus System
- The first measurement is compromised and the third is not;
- The third measurement is compromised and the first is not;
- Both the first and third measurements are compromised;
- Neither the first nor third measurements are compromised;
- The first measurement is compromised and the fifteenth is not;
- The fifteenth measurement is compromised and the first is not;
- Both the first and fifteenth measurements are compromised;
- Neither the first nor the fifteenth measurements are compromised.
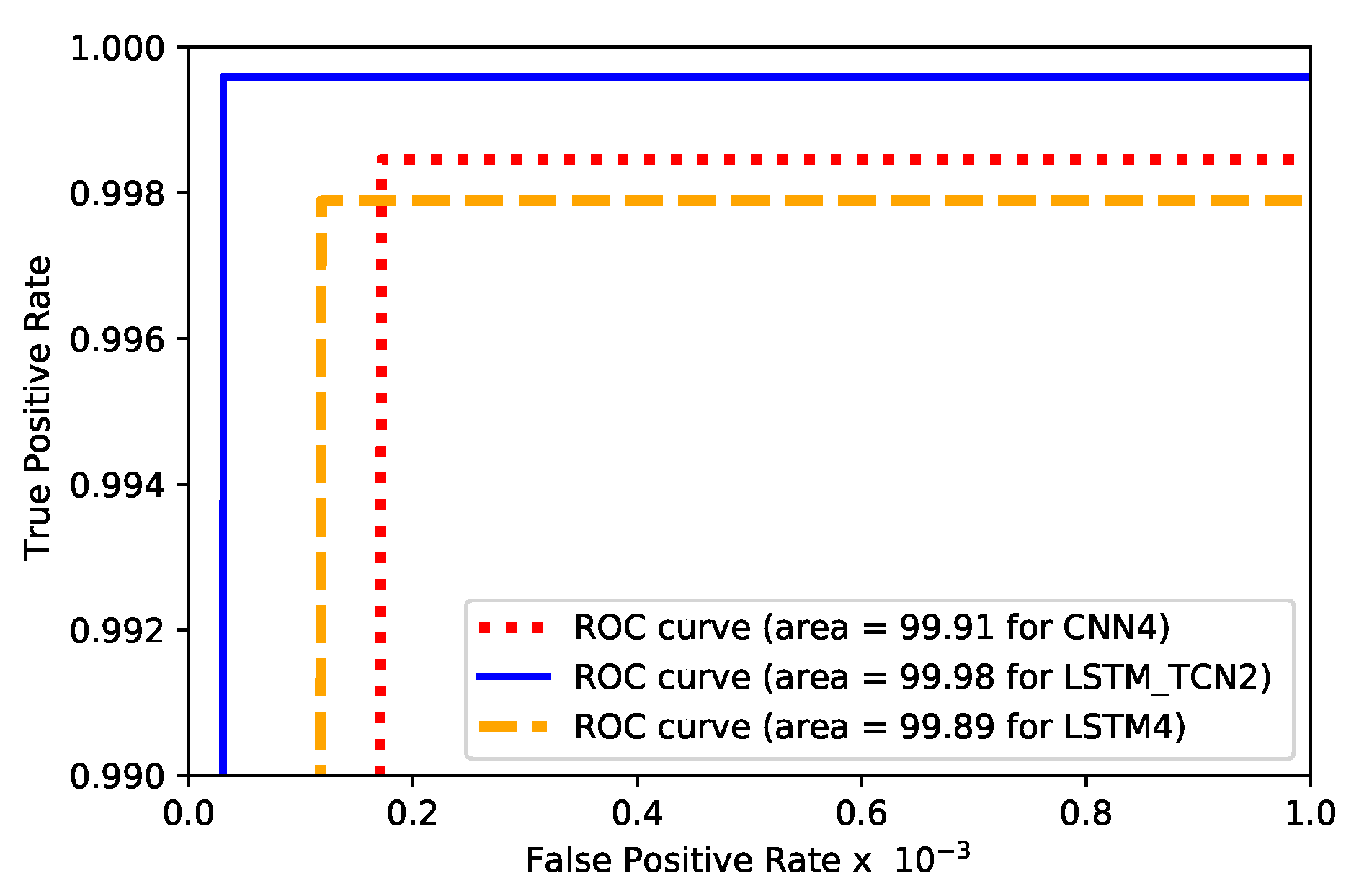
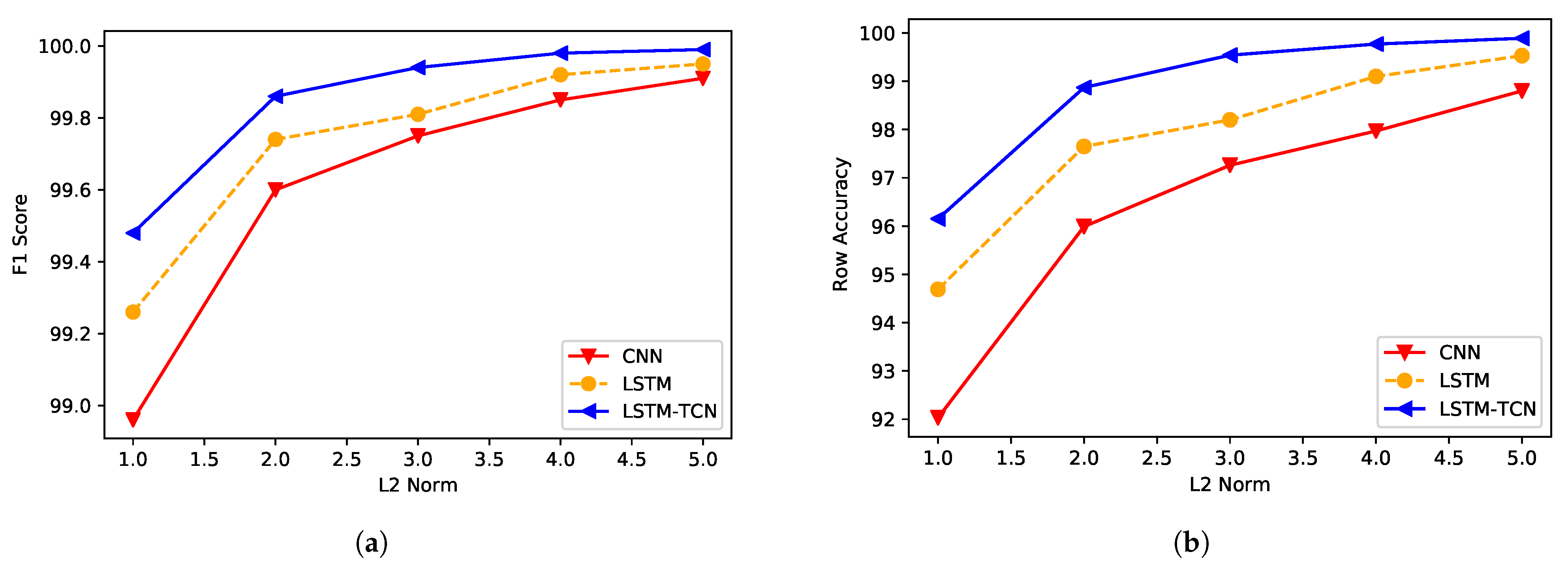
5.2.2. IEEE 118-Bus System
5.2.3. Robustness
5.2.4. Scalability
5.2.5. Model Complexity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fadlullah, Z.M.; Fouda, M.M.; Kato, N.; Takeuchi, A.; Iwasaki, N.; Nozaki, Y. Toward intelligent machine-to-machine communications in smart grid. IEEE Commun. Mag. 2011, 49, 60–65. [Google Scholar] [CrossRef]
- Fouda, M.M.; Fadlullah, Z.M.; Kato, N.; Lu, R.; Shen, X.S. A Lightweight Message Authentication Scheme for Smart Grid Communications. IEEE Trans. Smart Grid 2011, 2, 675–685. [Google Scholar] [CrossRef] [Green Version]
- Fadlullah, Z.M.; Fouda, M.M.; Kato, N.; Shen, X.; Nozaki, Y. An early warning system against malicious activities for smart grid communications. IEEE Netw. 2011, 25, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Fouda, M.M.; Fadlullah, Z.M.; Kato, N. Assessing attack threat against ZigBee-based home area network for Smart Grid communications. In Proceedings of the 2010 International Conference on Computer Engineering & Systems, Cairo, Egypt, 30 November–2 December 2010; pp. 245–250. [Google Scholar] [CrossRef]
- Fouda, M.M.; Fadlullah, Z.M.; Kato, N.; Lu, R.; Shen, X. Towards a light-weight message authentication mechanism tailored for Smart Grid communications. In Proceedings of the 2011 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Shanghai, China, 10–15 April 2011; pp. 1018–1023. [Google Scholar] [CrossRef]
- Liang, G.; Zhao, J.; Luo, F.; Weller, S.R.; Dong, Z.Y. A Review of False Data Injection Attacks Against Modern Power Systems. IEEE Trans. Smart Grid 2017, 8, 1630–1638. [Google Scholar] [CrossRef]
- Faheem, M.; Shah, S.; Butt, R.; Raza, B.; Anwar, M.; Ashraf, M.; Ngadi, M.; Gungor, V. Smart grid communication and information technologies in the perspective of Industry 4.0: Opportunities and challenges. Comput. Sci. Rev. 2018, 30, 1–30. [Google Scholar] [CrossRef]
- Wang, W.; Lu, Z. Cyber security in the Smart Grid: Survey and challenges. Comput. Netw. 2013, 57, 1344–1371. [Google Scholar] [CrossRef]
- Yan, Y.; Qian, Y.; Sharif, H.; Tipper, D. A Survey on Cyber Security for Smart Grid Communications. IEEE Commun. Surv. Tutor. 2012, 14, 998–1010. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Tang, J.; Cheng, Y.; Li, H.; Campbell, K.A.; Han, Z. Real-Time Detection of False Data Injection in Smart Grid Networks: An Adaptive CUSUM Method and Analysis. IEEE Syst. J. 2016, 10, 532–543. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Ning, P.; Reiter, M.K. False Data Injection Attacks against State Estimation in Electric Power Grids. In Proceedings of the 16th ACM Conference on Computer and Communications Security, CCS ’09, Chicago, IL USA, 9–13 November 2009; pp. 21–32. [Google Scholar] [CrossRef]
- Ibrahem, M.I.; Nabil, M.; Fouda, M.M.; Mahmoud, M.M.E.A.; Alasmary, W.; Alsolami, F. Efficient Privacy-Preserving Electricity Theft Detection with Dynamic Billing and Load Monitoring for AMI Networks. IEEE Internet Things J. 2021, 8, 1243–1258. [Google Scholar] [CrossRef]
- Badr, M.M.; Ibrahem, M.I.; Mahmoud, M.; Fouda, M.M.; Alsolami, F.; Alasmary, W. Detection of False-Reading Attacks in Smart Grid Net-Metering System. IEEE Internet Things J. 2022, 9, 1386–1401. [Google Scholar] [CrossRef]
- Kurt, M.N.; Yılmaz, Y.; Wang, X. Distributed Quickest Detection of Cyber-Attacks in Smart Grid. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2015–2030. [Google Scholar] [CrossRef]
- Liu, Y.; Ning, P.; Reiter, M.K. False Data Injection Attacks against State Estimation in Electric Power Grids. ACM Trans. Inf. Syst. Secur. 2011, 14, 1–33. [Google Scholar] [CrossRef]
- Hao, J.; Piechocki, R.J.; Kaleshi, D.; Chin, W.H.; Fan, Z. Sparse Malicious False Data Injection Attacks and Defense Mechanisms in Smart Grids. IEEE Trans. Ind. Inform. 2015, 11, 1198–1209. [Google Scholar] [CrossRef] [Green Version]
- Deng, R.; Xiao, G.; Lu, R.; Liang, H.; Vasilakos, A.V. False Data Injection on State Estimation in Power Systems—Attacks, Impacts, and Defense: A Survey. IEEE Trans. Ind. Inform. 2017, 13, 411–423. [Google Scholar] [CrossRef]
- Bi, S.; Zhang, Y.J. Using Covert Topological Information for Defense Against Malicious Attacks on DC State Estimation. IEEE J. Sel. Areas Commun. 2014, 32, 1471–1485. [Google Scholar] [CrossRef] [Green Version]
- Musleh, A.S.; Chen, G.; Dong, Z.Y. A Survey on the Detection Algorithms for False Data Injection Attacks in Smart Grids. IEEE Trans. Smart Grid 2020, 11, 2218–2234. [Google Scholar] [CrossRef]
- Wang, S.; Bi, S.; Zhang, Y.J.A. Locational Detection of the False Data Injection Attack in a Smart Grid: A Multilabel Classification Approach. IEEE Internet Things J. 2020, 7, 8218–8227. [Google Scholar] [CrossRef]
- Mukherjee, D.; Chakraborty, S.; Ghosh, S. Deep learning-based multilabel classification for locational detection of false data injection attack in smart grids. Electr. Eng. 2022, 104, 259–282. [Google Scholar] [CrossRef]
- Ozay, M.; Esnaola, I.; Yarman Vural, F.T.; Kulkarni, S.R.; Poor, H.V. Machine Learning Methods for Attack Detection in the Smart Grid. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1773–1786. [Google Scholar] [CrossRef] [Green Version]
- Kurt, M.N.; Ogundijo, O.; Li, C.; Wang, X. Online Cyber-Attack Detection in Smart Grid: A Reinforcement Learning Approach. IEEE Trans. Smart Grid 2019, 10, 5174–5185. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef] [Green Version]
- Malhotra, P.; Ramakrishnan, A.; Anand, G.; Vig, L.; Agarwal, P.; Shroff, G. LSTM-based Encoder-Decoder for Multi-sensor Anomaly Detection. arXiv 2016, arXiv:1607.00148. [Google Scholar]
- Zhou, S.; Shen, W.; Zeng, D.; Fang, M.; Wei, Y.; Zhang, Z. Spatial–temporal convolutional neural networks for anomaly detection and localization in crowded scenes. Signal Process. Image Commun. 2016, 47, 358–368. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, Y.; Niu, C.; Liu, R.; Sun, W.; Pei, D. Robust Anomaly Detection for Multivariate Time Series through Stochastic Recurrent Neural Network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD ’19, Anchorage, AK, USA, 4–8 August 2019; pp. 2828–2837. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, D.; Zhang, X.; Yuan, Z.; Cheng, X. Learning Graph Structures With Transformer for Multivariate Time-Series Anomaly Detection in IoT. IEEE Internet Things J. 2022, 9, 9179–9189. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Duan, J.; Huang, C.; Cao, D.; Tong, Y.; Xu, B.; Bai, J.; Tong, J.; Zhang, Q. Multivariate Time-Series Anomaly Detection via Graph Attention Network. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 841–850. [Google Scholar] [CrossRef]
- He, Y.; Zhao, J. Temporal Convolutional Networks for Anomaly Detection in Time Series. J. Phys. Conf. Ser. 2019, 1213, 042050. [Google Scholar] [CrossRef] [Green Version]
- Karim, F.; Majumdar, S.; Darabi, H. Insights Into LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2019, 7, 67718–67725. [Google Scholar] [CrossRef]
- Zhao, F.; Huang, Y.; Wang, L.; Tan, T. Deep semantic ranking based hashing for multi-label image retrieval. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1556–1564. [Google Scholar] [CrossRef]
- Sainath, T.N.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, Long Short-Term Memory, fully connected Deep Neural Networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 4580–4584. [Google Scholar] [CrossRef]
- Anwar, A.; Mahmood, A.N.; Tari, Z. Identification of vulnerable node clusters against false data injection attack in an AMI based Smart Grid. Inf. Syst. 2015, 53, 201–212. [Google Scholar] [CrossRef]
- Esmalifalak, M.; Liu, L.; Nguyen, N.; Zheng, R.; Han, Z. Detecting Stealthy False Data Injection Using Machine Learning in Smart Grid. IEEE Syst. J. 2017, 11, 1644–1652. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar] [CrossRef] [Green Version]
- Lin, M.; Chen, Q.; Yan, S. Network In Network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Gan, D. Matpower. PSERC. 1997. Available online: http://www.pserc.cornell.edu/matpower (accessed on 11 March 2020).
- Moslemi, R.; Mesbahi, A.; Velni, J.M. A fast, decentralized covariance selection-based approach to detect cyber attacks in smart grids. IEEE Trans. Smart Grid 2017, 9, 4930–4941. [Google Scholar] [CrossRef]
- Sedghi, H.; Jonckheere, E. Statistical structure learning to ensure data integrity in smart grid. IEEE Trans. Smart Grid 2015, 6, 1924–1933. [Google Scholar] [CrossRef]
- Chollet, F. Keras: The Python Deep Learning Library. Astrophysics Source Code Library. 2018; Record ascl:1806.022. Available online: https://github.com/fchollet/keras (accessed on 14 December 2021).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
| Stage | Layer (Type) | Kernal | Output Shape | No. of Parameters |
|---|---|---|---|---|
| 0 | input_1 | − | 0 | |
| 1 | permute | − | 0 | |
| 2 | Conv1D | 12,288 | ||
| 3 | batch_normalization | − | 512 | |
| 4 | RELU | − | 0 | |
| 5 | Conv1D | 98,560 | ||
| 6 | batch_normalization | − | 1024 | |
| 7 | RELU | − | 0 | |
| 8 | global_average_pooling1d | − | 0 | |
| 9 | LSTM | − | 98,432 | |
| 10 | dropout | − | 75,776 | |
| 11 | concatenate | − | 0 | |
| 12 | dense | − | 7315 | |
| Total no. of parameters: 195,475 | ||||
| No. of trainable parameters: 194,707 | ||||
| No. of non-trainable parameters: 768 | ||||
| Model | Layers | Precision % | Recall % | F1-Score % | RACC % | Number of Parameters |
|---|---|---|---|---|---|---|
| CNN | 2 | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| LSTM | 2 | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| LSTM-TCN | 2 | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
| Compromised Location | CNN | LSTM | LSTM-TCN |
|---|---|---|---|
| 1st | 80.44 | 82.00 | 93.78 |
| 3rd | 80.77 | 80.50 | 94.57 |
| 1st & 3rd | 45.45 | 71.21 | 95.45 |
| Neither | 81.35 | 81.14 | 94.51 |
| 1st | 76.18 | 81.12 | 93.93 |
| 15th | 80.44 | 79.75 | 94.46 |
| 1st & 15th | 74.65 | 77.46 | 94.37 |
| Neither | 81.41 | 81.28 | 94.53 |
| Model | Layers | Precision % | Recall % | F1-Score % | RACC % | Number of Parameters |
|---|---|---|---|---|---|---|
| CNN | 2 | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| LSTM | 2 | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| LSTM-TCN | 2 | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hegazy, H.I.; Tag Eldien, A.S.; Tantawy, M.M.; Fouda, M.M.; TagElDien, H.A. Real-Time Locational Detection of Stealthy False Data Injection Attack in Smart Grid: Using Multivariate-Based Multi-Label Classification Approach. Energies 2022, 15, 5312. https://doi.org/10.3390/en15145312
Hegazy HI, Tag Eldien AS, Tantawy MM, Fouda MM, TagElDien HA. Real-Time Locational Detection of Stealthy False Data Injection Attack in Smart Grid: Using Multivariate-Based Multi-Label Classification Approach. Energies. 2022; 15(14):5312. https://doi.org/10.3390/en15145312
Chicago/Turabian StyleHegazy, Hanem I., Adly S. Tag Eldien, Mohsen M. Tantawy, Mostafa M. Fouda, and Heba A. TagElDien. 2022. "Real-Time Locational Detection of Stealthy False Data Injection Attack in Smart Grid: Using Multivariate-Based Multi-Label Classification Approach" Energies 15, no. 14: 5312. https://doi.org/10.3390/en15145312
APA StyleHegazy, H. I., Tag Eldien, A. S., Tantawy, M. M., Fouda, M. M., & TagElDien, H. A. (2022). Real-Time Locational Detection of Stealthy False Data Injection Attack in Smart Grid: Using Multivariate-Based Multi-Label Classification Approach. Energies, 15(14), 5312. https://doi.org/10.3390/en15145312







