Multi-Objective Constructal Design for Square Heat-Generation Body with “Arrow-Shaped” High-Thermal-Conductivity Channel
Abstract
:1. Introduction
2. Square HGB Model
2.1. Physical Model
2.2. Mathematical Model
3. Multi-Objective Constructal Design for “Arrow-Shaped” HTCC
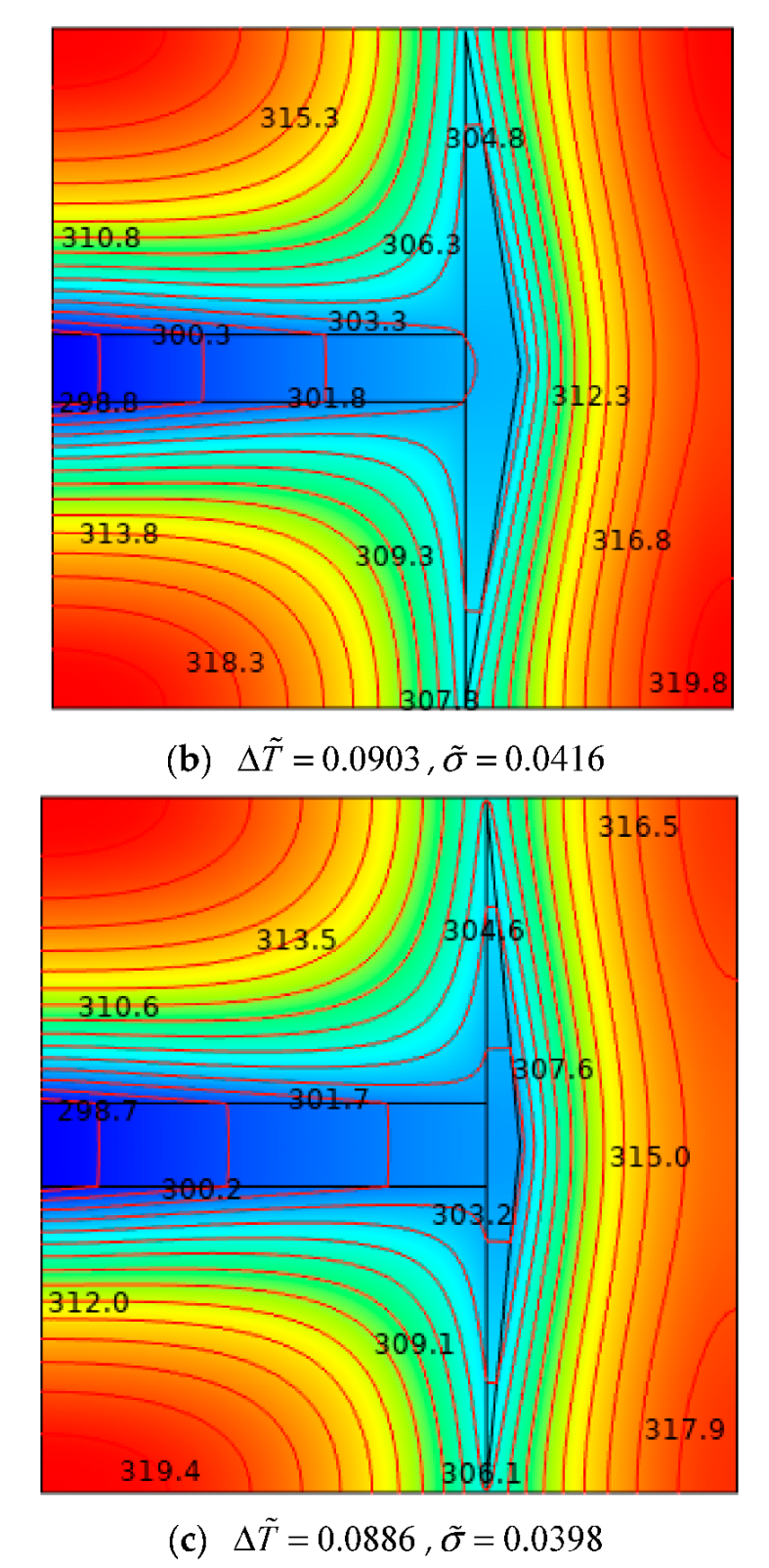
3.1. Multi-Objective Constructal Design under Single-DOF Optimization
3.2. Multi-Objective Constructal Design under Two-DOF Optimization
3.3. Multi-Objective Constructal Design under Three-DOF Optimization
4. Conclusions
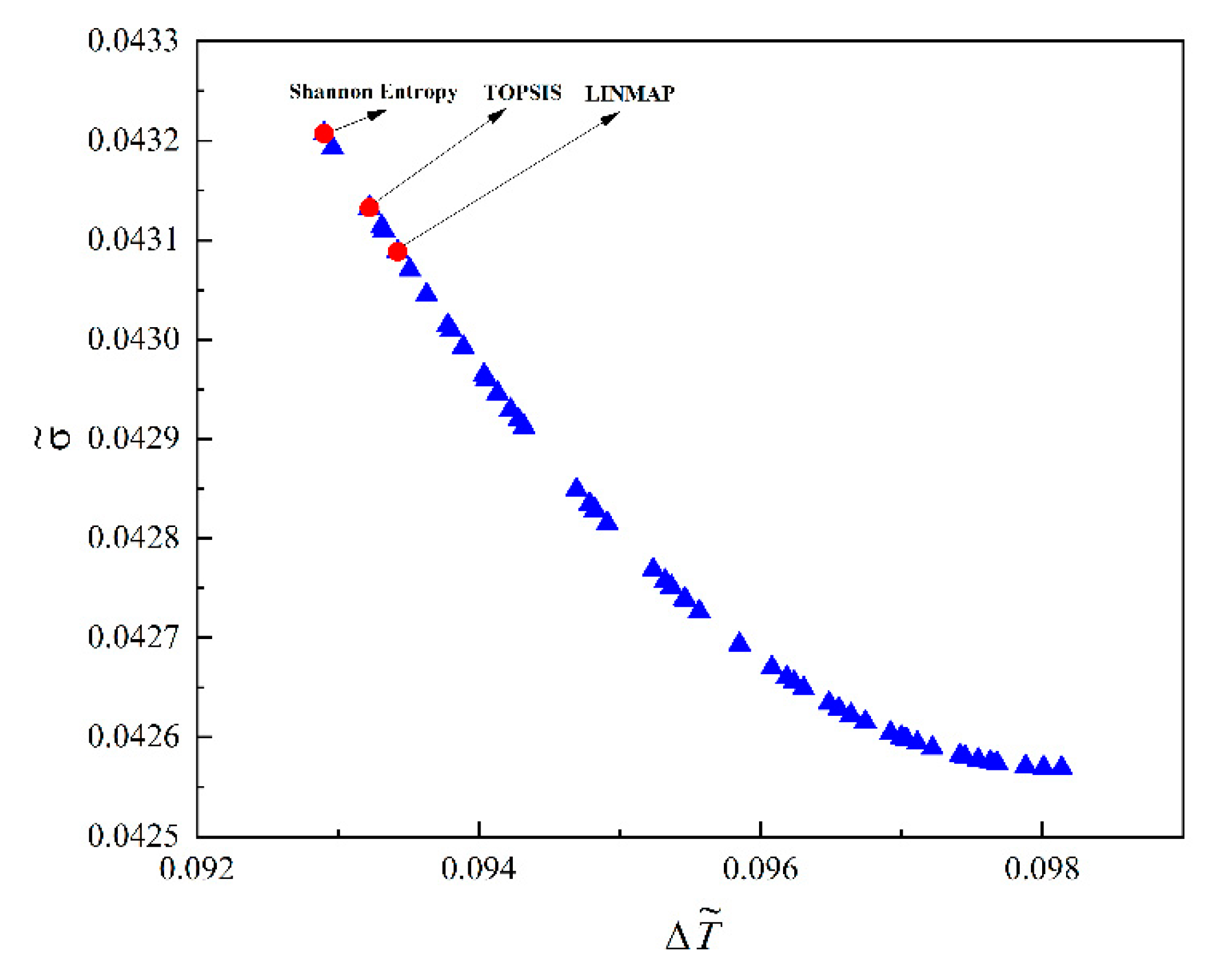
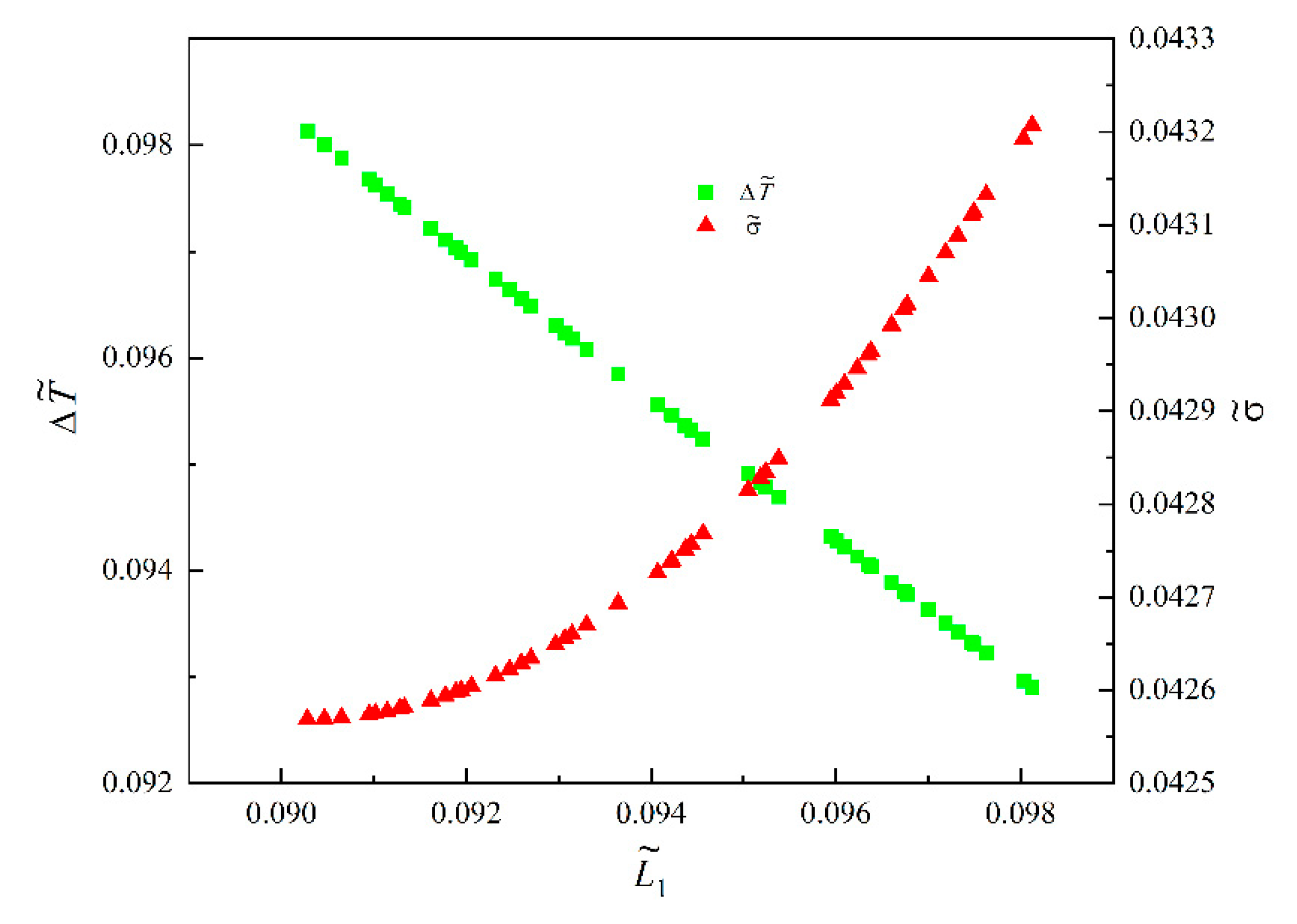
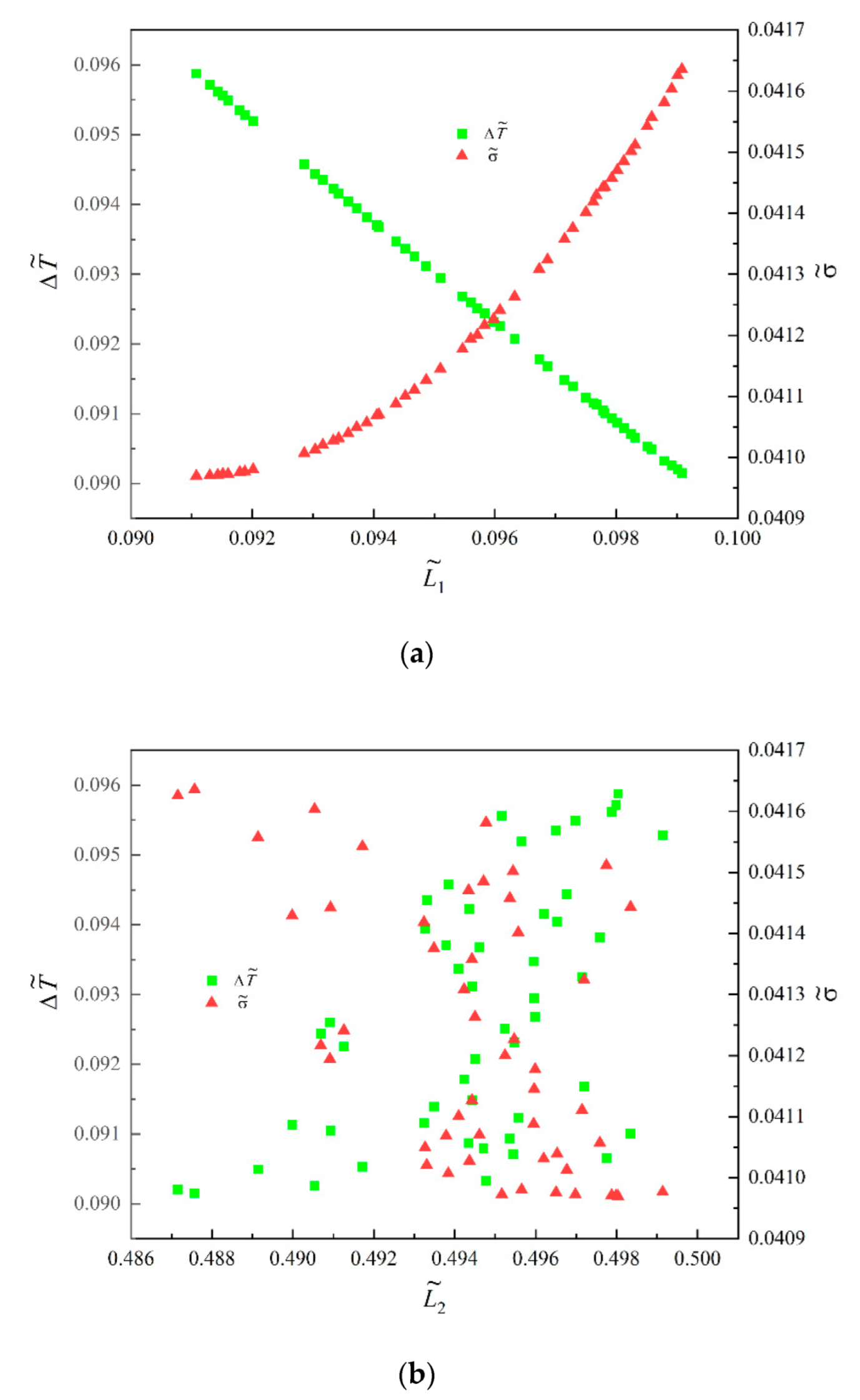
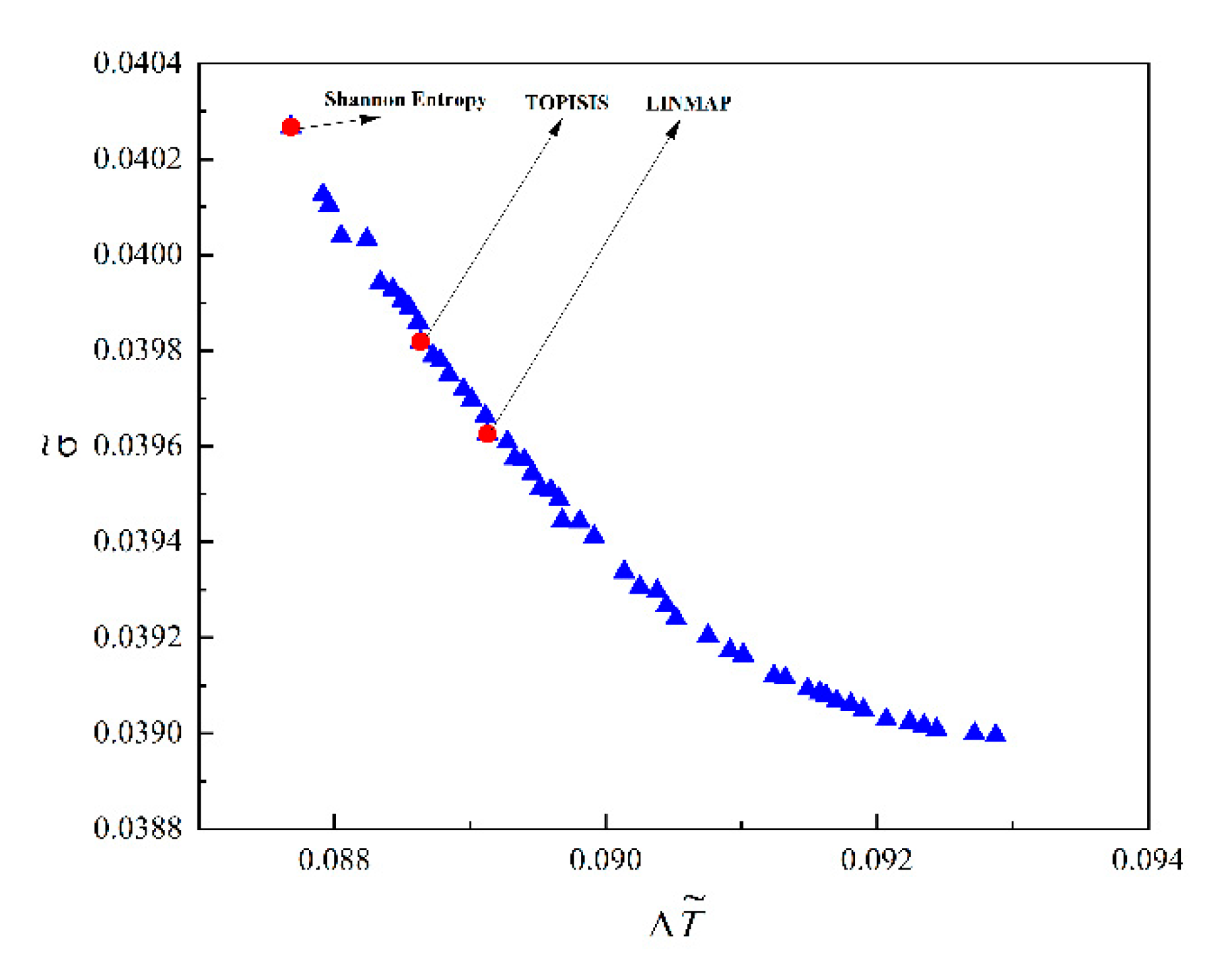
- In the Pareto frontiers of and obtained by MOO with single-DOF, two-DOF, and three-DOF optimizations, with the increase of , decreased continuously. and could not reach their optimal values under single-objective optimization at the same time; however, they could effectively compromise the two objectives and reduce the conflict between them.
- Under the optimization of single DOF, two DOF and three DOF, the deviation index of the optimal result based on the TOPSIS decision method was the smallest, so the optimal result with the TOPSIS decision method was selected as the design scheme for the best compromise between the maximum thermal resistance and the loss of heat transfer irreversibility of the square HGB.
- Compared with the two-DOF and single-DOF optimizations, the of square HGB under three-DOF optimization was reduced by 1.9% and 4.9%, respectively, and the of square HGB under three-DOF optimization was reduced by 4.3% and 7.7%, respectively. The and of the square HGB could be further reduced by increasing the DOF optimization of the “arrow-shaped” HTCC, which could further improve the comprehensive thermal performance of the square HGB. It may be possible to further improve the comprehensive thermal conductivity of the square heat-generation body by establishing HTCCs with more degrees of freedom.
- Constructal theory and NSGA-II are powerful tools for thermal performance improvements of a square HGB with “arrow-shaped” HTCC, and the optimization methods can be applied to many problems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Area of high thermal conductivity material () | |
| Length of square heat-generation body () | |
| Length of rectangular area of “arrow-shaped” channel () | |
| Width of rectangular area of “arrow-shaped” channel () | |
| Length of arrowhead area of “arrow-shaped” channel () | |
| Width of arrowhead area of “arrow-shaped” channel () | |
| Ratio of thermal conductivity (-) | |
| Thermal conductivity of heat-generation body () | |
| Thermal conductivity of high-thermal-conductivity channel () | |
| Heat generation rate per unit volume () | |
| Temperature () | |
| Greek Symbols | |
| Porosity of high-thermal-conductivity channel (-) | |
| Entropy-generation rate () | |
| Superscript | |
| Dimensionless | |
| Subscripts | |
| Minimum | |
| Abbreviations | |
| HGB | Heat-generation body |
| HTCC | High-thermal-conductivity channel |
| MTD | Maximum temperature difference |
| EGR | Entropy-generation rate |
| MOO | Multi-objective optimization |
| DOF | Degree of freedom |
References
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Bejan, A. Entropy Generation Minimization; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Chen, L.G.; Wu, C.; Sun, F.R. Finite time thermodynamic optimization or entropy generation minimization of energy systems. J. Non-Equilib. Thermodyn. 1999, 24, 327–359. [Google Scholar] [CrossRef]
- Farzaneh-Gord, M.; Ameri, H.; Arabkoohsar, A. Tube-in-tube helical heat exchangers performance optimization by entropy generation minimization approach. Appl. Therm. Eng. 2016, 108, 1279–1287. [Google Scholar] [CrossRef]
- Ebrahimi-Moghadam, A.; Moghadam, A.J. Optimal design of geometrical parameters and flow characteristics for Al2O3/water nanofluid inside corrugated heat exchangers by using entropy generation minimization and genetic algorithm methods. Appl. Therm. Eng. 2019, 149, 889–898. [Google Scholar] [CrossRef]
- Chauhan, P.R.; Kumar, R.; Bharj, R.S. Optimization of the circular microchannel heat sink under viscous heating effect using entropy generation minimization method. Therm. Sci. Eng. Prog. 2019, 13, 100365. [Google Scholar] [CrossRef]
- Nayak, P.K.; Tripathy, S.K.; Senapati, A.K. Heat transfer and entropy generation through finned tubeess and behavioral analysis of employees using statistical and correlation methods. Turk. J. Comput. Math. Educ. 2021, 12, 606–621. [Google Scholar]
- Bejan, A. Constructal-theory network of conducting paths for cooling a heat generating volume. Int. J. Heat Mass Transf. 1997, 40, 799–816. [Google Scholar] [CrossRef]
- Bejan, A.; Lorente, S. Design with Constructal Theory; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Chen, L.G. Progress in study on constructal theory and its applications. Sci. China Technol. Sci. 2012, 55, 802–820. [Google Scholar] [CrossRef]
- Bejan, A.; Gunes, U.; Sahin, B. The evolution of air and maritime transport. Appl. Phys. Rev. 2019, 6, 21319. [Google Scholar] [CrossRef]
- Chen, L.G.; Feng, H.J.; Xie, Z.H.; Sun, F.R. Progress of constructal theory in China over the past decade. Int. J. Heat Mass Transf. 2019, 130, 393–419. [Google Scholar] [CrossRef]
- Lorente, S.; Bejan, A. Current trends in constructal law and evolutionary design. Heat Transf.-Asian Res. 2019, 48, 357–389. [Google Scholar] [CrossRef]
- Chen, L.G.; Yang, A.B.; Feng, H.J.; Ge, Y.L.; Xia, S.J. Constructal design progress for eight types of heat sinks. Sci. China Technol. Sci. 2020, 63, 879–911. [Google Scholar] [CrossRef]
- Lorente, S. Vascular systems for the thermal and hygric management. Adv. Heat Transf. 2021, 53, 159–185. [Google Scholar]
- Chen, L.G.; Wu, W.J.; Feng, H.J. Constructal Design for Heat Conduction; Book Publisher International: London, UK, 2021. [Google Scholar]
- Bejan, A. Heat Transfer: Evolution, Design and Performance; John Wiley & Sons: New York, NY, USA, 2022. [Google Scholar]
- Bejan, A. Evolution, physics, and education. Biosystems 2022, 215, 104663. [Google Scholar] [CrossRef]
- Lorenzini, G.; Barreto, E.X.; Beckel, C.C.; Schneider, P.S.; Isoldi, L.A.; dos Santos, E.D. Constructal design of I-shaped high conductive pathway for cooling a heat-generating medium considering the thermal contact resistance. Int. J. Heat Mass Transf. 2016, 93, 770–777. [Google Scholar] [CrossRef]
- Lorenzini, G.; Barreto, E.X.; Beckel, C.C.; Schneider, P.S.; Isoldi, L.A.; dos Santos, E.D.; Rocha, L.A.O. Geometrical evaluation of T-shaped design conductive pathway with thermal contact resistance for cooling of heat-generating medium. Int. J. Heat Mass Transf. 2017, 108, 1884–1893. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Rezaei, E. Proposing a new algorithm for the optimization of conduction pathways based on a recursive localization. Appl. Therm. Eng. 2019, 151, 146–153. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Parsa, H.; Najafian, J. Proposing an optimal tree-like design of highly conductive material configuration with unequal branches for maximum cooling a heat generating piece. Int. J. Heat Mass Transf. 2019, 142, 118422. [Google Scholar] [CrossRef]
- Fagundes, T.M.; Lorenzini, G.; da Estrada, E.S.D.; Isoldi, L.A.; dos Santos, E.D.; Rocha, L.A.O.; da Silva Neto, A.J. Constructal design of conductive asymmetric tri-forked pathways. J. Eng. Thermophys. 2019, 28, 26–42. [Google Scholar] [CrossRef]
- Zhang, F.Y.; Feng, H.J.; Chen, L.G.; You, J.; Xie, Z.H. Constructal design of an arrow-shaped high thermal conductivity channel in a square heat generation body. Entropy 2020, 22, 475. [Google Scholar] [CrossRef]
- Cetkin, E.; Oliani, A. The natural emergence of asymmetric tree-shaped pathways for cooling of a non-uniformly heated domain. J. Appl. Phys. 2015, 118, 24902. [Google Scholar] [CrossRef] [Green Version]
- Ghodoossi, L.; Egrican, N. Conductive cooling of triangular shaped electronics using constructal theory. Energy Convers. Manag. 2004, 45, 811–828. [Google Scholar] [CrossRef]
- Da Silva, A.K.; Vasile, C.; Bejan, A. Dics cooled with high-conductivity inserts that extend inward from the perimeter. Int. J. Heat Mass Transf. 2004, 47, 4257–4263. [Google Scholar] [CrossRef]
- Sharfi, F.; Salimpuor, R.M.; Campo, A. Cooling a solid disc with uniform heat generation using inserts of high thermal conductivity within the constructal design platform. Int. J. Thermal Environ. Eng. 2016, 12, 15–26. [Google Scholar]
- Liu, H.L.; Li, B.T.; Hong, J. Generating constructal-conduction-networks for cooling discs at macro and micro scales. Int. Commun. Heat Mass Transf. 2019, 109, 104318. [Google Scholar] [CrossRef]
- Konan, H.C.; Cetkin, E. Snowflake shaped high-conductivity inserts for heat transfer enhancement. Int. J. Heat Mass Transf. 2018, 127, 473–482. [Google Scholar] [CrossRef]
- Hajmohammadi, M.R.; Rasouli, E.; Elmi, M.A. Geometric optimization of a highly conductive insert intruding an annular fin. Int. J. Heat Mass Transf. 2020, 146, 118910. [Google Scholar] [CrossRef]
- Li, Y.L.; Feng, M.L. Optimal design of conductive natural branched pathways for cooling a heat-generating volume. Heat Transf. 2021, 50, 2571–2591. [Google Scholar] [CrossRef]
- Ghodoossi, L. Entropy generation rate in uniform heat generating area cooled by conducting paths: Criterion for rating the performance of constructal designs. Energy Convers. Manag. 2004, 45, 2951–2969. [Google Scholar] [CrossRef]
- You, J.; Feng, H.J.; Chen, L.G.; Xie, Z.H. Constructal design of nonuniform heat generating area based on triangular elements: A case of entropy generation minimization. Int. J. Therm. Sci. 2019, 139, 403–412. [Google Scholar] [CrossRef]
- Feng, H.J.; You, J.; Chen, L.G.; Ge, Y.L.; Xia, S.J. Constructal design of a non-uniform heat generating disc based on entropy generation minimization. Eur. Phys. J. Plus 2020, 135, 257. [Google Scholar] [CrossRef]
- Ribeiro, P.; Queiros-Condé, D. On the entropy production of the elemental construct of the constructal designed plate generating heat. Int. J. Therm. Sci. 2019, 145, 106043. [Google Scholar] [CrossRef]
- Zhu, H.W.; Chen, L.G.; Ge, Y.L.; Feng, H.J. Constructal entropy generation rate minimization of heat conduction for leaf-shaped quadrilateral heat generation body. Eur. Phys. J. Plus 2022, 137, 275. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mohammadi, A.H.; Dehghani, S.; Barranco-Jimenez, M.A. Multi-objective thermodynamic-based optimization of output power of Solar Dish-Stirling engine by implementing an evolutionary algorithm. Energy Convers. Manag. 2013, 75, 438–445. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ahmadi, M.A.; Mohammadi, A.H.; Feidt, M.; Pourkiaei, S.M. Multi-objective optimization of an irreversible Stirling cryogenic refrigerator cycle. Energy Convers. Manag. 2014, 82, 351–360. [Google Scholar] [CrossRef]
- Jokar, M.A.; Ahmadi, M.H.; Sharifpur, M.; Meyer, J.P.; Pourfayaz, F.; Ming, T.Z. Thermodynamic evaluation and multi-objective optimization of molten carbonate fuel cell-supercritical CO2 Brayton cycle hybrid system. Energy Convers. Manag. 2017, 153, 538–556. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Jokar, M.A.; Ming, T.Z.; Feidt, M.; Pourfayaz, F.; Astaraei, F.R. Multi-objective performance optimization of irreversible molten carbonate fuel cell–Braysson heat engine and thermodynamic analysis with ecological objective approach. Energy 2018, 144, 707–722. [Google Scholar] [CrossRef]
- Ghasemkhani, A.; Farahat, S.; Naserian, M.M. Multi-objective optimization and decision making of endoreversible combined cycles with consideration of different heat exchangers by finite time thermodynamics. Energy Convers. Manag. 2018, 171, 1052–1062. [Google Scholar] [CrossRef]
- Han, Z.H.; Mei, Z.K.; Li, P. Multi-objective optimization and sensitivity analysis of an organic Rankine cycle coupled with a one-dimensional radial-inflow turbine efficiency prediction model. Energy Convers. Manag. 2018, 166, 37–47. [Google Scholar] [CrossRef]
- Wang, M.; Jing, R.; Zhang, H.R.; Meng, C.; Li, N.; Zhao, Y.R. An innovative Organic Rankine Cycle (ORC) based Ocean Thermal Energy Conversion (OTEC) system with performance simulation and multi-objective optimization. Appl. Therm. Eng. 2018, 145, 743–754. [Google Scholar] [CrossRef]
- Hu, S.Z.; Li, J.; Yang, F.B.; Yang, Z.; Duan, Y.Y. How to design organic Rankine cycle system under fluctuating ambient temperature: A multi-objective approach. Energy Convers. Manag. 2020, 224, 113331. [Google Scholar] [CrossRef]
- Ghorani, M.M.; Haghighi, M.H.S.; Riasi, A. Entropy generation minimization of a pump running in reverse mode based on surrogate models and NSGA-II. Int. Commun. Heat Mass Transf. 2020, 118, 104898. [Google Scholar] [CrossRef]
- Sadeghi, S.; Ghandehariun, S.; Naterer, G.F. Exergoeconomic and multi-objective optimization of a solar thermochemical hydrogen production plant with heat recovery. Energy Convers. Manag. 2020, 225, 113441. [Google Scholar] [CrossRef]
- Ge, Y.; Han, J.T.; Zhu, X.X. Performance analysis and multi-objective optimization of two organic Rankine cycles with different fluids for low grade waste heat recovery. J. Thermal Sci. 2022, 31, 650–662. [Google Scholar] [CrossRef]
- Shi, S.S.; Ge, Y.L.; Chen, L.G.; Feng, F.J. Performance optimizations with single-, bi-, tri- and quadru-objective for irreversible Atkinson cycle with nonlinear variation of working fluid’s specific heat. Energies 2021, 14, 4175. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Feng, H.J.; Chen, L.G.; Ge, Y.L. Multi-objective constructal design for compound heat dissipation channels in a three-dimensional trapezoidal heat generation body. Int. Commun. Heat Mass Transf. 2021, 127, 105584. [Google Scholar] [CrossRef]
- Feng, H.J.; Tang, W.; Chen, L.G.; Shi, J.C.; Wu, Z.X. Multi-objective constructal optimization for marine condensers. Energies 2021, 14, 5545. [Google Scholar] [CrossRef]
- Feng, H.J.; Chen, L.G.; Xie, Z.J.; Tang, W.; Ge, Y.L. Multi-objective constructal design for a marine boiler considering entropy generation rate and power consumption. Energy Rep. 2022, 8, 1519–1527. [Google Scholar] [CrossRef]
- Feng, H.J.; Zhang, Z.M.; Chen, L.G.; Ge, Y.L.; Yu, J.Y. Constructal design for tree-shaped compound heat dissipation channel in a disc heat generation body. Int. Commun. Heat Mass Transf. 2022, 132, 105929. [Google Scholar] [CrossRef]
- Sun, K.; Feng, H.J.; Chen, L.G.; Ge, Y.L. Constructal design of a cooling channel with semi-circular sidewall ribs in a rectangular heat generation body. Int. Commun. Heat Mass Transf. 2022, 134, 106040. [Google Scholar] [CrossRef]
- Kalkan, O.; Celen, A.; Bakirci, K. Multi-objective optimization of a mini channeled cold plate for using thermal management of a Li-Ion battery. Energy 2022, 251, 123949. [Google Scholar] [CrossRef]
- Tang, C.Q.; Chen, L.G.; Feng, H.J.; Ge, Y.L. Four-objective optimization for an irreversible closed modified simple Brayton cycle. Entropy 2021, 23, 282. [Google Scholar] [CrossRef] [PubMed]




| Optimization Methods | Decision Methods | Design Variables | Optimization Objectives | Deviation Indexes [56] | |
|---|---|---|---|---|---|
| Multi-objective optimization | LINMAP | 0.0973 | 0.0934 | 0.0431 | 0.2020 |
| TOPISIS | 0.0976 | 0.0932 | 0.0431 | 0.1862 | |
| Shannon Entropy | 0.0981 | 0.0929 | 0.0432 | 0.197 | |
| Single-objective optimizations | 0.0981 | 0.0929 | 0.0432 | 0.1997 | |
| 0.0903 | 0.0981 | 0.0426 | 0.8003 | ||
| Optimization Methods | Decision Methods | Design Variables | Optimization Objectives | Deviation Indexes | ||
|---|---|---|---|---|---|---|
| Multi-objective optimization | LINMAP | 0.0983 | 0.4954 | 0.0907 | 0.0415 | 0.1867 |
| TOPISIS | 0.0988 | 0.4948 | 0.0903 | 0.0416 | 0.1628 | |
| Shannon Entropy | 0.0991 | 0.4876 | 0.0902 | 0.0416 | 0.1860 | |
| Single-objective optimizations | 0.0991 | 0.4876 | 0.0902 | 0.0416 | 0.1860 | |
| 0.0911 | 0.4980 | 0.0959 | 0.0410 | 0.8140 | ||
| Optimization Methods | Decision Methods | Design Variables | Optimization Objectives | Deviation Indexes | |||
|---|---|---|---|---|---|---|---|
| Multi-objective optimization | LINMAP | 0.1199 | 0.4905 | 0.6483 | 0.0891 | 0.0396 | 0.3202 |
| TOPISIS | 0.1195 | 0.4914 | 0.6399 | 0.0886 | 0.0398 | 0.3010 | |
| Shannon Entropy | 0.1198 | 0.4794 | 0.6258 | 0.0877 | 0.0403 | 0.3575 | |
| Single-objective optimizations | 0.1198 | 0.4794 | 0.6258 | 0.0877 | 0.0403 | 0.3575 | |
| 0.1170 | 0.4911 | 0.7019 | 0.0929 | 0.0390 | 0.6425 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Chen, L.; Ge, Y.; Shi, S.; Feng, H. Multi-Objective Constructal Design for Square Heat-Generation Body with “Arrow-Shaped” High-Thermal-Conductivity Channel. Energies 2022, 15, 5235. https://doi.org/10.3390/en15145235
Zhu H, Chen L, Ge Y, Shi S, Feng H. Multi-Objective Constructal Design for Square Heat-Generation Body with “Arrow-Shaped” High-Thermal-Conductivity Channel. Energies. 2022; 15(14):5235. https://doi.org/10.3390/en15145235
Chicago/Turabian StyleZhu, Hongwei, Lingen Chen, Yanlin Ge, Shuangshuang Shi, and Huijun Feng. 2022. "Multi-Objective Constructal Design for Square Heat-Generation Body with “Arrow-Shaped” High-Thermal-Conductivity Channel" Energies 15, no. 14: 5235. https://doi.org/10.3390/en15145235
APA StyleZhu, H., Chen, L., Ge, Y., Shi, S., & Feng, H. (2022). Multi-Objective Constructal Design for Square Heat-Generation Body with “Arrow-Shaped” High-Thermal-Conductivity Channel. Energies, 15(14), 5235. https://doi.org/10.3390/en15145235







