Abstract
When designing biomass-to-biofuel supply chains, the biomass uncertainty, seasonality and geographical dispersion that affect economic viability need to be considered. This work presents a novel methodology that can optimize the design of biofuel supply chains by adopting a decentralized network structure consisting of a mix of fixed and mobile processing facilities. The model considers a variable biomass yield profile and the mobile fast pyrolysis technology. The mixed-integer linear programming model developed identifies the optimal biofuel production and biomass harvesting schedule schemes under the objective of profit maximization. It was applied in the case study of marginal lands in Scotland, which are assumed to be planted with Miscanthus. The trade-offs observed between economies of scale against the transportation costs, the effect of the relocation costs and the contribution of storage capacity were investigated. The results showed that, in most cases, harvesting is most concentrated during the month of the highest biomass yield, provided that storage facilities are available. Storage capacity plays an important role to widen the operational time window of processing facilities since scenarios with restricted or costly storage resulted in facilities of higher capacity operating within a narrower time window, leading to higher investment costs. Relocation costs proved to have a minor share in the total transportation costs.
Keywords:
biofuel; biomass; supply chain; optimization; mobile; miscanthus; fast pyrolysis; logistics 1. Introduction
In the context of energy supply diversification and sustainability, energy production has to switch more towards renewable energy sources to minimize the environmental impact from fossil fuels and to maximize energy security. Energy security comprises of the continuous and reliable availability of adequate energy in varied forms and at reasonable prices, ensuring the well-being of citizens and the proper functioning of the economy, without causing unacceptable or irreversible effects on the environment under the framework of sustainable development [1].
Diversification in generating power and producing fuels requires multiple alternate energy options such as biomass, which is a key sustainable energy source. Biomass includes the biodegradable fraction of products, waste and residues from biological origin from agriculture (including vegetal and animal substances), forestry and related industries including fisheries and aquaculture, as well as the biodegradable fraction of industrial and municipal waste [2].
Biomass has a multifaceted role in energy systems as, in addition to power and heating generation, a variety of biomass materials can produce biofuels finding extensive but not exclusive applications in the transportation sector. According to the European Union’s (EU) long-term strategy, the objective is to achieve a climate-neutral EU by 2050, in line with the objectives of the Paris Agreement and in the light of the latest available science and of the need to step up global climate action [3]. Sustainable biofuels could contribute to the decarbonization of the transport sector (road, aviation, etc.) in line with the objective of reaching a climate-neutral economy while ensuring a high level of affordable and accessible transport connectivity [4].
Biomass accounts for over 70% of the renewable energy production globally, while having a 4% share in fuel demand for road transport, in the form of biofuels. Furthermore, second- and third-generation biomass sources have the advantage of not being competitive to food and feed feedstock as they do not occupy land dedicated to the production of agricultural commodities. According to the EU Renewable Energy Directive 2018/2001, the contribution of advanced biofuels and biogas as a share of the final consumption of energy in the transport sector will be at least 0.2% in 2022, at least 1% in 2025 and at least 3.5% in 2030. The term ‘advanced biofuels’ encompasses second-generation biofuels that are interlinked to second-generation biomass sources such as agricultural residues, biomass fractions from mixed municipal and industrial wastes, animal manure, wastes and residues from forestry, etc. This would mean avoiding the potential deforestation with the consequent loss of carbon stocks, which is referred to as indirect land-use change (iLUC) [5], which is primarily evident with first-generation biomass sources.
In this respect, the design of biomass-to-biofuel supply chains is of crucial importance to obtain the set goals and obligations and to enhance the viable penetration of biofuels in the fuel market. The detailed biofuels’ production system planning consists of multiple layers of complexity, including a series of resources, locations, technologies, processes and products considered under technological, economic, environmental and logical constraints. This combined framework complicates both the architecture and the representation of the physical system, while the elaboration of production planning schemes can turn into a quite tedious task. Biomass supply chain systems can be appropriately addressed using optimization methodologies with the most prevalent discipline being that of Mathematical Programming (MP). MP, and especially mixed integer linear programming (MILP), deals with and efficiently expresses such supply chain problems, prescribing solutions about resource allocation, material transportation flows, facility location and relocation, technology and capacity selection, harvest scheduling and various multilevel operations.
Given that the typical design of a biomass supply chain is based on fixed centralized facilities, material transportation constitutes a fundamental concern for the whole system’s logistics and profitability. The high capacity biorefineries require larger volumes of biomass to be processed to boost productivity and exploit economies of scale. However, biomass sources are quite scattered, increasing routing complexity, hindering high biomass utilization rates and burdening the supply chain’s economics as shipping biomass over longer distances causes a significant increase in transportation costs [6,7].
Promising options to facilitate the utilization of spatially-dispersed biomass and enhance the biomass supply chain’s flexibility are preprocessing technologies. One such option is pelleting, which exhibits benefits by reducing the storage and handling requirements and, consequently, the transportation cost, increases the energy density of the biofuel and, overall, improves the biomass’s quality and durability [8]. Fast pyrolysis is another preprocessing technology, which converts biomass into bio-oil, a denser and higher energy content intermediate product that can be easily transported and stored. It also outputs two secondary products: biochar and syngas [9,10], which find applications in improving the physical, chemical and biological properties of soil for enhanced agricultural performance [11] and power generation in various types of equipment, respectively. The crude pyrolysis oil cannot be used in the current energy infrastructure but requires upgrading and further refining to meet the required end-user’s specifications [12]. Mobile fast pyrolysis combines the advantages of mobility, storability, higher energy capacity and flexibility, succeeding in reducing the transportation effort and cost, and with a smaller environmental footprint [9].
This study considers all the above aspects and aims to address the limitations of previous modeling attempts by developing a deterministic bottom-up MILP model for the optimization of a biomass-to-biofuel supply network design. The proposed methodology is designed and modeled to be able to adapt to and deal with any consideration of a biomass supply chain, allowing different technological and (pre and post) processing components, any kind of feedstock and various types of storage, while its interconnection with a Geographic Information System (GIS) expands its applicability to any region and scale of interest. One of the model’s novelties lies in incorporating a detailed routing of mobile facilities’ decisions in the supply chain model formulation, taking into consideration the distance travelled, so that the relocation costs can be calculated more accurately. Furthermore, this model adopts a non-linear biomass growth rate, allowing for a more detailed biomass harvesting schedule throughout the year.
The biomass supply chain model is applied to a case study of marginal lands in Scotland planted with Miscanthus to produce biofuels by using fixed and mobile fast pyrolysis plants together with upgrading technologies. Starting from a base case reference scenario, different scenarios are explored to investigate the effect of mobile facilities and the biomass growth curve to the overall supply chain performance.
After this introductory section, the remainder of the article is organized as follows. A literature review on existing relevant works on biomass supply chains is provided in Section 2. Section 3 starts with the conceptual model design, the aspects to be modeled and the presentation of the specific case study. In the same section, the model’s philosophy, characteristics, and mathematical structure are given in detail. Section 4 presents the nine scenarios analyzed, followed by the results’ presentation and discussion in Section 5. The last section summarizes the key findings and concluding remarks and provides some future research directions.
2. Literature Review
The bibliography abounds with methodologies and applications on biomass-to-biofuel supply chains. The present literature review focuses on studies mainly using the MILP approach to design the optimal biomass supply chain and designate the related strategic and tactical decisions. The common objective is to determine the whole superstructure of the supply chain starting from the fields to the pretreatment facilities, continuing to the intermediate processing facilities and final upgrading units up to the end users. The detailed decisions refer, inter alia, to facility siting and material flows (biomass supply, intermediate products and biofuel).
Examples of relevant work include Moretti et al. [13], who designed an advanced biofuel supply chain model with fixed facilities, incorporating a piecewise linear cost function to represent the economies of scale in the investment cost of the conversion facility producing methanol via biomass gasification. Kwon and Han [14] developed a MILP model for the optimal location of a biorefinery producing bioethanol from organic waste using anaerobic digestion, by minimizing the total ethanol levelized cost. Kwon et al. [15] developed a multiperiod deterministic MILP model for the production of biodiesel from waste to satisfy demand, choosing a five-year time interval, which makes the addition of storage locations and mobile refineries impractical. Mohd Yahya et al. [16] optimized a biomass-to-power supply chain based on carbon reduction targets following a combined methodology of three consecutive stages: Carbon Emission Pinch Analysis, MP and multistakeholder analysis. Results showed that co-firing plants were the most beneficial, but the transportation costs were highly susceptible to the plants’ location as also to biomass seasonality. Jonkman et al. [17] investigated a bio-based supply chain by developing an optimization methodology taking into account the individual goals of multiple actors, and including both an economic and a carbon footprint objective function. Baghizadeh et al. [18] introduced an aggregated approach concerning the forest industry and its multiplicity of products including biofuel. They developed a multiobjective, multiproduct, multiperiod mixed integer non-linear programming model for a sustainable forest supply chain by simultaneously addressing economic, environmental and social aspects under demand uncertainty. They showcased that increasing the capacity of some facilities (sawmills, ethanol production center, etc.) while also enlarging the transport fleet had a significant impact on profit maximization, instead of choosing to establish new facilities.
Up to now, few researchers have investigated the use of mobile biomass processing facilities. A recent study by Allman et al. [19] presented a model incorporating mobile gasifiers and turbines using the distances between nodes to calculate the relocation cost for specific configurations of a biomass waste-to-energy supply chain. Other forms of mobile processing facilities were investigated by Albashabsheh and Heier Stamm [20] who incorporated mobile densification in a MILP model through the use of mobile pelleting machines to reduce transportation costs for ethanol production from lignocellulosic biomass. Albashabsheh and Heier Stamm [21] also reviewed densification as part of the biomass supply chain optimization, finding that pyrolysis and pelleting achieve the highest density intermediates, offering simpler and less expensive transportation and handling. An early study by Sharifzadeh et al. [22] introduced centralized, decentralized and mobile pyrolysis plants in a MILP model integrating uncertainty. The relocation cost was considered as a fixed value, neglecting the transportation distance between the relocation sites. The results showed that mobile pyrolysis facilities are economically advantageous under uncertainty conditions. Mirkouei et al. [23] developed a stochastic model and a multicriteria decision-making framework to investigate fixed and mobile processing units including economic and environmental aspects throughout the supply chain. The relocation cost of the mobile facilities was considered minimal and neglected since they considered a 20-year period with a 1-year time step. Paolucci et al. [24] designed a pyrolysis-based biomass-to-energy production supply chain under a spatially explicit framework, to optimize economic and environmental objectives through a two-tier approach. You and Wang [25] developed a multiobjective MILP model for a biomass-to-liquid supply chain considering a distributed–centralized network including fast pyrolysis in the technology selection options. The bi-criterion target referred to the minimization of the total annualized cost and greenhouse gas (GHG) emissions generating Pareto optimal solutions that corresponded to differentiated supply chain network structures in relation to different environmental performances.
Modern supply chain networks are integrally coupled with GISs in order to use their detailed and accurate data to ensure their proper dimensioning, economics calculation integrity and overall sustainable function. Examples of GIS-based models include Wu et al. [26], who applied a GIS in designing and optimizing an agri-biomass supply chain by taking advantage of economies of scale to minimize supply costs and considering centralized large capacity conversion facilities and centralized storage sites. Razm et al. [27] used a GIS to obtain a more detailed geographical map of Iran and Armenia, to construct a biomass-to-bioenergy supply network for optimizing multiple objectives of economic performance, environmental impact and social opportunities. GIS software contributed to the development of a linear programming model by Razak et al. [28], optimizing the logistics’ costs and GHG emissions.
Based on the research reviewed, only a small number of studies considered mobile facilities in a detailed scheduling approach in their model formulation, as the usual case is to depend on centralized processing facilities with a high capacity, neglecting the detailed routing of smaller capacity mobile processing facilities and attributing a fixed cost to relocation instances. Another issue not addressed in the above-mentioned studies concerns the use of the biomass growth rate as a non-linear function, along with the possibility to harvest at different periods, which is especially important for biomass production in marginal lands. This feature is crucial for the optimal scheduling of the facilities and the overall functioning of the supply chain. An interesting ‘dilemma’ arises about the time of biomass harvesting, choosing between (a) the business-as-usual scenario, harvesting at specific months when the yield is maximum, and (b) harvesting at extended time periods with a reduced yield but benefiting from evening out the supply and utilization rates of facilities throughout the year.
3. Methodology
3.1. Conceptual Model Design
The proposed supply chain design indicates a differentiated approach for producing biofuel through the combination of high productivity based on centralized processing facilities, and flexibility gained from the existence of mobile conversion units. The basic concept is to enhance the biomass-to-biofuel network with more conversion and storing options and to detach the production stages of biofuel precursors from the upgrading stage. The methodology developed allows a full customization of the supply chain modules, starting from any feedstock source and the use of a variety of processing technologies, e.g., pyrolysis, gasification, combustion, etc. Its scope is broad being able to cover any region scale (local, regional, national) that contains biomass fields and hosts existing and candidate processing units.
Figure 1 illustrates an instance of the proposed superstructure focusing on the fast pyrolysis technology, which consists of mobile fast pyrolysis (MFP), fixed fast pyrolysis (FFP), fixed upgrading (FU) and storage entities. The multiple material streams that link these entities, are:
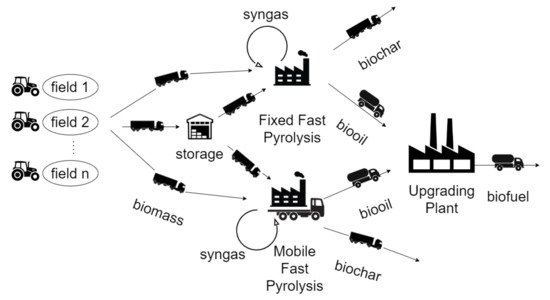
Figure 1.
Biomass-to-biofuel supply chain structure.
- Biomass flows from fields to MFP and FFP units.
- Biomass flow from fields to storage sites.
- Biomass flows from storage to MFP and FFP units.
- Bio-oil flow from FFP to FU unit.
- Bio-oil flow from MFP to FU unit.
- Biochar outputs from FFP and MFP units.
- Syngas outputs from FFP and MFP units (used internally in the fast pyrolysis process to supplement the required process heat).
- Biofuel output from FU unit.
Biomass and bio-oil transportation is carried out through trailer and tanker trucks, respectively.
Such a supply chain network model belongs to the typical location–allocation problems in which both the number, the size and the siting of new facilities has to be determined, though this work goes further by also incorporating the relocation option for MFP units. The location dimension includes one set of known sites (fields) and four sets of candidate to be determined nodes (facilities):
- Biomass fields, where biomass can be planted, harvested and collected.
- Intermediate storage facilities, where biomass can be stored for later usage.
- FFP facilities of varying capacity, where biomass can be converted to bio-oil, biochar and pyrolysis gas.
- MFP facilities having the relocation capability, where biomass can be converted to bio-oil, biochar and pyrolysis gas.
- FU facilities of varying capacity, where the bio-oil from the fast pyrolysis conversion process is transformed to biofuel (end product).
This supply chain’s rationale is to ensure the processing facilities are closer to sources of feedstock (biomass fields) in a decentralized approach, instead of the typical biomass concentration from multiple points to central processing plants. Potential gains lie in changing the synthesis of material flows by reducing transportation of biomass streams by partially substituting them with bio-oil. This liquid precursor of biofuel is a denser material of higher energy content, corresponding to significantly lower transportation costs and enabling shipment over larger distances. Bio-oil requires less space for storage, it is less susceptible to degradation and needs no pretreatment or densification before transportation, as compared to raw biomass. The mobility of processing units also contributes to mitigate the seasonality of biomass availability and constrained temporal uncertainty as, within a reasonable range, they can travel between different fields in relation to biomass availability and yield efficiency over time. Despite the fact that MFP units present higher unitary investment costs, their inherent flexibility may offset the increased start-up costs and technical minima of large, fixed facilities, which cannot cut down or stop their operation depending on the magnitude of biomass feeding. The relocating and storage capability increases the system’s flexibility and adaptability to changes while simultaneously improving utilization rates, which are desirable for such capital-intensive complex facilities.
The current work considers the following inputs for the biomass-to-biofuel network operation:
- coordinates of all sites and nodes for the calculation of the intra-node distances
- annual biomass growth curve profile
- selling price of biochar and biofuel
- cost of biomass harvesting/purchasing
- cost of biomass pretreating/drying before the fast pyrolysis processes
- conversion factors from biomass to bio-oil and biochar, and from bio-oil to biofuel
- technical minimum and maximum for the facilities’ capacity
- capital and operating costs of facilities
- insurance and maintenance costs of facilities
- biomass storage cost
- cost of transporting biomass with trailer trucks and bio-oil with tanker trucks
The problem’s objective is to determine the optimal combination of:
- (a)
- the harvesting schedule for biomass at each field,
- (b)
- the number, capacity and location of the FFP and FU facilities and their processing schedule,
- (c)
- the total number of MFP facilities and their routing schedule,
- (d)
- the monthly material flows throughout the supply chain and
- (e)
- the storage capacity and inventory levels on a monthly basis
by maximizing the supply chain’s total profit, which derives from revenues from selling biochar and biofuel minus the expenses such as the annualized investment costs, conversion costs, storage costs, transportation costs, operations and maintenance costs, etc.
The specific problem considers economies of scale in investment costs to decide the size of fixed facilities. The proposed configuration determines the time slot for harvesting biomass, allowing the intermediate warehouses to store collected biomass and gradually feed it into the facilities (FFP and/or MFP) to levelize both the annual biomass availability and the annual processing schedule while also enhancing the utilization of facilities. The storage option is used to rationalize the capacity chosen for the centralized processing facilities, thus constraining the total investment costs.
The proposed supply chain formulation is considered to be supply-driven, meaning that no biochar and biofuel demand profiles are considered. Expressed otherwise, it is assumed that biochar and biofuel demand is sufficient to absorb all products. This assumption is reasonable, reflecting the current need for constant supply of liquid biofuels throughout the year and the limited amounts currently available to meet the existing demand [13]. Both biochar and biofuel are considered to be sold at the end gate of the FU.
The biomass-to-biofuel problem is studied over a yearly time horizon with a monthly time step, assuming that the time needed for MFP relocation is negligible compared to the monthly time step.
Further assumptions of the model include that the candidate locations for all fields and processing facilities are known. The storage is assumed to be cyclical, meaning that the starting inventory in the first month depends on the ending inventory of the twelfth month, simulating in this way an equilibrium of multiple years. The thermal needs of the pyrolysis reactor are supplemented by all the pyrolysis gas outputs. It is also assumed that the entire biomass of a field is harvested within a single month.
The sets, parameters, and decision variables are described in the Nomenclature.
3.2. Model Formulation
3.2.1. Philosophy and Description
The biomass-to-biofuel supply chain problem is developed as a multiperiod MILP model incorporating continuous and binary decision variables. It is a deterministic engineering model able to represent many types of biomass processing technologies and routing patterns while it handles numerous techno-economic and geographical data. The time frame considered is a single year with monthly time steps.
3.2.2. Objective Function
The model’s objective function (1) aims at maximizing the total profit of the biomass supply chain considering the annual revenues and expenses.
The revenues are drawn from selling biofuel (RF) after bio-oil upgrading stage (FU) and biochar (RC) from FFP and MFP facilities, as calculated by Equations (2) and (3), respectively.
The cost dimension is the sum of:
- annualized investment costs of facilities (AIC),
- transportation costs for biomass and bio-oil (TC),
- processing costs for conversion in fast pyrolysis and in upgrading facilities (CC),
- inventory handling cost in storage facilities (SC),
- maintenance and insurance costs of the various facilities (MIC),
- biomass harvesting/purchasing cost (BC).
Three types of capital costs are considered: investment cost of FFP (ICFFP), FU (ICFU) and MFP (ICMFP) facilities. The investment costs of FU (4) and FFP (5) facilities incorporate economies of scale dependent on their capacity size. To represent the effect of economies of scale, piecewise continuous linear cost/capacity functions are engaged, which are appropriately linearized through the set of Equations (7)–(16).
The purchasing cost of each MFP facility (CMFP) is fixed and their total investment cost is given by Equation (6).
The piecewise cost functions as non-linear functions are incorporated in the model by applying appropriate linearization techniques [29].
Piecewise linearized cost constraints for the FU facilities
Piecewise linearized cost constraints for the FFP facilities
All investment costs are annualized based on their expected lifetime and a discount rate (r) in Equation (17).
The transportation cost is calculated for each active arc in the supply chain superstructure:
- the biomass from the fields to the FFP facilities Equation (18)
- the biomass from the fields to the MFP facilities Equation (19)
- the biomass from the fields to the storage facilities Equation (20)
- the biomass from the storage facilities to the FFP facilities Equation (21)
- the biomass from the storage facilities to the MFP facilities Equation (22)
- the bio-oil from the FFP to the FU facilities Equation (23)
- the bio-oil from the MFP to the FU facilities Equation (24)
- the total relocation cost of the MFP facilities Equation (25)
Equation (26) gives the sum of all transportation cost components.
The conversion costs mainly consist of material drying, labor cost, feeding and energy required at facilities. The processing costs of dry biomass in the FFP (CCFFP) and MFP (CCMFP) and of bio-oil in the FU (CCFU) facilities constitute the total conversion cost in Equation (27).
Each conversion cost component is calculated by Equations (28)–(30), respectively.
The inventory cost is calculated based on a unitary storage cost in Equation (31)
The annual maintenance and insurance costs depend on the total investment costs of the facilities.
The total biomass cost is calculated as follows.
3.2.3. Constraints and Equations
Equation (34) describes the biomass flow from fields and storage points to FFP facilities where the conversion to bio-oil takes place according to the respective bio-oil yield factor.
Similarly, Equation (35) expresses the balance of the total biomass transported to the MFP facilities and bio-oil extracted.
Equation (36) represents the biomass inventory balance having as inflow the biomass coming from the fields at the current time period t and the inventory stored from the previous time period t − 1 and biomass outflow to FFP and MFP facilities at the time period t.
The next constraint correlates the total feedstock supply with the biomass growth function, specifically, with the biomass yield (t/ha) and the field area (ha). The binary variable in Equation (38) controls which month biomass will be harvested from each field.
Equations (39) and (40) refer to the maximum possible biomass to be processed at FFP and MFP facilities due to capacity constraints.
The next set of constraints expresses the upper limit of bio-oil able to be processed to biofuel in the FU facilities according to their capacity.
In Equation (42), the total biomass inventory must not exceed storage capacity depending on the biomass bulk density, storage height and storage area.
Τhe area of a storage facility must be zero if the storage facility is not selected, which is ensured by constraint (43) with the implementation of the big-M constraint method.
The existence of the MFP facilities in the candidate locations is ensured by constraint (44). The sum of the binary variable which indicates that the MFP unit v is located at location m, must be equal to the binary variable , which indicates whether the MFP unit number v is selected.
To deal with non-linearities presented by the product of two binary variables, three extra constraints are added as follows [30].
3.3. Case Study
The proposed model is applied to the case study of marginal lands in Scotland, based on data from the Scottish Vacant and Derelict Land Survey [31]. Miscanthus × Giganteus, a perennial energy crop, is assumed to be used for biomass production. Yield rates for Miscanthus × Giganteus on monthly basis were adapted from Mos et al. [32] (see Figure 2) as well as a constant moisture content of 20% [33]. The period under study begins considering that Miscanthus cultivation has reached the maturity phase [34] and the construction of any facilities is finalized.
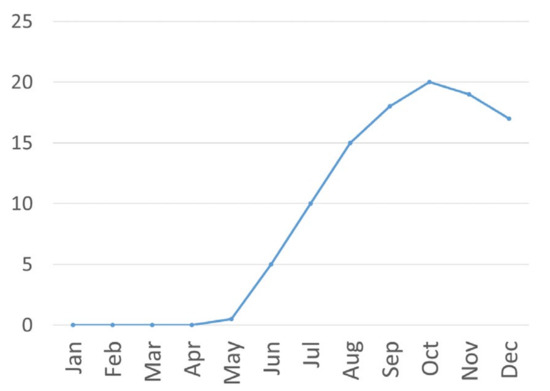
Figure 2.
Monthly yield rates for Miscanthus (t/ha).
Figure 3 shows the geographical locations of the nodes constituting the biomass-to-biofuel supply chain. The geographical data on marginal land from the Scottish Vacant and Derelict Land Survey were introduced in the ArcGIS Pro software. To reduce the complexity and render the model computationally feasible, the fields were grouped into 15 clusters with an additional centralized cluster using the embedded k-means clustering method. The underlying concept is that biomass is transported from fields to the center of each cluster. Subsequently, the driving distances between all cluster nodes were calculated with ArcGIS.
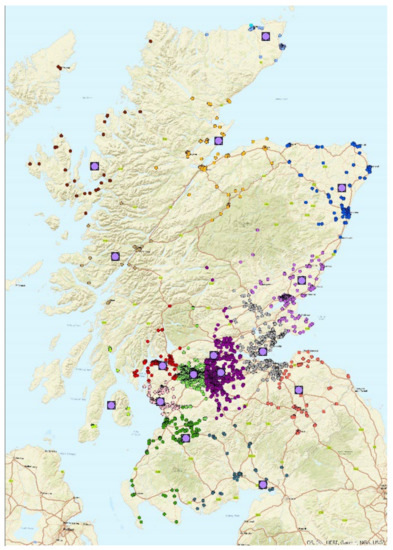
Figure 3.
Clusters of marginal lands in Scotland. The small nodes depict the individual marginal fields spatially grouped by color. The big purple nodes depict the node centers of each colored group.
4. Results
4.1. Scenarios and Inputs
A scenario analysis is performed to investigate the effect of specific parameters on the design and profitability of the proposed biomass-to-biofuel supply chain network. In particular, a reference and eight alternative scenarios are developed as follows:
- 1.
- Scenario base case (BC)—The BC scenario has full degrees of freedom to select the optimal mix of fixed and mobile facilities.
- 2.
- Scenario only fixed (OF)—The OF scenario represents the typical centralized biomass supply chain scheme without the existence of mobile facilities.
- 3.
- Scenario double distance (D100)—The D100 scenario stems from BC but the transportation cost is augmented by 100%.
- 4.
- Scenario no storage (NS)—The NS scenario stands without the warehouse option
- 5.
- Scenario double storage cost (S100)—The S100 scenario stems from BC but with an increased storage cost by 100%.
- 6.
- Scenario reduced yields (RY)—The RY scenario considers smaller yields at MFP compared to FFP facilities, namely 51% for bio-oil and 25% for biochar.
- 7.
- Scenario reduced MFP investment by 30% (M30)—The M30 scenario investigates the effect of a reduced investment cost of MFP facilities.
- 8.
- Scenario double MFP’s lifetime (LT100)—The LT100 scenario considers MFP and FFP facilities having the same lifetime of 20 years, thus reducing the related annualized costs.
- 9.
- Scenario storage three month perish (P3)—The P3 scenario allows a maximum biomass storage time of three months.
The proposed MILP model is implemented in GAMS and solved using the commercial solver XPRESS using a Processor 11th Gen Intel(R) Core(TM) i9-11900K @ 3.50 GHz, 8 Core(s), 16 Logical Processor(s) with 32 GB of RAM. The data used in this work are summarized in Table 1.

Table 1.
Data input.
4.2. Optimization Outcomes
The overview of the outcomes of the nine scenarios is shown in Table 2, revealing a trade-off between economies of scale of larger units and the flexibility of small-scale mobile units. Without the option of MFP units, the OF scenario prescribes the establishment of three FFP facilities, two more compared to BC. These two extra facilities are located close to biomass fields to overcome the large biomass transportation costs at the expense of quite moderate annual utilization rates near 50%. The selection of one MFP facility in BC that is increased to three mobile units in D100 shows that as the spatial density of the supply chain network becomes sparser (larger distances between nodes) meaning higher transportation costs, the advantages of mobile processing facilities become more pronounced. The increased number of MFP units limits the inefficient transportation of low-density biomass with trailer trucks and promotes the more cost-efficient use of tanker trucks to transfer bio-oil to FU facilities.

Table 2.
Overview of scenario results.
Increased selection of MFP units is also noticed when their capital costs are reduced (Scenario M30), indicating both the need but also the feasibility for this technology option to become more cost competitive. Due to this capital cost gain, M30 scenario presents the highest profitability among all scenarios, followed by LT100 and BC. Both LT100 and RY scenarios’ results complement the need for the MFP technology to advance both in lifetime and bio-oil yield and become more commercially mature.
Scenarios that do not use MFP at all include RY due to the obvious disadvantage of reduced product yields from MFP units, which it is assumed increases the cost per unit of the product, ultimately leading to the same system as in the OF scenario, scenario P3, where biomass has a limited storage lifetime, and scenario NS, where storage of biomass is not allowed at all. Therefore, ensuring similar yields with FFP units and using biomass storage improves the potential for using MFP units in a biomass-to-biofuel supply chain. It is also interesting to note that FFP units are selected in all scenarios, indicating that the economies of scale of these units are significant for locations where biomass is densely available, and MFP units have a complementary role to process biomass in more distant locations, with sparser biomass availability.
Another conclusion is that significantly higher capacities of FFP are selected in the scenarios without MFP (OF, RY, NS and P3), for the last two, this is also due to the limited timeframe available for processing the biomass due to limited or no storage. This inevitably leads to reduced utilization rates of the FFP units, which is undesirable for high capital cost equipment.
Focusing on the profitability of the various scenarios, the only options that can increase the system profit are to reduce the MFP capital cost, either directly (M30) or by extending the technology lifetime (LT100). In all other cases the profitability is reduced, with the most severe reduction when biomass storage is not allowed (NS), followed by the increased transportation cost (or, equivalently, more sparse nature of the biomass availability locations) (D100). These indicate the need for attention on the supply of biomass for an extended time period, to allow a wider operation time window for the processing facilities, as well as on the transportation costs.
Focusing more on the need for the supply of biomass for extended time periods, since Miscanthus can only be harvested at specific periods within the year, it is crucial to establish an optimal harvest and storage scheme to levelize biomass supply. Figure 4 shows the biomass production and storage fluctuations over the year, concluding that September and mainly October are the best options for harvesting because of the higher Miscanthus yield. The current storage cost justifies the narrow harvesting period, securing a more balanced supply of biomass in later months to the processing facilities when Miscanthus is either unavailable or with reduced yields. Deviations occur only in scenarios NS and P3, in which a wider biomass harvesting period is realized over the last five months due to the zero or limited storage capability, respectively. Specifically, NS scenario allows profit maximization when Miscanthus is harvested at constant volume rates from August until December, leading to lower amounts of material collected overall (see Table 2). Presenting a lower variation, P3 scenario focuses on harvesting in October for about 70% of the respective biomass amount occurring in other scenarios. Its time-limited capability to store biomass forces larger facilities to be installed for processing biomass that operate on a narrower time window, thus affecting their annual utilization rates and leading to higher fixed operating costs. As seen in Table 2, the average annual utilization rates for scenarios NS and P3 are 29% and 44%, respectively, whereas in other scenarios, such as BC, the corresponding value reaches 93%. The storage capacity drawback is also reflected in the profitability indices as the above-mentioned scenarios lag behind with values of 22.96% and 6.88%, respectively, compared to BC’s value. The double inventory cost of S100 exerts pressure on the supply chain similarly to NS and P3, forcing it to increase facility sizes and also reduce the inventory levels in relation to the other scenarios. In short, decreasing the supply chain’s ability to store biomass increases the fixed plant’s capacity to compensate for the shorter processing time window, thus increasing capital costs.
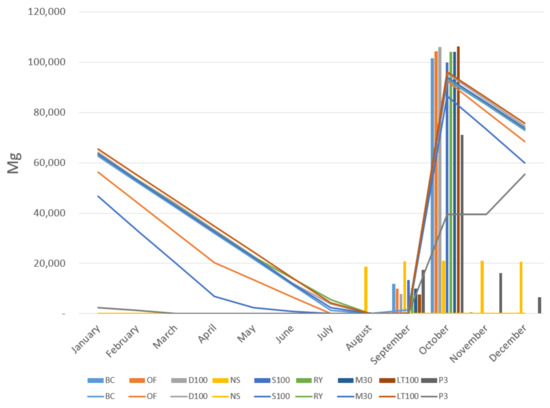
Figure 4.
Monthly dry biomass production (bars)–inventory (lines) balance.
Figure 5 depicts the cost breakdown of biofuel production (EUR/L) across all scenarios showing the uniform prevailing share of conversion cost and the minimal cost differences in aggregate level. In cases of increased MFP units’ utilization (e.g., M30), the transportation costs are lower in contrast to scenarios with large FFP facilities (e.g., NS), in which the investment costs are higher. The storage costs are relatively low in all scenarios with the exceptions of P3 and NS with small up to zero share and S100 presenting the highest storage cost. As a general conclusion, there is a trade-off between biomass storage cost and investment cost for higher capacity facilities, with the best options using storage to allow year-round operation of the processing facilities, thus reducing the required capacity and the related capital cost.
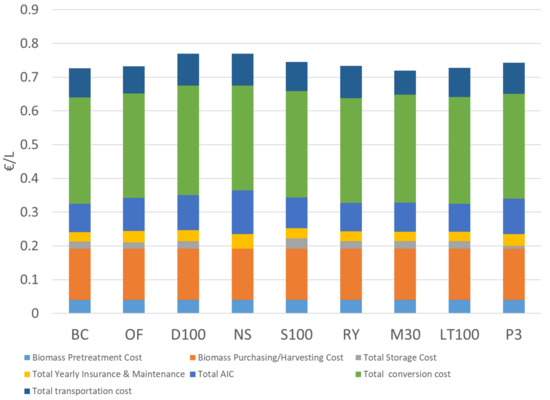
Figure 5.
Cost breakdown of biofuel production.
Figure 6 focuses explicitly on the transportation costs, revealing the negligible contribution of relocation cost, even in cases of high MFP facilities’ usage. It remains low, only accounting for 1.17% of the total transportation cost and 0.14% of the total supply chain cost as shown in Table 3.
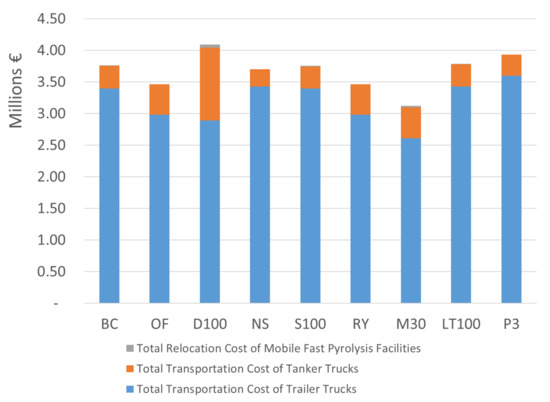
Figure 6.
Transportation cost breakdown.

Table 3.
Percentage contribution of relocation cost to transportation and total cost.
Focusing on the detailed design of the BC scenario, it can be concluded that the economic performance against the typical OF scenario is improved by combining the advantage of FFP facilities of lower unitary capital cost and higher productivity, and of MFP facilities of lower transportation costs and higher flexibility. However, the profitability improvement is quite small overall, indicating that the wins on transportation efficiencies against loss of economies of scale at processing are marginal in the studied case. The Miscanthus fields are fully harvested, processed at different time periods and transferred to the processing facilities. The optimal solution indicates the installation of one FFP, one MFP and one FU unit with capacities of 291 Mg/d, 50 Mg/d and 200 Mg/d, respectively, where both the FFP and FU are located at the red square location of Figure 7. The model forces the siting of the FFP and FU facilities in a centralized location with large amounts of biomass in its vicinity. On the contrary, biomass that is dispersed in North Scotland, is served by an MFP facility able to relocate according to the feedstock availability. In specifics, during the period of June–October, the MFP facility moves between four locations as illustrated with the green route in Figure 7. After this ‘on site’ processing of biomass, the bio-oil produced is transferred by tanker trucks to centralized facilities.
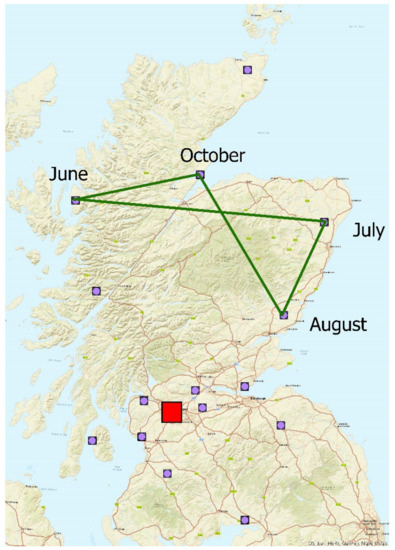
Figure 7.
Biomass supply chain setup and MFP routing (BC scenario). The purple nodes depict the node centers of each group of marginal fields. The red square depicts the establishment of an FFP and FU facility. The green line illustrates the routing of the MFP unit in monthly basis.
5. Discussion
The analysis revealed that MFP units can operate in conjunction with the fixed facilities to boost economic performance by providing increased flexibility with reduced transportation costs. When transportation distances or costs increase, the use of MFP units is promoted due to the comparative advantage of transporting the denser bio-oil over bulky biomass. In all cases, the relocation cost of mobile units accounts for a very small share of the total transportation cost. This could recommend that a simpler model formulation without representing the detailed relocation costs can also be adopted without a significant loss of accuracy in the case of the monthly-allowed MFP movement. The significance of mobile units is acknowledged in different studies in the literature. Specifically, uncertainty favors the deployment of MFP units [22]; modular gasifiers cause a 1 to 4% reduction in biomass processing waste costs [19], while mobile densification can be attractive in cases of varying distances, capital and processing costs [20]. Under the same perspective, our methodological approach contributes to the detailed modeling and evaluation of mobile units, ascertaining their benefits in the context of biomass supply chains under the examination of different scenarios. Regarding storage and given the intense seasonality and the variable yield profile of Miscanthus, the warehouse’s role was highlighted as significant in leveling feedstock supply to the processing facilities over wider time periods, thus achieving higher utilization rates for the high capital cost fixed processing facilities. It is indicative that in the case without biomass storage (NS scenario), the profit reduction is almost 23% compared to the BC scenario.
The present study introduces a formulation for the detailed relocation cost of MFP units and integrates the harvesting schedule aspect into the supply chain optimization, differently from the typical continuous biomass supply assumption. Therefore, the proposed model contributes to the academic knowledge by embedding, for the first time in a single model, a detailed calculation of the relocation costs of mobile processing units with seasonal availability of biomass. Researchers can use the model for additional case study applications and for further investigations of the potential for combining fixed with mobile facilities in other biofuel, biomass energy or even biomaterial supply chains. The proposed approach is particularly beneficial for investigating biomass types with seasonal availability as well as with high biomass/land availability dispersion. This methodology can also support a number of stakeholders, such as farm owners, biofuel producers, energy companies, technology providers, policy institutions, local and public authorities, etc., in the decision-making process for evaluating the exploitation potential of dispersed, marginal or degraded land. Business entities are offered a strategic tool to investigate the effect of different parameters in the techno-economic robustness and viability of a biomass supply chain. Policy makers can run various scenarios of policy support measures for biofuel production stimulation from a variety of feedstocks and understand the potential impact of their policies on the biofuel production costs. It can also support decisions on the optimal scale of intervention, i.e., centralized or decentralized, with the potential use of mobile units.
This study implemented a detailed decentralized approach considering biomass growth variability attempting to address new aspects and fill gaps in the related research field, but there are still some limitations. Due to the lack of experimental data, (a) the biomass moisture content was assumed constant, and (b) though marginal lands are expected to produce less biomass compared to agricultural lands, the present model did not take into account differentiated land yields among candidate locations for planting and harvesting. Another limitation lies in considering the negligible MFP setup time and costs, but taking them into account in the relocation cost, especially when time discretization is denser and MFP movements are more frequent, could make their effect more considerable on the total transportation costs.
Future research directions can include the incorporation of environmental aspects along the supply chain, to investigate the impact of mobile facilities on the supply chain’s environmental performance and possible trade-offs in the context of GHG emissions. Additionally, a portfolio of candidate biomass sources could be considered in order to diversify the annual biomass supply mix, mitigate the risks originating from feedstock availability and enhance feedstock supply security. Finally, the ‘softer’ benefits from adopting mobile processing facilities should be investigated in the future since the flexibility offered against changes over time for land and biomass availability, and the related risk reduction on the investment, have not been considered in this study.
6. Conclusions
This work presented a deterministic multiperiod MILP biomass-to-biofuel supply chain model designed to include fixed and mobile facilities as candidate processing options. It is a parametric model, able to cover any geographical area, exploiting its interoperability with GIS output data. The model was applied in a case study of marginal lands in Scotland planted with Miscanthus. Nine scenarios were investigated to explore the variations in the supply chain’s optimal design in the context of mobile facility techno-economic characteristics, transportation burden and storage availability. The aim was to investigate the role and potential benefits of adding MFP units to the design, operation and profitability of the biofuel supply chain, under a variable growth rate of biomass that is located in spatially-dispersed fields.
The model application demonstrated that the addition of mobile processing options and the decentralized conversion of biomass to a denser, more easily transportable intermediate material can boost the economic performance of biomass supply chains and enable the exploitation of lands that would otherwise remain unused. Furthermore, it is possible under certain conditions that a wider processing time window, facilitated by biomass harvesting beyond the maximum yield timing and combined with appropriate storage planning, may enable smaller capacity facilities, thus decreasing overall system costs.
Author Contributions
F.P.: conceptualization, methodology, visualization, writing—original draft preparation, data curation; P.N.G.: conceptualization, methodology, writing—review and editing, validation. A.R.: conceptualization, methodology, writing—review and editing, supervision, validation, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This study is part of the CERESiS project, which has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 101006717.
Data Availability Statement
Data are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Sets | |
| brp | Set of breakpoints for the investment cost curve of FFP facility |
| bru | Set of breakpoints for the investment cost curve of FU facility |
| f | Set of all fields |
| m, m′ | Set of candidate locations for the relocation of MFP facilities |
| n | Set of all nodes in the supply chain superstructure |
| p | Set of candidate locations for FFP facilities |
| s | Set of candidate location for storage facilities |
| t | Set of monthly time periods |
| u | Set of candidate locations for FU facilities |
| v | Set of MFP facilities (vehicles) |
| Parameters | |
| Total annualized investment costs (EUR) | |
| Area of field f (ha) | |
| Total biomass purchasing/harvesting cost (EUR/yr) | |
| Total conversion cost (EUR/yr) | |
| Conversion cost of FFP facilities (EUR/yr) | |
| Conversion cost of FU facilities (EUR/yr) | |
| Conversion cost of MFP facilities (EUR/yr) | |
| Purchasing cost of MFP facility (EUR) | |
| Cost of purchasing/harvesting biomass (EUR/tdry-biomass) | |
| Conversion cost in FFP facility (EUR/tdry-biomass) | |
| Conversion cost in FU facility (EUR/tbiofuel) | |
| Conversion cost in MFP facility (EUR/tdry-biomass) | |
| Cost of transporting MFP for 1 km (EUR/km) | |
| Cost of transporting 1 ton of bio-oil for 1 km (EUR/t km) | |
| Cost of transporting 1 ton of biomass for 1 km (EUR/t km) | |
| Distance between nodes (km) | |
| Height of storage facility (m) | |
| Storage cost per ton of biomass per month (EUR/tdry-biomass/month) | |
| Total investment cost of FFP facilities (EUR) | |
| Total investment cost of FU facilities (EUR) | |
| Total investment cost of MFP facilities (EUR) | |
| Capacity of MFP facility (tdry-biomass/month) | |
| Lifetime of FFP facility (yr) | |
| Lifetime of FU facility (yr) | |
| Lifetime of MFP facility (yr) | |
| A sufficiently big enough number for the Big-M linearization method | |
| Cost breakpoint values of the FFP facility in the capacity/cost curve (EUR) | |
| Break points of the capacity per month/cost curve of the FFP facility (tdry-biomass) | |
| Break points of the FU facility cost in the capacity/cost curve (EUR) | |
| Βreak points of the capacity per month/cost curve of the FU facility (tbio-oil) | |
| Selling price of biochar (EUR) | |
| Selling price of biofuel (EUR) | |
| Biomass availability at time period t (tdry-biomass/ha) | |
| Biochar revenue (EUR/yr) | |
| Biofuel revenue (EUR/yr) | |
| Discount rate (%) | |
| Total transportation cost (EUR/yr) | |
| Transportation cost of biomass from fields to MFP facilities (EUR/yr) | |
| Transportation cost of biomass from fields to FFP facilities (EUR/yr) | |
| Transportation cost of biomass from fields to storage facilities (EUR/yr) | |
| Total relocation cost of MFP facilities (EUR/yr) | |
| Transportation cost of bio-oil from MFP to FU facilities (EUR/yr) | |
| Transportation cost of bio-oil from FFP to FU facilities (EUR/yr) | |
| Transportation cost of biomass from storage to MFP facilities (EUR/yr) | |
| Transportation cost of biomass from storage to FFP facilities (EUR/yr) | |
| Conversion factor of biomass to biochar in FFP facility (tbiochar/tdry-biomass) | |
| Conversion factor of biomass to biochar in MFP facility (tbiochar/tdry-biomass) | |
| Conversion factor of bio-oil to biofuel in FU facility (tbiofuel/tbio-oil) | |
| Conversion factor of biomass to bio-oil in FFP facility (tbio-oil/tdry-biomass) | |
| Conversion factor of biomass to bio-oil in MFP facility (tbio-oil/tdry-biomass) | |
| Moisture content of biomass (%) | |
| Biomass bulk density (tdry-biomass/m3) | |
| Annual maintenance costs of FFP facilities (% of investment) | |
| Annual maintenance costs of FU facilities (% of investment) | |
| Annual insurance costs (% of investment) | |
| Annual maintenance costs of MFP facilities (% of investment) | |
| Binary variables | |
| 1 if field f is harvested at time period t, 0 otherwise | |
| 1 if MFP facility v is relocated from mobile candidate location m to m′ at time period t, 0 otherwise | |
| 1 if MFP facility v is located at candidate mobile location m at time period t, 0 otherwise | |
| 1 if FFP facility p is established, 0 otherwise | |
| 1 if storage facility s is established, 0 otherwise | |
| 1 if FU facility u is established, 0 otherwise | |
| 1 if MFP facility v is used, 0 otherwise | |
| Auxiliary binary variable for piecewise linearization of cost of FFP facility | |
| Auxiliary binary variable for piecewise linearization of cost of FU facility | |
| Continuous variables | |
| Storage area of storage facility s (m2) | |
| Amount of biomass stored at storage facility s at time period t (tdry-biomass) | |
| Capacity of FFP facility p (tdry-biomass/month) | |
| Capacity of FU facility u (tbio-oil/month) | |
| Amount of biomass transported from field f to MFP facility v at location m at time period t (tdry-biomass) | |
| Amount of biomass transported from field f to FFP facility p at time period t (tdry-biomass) | |
| Amount of biomass transported from field f to storage facility s at time period t (tdry-biomass) | |
| Amount of bio-oil transported from MFP facility v at location m to FU u at time period t (tbio-oil) | |
| Amount of bio-oil transported from FFP facility p to FU facility u at time period t (tbio-oil) | |
| Amount of biomass transported from storage facility s to MFP facility v at location m at time period t (tdry-biomass) | |
| Amount of biomass transported from storage facility s to FFP facility p at time period t (tdry-biomass) | |
| Auxiliary continuous variable for the piecewise linearization of FFP facility cost (0,1) | |
| Auxiliary continuous variable for the piecewise linearization of FU facility cost (0,1) | |
References
- Goldemberg, T.; Johansson, J. World Energy Assessment Overview 2004; United Nations Development Programme: New York, NY, USA, 2004. [Google Scholar]
- European Parliament and Council. Directive 2001/77/EC on the Promotion of Electricity Produced from Renewable Energy Sources in the Internal Energy Market. Off. J. 2001, 6, 12–25. [Google Scholar]
- United Nations Framework Convention on Climate Change. Long-Term Low Greenhouse Gas Emission Development Strategy of the European Union and Its Member States; UNFCCC: Bonn, Germany, 2020; Volume 2019, pp. 1–7. Available online: http://www4.unfccc.int/submissions/INDC/PublishedDocuments/Latvia/1/LV-03-06-EUINDC.pdf (accessed on 25 May 2022).
- EP. The European Green Deal-European Parliament Resolution of 15 January 2020 on the European Green Deal (2019/2956(RSP)). 2019. Available online: https://www.europarl.europa.eu/doceo/document/TA-9-2020-0005_EN.html (accessed on 25 May 2022).
- International Energy Agency. Technology Roadmap: Delivering Sustainable Bioenergy; IEA: Paris, France, 2017; Volume 63, pp. 87–91.
- Leboreiro, J.; Hilaly, A.K. Biomass transportation model and optimum plant size for the production of ethanol. Bioresour. Technol. 2011, 102, 2712–2723. [Google Scholar] [CrossRef] [PubMed]
- Vitale, I.; Dondo, R.G.; González, M.; Cóccola, M.E. Modelling and optimization of material flows in the wood pellet supply chain. Appl. Energy 2022, 313, 118776. [Google Scholar] [CrossRef]
- Zimon, D.; Woźniak, J.; Domingues, P.; Ikram, M.; Kuś, H. Proposition of Improving Selected Logistics Processes of Pellet production. Int. J. Qual. Res. 2021, 15, 387–402. [Google Scholar] [CrossRef]
- Bridgwater, A.V. Review of fast pyrolysis of biomass and product upgrading. Biomass Bioenergy 2012, 38, 68–94. [Google Scholar] [CrossRef]
- Jalalifar, S.; Abbassi, R.; Garaniya, V.; Hawboldt, K.; Ghiji, M. Parametric analysis of pyrolysis process on the product yields in a bubbling fluidized bed reactor. Fuel 2018, 234, 616–625. [Google Scholar] [CrossRef]
- Bolan, N.; Hoang, S.A.; Beiyuan, J.; Gupta, S.; Hou, D.; Karakoti, A.; Joseph, S.; Jung, S.; Kim, K.-H.; Kirkham, M.; et al. Multifunctional applications of biochar beyond carbon storage. Int. Mater. Rev. 2022, 67, 150–200. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Sadeqzadeh, M.; Guo, M.; Borhani, T.N.; Konda, N.M.; Garcia, M.C.; Wang, L.; Hallett, J.; Shah, N. The multi-scale challenges of biomass fast pyrolysis and bio-oil upgrading: Review of the state of art and future research directions. Prog. Energy Combust. Sci. 2019, 71, 1–80. [Google Scholar] [CrossRef]
- Moretti, L.; Milani, M.; Lozza, G.G.; Manzolini, G. A detailed MILP formulation for the optimal design of advanced biofuel supply chains. Renew. Energy 2021, 171, 159–175. [Google Scholar] [CrossRef]
- Kwon, O.; Han, J. Waste-to-bioethanol supply chain network: A deterministic model. Appl. Energy 2021, 300, 117381. [Google Scholar] [CrossRef]
- Kwon, O.; Kim, J.; Han, J. Organic waste derived biodiesel supply chain network: Deterministic multi-period planning model. Appl. Energy 2021, 305, 117847. [Google Scholar] [CrossRef]
- Yahya, N.S.M.; Ng, L.Y.; Andiappan, V. Optimisation and planning of biomass supply chain for new and existing power plants based on carbon reduction targets. Energy 2021, 237, 121488. [Google Scholar] [CrossRef]
- Jonkman, J.; Kanellopoulos, A.; Bloemhof, J.M. Designing an eco-efficient biomass-based supply chain using a multi-actor optimisation model. J. Clean. Prod. 2019, 210, 1065–1075. [Google Scholar] [CrossRef]
- Baghizadeh, K.; Zimon, D.; Jum’A, L. Modeling and Optimization Sustainable Forest Supply Chain Considering Discount in Transportation System and Supplier Selection under Uncertainty. Forests 2021, 12, 964. [Google Scholar] [CrossRef]
- Allman, A.; Lee, C.; Martín, M.; Zhang, Q. Biomass waste-to-energy supply chain optimization with mobile production modules. Comput. Chem. Eng. 2021, 150, 107326. [Google Scholar] [CrossRef]
- Albashabsheh, N.T.; Stamm, J.L.H. Optimization of lignocellulosic biomass-to-biofuel supply chains with mobile pelleting. Transp. Res. Part E Logist. Transp. Rev. 2019, 122, 545–562. [Google Scholar] [CrossRef]
- Albashabsheh, N.T.; Stamm, J.L.H. Optimization of lignocellulosic biomass-to-biofuel supply chains with densification: Literature review. Biomass Bioenergy 2020, 144, 105888. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Garcia, M.C.; Shah, N. Supply chain network design and operation: Systematic decision-making for centralized, distributed, and mobile biofuel production using mixed integer linear programming (MILP) under uncertainty. Biomass Bioenergy 2015, 81, 401–414. [Google Scholar] [CrossRef] [Green Version]
- Mirkouei, A.; Haapala, K.R.; Sessions, J.; Murthy, G.S. A mixed biomass-based energy supply chain for enhancing economic and environmental sustainability benefits: A multi-criteria decision making framework. Appl. Energy 2017, 206, 1088–1101. [Google Scholar] [CrossRef]
- Paolucci, N.; Bezzo, F.; Tugnoli, A. A two-tier approach to the optimization of a biomass supply chain for pyrolysis processes. Biomass Bioenergy 2016, 84, 87–97. [Google Scholar] [CrossRef]
- You, F.; Wang, B. Life Cycle Optimization of Biomass-to-Liquid Supply Chains with Distributed–Centralized Processing Networks. Ind. Eng. Chem. Res. 2011, 50, 10102–10127. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, J.; Yi, W.; Cai, H.; Li, Y.; Su, Z. Agri-biomass supply chain optimization in north China: Model development and application. Energy 2021, 239, 122374. [Google Scholar] [CrossRef]
- Razm, S.; Nickel, S.; Sahebi, H. A multi-objective mathematical model to redesign of global sustainable bioenergy supply network. Comput. Chem. Eng. 2019, 128, 1–20. [Google Scholar] [CrossRef]
- Razak, N.H.; Hashim, H.; Yunus, N.A.; Klemeš, J.J. Integrated GIS-AHP optimization for bioethanol from oil palm biomass supply chain network design. Chem. Eng. Trans. 2021, 83, 571–576. [Google Scholar] [CrossRef]
- Winston, W.L.; Goldberg, J.B. Operations Research: Applications and Algorithms; Belmont: Nashville, TN, USA, 2004; Volume 73. [Google Scholar]
- Tan, W.; Khoshnevis, B. A linearized polynomial mixed integer programming model for the integration of process planning and scheduling. J. Intell. Manuf. 2004, 15, 593–605. [Google Scholar] [CrossRef]
- SVDLS. Scottish Vacant and Derelict Land Survey. 2021. Available online: https://www.gov.scot/publications/scottish-vacant-and-derelict-land-survey---site-register/ (accessed on 25 November 2021).
- Mos, M.; Robson, P.R.H.; Buckby, S.; Hastings, A.F.; Helios, W.; Jama-Rodzeńska, A.; Kotecki, A.; Kalembasa, D.; Kalembasa, S.; Kozak, M.; et al. Seasonal Dynamics of Dry Matter Accumulation and Nutrients in a Mature Miscanthus × giganteus Stand in the Lower Silesia Region of Poland. Agronomy 2021, 11, 1679. [Google Scholar] [CrossRef]
- Sustainable Energy Authority of Ireland. Miscanthus Factsheet. 2013, p. 4. Available online: https://www.ifa.ie/wp-content/uploads/2013/10/Miscanthus-Factsheet-SEAI.pdf (accessed on 25 May 2022).
- Ben Fradj, N.; Jayet, P.-A. Impacts of promoting perennial crops in the French agriculture. In Proceedings of the EAAE 2011, Zurich, Switzerland, 30 August–2 September 2011; pp. 1–10. [Google Scholar]
- Van der Meulen, S.; Grijspaardt, T.; Mars, W.; van der Geest, W.; Roest-Crollius, A.; Kiel, J. Cost Figures for Freight Transport—Final Report; Research to Progress; Panteia: Zoetermeer, The Netherlands, 2020; pp. 1–85. [Google Scholar]
- Rentizelas, A.; Tolis, A.; Tatsiopoulos, I.P. Logistics issues of biomass: The storage problem and the multi-biomass supply chain. Renew. Sustain. Energy Rev. 2009, 13, 887–894. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Nanda, S.; Guayaquil-Sosa, J.F.; Berruti, F. Pyrolysis of Miscanthus and characterization of value-added bio-oil and biochar products. Can. J. Chem. Eng. 2020, 99, S55–S68. [Google Scholar] [CrossRef]
- United Nations Industrial Development Organization. Market Analysis of Biochar Produced by Small-Scale Pyrolysis Units in Vietnam; United Nations Industrial Development Organization: Vienna, Austria, 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).