Nonlinear Self-Synchronizing Current Control for Grid-Connected Photovoltaic Inverters ^†

Abstract

Three-phase inverters for photovoltaic grid-connected applications typically require some form of grid voltage phase-angle detection in order to properly synchronize to the grid and control real and reactive power generation. Typically, a phase-locked loop scheme is used to determine this real-time phase angle information. However, in the present work, a novel method is proposed whereby the phase angle of the grid can be accurately identified solely via the grid current feedback. This phase-angle observer is incorporated into a current controller which can manage the real and reactive power of the grid-connected PV inverter system. Moreover, the maximum power point of the photovoltaic arrays is achieved without using a DC–DC converter. The proposed method achieves the grid current and DC-link voltage control objectives without the knowledge of the grid information and without the need for a cascaded control scheme. The design of this combined observer/controller scheme is motivated and validated via a Lyapunov stability analysis. The experimental setup is prototyped utilizing a real-time Typhoon HIL 603 and National Instrument cRIO embedded controller in order to validate the proposed observer/controller scheme under different operation scenarios such as irradiation changes, frequency changes, reactive power injection, and operation with a distorted grid. The results show that the DC-link voltage and the active and reactive powers are well regulated from the proposed control scheme without the measurement of the grid phase and frequency.

1. Introduction

Solar energy is the most abundant and the cleanest form of renewable energy sources available in the world, which is used for a variety of applications, such as generation of electricity for domestic, commercial, or industrial applications [1,2]. Nowadays, photovoltaic (PV) generation is becoming a vital part of modern energy systems due to the cost reduction of manufacturing PV modules. Additionally, improvements in the energy extraction from solar panels has made PV generation more efficient and reliable than other generating sources [2,3]. Electrical power generated by PV array depends on the temperature and the solar irradiation, which has a strong nonlinear effect. Recently, the proliferation of installed grid-connected PV systems have begun to impact the stability of the power grid [4,5]. Thus, real-time control of grid-connected inverter systems has drawn recent attention in the literature [6,7]. The affects seen on the power system due to the stochastic nature of PV power outputs has drawn attention to the control system aspect of PV systems [8]. In the literature, connecting PV arrays to the utility grid has been accomplished in many forms and configurations [8,9]. Traditional PV systems utilize a two-stage power converter system with closed loop control schemes utilized throughout. A DC–DC converter is typically utilized as a first stage to regulate the voltage of the DC-link capacitor, thereby ensuring maximum power point operation for the PV arrays. The second stage is the DC–AC power converter, which injects AC power into the grid and/or supports a local load [10]. Using a two-stage topology results in a reduction of the system efficiency as well as an increase in the system cost [2]. For these reasons, a single-stage, three-phase, grid-connected PV system with maximum power point tracking (MPPT) and DC–AC converter will be used in this work.

Unintentional connection of the PV-based grid-connected inverter systems to the utility grid is undesirable as this could lead to system to instability [11]. Thus, in order to perform safe connection between the distribution generation unit (such as the PV-based inverter) and the grid, a synchronization unit is necessary to obtain the grid’s phase angle and frequency before connection to avoid an instantaneous out of phase connection. The main method that is used in the literature for this purpose is a Phase Locked Loop (PLL). Moreover, the grid’s information that is extracted from PLLs is used in the coordinate transformation in three-phase systems [12,13,14]. A PLL system is mainly integrated with the primary current control scheme as an outer loop, thus creating a cascaded control system [13,15]. In such cascaded schemes, the dynamics of the outer loop (in this case the PLL) should be slower (bandwidth) than the inner loop (current control loop) to maintain the stability of the system. On the other hand, the slow dynamic of a PLL-loop means delays in the detection of the grid’s phase and frequency, both of which are necessary for the current control loop. Moreover, adding a PLL loop to the main control loop will add more complexity to the system [16]. Many approaches have been proposed in the literature to improving the performance of the PLL schemes to address any potential instability issues resulting from the interaction between the PLL schemes and current control loop [17,18]. These challenges have motivated researchers to develop control schemes for grid-connected inverters that do not require a synchronization system such as PLLs [19,20,21,22]. For instance, the authors in [23] proposed a direct power controller for a single-phase grid-connected inverter without a PLL scheme. Moreover, we proposed in our work in [24] a method for a PLL-less current control scheme for three-phase, grid-connected inverters. Although these methods do not need a PLL scheme, they do not consider a grid-connected PV system or the additional dynamics this would entail. Previous studies [19,20,21,22,23,24] have considered a fixed dc voltage as an input. Hence, the dynamic of the PV panels, dc voltage regulator, and maximum power point tracking algorithm are not included in their control schemes.

A few works have investigated a PLL-less synchronization procedure for PV inverter systems. For example, in [25], the authors propose a current control scheme for single-phase PV inverter systems without a PLL scheme. The problem with this approach is that the control scheme has multiple current loops, which is problematic in managing the bandwidths with the various loops to insure the stability of the whole system. In [26], we propose a PLL-less current control scheme for PV inverter systems. Simulation results demonstrated the effectiveness of this approach to simultaneously control the grid current, DC-link voltage, and estimate the grid phase and frequency.

In this paper, a single-stage, three-phase, grid-connected photovoltaic system is controlled by a novel nonlinear current controller. The main contribution of the proposed controller is that the current tracking objective is achieved without knowledge of the grid phase angle and frequency. To do so, an estimated rotating reference frame (γδ-frame) is utilized [27]. Moreover, the proposed control scheme ensures that tracking of the DC-link capacitor reference voltage-generated from MPPT algorithm is achieved. This algorithm ensures the PV array(s) achieves their maximum power operating point. Within the control scheme, adaptive compensation terms facilitate the voltage and current tracking objectives and simultaneously account for the unavailable grid frequency and phase, hence eliminating the need for an additional feedback system for synchronization, such as a PLL. The voltage sensors required for PLL-type systems are expensive and introduce electrical noise and dc offsets, which must be compensated for in other ways.

The main contributions of the present work over our previous published work [26] and other works in the literature are:

1.

The proposed controller/observer scheme eliminates the need for a cascaded control scheme. A cascaded approach is necessary in traditional control schemes for such an application to regulate the DC-link capacitor voltage, control the grid current, and determine the grid information extraction loop (PLL).

2.

In terms of the control design, a new term has been added to both the DC-link voltage dynamics and grid current dynamics which accounts for un-modeled dynamics terms. Inclusion of these terms was motivated by validation experiments. Then, during the control design process, adaptive compensation terms have been included in the control to compensate for these uncertainties.

3.

In terms of validation, an experimental setup has been prototyped to further validate the proposed scheme, including both control and observer aspects. A combination between Typhoon HIL [28,29,30,31] and National Instrument real time compact RIO has been used for this purpose. Furthermore, the proposed controller/observer scheme has been tested in different operating scenarios including sudden change to solar irradiance, grid frequency fluctuation, reactive power injection, and distorted grid utility.

2. System Model

A single-stage, three-phase, PV grid-connected inverter system with an inductive filter is shown in Figure 1. By applying Kirchhoff’s voltage law, the dynamic mathematical model for this system can be represented as

$$v_{abc}\triangleq L{\dot{I}}_{abc}+R{I}_{abc}+e_{abc},$$

(1)

where $v_{abc}\left(t\right)\in {ℝ}^{3\times 1}$ are the phase voltages, $I_{abc}\left(t\right)\in {ℝ}^{3\times 1}$ are the phase currents, and $e_{abc}\in {ℝ}^{3\times 1}$ are the voltages of the point of common coupling (PCC) at which the system is connected to the public utility grid. Assuming a switching average model, the three-phase inverter output voltages as the product to the DC-link voltage $V_{dc}$ and the duty cycles of their respective switching legs can be represented as

$$v_{abc}\triangleq V_{dc}{D}_{abc}$$

(2)

where the duty cycles, $D_{abc}\left(t\right)\in \left[0,1\right]$. Moreover, assuming a balanced utility grid, the three-phase PCC voltages can be rewritten as

$$e_{abc}\triangleq E_m\cos \left(\theta \pm \varphi \right)$$

(3)

where $E_m$ is the amplitude of the PCC voltage, $\theta \left(t\right)$ is the phase angle of the same voltage which will be donated as a grid phase angle, and $\varphi =0 \mathrm{and} 120$ to represent balanced three-phase voltages. By substituting (2) and (3) into (1), the three-phase grid current dynamics can be obtained as

$$L{\dot{I}}_{abc}=V_{dc}{D}_{abc}-R{I}_{abc}-E_m\cos \left(\theta \pm \varphi \right).$$

(4)

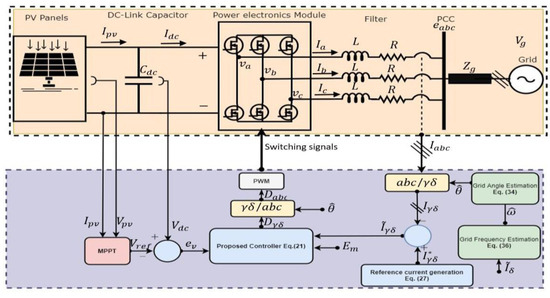
Figure 1. Three-Phase Grid Connected PV System and proposed control scheme.

From Figure 1, the dynamic equation of the DC-link capacitor of the PV System can be obtained by applying Kirchhoff’s current law (KCL) at the capacitor node as follows:

$$C{\dot{V}}_{dc}=I_{pv}-I_{dc}$$

(5)

where $I_{pv}$ is the output current from PV panels, and $I_{dc}$ is the DC input current to the inverter.

By using the standard Clarke and Park transformations, the $dq$-reference frame model for the system dynamics is obtained as

$$L\left[\begin{array}{c}{\dot{I}}_d\\ {\dot{I}}_q\end{array}\right]=V_{dc}\left[\begin{array}{c}{D}_d\\ D_q\end{array}\right]-\left[\begin{array}{cc}R& -\omega L\\ \omega L& R\end{array}\right]\left[\begin{array}{c}{I}_d\\ I_q\end{array}\right]-E_m\left[\begin{array}{c}1\\ 0\end{array}\right]$$

(6)

where $\omega \left(t\right)\triangleq \dot{\theta }\left(t\right)$ is the grid frequency.

In this work, the grid angle $\theta \left(t\right)$ is an unmeasurable and unknown parameter. Therefore, designing an observer for the grid angle $\widehat{\theta }\left(t\right)$ is required to perform the $dq$ transformations in the estimated reference frame [27]. This results in a rotating orthogonal axis system denoted as $\gamma \delta$. After performing the transformation in the $\gamma \delta$ frame, the system shown in (6) can be written as

$$L\left[\begin{array}{c}{\dot{I}}_{\gamma }\\ {\dot{I}}_{\delta }\end{array}\right]=V_{dc}\left[\begin{array}{c}{D}_{\gamma }\\ D_{\delta }\end{array}\right]-\left[\begin{array}{cc}R& -\dot{\widehat{\theta }}L\\ \dot{\widehat{\theta }}L& R\end{array}\right]\left[\begin{array}{c}{I}_{\gamma }\\ I_{\delta }\end{array}\right]-E_m\left[\begin{array}{c}\cos \tilde{\theta }\\ \sin \tilde{\theta }\end{array}\right]+d_i\left[\begin{array}{c}1\\ 0\end{array}\right]$$

(7)

where $\tilde{\theta }\left(t\right)$ is the error between the actual grid phase angle, and the observed phase angle will be defined later. In (7), $d_i\left(t\right)\in ℝ$ is an unknown, slowly time-varying term added to compensate for any unknown disturbance and imperfect inverter modelling.

The dynamic equation of the DC-link capacitor in (5) can be modified by using the active power balance principle between the dc and ac system sides as follows:

$$P_{dc}\triangleq P_{ac}$$

(8)

where

$$P_{dc}=V_{dc}{I}_{dc}$$

(9)

and

$$P_{ac}=e_{abc}{i}_{abc}=E_m\cos \left(\theta \pm \varphi \right)I_{abc}$$

(10)

Based on the Clarke transformation, (10) in the $\alpha \beta$-frame can be written after some mathematical simplifications as

$$P_{ac}=\frac{3}{2}{E}_m\left[\cos \theta \sin \theta \right]\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]$$

(11)

By performing the transformation of $\alpha \beta \mathrm{to} \gamma \delta$ on (11), and after some mathematical simplifications, the power equation can be obtained in $\gamma \delta$- estimated frame as follows:

$$P_{ac}=\frac{3}{2}{E}_m\left(I_{\gamma }\cos \tilde{\theta }+I_{\delta }\sin \tilde{\theta }\right).$$

(12)

Using (8), (9), and (12), the $I_{dc}$ equation can be written as

$$I_{dc}=\frac{3}{2}\frac{E_m}{V_{dc}}\left(I_{\gamma }\cos \tilde{\theta }+I_{\delta }\sin \tilde{\theta }\right)$$

(13)

Finally, the dynamic equation of the DC-link capacitor voltage for the PV inverter system in the $\gamma \delta$ estimated reference frame is obtained by substituting (13) into (5) as shown in (14):

$$C{\dot{V}}_{dc}=I_{pv}-\frac{3}{2}\frac{E_m}{V_{dc}}\left(I_{\gamma }\cos \tilde{\theta }+I_{\delta }\sin \tilde{\theta }\right)+d_v$$

(14)

where $d_v\left(t\right)\in ℝ$ is a term added to compensate for any slowly time-varying, external, unknown disturbance.

3. Control System Development

The main objective of the proposed controller/observer scheme is designing duty cycle control signals $D_{\gamma } \mathrm{and} D_{\delta }$ of the PV single-stage, three-phase, grid-connected inverter system in the absence of the grid angle $\theta \left(t\right)$ and frequency $\omega \left(t\right)$ measurements. The $I_{\gamma }\left(t\right)$ and $I_{\delta }\left(t\right)$ can follow their respective reference currents $I_{\gamma }^{*}\left(t\right)$ and $I_{\delta }^{*}\left(t\right)$,$hence, I_{\gamma }\left(t\right)\to I_{\gamma }^{*}\left(\mathrm{t}\right)\mathrm{and}{I}_{\delta }\left(t\right)\to I_{\delta }^{*}\left(\mathrm{t}\right)$ as $t\to \infty .$ Additionally, the PV array must operate at the maximum power point. To ensure this, the reference active current $I_{\gamma }^{*}\left(t\right)$ is designed in order to make sure that the DC-link capacitor voltage tracks its reference trajectory. Hence, $V_{dc}\left(t\right)\to V_{ref}\left(t\right)$ as $t\to \infty$ where the reference voltage trajectory $V_{ref}\left(t\right)$ is obtained from a standard MPPT algorithm. The subsequent stability analysis will prove that when the grid angle observer converges, $\tilde{\theta }\left(t\right)=0$, then $I_{\gamma }\left(t\right)=I_d\left(t\right), I_{\delta }\left(t\right)=I_q\left(t\right)$, which means that the active and reactive power that will be injected into the grid are controllable. The following assumptions are made to facilitate this control development.

Assumption 1.

$\alpha \beta$-frame currents $I_{\alpha }\left(t\right),I_{\beta }\left(t\right)$ are measurable. $V_{pcc}\left(t\right)$,$V_{dc}\left(t\right),I_{PV}\left(t\right)$ are also measurable.

Assumption 2.

The nominal system parameters $R,L$ are known a priori.

Assumption 3.

The grid frequency$\omega \left(t\right)$is unknown but is assumed to be a positive constant. Additionally, the grid phase angle$\theta \left(t\right)$is unknown.

Assumption 4.

The disturbance terms$d_i\left(t\right), d_v\left(t\right)$are assumed to be slowly time-varying; hence,$\dot{d_i}\left(t\right),\dot{d_v}\left(t\right)\cong 0.$

3.1. Error System Development

To facilitate the subsequent control development, the following current tracking errors are defined as

$$\left[\begin{array}{c}{\tilde{I}}_{\gamma }\\ {\tilde{I}}_{\delta }\end{array}\right]\triangleq \left[\begin{array}{c}{I}_{\gamma }^{*}\\ I_{\delta }^{*}\end{array}\right]-\left[\begin{array}{c}{I}_{\gamma }\\ I_{\delta }\end{array}\right]$$

(15)

The tracking error dynamics of the DC-link voltage for the PV inverter system are defined as

$$e_v\triangleq V_{dc}-V_{ref}.$$

(16)

Since the grid phase angle and frequency are unknown, the estimation error signals are defined as

$$\tilde{\omega }\triangleq \omega -\widehat{\omega }$$

(17)

$$\tilde{\theta }\triangleq \theta -\widehat{\theta }$$

(18)

Taking the time derivative of (15), pre-multiplying by $L$, and utilizing the system dynamics from (7), the open loop error dynamics for the current are obtained as follows:

$$L\left[\begin{array}{c}{\dot{\tilde{I}}}_{\gamma }\\ {\dot{\tilde{I}}}_{\delta }\end{array}\right]=L\left[\begin{array}{c}{\dot{I}}_{\gamma }^{*}\\ {\dot{I}}_{\delta }^{*}\end{array}\right]+\left[\begin{array}{cc}R& -\dot{\widehat{\theta }}L\\ \dot{\widehat{\theta }}L& R\end{array}\right]\left[\begin{array}{c}{I}_{\gamma }\\ I_{\delta }\end{array}\right]+E_m\left[\begin{array}{c}\cos \tilde{\theta }\\ \sin \tilde{\theta }\end{array}\right]-V_{dc}\left[\begin{array}{c}{D}_{\gamma }\\ D_{\delta }\end{array}\right]-d_i\left[\begin{array}{c}1\\ 0\end{array}\right].$$

(19)

To simplify the analysis, assume that $\tilde{\theta }\left(t\right)$ is small and centered about 0; hence, $\cos \tilde{\theta }\approx 1$. Based on this assumption, (19) can be simplified in the following form:

$$L\left[\begin{array}{c}{\dot{\tilde{I}}}_{\gamma }\\ {\dot{\tilde{I}}}_{\delta }\end{array}\right]=L\left[\begin{array}{c}{\dot{I}}_{\gamma }^{*}\\ {\dot{I}}_{\delta }^{*}\end{array}\right]+\left[\begin{array}{cc}R& -\dot{\widehat{\theta }}L\\ \dot{\widehat{\theta }}L& R\end{array}\right]\left[\begin{array}{c}{I}_{\gamma }\\ I_{\delta }\end{array}\right]+E_m\left[\begin{array}{c}1\\ \sin \tilde{\theta }\end{array}\right]-V_{dc}\left[\begin{array}{c}{D}_{\gamma }\\ D_{\delta }\end{array}\right]-d_i\left[\begin{array}{c}1\\ 0\end{array}\right].$$

(20)

3.2. Control Design

Motivated by the subsequent stability analysis and using the open loop error dynamics for the current in (20), the following duty cycle control inputs are defined as follows:

$$\left[\begin{array}{c}{D}_{\gamma }\\ D_{\delta }\end{array}\right]\triangleq \frac{1}{V_{dc}}\left(\begin{array}{c}L\left[\begin{array}{c}{\dot{I}}_{\gamma }^{*}\\ {\dot{I}}_{\delta }^{*}\end{array}\right]+\left[\begin{array}{cc}R& -\dot{\widehat{\theta }}L\\ \dot{\widehat{\theta }}L& R\end{array}\right]\left[\begin{array}{c}{I}_{\gamma }\\ I_{\delta }\end{array}\right]+\left[\begin{array}{c}{E}_m\\ 0\end{array}\right]+k_1\left[\begin{array}{c}{\tilde{I}}_{\gamma }\\ {\tilde{I}}_{\delta }\end{array}\right]-\widehat{d_i}\left[\begin{array}{c}1\\ 0\end{array}\right]\end{array}\right)$$

(21)

where $k_1\in {ℝ}^{+}$ is a positive control gain and $\widehat{d_i}\left(t\right)$ is the estimation of the unknown disturbance $d_i\left(t\right)$. The update law of $d_i\left(t\right)$ is designed based on the subsequent stability analysis and found to be as follows:

$$\dot{\widehat{d_i}}=-k_d{}_i{\tilde{I}}_{\gamma }$$

(22)

where $k_{d_i}\in {ℝ}^{+}$ is a positive estimation gain. The closed loop error dynamics of the current are obtained by substituting (21) into the open loop error dynamics in (20) as follows:

$$L\left[\begin{array}{c}{\dot{\tilde{I}}}_{\gamma }\\ {\dot{\tilde{I}}}_{\delta }\end{array}\right]=-k_1\left[\begin{array}{c}{\tilde{I}}_{\gamma }\\ {\tilde{I}}_{\delta }\end{array}\right]+\left[\begin{array}{c}0\\ E_m\sin \tilde{\theta }\end{array}\right]-\widetilde{d_i}\left[\begin{array}{c}1\\ 0\end{array}\right]$$

(23)

where $\widetilde{d_i}\left(t\right)$ is the estimation error defined as:

$${\tilde{d}}_i\triangleq d_i-{\widehat{d}}_i$$

(24)

Taking the time derivative of (16), and pre-multiplying it by $C$, and using the DC-link dynamic from (14) as well as the assumption $\cos \tilde{\theta }\approx 1$, the open loop error dynamic of the DC- link voltage can be obtained as

$$C\dot{e_v}=I_{pv}-\frac{3}{2}\frac{E_m}{V_{dc}}\left(I_{\gamma }+I_{\delta }\sin \tilde{\theta }\right)+d_v-C{\dot{V}}_{ref}$$

(25)

Utilizing the tracking error of the current $I_{\gamma }\left(t\right)$ from (15), the above equation in (25) can be rewritten as

$$C\dot{e_v}=I_{pv}-\frac{3}{2}\frac{E_m}{V_{dc}}\left(I_{\gamma }^{*}-{\tilde{I}}_{\gamma }+I_{\delta }\sin \tilde{\theta }\right)+d_v-C{\dot{V}}_{ref}.$$

(26)

Motivated by subsequent stability analysis, $I_{\gamma }^{*}\left(t\right)$ can be designed based on the Equation (26) as follows:

$$I_{\gamma }^{*}\triangleq \frac{2}{3}\frac{V_{dc}}{E_m}\left[I_{pv}-C{\dot{V}}_{ref}+k_v{e}_v+{\widehat{d}}_v\right]$$

(27)

where $K_v\in {ℝ}^{+}$ is a positive control gain and ${\widehat{d}}_v\left(t\right)$ is the estimation of the unknown disturbance with the following updating law, which is obtained based on the subsequent stability analysis:

$${\dot{\widehat{d}}}_v=-k_d{}_v{e}_v$$

(28)

where $k_{d_v}\in {ℝ}^{+}$ is a positive estimation gain.

Remark 1.

$I_{\gamma }^{*}\left(t\right)$is designed to stabilize the DC-link voltage and to make sure that the PV arrays are operating at their maximum power point. Moreover,$I_{\delta }^{*}\left(t\right)$could be selected to control the amount of the injected reactive power to the grid.

The closed loop error dynamics for $e_v\left(t\right)$ can be obtained by substituting (27) into (25) as follows:

$$C{\dot{e}}_v=\frac{3}{2}\frac{E_m}{V_{dc}}\left({\tilde{I}}_{\gamma }-I_{\delta }\sin \tilde{\theta }\right)-k_v{e}_v-{\tilde{d}}_v$$

(29)

where ${\tilde{d}}_v\left(t\right)$ is the estimation error of the unknown disturbance defined as

$${\tilde{d}}_v\triangleq d_v-{\widehat{d}}_v.$$

(30)

In order to design the grid phase-angle observer, the derivative of (18) is taken to obtain

$$\dot{\tilde{\theta }}=\omega -\dot{\widehat{\theta }}.$$

(31)

Then, motivated by the subsequent stability analysis and the above equation in (31), the angle observer can be obtained after some mathematical operations as follows:

$$\dot{\widehat{\theta }}\triangleq \widehat{\omega }+{\tilde{I}}_{\delta }+E_m\sin \tilde{\theta }-\frac{3}{2}\frac{e_v}{V_{dc}}{I}_{\delta }$$

(32)

It is notable that the above update law for the grid angle observer is unrealizable due to the unknown and unmeasurable signals such as $\tilde{\theta }\left(t\right)$. To make this observer realizable and implementable, substitute $E_m\sin \tilde{\theta }$ term from the closed loop error dynamics of ${\tilde{I}}_{\delta }\left(t\right)$ from (23) into (32) to obtain

$$\dot{\widehat{\theta }}\triangleq \widehat{\omega }+\left(k_1+1\right){\tilde{I}}_{\delta }+L{\dot{\tilde{I}}}_{\delta }-\frac{3}{2}\frac{e_v}{V_{dc}}{I}_{\delta }.$$

(33)

Integrating both sides of (33) yields the following realizable form:

$$\widehat{\theta }=L{\tilde{I}}_{\delta }+{{\displaystyle \int }}^{}\left[\widehat{\omega }+\left(k_1+1\right){\tilde{I}}_{\delta }-\frac{3}{2}\frac{e_v}{V_{dc}}{I}_{\delta }\right]d\sigma$$

(34)

where $\widehat{\omega }$(t)$\in ℝ$ is the subsequently designed update law for the unknown grid frequency. Note that a realizable form of $\dot{\widehat{\theta }}\left(t\right)$ is still undefined, which is necessary for generating the duty cycle control inputs $D_{\gamma }\left(t\right),D_{\delta }\left(t\right)$ as shown in (21). For this reason, $\widehat{\omega }\left(t\right)$ is subsequently designed. Given the relationship between these variables, this substitution is easily justified. Motivated by the stability analysis, the unrealizable design form for the grid frequency estimator is obtained as follows:

$$\dot{\widehat{\omega }}=k_{\omega }{E}_m\sin \tilde{\theta }$$

(35)

where $k_{\omega }\in {ℝ}^{+}$ is a positive estimator gain. To obtain a realizable form of this estimator, again the term $E_m\sin \tilde{\theta }$ from (23) should be used in (35) and then the integration of both sides is taken to obtain

$$\widehat{\omega }=k_{\omega }\left(L{\tilde{I}}_{\delta }+k_1{{\displaystyle \int }}^{}{\tilde{I}}_{\delta }\left(\sigma \right)\right)d\sigma$$

(36)

3.3. Stability Analysis

Theorem 1.

The closed loop error dynamics from (23) and (29) ensure that the error signals defined in (15), (16), and (18) are regulated as${\tilde{I}}_{\gamma }\left(t\right), {\tilde{I}}_{\delta }\left(t\right), e_v\left(t\right),\tilde{\theta }\left(t\right)\to 0$as$t\to \infty .$

Proof of Theorem 1.

To analyze the stability of the system, a Lyapunov function is chosen as follows:

$$V=\frac{C}{2}{e}_v^2+\frac{1}{2}L{\tilde{I}}_{\gamma }{}^2+\frac{1}{2}L{\tilde{I}}_{\delta }{}^2+E_m\left(1-\cos \tilde{\theta }\right)+\frac{1}{2k_{\omega }}{\tilde{\omega }}^2+\frac{1}{2k_d{}_i}{\tilde{d}}_i{}^2+\frac{1}{2k_d{}_v}{\tilde{d}}_v{}^2.$$

(37)

Assumption 5.

$V\left(t\right)$in (37) is positive definite in the local region$\tilde{\theta }\left(t\right)\in \left(-2\pi ,2\pi \right)$. Assuming that$\tilde{\theta }$is wrapped such that its effective domain is$\tilde{\theta }\left(t\right)\in \left[-\pi ,\pi \right)$, the function is effectively globally positive definite.

The time derivative of $V\left(t\right)$ is taken as follows:

$$\dot{V}=C{e}_v{\dot{e}}_v+L{\tilde{I}}_{\gamma }{\dot{\tilde{I}}}_{\gamma }+L{\tilde{I}}_{\delta }{\dot{\tilde{I}}}_{\delta }+E_m\dot{\tilde{\theta }}\sin \tilde{\theta }-\frac{1}{k_{\omega }}\tilde{\omega }\dot{\widehat{\omega }}-\frac{1}{k_d{}_i}{\tilde{d}}_i\dot{{\widehat{d}}_i}-\frac{1}{k_d{}_v}{\tilde{d}}_v\dot{{\widehat{d}}_v}$$

(38)

Substituting the closed loop error dynamics from (23) and (29) as well as the update laws from (22), (28), (32), and (35) a long (31) into the above equation and simplifying, $\dot{V}\left(t\right)$ can be upper bounded as

$$\dot{V}\le -k_v{e}_v^2-k_1{\tilde{I}}_{\gamma }^2-k_1{\tilde{I}}_{\delta }^2-E_m^2{\sin }^2\tilde{\theta }+\frac{3}{2}\frac{E_m}{V_{dc}}\left|e_v\right|\left|{\tilde{I}}_{\gamma }\right|.$$

(39)

By using the inequality $\left|e_v\right|\left|{\tilde{I}}_{\gamma }\right|\le \frac{1}{2}{\left|e_v\right|}^2+\frac{1}{2}{\left|{\tilde{I}}_{\gamma }\right|}^2$, $\dot{V}$(t) can be further upper bounded as

$$\dot{V}\le -k_v{e}_v^2-k_1{\tilde{I}}_{\gamma }^2-k_1{\tilde{I}}_{\delta }^2-E_m^2{\sin }^2\tilde{\theta }+\frac{3E_m}{4V_{dc}}{\left|e_v\right|}^2+\frac{3E_m}{4V_{dc}}{\left|{\tilde{I}}_{\gamma }\right|}^2$$

(40)

$$\dot{V}\le -\left(k_v-\frac{3E_m}{4V_{dc}}\right)e_v^2-\left(k_1-\frac{3E_m}{4V_{dc}}\right){\tilde{I}}_{\gamma }^2-k_1{\tilde{I}}_{\delta }^2-E_m^2{\sin }^2\tilde{\theta }.$$

(41)

It is clear that $\dot{V}\left(t\right)$ is a negative semi-definite function if $k_v>\frac{3E_m}{4V_{dc}}$ and $k_1>\frac{3E_m}{4V_{dc}}$. From $V\left(t\right),\dot{V}\left(t\right)$ it is clear that $e_v,{\tilde{I}}_{\gamma },{\tilde{I}}_{\delta },{\sin }^2\tilde{\theta },\tilde{\omega },{\tilde{d}}_i,{\tilde{d}}_v\in {ℒ}_{\infty }$. Since ${\tilde{I}}_{\gamma },{\tilde{I}}_{\delta },\tilde{\theta }\in {ℒ}_{\infty }$, from closed loop error dynamics for ${\tilde{I}}_{\gamma }$, ${\tilde{I}}_{\delta }$ and $e_v$ it is shown that ${\dot{\tilde{I}}}_{\gamma },{\dot{\tilde{I}}}_{\delta },{\dot{e}}_v\in {ℒ}_{\infty }$. Moreover, $\tilde{\omega }\in {ℒ}_{\infty }$ and from Assumption 3, $\omega \in {ℒ}_{\infty }$ and therefore $\widehat{\omega }\in {ℒ}_{\infty }$. Since $d_i$ and $d_v$ are bounded by assumption, then from (24) and (30) one can conclude that ${\widehat{d}}_i$, ${\widehat{d}}_v\in {ℒ}_{\infty }$. Since ${\tilde{I}}_{\gamma },{\tilde{I}}_{\delta },\tilde{\theta },\widehat{\omega }\in {ℒ}_{\infty }$, from definition of $\dot{\widehat{\theta }}$ it is clear that $\dot{\widehat{\theta }}\in {ℒ}_{\infty }$. Now, $\omega ,\dot{\widehat{\theta }}\in {ℒ}_{\infty }$ and from definition of $\dot{\tilde{\theta }}$, $\dot{\tilde{\theta }}\in {ℒ}_{\infty }$. Finally ${\dot{\tilde{I}}}_{\gamma },{\dot{\tilde{I}}}_{\delta },{\dot{e}}_v,\dot{\tilde{\theta }}\in {ℒ}_{\infty }$ and $\ddot{V}\left(t\right)\in {ℒ}_{\infty }$, by Barbalat’s Lemma it is clear that $\dot{V}\left(t\right)\to 0$ as $t\to \infty$ and thus ${\tilde{I}}_{\gamma },{\tilde{I}}_{\delta },e_v,\tilde{\theta }\to 0$ as $t\to \infty$. □

4. Experimental Results

To validate the proposed controller, a hardware-in-the-loop setup has been implemented. The PV panels and the grid-connected inverter system shown in Figure 1 were emulated in Typhoon HIL603 hardware using the small-time step library. The control algorithm was implemented inside LabVIEW FPGA and then programmed into the National Instruments CompactRIO (cRIO) 9032. A digital output module NI 9401 on the cRIO is used to send the switching signals generated by the controller to the HIL603 via a digital input module. Moreover, the analog output module of the HIL603 is used to measure the emulated currents and the voltages of the inverter model and sends them to the controller via the analog input module NI 9222 of the cRIO. Analog input module NI 9015 is used to measure the DC-link voltage and PV current. Figure 2 shows the experimental setup components that are used in this C-HIL validation setup. Table 1 details the PV panels parameters that are used in Typhoon PV model generation. Table 2 summarizes the system parameters and the controller gains that are used throughout the following experiments. The controller gains have been found to meet the stability analysis conditions and have the best performance.

Figure 2. C-HIL Experimental setup used for control system validation.

Table 1. Photovoltaic Panels, System and Controller Parameters.

Parameters	Value
$\mathrm{Nominal}\mathrm{open}\mathrm{circuit}\mathrm{voltage}\mathrm{of}\mathrm{PV}\mathrm{array},V_{oc}$	32.9 V
$\mathrm{Nominal}\mathrm{short}\mathrm{circuit}\mathrm{current}\mathrm{of}\mathrm{PV}\mathrm{array},I_{sc}$	8.21 A
Panels connected in series	20
Solar cells in a string	54
Solar cells strings connected in parallel	3

Table 2. System Parameters and Controller gains.

Parameters	Value
Nominal Line Inductance, L	$10\mathrm{mH}$
Nominal Line Resistance, R	$0.1 \Omega$
$\mathrm{Switching}\mathrm{Frequency},f_{sw}$	$10\mathrm{kHz}$
$\mathrm{Grid}\mathrm{Voltage},V_g$	$110{\mathrm{V}}_{\mathrm{rms}}$
$\mathrm{Control}\mathrm{Gain},k_1$	20
$\mathrm{Control}\mathrm{Gain},k_{\omega }$	0.001
$\mathrm{Control}\mathrm{Gain},k_v$	1
$\mathrm{Estimation}\mathrm{Gains},k_{di,}{k}_{dv}$	10
$\mathrm{Nominal}\mathrm{System}\mathrm{Frequency},\omega$	377 rad/s

4.1. Tracking Performance of Proposed Controller

In the first scenario, the tracking performance of the proposed controller/observer scheme, the PV system experiences standard atmospheric conditions for which the irradiation and the temperature are $1000 \mathrm{W}/{\mathrm{m}}^2$ and $25 °\mathrm{C}$, respectively. The $\gamma \delta$-axis currents with their respective reference currents are shown in Figure 3 and Figure 4. It can be seen that $\gamma \delta$-axis currents successfully follow the reference currents. The root mean square (RMS) of the steady-state errors for active and reactive currents ${\tilde{I}}_{\gamma }\left(t\right)$ and ${\tilde{I}}_{\delta }\left(t\right)$ are calculated to be 0.45 A and 0.06 A, respectively. Figure 5 shows the voltage of the DC-link capacitor and the reference voltage generated by the MPPT algorithm (the MPPT algorithm will not be studied in this work). It is clear that the DC-link voltage tracks its reference voltage with the RMS steady-state error, which is around 0.1 V. The controller output (Duty cycle) that is needed for the proposed controller/observer scheme for the PV single-stage, three-phase, grid-connected inverter is shown in Figure 6. The observer of the grid angle follows the angle generated from PLL as shown in Figure 7. The PLL algorithm is used here only for comparison and is never used in the control scheme.

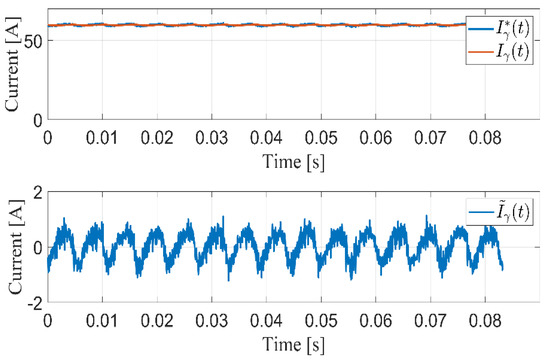
Figure 3. Injected grid current in $\gamma$-axis for steady-state operation.

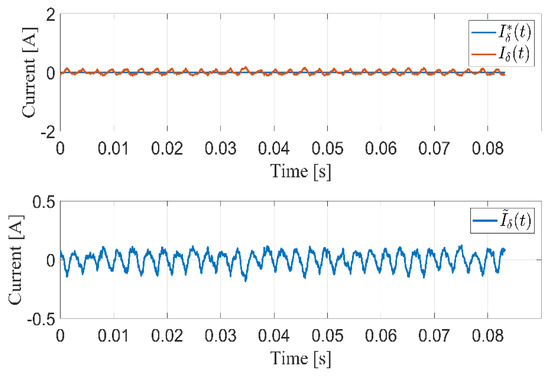
Figure 4. Injected grid current in $\delta$-axis for steady-state operation.

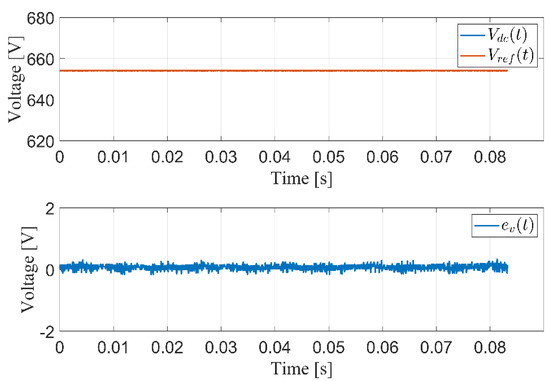
Figure 5. DC-link bus performance in steady state operation.

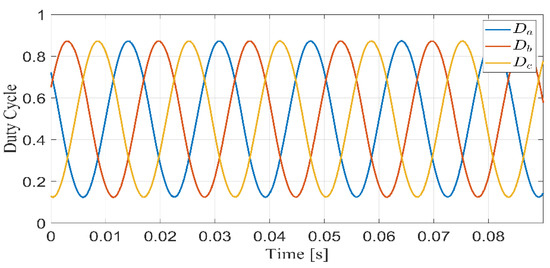
Figure 6. Duty cycle for the inverter.

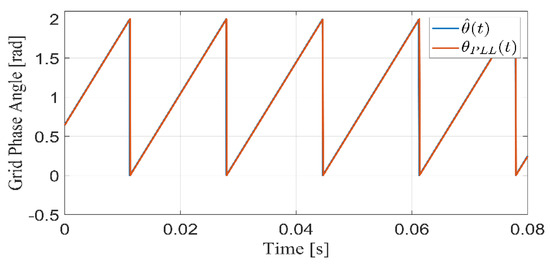
Figure 7. Performance of the proposed observer and PLL-based grid phase angle.

Under real-world conditions, the irradiation of the sun is continuously changing, which affects the output power of the PV panels. For this reason, the controller for such a system should be tested in the presence of irradiation changes. In this test, a sudden change in irradiation occurs at 3.6 s. from $1000 \mathrm{W}/{\mathrm{m}}^2$ to $800 \mathrm{W}/{\mathrm{m}}^2$. It can be seen that the $\gamma$-axis currents follow the reference currents smoothly and very quickly, as shown in Figure 8. Moreover, the DC-link voltage $V_{dc}\left(t\right)$ follows the reference voltage $V_{ref}\left(t\right)$, which is generated from the MPPT algorithm, as shown in Figure 9. It is clear from this figure that the voltage control works very well. Figure 10 shows the output active power changes based on the irradiation step change. It is clear that the active power is reduced according to irradiation drop with smooth performance. Figure 11 demonstrates the tracking performance of the proposed grid phase angle and frequency observer scheme. The grid frequency is changed from $60 \mathrm{Hz}$ to $58 \mathrm{Hz}$ and then back to $60 \mathrm{Hz}$. It is seen that the proposed observer estimates the grid frequency without any over or undershoot.

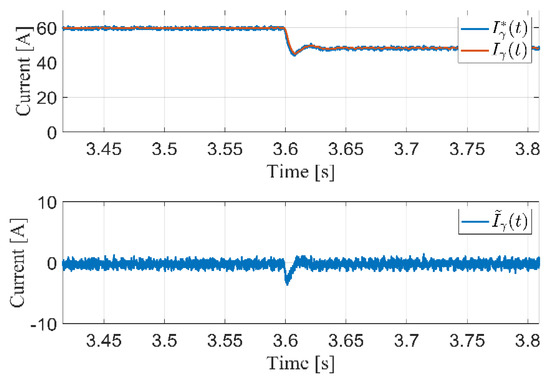
Figure 8. Current tracking performance for irradiation change from 1000 $\mathrm{W}/{\mathrm{m}}^2$ to 800$\mathrm{W}/{\mathrm{m}}^2$.

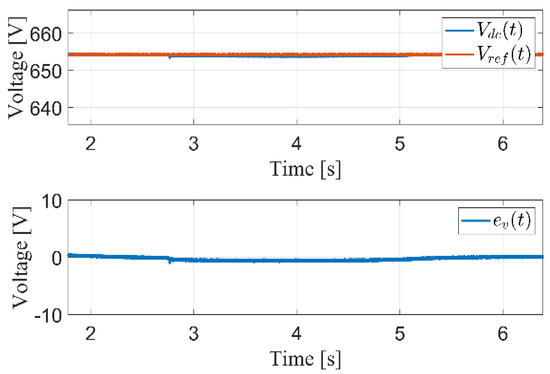
Figure 9. DC-link bus performance for irradiation changes from 1000 $\mathrm{W}/{\mathrm{m}}^2$ to 800 $\mathrm{W}/{\mathrm{m}}^2$.

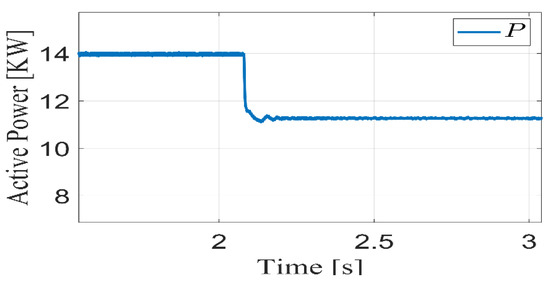
Figure 10. Active power performance during the irradiance changes.

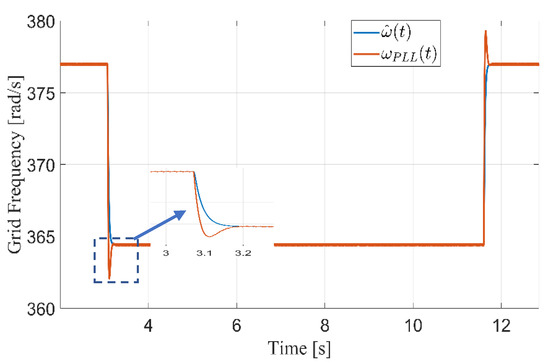
Figure 11. Tracking performance of the estimation of the grid frequency.

4.2. Proposed Controller Performance under Low- Voltage Ride-Through (LVRT) Scenario

Generally, LVRT is a common disturbance in the utility grid voltage which creates a severe operating condition for PV grid-connected inverters. An LVRT scenario has been employed to test the robustness of our proposed controller/observer scheme against this type of grid disturbance. This scenario is emulated by dropping the magnitude of the grid voltage from $110 {\mathrm{V}}_{\mathrm{rms}}$ to $80 {\mathrm{V}}_{\mathrm{rms}}$ for $150 \mathrm{ms}$. Figure 12 shows the active power injected into the grid during this kind of disturbance along with the grid voltage profile. As can be seen, the controller maintains constant power output to the grid. Since the grid voltage decreases, the only way to keep the power constant is to increase the current supplied from the PV system. In this case, the current limiter is added to the circuit in order to keep the current within the PV panel-rated current if the voltage drops to severe levels. Figure 13 shows the tracking performance of the injected current in this operating point.

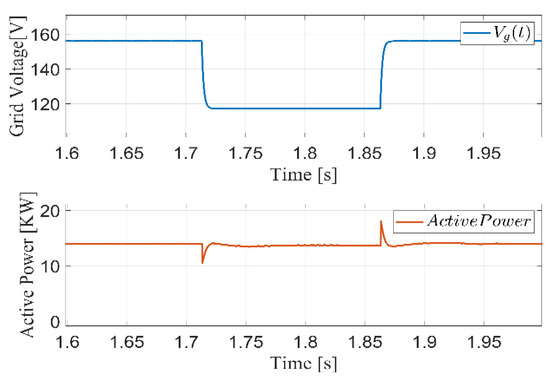
Figure 12. System performance due to LVRT scenario (Voltage drop from 110 V_rms to 80 V_rms).

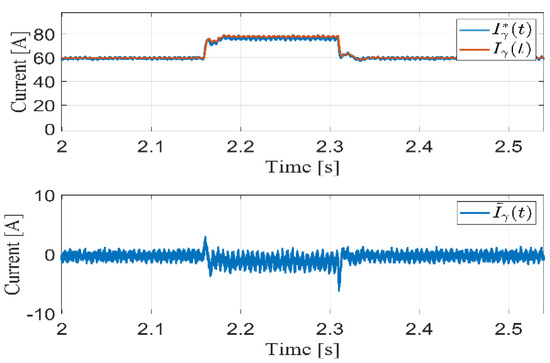
Figure 13. Current tracking performance corresponding to LVRT condition.

4.3. Proposed Controller Performance in the Presence of Harmonic Rich Grid

Harmonics are very common in grid voltage. The effect of these harmonics on renewable based power systems must be tested. In this scenario, the gird voltage with a Total Harmonics Distortion (THD) of 16% is used in order to demonstrate the capability of the proposed controller to harvest the maximum power from the PV panels and to inject power into the grid. Figure 14 shows the active power that is injected into the grid. Figure 15 shows the controller performance—in this case, in terms of the error signals for the injected currents and DC-Link voltage. Moreover, Figure 16 shows the proposed observer performance for the phase angle and frequency of the grid voltage.

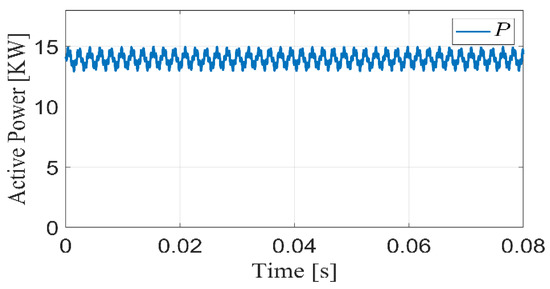
Figure 14. Active power injected into the grid under distorted grid.

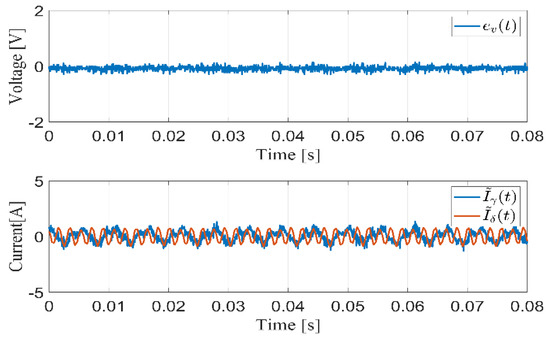
Figure 15. Steady-state error signals under distorted grid conditions.

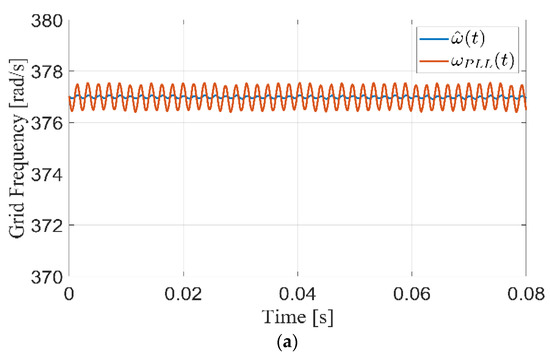
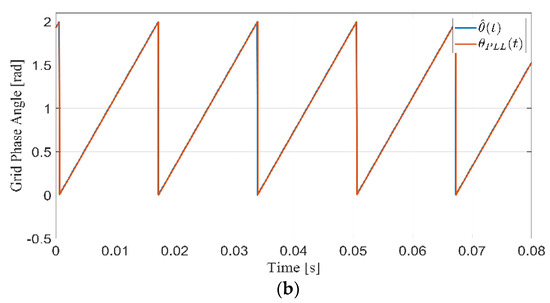
Figure 16. Steady-state observer performance under distorted grid (a) grid frequency [rad/s] (b) grid phase angle [rad].

4.4. Proposed Controller Performance under Reactive Power Injection Condition

The proposed controller has been designed to handle both active power harvesting and reactive power injection operating conditions. In this test, the reactive power injection condition is applied by increasing the q-axis reference current to inject 7.5 KVAR into the grid. Figure 17 shows the performance during the injection condition. It is seen that the reactive power is injected with a small percentage overshoot of less than 5%. Moreover, Figure 17 shows the power factor at the grid side before and after reactive power injection. The power factor is unity before the injection instant and is calculated to be 0.86 after the injection of reactive power since the phase angle between the voltage and current is around ${30}^{°}$.

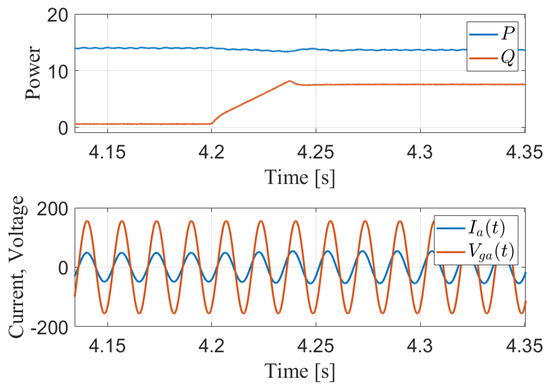
Figure 17. Active and reactive power performance during reactive power injection condition and power factor change due to the injection.

5. Conclusions

A current and voltage control scheme for a single-stage, PV grid-connected, three-phase inverter has been proposed. The proposed controller/observer scheme achieves the grid current and DC-link voltage control objectives without the knowledge of the grid information and without the need for a cascaded control scheme. Moreover, self-synchronization between the PV inverter and the grid has been guaranteed without using a PLL scheme or a synchronization unit. The proposed scheme adaptively estimated the grid phase angle and frequency. The controller and estimation schemes are validated by a Lyapunov stability analysis, and the closed loop stability has been proven. From the hardware-in-the loop experimental results, it is clear that the proposed scheme has acceptable performance for both transient and steady-state operations. Many other real-world test cases have also been evaluated. In all cases, the proposed scheme demonstrated acceptable operations in the presence of missing system information.