Implementation of an Improved Motor Control for Electric Vehicles
Abstract
:1. Introduction
2. Construction of Motor Controller
2.1. Model of Induction Motors
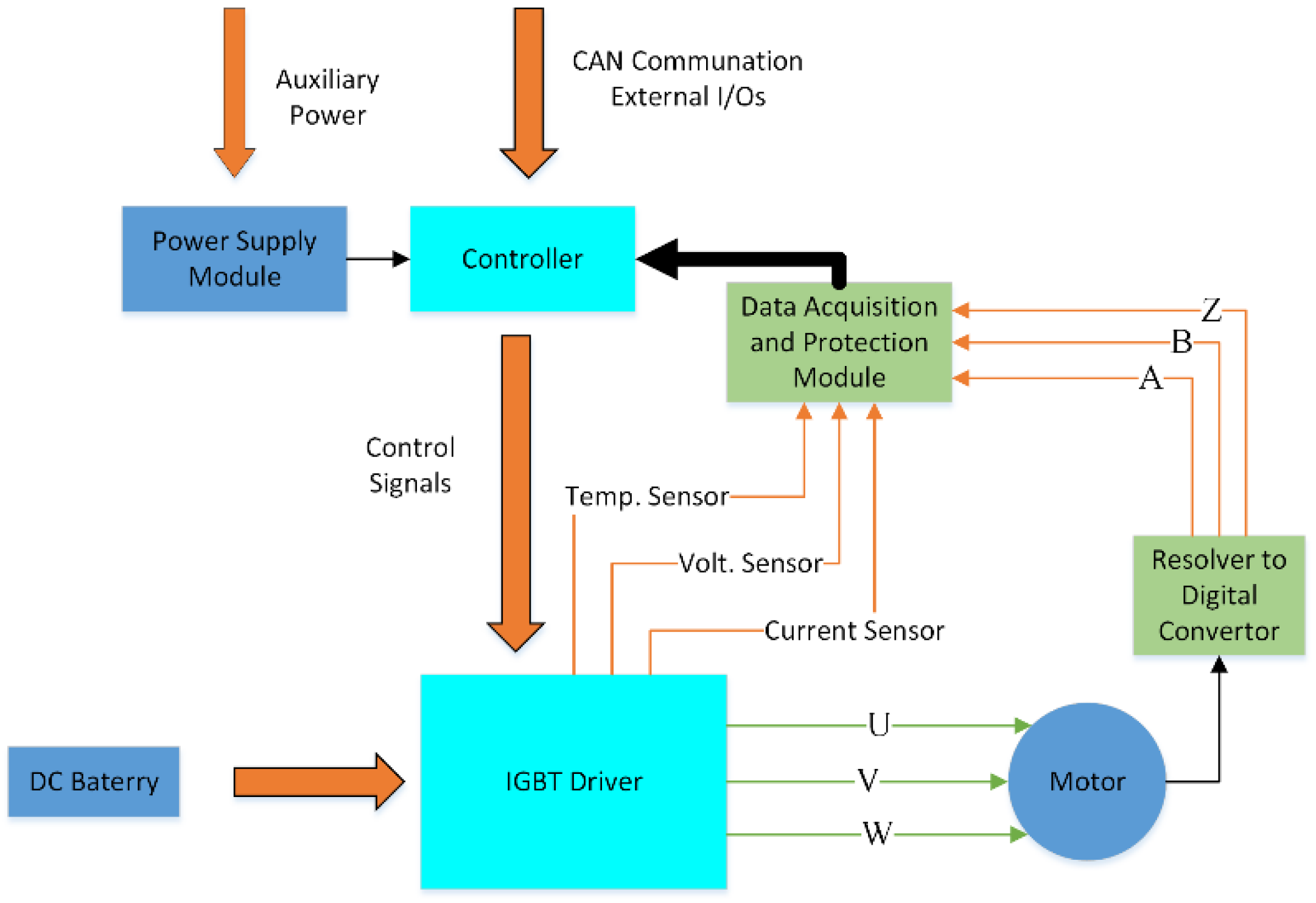
2.2. Hardware of the System
3. Implementation of Algorithm
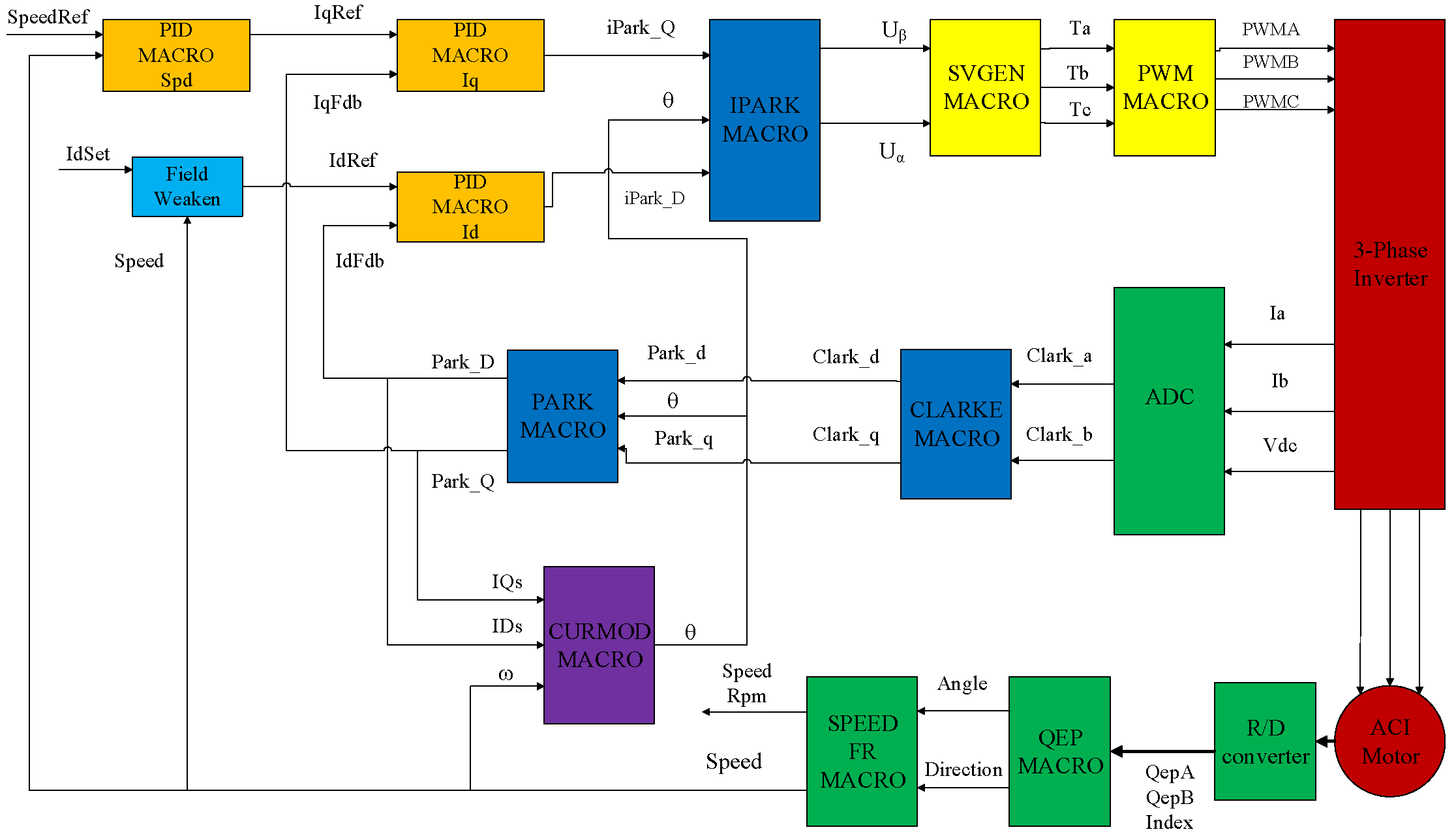
3.1. Scheme of FOC for AC Induction Motors
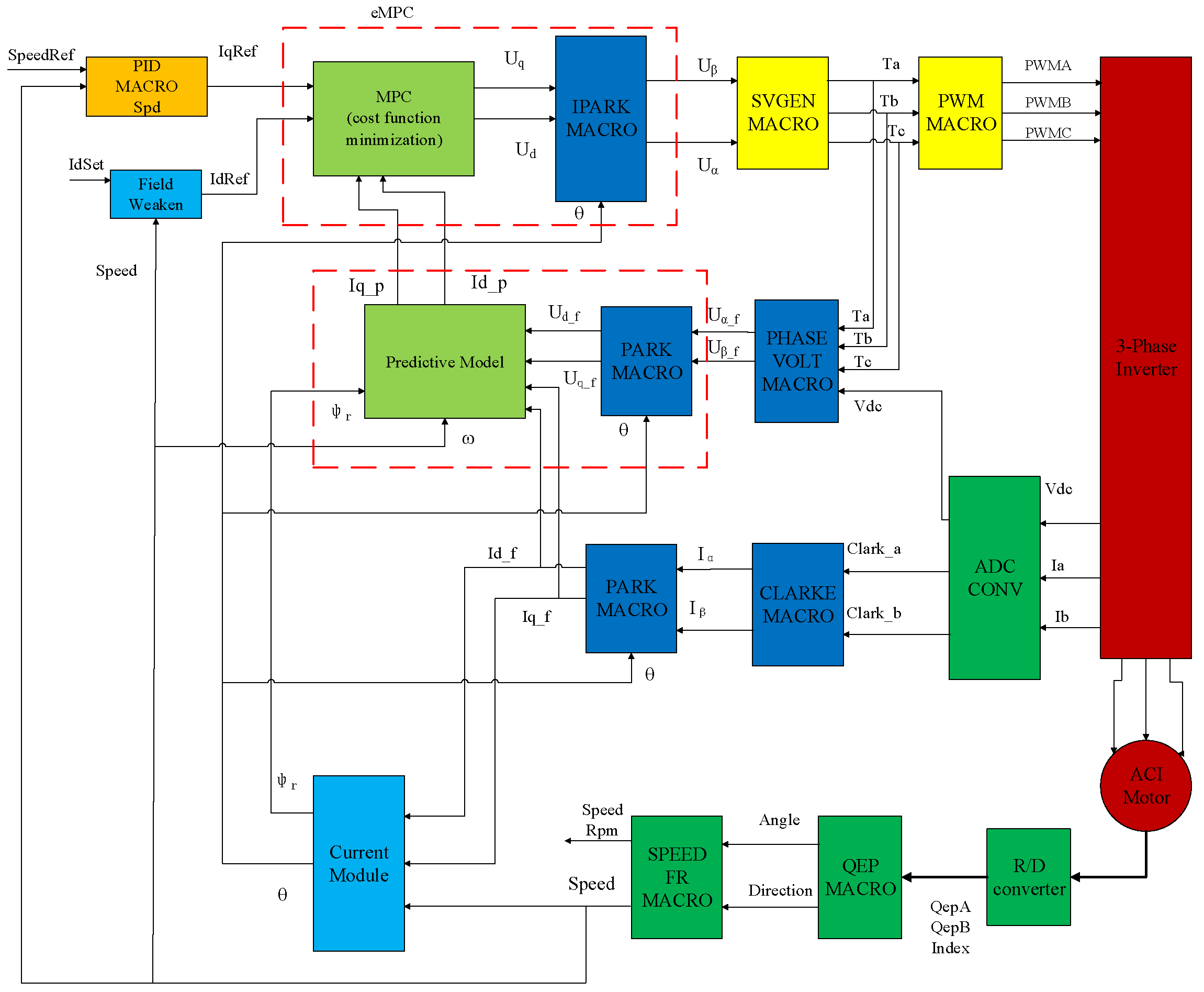
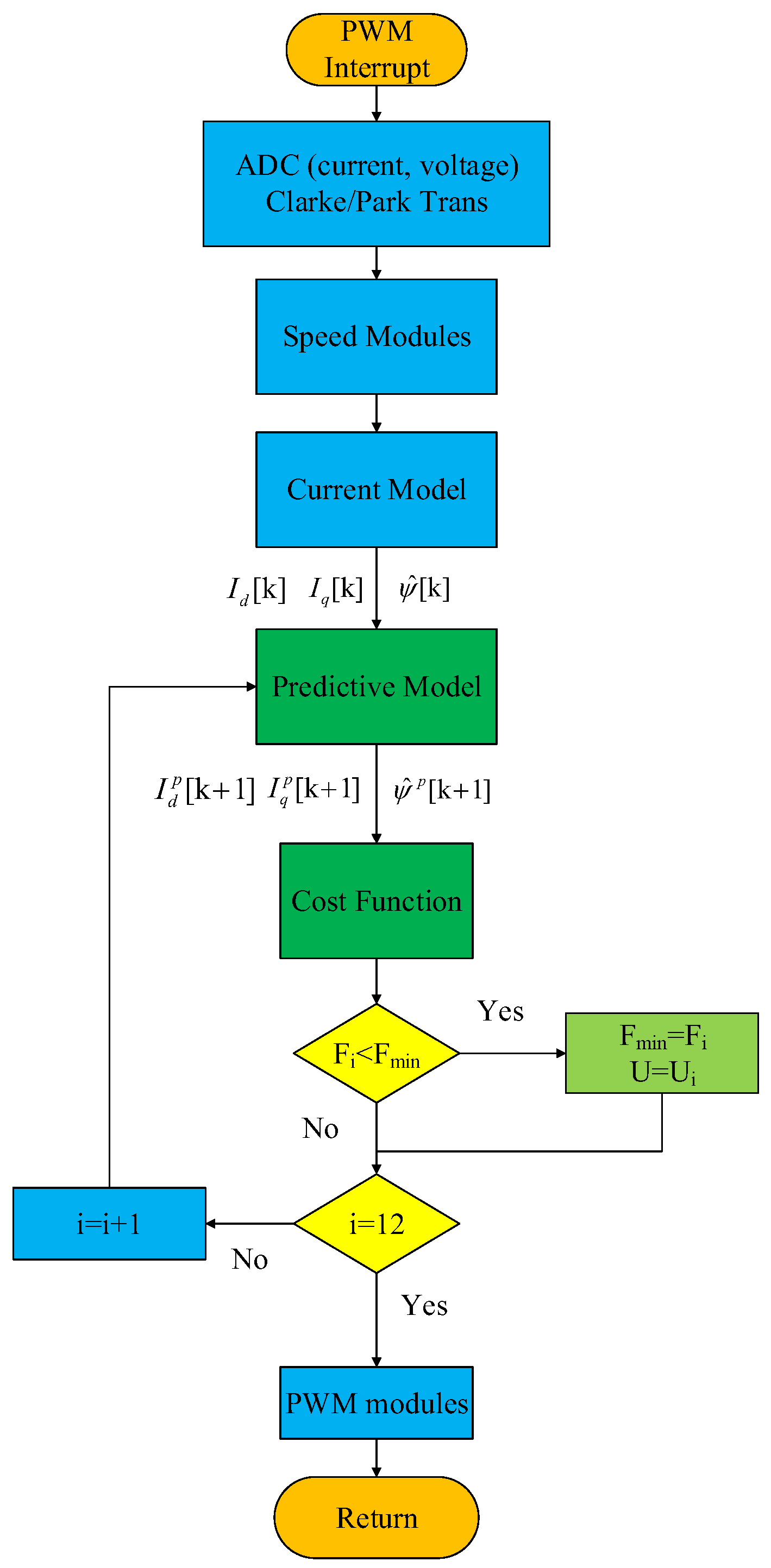
3.2. Scheme of MPC for AC Induction Motors
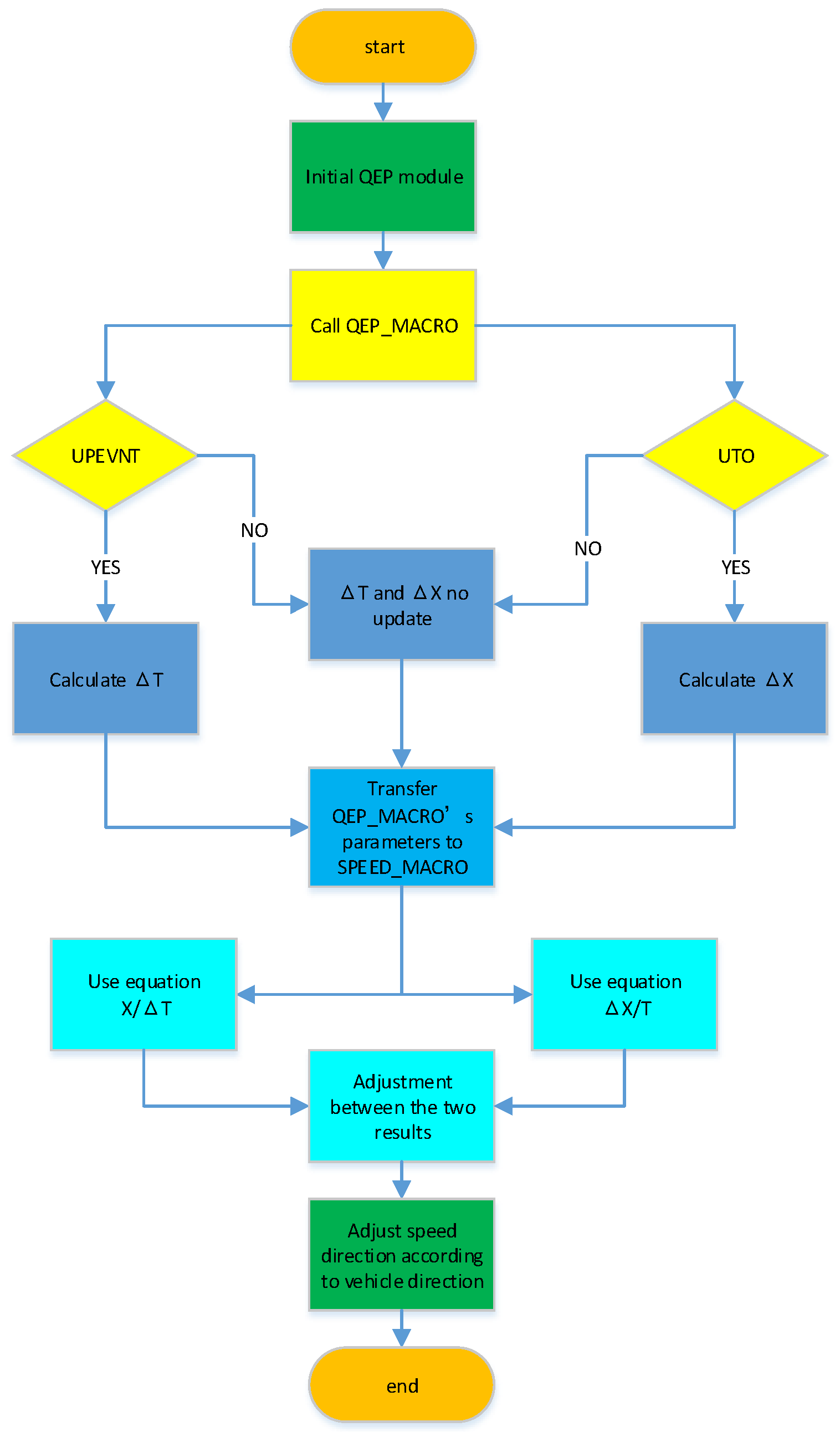
3.3. Speed Calculation Algorithm
3.4. Speed Sensorless MPC
3.4.1. Flux Linkage Estimation
3.4.2. Speed Estimation
3.4.3. Speed-Adaptive Flux Observer
3.5. Implementation on Microprocessor
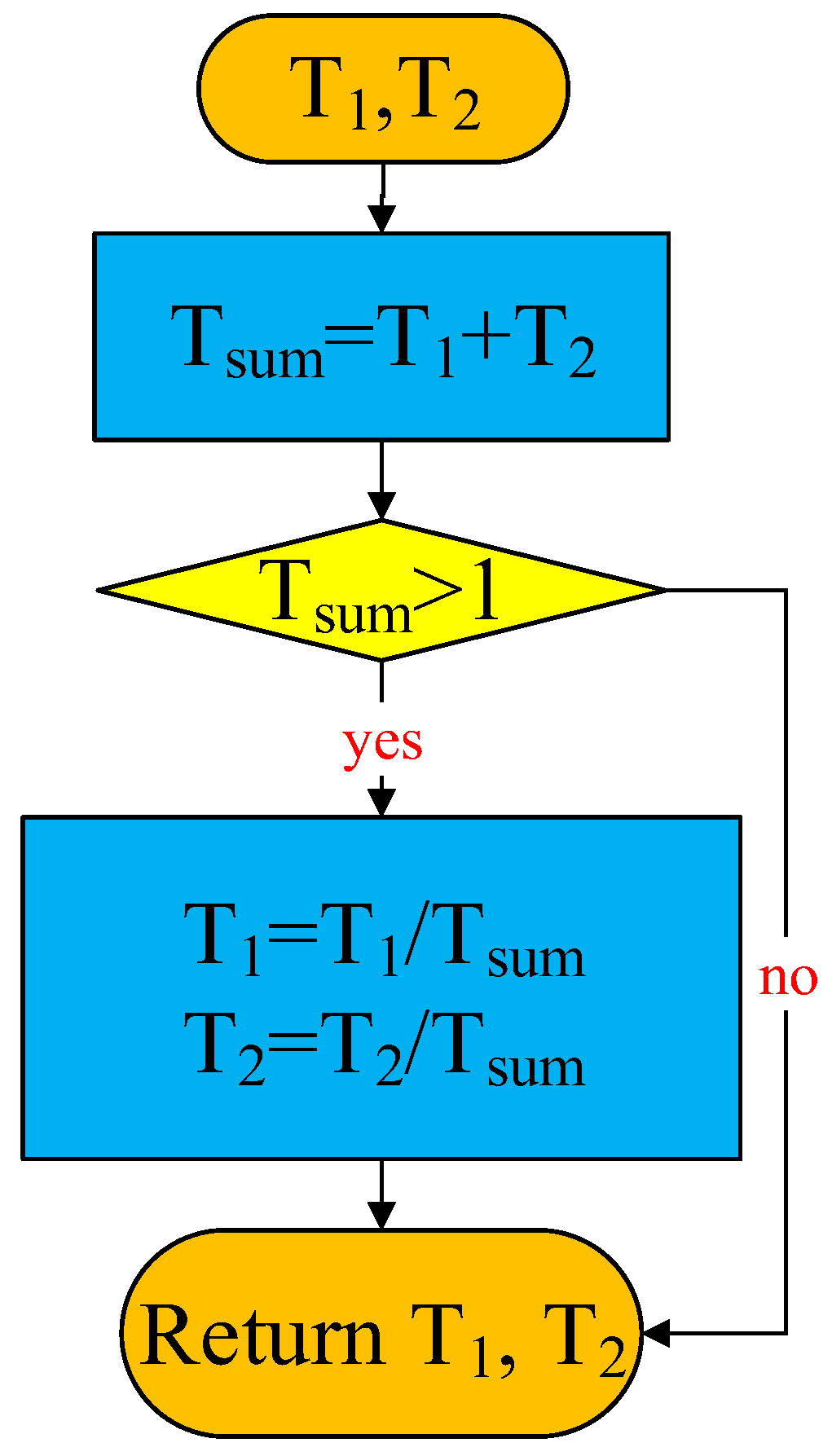
3.5.1. Discretization and Normalization
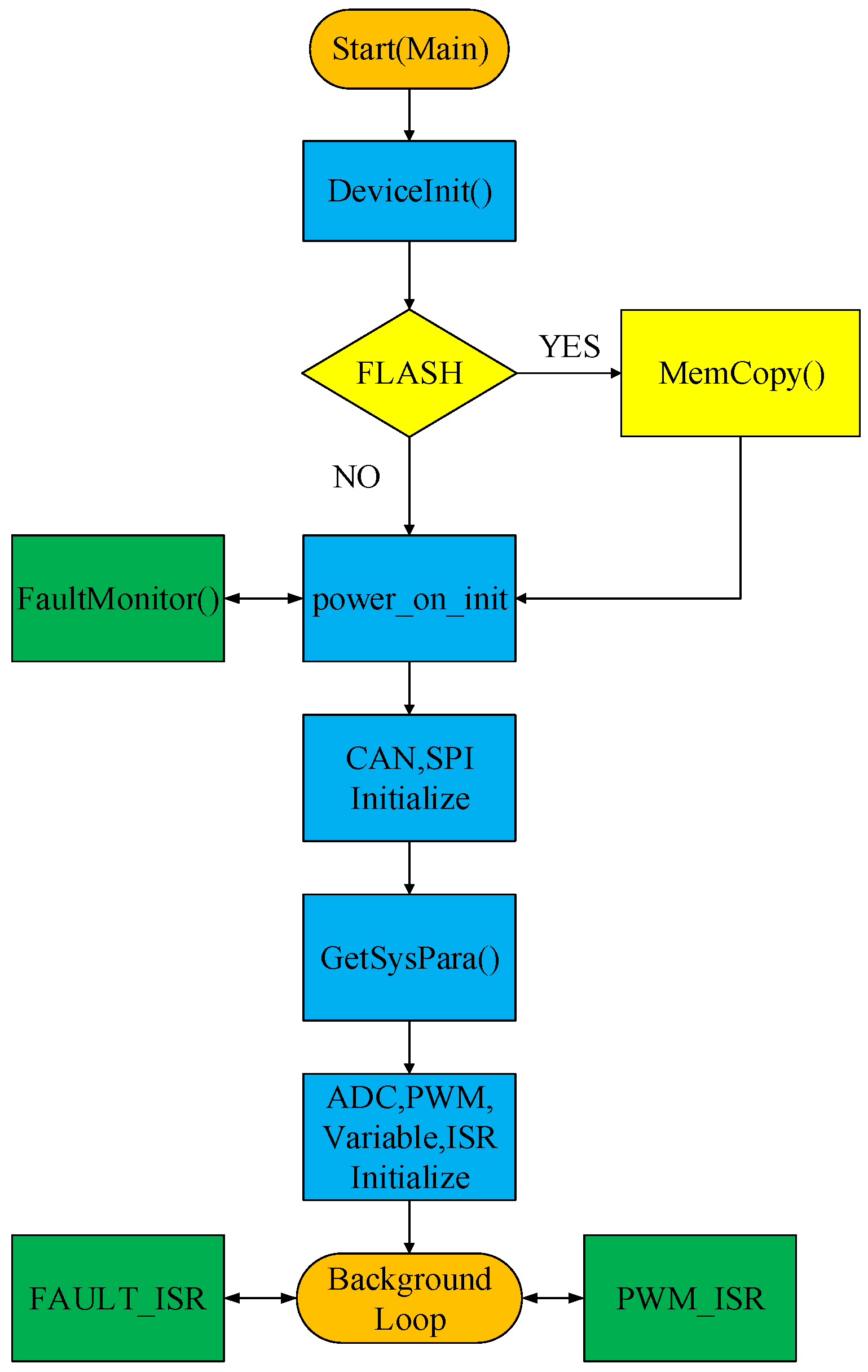
3.5.2. Main Program
4. Practical Problems
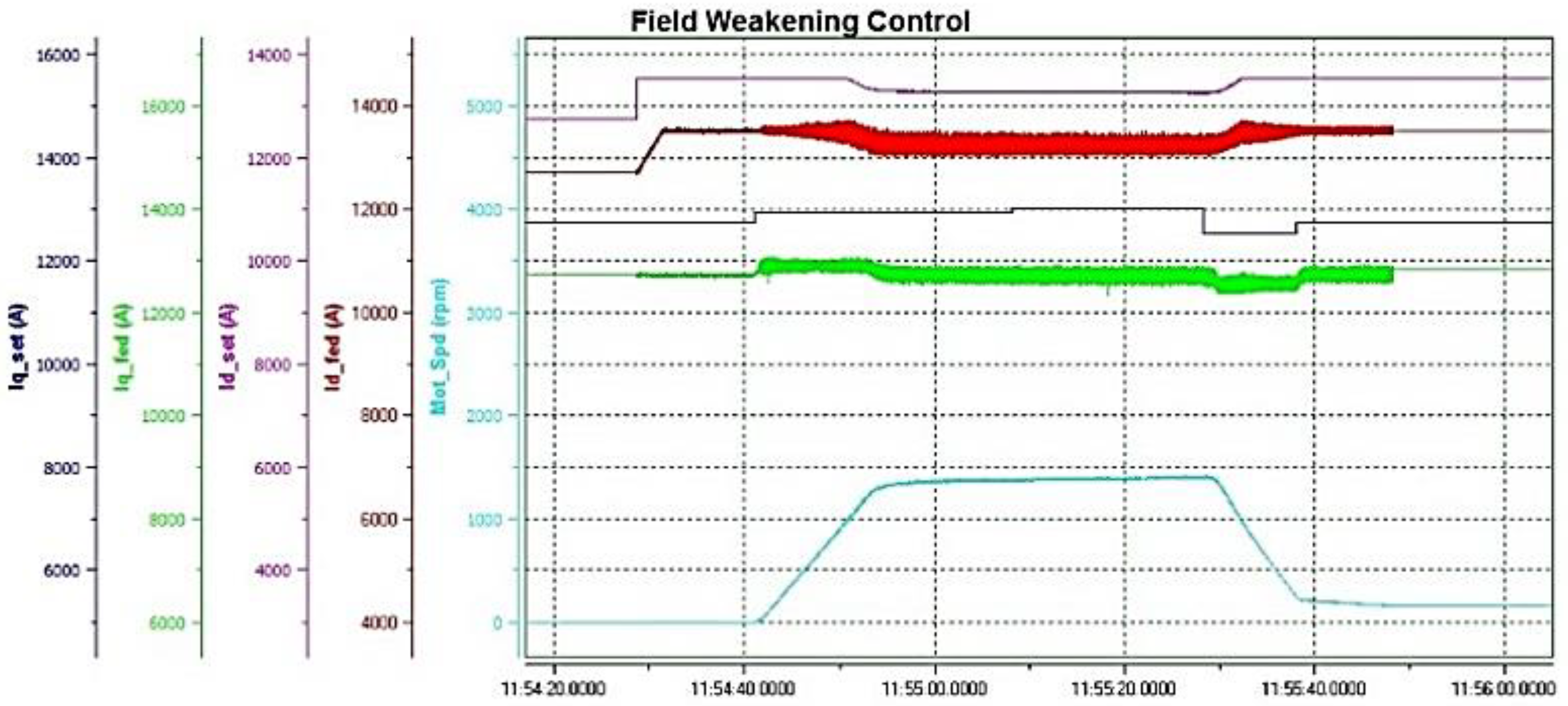
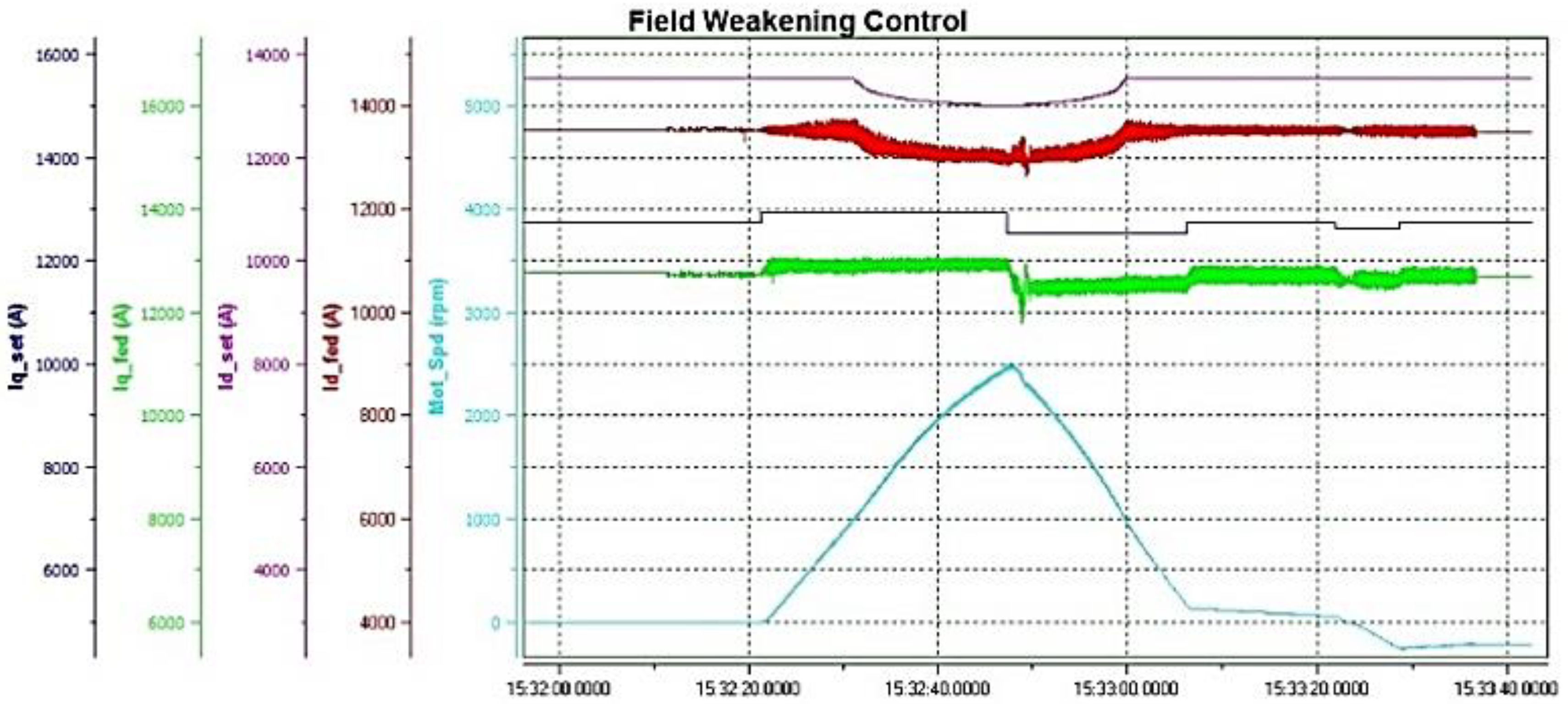
4.1. Field-Weakening Control Strategy
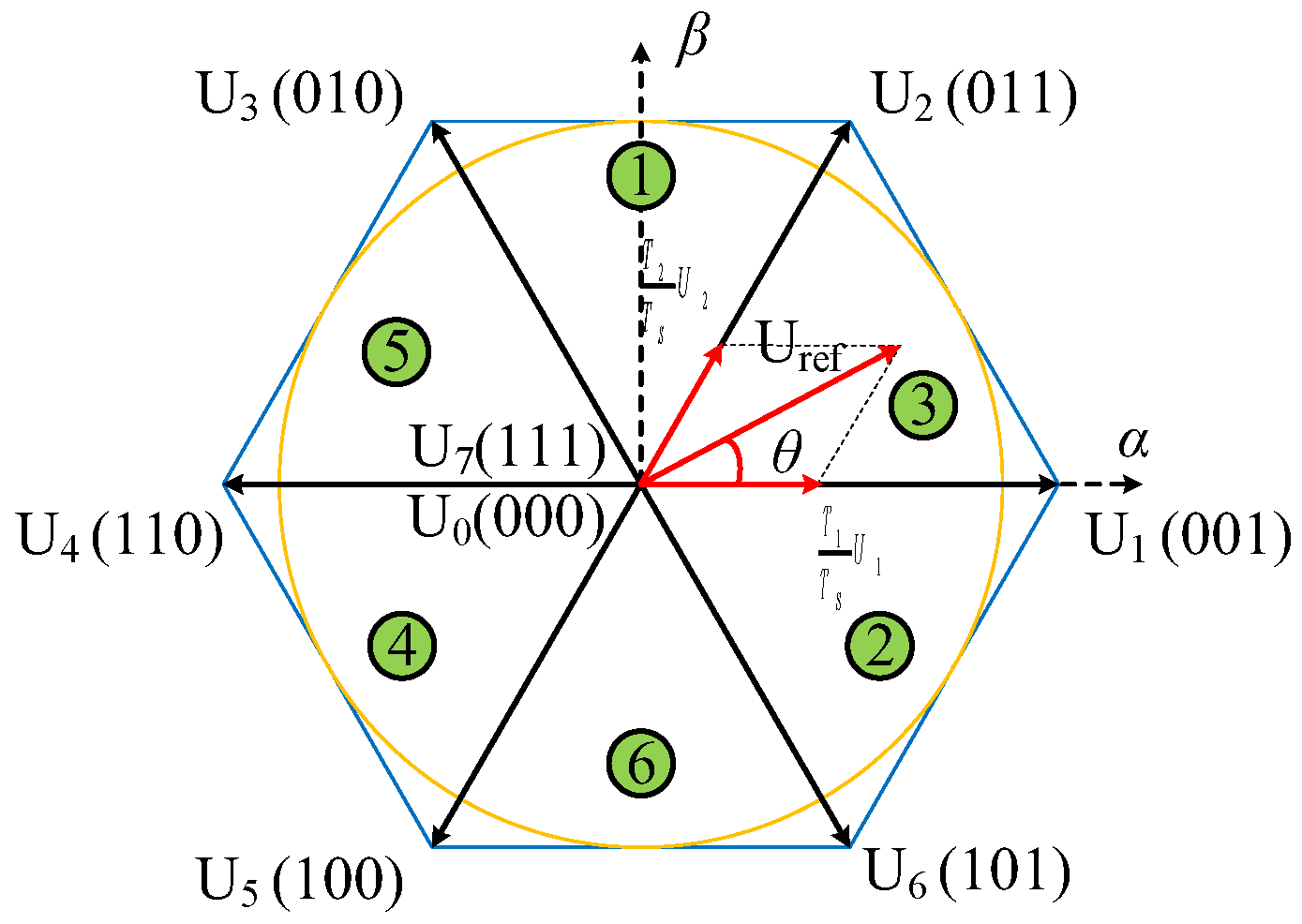
4.2. Overmodulation
4.3. PC Software
5. Experimental Results and Discussion
5.1. Field Weakening Control
5.2. Overmodulation
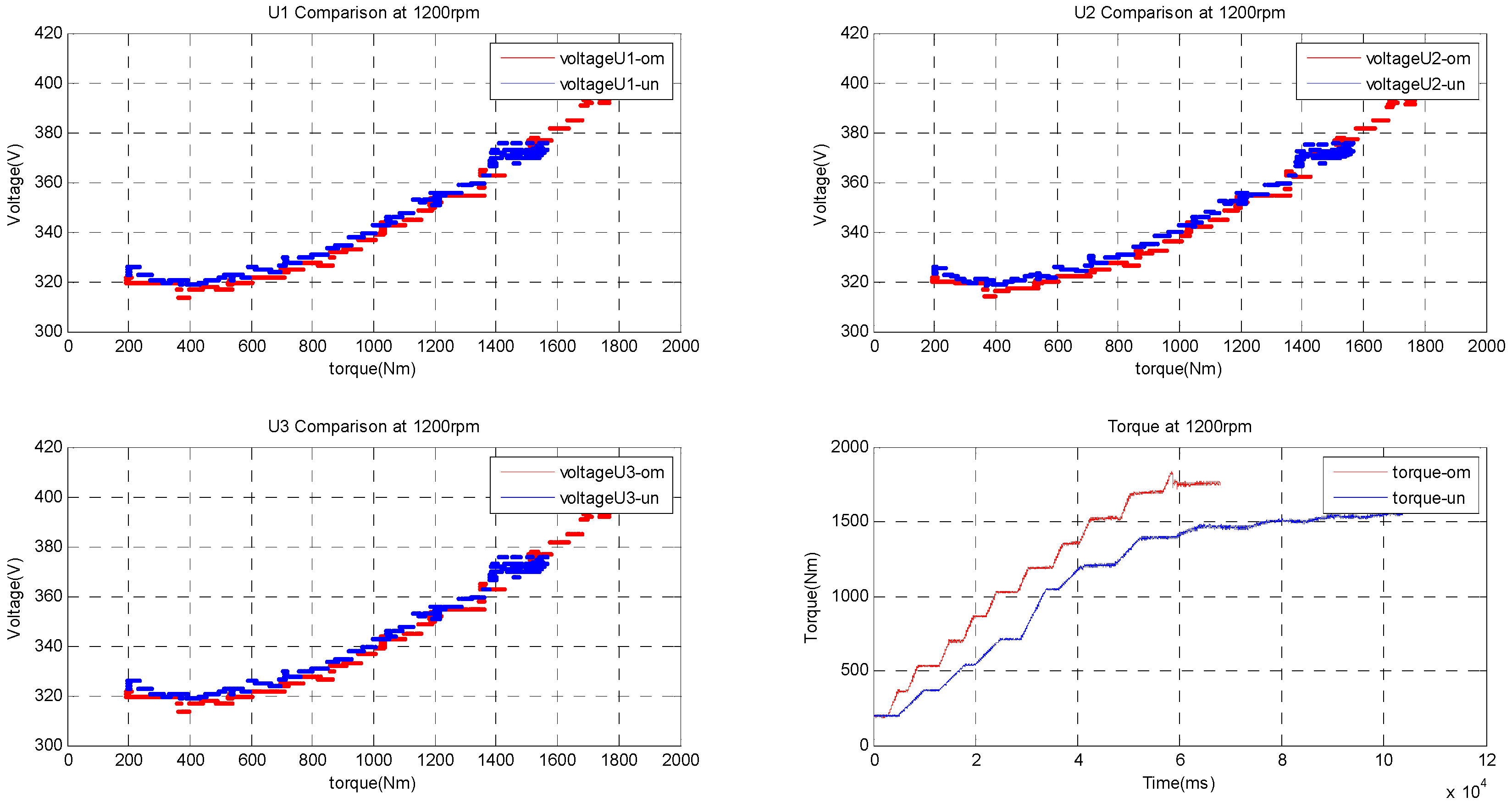
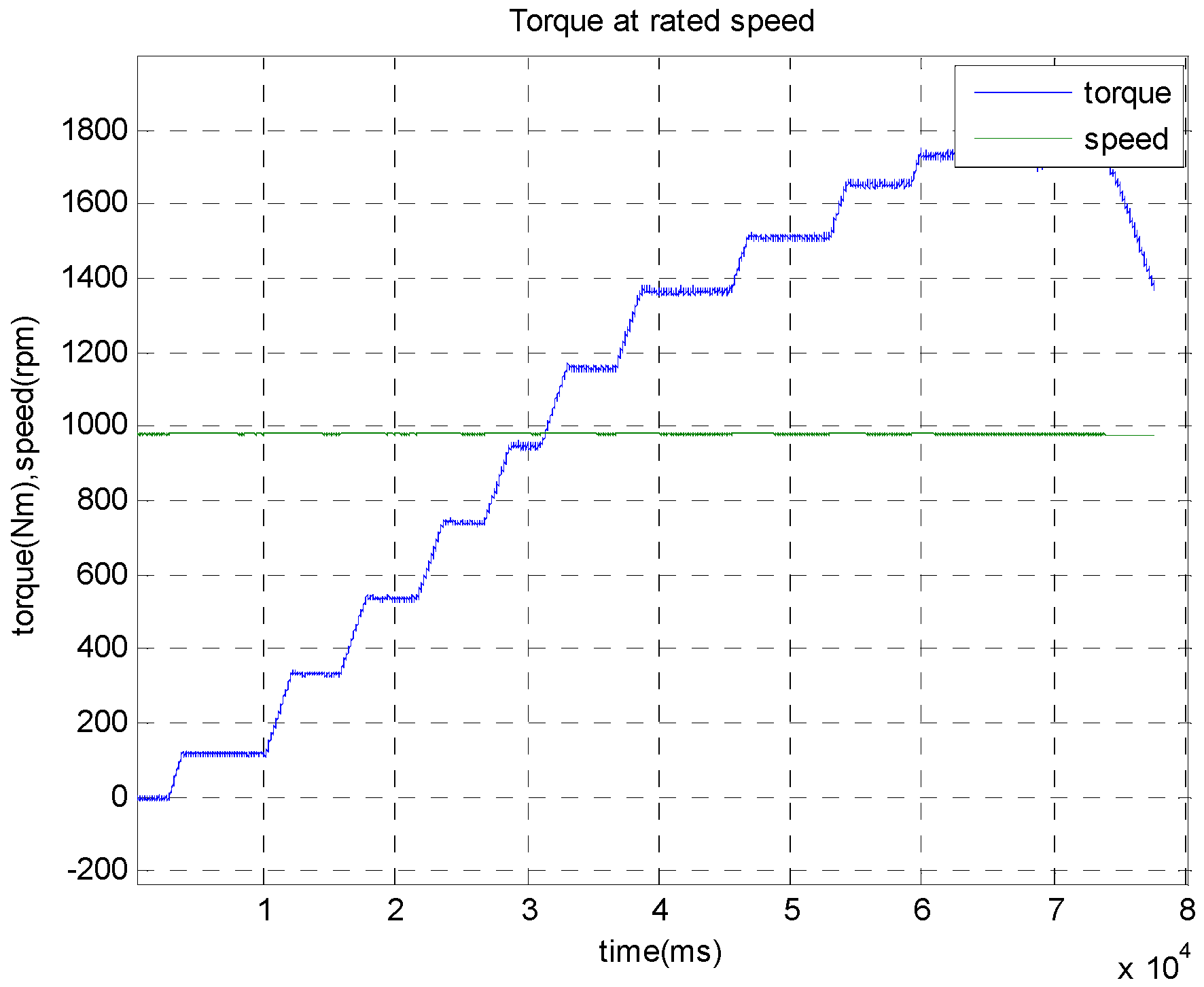
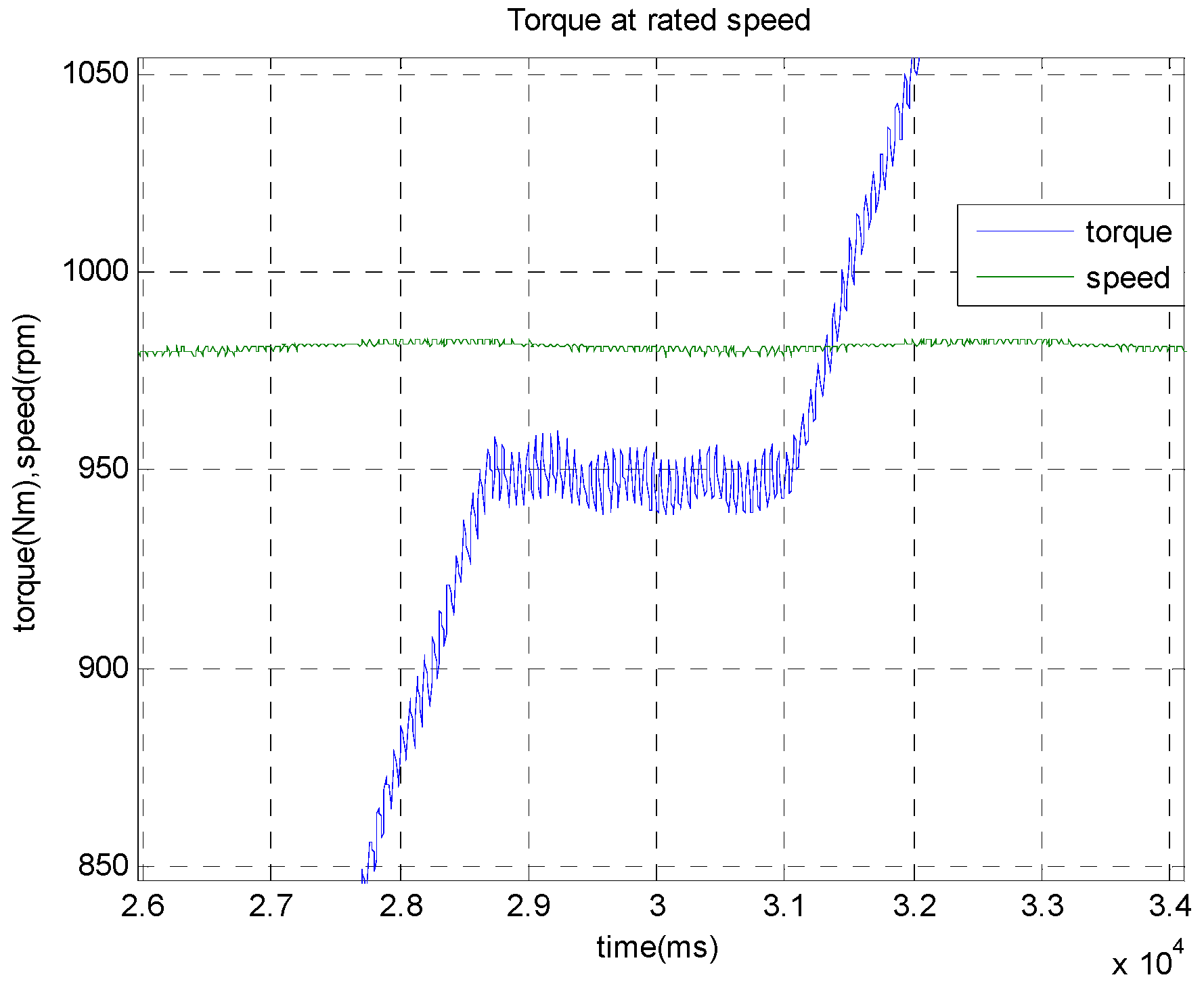
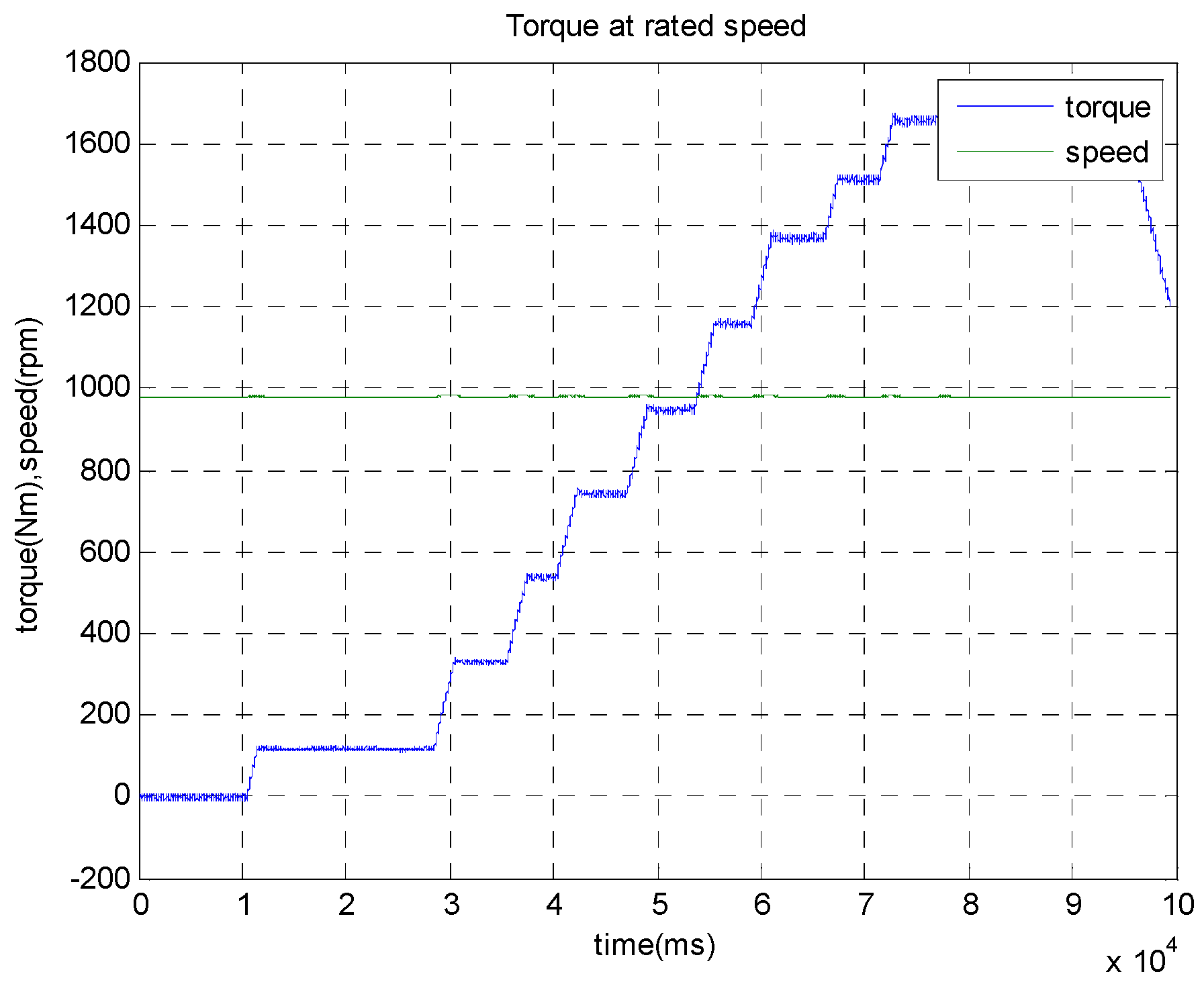
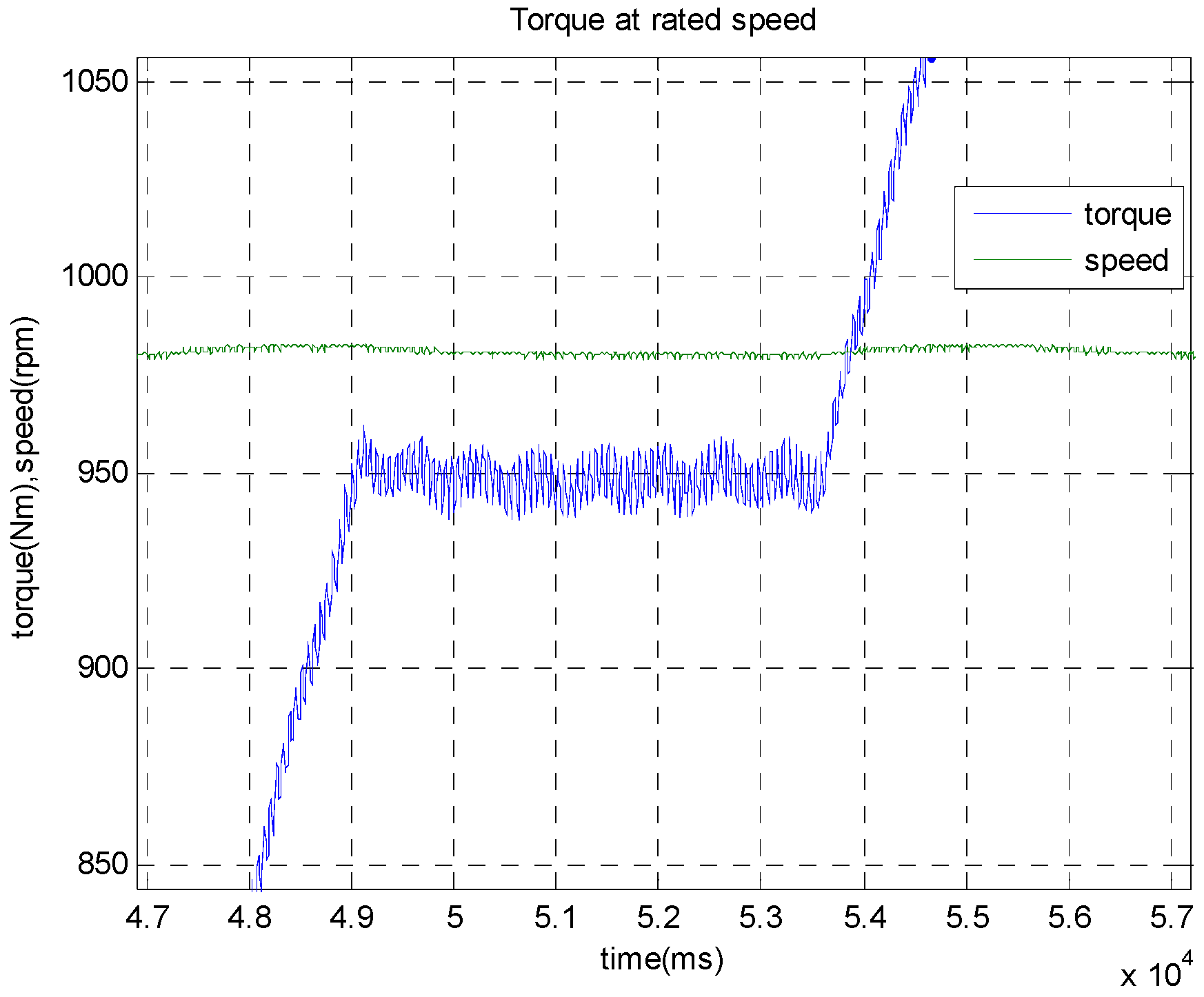
5.3. Torque Peformances
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xu, W.; Zhu, J.; Guo, Y.; Wang, S.; Wang, Y.; Shi, Z. Survey on electrical machines in electrical vehicles. In Proceedings of the 2009 International Conference on Applied Superconductivity and Electromagnetic Devices, ASEMD 2009, Chengdu, China, 25–27 September 2009; pp. 167–170. [Google Scholar]
- Lei, G.; Wang, T.S.; Guo, Y.G.; Zhu, J.G.; Wang, S.H. System-Level Design Optimization Methods for Electrical Drive Systems: Deterministic Approach. IEEE Trans. Ind. Electron. 2014, 61, 6591–6602. [Google Scholar] [CrossRef]
- Lei, G.; Wang, T.S.; Zhu, J.G.; Guo, Y.G.; Wang, S.H. System-Level Design Optimization Method for Electrical Drive Systems-Robust Approach. IEEE Trans. Ind. Electron. 2015, 62, 4702–4713. [Google Scholar] [CrossRef]
- Chan, C.C. The state of the art of electric and hybrid vehicles. Proc. IEEE 2002, 90, 247–275. [Google Scholar] [CrossRef] [Green Version]
- Berrezzek, F.; Bensaker, B. Flatness based nonlinear sensorless control of induction motor systems. Int. J. Power Electron. Drive Syst. 2016, 7, 265. [Google Scholar]
- Men, X.; Guo, Y.; Wu, G.; Shi, C.; Zhu, J. Implementation of a motor control system for electric bus based on DSP. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar]
- Dannehl, J.; Fuchs, F.W. Flatness-based control of an induction machine fed via voltage source inverter-concept, control design and performance analysis. In Proceedings of the IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 5125–5130. [Google Scholar]
- Fan, L.; Zhang, L. An improved vector control of an induction motor based on flatness. Procedia Eng. 2011, 15, 624–628. [Google Scholar] [CrossRef]
- Casadei, D.; Profumo, F.; Serra, G.; Tani, A. FOC and DTC: Two viable schemes for induction motors torque control. IEEE Trans. Power Electron. 2002, 17, 779–787. [Google Scholar] [CrossRef] [Green Version]
- Bose, B.K.; Simoes, M.G.; Crecelius, D.R.; Rajashekara, K.; Martin, R. Speed sensorless hybrid vector controlled induction motor drive. In Proceedings of the Conference Record of the 1995 IEEE Industry Applications Conference Thirtieth IAS Annual Meeting, Orlando, FL, USA, 8–12 October 1995; pp. 137–143. [Google Scholar]
- Men, X.; Wu, G.; Guo, Y.; Zhu, Z.; Gao, J. Development of an Advanced Motor Control System for Electric Vehicles; SAE Technical Papers; SAE International: Detroit, MI, USA, 2019. [Google Scholar]
- Vazquez, S.; Leon, J.; Franquelo, L.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model predictive control: A review of its applications in power electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R.; Zanchetta, P.; Abu-Rub, H.; Young, H.A.; Rojas, C.A. State of the art of finite control set model predictive control in power electronics. IEEE Trans. Ind. Inform. 2013, 9, 1003–1016. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H. Generalized two-vector-based model-predictive torque control of induction motor drives. IEEE Trans. Power Electron. 2015, 30, 3818–3829. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H.; Li, Z. A simple SVM-based deadbeat direct torque control of induction motor drives. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Korea, 26–29 October 2013; pp. 2201–2206. [Google Scholar]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives; John Wiley & Sons: New York, NY, USA, 2012; Volume 40. [Google Scholar]
- Miranda, H.; Cortés, P.; Yuz, J.I.; Rodríguez, J. Predictive torque control of induction machines based on state-space models. IEEE Trans. Ind. Electron. 2009, 56, 1916–1924. [Google Scholar] [CrossRef]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers; McGraw-Hill Higher Education: Boston, MA, USA, 2010. [Google Scholar]
- Zhang, Y.; Yang, H. Two-vector-based model predictive torque control without weighting factors for induction motor drives. IEEE Trans. Power Electron. 2016, 31, 1381–1390. [Google Scholar] [CrossRef]
- Cortés, P.; Kouro, S.; La Rocca, B.; Vargas, R.; Rodríguez, J.; León, J.I.; Vazquez, S.; Franquelo, L.G. Guidelines for weighting factors design in model predictive control of power converters and drives. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Churchill, Australia, 10–13 February 2009; pp. 1–7. [Google Scholar]
- Akin, B.; Bhardwaj, M. Sensored Field Oriented Control of 3-Phase Induction Motors; Texas Instrument Guide; Texas Instruments Incorporated: Dallas, TX, USA, 2013; p. 2019. [Google Scholar]
- Mariethoz, S.; Domahidi, A.; Morari, M. High-bandwidth explicit model predictive control of electrical drives. IEEE Trans. Ind. Appl. 2012, 48, 1980–1992. [Google Scholar] [CrossRef]
- Geyer, T.; Papafotiou, G.; Morari, M. Model predictive direct torque control—Part I: Concept, algorithm, and analysis. IEEE Trans. Ind. Electron. 2009, 56, 1894–1905. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Z. Speed sensorless control for three-level inverter-fed induction motors using an extended Luenberger observer. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–5. [Google Scholar]
- Zhang, Y.; Zhu, J. An improved direct torque control for three-level inverter-fed induction motor sensorless drive. IEEE Trans. Power Electron. 2012, 27, 1502–1513. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H.; Xia, B. Model-predictive control of induction motor drives: Torque control versus flux control. IEEE Trans. Ind. Appl. 2016, 52, 4050–4060. [Google Scholar] [CrossRef]
- Seman, S.; Niiranen, J.; Arkkio, A. Ride-through analysis of doubly fed induction wind-power generator under unsymmetrical network disturbance. IEEE Trans. Power Syst. 2006, 21, 1782. [Google Scholar] [CrossRef]
- Lee, D.; Lee, G. A novel overmodulation technique for space-vector PWM inverters. IEEE Trans. Power Electron. 1998, 13, 1144–1151. [Google Scholar]
- Zhang, Y.; Xia, B.; Yang, H. Performance evaluation of an improved model predictive control with field oriented control as a benchmark. IET Electr. Power Appl. 2017, 11, 677–687. [Google Scholar] [CrossRef]

| Comparison | FOC | DTC | MPC |
|---|---|---|---|
| Speed Estimation | Encoder output | Encoder output | Encoder output |
| Speed Controller | PI | PI | Cost function definition |
| Flux-linkage Estimation | N/A | abc-αβ transformation | abc-dq transformation |
| Flux-linkage Controller | N/A | Hysteresis controller | Cost function definition |
| Current/Torque Estimation | abc-dq transformation | Calculation from flux-linkage and currents | abc-dq transformation |
| Current/Torque Controller | PI | Hysteresis controller | Cost function definition |
| Inverter Control | PWM | Look-up table | Cost function definition |
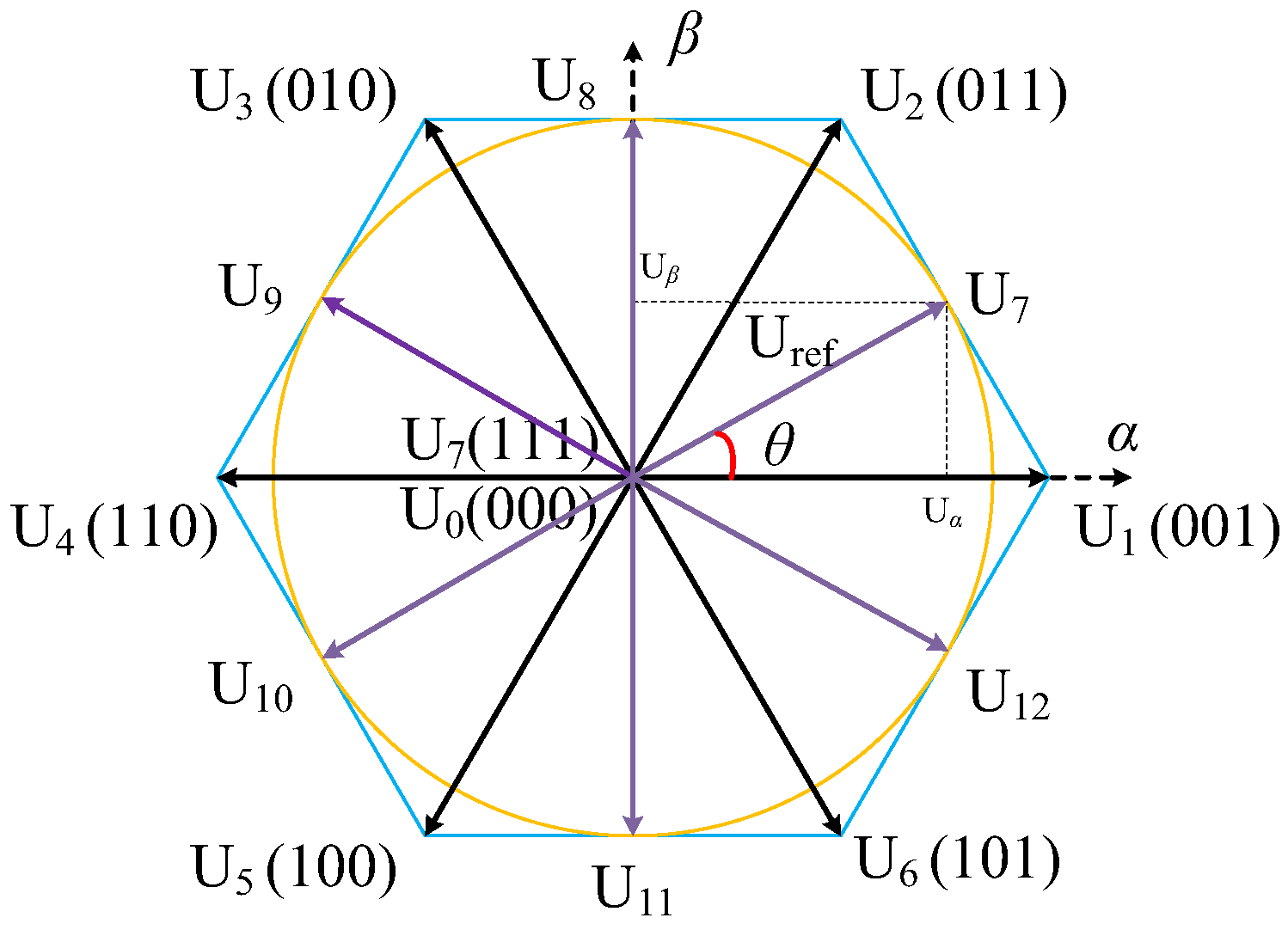
| Sector | Vector | t1 | t2 |
|---|---|---|---|
| 1 | U3, U2 | Z | Y |
| 2 | U1, U6 | Y | −X |
| 3 | U1, U2 | −Z | X |
| 4 | U5, U4 | −X | Z |
| 5 | U3, U4 | X | −Y |
| 6 | U5, U6 | −Y | −Z |
| Vector | ||
|---|---|---|
| U1 | 0 | |
| U2 | ||
| U3 | ||
| U4 | 0 | |
| U5 | ||
| U6 | ||
| U7 | ||
| U8 | 0 | |
| U9 | ||
| U10 | ||
| U11 | 0 | |
| U12 |
| Motor Parameters | Value | Unit |
|---|---|---|
| Rated power | 100 | kW |
| Rated voltage | 350 | V |
| Rated current | 178 | A |
| Rated speed | 980 | rpm |
| Number of pole pairs | 3 | |
| Rr | 0.014 | Ω |
| Lr | 10.5 | mH |
| Rs | 0.019 | Ω |
| Ls | 10.9 | mH |
| Peak power | 250 | kW |
| Max torque | 2400 | Nm |
| Switching frequency | 2~20 | kHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Men, X.; Guo, Y.; Wu, G.; Chen, S.; Shi, C. Implementation of an Improved Motor Control for Electric Vehicles. Energies 2022, 15, 4833. https://doi.org/10.3390/en15134833
Men X, Guo Y, Wu G, Chen S, Shi C. Implementation of an Improved Motor Control for Electric Vehicles. Energies. 2022; 15(13):4833. https://doi.org/10.3390/en15134833
Chicago/Turabian StyleMen, Xiaojin, Youguang Guo, Gang Wu, Shuangwu Chen, and Chun Shi. 2022. "Implementation of an Improved Motor Control for Electric Vehicles" Energies 15, no. 13: 4833. https://doi.org/10.3390/en15134833
APA StyleMen, X., Guo, Y., Wu, G., Chen, S., & Shi, C. (2022). Implementation of an Improved Motor Control for Electric Vehicles. Energies, 15(13), 4833. https://doi.org/10.3390/en15134833







