A Simplified Solution Method for End-of-Term Storage Energy Maximization Model of Cascaded Reservoirs
Abstract
:1. Introduction
2. Materials and Methods
2.1. End-of-Term Storage Energy Maximization Model
2.1.1. Objective Function
2.1.2. Constraint Conditions
2.2. Solution Method
2.2.1. Optimization Model Solution Simplification
2.2.2. DPSA
2.2.3. Optimization Model Solution Process
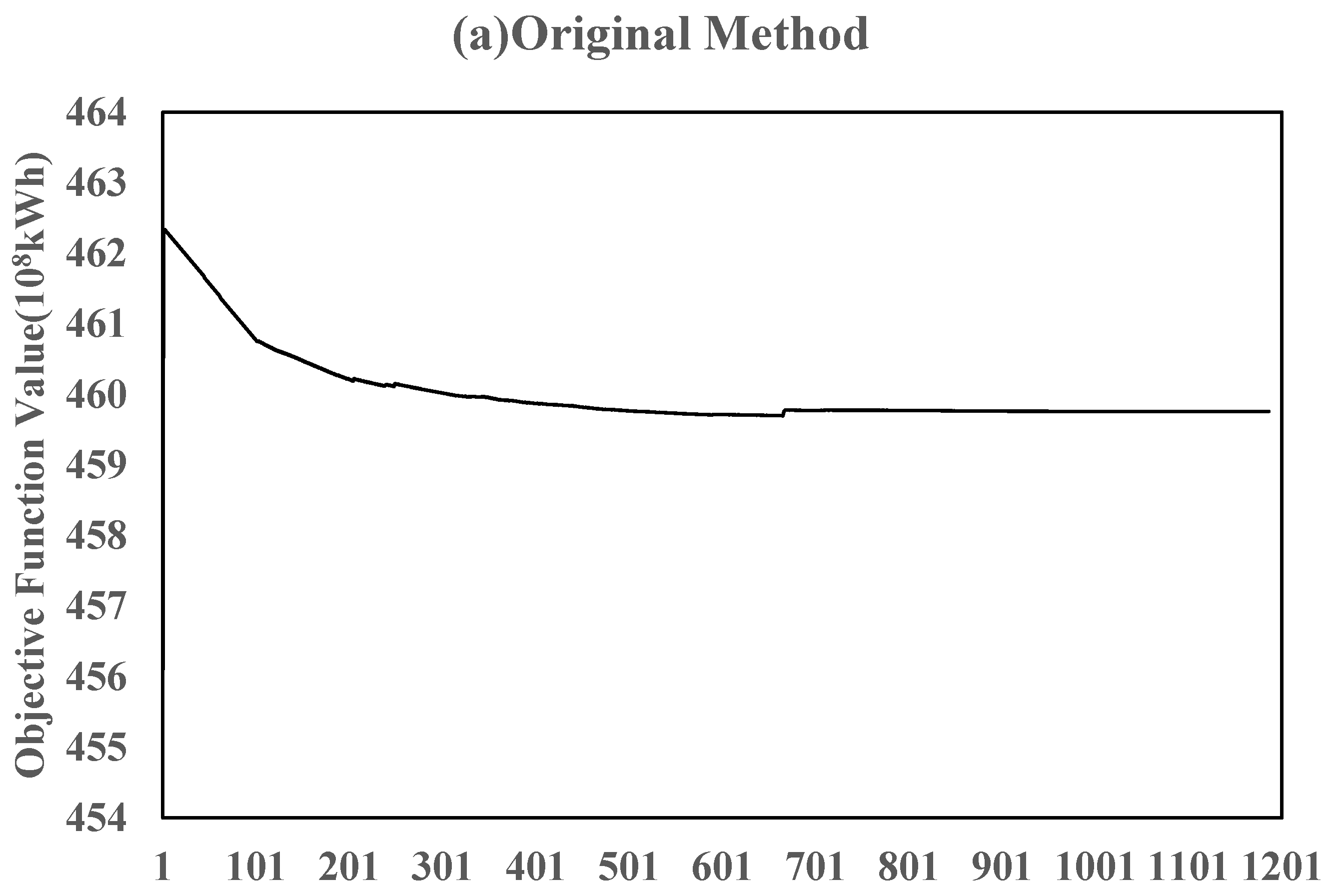
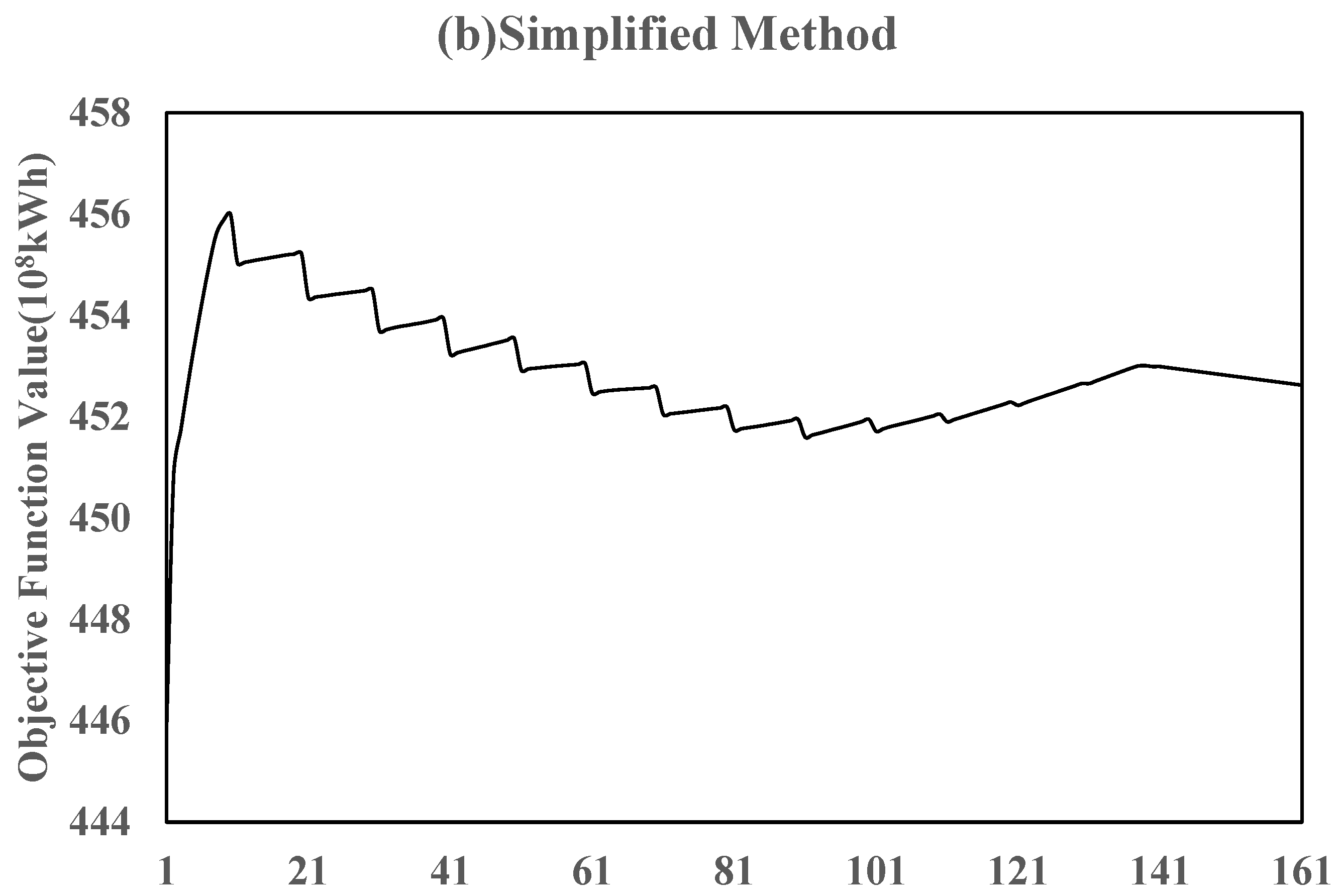
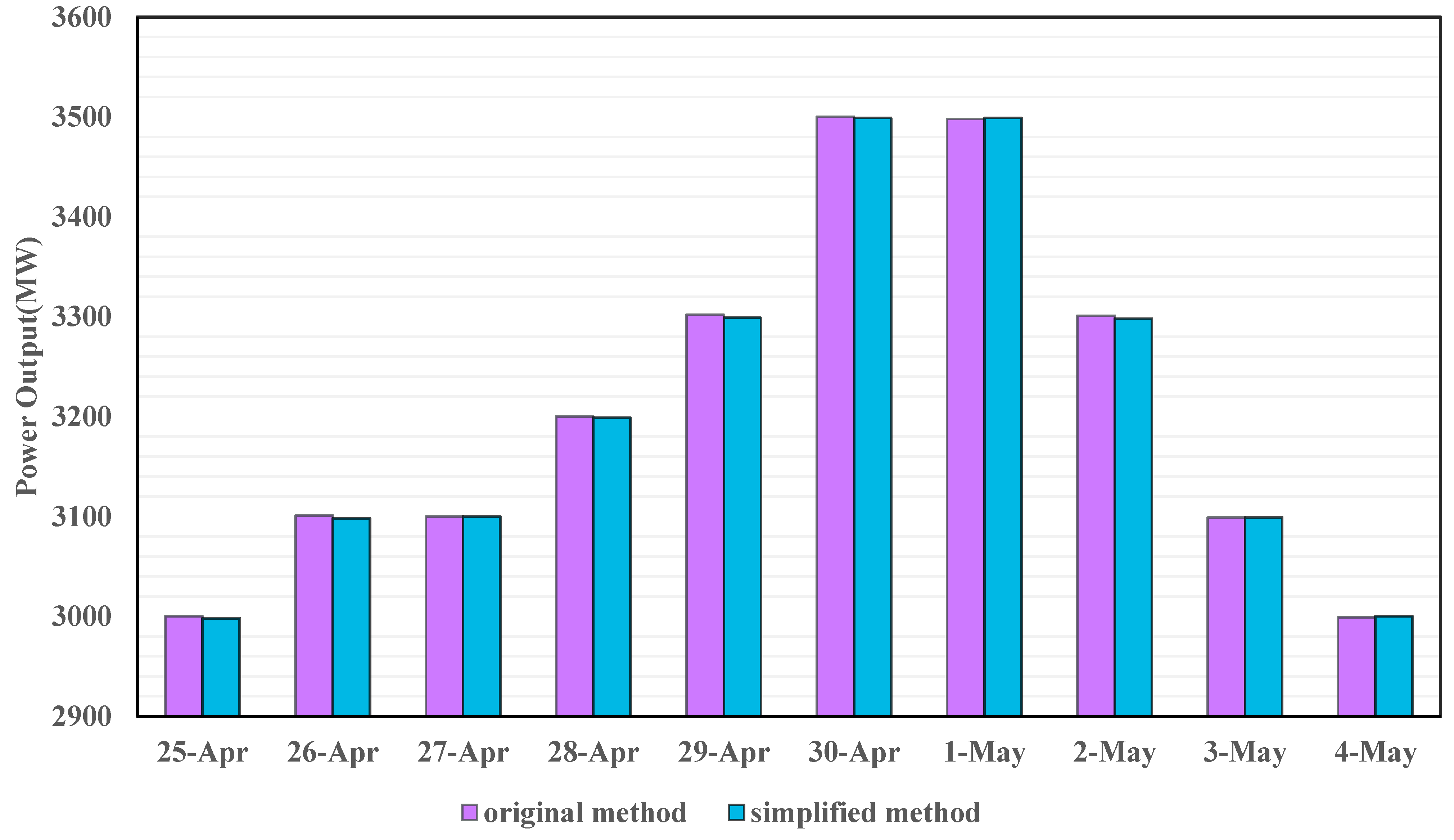
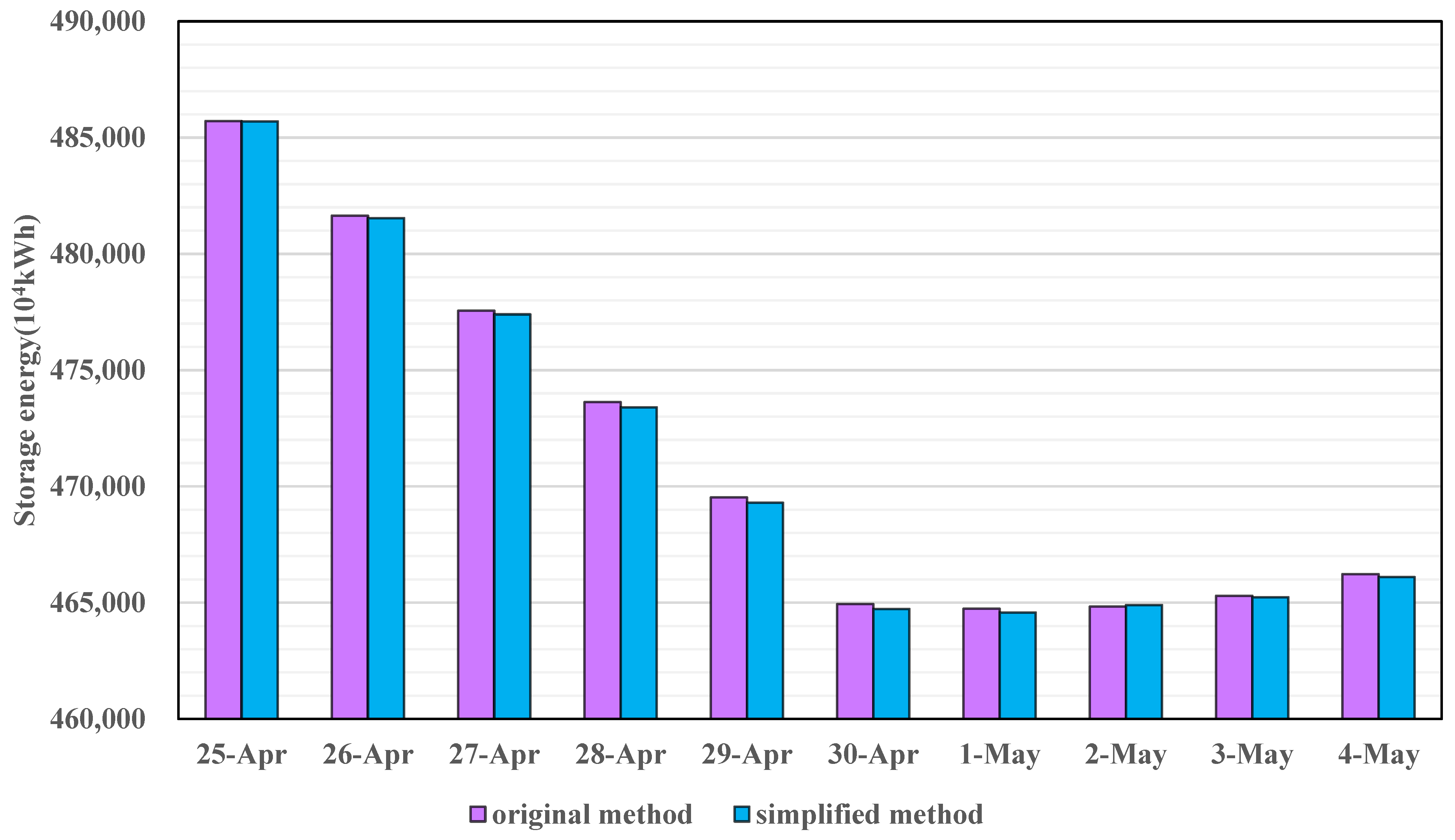
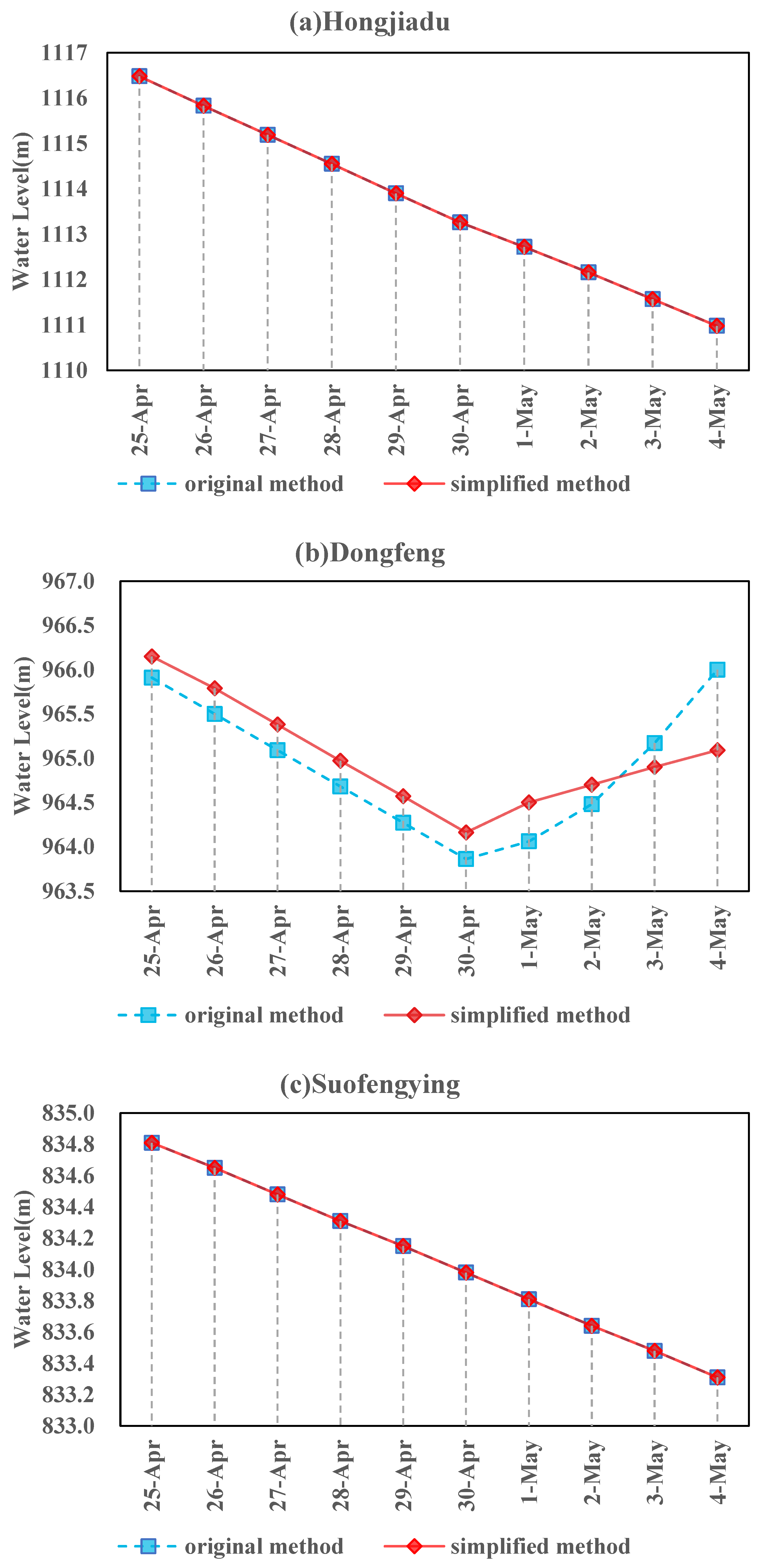
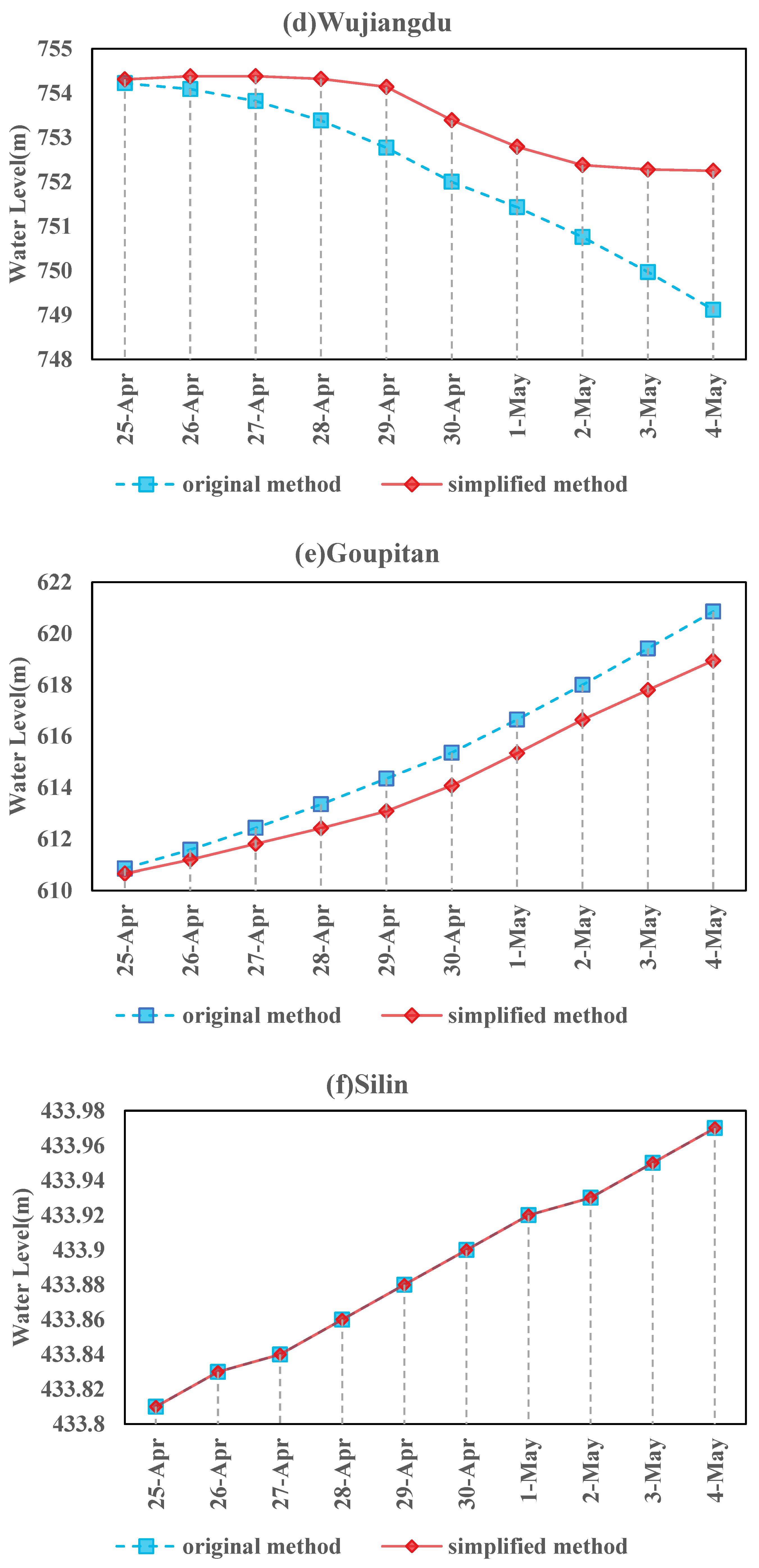
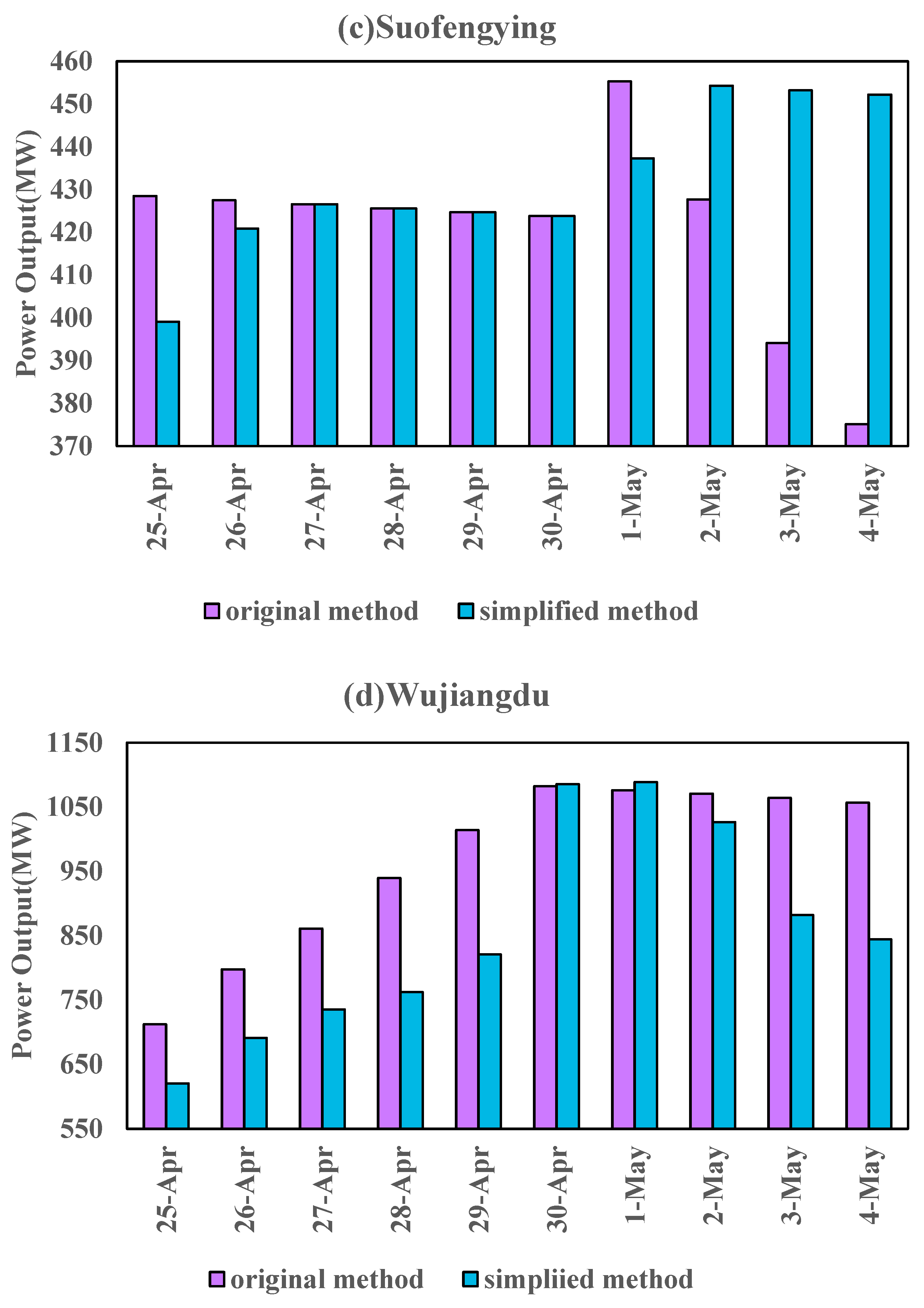
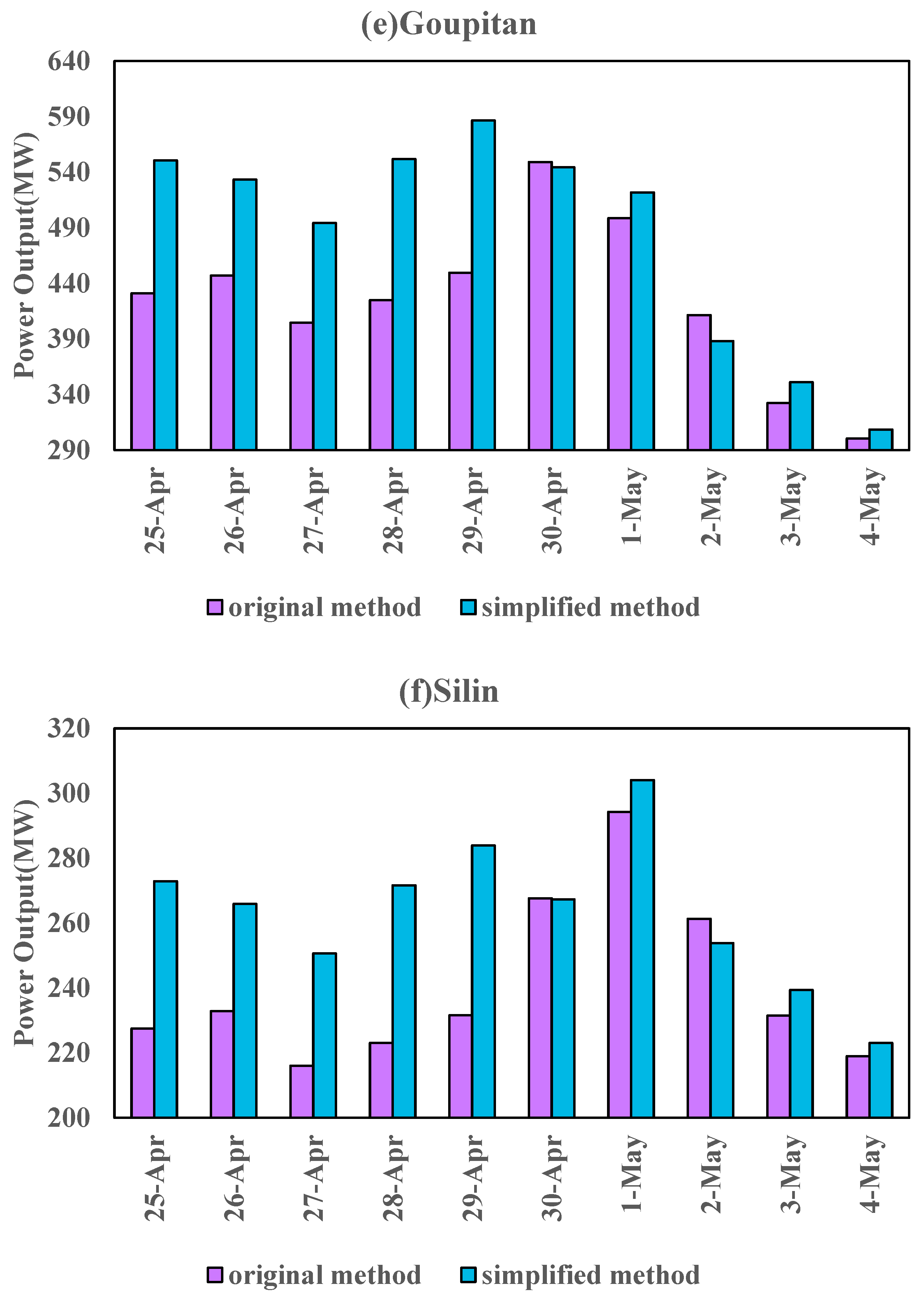
3. Case Study
4. Discussion
5. Conclusions
Future Possible Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| ACO | ant colony algorithm |
| BD | bundle method |
| CP | cutting plane method |
| DC-CP | dynamically constrained cutting plane method |
| DP | dynamic programming |
| DPSA | successive approximation of dynamic programming |
| GA | genetic algorithm |
| GD | generation dispatch problem |
| LP | linear programming |
| LR | Lagrangian relaxation method |
| NLP | nonlinear programming |
| POA | progressive optimality algorithm |
| PSO | particle swarm optimization |
| UC | unit commitment problem |
| Variables | |
| the storage energy of reservoir m at the end of scheduling term, 104 kWh | |
| the number of reservoirs in the cascaded hydropower system | |
| the end-of-term storage energy of cascaded hydropower system, 104 kWh | |
| the water storage of reservoir m at the end of the dispatching period T, m3 | |
| the mean rate of consumption of reservoir m, m3/kWh | |
| the water storage above the dead water level of all upstream reservoirs of reservoir m at the end of the dispatching term, m3 | |
| the direct upstream reservoirs array of reservoir m | |
| k | the serial number of direct upstream reservoirs of reservoir m |
| the number of direct upstream reservoirs of reservoir m | |
| the water storage of direct upstream reservoirs of kth reservoir at the end of period T, m3 | |
| water storage above the dead water level of all direct upstream reservoirs of kth reservoir at the end of period T, m3 | |
| t | the scheduling period, |
| the water storage of reservoir m in period t, m3 | |
| reservoir inflow of reservoir m in period t, m3/s | |
| power discharge of reservoir m in period t, m3/s | |
| spill of reservoir m in period t, m3/s | |
| storage outflow of reservoir m in period t, m3/s | |
| the interval inflow of reservoir m in period t, m3/s | |
| water level of reservoir m in period t, m | |
| power output of reservoir m in period t, MW | |
| Lagrange multiplier | |
| Parameters | |
| p | a parameter of aggregate function method, which is set to be 0.01 |
References
- Zeng, M.; Zhang, K.; Liu, D. Overall review of pumped-hydro energy storage in China: Status quo, operation mechanism and policy barriers. Renew. Sustain. Energy Rev. 2013, 17, 35–43. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, S.; Ye, Y.; Liu, R.; Shang, L.; Liu, C.; Meng, X.; Li, X.; Fan, Q. China’ energy-water nexus: Hydropower generation potential of joint operation of the Three Gorges and Qingjiang cascade reservoirs. Energy 2018, 142, 14–32. [Google Scholar] [CrossRef]
- Wu, X.; Cheng, C.; Zeng, Y.; Lund, J.R. Centralized versus Distributed Cooperative Operating Rules for Multiple Cascaded Hydropower Reservoirs. J. Water Resour. Plan. Manag. 2016, 142, 05016008. [Google Scholar] [CrossRef]
- Liao, S.; Liu, H.; Liu, Z.; Liu, B.; Li, G.; Li, S. Medium-term peak shaving operation of cascade hydropower plants considering water delay time. Renew. Energy 2021, 179, 406–417. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal Operation of Multireservoir Systems: State-of-the-Art Review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Yeh, W.W.-G. Reservoir Management and Operations Models: A State-of-the-Art Review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Yoo, J.-H. Maximization of hydropower generation through the application of a linear programming model. J. Hydrol. 2009, 376, 182–187. [Google Scholar] [CrossRef]
- Barros, M.T.L.; Tsai, F.T.-C.; Yang, S.-L.; Lopes, J.E.G.; Yeh, W.W.-G. Optimization of Large-Scale Hydropower System Operations. J. Water Resour. Plan. Manag. 2003, 129, 178–188. [Google Scholar] [CrossRef]
- Cheng, C.-T.; Liao, S.-L.; Tang, Z.-T.; Zhao, M.-Y. Comparison of particle swarm optimization and dynamic programming for large scale hydro unit load dispatch. Energy Convers. Manag. 2009, 50, 3007–3014. [Google Scholar] [CrossRef]
- Feng, Z.-K.; Niu, W.-J.; Cheng, C.-T.; Wu, X.-Y. Optimization of large-scale hydropower system peak operation with hybrid dynamic programming and domain knowledge. J. Clean. Prod. 2018, 171, 390–402. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J.; Yang, D. Improved Dynamic Programming for Hydropower Reservoir Operation. J. Water Resour. Plan. Manag. 2014, 140, 365–374. [Google Scholar] [CrossRef]
- Oliveira, R.; Loucks, D.P. Operating rules for multireservoir systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
- Kumar, D.N.; Reddy, M.J. Multipurpose Reservoir Operation Using Particle Swarm Optimization. J. Water Resour. Plan. Manag. 2007, 133, 192–201. [Google Scholar] [CrossRef]
- Kumar, D.N.; Reddy, M.J. Ant Colony Optimization for Multi-Purpose Reservoir Operation. Water Resour. Manag. 2006, 20, 879–898. [Google Scholar] [CrossRef]
- Giles, J.E.; Wunderlich, W.O. Weekly Multipurpose Planning Model for TVA Reservoir System. J. Water Resour. Plan. Manag. Div. 1981, 107, 495–511. [Google Scholar] [CrossRef]
- Trott, W.J.; Yeh, W.W.-G. Optimization of Multiple Reservoir System. J. Hydraul. Div. 1973, 99, 1865–1884. [Google Scholar] [CrossRef]
- Opan, M. Irrigation-energy management using a DPSA-based optimization model in the Ceyhan Basin of Turkey. J. Hydrol. 2010, 385, 353–360. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, P.; Chen, X.; Wang, L.; Ai, X.; Feng, M.; Liu, D.; Liu, Y. Optimal Operation of Multi-reservoir Systems Considering Time-lags of Flood Routing. Water Resour. Manag. 2015, 30, 523–540. [Google Scholar] [CrossRef]
- He, Z.; Wang, C.; Wang, Y.; Wei, B.; Zhou, J.; Zhang, H.; Qin, H. Dynamic programming with successive approximation and relaxation strategy for long-term joint power generation scheduling of large-scale hydropower station group. Energy 2021, 222, 119960. [Google Scholar] [CrossRef]
- Fisher, M.L. The Lagrangian Relaxation Method for Solving Integer Programming Problems. Manag. Sci. 1981, 27, 1–18. [Google Scholar] [CrossRef]
- Fisher, M.L. An Applications Oriented Guide to Lagrangian Relaxation. Interfaces 1985, 15, 10–21. [Google Scholar] [CrossRef]
- Guan, X.; Ni, E.; Li, R.; Luh, P.B. An optimization-based algorithm for scheduling hydrothermal power systems with cascaded reservoirs and discrete hydro constraints. IEEE Trans. Power Syst. 1997, 12, 1775–1780. [Google Scholar] [CrossRef] [Green Version]
- Redondo, N.J.; Conejo, A. Short-term hydro-thermal coordination by Lagrangian relaxation: Solution of the dual problem. IEEE Trans. Power Syst. 1999, 14, 89–95. [Google Scholar] [CrossRef]
- Soares, S.; Ohishi, T.; Cicogna, M.; Arce, A. Dynamic dispatch of hydro generating units. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 2, p. 6. [Google Scholar]
- Zhai, Q.; Guan, X.; Cui, J. Unit commitment with identical units successive subproblem solving method based on Lagrangian relaxation. IEEE Trans. Power Syst. 2002, 17, 1250–1257. [Google Scholar] [CrossRef]
- Finardi, E.C.; Scuzziato, M.R. A comparative analysis of different dual problems in the Lagrangian Relaxation context for solving the Hydro Unit Commitment problem. Electr. Power Syst. Res. 2014, 107, 221–229. [Google Scholar] [CrossRef]
- Pursimo, J.; Antila, H.; Vilkko, M.; Lautala, P. A short-term scheduling for a hydropower plant chain. Int. J. Electr. Power Energy Syst. 1998, 20, 525–532. [Google Scholar] [CrossRef]
- Wang, J. Short-term generation scheduling model of Fujian hydro system. Energy Convers. Manag. 2009, 50, 1085–1094. [Google Scholar] [CrossRef]
- Finardi, E.; Takigawa, F.; Brito, B. Assessing solution quality and computational performance in the hydro unit commitment problem considering different mathematical programming approaches. Electr. Power Syst. Res. 2016, 136, 212–222. [Google Scholar] [CrossRef]
- Liu, B.; Cheng, C.; Wang, S.; Liao, S.; Chau, K.-W.; Wu, X.; Li, W. Parallel chance-constrained dynamic programming for cascade hydropower system operation. Energy 2018, 165, 752–767. [Google Scholar] [CrossRef]
- Liu, P.; Guo, S.; Xu, X.; Chen, J. Derivation of Aggregation-Based Joint Operating Rule Curves for Cascade Hydropower Reservoirs. Water Resour. Manag. 2011, 25, 3177–3200. [Google Scholar] [CrossRef]
- Li, X. An entropy-based aggregate method for minimax optimization. Eng. Optim. 1992, 18, 277–285. [Google Scholar] [CrossRef]
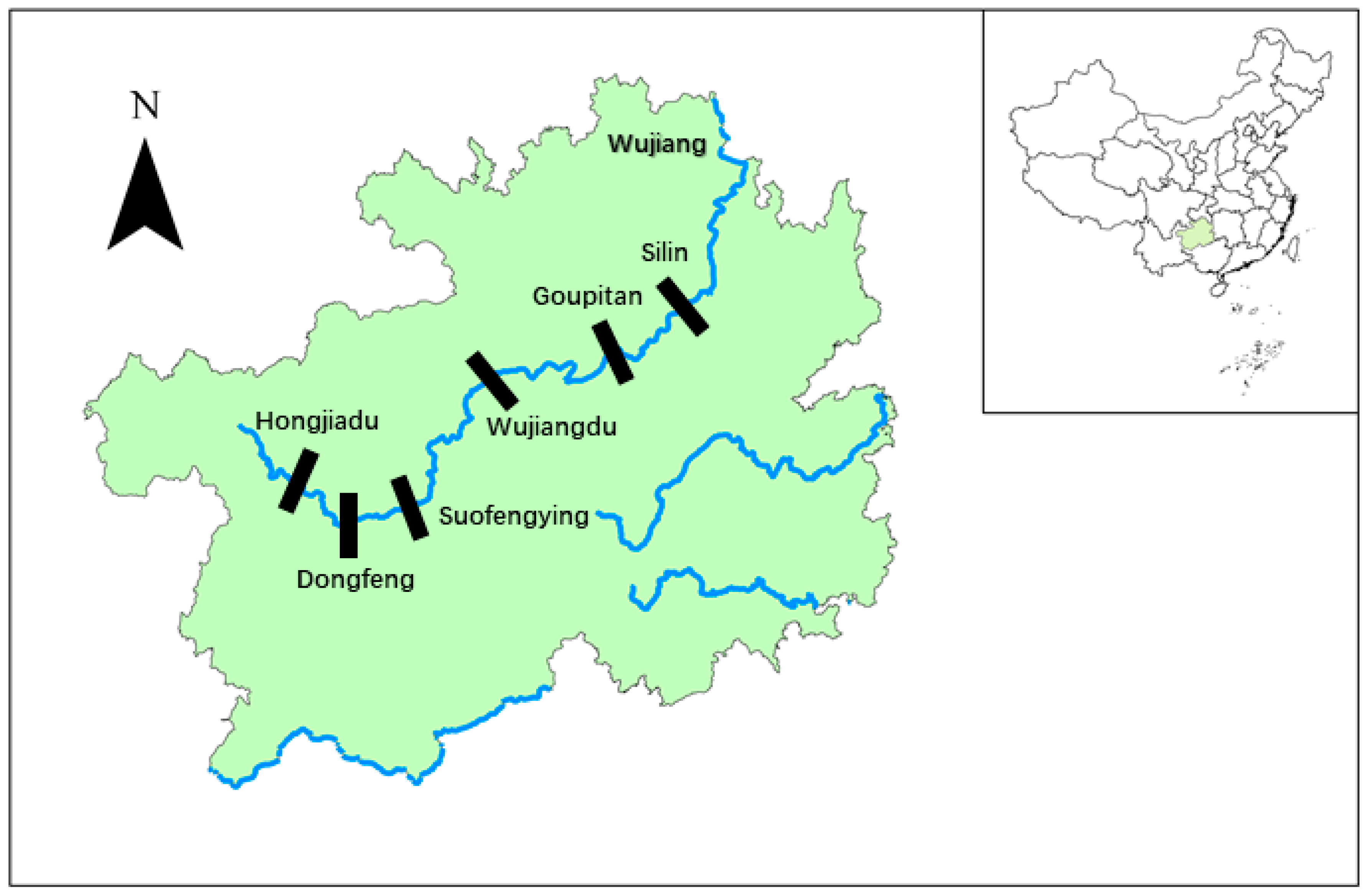

| Hydropower Plant | Regulation Performance | Installed Capacity (MW) | Dead Water Level (m) | Normal High Water Level (m) | Regulation Storage (108 m3) |
|---|---|---|---|---|---|
| Hongjiadu | Pluriennal Regulation | 600 | 1076 | 1140 | 33.61 |
| Dongfeng | Incomplete Annual Regulation | 695 | 936 | 970 | 4.9 |
| Suofengying | Daily Regulation | 600 | 822 | 837 | 0.674 |
| Wujiangdu | Incomplete Annual Regulation | 1250 | 720 | 760 | 13.6 |
| Goupitan | Pluriennal Regulation | 3000 | 585 | 630 | 31.54 |
| Silin | Daily Regulation | 1050 | 431 | 440 | 3.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Cheng, R.; Cheng, C. A Simplified Solution Method for End-of-Term Storage Energy Maximization Model of Cascaded Reservoirs. Energies 2022, 15, 4503. https://doi.org/10.3390/en15124503
Wu X, Cheng R, Cheng C. A Simplified Solution Method for End-of-Term Storage Energy Maximization Model of Cascaded Reservoirs. Energies. 2022; 15(12):4503. https://doi.org/10.3390/en15124503
Chicago/Turabian StyleWu, Xinyu, Ruixiang Cheng, and Chuntian Cheng. 2022. "A Simplified Solution Method for End-of-Term Storage Energy Maximization Model of Cascaded Reservoirs" Energies 15, no. 12: 4503. https://doi.org/10.3390/en15124503
APA StyleWu, X., Cheng, R., & Cheng, C. (2022). A Simplified Solution Method for End-of-Term Storage Energy Maximization Model of Cascaded Reservoirs. Energies, 15(12), 4503. https://doi.org/10.3390/en15124503







