Optimizing Low-Carbon Pathway of China’s Power Supply Structure Using Model Predictive Control
Abstract
:1. Introduction
- (1)
- Establish the concept of CCI to describe the relationship between installed capacity and annual generation, put forward a statistical-based CCI simulation method for renewable energy units, and extend the method to annual power structure planning;
- (2)
- Establish a two-layer optimization structure, regard power structure planning as two stages of installed capacity optimization and power generation optimization, and solve the optimization problem in stages;
- (3)
- Apply the MPC framework to power supply structure planning, regard the problem as a dynamic programming problem, solve the optimization problem from the control perspective, adjust the control strategy of each rolling time domain according to different states, and finally obtain the optimal solution.
2. Introduction of Related Concepts
2.1. CCI of the Generator
2.2. Forecast of CCI for Renewable Energy Units
2.3. Latin Hypercube Sampling
- Determine the number of samples L, that is, the total number of CCI values required for renewable energy units;
- Divide the cumulative probability distribution (0, 1) interval into L segments equally;
- In each of these L segments, a value is randomly selected as the probability value of CCI;
- Map the extracted values to the standard normal distribution samples through the inverse function of the standard normal cumulative distribution;
- By shuffling the sequence of the obtained samples and further improving the randomness of the samples, the CCI sequence in a certain scenario is obtained.
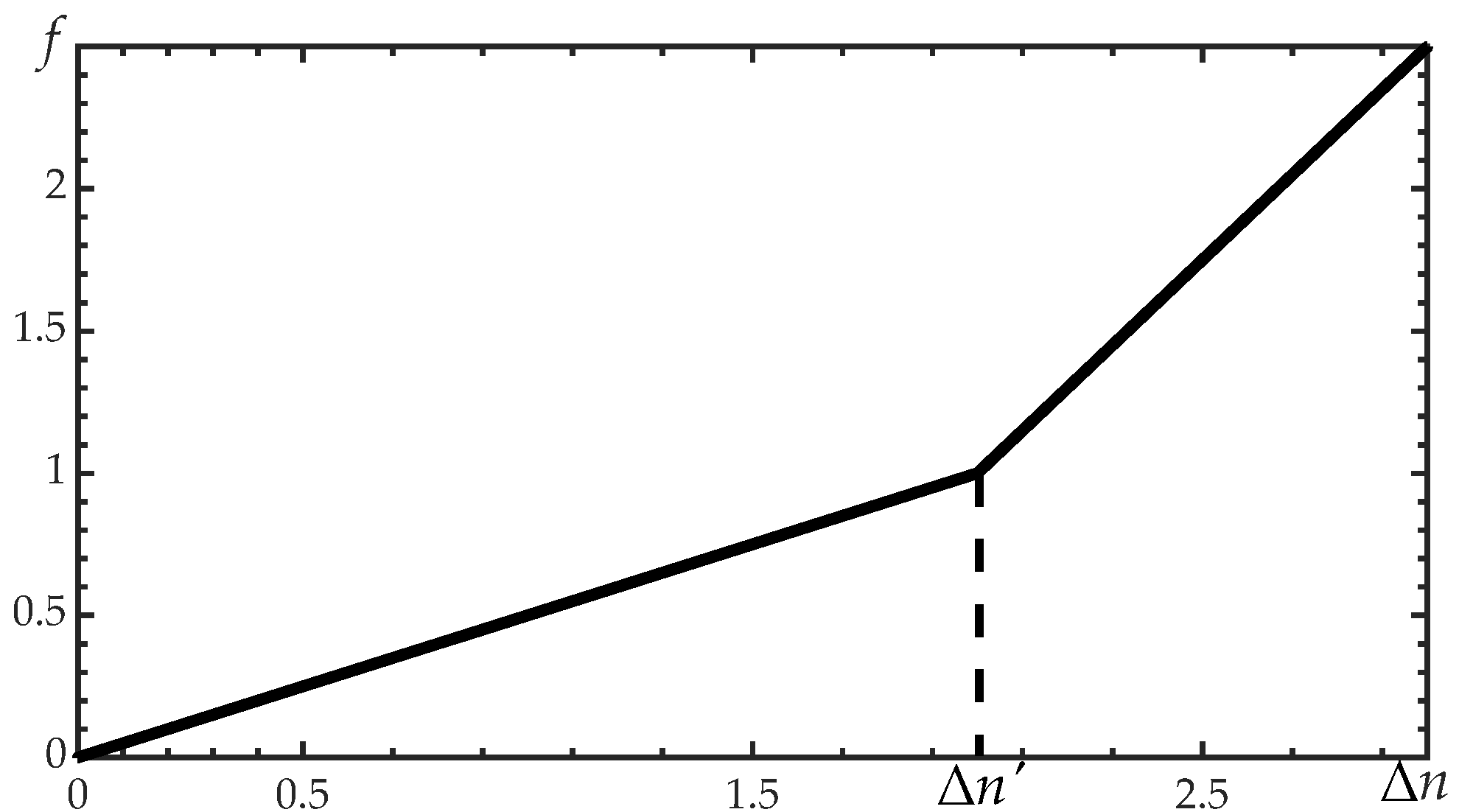
2.4. Annual Peak Shaving Cost of Power Generation Technology
3. Two-Layer Optimization Model Based on MPC
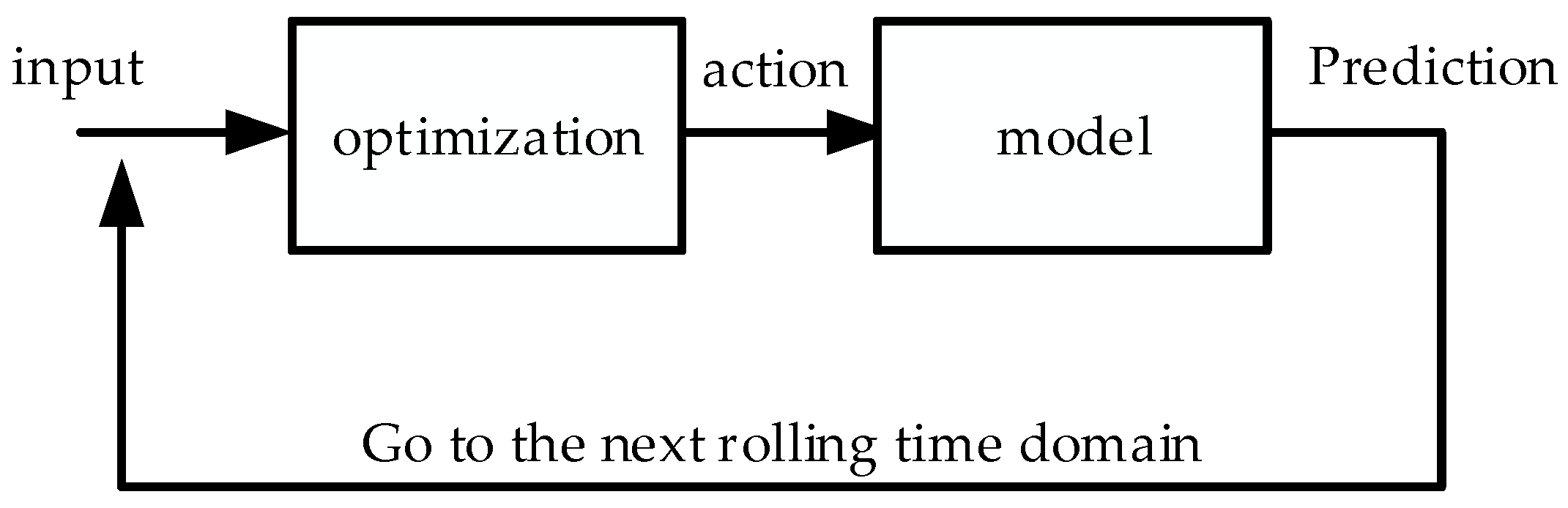
3.1. Necessity and Basic Architecture of Model
3.2. Upper-Layer Installed Capacity Planning Model
3.3. Lower-Layer CCI Optimization Model
3.4. Model Solution
- Predict exogenous variables, including the carbon emission coefficient, various costs, annual electricity demand and peak load in a year, the CCI of wind and solar power generation, etc. The prediction methods of the exogenous variables are shown as follows:
- 2.
- Define k representing the number of loops, then enter the initial value of the state variable and set k = 1, ;
- 3.
- Solve the upper-layer optimization problem established in Section 3.2. After temporarily regarding the CCI value in the rolling time domain as a constant, we rewrote the variables in this optimization model with state variables. We then used the number in parentheses to denote the element label of the vector and summarized the equivalent reformulation as follows:for other constraints in Section 3.2, the variables in the model can be replaced by state variables according to Equation (14), which are not repeated here. Through this step, we obtain of each year during the planning period; therefore, the installed capacity is obtained.
- 4.
- Solve the lower-layer optimization problem established in Section 3.3. Based on the obtained G in step 3, solve the optimal CCI for each year according to the optimization model established in Section 3.3, and get the results to replace the elements of the state vector. It is worth noting that and , i.e., and , are exogenous variables, and the substitution process does not change their values;
- 5.
- Determine if k is equal to the set number of cycles. If they are not equal, set k = k + 1, then take the state variable of the second year in the rolling time domain as the initial state variable, i.e., , and return to step 3; if they are equal, stop the loop;
- 6.
- Finally, we obtain k groups of optimal solution matrices from k loops, then take out the initial state vector in the solution matrix of the first loop and the second column vector in each matrix to form a new matrix A. The reformulated matrix is the final optimal solution from the MPC framework, and we obtain our results as Equation (24).
| Algorithm 1. MPC framework |
| 1: Predict exogenous variables. |
| 2. Input: initial value of the state vector, planning period T, and the number of cycles. |
| 3: if k = 1, then |
| 4: Solve the upper-layer optimization model. |
| 5: Solve the lower-layer optimization model, and obtain an optimal solution matrix. |
| 6: Set . |
| 7: for k = 2, …, T + 1, do |
| 8: Set . |
| 9: Solve the upper-layer optimization model for . |
| 10: Solve the lower-layer optimization model, and obtain an optimal solution matrix. |
| 11: return A, G, W, and em. |
4. Case Study
4.1. Base Data
- Carbon dioxide emissions in the power industry only come from thermal power units, ignoring the impact of transportation and thermodynamics on carbon emissions in the power industry;
- The installed capacity data in the past years all meet the load peak requirements and can be used as the lower limit constraint value of the installed capacity in the past years;
- Considering the improvement in the tolerance of the thermal power reserve due to technological progress, the minimum power generation ratio of the units that generate stable power decreases by an equal rate of change;
- Peak load and annual electricity demand increase in equal proportions;
- Ignoring increases in fuel costs due to energy shortages and political factors, all costs are subject to a fixed rate of change;
- The thermal power unit absorbs 90% of the carbon dioxide after a CCS retrofit.
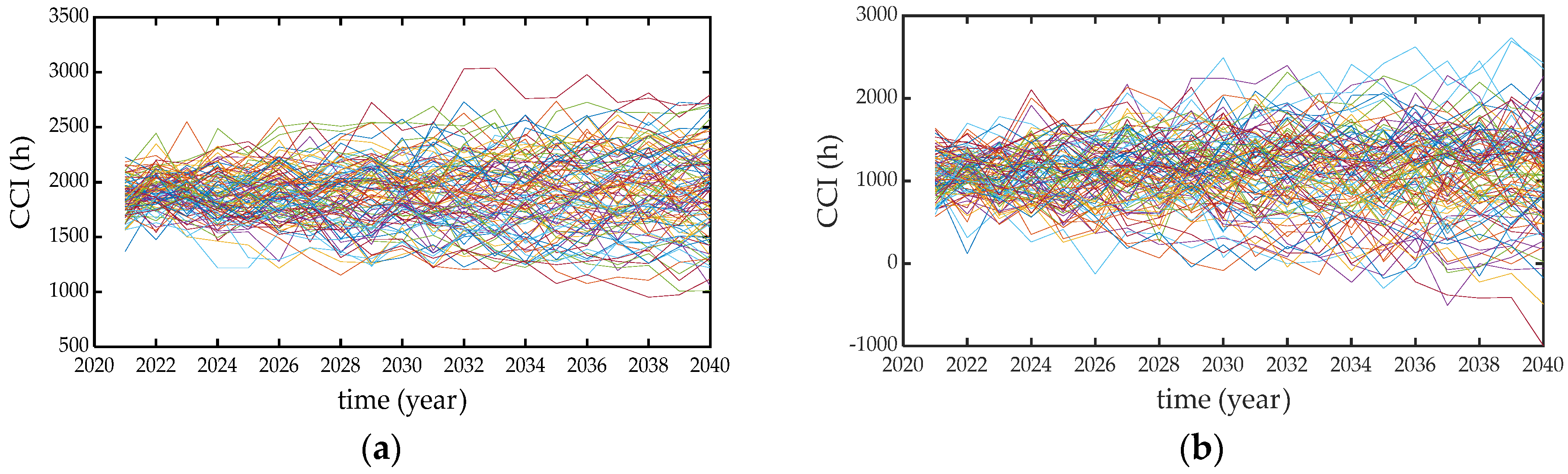
4.2. Results of the Case
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Power Generation Technology | Unit Cost | Change Rate (%) |
|---|---|---|
| Thermal power | C10 | −0.2 |
| C20 | 5 | |
| C30 | 10 | |
| Hydropower | C10 | 1 |
| C20 | 0 | |
| C30 | 0 | |
| Nuclear power | C10 | −0.8 |
| C20 | 5 | |
| C30 | 1 | |
| Wind power | C10 | −2 |
| C20 | −2.5 | |
| C30 | 1 | |
| Solar power | C10 | −5 |
| C20 | −0.5 | |
| C30 | 1 | |
| Others | C10 | −1 |
| C20 | −0.5 | |
| C30 | 1 |
| Power Generation Technology | n′ (h) | k1 | k2 |
|---|---|---|---|
| Thermal power | 4540 | 1 | 5 |
| Hydropower | 3300 | 2 | 6 |
| Nuclear power | 7000 | 7 | 8 |
| Others | 4700 | 3 | 4 |
| Parameter | Initial Value (million kW/billion kWh) | Change Rate (%) |
|---|---|---|
| Ppeak | 2162.49 | 3 |
| W | 7317.00 | 6 |
References
- Godde, C.M.; Mason-D’Croz, D.; Mayberry, D.E.; Thornton, P.K.; Herrero, M. Impacts of climate change on the livestock food supply chain; a review of the evidence. Glob. Food Secur. 2021, 28, 100488. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.B.; Bai, X.; Li, W.; Wang, N. Impacts of climate change on water resources and grain production. Technol. Forecast. Soc. Chang. 2019, 143, 76–84. [Google Scholar] [CrossRef]
- Altieri, M.A.; Nicholls, C.I. The adaptation and mitigation potential of traditional agriculture in a changing climate. Clim. Chang. 2017, 140, 33–45. [Google Scholar] [CrossRef]
- Cuthbert, M.O.; Gleeson, T.; Moosdorf, N.; Befus, K.M.; Schneider, A.; Hartmann, J.; Lehner, B. Global patterns and dynamics of climate-groundwater interactions. Nat. Clim. Chang. 2019, 9, 137–141. [Google Scholar] [CrossRef]
- Wanders, N.; Wada, Y. Human and climate impacts on the 21st century hydrological drought. J. Hydrol. 2015, 526, 208–220. [Google Scholar] [CrossRef]
- Alfieri, L.; Burek, P.; Feyen, L.; Forzieri, G. Global warming increases the frequency of river floods in Europe. Hydrol. Earth Syst. Sci. 2015, 19, 2247–2260. [Google Scholar] [CrossRef] [Green Version]
- Simpson, N.P.; Mach, K.J.; Constable, A.; Hess, J.; Hogarth, R.; Howden, M.; Lawrence, J.; Lempert, R.J.; Muccione, V.; Mackey, B.; et al. A framework for complex climate change risk assessment. One Earth 2021, 4, 489–501. [Google Scholar] [CrossRef]
- Preston, B.J. The Influence of the Paris Agreement on Climate Litigation: Legal Obligations and Norms (Part I). J. Environ. Law 2021, 33, 1–32. [Google Scholar] [CrossRef]
- Schleussner, C.-F.; Rogelj, J.; Schaeffer, M.; Lissner, T.; Licker, R.; Fischer, E.M.; Knutti, R.; Levermann, A.; Frieler, K.; Hare, W. Science and policy characteristics of the Paris Agreement temperature goal. Nat. Clim. Chang. 2016, 6, 827–835. [Google Scholar] [CrossRef] [Green Version]
- He, J.K. China’s INDC and non-fossil energy development. Adv. Clim. Chang. Res. 2015, 6, 210–215. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, J.Z.; Su, Z.Y. Power generation and renewable potential in China. Renew. Sustain. Energy Rev. 2014, 40, 727–740. [Google Scholar] [CrossRef]
- Shuai, Y.; Zhao, B.; Jiang, D.; He, S.; Lyu, J.; Yue, G. Status and prospect of coal-fired high efficiency and clean power generation technology in China. Therm. Power Gener. 2022, 51, 1–10. [Google Scholar]
- Jiang, Y.; Lei, Y.L.; Yan, X.; Yang, Y.Z. Employment impact assessment of carbon capture and storage (CCS) in China’s power sector based on input-output model. Environ. Sci. Pollut. Res. 2019, 26, 15665–15676. [Google Scholar] [CrossRef] [PubMed]
- Tock, L.; Marechal, F. Environomic optimal design of power plants with CO2 capture. Int. J. Greenh. Gas Control 2015, 39, 245–255. [Google Scholar] [CrossRef]
- Sifat, N.S.; Haseli, Y. A Critical Review of CO2 Capture Technologies and Prospects for Clean Power Generation. Energies 2019, 12, 4143. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.K.; Thakur, N.S. Assessing the impact of small hydropower projects in Jammu and Kashmir: A study from north-western Himalayan region of India. Renew. Sustain. Energy Rev. 2017, 80, 679–693. [Google Scholar] [CrossRef]
- Zelenakova, M.; Fijko, R.; Diaconu, D.C.; Remenakova, I. Environmental Impact of Small Hydro Power Plant-A Case Study. Environments 2018, 5, 12. [Google Scholar] [CrossRef] [Green Version]
- Zeng, M.; Liu, Y.X.; Ouyang, S.J.; Shi, H.; Li, C.X. Nuclear energy in the Post-Fukushima Era: Research on the developments of the Chinese and worldwide nuclear power industries. Renew. Sustain. Energy Rev. 2016, 58, 147–156. [Google Scholar] [CrossRef] [Green Version]
- IEA. World Energy Outlook 2021; OECD: Paris, France, 2021. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Zuo, J.A.; Fan, L.L.; Zillante, G. Impacts of renewable energy regulations on the structure of power generation in China—A critical analysis. Renew. Energy 2011, 36, 24–30. [Google Scholar] [CrossRef]
- Wu, Q.L.; Peng, C.Y. Scenario Analysis of Carbon Emissions of China’s Electric Power Industry Up to 2030. Energies 2016, 9, 988. [Google Scholar] [CrossRef] [Green Version]
- Shen, W.; Qiu, J.; Meng, K.; Chen, X.; Dong, Z.Y. Low-Carbon Electricity Network Transition Considering Retirement of Aging Coal Generators. IEEE Trans. Power Syst. 2020, 35, 4193–4205. [Google Scholar] [CrossRef]
- Wu, J.J.; Tang, G.H.; Wang, R.; Sun, Y.W. Multi-Objective Optimization for China’s Power Carbon Emission Reduction by 2035. J. Therm. Sci. 2019, 28, 184–194. [Google Scholar] [CrossRef]
- Li, Z.; Chen, S.; Dong, W.; Liu, P.; Du, E.; Ma, L.; He, J. Low Carbon Transition Pathway of Power Sector Under Carbon Emission Constraints. Proc. Chin. Soc. Electr. Eng. 2021, 41, 3987–4000. [Google Scholar] [CrossRef]
- Shu, Y.; Zhang, L.; Zhang, Y.; Wang, Y.; Lu, G.; Yuan, B.; Xia, P. Carbon Peak and Carbon Neutrality Path for China’s Power Industry. Eng. Sci. 2021, 23, 1–14. [Google Scholar] [CrossRef]
- Yao, X.L.; Lei, H.T.; Yang, L.L.; Shao, S.; Ahmed, D.; Ismaail, M. Low-carbon transformation of the regional electric power supply structure in China: A scenario analysis based on a bottom-up model with resource endowment constraints. Resour. Conserv. Recycl. 2021, 167, 105315. [Google Scholar] [CrossRef]
- Mirjat, N.H.; Uqaili, M.A.; Harijan, K.; Walasai, G.D.; Mondal, M.A.H.; Sahin, H. Long-term electricity demand forecast and supply side scenarios for Pakistan (2015–2050): A LEAP model application for policy analysis. Energy 2018, 165, 512–526. [Google Scholar] [CrossRef]
- Wang, B.; Wang, L.M.; Zhong, S.; Xiang, N.; Qu, Q.S. Low-Carbon Transformation of Electric System against Power Shortage in China: Policy Optimization. Energies 2022, 15, 1574. [Google Scholar] [CrossRef]
- Yang, M.; Patino-Echeverri, D.; Yang, F.X. Wind power generation in China: Understanding the mismatch between capacity and generation. Renew. Energy 2012, 41, 145–151. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.X.; Wang, X.F. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- van der Meer, D.W.; Widen, J.; Munkhammar, J. Review on probabilistic forecasting of photovoltaic power production and electricity consumption. Renew. Sustain. Energy Rev. 2018, 81, 1484–1512. [Google Scholar] [CrossRef]
- Zhao, L.J.; Nazir, M.S.; Nazir, H.; Abdalla, A.N. A review on proliferation of artificial intelligence in wind energy forecasting and instrumentation management. Environ. Sci. Pollut. Res. 2022, 29, 43690–43709. [Google Scholar] [CrossRef] [PubMed]
- Alimohammadisagvand, B. Influence of Demand Response Actions on Thermal Comfort and Electricity Cost for Residential Houses. Article Dissertation, Aalto University, Espoo, Finland, 2018. [Google Scholar]
- Alimohammadisagvand, B.; Jokisalo, J.; Sirén, K. The potential of predictive control in minimizing the electricity cost in a heat-pump heated residential house. In Proceedings of the 3rd IBPSA-England Conference BSO 2016, Great North Museum, Newcastle, UK, 12–14 September 2016. [Google Scholar]
- Muratori, M.; Rizzoni, G. Residential Demand Response: Dynamic Energy Management and Time-Varying Electricity Pricing. IEEE Trans. Power Syst. 2016, 31, 1108–1117. [Google Scholar] [CrossRef]
- de Siqueira, L.; Peng, W. Control strategy to smooth wind power output using battery energy storage system: A review. J. Energy Storage 2021, 35, 102252. [Google Scholar] [CrossRef]
- Fan, M. A Novel Optimal Generation Dispatch Algorithm to Reduce the Uncertainty Impact of Renewable Energy. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016. [Google Scholar] [CrossRef]
- Ye, L.; Lu, P.; Zhao, Y.; Dai, B.; Tang, Y. Review of Model Predictive Control for Power System With Large-scale Wind Power Grid-connected. Proc. Chin. Soc. Electr. Eng. 2021, 41, 6181–6197. [Google Scholar]
- Shiroei, M.; Ranjbar, A.M.; Amraee, T. A functional model predictive control approach for power system load frequency control considering generation rate constraint. Int. Trans. Electr. Energy Syst. 2013, 23, 214–229. [Google Scholar] [CrossRef]
- Zheng, Y.; Hill, D.J.; Meng, K.; Luo, F.J.; Dong, Z.Y. Optimal Short-term Power Dispatch Scheduling for a Wind Farm with Battery Energy Storage System. In Proceedings of the 9th IFAC Symposium on Control of Power and Energy Systems (CPES 2015), New Delhi, India, 9–11 December 2015. [Google Scholar] [CrossRef]
- Vand, B.; Ruusu, R.; Hasan, A.; Delgado, B.M. Optimal management of energy sharing in a community of buildings using a model predictive control. Energy Convers. Manag. 2021, 239, 114178. [Google Scholar] [CrossRef]
- Kellett, C.M.; Weller, S.R.; Faulwasser, T.; Grune, L.; Semmler, W. Feedback, dynamics, and optimal control in climate economics. Annu. Rev. Control 2019, 47, 7–20. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Wang, X.; Rong, S.A. Probabilistic Load Flow Method Based on Modified Latin Hypercube-Important Sampling. Energies 2018, 11, 3171. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.; Chen, Y.Y.; Liu, J.K. Reliability sensitivity analysis using axis orthogonal importance Latin hypercube sampling method. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef] [Green Version]
- Tian, X.; Fan, C. Analysis of Deep Peak Regulation and Its Benefit of Thermal Units in Power System With Large Scale Wind Power Integrated. Power Syst. Technol. 2017, 41, 2255–2263. [Google Scholar]
- Lin, L.; Xu, B.Q.; Xia, S.W. Multi-Angle Economic Analysis of Coal-Fired Units with Plasma Ignition and Oil Injection during Deep Peak Shaving in China. Appl. Sci. 2019, 9, 5399. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhang, N.; Dai, H.; Zhang, S.; Wu, X.; Xue, M. Model Construction and Pathways of Low-Carbon Transition of China’s Power System. Electr. Power 2021, 54, 1–11. [Google Scholar]
- Wang, H.; Rong, J. Analysis on China’s Nuclear Energy Development Path under the Goal of Peaking Carbon Emissions and Achieving Carbon Neutrality. Electr. Power 2021, 54, 86–94. [Google Scholar]
- Zhao, X.F.; Wu, L.; Qi, Y. The energy injustice of hydropower: Development, resettlement, and social exclusion at the Hongjiang and Wanmipo hydropower stations in China. Energy Res. Soc. Sci. 2020, 62, 101366. [Google Scholar] [CrossRef]


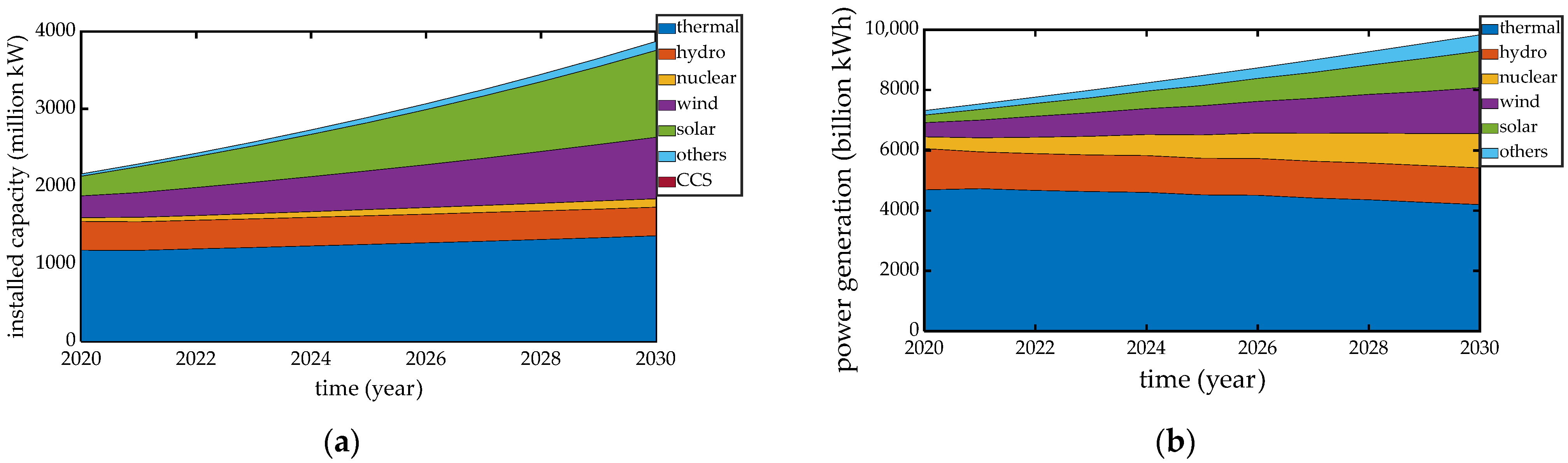

| Power Generation Technology | C10 (yuan/kW) 1 | C20 (yuan/kWh) 1 | C30 (yuan/tCO2) 1 |
|---|---|---|---|
| Thermal power | 5520 | 310.5 | 82.8 |
| Nuclear power | 19,320 | 172.5 | 0 |
| Wind power | 7719 | 103.5 | 0 |
| Solar power | 4485 | 69 | 0 |
| Time (Year) | CCIs of Wind Generation (h) | CCIs of Solar Generation (h) |
|---|---|---|
| 2021 | 1847.886522 | 1016.125731 |
| 2022 | 1913.541309 | 1067.513049 |
| 2023 | 1902.93377 | 1057.050932 |
| 2024 | 1907.364856 | 1060.14718 |
| 2025 | 1865.555989 | 1041.880608 |
| 2026 | 1870.00318 | 1055.535528 |
| 2027 | 1882.558415 | 1079.256736 |
| 2028 | 1870.740671 | 1108.316839 |
| 2029 | 1878.5824 | 1080.04406 |
| 2030 | 1889.170836 | 1102.518975 |
| 2031 | 1867.022553 | 1154.598184 |
| 2032 | 1878.976875 | 1101.724634 |
| 2033 | 1911.402465 | 1139.257536 |
| 2034 | 1888.15016 | 1210.713959 |
| 2035 | 1876.303183 | 1148.691111 |
| 2036 | 1894.921912 | 1170.002537 |
| 2037 | 1904.653039 | 1147.8856 |
| 2038 | 1880.995522 | 1151.924091 |
| 2039 | 1904.351957 | 1148.916736 |
| 2040 | 1903.463496 | 1163.986872 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Chu, X. Optimizing Low-Carbon Pathway of China’s Power Supply Structure Using Model Predictive Control. Energies 2022, 15, 4450. https://doi.org/10.3390/en15124450
Ma Y, Chu X. Optimizing Low-Carbon Pathway of China’s Power Supply Structure Using Model Predictive Control. Energies. 2022; 15(12):4450. https://doi.org/10.3390/en15124450
Chicago/Turabian StyleMa, Yue, and Xiaodong Chu. 2022. "Optimizing Low-Carbon Pathway of China’s Power Supply Structure Using Model Predictive Control" Energies 15, no. 12: 4450. https://doi.org/10.3390/en15124450
APA StyleMa, Y., & Chu, X. (2022). Optimizing Low-Carbon Pathway of China’s Power Supply Structure Using Model Predictive Control. Energies, 15(12), 4450. https://doi.org/10.3390/en15124450






