Load Frequency Robust Control Considering Intermittent Characteristics of Demand-Side Resources
Abstract
:1. Introduction
- Focusing on the unique characteristics of DSRs, dissecting their causes and designing an intermittent control strategy to overcome their negative impact on the grid.
- A critical analysis of stability and robust performance is provided for new LFC systems, considering the parameter uncertainties of the power system.
2. The Intermittent Characteristics of DSRs and Coordinated LFC Model
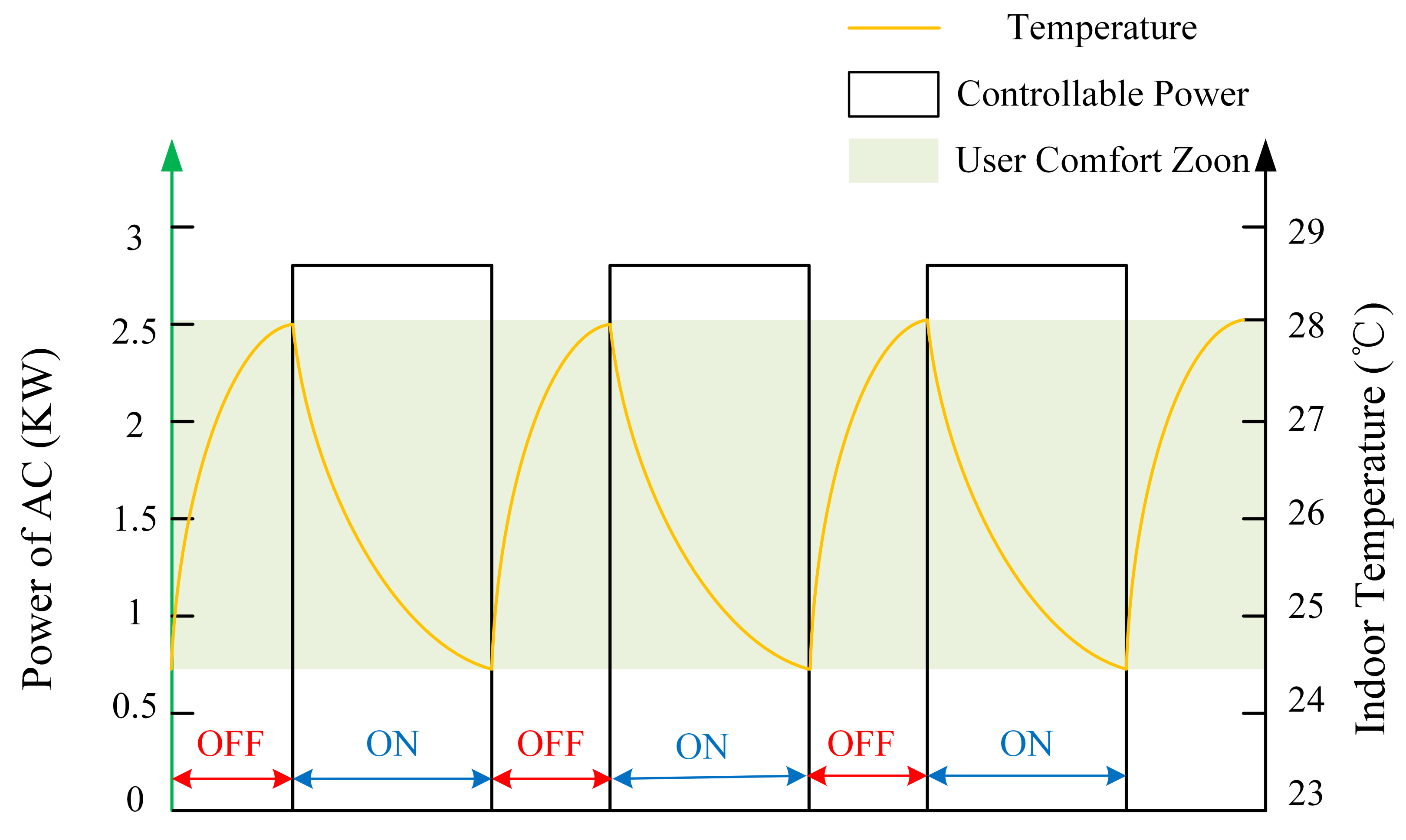
2.1. Cause of Intermittency of DSRs
2.2. Control Strategies for the Intermittent Characteristics of DSRs
2.3. LFC Model with DSRs
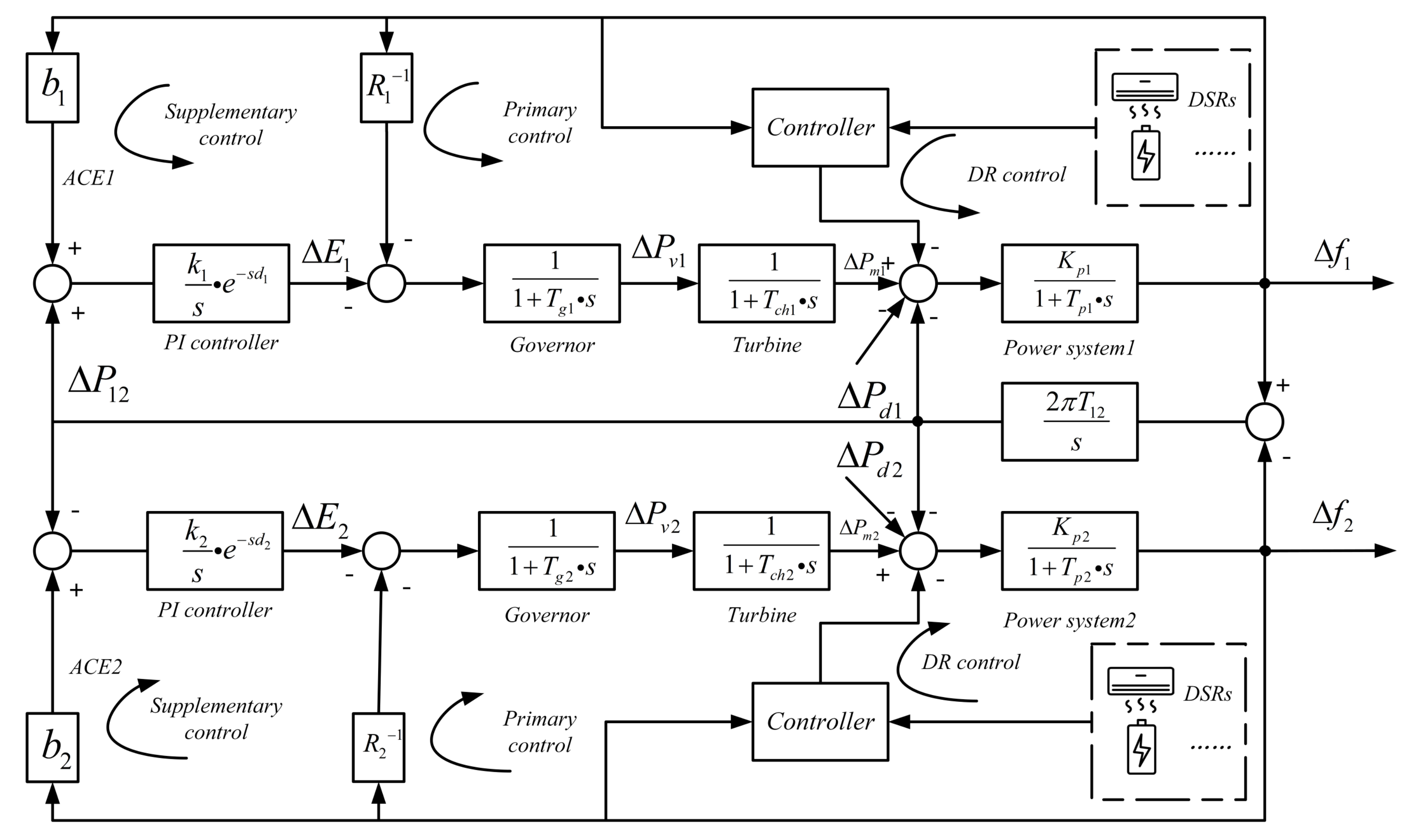
2.3.1. Open-Loop LFC System Model
- is controllable and
- The uncertainty term is bounded and satisfies , where is the norm of the matrix and h is a constant greater than zero. The uncertainty can be described by the following matrix:
2.3.2. Closed-Loop LFC System Model and Robust H∞ Performance
3. Main Result
3.1. Preliminaries
3.2. Controller Design
- (a)
- (b)
- (c)
- (d)
- (e)
- (f)
3.3. Analysis of H∞ Performance
4. Case Study
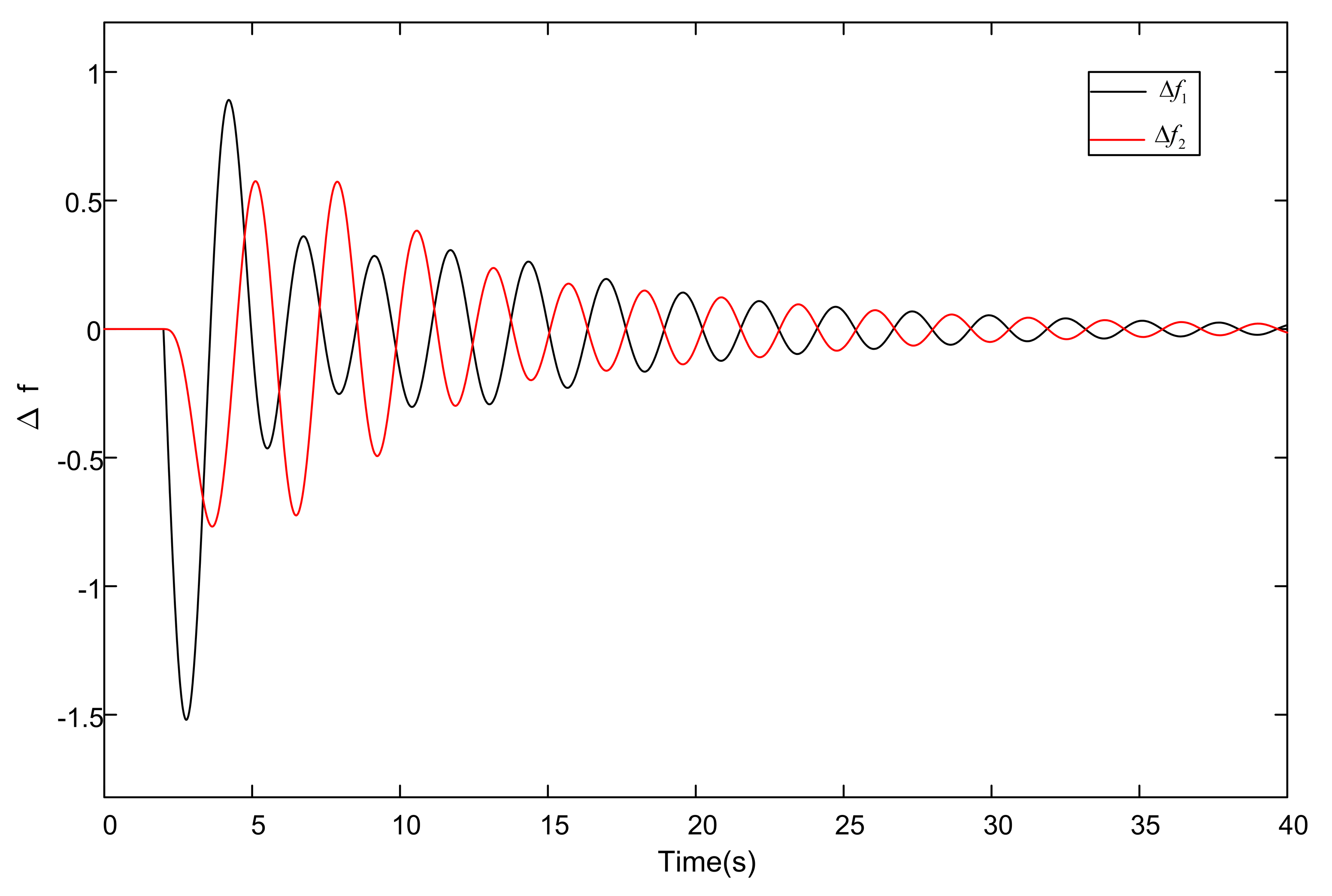
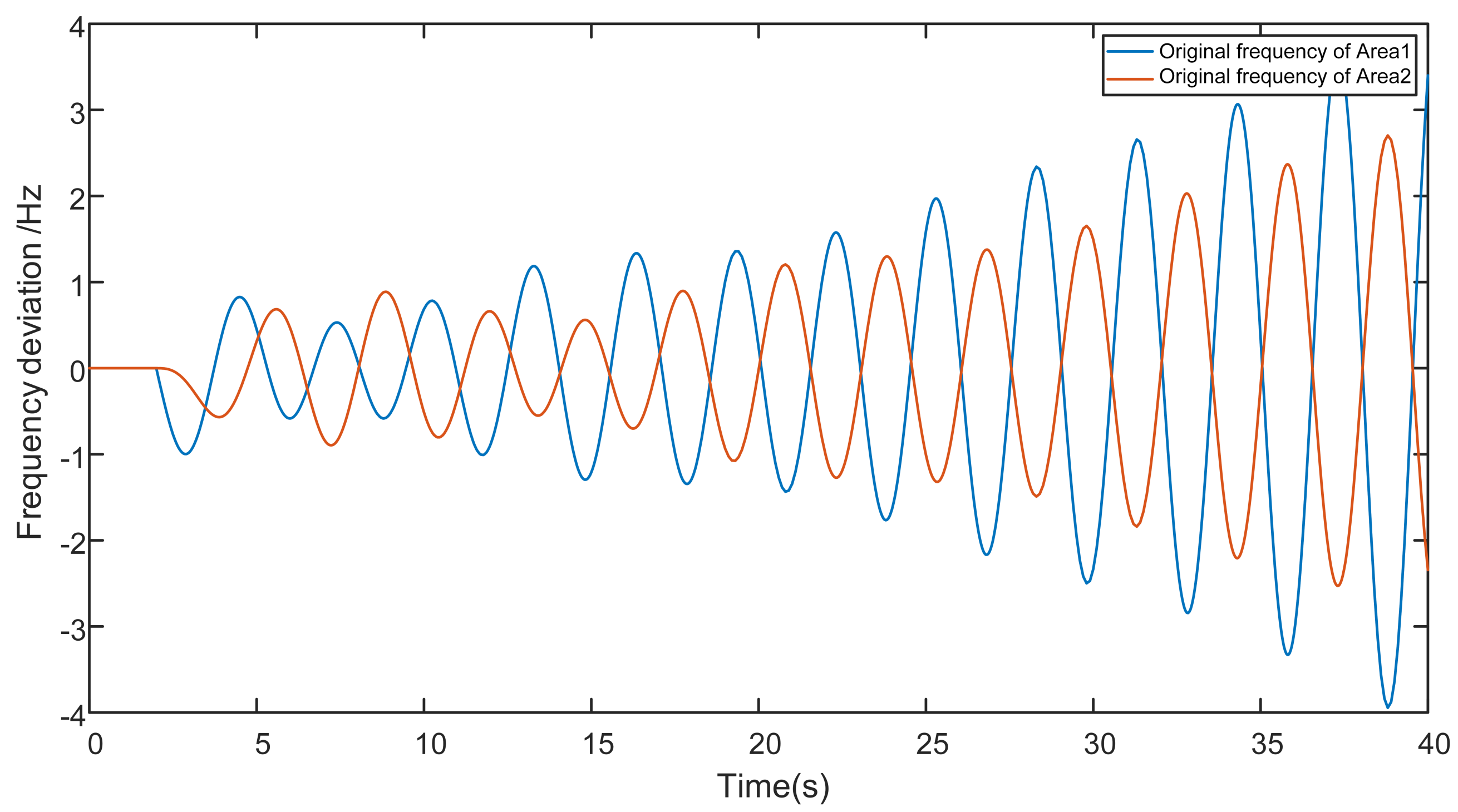
4.1. The Open-Loop LFC System
4.2. The Close-Loop LFC System
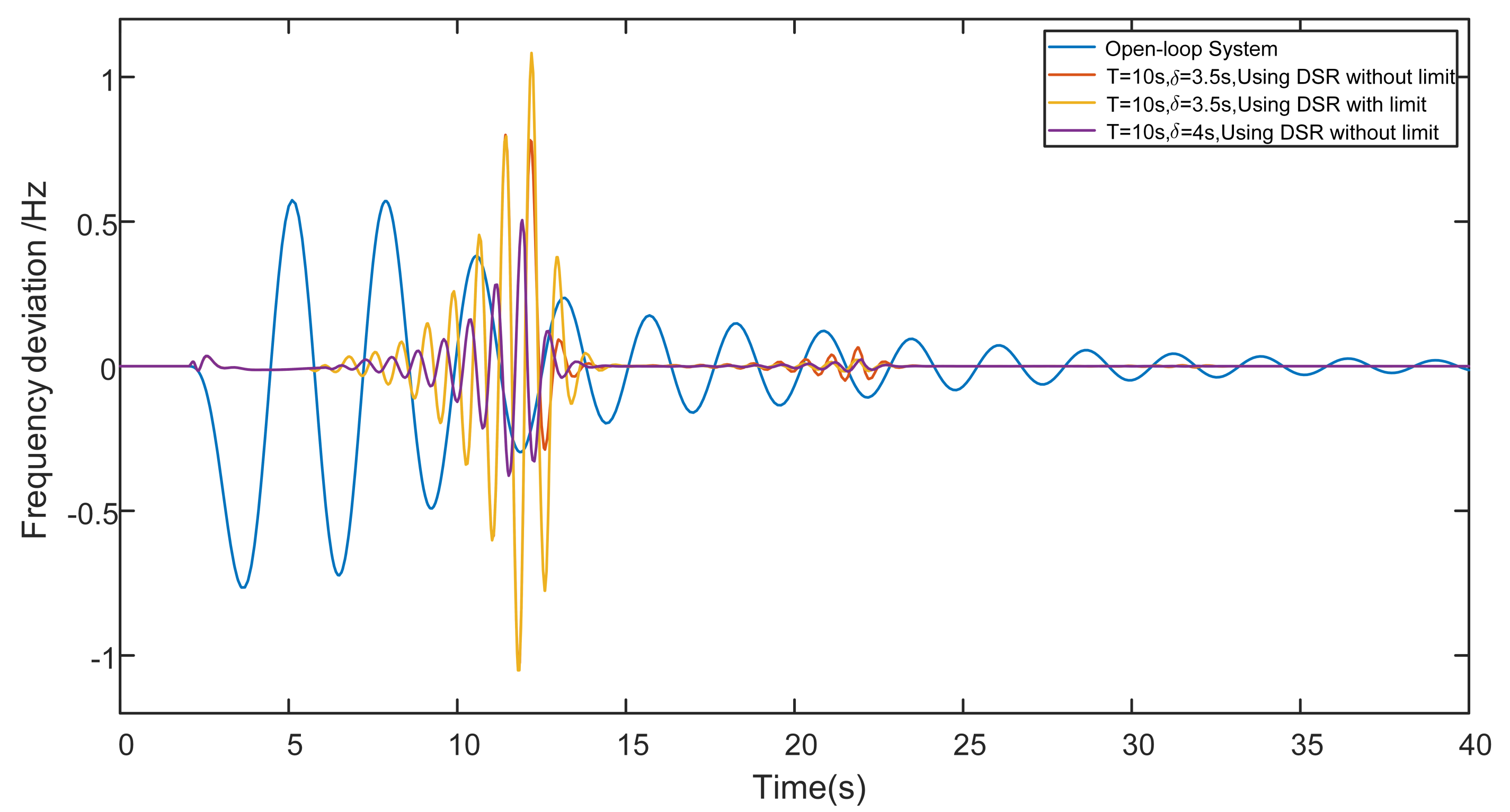
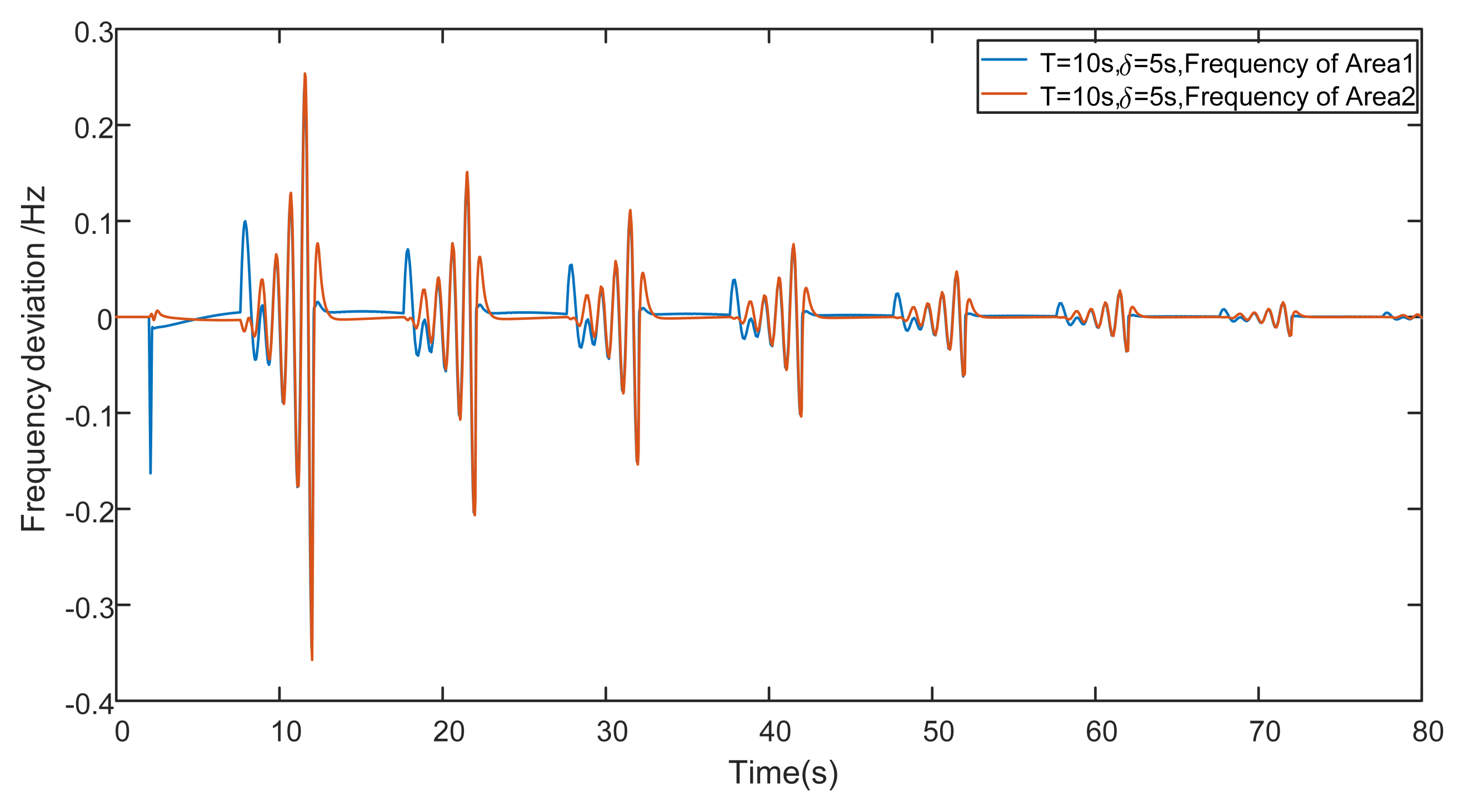
4.2.1. Load-Side and Generation-Side Cooperative Control
- As mentioned in Section 2.2, the intermittent control parameters should not only take into account the comfort of the user but also the stability of the system, otherwise the intermittent input itself is a strong source of disturbance for the LFC system, and a review of the relevant literature [28,29] shows that these two parameters are generally a fixed value in a certain region and can be obtained directly.
- In Formulas (1) and (2) we present the input expression for a DSR resource with intermittent characteristics, which should be related only to the frequency deviation of the system.The DSRs are generally considered to be incapable of detecting any status information other than local frequency deviations in the system, such as the tie line power deviation and the active change in system load , etc. Therefore, we only need to solve for two parameters.
4.2.2. Load-Side and Generation-Side Cooperative Control with Parameter Uncertainty
5. Conclusions
- The intermittent characteristics of demand-side resources are pervasive and are essentially a compromise of demand response for the comfort of the users, which may affect the steady and safety operation of the power system.
- Demand-side resources have great potential in grid frequency regulation, pressure on regulation from the generation side would be greatly mitigated if they could be coordinated and complemented with generation-side resources.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Abbreviations
| DSRs | Demand-Side Resources |
| LFC | Load Frequency Conrol |
| AGC | Automation Generation Control |
| AC | Air Conditioner |
Nomenclature
| Controller parameters to be determined | |
| Constants greater than zero | |
| Power variation for secondary frequency regulation | |
| Electromagnetic power deviation | |
| Mechanical power deviation | |
| Control gain for secondary frequency regulation, Time lag | |
| Governor and turbine time constants | |
| Power system gain and time constants |
Appendix A
Appendix B
References
- Shayeghi, H.A.S.H.; Shayanfar, H.A.; Jalili, A. Load frequency control strategies: A state-of-the-art survey for the researcher. Energy Convers. Manag. 2009, 50, 344–353. [Google Scholar] [CrossRef]
- Meng, L.; Zafar, J.; Khadem, S.K.; Collinson, A.; Murchie, K.C.; Coffele, F.; Burt, G.M. Fast Frequency Response From Energy Storage Systems Review of Grid Standards, Projects and Technical Issues. IEEE Trans. Smart Grid 2020, 11, 1566–1581. [Google Scholar] [CrossRef] [Green Version]
- Yao, J.G.; Zhang, K.F.; Ding, Z.T.; Li, Y.P.; Yang, S.C.; Xia, M. Concept Extension and Research Focus of Dynamic Demand Response. Autom. Electr. Power Syst. 2019, 43, 9. (In Chinese) [Google Scholar]
- Short, J.A.; Infield, D.G.; Freris, L.L. Stabilization of Grid Frequency Through Dynamic Demand Control. IEEE Trans. Power Syst. 2007, 22, 1284–1293. [Google Scholar] [CrossRef] [Green Version]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A Survey on Demand Response Programs in Smart Grids: Pricing Methods and Optimization Algorithms. IEEE Commun. Surv. Tutor. 2015, 17, 152–178. [Google Scholar] [CrossRef]
- Gao, C.; Liang, T.; Li, Y. A Survey on Theory and Practice of Automated Demand Response. Power Syst. Technol. 2014, 38, 8. (In Chinese) [Google Scholar]
- Shen, Y.; Li, Y.; Gao, C.; Zhou, L. Application of Demand Response in Ancillary Service Market. Autom. Electr. Power Syst. 2017, 41, 11. (In Chinese) [Google Scholar]
- Han, B.; Yao, J.; Yu, Y. Discussion on Active Load Response at Receiving End Power Grid for Mitigating UHVDC Blocking Fault. Autom. Electr. Power Syst. 2016, 40, 6. (In Chinese) [Google Scholar]
- Pourmousavi, S.A.; Nehrir, M.H. Introducing Dynamic Demand Response in the LFC Model. IEEE Trans. Power Syst. 2014, 29, 1562–1572. [Google Scholar] [CrossRef]
- Yi, T.; Feng, L.; Qian, C.; Li, M.; Qi, W.; Ming, N.; Gang, C. Frequency prediction method considering demand response aggregate characteristics and control effects. Appl. Energy 2018, 229, 936–944. [Google Scholar]
- Molina-Garcia, A.; Bouffard, F.; Kirschen, D.S. Decentralized Demand-Side Contribution to Primary Frequency Control. IEEE Trans. Power Syst. 2011, 26, 411–419. [Google Scholar] [CrossRef]
- Liu, H.; Huang, K.; Wang, N.; Qi, J.; Wu, Q.; Ma, S.; Li, C. Optimal dispatch for participation of electric vehicles in frequency regulation based on area control error and area regulation requirement. Appl. Energy 2019, 240, 46–55. [Google Scholar] [CrossRef]
- Bai, L.; Li, F.; Cui, H.; Jiang, T.; Sun, H.; Zhu, J. Interval optimization based operating strategy for gas-electricity integrated energy systems considering demand response and wind uncertainty. Appl. Energy 2016, 167, 270–279. [Google Scholar] [CrossRef] [Green Version]
- Zhao, C.; Wang, J.; Watson, J.P.; Guan, Y. Multi-stage robust unit commitment considering wind and demand response uncertainties. In Proceedings of the IEEE PES General Meeting, Conference & Exposition, Virtual Event, 26–29 July 2021. [Google Scholar]
- Ziping, W.U.; Gao, W.; Gao, T.; Yan, W.; Wang, X. State-of-the-art review on frequency response of wind power plants in power systems. J. Mod. Power Syst. Clean Energy 2018, 6, 1–16. [Google Scholar]
- Han, Z.; He, R.; Xu, Y. Study on Resonance Mechanism of Power System Low Frequency Oscillation Induced by Turbo-pressure Pulsation. Proc. CSEE 2008, 28, 5. (In Chinese) [Google Scholar]
- Milano, F.; Zarate-Minano, R. A Systematic Method to Model Power Systems as Stochastic Differential Algebraic Equations. IEEE Trans. Power Syst. 2013, 28, 4537–4544. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, X.; Ning, L.; Wei, Z.; Sun, G. Robust stochastic stability of power system with time-varying delay under Gaussian random perturbations. Neurocomputing 2015, 162, 1–8. [Google Scholar] [CrossRef]
- Mi, Y.; Fu, Y.; Li, D.; Wang, C.; Loh, P.C.; Wang, P. The sliding mode load frequency control for hybrid power system based on disturbance observer. Int. J. Electr. Power Energy Syst. 2016, 74, 446–452. [Google Scholar] [CrossRef]
- Preece, R.; Woolley, N.C.; Milanovic, J.V. The Probablistic Collocation Method for Power System Damping and Voltage Collapse Studies in the Presence of Uncertainties. IEEE Trans. Power Syst. 2013, 28, 2253–2262. [Google Scholar] [CrossRef]
- Xia, W.; Cao, J. Pinning synchronization of delayed dynamical networks via periodically intermittent control. Chaos 2009, 19, 821–891. [Google Scholar] [CrossRef]
- Żochowski, M. Intermittent dynamical control. Phys. D Nonlinear Phenom. 2000, 145, 181–190. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Studies in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1994; Volume 15. [Google Scholar]
- Xie, L.; Fu, M.; Souza, C.D. H∞ control and quadratic stabilization of systems with parameter uncertainty via output feedback. Autom. Control IEEE Trans. 1992, 37, 1253–1256. [Google Scholar] [CrossRef]
- Halanay, A. Differential equations: stability, oscillations, time lags. Siam Rev. 1975, 10, 93–94. [Google Scholar]
- Li, C.; Liao, X.; Huang, T. Exponential stabilization of chaotic systems with delay by periodically intermittent control. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 043103. [Google Scholar] [CrossRef]
- Liu, Z.W.; Yu, X.; Guan, Z.H.; Hu, B.; Li, C. Pulse-Modulated Intermittent Control in Consensus of Multiagent Systems. IEEE Trans. Syst. Man Cybern. Syst. 2016, 47, 1–11. [Google Scholar] [CrossRef]
- Hu, X. Research on Modeling and Control Strategy for Air Conditioning Loads to Participate in Demand Response in Power System. Ph.D. Thesis, Southeast University, Nanjing, China, 2017. (In Chinese). [Google Scholar]
- Lei, Z.; Yang, L.; Ciwei, G. Improvement of Temperature Adjusting Method for Aggregated Air-conditioning Loads and Its Control Strategy. Proc. CSEE 2014, 34, 5579–5589. (In Chinese) [Google Scholar]



| Area | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 120 | 20 | 0.31 | 0.25 | 0.425 | 2.4 | 0.67 | 0.1 |
| 1 | 120 | 20 | 0.3 | 0.3 | 0.425 | 2.4 | 0.6 | 0.1 |
| Method | Maximum Frequency Deviation | Transient Time |
|---|---|---|
| Open-Loop System | 0.78 Hz | 36.5 s |
| This Paper ( 3.5 s) | 0.72 Hz | 23.5 s |
| This Paper ( 4 s) | 0.52 Hz | 21.5 s |
| Method | Maximum Frequency Deviation | Transient Time |
|---|---|---|
| Open-Loop System | Unstable system(∞) | Unstable system(∞) |
| This Paper ( 5 s) | 0.35 Hz | 72 s |
| This Paper ( 6 s) | 0.19 Hz | 33 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ming, G.; Geng, J.; Liu, J.; Chen, Y.; Yuan, K.; Zhang, K. Load Frequency Robust Control Considering Intermittent Characteristics of Demand-Side Resources. Energies 2022, 15, 4370. https://doi.org/10.3390/en15124370
Ming G, Geng J, Liu J, Chen Y, Yuan K, Zhang K. Load Frequency Robust Control Considering Intermittent Characteristics of Demand-Side Resources. Energies. 2022; 15(12):4370. https://doi.org/10.3390/en15124370
Chicago/Turabian StyleMing, Guoxin, Jian Geng, Jiantao Liu, Yiyuan Chen, Kun Yuan, and Kaifeng Zhang. 2022. "Load Frequency Robust Control Considering Intermittent Characteristics of Demand-Side Resources" Energies 15, no. 12: 4370. https://doi.org/10.3390/en15124370
APA StyleMing, G., Geng, J., Liu, J., Chen, Y., Yuan, K., & Zhang, K. (2022). Load Frequency Robust Control Considering Intermittent Characteristics of Demand-Side Resources. Energies, 15(12), 4370. https://doi.org/10.3390/en15124370






