An Efficient Approach for Peak-Load-Aware Scheduling of Energy-Intensive Tasks in the Context of a Public IEEE Challenge
Abstract
:1. Introduction
2. Problem Description
3. Use Case
4. Approach
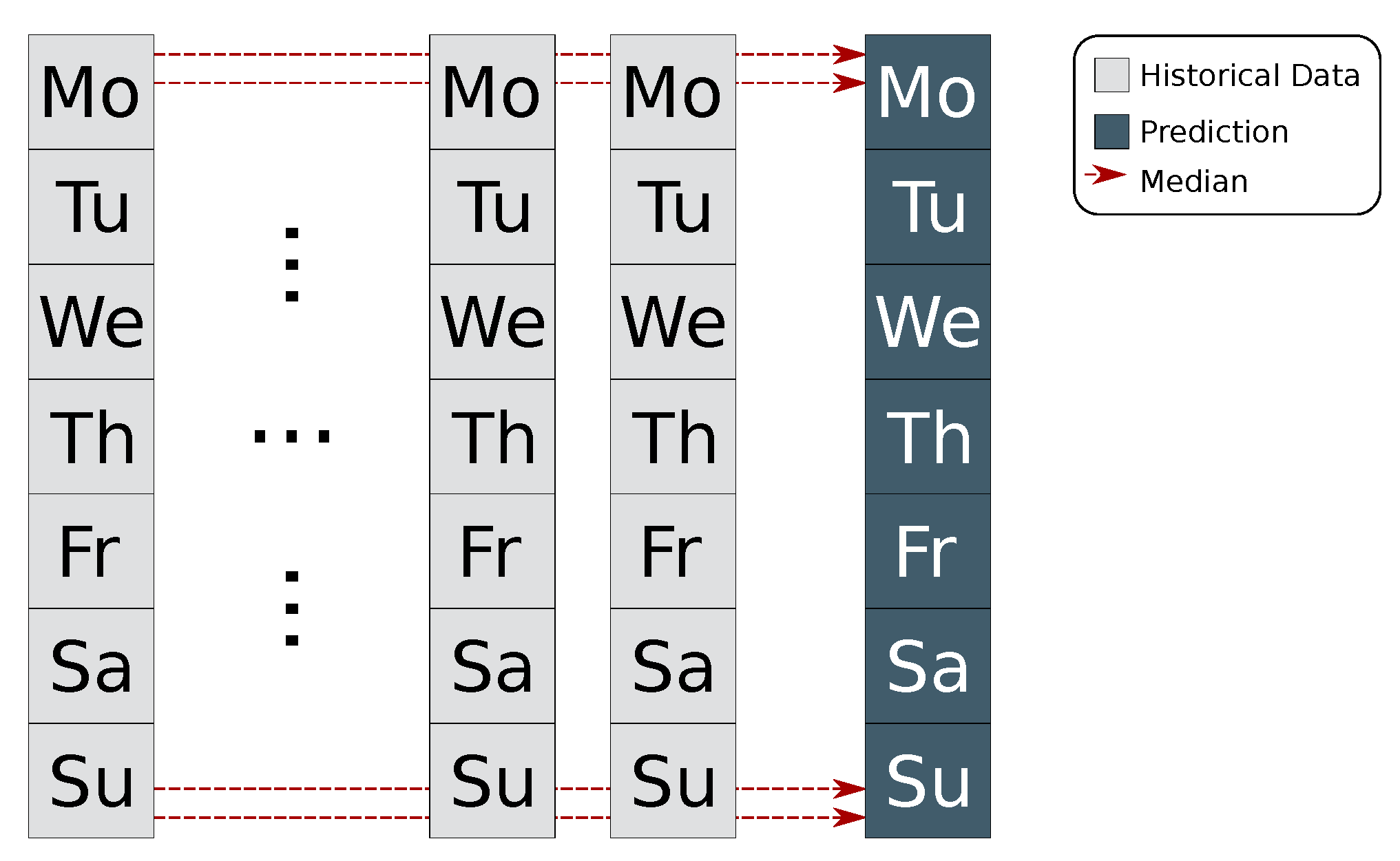
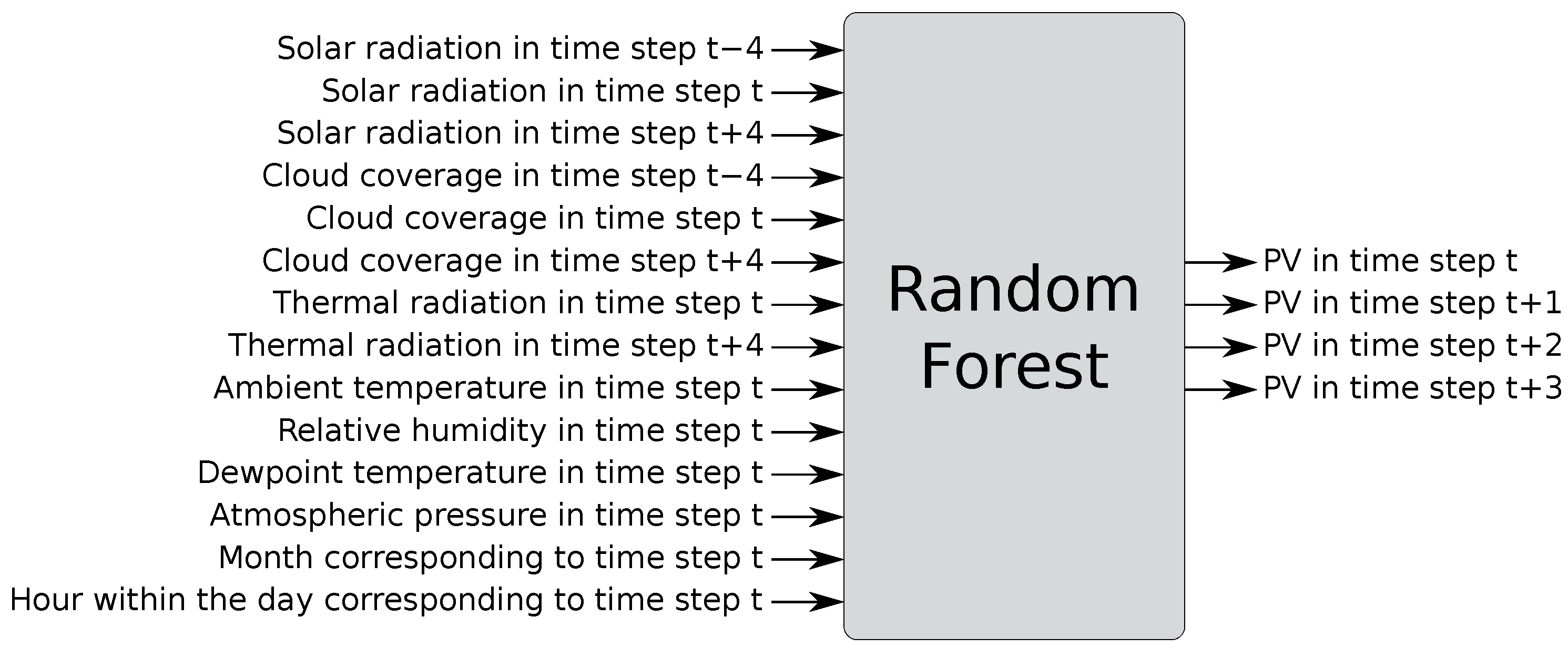
4.1. Building Load Prediction
4.2. Photovoltaics Prediction
4.3. Optimization
- (1)
- Separate building assignment;
- (2)
- Variable reduction;
- (3)
- Solver parameter tuning;
- (4)
- Problem decomposition;
- (5)
- Linearization.
4.3.1. Separate Building Assignment
4.3.2. Variable Reduction
| Algorithm 1: Computation of first possible start day. |
 |
4.3.3. Solver Parameter Tuning
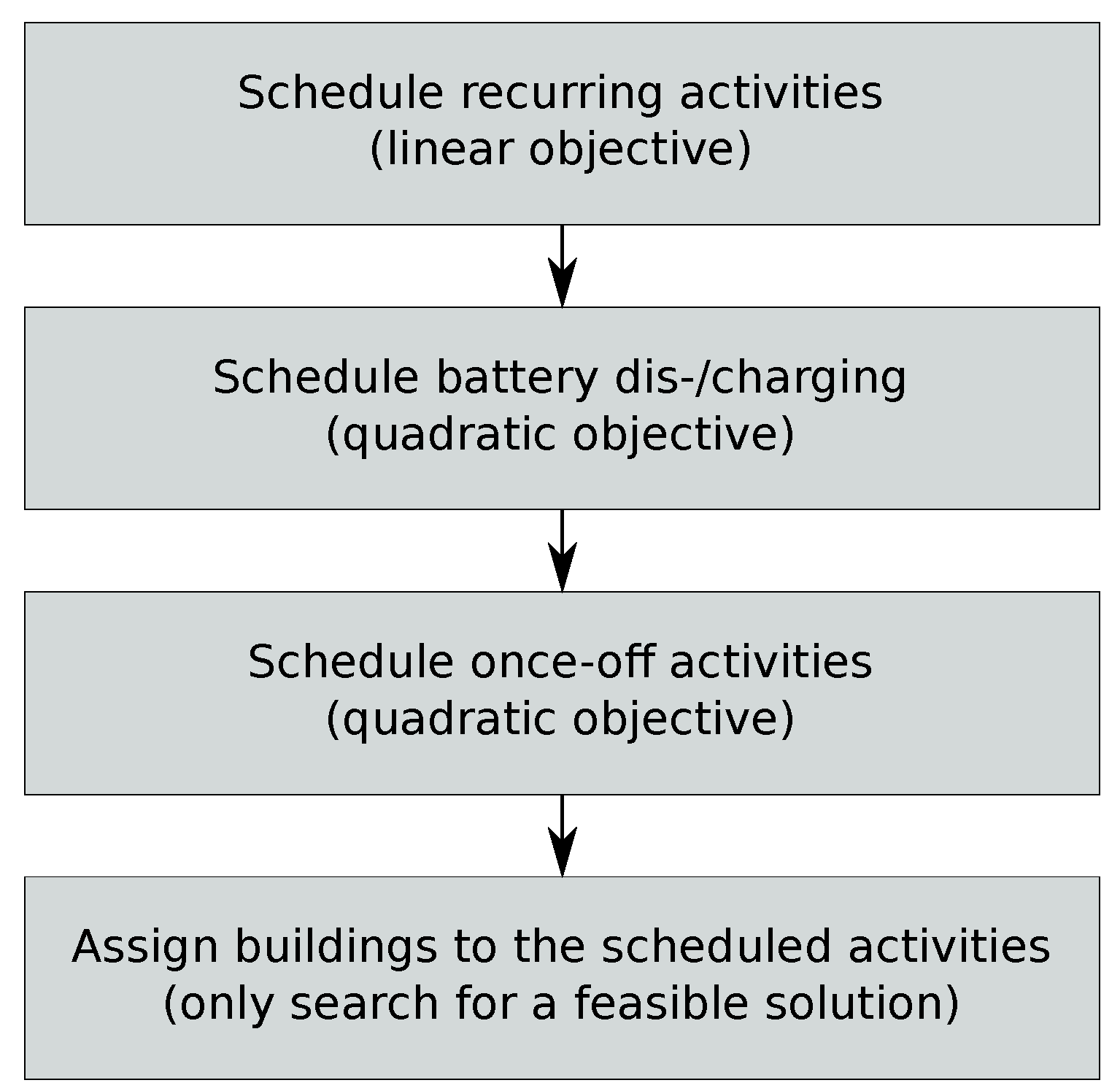
4.3.4. Problem Decomposition
4.3.5. Linearization
5. Simulation Experiments
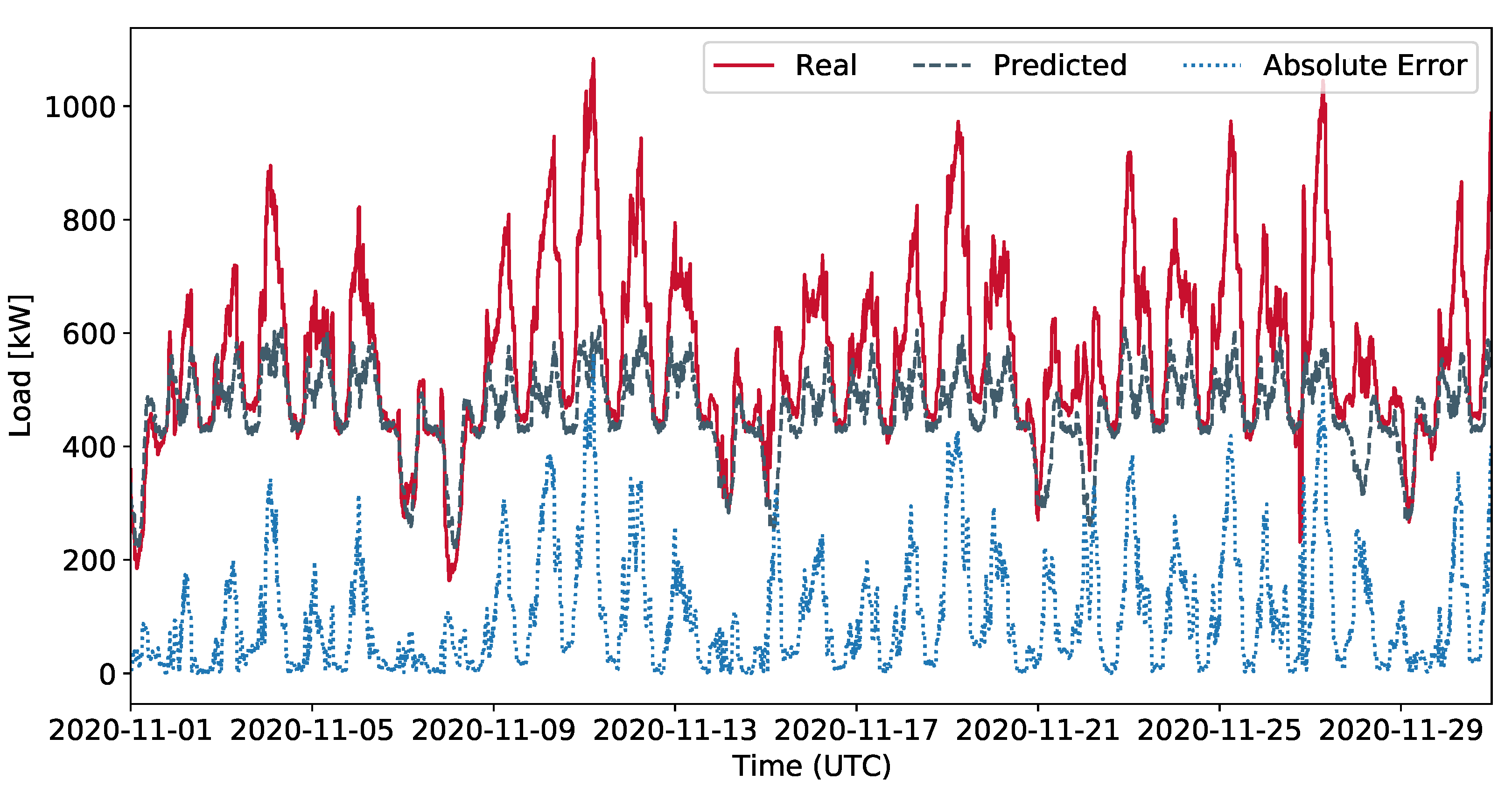
5.1. Predictions
5.2. Optimizations
- c_q_f: Combined optimization of all activities and batteries with quadratic objective and a full number of binary variables;
- c_q_r: Combined optimization of all activities and batteries with quadratic objective and a reduced number of binary variables (improvement (2));
- c_l_r: Combined optimization of all activities and batteries with linear objective (improvement (5)) and a reduced number of binary variables (improvement (2));
- s_q_f: Separate optimizations of recurring activities, batteries, and once-off activities (improvement (4)) with quadratic objective and the full number of binary variables;
- s_q_r: Separate optimizations of recurring activities, batteries, and once-off activities (improvement (4)) with quadratic objective and a reduced number of binary variables (improvement (2));
- s_l_r: Separate optimizations of recurring activities, batteries, and once-off activities (improvement (4)) with linear objective for recurring activities (improvement (5)) and a reduced number of binary variables (improvement (2)).
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Parameters | |
| Energy price at time step t | |
| Peak load charge | |
| Efficiency of stationary battery s | |
| Capacity of stationary battery s | |
| First possible start day of activity a | |
| Last possible start day of activity a | |
| Duration of activity a in number of time steps | |
| Mapping of time step t to time step in first full week | |
| Number of large rooms required by activity a | |
| Number of small rooms required by activity a | |
| Load of activity a | |
| Base load of building b at time step t | |
| Production of PV system p at time step t | |
| Base load at time step t | |
| Charging/discharging power of stationary battery s | |
| Number of large rooms of building b | |
| Number of small rooms of building b | |
| Number of buildings | |
| Number of once-off activities | |
| Number of PV systems | |
| Number of recurring activities | |
| Number of stationary batteries | |
| Penalty of once-off activity o | |
| Remuneration of once-off activity o | |
| T | Length of planning horizon |
| Last time step of office hours during a day | |
| First time step of office hours during a day | |
| Last time step of last full week of planning horizon | |
| Last time step of working days of first full week of planning horizon | |
| First time step of working days of first full week of planning horizon | |
| Weekday corresponding to time step t | |
| Sets | |
| A | Set of all activities |
| B | Set of buildings |
| Set of activities preceding activity a | |
| O | Set of once-off activities |
| Set of scheduled once-off activities | |
| P | Set of PV systems |
| R | Set of recurring activities |
| S | Set of stationary batteries |
| , | Set of possible start times of activity a |
| Variables | |
| Battery level of battery s at time step t | |
| Binary flag indicating charging of battery s at time step t | |
| Binary flag indicating discharging of battery s at time step t | |
| Binary flag indicating start of activity a at time step t | |
| Load of stationary battery s at time step t | |
| Square of the peak load | |
| Peak load | |
| Total load at time step t | |
| Time step of (first) start of activity a | |
| Number of rooms of building b assigned to activity a |
References
- Tol, R.S. Europe’s Climate Target for 2050: An Assessment. Intereconomics 2021, 56, 330–335. [Google Scholar] [CrossRef] [PubMed]
- Roesch, M.; Linder, C.; Zimmermann, R.; Rudolf, A.; Hohmann, A.; Reinhart, G. Smart Grid for Industry Using Multi-Agent Reinforcement Learning. Appl. Sci. 2020, 10, 6900. [Google Scholar] [CrossRef]
- Stadie, M.; Rodemann, T.; Burger, A.; Jomrich, F.; Limmer, S.; Rebhan, S.; Saeki, H. V2B Vehicle to Building Charging Manager. In Proceedings of the EVTeC: 5th International Electric Vehicle Technology Conference 2021, Yokohama, Japan, 24–26 May 2021. [Google Scholar]
- Bergmeir, C. IEEE-CIS Technical Challenge on Predict+Optimize for Renewable Energy Scheduling. 2021. Available online: https://ieee-dataport.org/competitions/ieee-cis-technical-challenge-predictoptimize-renewable-energy-scheduling (accessed on 16 May 2022).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual; Gurobi Optimization, LLC: Houston, TX, USA, 2022. [Google Scholar]
- Mamun, A.A.; Sohel, M.; Mohammad, N.; Haque Sunny, M.S.; Dipta, D.R.; Hossain, E. A Comprehensive Review of the Load Forecasting Techniques Using Single and Hybrid Predictive Models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
- Nti, I.K.; Teimeh, M.; Nyarko-Boateng, O.; Adekoya, A.F. Electricity load forecasting: A systematic review. J. Electr. Syst. Inf. Technol. 2020, 7, 1–19. [Google Scholar] [CrossRef]
- Groß, A.; Lenders, A.; Schwenker, F.; Braun, D.A.; Fischer, D. Comparison of short-term electrical load forecasting methods for different building types. Energy Inform. 2021, 4, 1–16. [Google Scholar]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; de Pison, F.M.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 1–26. [Google Scholar] [CrossRef]
- Schmitt, T.; Rodemann, T.; Adamy, J. Multi-objective model predictive control for microgrids. Automatisierungstechnik 2020, 68, 687–702. [Google Scholar] [CrossRef]
- Altin, N.; Eyimaya, S.E. A Review of Microgrid Control Strategies. In Proceedings of the 2021 10th International Conference on Renewable Energy Research and Application, Istanbul, Turkey, 26–29 September 2021; pp. 412–417. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, X.; Du, J.; Kong, F. Smart Charging for Electric Vehicles: A Survey From the Algorithmic Perspective. IEEE Commun. Surv. Tutor. 2016, 18, 1500–1517. [Google Scholar] [CrossRef] [Green Version]
- Naharudinsyah, I.; Limmer, S. Optimal Charging of Electric Vehicles with Trading on the Intraday Electricity Market. Energies 2018, 11, 1416. [Google Scholar] [CrossRef] [Green Version]
- Espín-Sarzosa, D.; Palma-Behnke, R.; Núñez Mata, O. Energy Management Systems for Microgrids: Main Existing Trends in Centralized Control Architectures. Energies 2020, 13, 547. [Google Scholar] [CrossRef] [Green Version]
- Hoke, A.; Brissette, A.; Chandler, S.; Pratt, A.; Maksimović, D. Look-ahead economic dispatch of microgrids with energy storage, using linear programming. In Proceedings of the 2013 1st IEEE Conference on Technologies for Sustainability (SusTech), Portland, OR, USA, 1–2 August 2013; pp. 154–161. [Google Scholar] [CrossRef]
- Torres, D.; Crichigno, J.; Padilla, G.; Rivera, R. Scheduling coupled photovoltaic, battery and conventional energy sources to maximize profit using linear programming. Renew. Energy 2014, 72, 284–290. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Q.; Xue, M.; Geng, G. Energy Management of Microgrid in Grid-Connected and Stand-Alone Modes. IEEE Trans. Power Syst. 2013, 28, 3380–3389. [Google Scholar] [CrossRef]
- Khani, H.; Zadeh, M.R.D. Online Adaptive Real-Time Optimal Dispatch of Privately Owned Energy Storage Systems Using Public-Domain Electricity Market Prices. IEEE Trans. Power Syst. 2015, 30, 930–938. [Google Scholar] [CrossRef]
- Sani Hassan, A.; Cipcigan, L.; Jenkins, N. Optimal battery storage operation for PV systems with tariff incentives. Appl. Energy 2017, 203, 422–441. [Google Scholar] [CrossRef]
- Koller, M.; Borsche, T.; Ulbig, A.; Andersson, G. Defining a degradation cost function for optimal control of a battery energy storage system. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, X.; Cao, Y.; Li, C.; Chung, C.Y.; Chan, K.W. Optimal scheduling of virtual power plant with battery degradation cost. IET Gener. Transm. Distrib. 2016, 10, 712–725. [Google Scholar] [CrossRef]
- Xu, B.; Zhao, J.; Zheng, T.; Litvinov, E.; Kirschen, D.S. Factoring the Cycle Aging Cost of Batteries Participating in Electricity Markets. IEEE Trans. Power Syst. 2018, 33, 2248–2259. [Google Scholar] [CrossRef] [Green Version]
- Maheshwari, A.; Paterakis, N.G.; Santarelli, M.; Gibescu, M. Optimizing the operation of energy storage using a non-linear lithium-ion battery degradation model. Appl. Energy 2020, 261, 114360. [Google Scholar] [CrossRef]
- Abdulla, K.; de Hoog, J.; Muenzel, V.; Suits, F.; Steer, K.; Wirth, A.; Halgamuge, S. Optimal Operation of Energy Storage Systems Considering Forecasts and Battery Degradation. IEEE Trans. Smart Grid 2018, 9, 2086–2096. [Google Scholar] [CrossRef]
- Li, Y.; Vilathgamuwa, D.M.; Choi, S.S.; Farrell, T.W.; Tran, N.T.; Teague, J. Nonlinear Model Predictive Control of Photovoltaic-Battery System for Short-Term Power Dispatch. In Proceedings of the IECON 2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 1884–1889. [Google Scholar] [CrossRef] [Green Version]
- Aaslid, P.; Belsnes, M.M.; Fosso, O.B. Optimal microgrid operation considering battery degradation using stochastic dual dynamic programming. In Proceedings of the 2019 International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Kumar, R.; Wenzel, M.J.; Ellis, M.J.; ElBsat, M.N.; Drees, K.H.; Zavala, V.M. A Stochastic Model Predictive Control Framework for Stationary Battery Systems. IEEE Trans. Power Syst. 2018, 33, 4397–4406. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, H.; Jin, X. Aging-aware predictive control of PV-battery assets in buildings. Appl. Energy 2019, 236, 478–488. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand Side Management in Smart Grid Using Heuristic Optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Ahmad, A.; Khan, A.; Javaid, N.; Hussain, H.M.; Abdul, W.; Almogren, A.; Alamri, A.; Azim Niaz, I. An Optimized Home Energy Management System with Integrated Renewable Energy and Storage Resources. Energies 2017, 10, 549. [Google Scholar] [CrossRef] [Green Version]
- Hussain, H.M.; Javaid, N.; Iqbal, S.; Hasan, Q.U.; Aurangzeb, K.; Alhussein, M. An Efficient Demand Side Management System with a New Optimized Home Energy Management Controller in Smart Grid. Energies 2018, 11, 190. [Google Scholar] [CrossRef] [Green Version]
- Lezama, F.; Soares, J.; Canizes, B.; Vale, Z. Flexibility management model of home appliances to support DSO requests in smart grids. Sustain. Cities Soc. 2020, 55, 102048. [Google Scholar] [CrossRef]
- Rana, M.J.; Rahi, K.H.; Ray, T.; Sarker, R. An efficient optimization approach for flexibility provisioning in community microgrids with an incentive-based demand response scheme. Sustain. Cities Soc. 2021, 74, 103218. [Google Scholar] [CrossRef]
- Sou, K.C.; Weimer, J.; Sandberg, H.; Johansson, K.H. Scheduling smart home appliances using mixed integer linear programming. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 5144–5149. [Google Scholar] [CrossRef] [Green Version]
- Bradac, Z.; Kaczmarczyk, V.; Fiedler, P. Optimal Scheduling of Domestic Appliances via MILP. Energies 2015, 8, 217–232. [Google Scholar] [CrossRef]
- Taik, S.; Kiss, B. Smart Household Electricity Usage Optimization Using MPC and MILP. In Proceedings of the 2019 22nd International Conference on Process Control (PC19), Strbske Pleso, Slovakia, 11–14 June 2019; pp. 31–36. [Google Scholar] [CrossRef]
- Limmer, S.; Lezama, F.; Soares, J.A.; Vale, Z. Coordination of Home Appliances for Demand Response: An Improved Optimization Model and Approach. IEEE Access 2021, 9, 146183–146194. [Google Scholar] [CrossRef]
- Enrich, R.; Skovron, P.; Tolos, M.; Torrent-Moreno, M. Microgrid management based on economic and technical criteria. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 551–556. [Google Scholar] [CrossRef]
- Alghamdi, H.; Alsubait, T.; Alhakami, H.; Baz, A. A review of optimization algorithms for university timetable scheduling. Eng. Technol. Appl. Sci. Res. 2020, 10, 6410–6417. [Google Scholar] [CrossRef]
- Olson, R.S.; Bartley, N.; Urbanowicz, R.J.; Moore, J.H. Evaluation of a Tree-based Pipeline Optimization Tool for Automating Data Science. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ’16), Denver, CO, USA, 20–24 July 2016; ACM: New York, NY, USA, 2016; pp. 485–492. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, T.; Limmer, S. Optimizing the Hyperparameters of a Mixed Integer Linear Programming Solver to Speed up Electric Vehicle Charging Control. In Applications of Evolutionary Computation, Proceedings of 23rd European Conference, EvoApplications 2020, Held as Part of EvoStar 2020, Seville, Spain, 15–17 April 2020; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12104, pp. 37–53. [Google Scholar] [CrossRef]


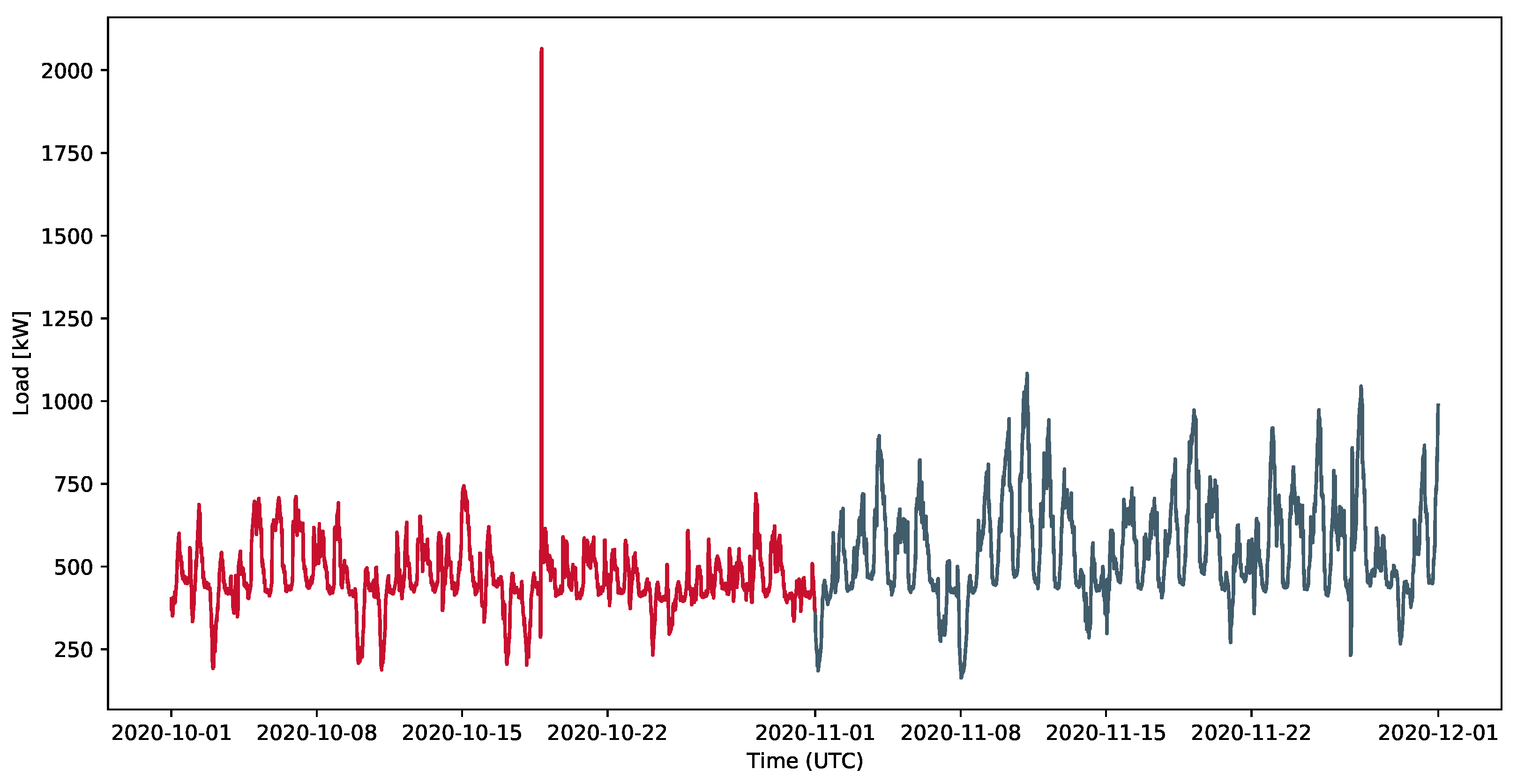
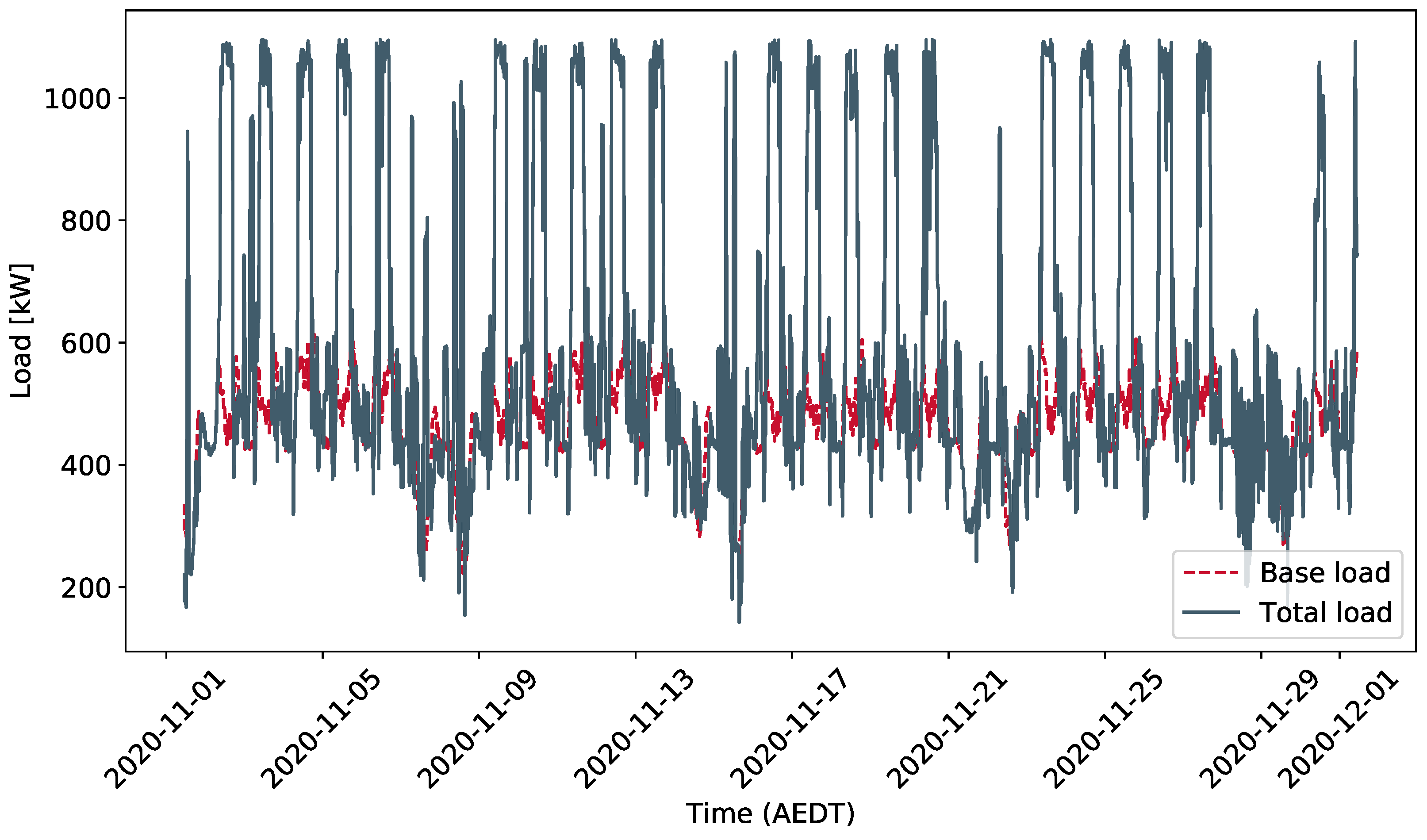
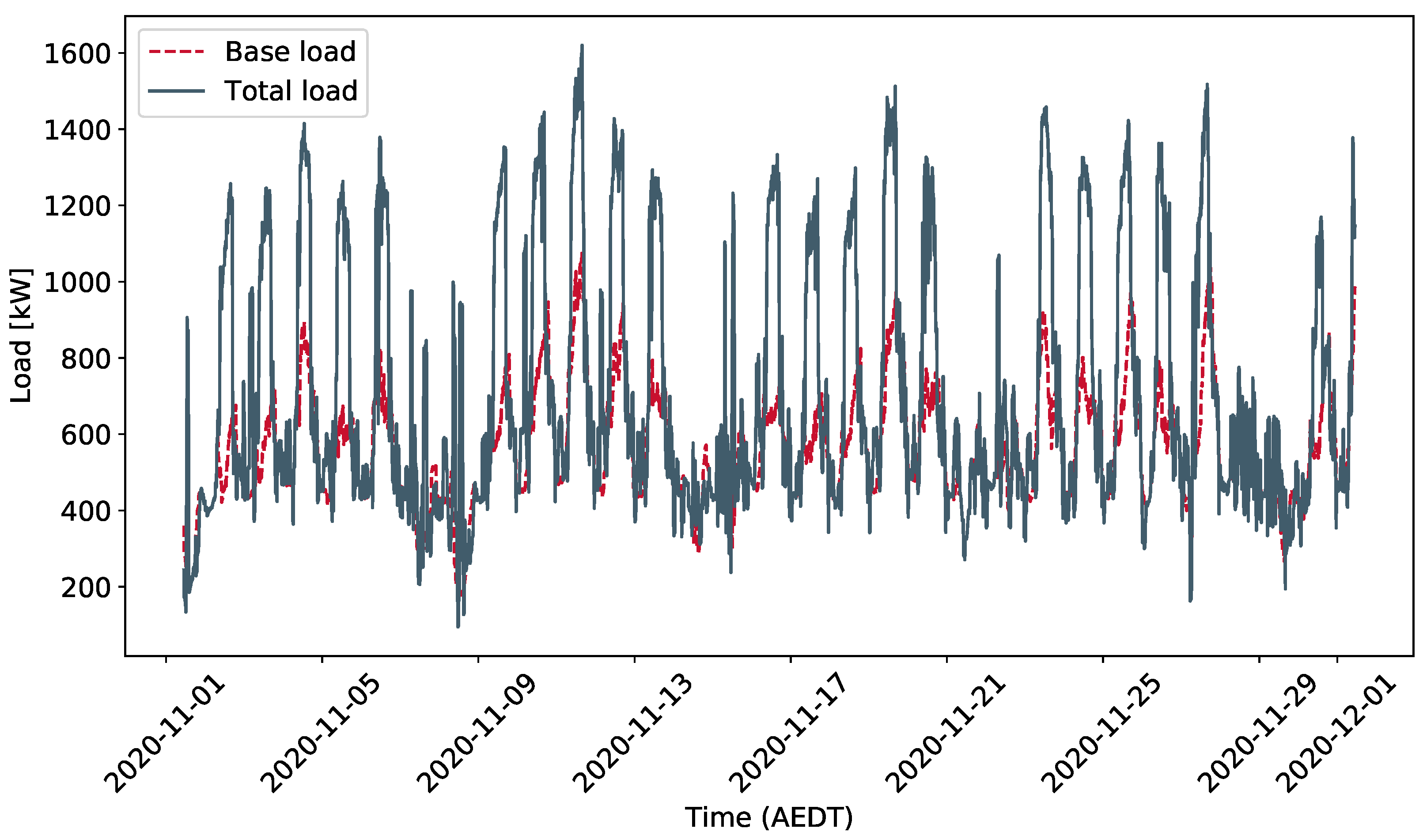
| Place | Electricity Cost | Prediction Error (MASE) |
|---|---|---|
| 1 | 328,359.20 | 0.744052 |
| 2 | 335,107.25 | 0.646022 |
| 3 | 339,160.43 | 0.855737 |
| 4 | 340,725.94 | 0.807299 |
| 5 | 342,810.02 | 0.774996 |
| 6 | 357,210.66 | 1.870326 |
| 7 | 363,168.14 | 0.847391 |
| Load/Production | Our Approach | Winning Submission | ||
|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | |
| Building0 | 37.31 | 52.68 | 34.46 | 48.11 |
| Building1 | 2.14 | 3.22 | 1.89 | 3.15 |
| Building3 | 68.27 | 103.78 | 61.38 | 95.19 |
| Building4 | 0.69 | 0.92 | 0.56 | 0.76 |
| Building5 | 6.25 | 12.58 | 8.92 | 10.53 |
| Building6 | 2.47 | 4.45 | 2.40 | 4.44 |
| Solar0 | 3.31 | 6.06 | 3.19 | 5.46 |
| Solar1 | 0.61 | 1.20 | 0.65 | 1.22 |
| Solar2 | 0.64 | 1.23 | 0.70 | 1.26 |
| Solar3 | 0.78 | 1.40 | 0.75 | 1.29 |
| Solar4 | 0.37 | 0.72 | 0.43 | 0.77 |
| Solar5 | 1.97 | 3.77 | 2.16 | 3.85 |
| Total Load | 102.17 | 144.83 | 82.49 | 120.72 |
| Problem | c_q_f | c_q_r | c_l_r | s_q_f | s_q_r | s_l_r |
|---|---|---|---|---|---|---|
| small0 | 26,299 | 25,971 | 25,006 | 24,489 | 24,669 | 24,399 |
| small1 | 26,092 | 24,920 | 24,211 | 23,414 | 23,414 | 23,443 |
| small2 | 25,696 | 26,145 | 23,706 | 23,485 | 23,665 | 23,341 |
| large0 | 25,184 | 25,105 | 23,575 | 23,859 | 23,839 | 23,640 |
| large1 | 25,364 | 25,365 | 24,096 | 24,314 | 24,283 | 23,925 |
| large2 | 24,209 | 24,168 | 23,028 | 23,021 | 22,972 | 22,651 |
| Mean | 25,474 | 25,279 | 23,937 | 23,764 | 23,807 | 23,567 |
| Problem | s_q_f | s_q_r | ||||
|---|---|---|---|---|---|---|
| Continuous | Integer | Binary | Continuous | Integer | Binary | |
| Before Pre-solving | ||||||
| small0 | 2882 | 6770 | 6770 | 2882 | 2922 | 2922 |
| large0 | 2882 | 27,320 | 27,320 | 2882 | 13,222 | 13,222 |
| After Pre-solving | ||||||
| small0 | 135 | 2935 | 2922 | 143 | 2935 | 2922 |
| large0 | 137 | 13,235 | 13,222 | 137 | 13,235 | 13,222 |
| Pred-Pred | Pred-Real | Real-Real | |
|---|---|---|---|
| Peak cost | 6588 | 14,549 | 10,842 |
| Energy cost | 17,870 | 21,262 | 21,237 |
| Once-off profit | 59 | 59 | 619 |
| Total cost | 24,399 | 35,752 | 31,460 |
| Problem | Recurring | Batteries | Once-Off |
|---|---|---|---|
| small0 | 2.5% | 0.8% | 2.2% |
| small1 | 0.0% | 0.6% | 2.1% |
| small2 | 0.0% | 0.5% | 2.0% |
| small3 | 0.0% | 0.7% | 0.0% |
| small4 | 0.0% | 0.7% | 0.0% |
| large0 | 1.4% | 0.7% | 4.9% |
| large1 | 1.5% | 1.0% | 4.7% |
| large2 | 1.6% | 0.5% | 4.2% |
| large3 | 1.6% | 0.9% | 4.4% |
| large4 | 1.6% | 1.1% | 3.7% |
| Problem | OS | PC (AUD) | EC (AUD) | OP (AUD) | TC (AUD) |
|---|---|---|---|---|---|
| small0 | 7 | 13,195 | 21,283 | 29 | 34,449 |
| small1 | 19 | 13,130 | 20,865 | 251 | 33,744 |
| small2 | 2 | 13,081 | 20,833 | 60 | 33,855 |
| small3 | 20 | 12,533 | 20,994 | 267 | 33,259 |
| small4 | 20 | 13,825 | 20,924 | 869 | 33,880 |
| large0 | 6 | 13,025 | 21,225 | 78 | 34,173 |
| large1 | 7 | 13,374 | 21,290 | 43 | 34,622 |
| large2 | 11 | 12,075 | 20,919 | 29 | 32,964 |
| large3 | 8 | 12,467 | 21,029 | 42 | 33,454 |
| large4 | 30 | 13,074 | 21,233 | 236 | 34,071 |
| Problem | OS | PC (AUD) | EC (AUD) | OP (AUD) | TC (AUD) | Gap (%) |
|---|---|---|---|---|---|---|
| small0 | 20 | 14,425 | 21,575 | 1491 | 34,509 | +0.17 |
| small1 | 19 | 13,726 | 21,131 | 1593 | 33,265 | −1.42 |
| small2 | 20 | 12,696 | 21,232 | 1500 | 32,428 | −4.22 |
| small3 | 20 | 13,289 | 21,181 | 1333 | 33,136 | −0.37 |
| small4 | 20 | 12,490 | 21,057 | 1056 | 32,490 | −4.10 |
| large0 | 99 | 12,912 | 21,619 | 1889 | 32,643 | −4.48 |
| large1 | 100 | 13,244 | 21,658 | 1847 | 33,055 | −4.53 |
| large2 | 97 | 12,160 | 21,238 | 1686 | 31,712 | −3.80 |
| large3 | 100 | 12,502 | 21,443 | 1725 | 32,219 | −3.69 |
| large4 | 94 | 12,927 | 21,602 | 1626 | 32,903 | −3.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Limmer, S.; Einecke, N. An Efficient Approach for Peak-Load-Aware Scheduling of Energy-Intensive Tasks in the Context of a Public IEEE Challenge. Energies 2022, 15, 3718. https://doi.org/10.3390/en15103718
Limmer S, Einecke N. An Efficient Approach for Peak-Load-Aware Scheduling of Energy-Intensive Tasks in the Context of a Public IEEE Challenge. Energies. 2022; 15(10):3718. https://doi.org/10.3390/en15103718
Chicago/Turabian StyleLimmer, Steffen, and Nils Einecke. 2022. "An Efficient Approach for Peak-Load-Aware Scheduling of Energy-Intensive Tasks in the Context of a Public IEEE Challenge" Energies 15, no. 10: 3718. https://doi.org/10.3390/en15103718
APA StyleLimmer, S., & Einecke, N. (2022). An Efficient Approach for Peak-Load-Aware Scheduling of Energy-Intensive Tasks in the Context of a Public IEEE Challenge. Energies, 15(10), 3718. https://doi.org/10.3390/en15103718






