Disturbance Observer-Based Model Predictive Super-Twisting Control for Soft Open Point
Abstract
:1. Introduction
- (1)
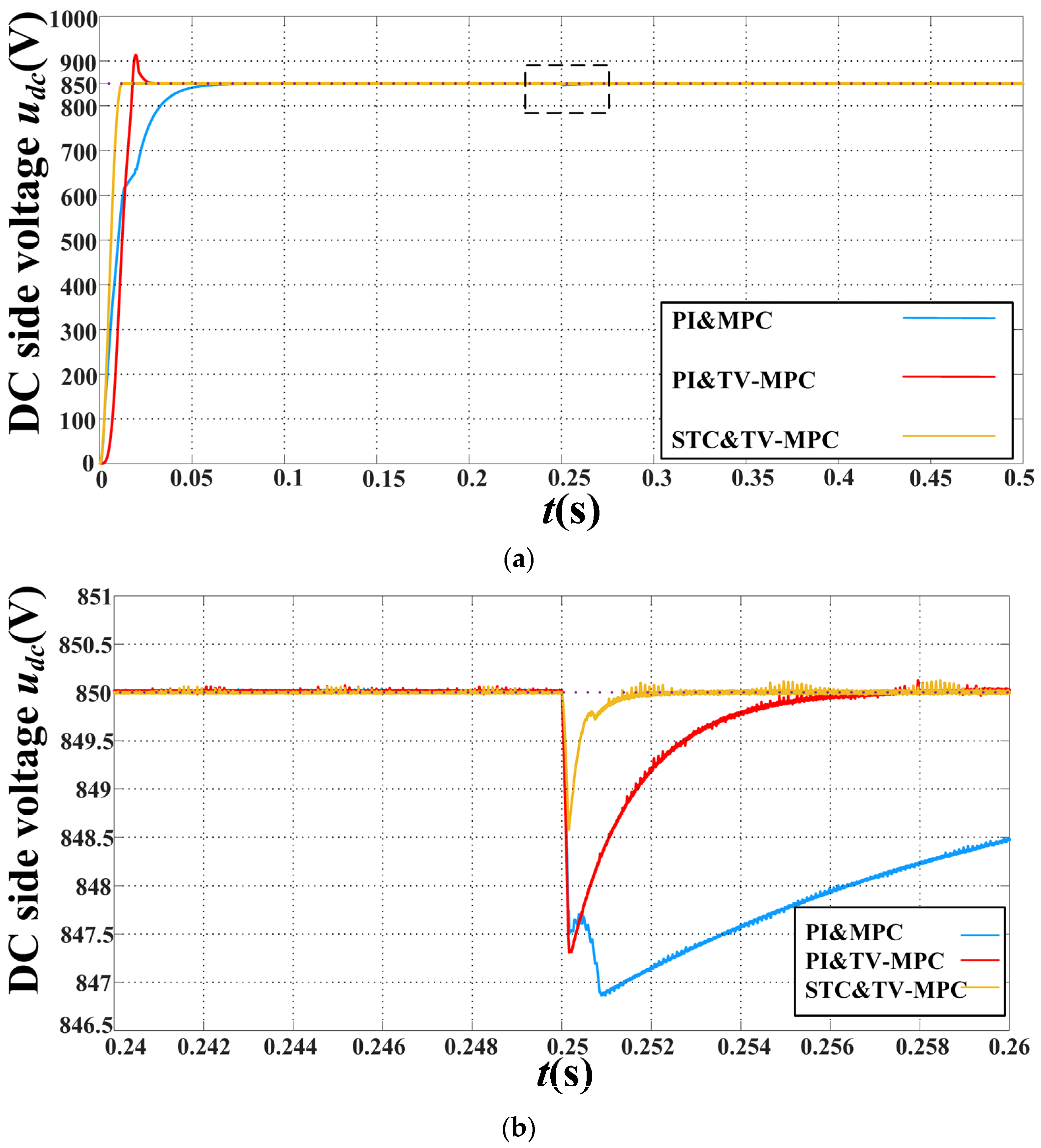
- Compared with traditional outer-loop PI controller, the start-up time and dynamic response of the DC-side voltage are improved by adopting the proposed method;
- (2)
- Compared with signal-vector method, the current harmonics are improved by applying the TV-MPC method in SOP system;
- (3)
- Parameter mismatches in the SOP system are considered and compensated for by STO, which improves the adaptation of the SOP system to the disturbances.
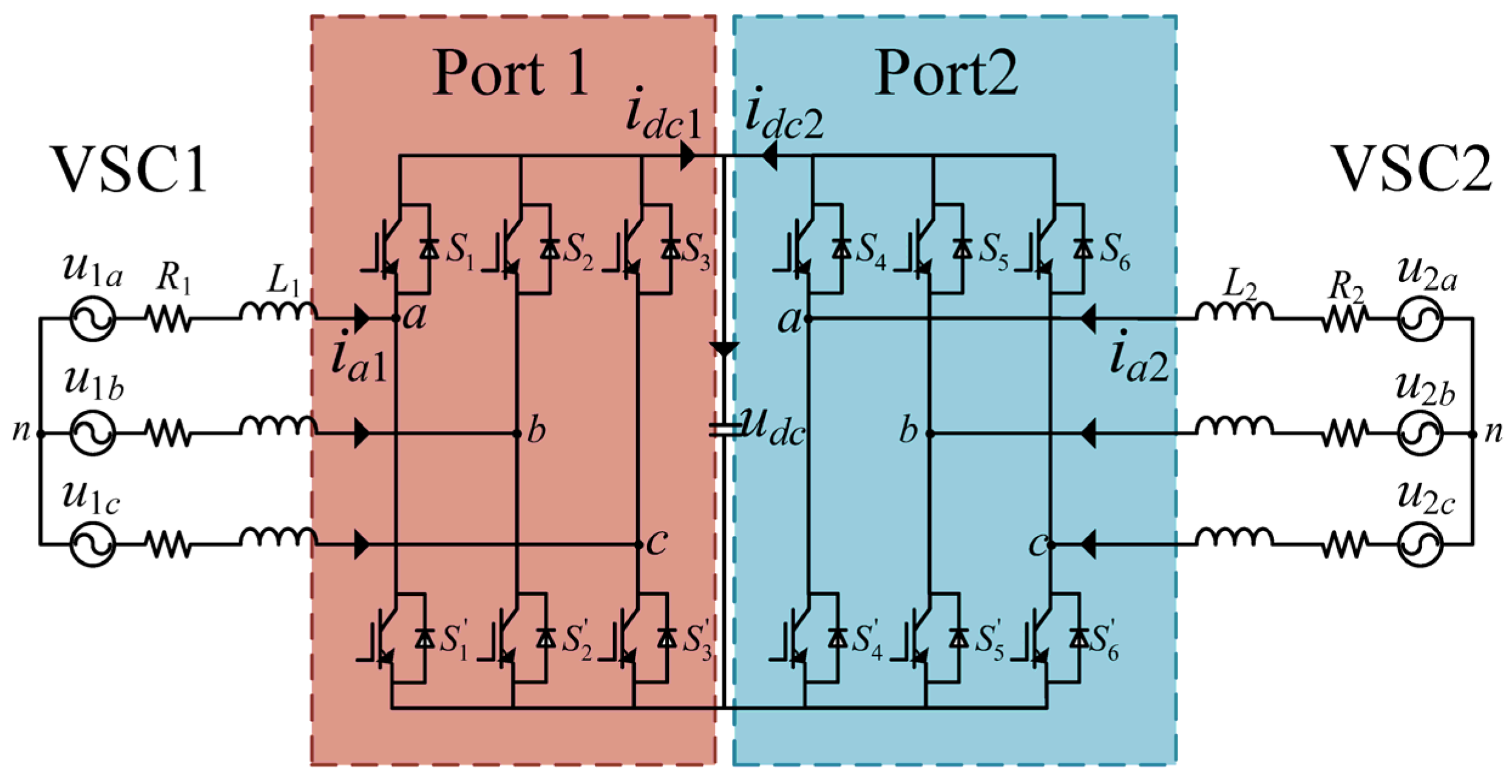
2. Mathematical Model of SOP
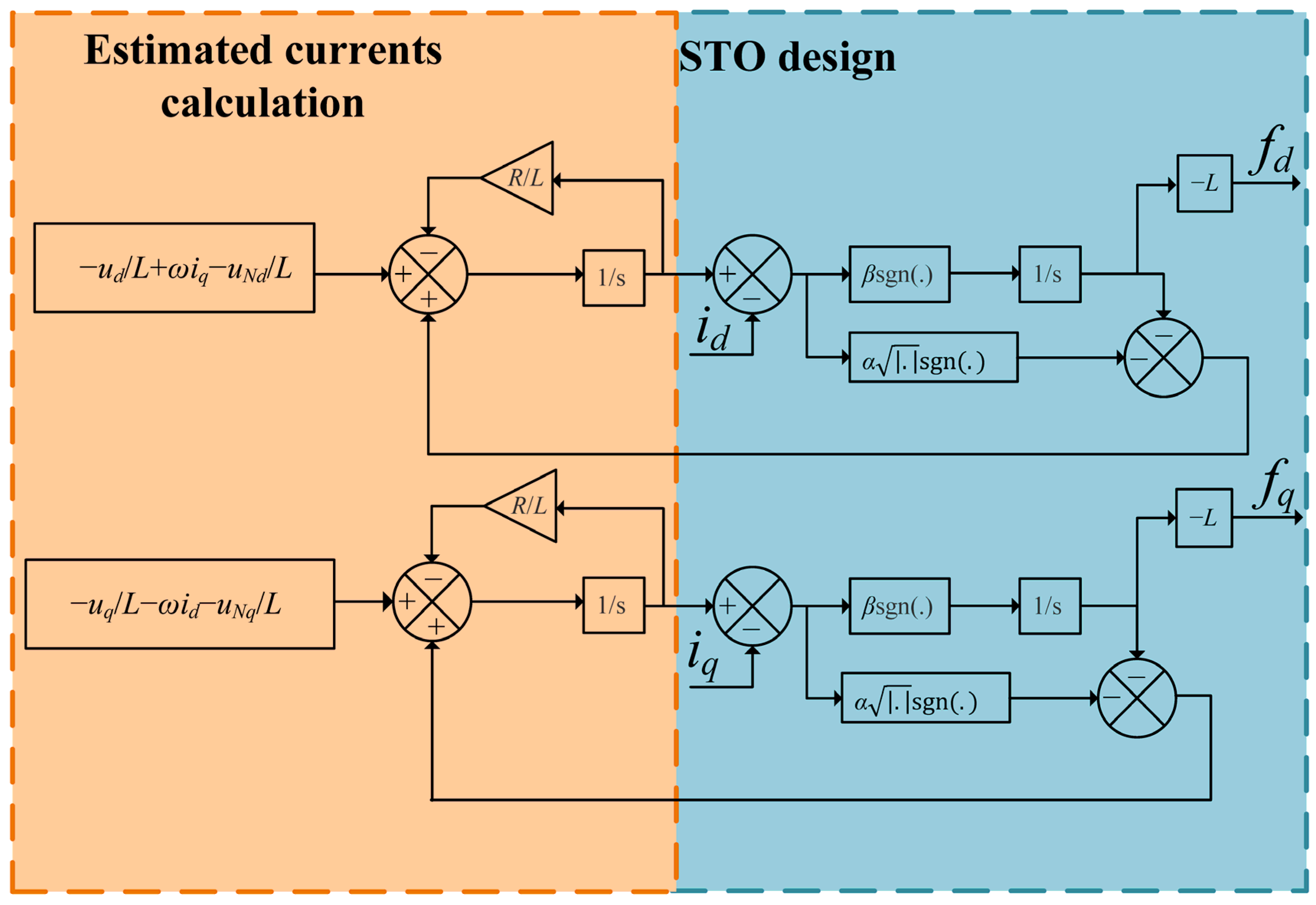
3. Design of Super-Twisting Observer under Parameter Mismatch
4. Design of Outer-Loop Super-Twisting Controller Design
5. Inner-Loop TV-MPC for SOP
5.1. Traditional MPC Method
5.2. TV-MPC Method
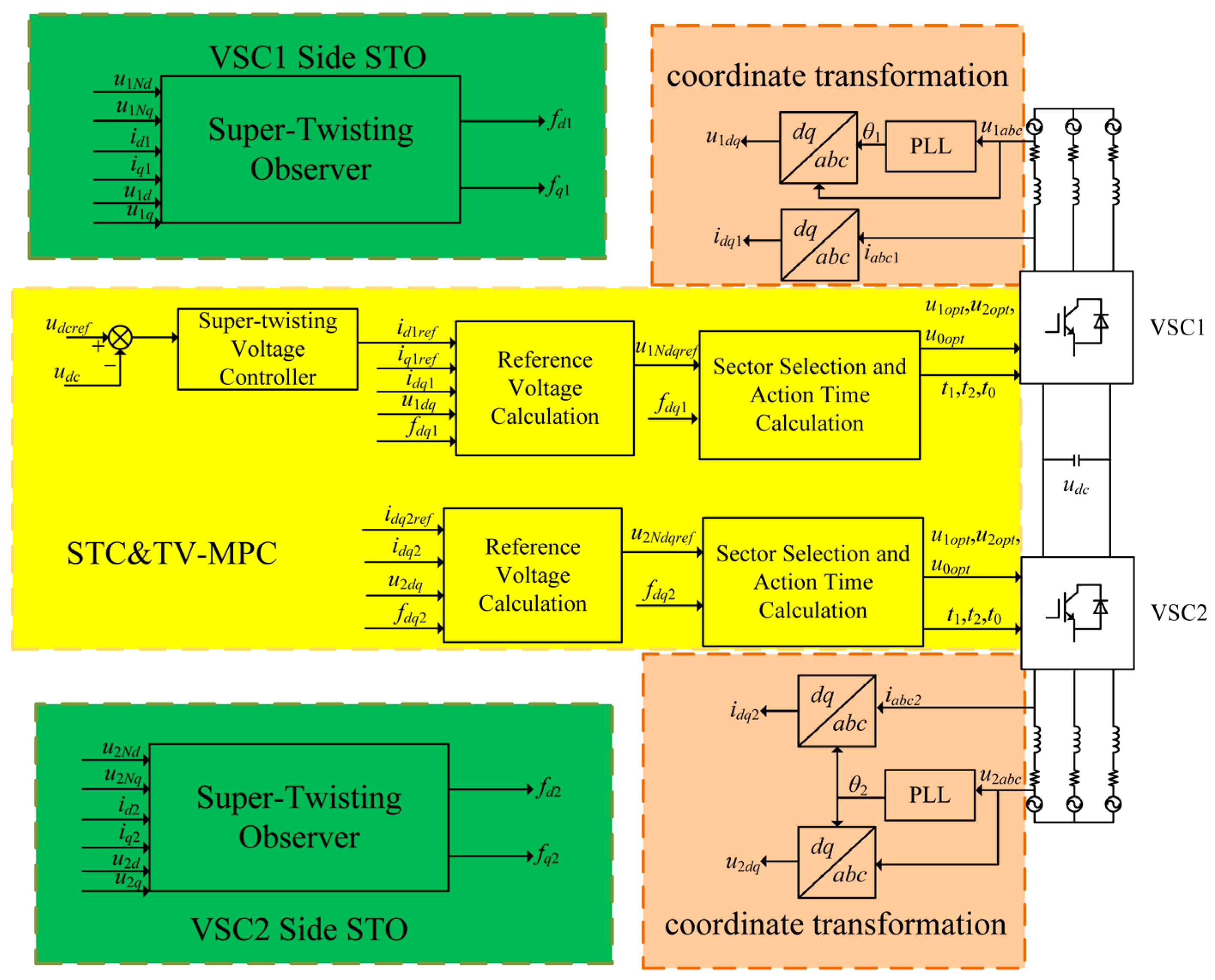
5.3. TV-MPC with STO
6. Simulations
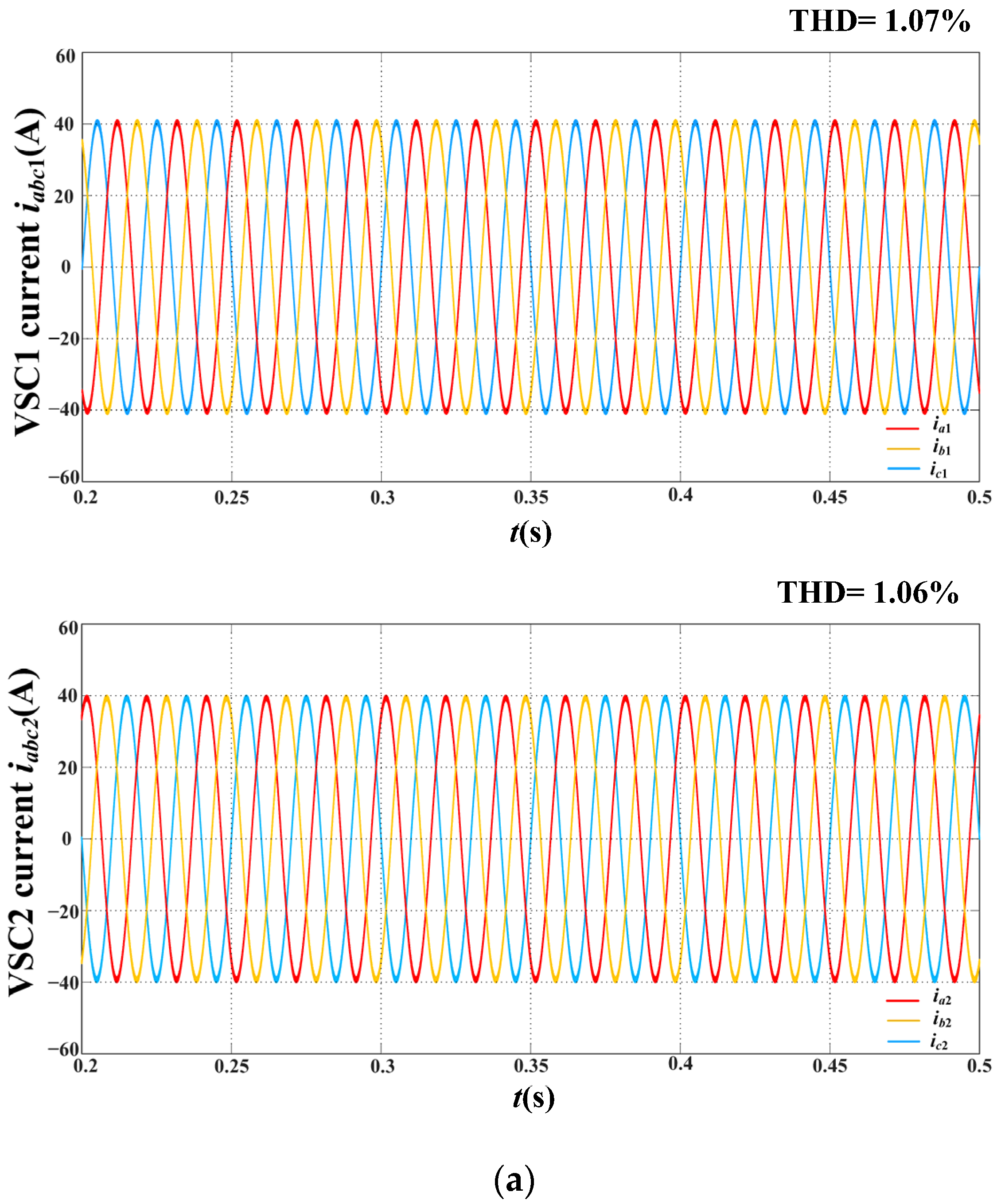
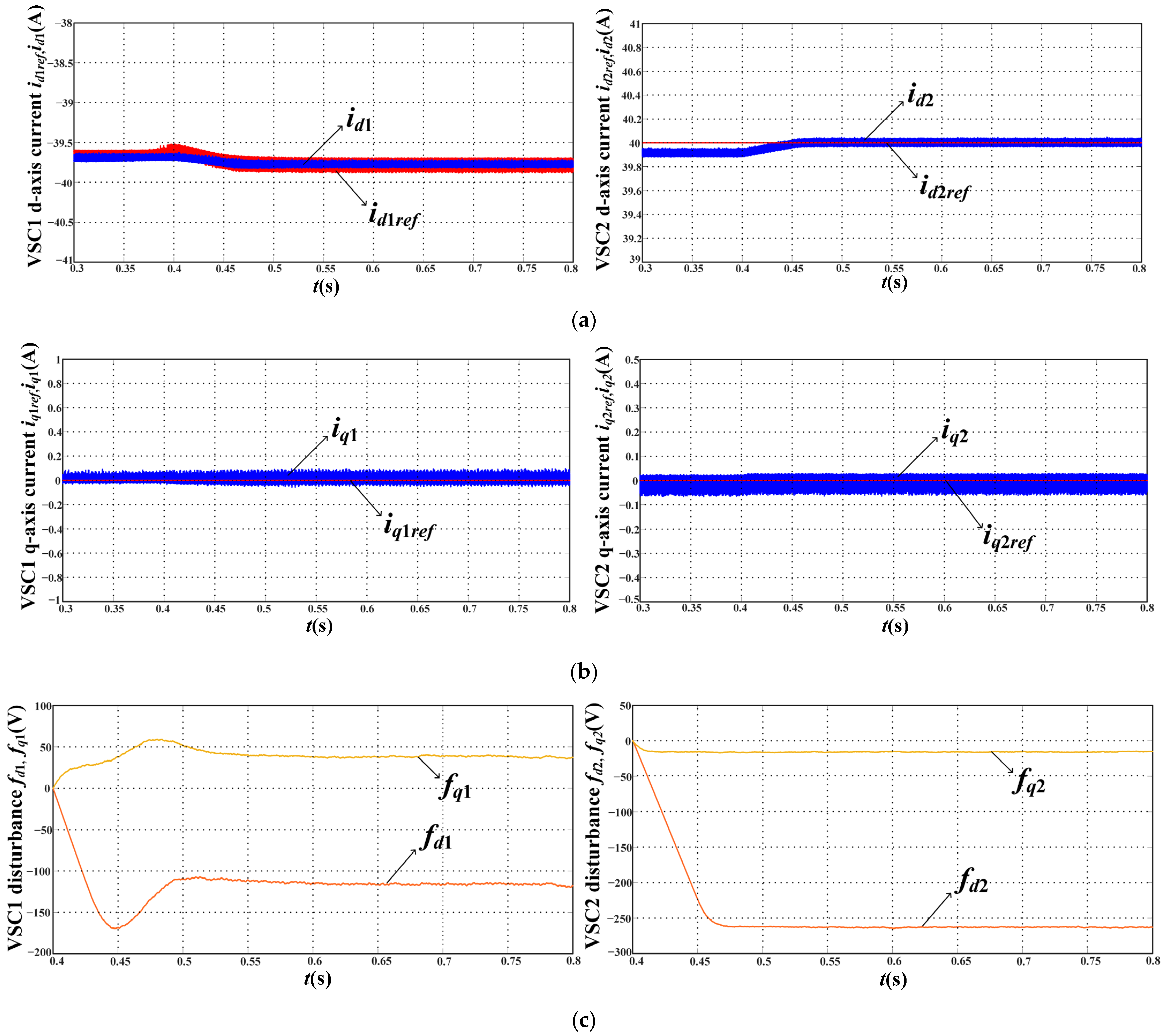
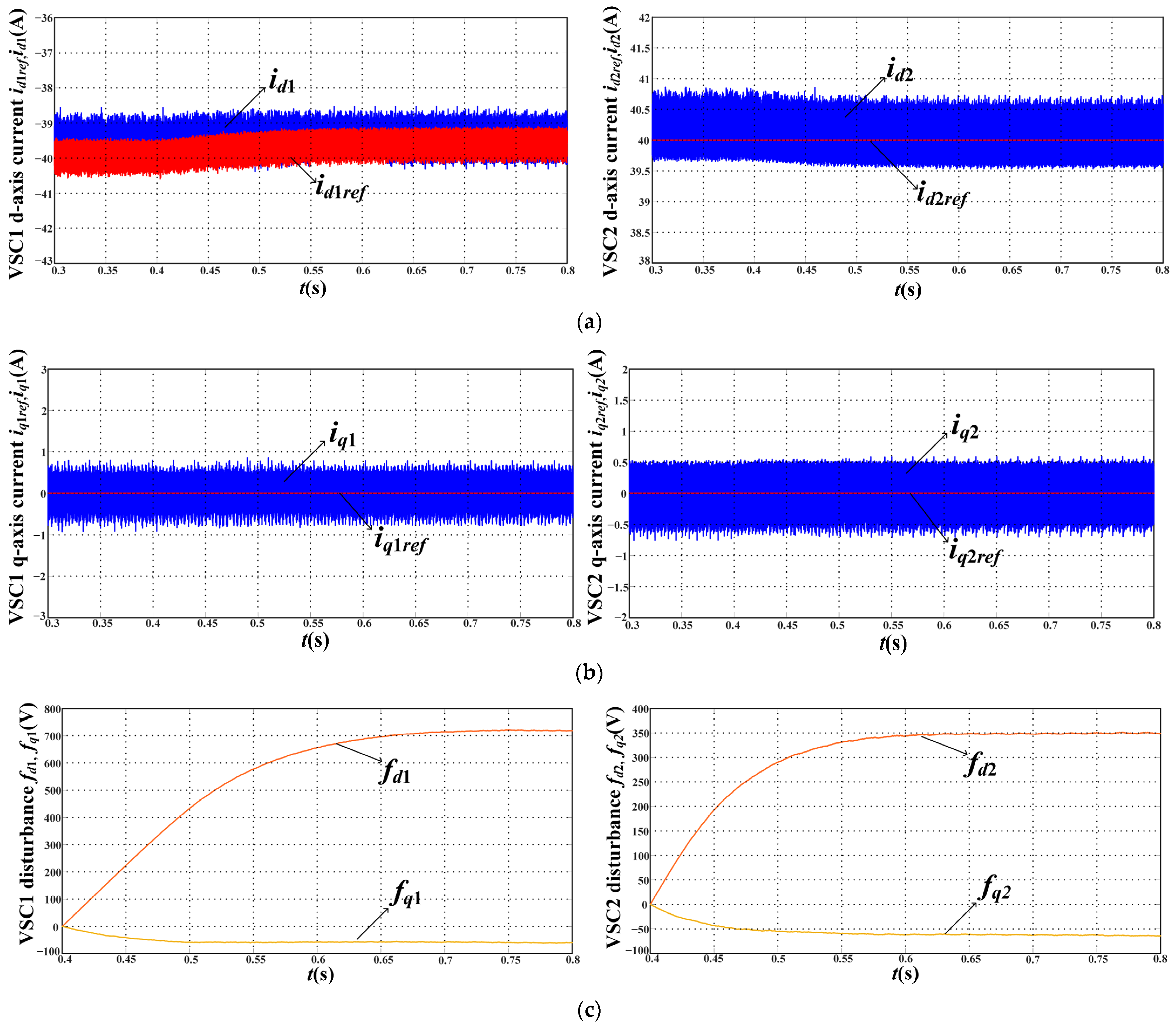
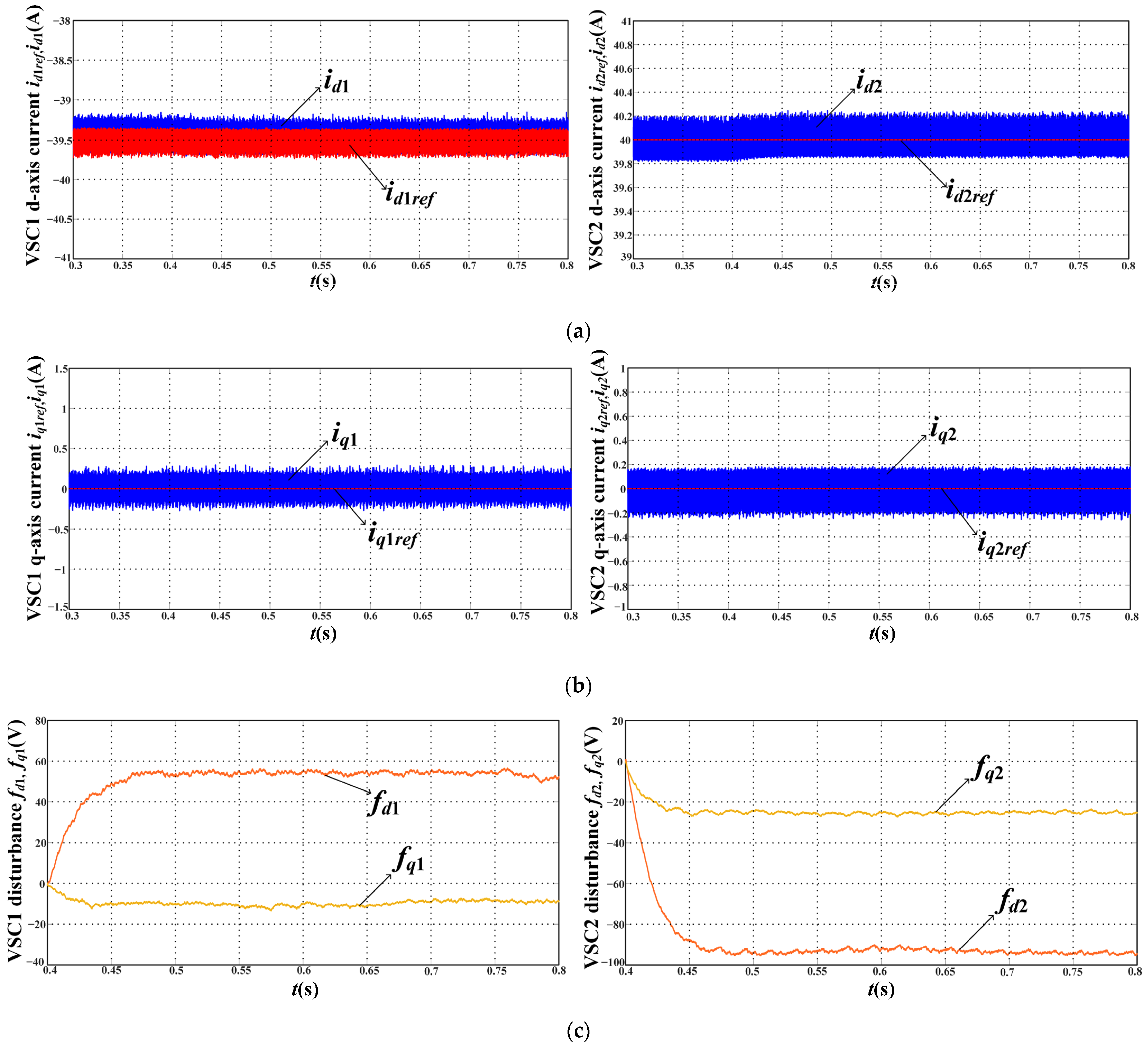
6.1. Current Pefromance of Steady-State
6.2. DC Voltage Performance
6.3. STC and TV-MPC with STO under Parameter Mismatches
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bahrami, S.; Amini, M.H.; Shafie-Khah, M.; Catalão, J.P.S. A Decentralized Renewable Generation Management and Demand Response in Power Distribution Networks. IEEE Trans. Sustain. Energy 2018, 4, 1783–1797. [Google Scholar] [CrossRef]
- Wang, C.; Song, G.; Li, P.; Ji, H.; Zhao, J.; Wu, J. Optimal siting and sizing of soft open points in active electrical distribution networks. Appl. Energy 2017, 189, 301–309. [Google Scholar] [CrossRef]
- Jiang, X.; Zhou, Y.; Ming, W.; Yang, P.; Wu, J. An Overview of Soft Open Points in Electricity Distribution Networks. IEEE Trans. Smart Grid 2022, 13, 1899–1910. [Google Scholar] [CrossRef]
- Wu, R.; Ran, L.; Weiss, G.; Yu, J. Control of a synchronverter-based soft open point in a distribution network. J. Eng. 2019, 16, 720–727. [Google Scholar] [CrossRef]
- Cao, W.; Wu, J.; Jenkins, N.; Wang, C.; Green, T. Operating principle of Soft Open Points for electrical distribution network operation. Appl. Energy 2016, 164, 245–257. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Qu, Z.; Yang, H.; Zhao, R.; Lu, Y.; Yang, Y. Research on an Improved Droop Control Strategy for Soft Open Point. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018; pp. 2000–2005. [Google Scholar]
- Falkowski, P.; Sikorski, A. Finite Control Set Model Predictive Control for Grid-Connected AC–DC Converters with LCL Filter. IEEE Trans. Ind. Electron. 2018, 4, 2844–2852. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, X.; Tan, G.; Zhang, W.; Wang, Q. A Dual-Vector Model Predictive Control Method with Minimum Current THD. IEEE Trans. Power Electron. 2021, 9, 9758–9762. [Google Scholar] [CrossRef]
- Li, H.; Lin, M.; Yin, M.; Ai, J.; Le, W. Three-Vector-Based Low-Complexity Model Predictive Direct Power Control Strategy for PWM Rectifier Without Voltage Sensors. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 1, 240–251. [Google Scholar] [CrossRef]
- Zhan, S.; Na, J.; Li, G.; Wang, B. Adaptive Model Predictive Control of Wave Energy Converters. IEEE Trans. Sustain. Energy 2020, 1, 229–238. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D.; Peng, Z. Cascade-Free Fuzzy Finite-Control-Set Model Predictive Control for Nested Neutral Point-Clamped Converters with Low Switching Frequency. IEEE Trans. Control Syst. Technol. 2019, 5, 2237–2244. [Google Scholar] [CrossRef]
- Xue, C.; Song, W.; Wu, X.; Feng, X. A Constant Switching Frequency Finite-Control-Set Predictive Current Control Scheme of a Five-Phase Inverter with Duty-Ratio Optimization. IEEE Trans. Power Electron. 2018, 4, 3583–3594. [Google Scholar] [CrossRef]
- Cortes, P.; Rodriguez, J.; Silva, C.; Flores, A. Delay compensation in model predictive current control of a three-phase inverter. IEEE Trans. Ind. Electron. 2011, 2, 1323–1325. [Google Scholar] [CrossRef]
- Jin, T.; Shen, X.; Su, T.; Flesch, R.C.C. Model Predictive Voltage Control Based on Finite Control Set with Computation Time Delay Compensation for PV Systems. IEEE Trans. Energy Convers. 2019, 1, 330–338. [Google Scholar] [CrossRef]
- Young, H.A.; Perez, M.A.; Rodriguez, J. Analysis of Finite-Control-Set Model Predictive Current Control with Model Parameter Mismatch in a Three-Phase Inverter. IEEE Trans. Ind. Electron. 2016, 5, 3100–3107. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhang, Y. Model Predictive Current Control for PMSM Drives with Parameter Robustness Improvement. in IEEE Trans. Power Electron. 2019, 2, 1645–1657. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Rodríguez, J. Torque Ripple Reduction of Predictive Torque Control for PMSM Drives with Parameter Mismatch. IEEE Trans. Power Electron. 2017, 9, 7160–7168. [Google Scholar] [CrossRef]
- Ghanes, M.; Trabelsi, M.; Abu-Rub, H.; Ben-Brahim, L. Robust Adaptive Observer-Based Model Predictive Control for Multilevel Flying Capacitors Inverter. IEEE Trans. Ind. Electron. 2016, 12, 7876–7886. [Google Scholar] [CrossRef]
- Yang, R.; Wang, M.; Li, L.; Wang, G.; Zhong, C. Robust Predictive Current Control of PMLSM With Extended State Modeling Based Kalman Filter: For Time-Varying Disturbance Rejection. IEEE Trans. Power Electron. 2020, 2, 2208–2221. [Google Scholar] [CrossRef]
- Yang, M.; Lang, X.; Long, J.; Xu, D. Flux Immunity Robust Predictive Current Control with Incremental Model and Extended State Observer for PMSM Drive. IEEE Trans. Power Electron. 2017, 12, 9267–9279. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiao, W.; Ha, D. A Sliding-Mode Duty-Ratio Controller for DC/DC Buck Converters with Constant Power Loads. IEEE Trans. Ind. Appl. 2014, 2, 1448–1458. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Mi, Y.; Fu, Y.; Wang, P. Frequency Control of an Isolated Micro-Grid Using Double Sliding Mode Controllers and Disturbance Observer. IEEE Trans. Smart Grid 2018, 2, 923–930. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Liang, J.; Gao, J.; Walker, P.D.; Zhang, N. Sliding-Mode Observer Based Voltage-Sensorless Model Predictive Power Control of PWM Rectifier Under Unbalanced Grid Conditions. IEEE Trans. Ind. Electron. 2018, 7, 5550–5560. [Google Scholar] [CrossRef] [Green Version]
- Xia, J.; Guo, Y.; Dai, B.; Zhang, X. Sensor Fault Diagnosis and System Reconfiguration Approach for an Electric Traction PWM Rectifier Based on Sliding Mode Observer. IEEE Trans. Ind. Appl. 2017, 5, 4768–4778. [Google Scholar] [CrossRef]
- Sebaaly, F.; Vahedi, H.; Kanaan, H.Y.; Moubayed, N.; Al-Haddad, K. Sliding Mode Fixed Frequency Current Controller Design for Grid-Connected NPC Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1397–1405. [Google Scholar] [CrossRef]
- Li, X.; Luo, X.; Li, S.; Li, J.; Guan, X. Consensus of second-order nonlinear multi-agent systems via sliding mode observer and controller. J. Syst. Eng. Electron. 2017, 4, 756–765. [Google Scholar]
- Sadeghi, R.; Madani, S.M.; Ataei, M.; Kashkooli, M.R.A.; Ademi, S. Super-Twisting Sliding Mode Direct Power Control of a Brushless Doubly Fed Induction Generator. IEEE Trans. Ind. Electron. 2018, 11, 9147–9156. [Google Scholar] [CrossRef]
- Hou, Q.; Ding, S.; Yu, X. Composite Super-Twisting Sliding Mode Control Design for PMSM Speed Regulation Problem Based on a Novel Disturbance Observer. IEEE Trans. Energy Convers. 2021, 4, 2591–2599. [Google Scholar] [CrossRef]
- Hou, Q.; Ding, S. GPIO Based Super-Twisting Sliding Mode Control for PMSM. IEEE Trans. Circuits Syst. II Express Briefs 2021, 2, 747–751. [Google Scholar] [CrossRef]
- Cao, Y.; Fu, Z.; Zhang, M.; Huang, J. Extended-State-Observer-Based Super Twisting Control for Pneumatic Muscle Actuators. Actuators 2021, 10, 35. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Laghrouche, S.; Depernet, D.; Djerdir, A.; Cirrincione, M. Disturbance-Observer-Based Complementary Sliding-Mode Speed Control for PMSM Drives: A Super-Twisting Sliding-Mode Observer-Based Approach. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5416–5428. [Google Scholar] [CrossRef]
- Luo, W.; Vazquez, S.; Liu, J.; Gordillo, F.; Franquelo, L.G.; Wu, L. Control System Design of a Three-Phase Active Front End Using a Sliding-Mode Observer. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 739–748. [Google Scholar] [CrossRef]
- Fu, D.; Zhao, X.; Zhu, J. A Novel Robust Super-Twisting Nonsingular Terminal Sliding Mode Controller for Permanent Magnet Linear Synchronous Motors. IEEE Trans. Power Electron. 2022, 3, 2936–2945. [Google Scholar] [CrossRef]
- Han, S.I. Fuzzy Supertwisting Dynamic Surface Control for MIMO Strict-Feedback Nonlinear Dynamic Systems with Supertwisting Nonlinear Disturbance Observer and a New Partial Tracking Error Constraint. IEEE Trans. Fuzzy Syst. 2019, 11, 2101–2114. [Google Scholar] [CrossRef]
- Xu, Y.; Ding, X.; Wang, J.; Wang, C. Robust three-vector-based low-complexity model predictive current control with supertwisting-algorithm-based second-order sliding-mode observer for permanent magnet synchronous motor. IET Power Electron. 2019, 11, 2895–2903. [Google Scholar] [CrossRef]
- Hur, N.; Jung, J.; Nam, K. A fast dynamic DC-link power-balancing scheme for a PWM converter-inverter system. IEEE Trans. Ind. Electron. 2001, 48, 794–803. [Google Scholar]
- Rodriguez, J.; Pontt, J.; Silva, C.; Correa, P.; Lezana, P.; Cortes, P.; Ammann, U. Predictive Current Control of a Voltage Source Inverter. IEEE Trans. Ind. Electron. 2007, 54, 495–503. [Google Scholar] [CrossRef]
- Guo, B.; Su, M.; Sun, Y.; Wang, H.; Dan, H.; Tang, Z.; Cheng, B. A Robust Second-Order Sliding Mode Control for Single-Phase Photovoltaic Grid-Connected Voltage Source Inverter. IEEE Access 2019, 7, 53202–53212. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. Strict Lyapunov Functions for the Super-Twisting Algorithm. IEEE Trans. Autom. Control 2012, 4, 1035–1040. [Google Scholar] [CrossRef]




| Sector | Voltage Vector Combination |
|---|---|
| I | V1, V2, V0 or V7 |
| II | V2, V3, V0 or V7 |
| III | V3, V4, V0 or V7 |
| IV | V4, V5, V0 or V7 |
| V | V5, V6, V0 or V7 |
| VI | V6, V1, V0 or V7 |
| Name | Symbol | Value |
|---|---|---|
| VSC1 grid voltage | u1 | 220 V |
| VSC2 grid voltage | u2 | 220 V |
| VSC1 resistance | R1 | 0.03 Ω |
| VSC2 resistance | R2 | 0.03 Ω |
| VSC1 inductance | L1 | 3 mH |
| VSC2 inductance | L2 | 3 mH |
| DC-side capacitance | C | 5000 μF f |
| Sampling time | Ts | 1 × 10−6 s |
| Method | Outer-Loop Controller Parameters |
|---|---|
| PI and MPC | kp = 3.5, ki = 4.125 |
| PI and TV-MPC | kp = 3.5, ki = 4.125 |
| STC and TV-MPC | k1= 150, k2 = 3000 |
| k1 | k2 | α1 | β1 | α2 | β2 |
|---|---|---|---|---|---|
| 100 | 200 | 50,000 | 1,500,000 | 50,000 | 1,500,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhou, H.; Su, H. Disturbance Observer-Based Model Predictive Super-Twisting Control for Soft Open Point. Energies 2022, 15, 3657. https://doi.org/10.3390/en15103657
Wang Z, Zhou H, Su H. Disturbance Observer-Based Model Predictive Super-Twisting Control for Soft Open Point. Energies. 2022; 15(10):3657. https://doi.org/10.3390/en15103657
Chicago/Turabian StyleWang, Zhengqi, Haoyu Zhou, and Hongyu Su. 2022. "Disturbance Observer-Based Model Predictive Super-Twisting Control for Soft Open Point" Energies 15, no. 10: 3657. https://doi.org/10.3390/en15103657
APA StyleWang, Z., Zhou, H., & Su, H. (2022). Disturbance Observer-Based Model Predictive Super-Twisting Control for Soft Open Point. Energies, 15(10), 3657. https://doi.org/10.3390/en15103657






