Parameter Effect Analysis of Non-Darcy Flow and a Method for Choosing a Fluid Flow Equation in Fractured Karstic Carbonate Reservoirs
Abstract
:1. Introduction
2. Method of Comparing Darcy Flow and Non-Darcy Flows
2.1. Non-Darcy Flow Mechanism and Equations
2.2. Analytical Solution of Darcy and Non-Darcy Equations
3. Comparison of Darcy and Non-Darcy Equations Based on Analytical Solution
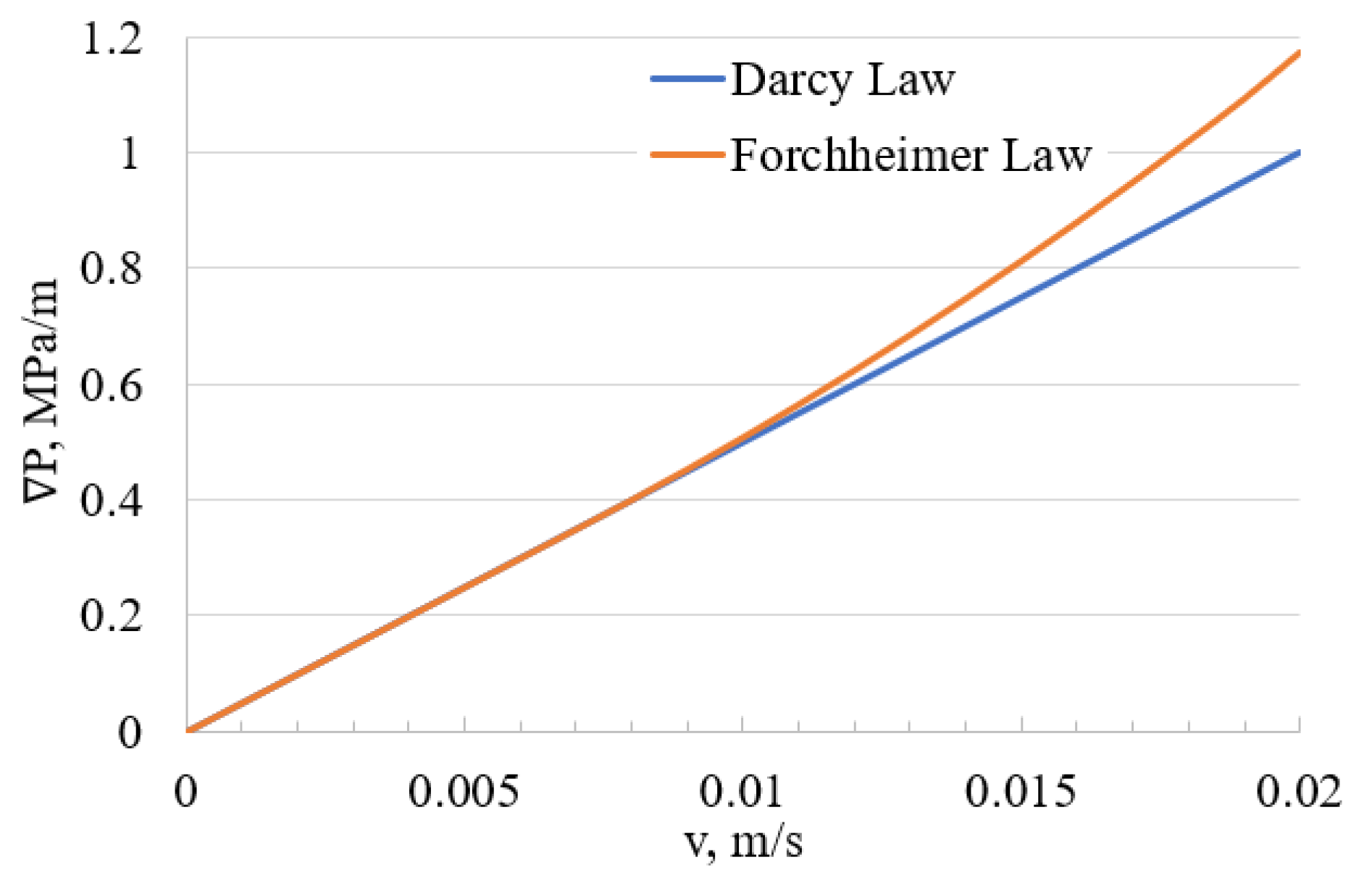
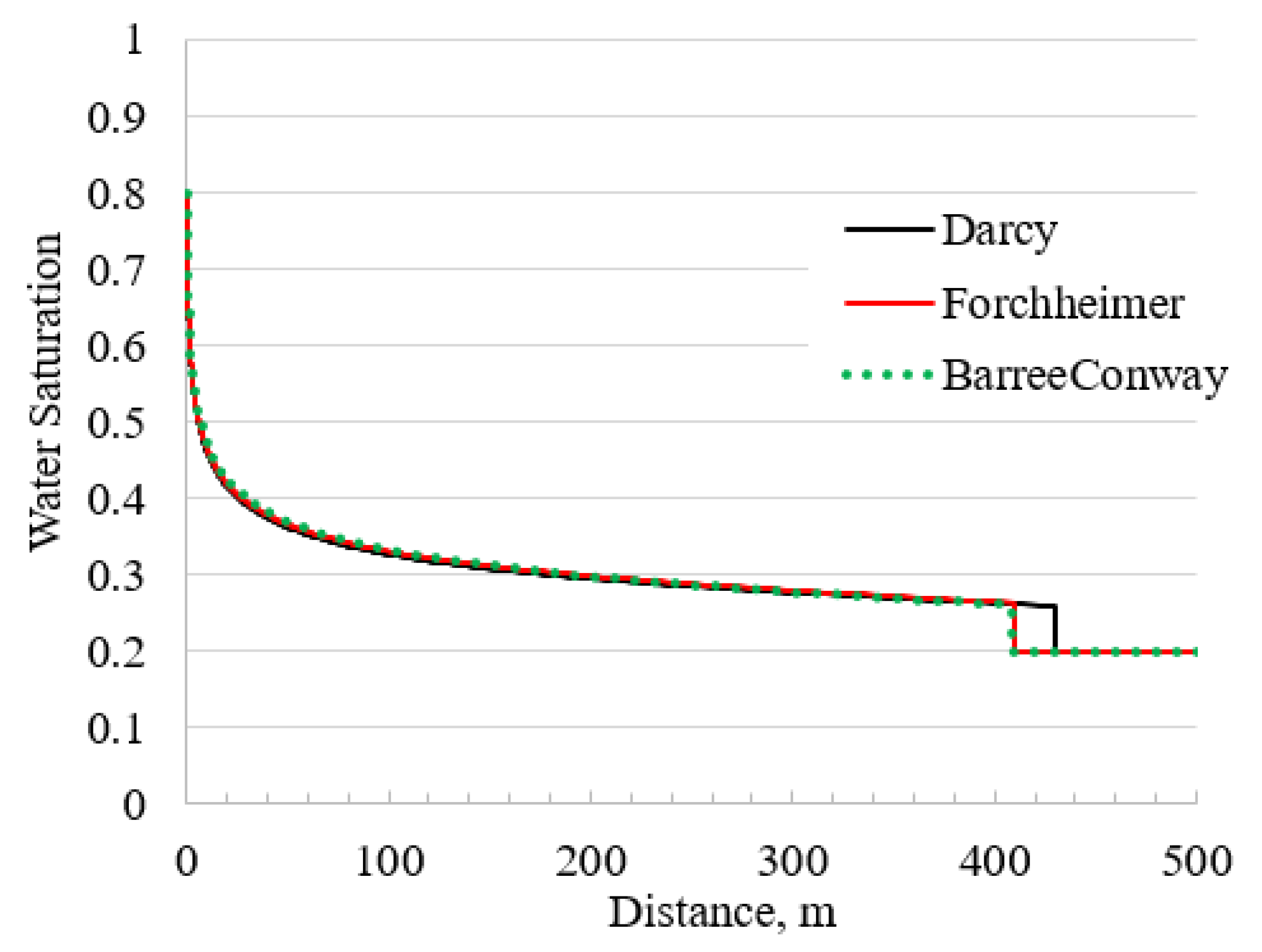
3.1. Comparison of Darcy and Forchheimer Equations
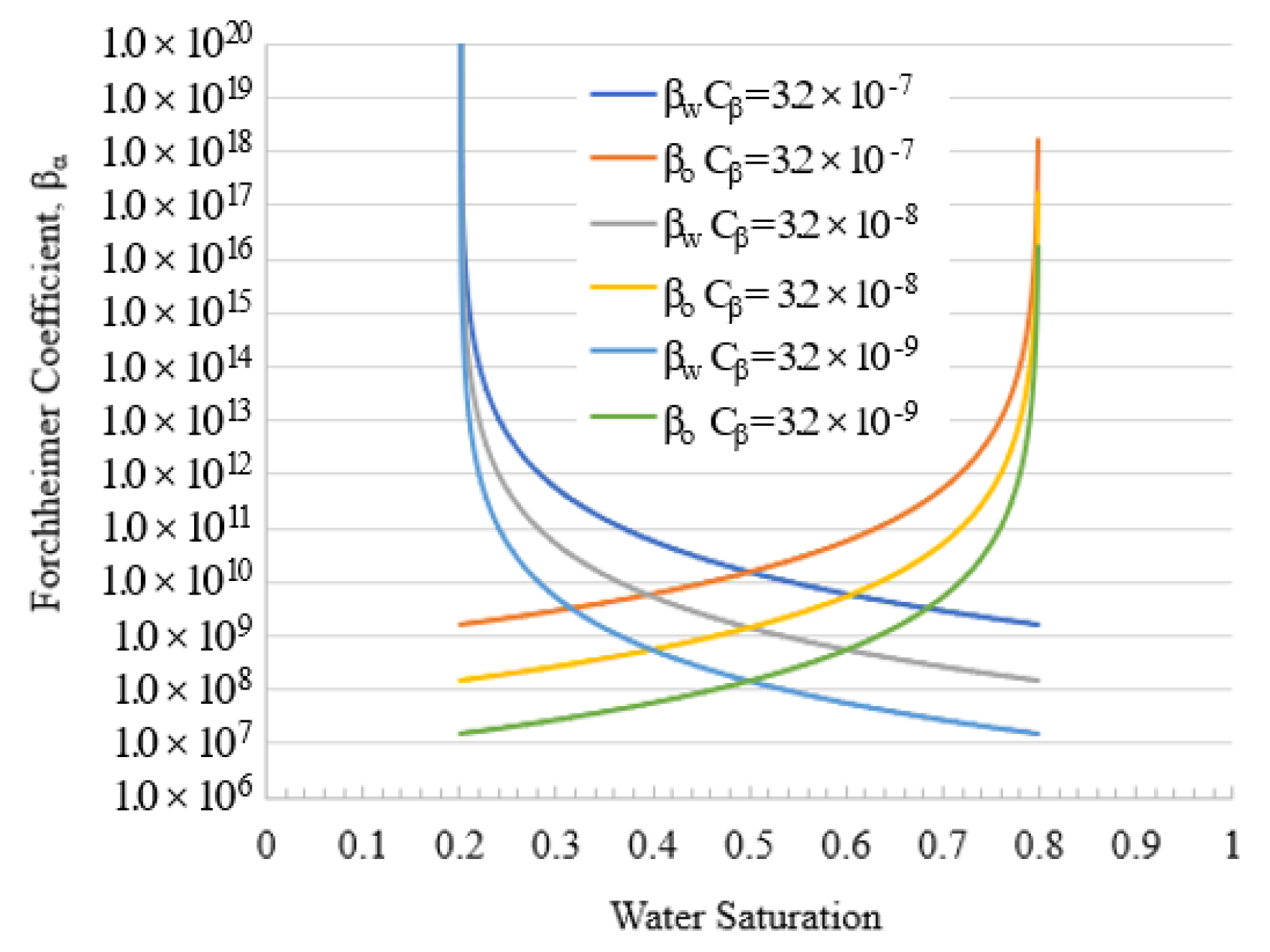
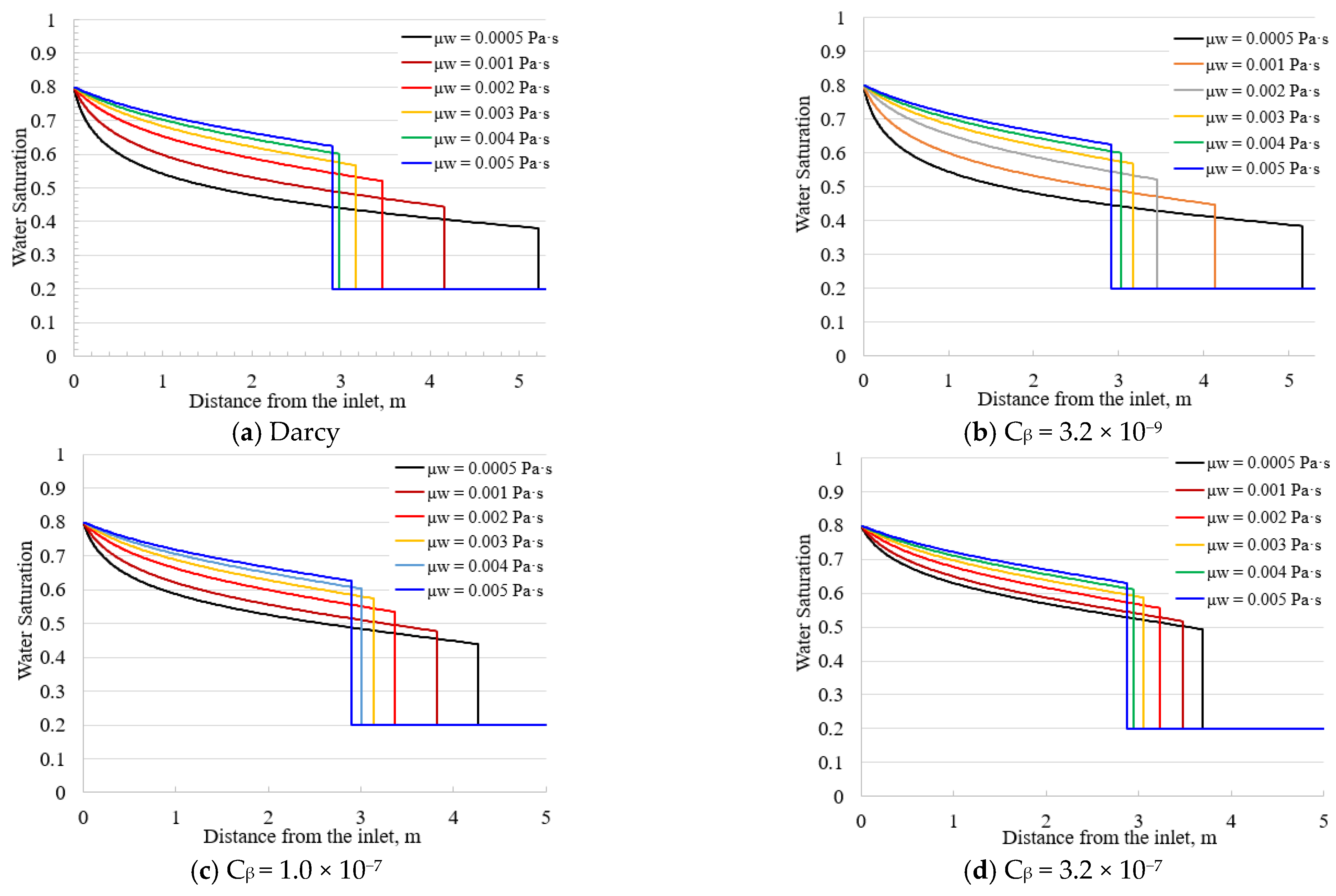
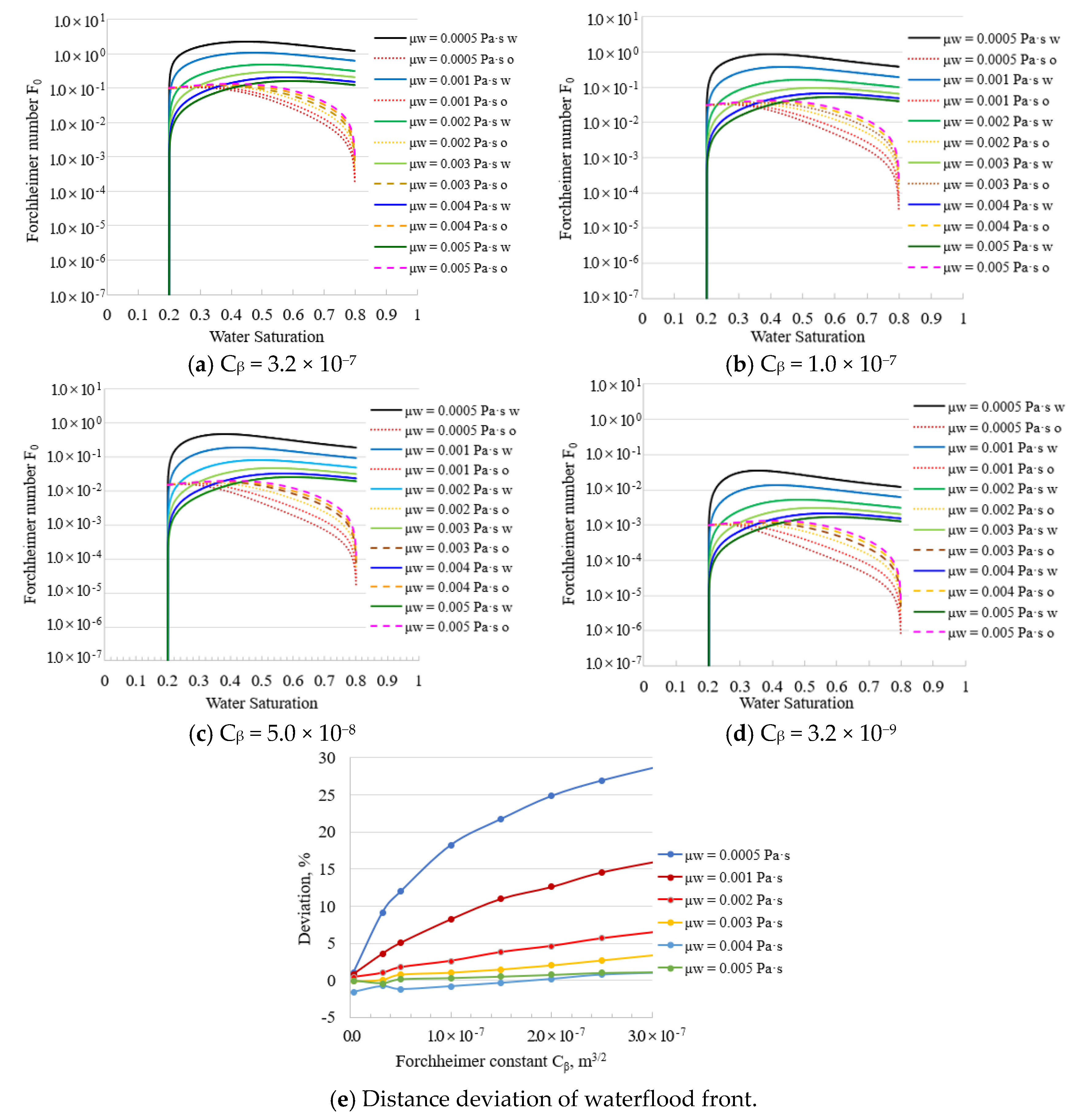
3.1.1. Forchheimer Constant Cβ
3.1.2. Fluid Viscosity
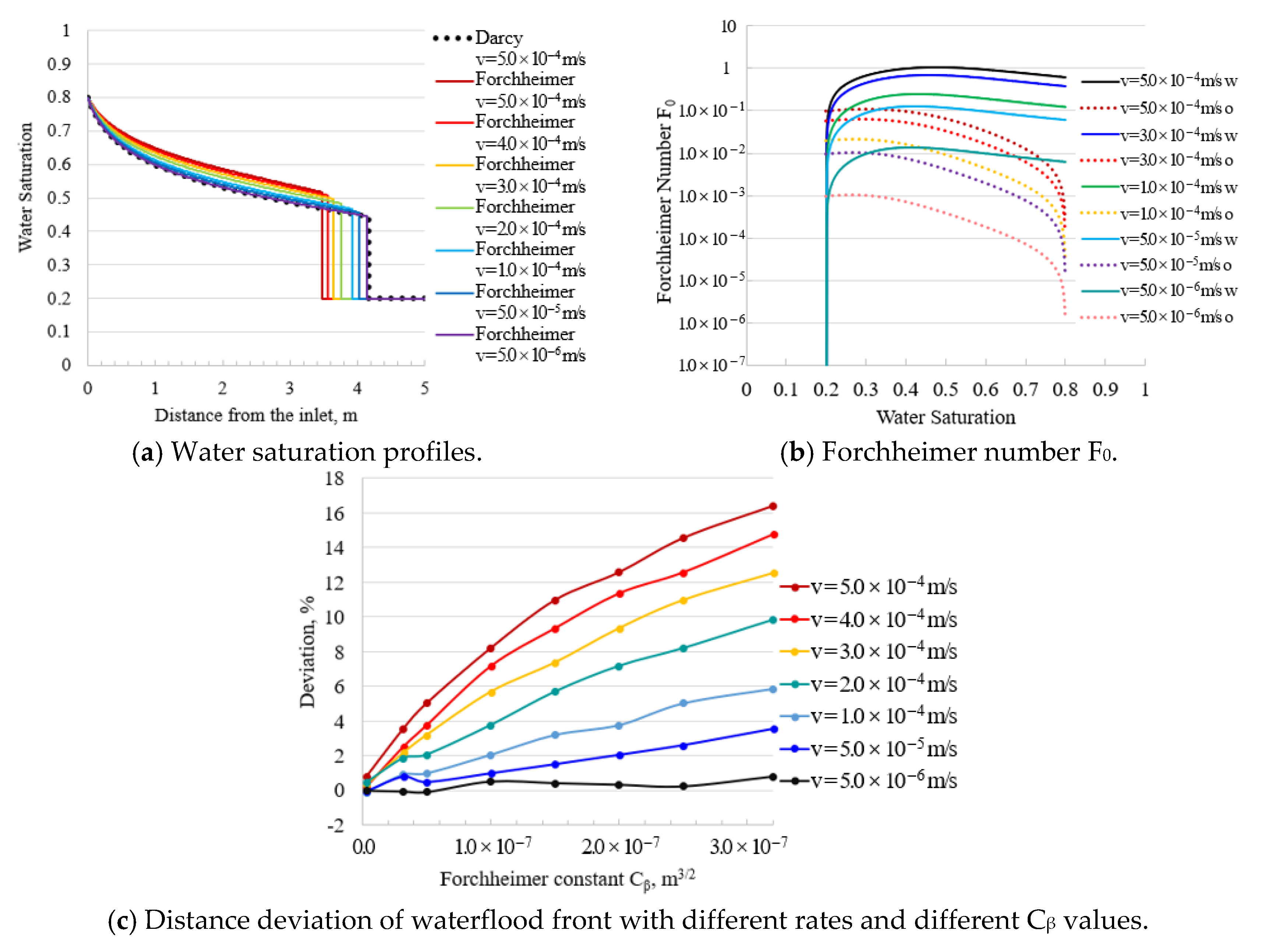
3.1.3. Flow Velocity
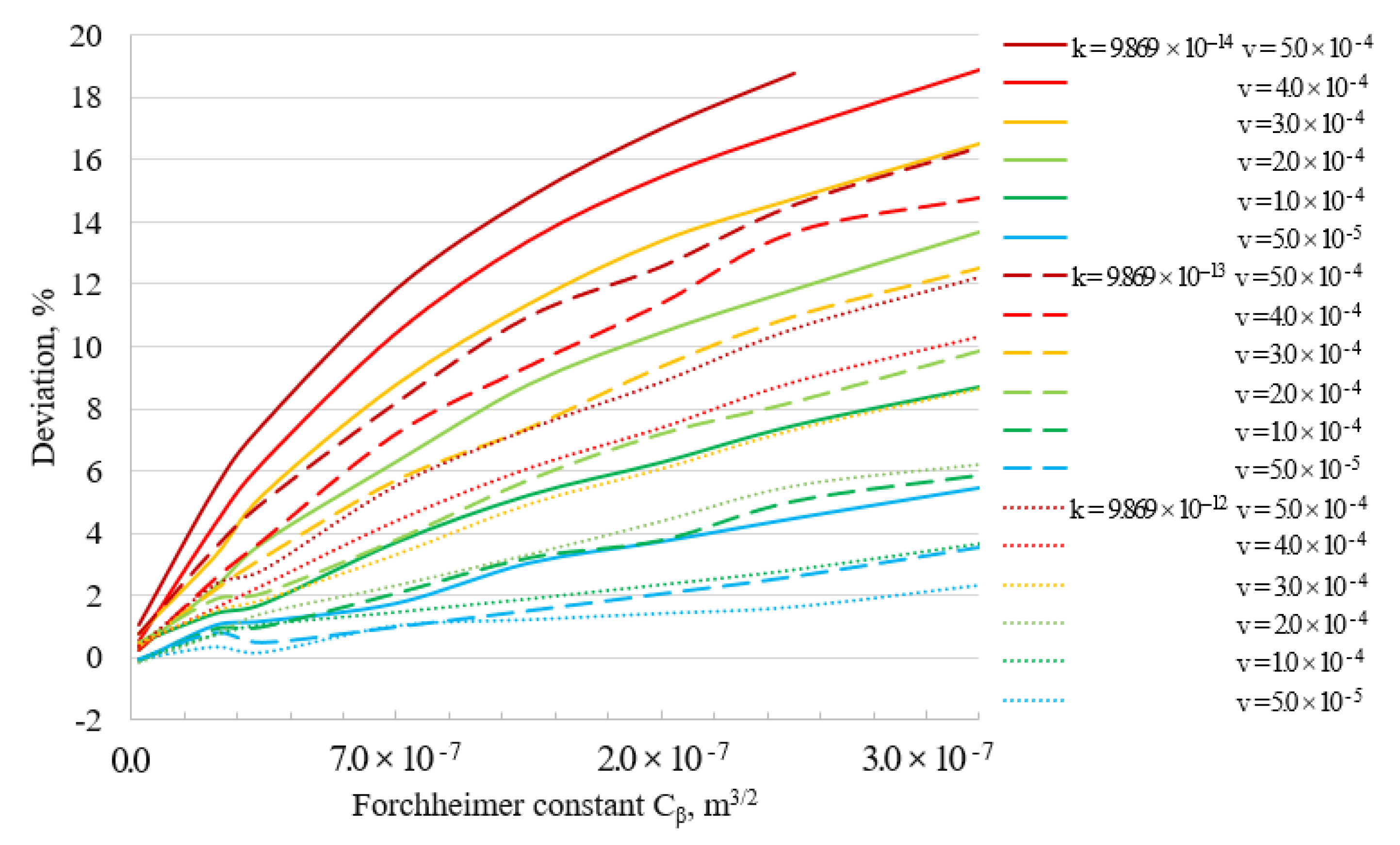
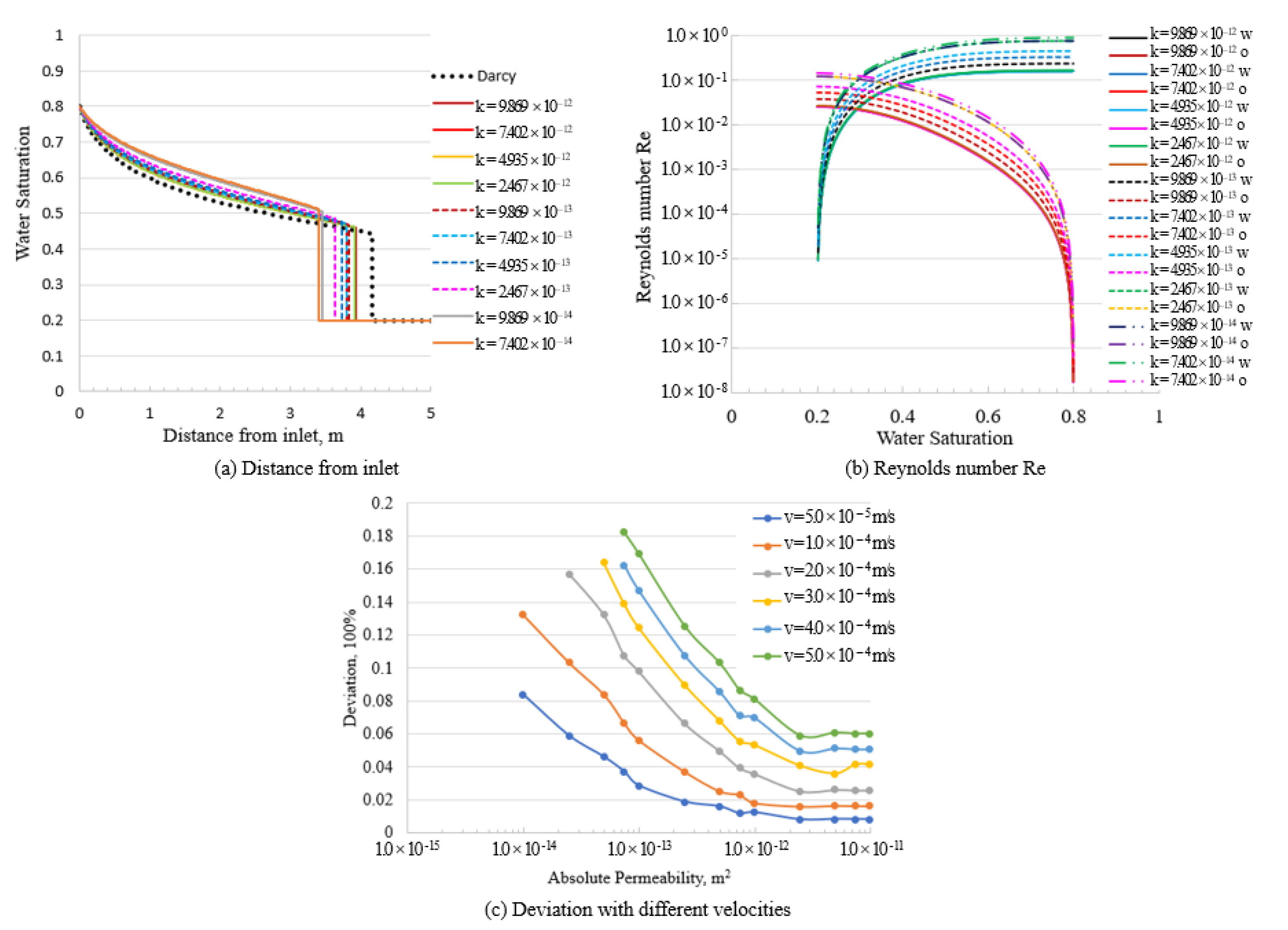
3.1.4. Absolute Permeability
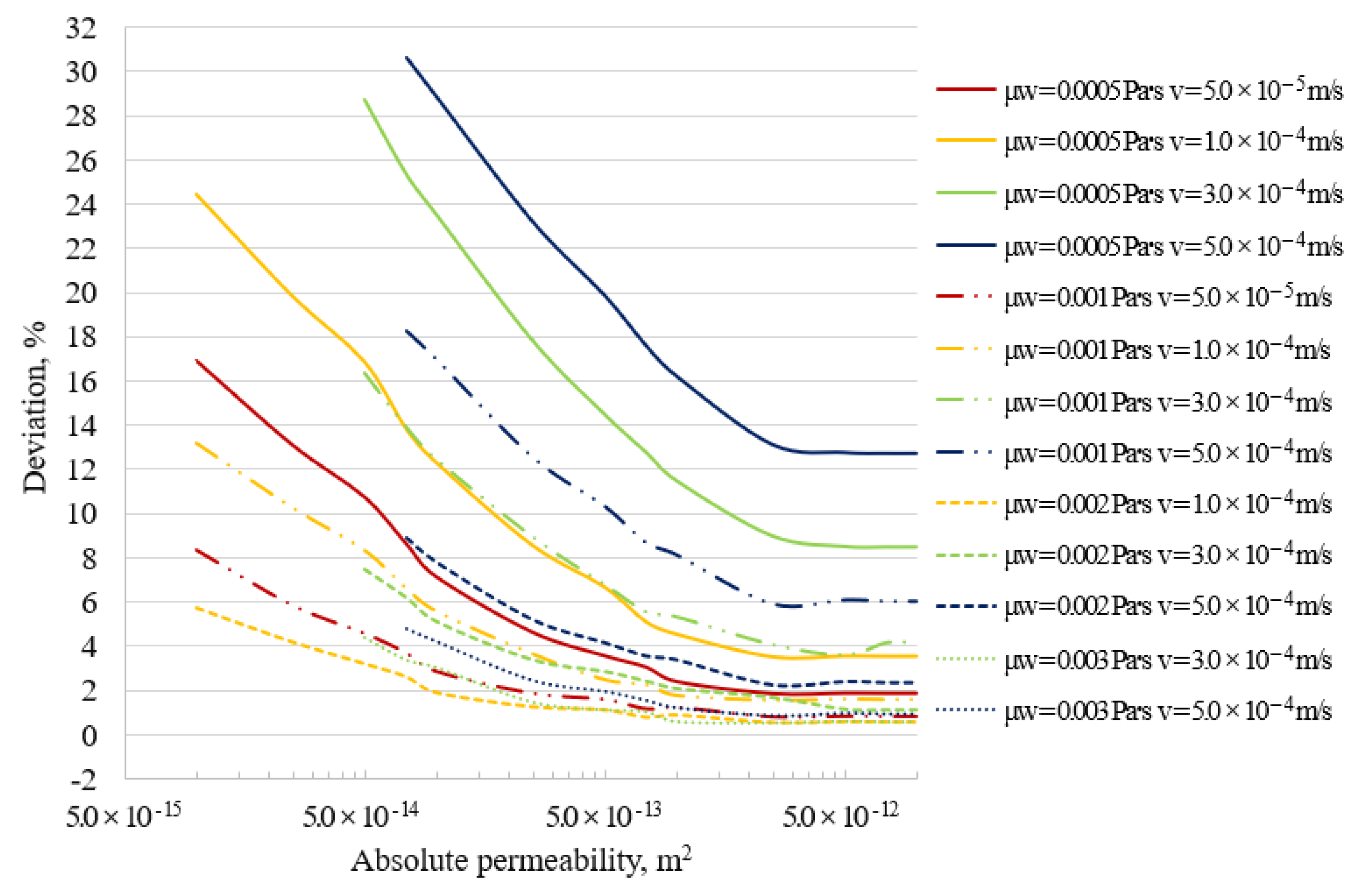
3.1.5. Effect of Parameters
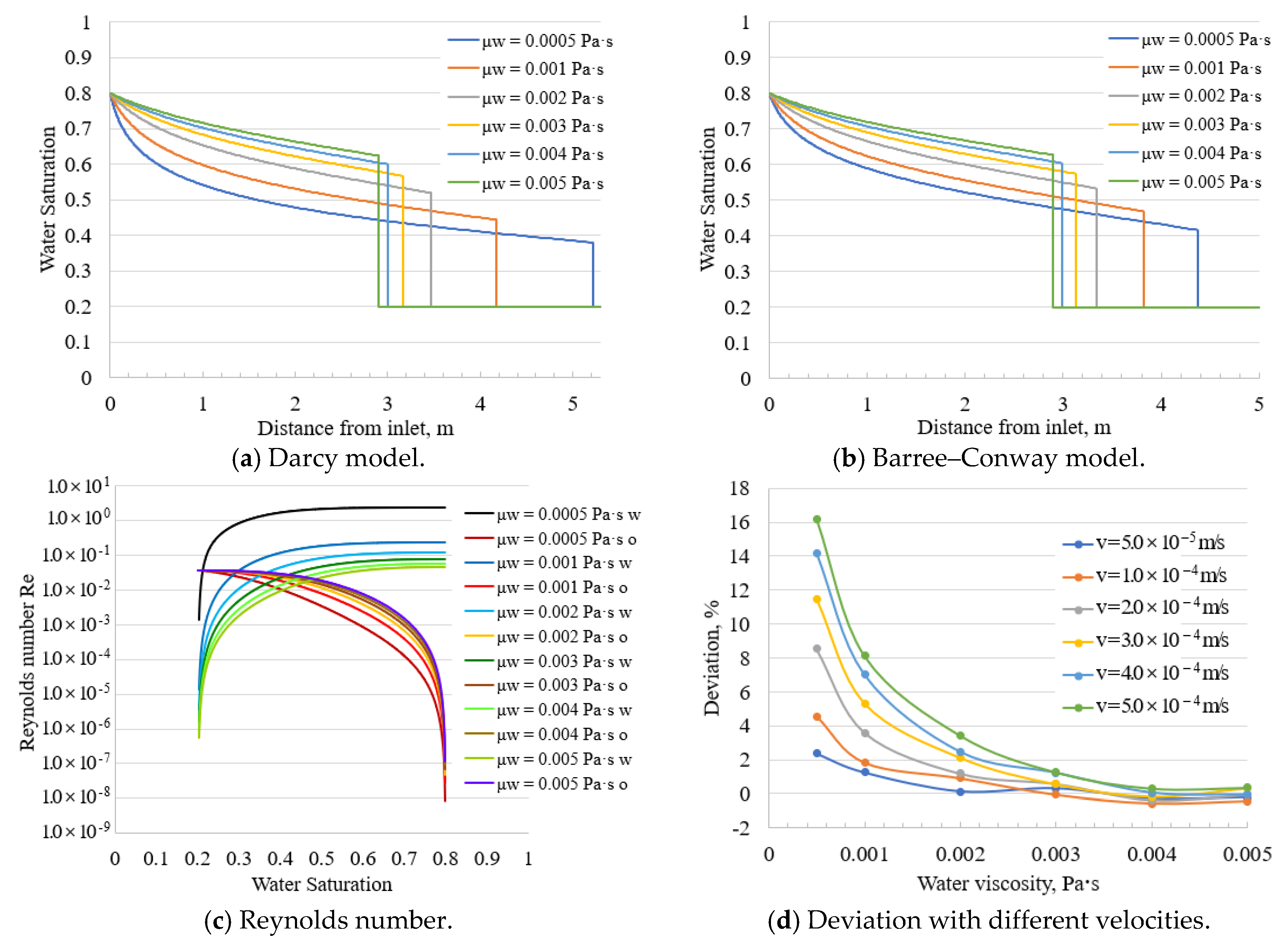
3.2. Comparison of Darcy and Barree–Conway Equations
3.2.1. Fluid Viscosity
3.2.2. Flow Velocity
3.2.3. Absolute Permeability
3.2.4. Effect of Parameters
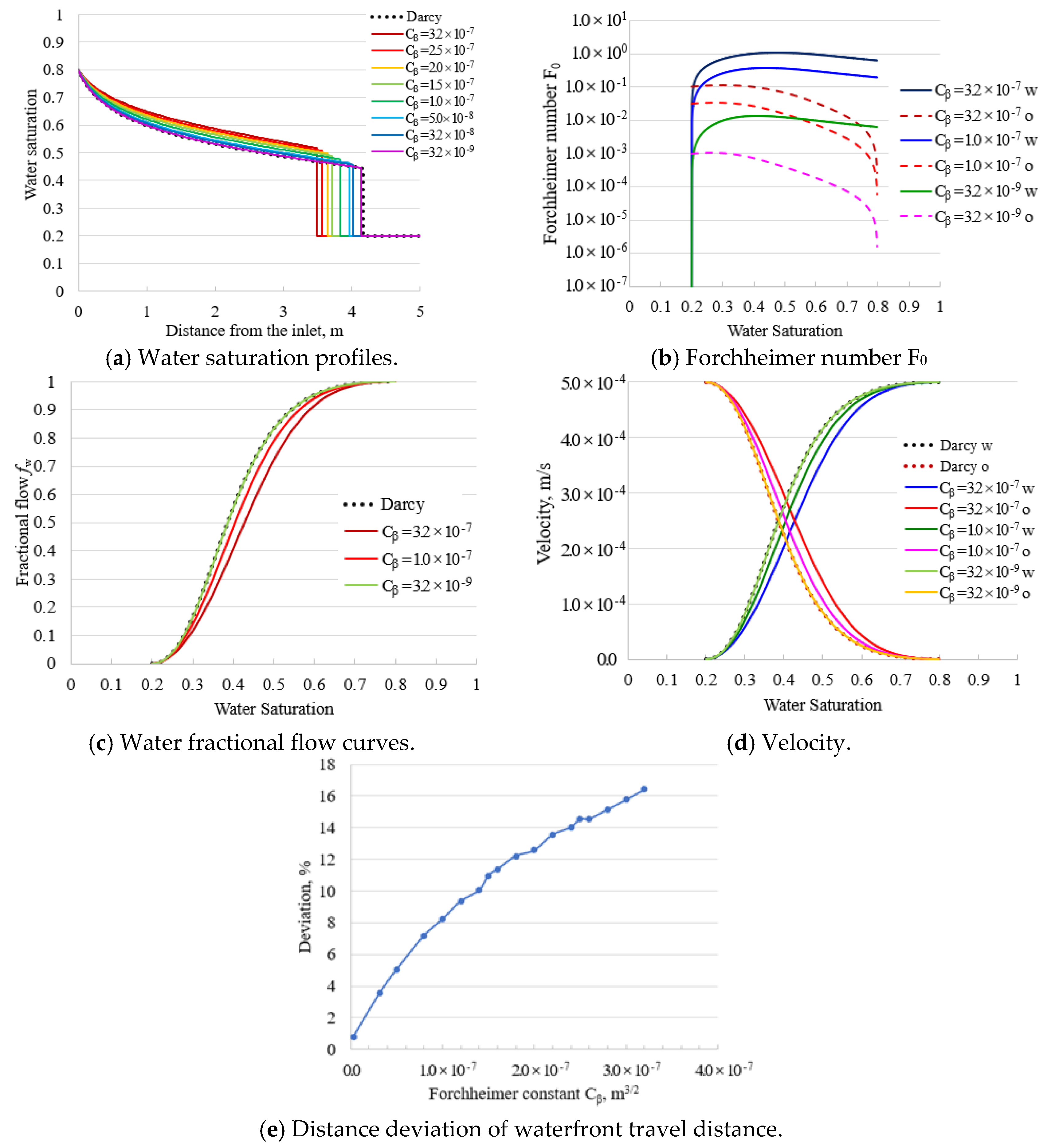
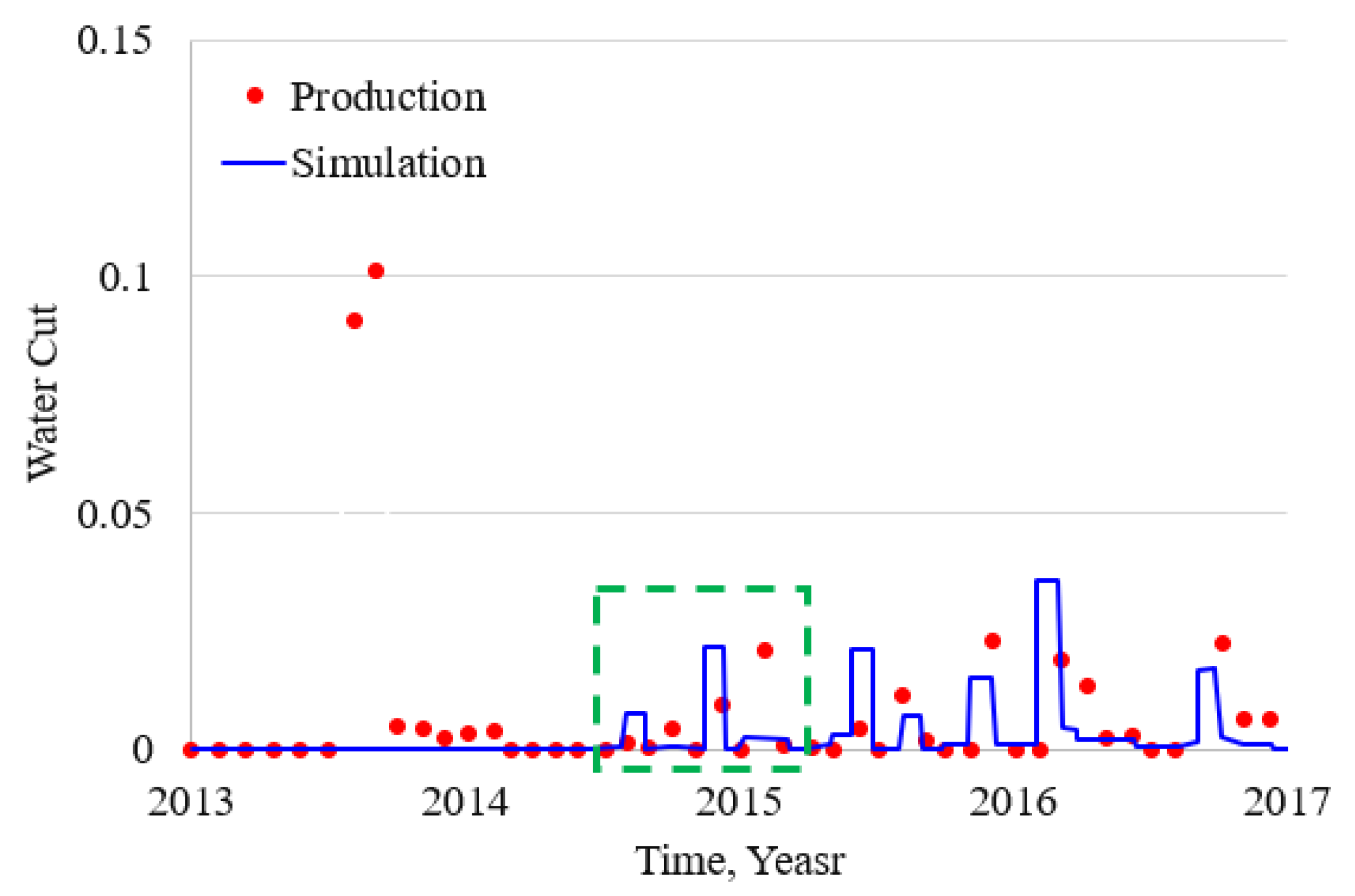
4. Applications of Tarim Fractured Karstic Carbonate Reservoir
5. Conclusions
- It is not very realistic that the non-Darcy flow equation is used to simulate fluid flow in fractured karstic carbonate reservoirs. It is the inertial term in Forchheimer model and the apparent permeability in the Barree–Conway model that make these equations more complex than the Darcy equation. Furthermore, it will dramatically increase the difficulty and expense of numerical simulation.
- The Forchheimer number and Reynolds number do not quantify the magnitude of the inertial effect. In addition, the crucial values of the Forchheimer number and Reynolds number are not constant and vary with the parameters of the rock and fluid properties. It is very difficult to determine whether to consider the non-Darcy effect only according to the Forchheimer/Reynolds number.
- The distance deviation of the waterflood front can better describe the inertial effect of multiphase flow. In numerical simulation, we are concerned with the displacement range and the sweeping efficiency. According to the distance deviation of the waterflood front between the Darcy and non-Darcy equations, we will not only choose the flow equation within the numerical error allowed, but also obtain the evaluation of the numerical error for a complex heterogeneous reservoir.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akbar, M.; Vissapragada, B.; Alghamdi, A.H. A snapshot of carbonate reservoir evaluation. Oilfield Rev. 2000, 12, 20–21. [Google Scholar]
- Srinivasan, S.; O’Malley, D.; Mudunuru, M.K. A machine learning framework for rapid forecasting and history matching in unconventional reservoirs. Sci. Rep. 2021, 11, 21730. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Sun, H.; Li, A. Modern System of multiphase flow in porous media and its development trend. Sci. China Press 2018, 63, 425–451. [Google Scholar] [CrossRef] [Green Version]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon; Technical Report; Dalmont: Paris, France, 1856. [Google Scholar]
- Forchheimer, P. Wasserbewegung durch boden. Z. Ver Deutsh. Ing. 1901, 45, 1782–1788. [Google Scholar]
- Whitaker, S. Advances in theory of fluid motion in porous media. Ind. Eng. Chem. 1969, 61, 14–28. [Google Scholar] [CrossRef]
- Jones, S.C. A Rapid Unsteady-State Klinkenberg Permeameter. Soc. Pet. Eng. J. 1972, 12, 383–397. [Google Scholar] [CrossRef]
- Geertsma, J. Estimating the Coefficient of Inertial Resistance in Fluid Flow through Porous Media. Soc. Pet. Eng. J. 1974, 14, 445–450. [Google Scholar] [CrossRef]
- Firoozabadi, A.; Katz, D.L. An analysis of high-velocity gas flow through porous media. J. Petrol. Technol 1979, 31, 211–216. [Google Scholar] [CrossRef]
- Ruth, D.; Ma, H. On the derivation of the Forchheimer equation by means of the averaging theorem. Transp. Porous Media 1992, 7, 255–264. [Google Scholar] [CrossRef]
- Barree, R.D.; Conway, W. Beyond Beta Factors: A Complete Model for Darcy, Forchheimer, and Trans-Forchheimer Flow in Porous Media. In Proceedings of the SPE Annual Technical Conference and Exhibition (SPE 2004), Houston, TX, USA, 26–29 September 2004; pp. 1–8. [Google Scholar]
- Barree, R.D.; Conway, M.W. Multiphase non-darcy flow in proppant packs. In Proceedings of the SPE Annual Technical Conference and Exhibition (SPE 2007), Anaheim, CA, USA, 11–14 November 2007; pp. 1–10. [Google Scholar]
- Chilton, T.H.; Colburn, A.P. Pressure drop in packed tubes. Ind Engng. Chem. 1931, 23, 913–919. [Google Scholar] [CrossRef]
- Green, L., Jr.; Duwez, P. Fluid flow through porous metals. J. Appl. Mech. 1951, 18, 39–45. [Google Scholar] [CrossRef]
- Ma, H.; Ruth, D.W. The microscopic analysis of high Forchheimer number flow in porous media. Transp. Porous Media 1993, 13, 139–160. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Engng. Prog. 1952, 48, 89–94. [Google Scholar]
- Evans, R.D.; Hudson, C.S.; Greenlee, J.E. The effect of an immobile liquid saturation on the non-darcy flow coefficient in porous media. SPE Prod. Eng. 1987, 2, 331–338. [Google Scholar] [CrossRef]
- Scheidegger, A.E. The Physics of Flow through Porous Media, 3rd ed.; University of Toronto Press, Scholarly Publishing: Toronto, ON, Canada, 1974; pp. 31–150. [Google Scholar]
- Blick, E.F.; Civan, F. Porous media momentum equation for highly accelerated flow. SPE Reserv. Engng. 1988, 3, 1048–1052. [Google Scholar] [CrossRef]
- Bear, J. Hydraulics of Groundwater; McGraw-Hill: New York, NY, USA, 1979; pp. 66–82. [Google Scholar]
- Wu, Y. Non-Darcy displacement of immiscible fluids in porous media. Water Resour. Res. 2001, 37, 2943–2950. [Google Scholar] [CrossRef]
- Bitao, L.; Jennifer, L.; Wu, Y.-S. Non-darcy porous media flow according to the barree and conway model: Laboratory and numerical modeling studies. In Proceeding of the SPE Rocky Mountain Petroleum Technology Conference (SPE 2009), Denver, CO, USA, 14–16 April 2009; pp. 1–10. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media. In Hydrology Papers; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Zhengwen, Z.; Reid, G. A criterion for Non-Darcy Flow in Porous Media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar]




| Parameters | Value | Unit |
|---|---|---|
| Porosity, ϕ | 0.30 | |
| Absolute permeability, k | 9.869 × 10−13 | m2 |
| Cross section area, A | 1.0 | m2 |
| Length of model, L | 5.0 | m |
| Injection rate, qt | 5.0 × 10−4 | m3/s |
| Water viscosity, μw | 1.0 × 10−3 | Pa·s |
| Oil viscosity, μo | 5.0 × 10−3 | Pa·s |
| Residual water saturation, Swr | 0.2 | |
| Residual oil saturation, Sor | 0.2 | |
| Maximum relative permeability, krw,max | 0.8 | |
| Maximum relative permeability, kro,max | 0.8 | |
| Power index of relative permeability, nw | 2 | |
| Power index of relative permeability, no | 2 | |
| Density of water, ρw | 1000 | kg/m3 |
| Density of oil, ρo | 800 | kg/m3 |
| Forchheimer flow constant, Cβ | 3.2 × 10−7 | m3/2 |
| Minimum permeability fraction, kmr | 0.01 | |
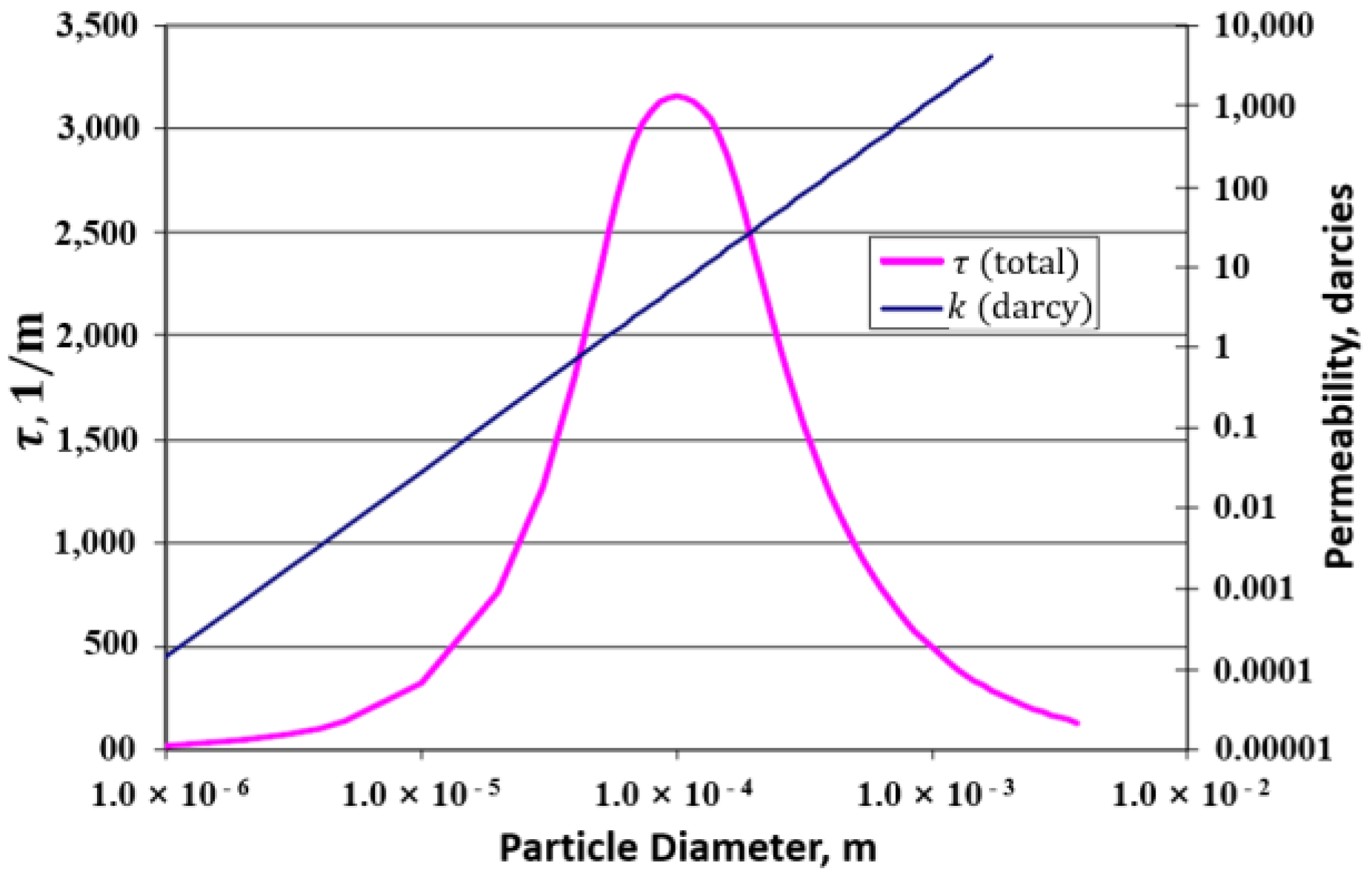
| Inverse of characteristic length, τ | 2.1× 103 | m−1 |
| Absolute Permeability k, m2 | Inverse of Characteristic Length τ, m−1 | |
|---|---|---|
| 1 | 9.869 × 10−12 | 3100 |
| 2 | 7.402 × 10−12 | 3100 |
| 3 | 4.935 × 10−12 | 3150 |
| 4 | 2.467 × 10−12 | 3000 |
| 5 | 9.869 × 10−13 | 2100 |
| 6 | 7.402 × 10−13 | 1900 |
| 7 | 4.935 × 10−13 | 1500 |
| 8 | 2.467 × 10−13 | 1100 |
| 9 | 9.869 × 10−14 | 650 |
| 10 | 7.402 × 10−14 | 550 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yao, J.; Huang, Z. Parameter Effect Analysis of Non-Darcy Flow and a Method for Choosing a Fluid Flow Equation in Fractured Karstic Carbonate Reservoirs. Energies 2022, 15, 3623. https://doi.org/10.3390/en15103623
Wang Y, Yao J, Huang Z. Parameter Effect Analysis of Non-Darcy Flow and a Method for Choosing a Fluid Flow Equation in Fractured Karstic Carbonate Reservoirs. Energies. 2022; 15(10):3623. https://doi.org/10.3390/en15103623
Chicago/Turabian StyleWang, Yueying, Jun Yao, and Zhaoqin Huang. 2022. "Parameter Effect Analysis of Non-Darcy Flow and a Method for Choosing a Fluid Flow Equation in Fractured Karstic Carbonate Reservoirs" Energies 15, no. 10: 3623. https://doi.org/10.3390/en15103623
APA StyleWang, Y., Yao, J., & Huang, Z. (2022). Parameter Effect Analysis of Non-Darcy Flow and a Method for Choosing a Fluid Flow Equation in Fractured Karstic Carbonate Reservoirs. Energies, 15(10), 3623. https://doi.org/10.3390/en15103623






