Multi-Stacked Superbuck Converter-Based Single-Switch Charger Integrating Cell Voltage Equalizer for Series-Connected Energy Storage Cells
Abstract
:1. Introduction
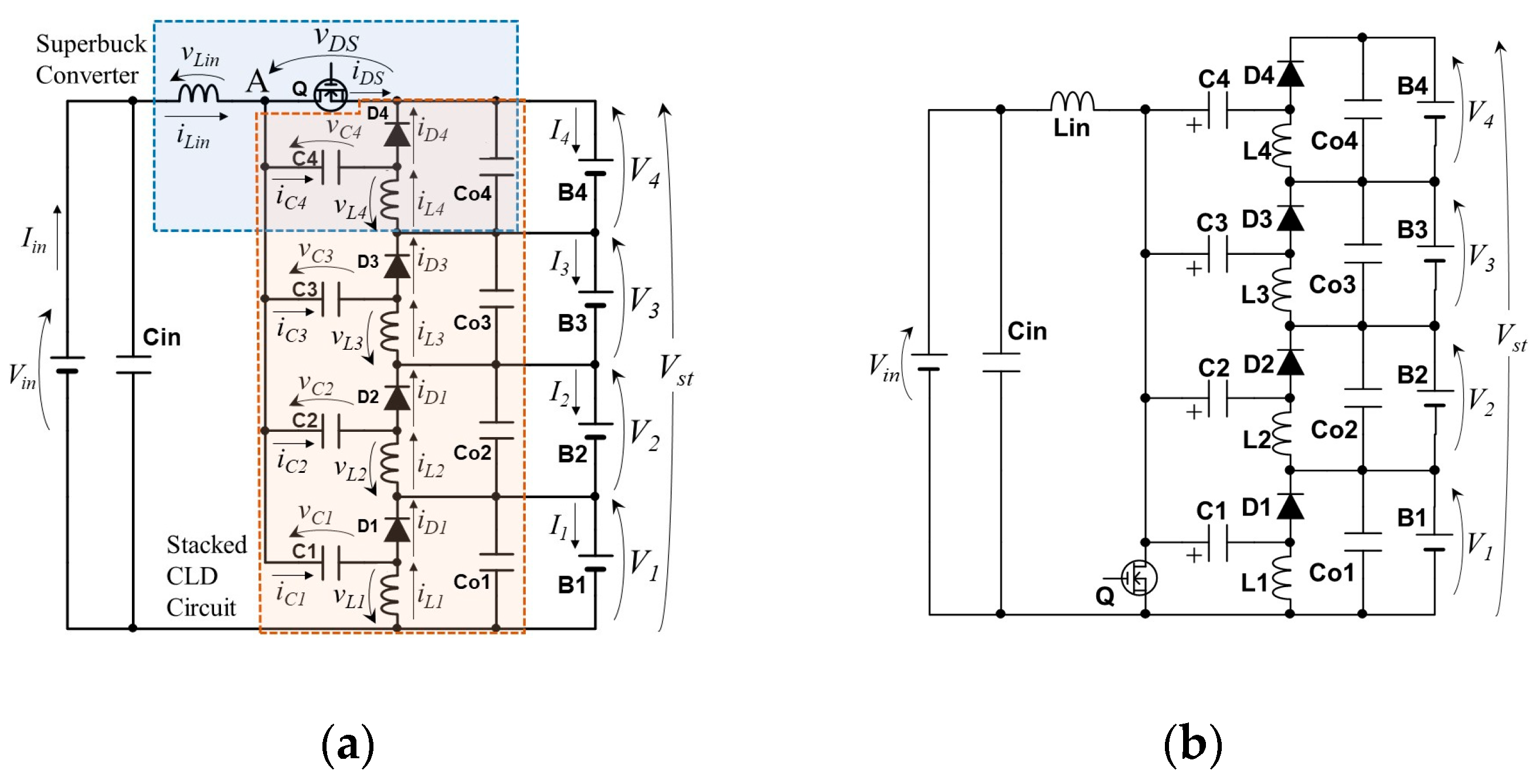
2. Proposed Integrated Chargers
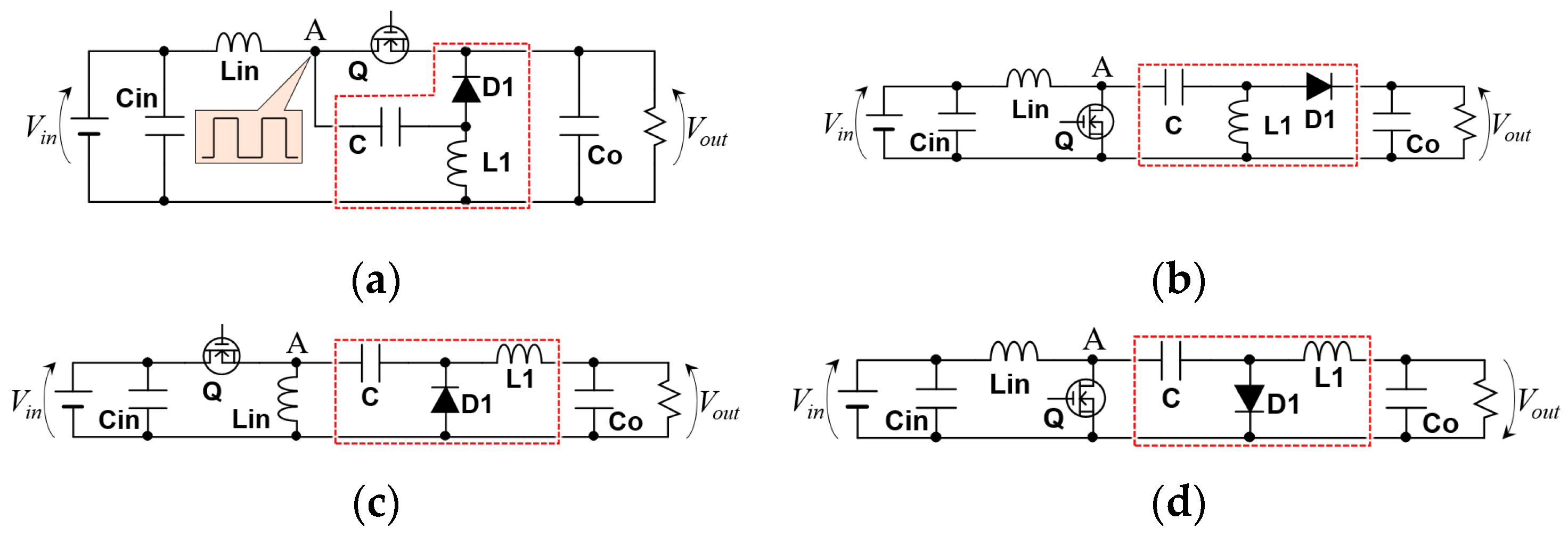
2.1. PWM Converters
2.2. Single-Switch Integrated Chargers
2.3. Benefits and Drawbacks
2.4. Comparison
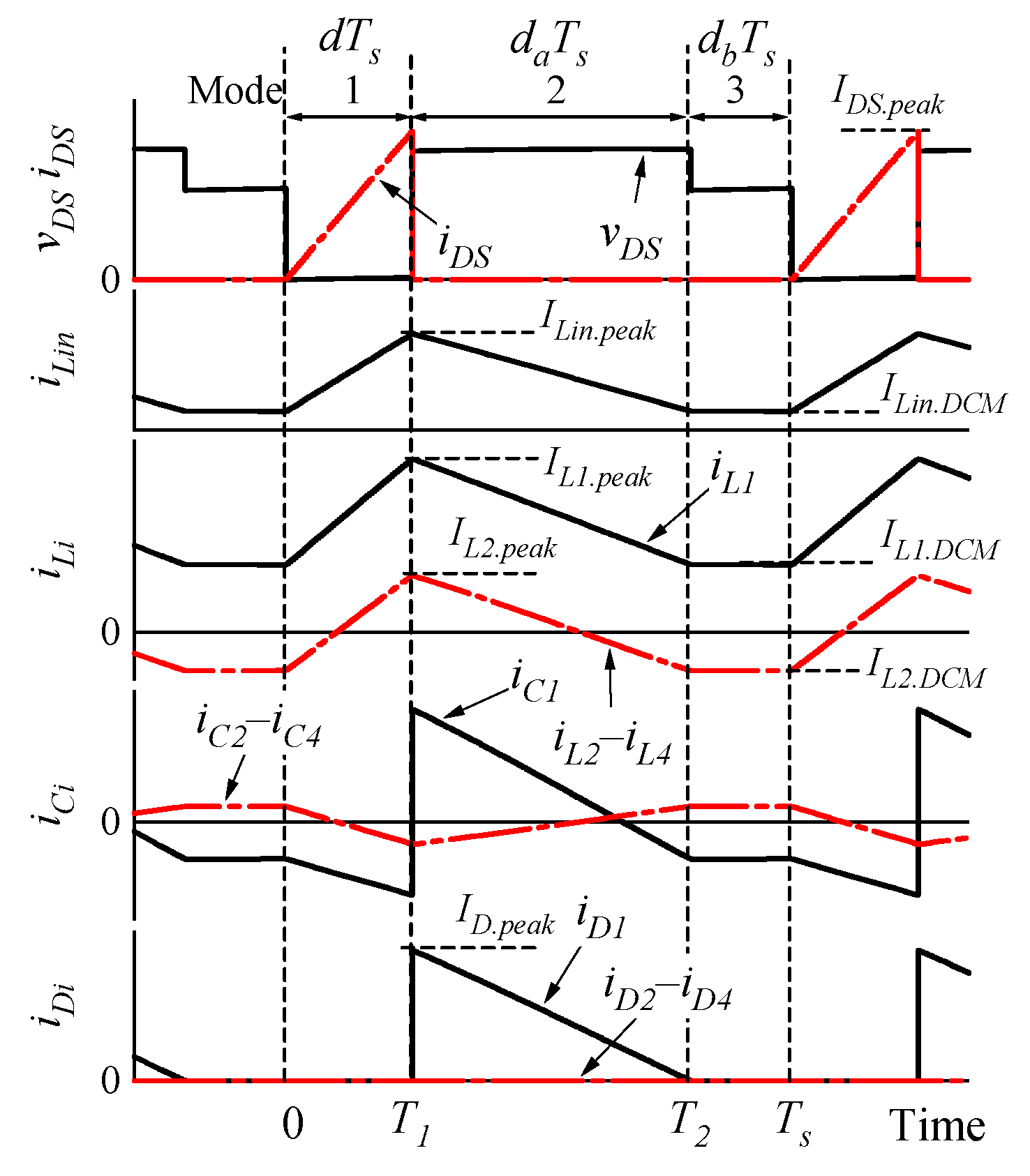
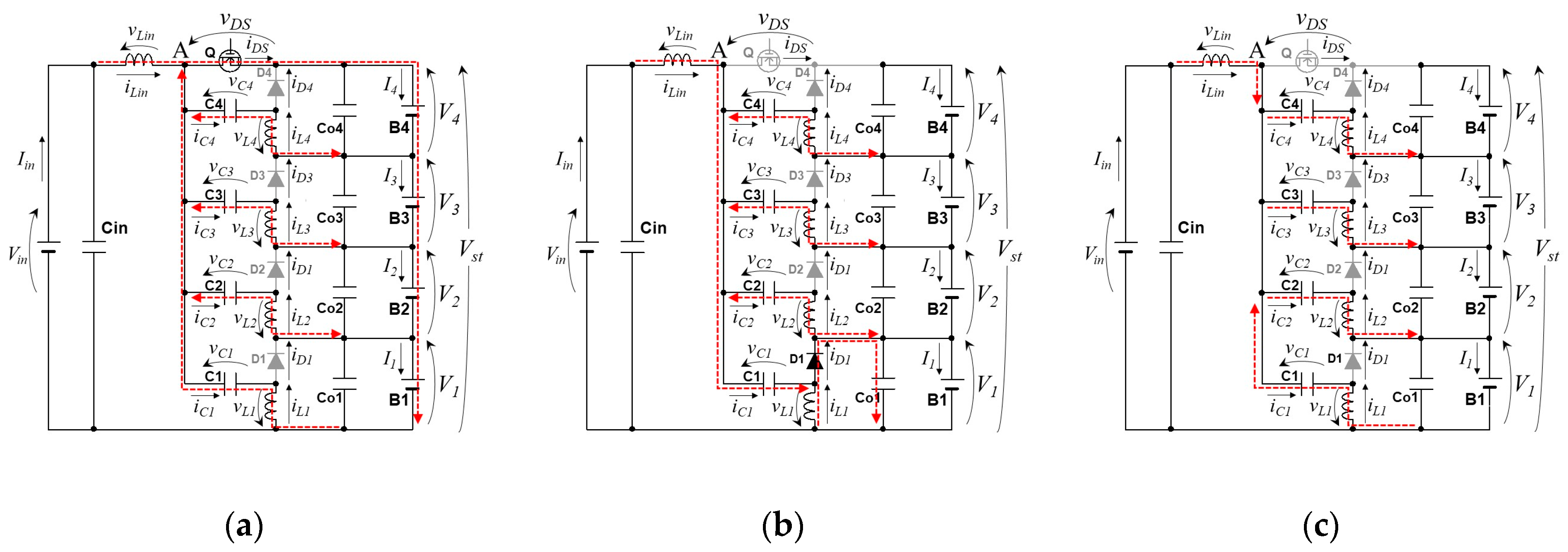
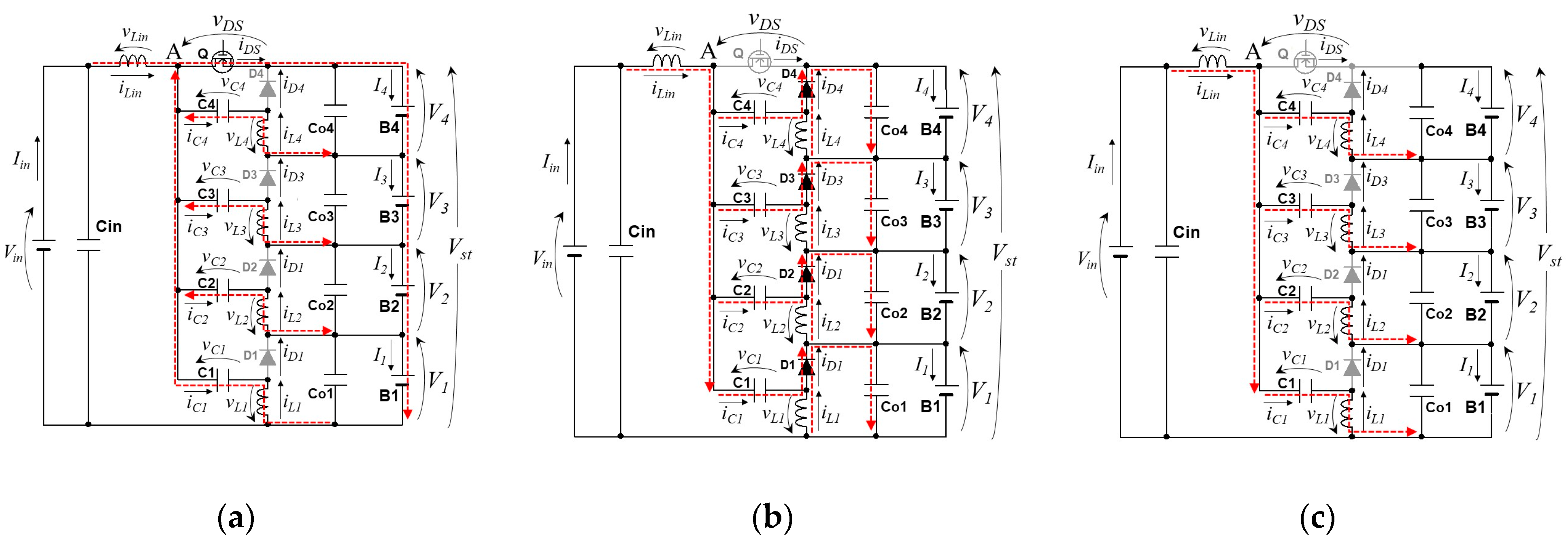
3. Operation Analysis
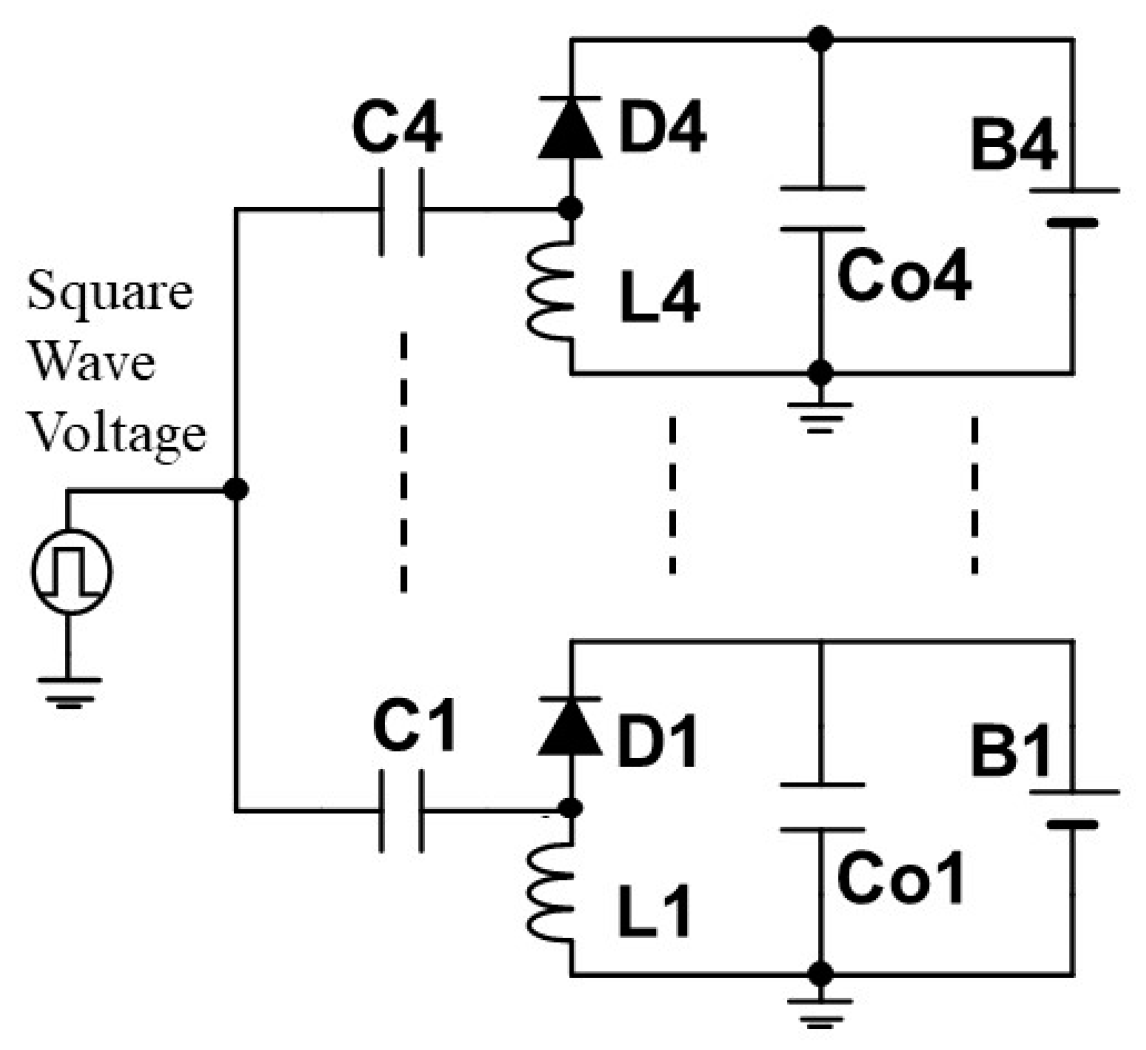
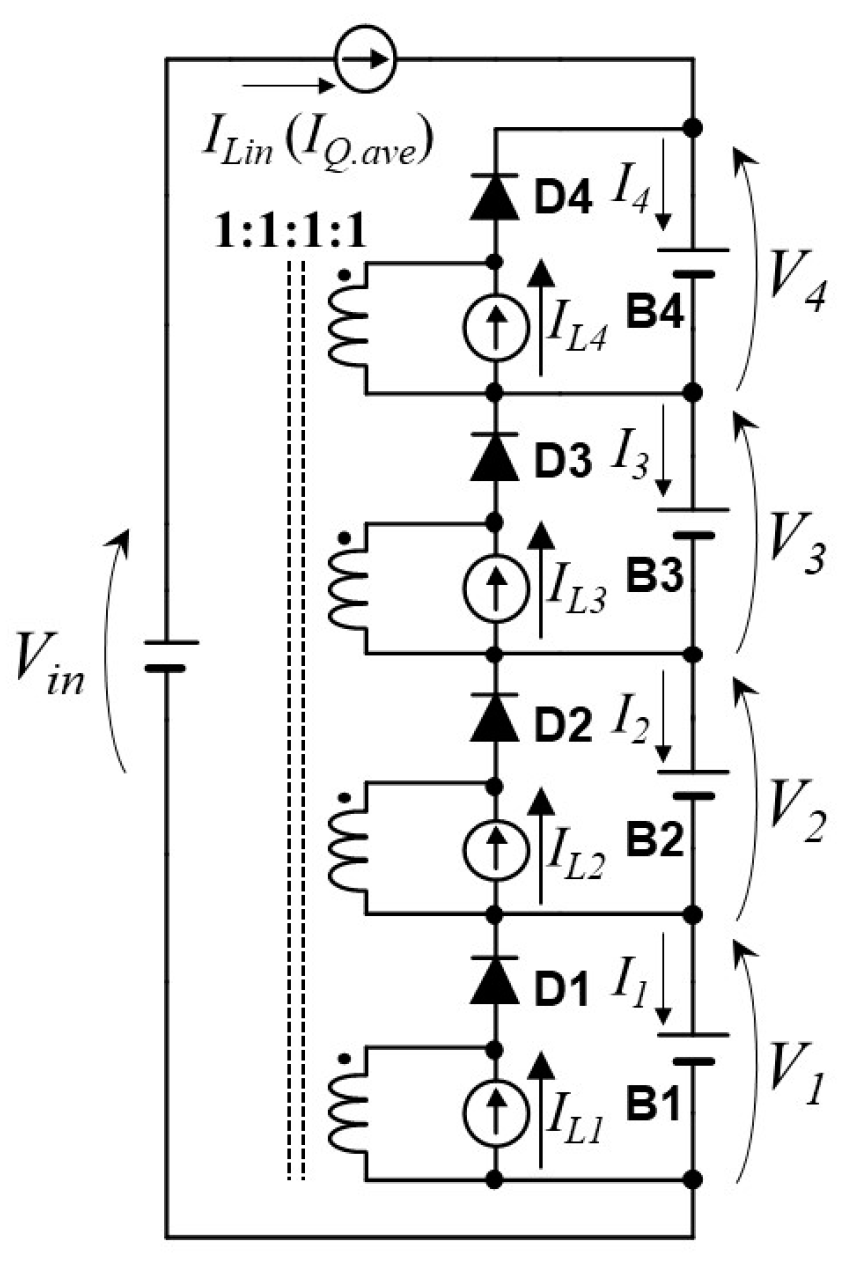
3.1. Voltage Equalization Mechanism
3.2. Operation under Voltage-Imbalanced Condition
3.3. Operation under Voltage-Balanced Condition
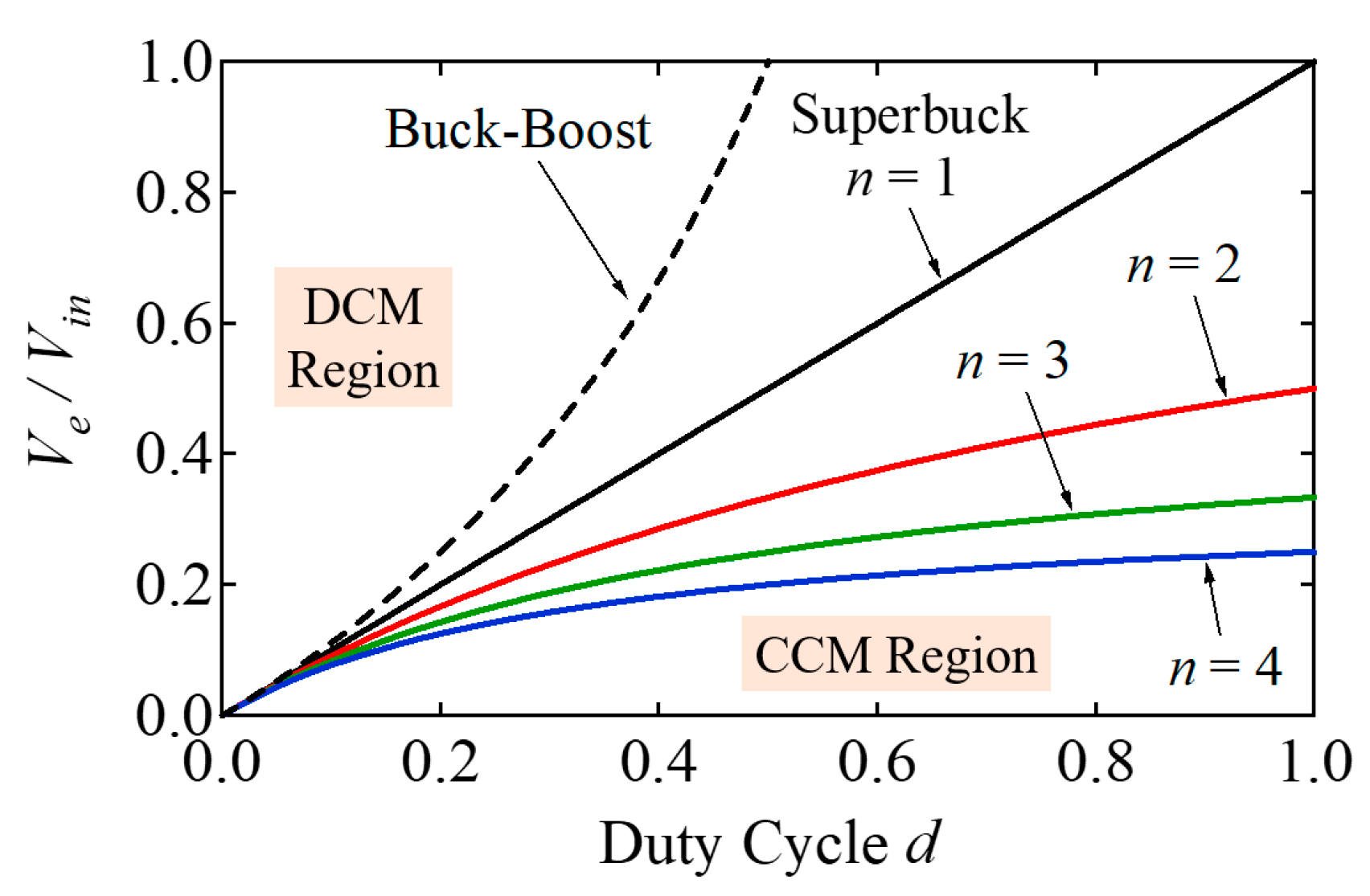
3.4. DCM Boundary
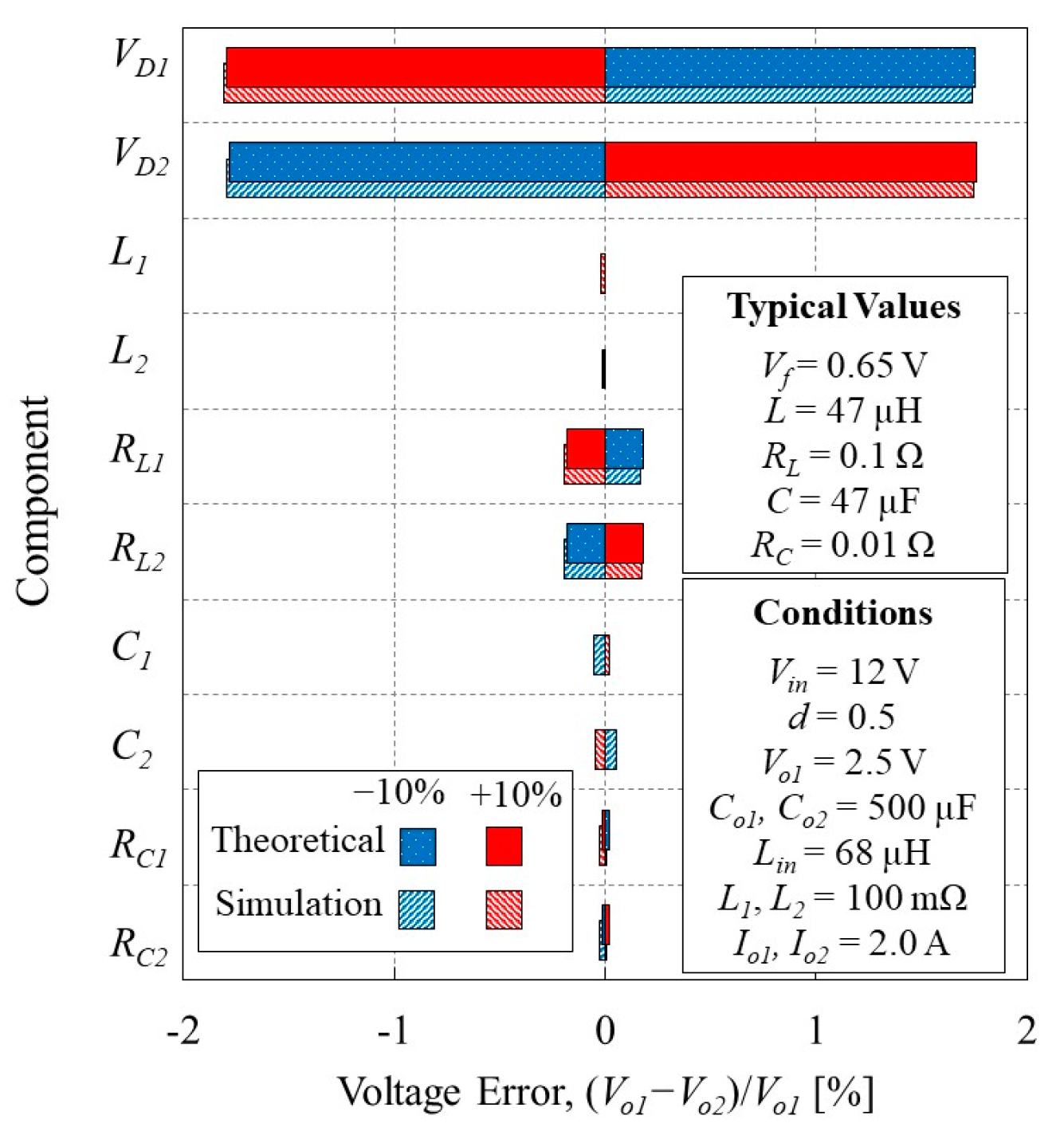
3.5. Impact of Component Tolerance on Voltage Equalization Performance
4. Design Example
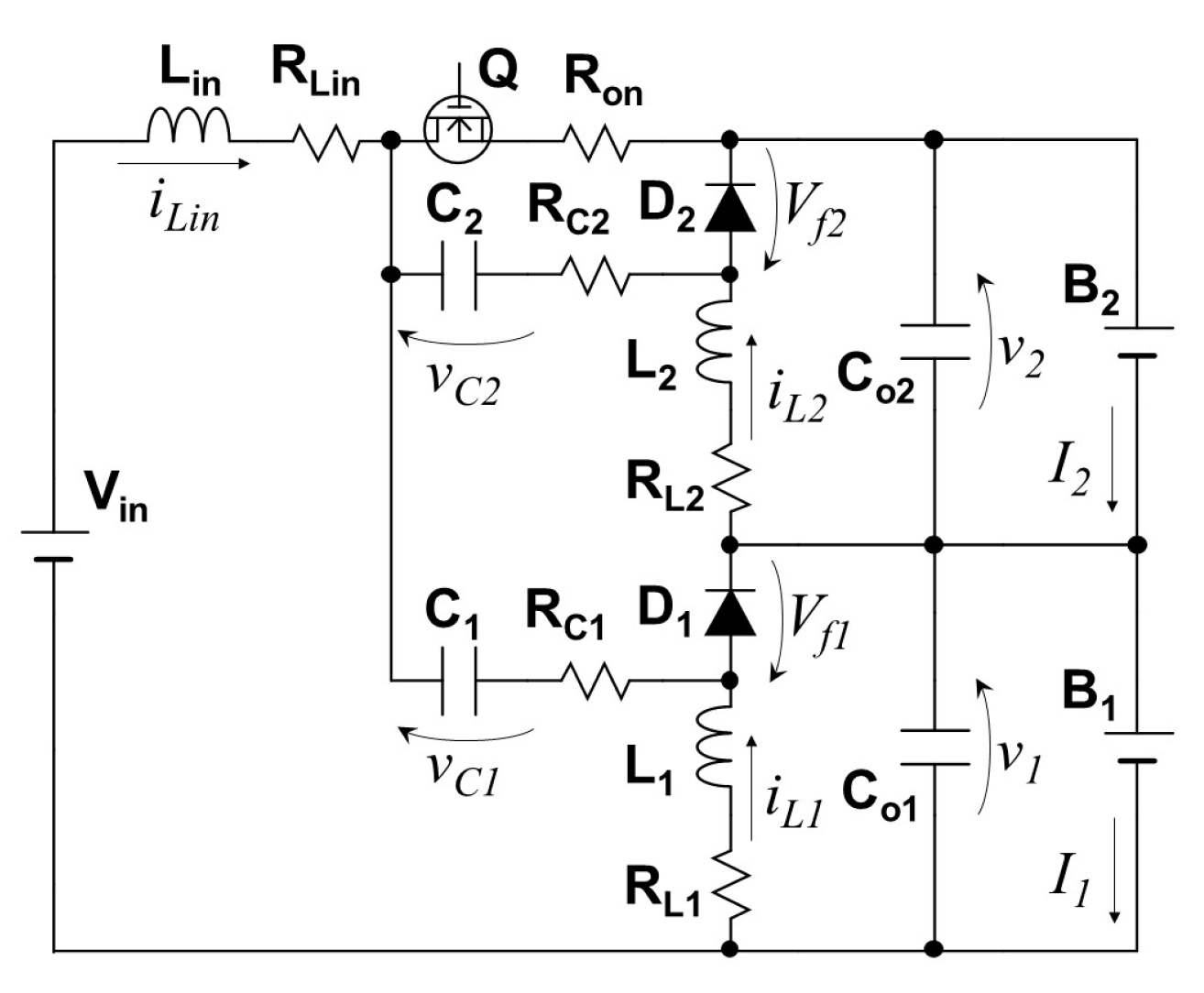
5. DC Equivalent Circuit and Its Simulation Results
5.1. Derivation of DC Equivalent Circuit
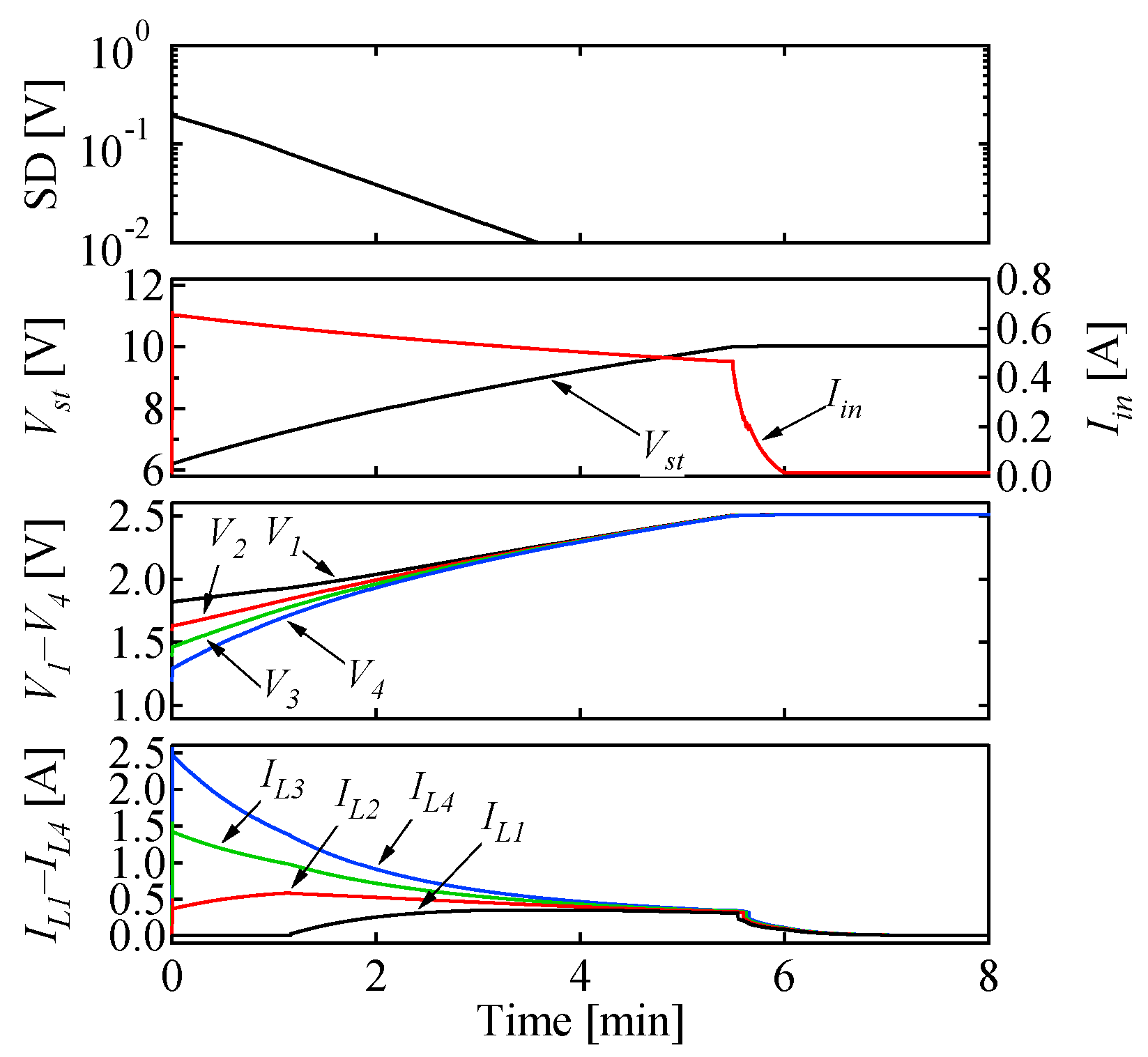
5.2. Simulation-Based Equalization
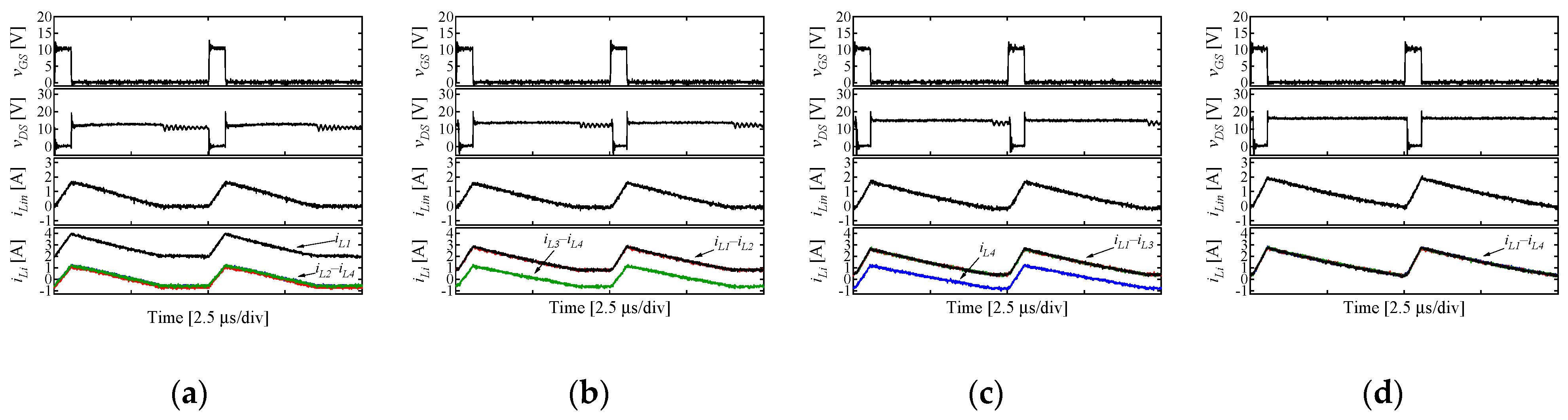
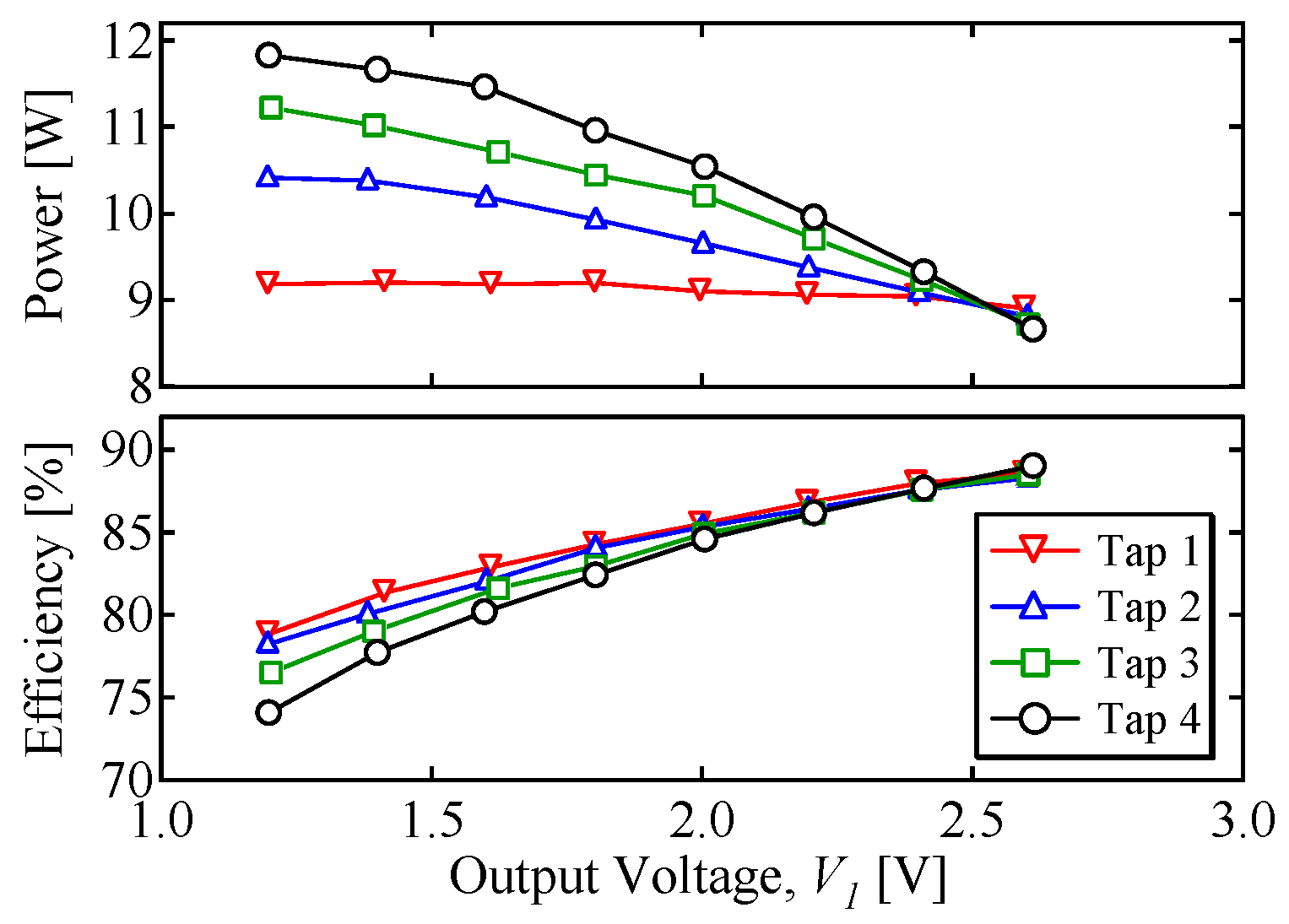
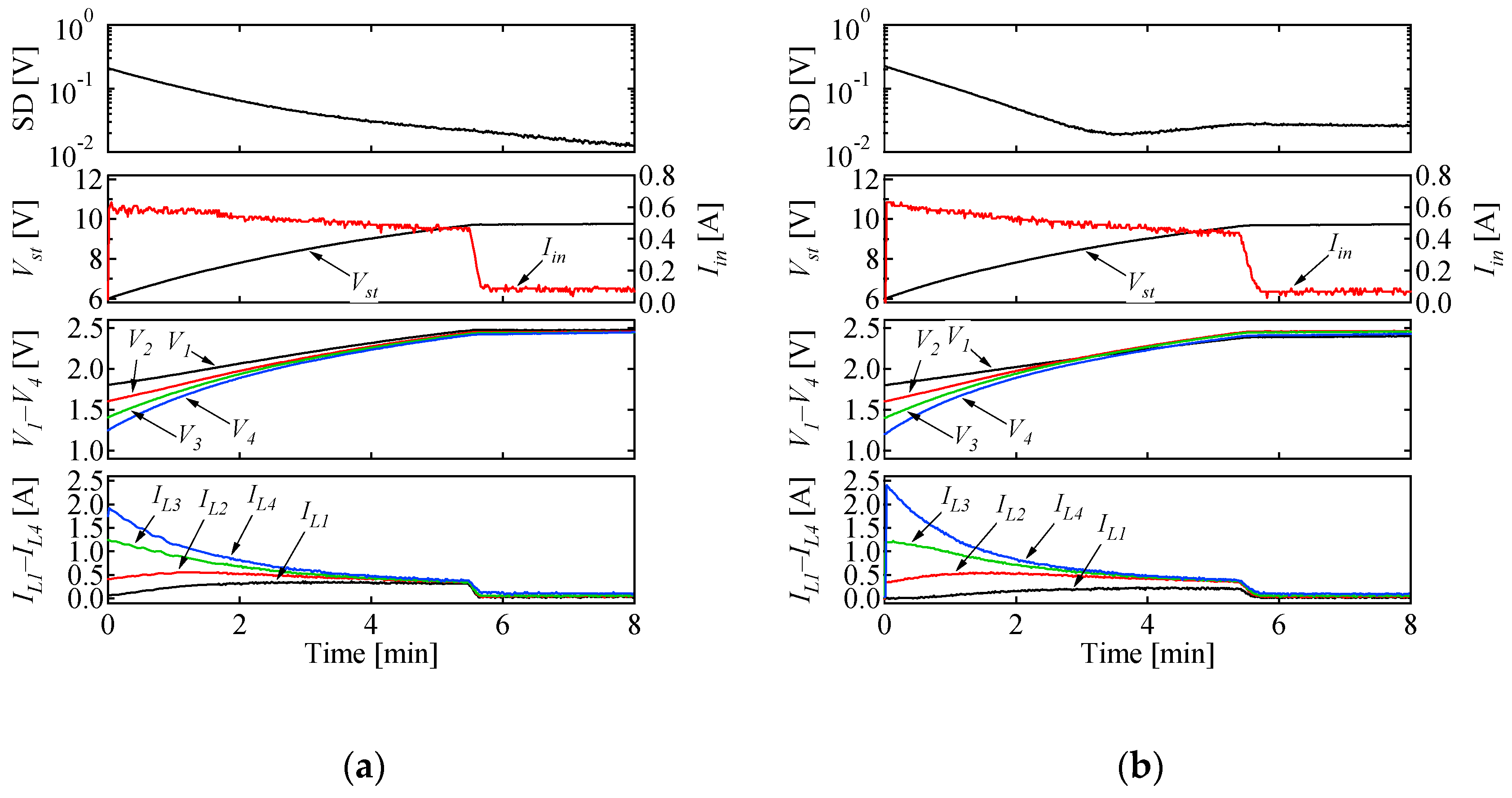
6. Experimental Results
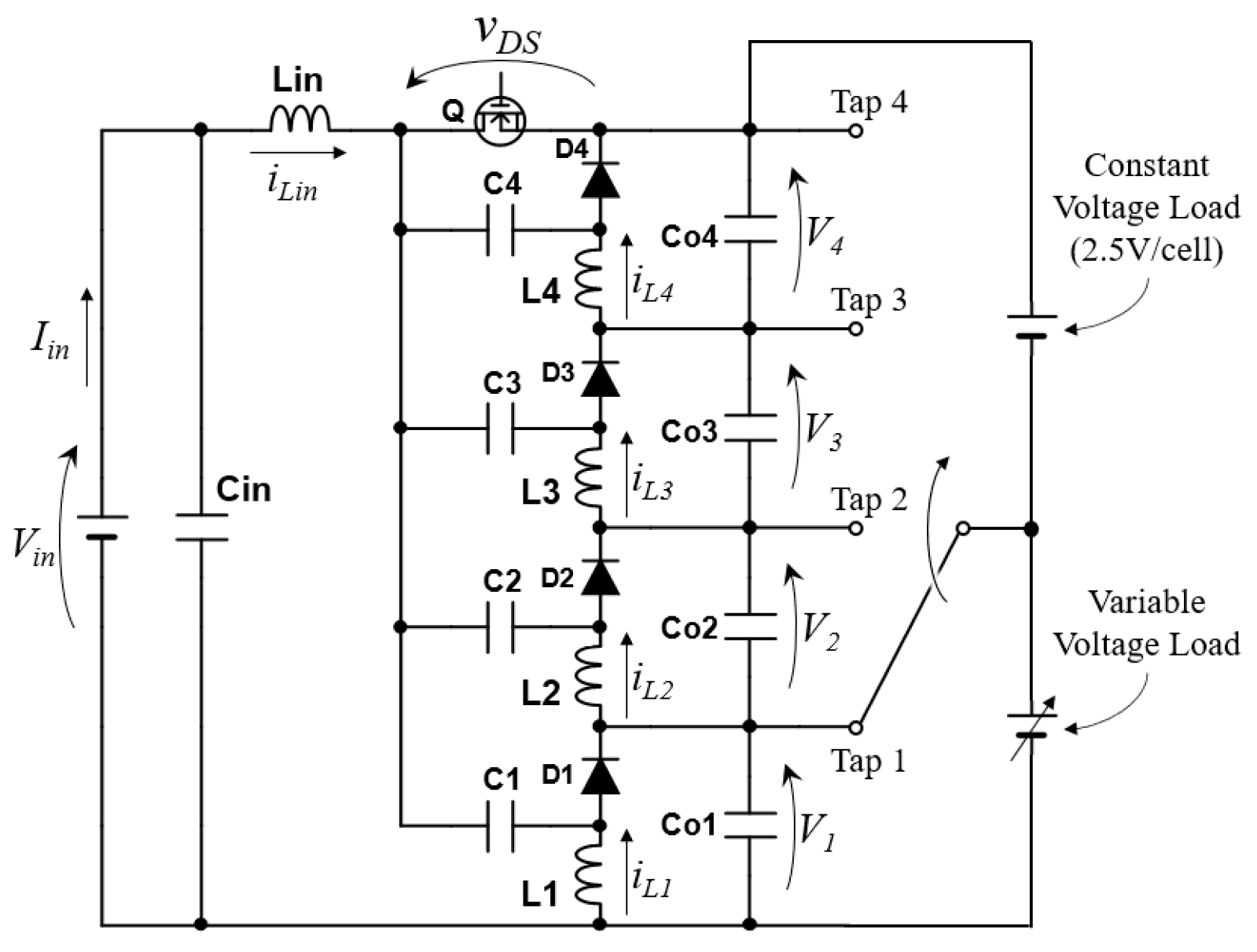
6.1. Prototype and Its Characteristics
6.2. Characteristics of Integrated Charger Alone
6.3. Charging Test for EDLCs
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kenney, B.; Darcovich, K.; MacNeil, D.D.; Davidson, I.J. Modelling the impact of variations in electrode manufacturing on lithium-ion battery modules. J. Power Sources 2012, 213, 391–401. [Google Scholar] [CrossRef]
- Zhou, L.; Zheng, Y.; Ouyang, M.; Lu, L. A study on parameter variation effects on battery packs for electric vehicles. J. Power Sources 2017, 364, 242–252. [Google Scholar] [CrossRef]
- Cassani, P.A.; Williamson, S.S. Design, testing, and validation of a simplified control scheme for a novel plug-in hybrid electric vehicle battery cell equalizer. IEEE Trans. Ind. Electron. 2010, 57, 3956–3962. [Google Scholar] [CrossRef]
- Phung, T.H.; Collet, A.; Crebier, J. An optimized topology for next-to-next balancing of series-connected lithium-ion cells. IEEE Trans. Power Electron. 2014, 29, 4603–4613. [Google Scholar] [CrossRef]
- Ewanchuk, J.; Salmon, J. A modular balancing bridge for series connected voltage sources. IEEE Trans. Power Electron. 2014, 29, 4712–4722. [Google Scholar] [CrossRef]
- Baughman, A.; Ferdowsi, M. Double-tiered switched-capacitor battery charge equalization technique. IEEE Trans. Ind. Appl. 2008, 55, 2277–2285. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Influence of high-frequency charge-discharge cycling induced by cell voltage equalizers on the life performance of lithium-ion cells. IEEE Trans. Veh. Technol. 2011, 60, 1505–1515. [Google Scholar] [CrossRef]
- Kim, M.Y.; Kim, C.H.; Kim, J.H.; Moon, G.W. A chain structure of switched capacitor for improved cell balancing speed of lithium-ion batteries. IEEE Trans. Ind. Electron. 2014, 61, 3989–3999. [Google Scholar] [CrossRef]
- Shang, Y.; Xia, B.; Lu, F.; Zhang, C.; Cui, N.; Mi, C.C. A switched-coupling-capacitor equalizer for series-connected battery strings. IEEE Trans. Power Electron. 2017, 32, 7694–7706. [Google Scholar] [CrossRef]
- Kutkut, N.H.; Divan, D.M.; Novotny, D.W. Charge equalization for series connected battery strings. IEEE Trans. Ind. Appl. 1995, 31, 562–568. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Single-switch cell voltage equalizer using multistacked buck-boost converters operating in discontinuous conduction mode for series-connected energy storage cells. IEEE Trans. Veh. Technol. 2011, 60, 3635–3645. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Double-switch single-transformer cell voltage equalizer using a half-bridge inverter and voltage multiplier for series-connected supercapacitors. IEEE Trans. Veh. Technol. 2012, 61, 3920–3930. [Google Scholar] [CrossRef]
- Uno, M.; Kukita, A. Double-switch equalizer using parallel- or series-parallel-resonant inverter and voltage multiplier for series-connected supercapacitors. IEEE Trans. Power Electron. 2014, 29, 812–828. [Google Scholar] [CrossRef]
- Arias, M.; Sebastian, J.; Hernando, M.M.; Viscarret, U.; Gil, I. Practical application of the wave-trap concept in battery–cell equalizers. IEEE Trans. Power Electron. 2015, 30, 5616–5631. [Google Scholar] [CrossRef]
- Uno, M.; Kukita, A. String-to-battery voltage equalizer based on half-bridge converter with multi-stacked current doublers for series-connected batteries. IEEE Trans. Power Electron. 2019, 34, 1286–1298. [Google Scholar] [CrossRef]
- Xu, A.; Xie, S.; Liu, X. Dynamic voltage equalization for series-connected ultracapacitors in EV/HEV applications. IEEE Trans. Veh. Technol. 2009, 58, 3981–3987. [Google Scholar]
- Kim, C.H.; Kim, M.Y.; Park, H.S.; Moon, G.W. A modularized two-stage charge equalizer with cell selection switches for series-connected lithium-ion battery string in a HEV. IEEE Trans. Power Electron. 2012, 27, 3764–3774. [Google Scholar] [CrossRef]
- Kim, C.H.; Kim, M.Y.; Moon, G.W. A modularized charge equalizer using a battery monitoring IC for series-connected Li-ion battery strings in electric vehicles. IEEE Trans. Power Electron. 2013, 28, 3779–3787. [Google Scholar] [CrossRef]
- Lee, K.M.; Lee, S.W.; Choi, Y.G.; Kang, B. Active balancing of Li-ion battery cells using transformer as energy carrier. IEEE Trans. Ind. Electron. 2017, 64, 1251–1257. [Google Scholar] [CrossRef]
- Lee, S.W.; Lee, K.M.; Choi, Y.G.; Kang, B. Modularized design of active charge equalizer for Li-ion battery pack. IEEE Trans. Power Electron. 2018, 65, 8697–8706. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, Q.; Cui, N.; Duan, B.; Zhou, Z.; Zhang, C. Multi-cell-to-multi-cell equalizers based on matrix and half-bridge LC converters for series-connected battery strings. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1755–1766. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, C.; Cui, N.; Guerrero, J.M. A cell-to-cell battery equalizer with zero-current switching and zero-voltage gap based on quasi-resonant LC converter and boost converter. IEEE Trans. Power Electron. 2015, 30, 3731–3747. [Google Scholar] [CrossRef] [Green Version]
- Uno, M.; Yoshino, K. Modular equalization system using dual phase-shift-controlled capacitively isolated dual active bridge converters to equalize cells and modules in series-connected lithium-ion batteries. IEEE Trans. Power Electron. 2021, 36, 2983–2995. [Google Scholar] [CrossRef]
- Kutkut, N.H.; Wiegman, H.L.N.; Divan, D.M.; Novotny, D.W. Charge equalization for an electric vehicle battery system. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 235–246. [Google Scholar] [CrossRef]
- Kutkut, N.H.; Wiegman, H.L.N.; Divan, D.M.; Novotny, D.W. Design considerations for charge equalization of an electric vehicle battery system. IEEE Trans. Ind. Appl. 1999, 35, 28–35. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, Y.H.; Liang, T.J.; Chen, S.M.; Horng, W.Y.; Chung, Y.Y. A novel high-efficiency compact-size low-cost balancing method for series connected battery applications. IEEE Trans. Power Electron. 2013, 28, 5927–5939. [Google Scholar] [CrossRef]
- Uno, M.; Kukita, A. Bidirectional PWM converter integrating cell voltage equalizer using series-resonant voltage multiplier for series-connected energy storage cells. IEEE Trans. Power Electron. 2015, 30, 3077–3090. [Google Scholar] [CrossRef]
- Uno, M.; Yashiro, K. Tapped-inductor-based single-magnetic bidirectional PWM converter integrating cell voltage equalizer for series-connected supercapacitors. IEEE Trans. Power Electron. 2020, 35, 13157–13171. [Google Scholar] [CrossRef]




| Topology | DCM Boundary | Current Ripple | Voltage Stress of Q and D | Capacitor Voltage VCk (k = 1…n) | |
|---|---|---|---|---|---|
| Input | Output | ||||
| Superbuck | Low | Low | |||
| SEPIC | Low | High | |||
| Zeta | High | Low | |||
| Ćuk | Low | Low | |||
| Component | Value, Part Number |
|---|---|
| Q | N-Ch MOSFET, ZXMN4A06GTA, Ron = 75 mΩ |
| Lin, L1–L4 | 10 µH, 33 mΩ |
| Cin | Aluminum Electrolytic Capacitor, 330 µF |
| C1–C4 | Ceramic Capacitor, 36 µF |
| D1–D4 | Schottky Barrier Diode, SL44, Vf = 0.35 V |
| Co1–Co4 | Ceramic Capacitor, 300 µF |
| Gate Driver | L6741 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uno, M.; Xu, Q.; Sato, Y. Multi-Stacked Superbuck Converter-Based Single-Switch Charger Integrating Cell Voltage Equalizer for Series-Connected Energy Storage Cells. Energies 2022, 15, 3619. https://doi.org/10.3390/en15103619
Uno M, Xu Q, Sato Y. Multi-Stacked Superbuck Converter-Based Single-Switch Charger Integrating Cell Voltage Equalizer for Series-Connected Energy Storage Cells. Energies. 2022; 15(10):3619. https://doi.org/10.3390/en15103619
Chicago/Turabian StyleUno, Masatoshi, Qi Xu, and Yusuke Sato. 2022. "Multi-Stacked Superbuck Converter-Based Single-Switch Charger Integrating Cell Voltage Equalizer for Series-Connected Energy Storage Cells" Energies 15, no. 10: 3619. https://doi.org/10.3390/en15103619
APA StyleUno, M., Xu, Q., & Sato, Y. (2022). Multi-Stacked Superbuck Converter-Based Single-Switch Charger Integrating Cell Voltage Equalizer for Series-Connected Energy Storage Cells. Energies, 15(10), 3619. https://doi.org/10.3390/en15103619






