1. Introduction
Assessing the performance of a geologic repository for the disposal of radioactive waste is a complex undertaking. The system to be examined consists of various natural features that interact with engineered components. A multitude of coupled physical, chemical, biological, and thermal processes must be considered, as they potentially affect the release of radionuclides from the waste canisters, and their transport through the engineered barrier system and the geosphere to the accessible environment. Safety-relevant features and processes extend over a wide range of spatial scales—from molecular to site to regional scales. Moreover, they include short-term events as well as processes that evolve over geologic times. Due to this expansive range of spatial and temporal scales and the fact that the repository is to be built in the deep subsurface with ideally minimal perturbation of the site, many of the properties cannot be measured with high resolution.
Numerical modeling is an essential tool in our efforts to understand the evolution of the disposal system and the risk it might pose to humans and the environment. A site-specific model—based on established physical principles as well as relevant site characterization data—provides insights into the interactions among the many linked components and coupled processes and their impact on repository behavior. It also allows one to calculate variables that cannot be directly observed, to forecast the evolution of the repository system, and to examine alternative or unlikely scenarios. It is understood that simulation results and inferred statements about exposure risks (or any other performance metric) are inherently uncertain; this uncertainty must be appropriately managed and communicated to decision makers, stakeholders, and the public.
Acknowledging the uncertainty in any estimation of repository performance naturally leads to the question as to whether there is a sufficient basis for our confidence in the model results, and what evidence needs to be presented to support the assertion that a specific model can be relied upon for making important design, engineering, or public policy decisions. To address this question, such a model should undergo a formal process referred to as “model validation.” Other terms used in this context include “verify”, “validate”, “corroborate”, “confirm” and expression such as “confidence building”. These terms are often put in quotes to indicate that they are not meant in their literal sense, as they imply that the model makes a definite statement about the absolute truth of a physical system. We omit the quotes as it is the intent of this discussion to clarify the meaning and limits of these terms when describing the quality of a model used in performance assessment studies (We concur with authors who state that the term “validation” could be misleading and should be replaced with a more neutral term, such as “evaluation.” However, while “model evaluation” may be preferable, existing literature and guidelines for modeling practitioners have almost exclusively used the term “validation.” We therefore continue using this established term, also to indicate that the concept of “pragmatic model validation” developed in this article attempts to address the validation issue as currently discussed in the context of nuclear waste isolation).
A frequently cited definition of model validation is the one provided by the International Atomic Energy Agency (IAEA) [
1]:
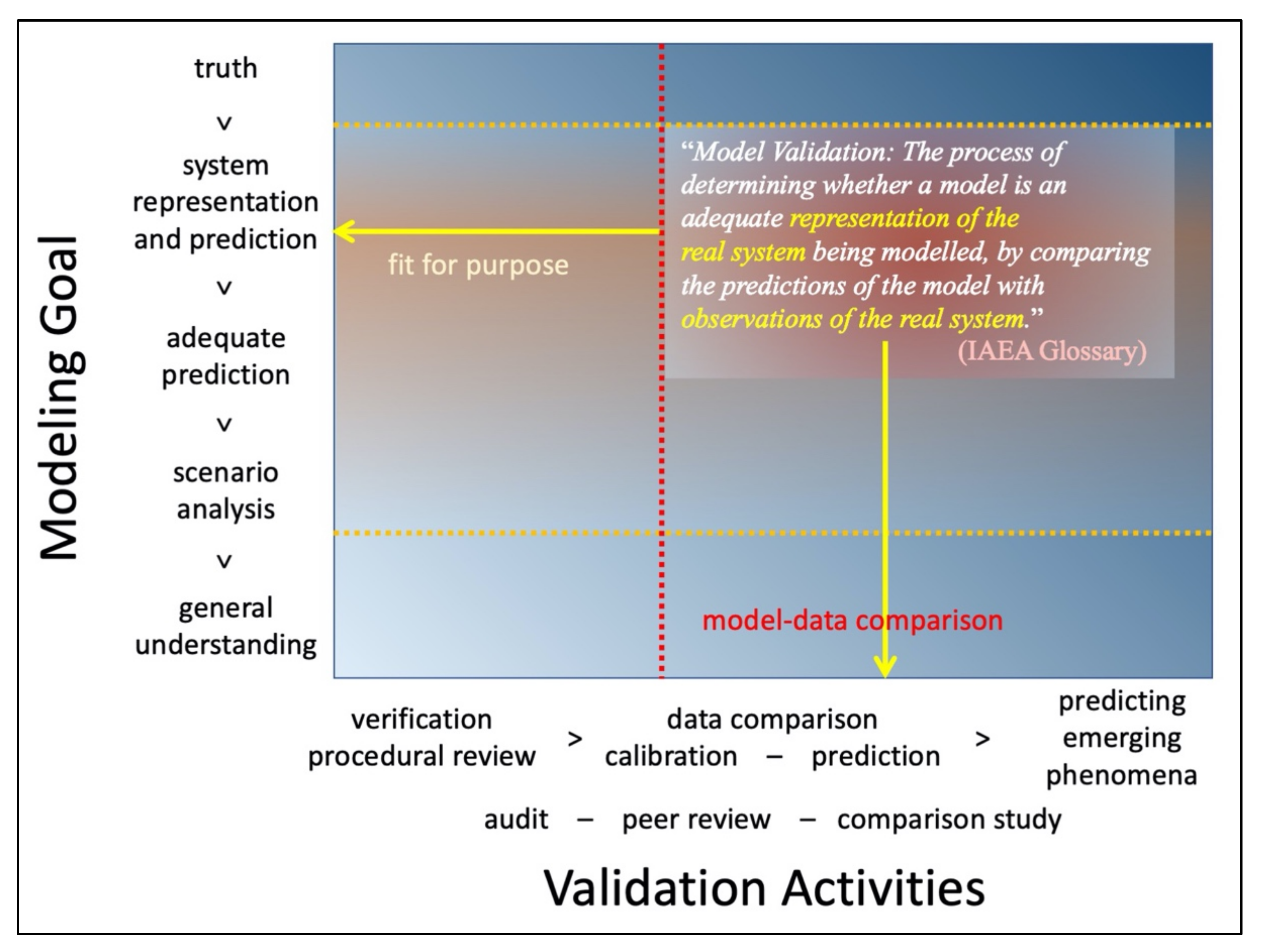
“Model Validation: The process of determining whether a model is an adequate representation of the real system being modelled, by comparing the predictions of the model with observations of the real system.” This definition not only declares what the main purpose of model validation is, but also explicitly states what approach should be used. Other definitions of validation are quite consistent in the key elements they contain, including: (a) the relation between the model and the real system; (b) the need for a comparison between model predictions and measured data; (c) the model’s limited domain of applicability; and (d) the importance of uncertainty quantification. Some definitions emphasize one aspect over the other, or are more or less prescriptive about the evidence that needs to be presented to satisfy validation acceptance criteria.
This article presents our perspective on the practicality of model validation in the context of quantitative assessments used for decision support in the highly regulated environment of radioactive waste management. We start with a short review of the philosophical roots of the discussion and some critical commentary (
Section 2). We then highlight the necessity for careful model evaluation (
Section 3) and outline the concept of “pragmatic model validation” (
Section 4). We provide a list of elements that could be applied as part of this pragmatic validation approach (
Section 5), before we summarize and conclude (
Section 6).
2. Criticism of Verifiability and Model Validation
The philosophical discourse about the fundamental (im)possibility of establishing the truth of any proposition, specifically one made about a physical system, has a long history which continues today. In the philosophy of science, the question of how the truth of a scientific statement, hypothesis, or theory can be verified has been expanded to the more fundamental question of whether such verification is possible even in principle. Some argue that, at best, a theory (or model) can only retain the status of being “not invalid”. The concept of falsifiability, proposed by Popper [
2], suggests that for a theory to be considered scientific, one must be able to test it in such a way that it could be demonstrated to be false. Falsifiability is not only formulated as an explicit opposite to verifiability, but also as a criterion for demarcation between science and non-science, and as a methodological guiding rule for research. While it is generally accepted that theories cannot be verified, falsifiability has also been questioned. In essence, taking the discrepancy between an observation and a prediction as a sufficient criterion to falsify a theory (or a model) can be misleading, as any observation is itself laden with auxiliary hypotheses.
Kuhn [
3] argued that experiments and observations are determined by the prevailing paradigm, and—conversely—the discrepancy between observational data and a prediction do not necessarily refute the underlying theory, as competing theories could be inherently incommensurable. Consequently, scientific truth cannot be established by objective criteria, but is determined by scientific consensus, which may change rather abruptly during a paradigm shift. Kuhn [
4] also proposes to examine the following five characteristics as criteria for theory choice, noting that the evaluation of these criteria remains subjective: a theory should be (1) accurate, i.e., empirically coherent with observations; (2) consistent, both internally and externally with other theories; (3) of broad scope, extending beyond what it was initially designed to explain; (4) the simplest explanation (“Occam’s razor”); and (5) fruitful in that it discloses new phenomena or relationships among phenomena.
The debate over the verifiability or falsifiability of theories ranges from thought-provoking to contentious; it is beyond the scope of this commentary to summarize this debate or to take a position, other than acknowledging that attempts at validating a numerical model will most likely face fundamental difficulties similar to those encountered by scientific theories. The similarities and differences between theories and models are discussed in the influential article by Oreskes et al. (1994) [
5], who examine the issue of verification, validation, and confirmation in the context of numerical models in the earth sciences—with frequent references to validation efforts for models developed to assess the safety of a repository for radioactive wastes.
Oreskes et al. (1994) [
5] reach the conclusion that “
Verification and validation of numerical models of natural systems is impossible.” They arrive at this statement by observing that all natural systems are open, with distributed input parameters that are incompletely known or conceptually inconsistent with the definition and scale on which they might be directly measured or inferred using auxiliary hypotheses, models, and assumptions. Even if not aiming for a statement that establishes truth (as the term verification implies), the legitimacy of an application-specific model cannot be established, either. Validating a numerical model by comparison of its predictions with observations only indicates consistency but does not ensure that the model represents the natural phenomena [
6]. While calibrating a numerical model may signify that it is empirically adequate, reproducing past observational data does not guarantee model performance when predicting the future, as any extrapolation requires a change in the model structure, which in turn affects processes, temporal and spatial scales, the influence of input parameters, and sensitivities of output variables. Even if data not used for model calibration are reasonably well reproduced, the model cannot be considered validated. This is referred to as the fallacy of “affirming the consequent,” in which a necessary condition—matching the data—is mistaken as being a sufficient condition—confirming the veracity of the model. While attaining empirical consistency between the model-calculated and measured data may increase the confidence in the model, it does not confirm that a particular model captures the natural world it seeks to represent. Such confirmation is always partial, i.e., it only supports the probability of the model’s utility relative to alternative models proposed to gain insights or make predictions.
Oreskes et al. (1994) [
5] consider this terminology—verification, validation, and confirmation—potentially misleading, specifically when used to indicate that the results of a numerical model are reliable enough to support important public policy decisions. They acknowledge that models may be useful to corroborate a hypothesis, to reveal discrepancies in other models, to perform sensitivity analyses, and to guide further studies. They conclude that models should be used to challenge existing formulations, rather than to validate or verify their ability to make predictions about a physical system.
Another criticism comes from a direct comparison—as part of a post audit—of relevant observations with predictions made by “validated” models that were developed specifically to make these predictions. For example, in a series of articles [
7,
8,
9,
10,
11], Bredehoeft and Konikow found that a significant fraction of models made poor predictions due to conceptual modeling errors. In these cases, new data revealed that the prevailing conceptual model was invalid, i.e., the models did not just require minor adjustments of input parameters, but a fundamental change in key aspects of how they represent the natural system. They specifically discuss “hydrologic surprises” that rendered an initial conceptual model of a proposed waste disposal site invalid [
11]. Note that some of these arguments have been rebutted [
12,
13,
14].
Using alternative models may reveal the impact of such conceptual model uncertainties. For example, Selroos et al. [
15] examined the uncertainties of models that predict groundwater flow and radionuclide transport from the waste canisters to the biosphere, where the fractured crystalline host rock is simulated using alternative modeling methods, such as stochastic continuum, discrete fracture network, and channel network approaches. The three modeling approaches yielded differences in variability, but overall similar travel times, release fluxes, and other performance metrics. They noted that the impact of conceptual uncertainty may be underestimated, as a common reference case was provided to the participants of this study, potentially constraining the flow modeling.
Similarly, based on a consistent set of characterization data, multiple alternative conceptual models of fracture flow and bentonite hydration were developed as part of Task 8 of the SKB Task Force. Not only did the predicted times for complete bentonite hydration vary over a relatively wide range, the modeling teams also developed different views regarding the key factors affecting the overall system behavior and, consequently, made different recommendations about research and site characterization needs [
16].
Differences or inconsistencies between reality and its representation in a numerical model are inherent in the modeling process and thus unavoidable. Any model is an abstraction of the real system, which implies that it is based on conceptual decisions, the choice of simplifying assumptions and the selection of input parameters with different levels of uncertainty. Whether the errors introduced by such simplifications and deficiencies can be considered acceptable depends fundamentally on the intended purpose of the model. This is the reason why conceptualization is the key step in model development and also the main target of a critical model validation effort.
As illustrated in this short summary, the mere possibility of model validation is being questioned based on philosophical, historical, and practical considerations. While the details of these arguments depend on the definition of the term “validation” and the claims ascribed to a “validated model”, the various critics arrive at similar conclusions and recommendations:
It is fundamentally impossible to confirm that a site-specific model properly represents the natural system [
5,
6,
7,
17,
18,
19];
Models should not be used for predictive purposes, unless the prediction domain is commensurable with the calibration domain; however, models are useful to challenge the conceptual understanding, examine assumptions, explore what-if scenarios, and perform sensitivity analyses [
5,
7,
20,
21,
22];
The term “validation” and similar terms should not be used, as they give a misleading impression of predictive model capabilities [
5,
7,
9,
19,
20,
23].
Despite the fundamental challenges and criticisms summarized above, there is an obvious mandate to carefully define approaches for the development and evaluation of numerical models, and to build confidence in performance predictions that are used for decision support. Heeding the cautionary remarks by its critics, we attempt to develop a pragmatic approach to model validation.
3. The Need for Model Evaluation
3.1. The Nature of Models
A model is a purposeful, simplified representation of the real disposal system. During the development of the conceptual model, each aspect of the system is suitably abstracted in an iterative process, accounting for each factor’s impact on repository performance, and the degree to which it can be supported by theory or site-specific data.
For site-specific simulations, it is essential to achieve an appropriate level of model complexity, which is a trade-off between the complexity of the real system as far as it can be observed or inferred, and the need to be commensurate with the requirements for the model. A model can be oversimplified or overly complex (i.e., overparameterized). An oversimplified model fails to capture the salient features of the system to be modeled, which likely leads to systematically wrong or overconfident predictions. Conversely, while an overparameterized model is fundamentally able to better fit the data (at the risk of overfitting), it results in highly correlated, highly uncertain parameter estimates that lead to model predictions that are also highly uncertain and unreliable [
24]. While sensitivity analyses can help assess the appropriate level of complexity, they obviously cannot identify potentially relevant features or processes that are not implemented in an oversimplified model, and they cannot readily examine parameter correlations and their impact on estimation and prediction uncertainties as they emerge in an overparameterized model. While modelers typically start with a simple model, then add complexity as new insights or data become available, one might argue that the appropriate model complexity is best approached by starting with a relatively rich, complex model—at least on the conceptual level—and then using a screening process or notional inversions with sub-space methods to screen out irrelevant or unsupported model components to arrive at a simpler model [
25,
26,
27].
Hydrogeological process models are typically based on well-established empirical laws. Moreover, the physical and conceptual boundaries, within which the given laws can be considered acceptable for practical purposes, are relatively well understood. These laws and their interactions with each other are described by a mathematical model and implemented using an appropriate numerical scheme into a computer code. Testing the correct implementation of the mathematical model into a software package is often referred to as “verification.” In addition, convergence studies are typically performed to confirm that the chosen space and time discretizations have sufficient resolution, and that all computational parameters are properly set to arrive at a solution that is accurate. For the remainder of this discussion, we assume that the code has been properly verified, and that the simulation results do not suffer from unacceptable numerical artifacts.
3.2. Calibration
A mathematical model typically consists of a set of coupled partial differential equations. These governing equations contain coefficients that emerge as the empirical laws are derived or upscaled from more fundamental descriptions of physical or chemical processes. New parameters may appear as the support scale is increased. These new parameters reflect a property that does not exist on the smaller scale, and smaller-scale properties may disappear as they are lumped into new parameters. By further increasing the scale, the value of the parameter may change, resulting in scale-dependent parameters. This is specifically true in highly heterogeneous systems, which cannot be described deterministically, but only statistically. Unless ergodicity prevails and heterogeneity can be appropriately characterized, spatial variability may significantly contribute to estimation and prediction uncertainties.
The coefficients of the mathematical model are often unknown, uncertain, problem- and site-specific input parameters to the simulator. They reflect material properties, but also geometrical aspects or initial and boundary conditions.
Despite the use of physics-based laws, hydrogeological models include a large collection of “auxiliary hypotheses,” many of which are untested or even impossible to confirm. This problem is acknowledged (and partly mitigated) by the fact that the parameters of site-specific hydrogeological models are adjusted and determined by calibrating the model against observational data. Many concepts, methods, and algorithms have been developed to calibrate a parsimonious or high-dimensional model to observed data (for a review of inverse approaches in hydrogeology, see [
28,
29,
30,
31,
32,
33,
34]). The parameters estimated by inverse modeling are inherently uncertain, but—more importantly—may be ambiguous or biased for the following reasons:
The mathematical model and/or auxiliary hypotheses are incomplete or are poor representations of the system to be modeled;
There is a discrepancy in the definition, state, location, or scale of the calculated model output variable and the corresponding observation used for model calibration;
Measured data have an error component that is systematic;
The model output has an error component that is systematic; systematic errors include errors in the conceptual model, (over)simplifications in the model structure (processes and features), model truncation errors, reduction in model dimensionality, symmetry assumptions, errors in initial and boundary conditions, etc.;
Data sets are incomplete, and the inverse problem is either underdetermined or regularized using an artificial or erroneous regularization term;
The data are not sufficiently informative about the parameters of interest, or the available data are not discriminative enough to sufficiently reduce correlations among the parameters;
Alternative conceptual models exist that are equally capable of reproducing the calibration data.
It is important to realize that such ambiguities and biases may remain undiscovered, specifically if the model is able to accurately reproduce historical data after model calibration. As long as the model is only used for predictions under conditions that are very similar to those prevalent during the collection of calibration data, it is likely that prediction results are acceptable (referred to as “interpolative prediction”). However, this drastically limits the applicability of the model, whose main purpose is not to reproduce the system state that is already revealed by the measured data, but to examine its behavior under different conditions, to explore unobservable variables, or to understand the underlying processes (referred to as “extrapolative prediction” or “explanatory simulations”). Any of these application modes contains an extrapolation—regarding conditions, processes, states, spatial and temporal scales—and potentially also leaves the realm of established theory and fundamental understanding.
3.3. Extrapolation
One might argue that the need for model validation arises whenever such an extrapolation from one model space to another is attempted. This pertains specifically to the step when we proceed from model calibration to model prediction: at this point, we leave the space where model development makes use of measured data of the system we want to simulate (e.g., deterministic or statistical conditioning data, prior information about parameters, site-characterization data, testing and monitoring data, and calibration data). As discussed above, calibration produces effective parameters, i.e., parameters that are process-specific, model-related and scale-dependent. Whenever the model structure, key processes or scales are changed to adapt the calibrated model to a particular prediction problem, the interpretation, reference frame, and numerical value of the effective parameters are likely to change as well—thus the need for validating the appropriateness of the prediction model for its intended use.
This notion is reflected in all validation approaches that recommend data-splitting or a prediction-outcome comparison, which in essence attempts to emulate the situation in which a model is used for predictive purposes outside its calibration space. It should be noted that data-splitting is often used with time-series data, which means the calibration and validation data sets are usually of the same type, are observed at the same location, and refer to the same reference scale. This similarity between calibration and prediction data limits the application range for which the model is tested, as only a minor extrapolation is examined.
While confidence in a model is likely to be increased by critically examining the process of model development—i.e., without relying on a comparison of model results with measurable quantities of interest—a test of the model’s ability to make reliable predictions is an essential part of most validation methodologies [
1,
35], whether they are proposed as part of a philosophical argument or for pragmatic validation of numerical models used for the licensing of a radioactive waste repository.
3.4. Model Space
As indicated above, the need for model validation arises whenever a transition between model spaces occurs. The model space is the envelope of all possible models [
36]. It describes the bounds on the system of interest, from which relevant parameterizations, idealizations and modeling principles are chosen. It is thus the ensemble of conceptualizations, assumptions, physical rules, mathematical equations, and parameters that give a theoretical, observational and/or empirical description of the processes and conditions that allow simulations of the system state and its evolution. The model space evolves as new information is gathered or different requirements are placed on the model [
37]. Generally, the model space is reduced during the conditioning and calibration activities but may then expand when applied to different prediction spaces. Conditioning constrains the model space by making assumptions and tailoring it to prior information about a particular site. Calibration is the process of reducing the model space by comparing model outputs to measured data, which can be viewed as assessing the probability of a chosen model parameter set to be consistent with observations. A mismatch indicates that the specific conceptual model chosen for the analysis is an unlikely representation of the real system. In general, adding site-specific information allows us to separate more likely from less likely conceptualizations of the system, thus narrowing the model space.
However, this narrowing also limits the application range of the model. To make a useful prediction, an extrapolation must be made from the calibration spaces to the targeted prediction space. The prediction space may either refer to the conditions under which validation test data are collected, or it may refer to the ultimate model purpose, where the actual outcome is unknown. In either case, the conditions to be represented for a prediction are—by definition—different from those prevailing during model calibration. The need to extrapolate to different spatial and temporal scales, different boundary conditions, and potentially different key processes widens the model space; it is the reason why model validation is necessary.
If the model at a given stage of a project (a) does not satisfactorily explain or reproduce observations, showing systematic deviations or large mismatches between data and observations; or (b) its calibrated parameters are inconsistent with prior information and substantiated assumptions, then the first step of the modeling process, i.e., model conceptualization, needs to be repeated in view of the new information and experience gained from the previous analyses. Predictions made with multiple alternative models, which cover different model spaces, are more likely to adequately span outcomes in the real system, with the caveat that all of them may be nonbehavioral, i.e., are not acceptable in reproducing the observed behavior [
38].
Validation can be viewed as a critical review of the model-development process with the aim to demonstrate that the targeted prediction space is adequately delineated by an ensemble of model outputs. The acceptable shape and extent of the prediction space is determined by the purpose of the model—the more specific the modeling objectives are, the narrower the targeted prediction space is, and the more stringent the validation acceptance criteria are. The targeted prediction space may be represented by observations of the real system under conditions that are similar to those affecting the unknown behavior of interest.
The validation process is intended to reduce the number of conceptual models and their associated model spaces to a set of “behavioral models” [
39], thus increasing the confidence in our assessment of the models’ strengths and limits [
40].
The concept of a model space and its evolution reveals that the object of validation is not a single numerical model, but the outcome produced by an ensemble of models. As each alternative model has its distinct model space, the prediction space is considerably wider if multiple models and their uncertainties are considered. If predictions made with alternative conceptualizations and methods do not diverge, but instead occupy a sufficiently small prediction space, then higher confidence can be gained that the ensemble of these predictions can be used as the basis for decision making [
41].
In this view, the object of validation is the model prediction space—rather than the models that define it. The shortened term “model validation” as used here shall refer to this model-development process and the interpretation outlined in this section.
4. Pragmatic Model Validation
4.1. Pragmatism in Validation
We introduce the term “pragmatic model validation” to emphasize the context and environment, in which we want to evaluate models. Pragmatic model validation has the goal to build confidence in the model’s ability to make reliable statements about a specific aspect of the repository system. It also recognizes that any model always contains residual uncertainty; the ambition is not to make assertions about the ultimate truth. This definition is an acknowledgment that finding the truth remains elusive, but that a critical fit-for-purpose assessment of a model is both crucial and valuable.
Pragmatic validation is demanding: the effort cannot just be abandoned as achieving truth or full confidence in predictions is a futile undertaking; instead, the inherent limitations of a model and the uncertainties in its predictions must be understood, and the domain of applicability must be determined and related to the intended use of the model. Finally, this information must be effectively communicated to the end-user of the model. Conversely, pragmatic validation limits the domain of model applicability, which in turn reduces the space of influential parameters, making its exploration more tangible.
The word “pragmatic” may also refer to the fact that validation of models representing subsurface systems is constrained by the scarcity of data. The validation process can help identify which data should be collected to increase model confidence by reducing prediction uncertainty. This relation between measured data, model parameters, and confidence in predictions can be formally examined in a data-worth analysis, which evaluates the relative contribution of an actual or potential data point to a reduction in uncertainties (a) in parameters inferred from the data through inverse modeling; and/or (b) in a target prediction of interest, which reflects the modeling purpose. A data-worth analysis takes place in the data space as well as multiple model spaces. It propagates data uncertainty to parameter uncertainty to prediction uncertainty, a process that examines sensitivities and information content of individual data points and the influence of parameters on model predictions. The relative importance of competing target predictions is also accounted for. The workflow for a pragmatic model validation and a data-worth analysis are thus similar. In fact, a data-worth analysis should be an integral part of model validation, demonstrating that data used for a prediction-outcome approach to model validation are indeed informative and related to the ultimate modeling purpose. Note that a data-worth analysis would be performed prior to the collection of validation data. The analysis forces the user to think about validation acceptance criteria, and to apply them once the data become available. Some background on the data-worth analysis workflow can be found in [
42,
43,
44].
In this interpretation, the term “pragmatic” is an acknowledgment of both the validation challenge, which must be accounted for when qualifying the credibility and applicability of a validated model, and the usefulness of the validation process itself, which helps identify data-collection and research needs for an improvement of system understanding and the reliability of model predictions.
Box [
45] coined the aphorism
“All models are wrong, but some models are useful.“ Box et al. [
46] offered the following explanation:
“All models are approximations. Assumptions, whether implied or clearly stated, are never exactly true. All models are wrong, but some models are useful. So the question you need to ask is not ‘Is the model true?’ (it never is) but ‘Is the model good enough for this particular application?’” These comments are relevant also for geoscientific modeling, where the abstraction process during conceptual model development introduces numerous, often strong approximations, and many assumptions are made due to generally poor coverage of characterization data and the impracticality of explicitly implementing multi-scale features and processes. Box’s aphorism can be viewed as a concise statement about the potential backdrop of a pragmatic approach to model validation.
Finally, due to the recognized fundamental limitations and practical constraints, pragmatic validation also refers to the validation approach itself. It indicates that the chosen approach is clearly targeted for a specific model use or to calculate specific quantities of interest. It submits that the model is used to address a practical problem by making predictions, from which recommendations are derived, i.e., it is used as a practical tool rather than just describing or mimicking nature.
Furthermore, pragmatic model validation invites the question about the effort that should be expended to appraise a model. For example: Is it sufficient to validate a model by benchmarking it against other models, or by testing just the individual components, or by comparing its outcome to literature data? Or is it necessary to perform a designated laboratory experiment or field test? Must it be demonstrated that the model is capable of performing over the entire spatial and temporal scales relevant for nuclear waste disposal? Merely addressing such questions indicates that a pragmatic approach is being taken, and the answer about what effort is considered reasonable is driven by the ultimate purpose of the model and its significance for decision making, specifically in areas where supporting information is uncertain or disputed, conclusive scientific evidence is not available, and the model outcome has important implications affecting a plurality of stakeholders.
4.2. Sensitivity Auditing
Saltelli et al. [
40] outline a protocol to be used for a critical appraisal of a model’s quality. The process they propose can be described as pragmatic in the sense that it provides practical guidelines with the aim to improve the quality of models used for the express purpose of supporting important policy decisions that involve considerable risks as well as unquantifiable, irreducible uncertainties. The approach is referred to as “sensitivity auditing” and goes beyond a mere evaluation of model uncertainties and parametric sensitivities. Note that sensitivity analyses do not reduce model uncertainties, but they make them transparent so that both modeling practitioners and recipients of modeling analyses are fully aware of the conditionality of the predictions. Sensitivity auditing is intended to skeptically review any inference made by the simulations. It attempts to establish whether a model is plausible regarding its assumptions, outcome, and usage. It not only examines the model, but also the auditing process itself. Rules are formulated and checklists generated for the entire modeling process to achieve transparency about the reliability of a specific model prediction. Following these rules is considered a minimum due-diligence requirement for the use of model-based inferences.
The formal process includes a global sensitivity analysis [
47] to identify the key factors affecting prediction uncertainty. Next, value-laden assumptions as well as other model- and problem-related statements are systematically qualified [
48]. Uncertainty analysis methods are used to obtain quantitative metrics about the model outputs of interests. Qualitative judgments about the information, such as its reliability, are added, along with an evaluative account of how the information was produced. Problem-specific pedigree criteria (such as theoretical understanding, empirical basis, methodological rigor, degree of validation, use of standards, quality control and safety culture, plausibility, influence on results, comparison of alternative conceptual models, agreement among peers, review process, value ladenness of estimates, assumptions and problem framing, and influence by situational limitations) are evaluated by assigning a numerical value to linguistic descriptions of the level to which each criterion is met. For example, for the pedigree criterion [
48] ‘degree of validation’, the description may range from ‘compared with independent measurements of the same variable’ to ‘compared with derived quantities from measurements of a proxy variable’ to ‘weak, indirect, or no validation’.
This system provides insight into two independent uncertainty aspects of a model-calculated number, one expressing its exactness, and the other expressing the methodological and epistemological limitations of the underlying knowledge base. These two aspects must be viewed together to arrive at a meaningful statement about a model’s quality. For example, inexactness or even ignorance about an input parameter may not invalidate a model if the parameter is non-influential, i.e., has a negligible effect on the prediction of interest. Conversely, model predictions can be reliable even if they are highly sensitive to certain input parameters, provided that these parameters can be determined with high confidence.
In general, the notion that model validation is an auditing process guided by critical questions redirects the attention from a stringent pass-fail comparison of model-calculated and measured data to a broader evaluation of a model’s adequacy through the judicious use of expert judgment as well as formal sensitivity and uncertainty analyses. Moreover, the model development and evaluation processes need to be thoroughly documented and externally reviewed.
In this view, confidence is obtained by the fact that the validation process helps identify and correct obvious flaws in the model [
19], that hypotheses and assumptions are properly tested [
49], and that scientifically appropriate methods are used [
50]. A rigorous validation process will ultimately improve the model and therefore the quality of inferences and decisions made based on the model output.
4.3. Validation Activities and Acceptance Criteria
The discussion of pragmatic validation reveals the wide range of interpretations and expectations the term “validation” evokes, with respect to both the ultimate purpose of the validation process and the most suitable method to achieve that goal. The essence of pragmatic validation is that it exposes a proposed modeling solution to the test of its usefulness. Expectations about what a validated model is supposed to accomplish are wide-ranging:
A validated model provides an improved, general understanding of the system, as the model results are examined from disparate lines of evidence. However, the model results are not to be interpreted as predictions about the real system behavior;
A validated model provides a consistent representation and explanation of the available, complementary data from different scientific disciplines (geology, hydrogeology, geochemistry, etc.);
A validated model is suitable to examine alternative cases and “what-if” scenarios. The model results are not accurate predictions but reveal relative changes in the expected system behavior as a function of the chosen scenarios;
A validated model can make specific predictions that are adequate for the purpose of the model. The model does not necessarily represent the real system, but its outcomes are acceptable as they support the ultimate project purpose. For example, the model may be used for conservative or bounding calculations, which—despite being unlikely, unreasonable, or even unphysical—may be adequate within a regulatory framework and may support a performance assessment study;
A validated model is an approximate representation of the real system. The degree of model fidelity is dictated by the accuracy with which the predictions need to be made, so they can support decision making.
The process of how to validate a model depends on which of the model-validation goals outlined in the preceding list need to be met. The validation process will be less elaborate and may be limited to component testing and peer review if the purpose of the model is to improve the general system understanding or to examine “what-if” scenarios; it will likely require comparison with experimental or monitoring data if decision-makers intend to rely on quantitative predictions; it will be an extensive, cross-disciplinary, continual research endeavor if fundamental statements about the nature of the world are to be made. The following activities may be part of a model validation exercise:
A validated model should comply with industry-standard QA/QC procedures and have passed a formal software qualification lifecycle test (“verification”);
A validated model should have undergone a detailed review of the procedures used for the construction of the conceptual and numerical models, including the evaluation (a) of available data, (b) of theoretical and empirical laws and principles, (c) of the abstraction process and conceptual model development, (d) the construction of the calculational model, and (e) the iterative refinement based on predictive simulations, sensitivity analyses, and uncertainty quantification [
40,
51];
A validated model should be calibrated against relevant data, with (a) residuals being devoid of a significant systematic component, (b) acceptably low estimation uncertainties, and (c) fairly weak parameter correlations. The criteria for acceptability are determined by the accuracy with which model outputs supporting the project objectives need to be calculated [
43];
A validated model should be peer-reviewed with a general consensus among experts and stakeholders that the model qualifies for its intended use, and that limitations, the range of application, and uncertainties are sufficiently understood and documented;
A validated model should be compared to alternative models [
52,
53] or approaches and perform equally well or better regarding relevant validation performance criteria [
54];
A validated model should reproduce—with acceptable accuracy—relevant data not used for model calibration. The type of data, the processes involved, the spatial and temporal scales, and the conditions prevailing during data collection should reflect those of the target predictions as closely as possible. The criteria for acceptability are determined by the accuracy with which model outputs supporting the project objectives need to be calculated;
A validated model should demonstrate that it can predict emerging phenomena [
4].
As indicated in the above list, model-validation activities and related acceptance criteria vary as they are related to the demands imposed on the model.
Figure 1 shows the approximate correspondence between the goals the validated model must meet and the required validation activities.
Figure 1 also indicates the region within the matrix that IAEA’s validation definition appears to target.
It is obvious that a good general system understanding is a pre-requisite for a model that is expected to provide reliable, quantitative predictions of a previously unobserved system behavior. This statement applies specifically to models that rely on an understanding of the underlying physical processes, as opposed to statistical models (including, for example, neural networks and machine-learning algorithms), which are data-driven approaches that infer input–output correlations with no or only a cursory use of physical concepts. The models of concern here are those that incorporate substantial mechanistic understanding rather than empirical correlations.
Similarly, following standards and best practices, and having the development of each model component checked individually and submitted to independent review, are certainly ways to increase the credibility of a model, regardless of its ultimate use.
5. The Pragmatic Model Validation Framework
As discussed above, pragmatic model validation involves a critical review of the model-development process with the goal of demonstrating that the acceptable region of uncertainty is adequately delineated by the model or an ensemble of model outputs. The acceptable level of prediction uncertainty is determined by the purpose of the study. While confidence in a model may be increased by critically examining the process of model development [
22,
40]—i.e., without relying on a comparison of model results to observations—a test of the model’s ability to make reliable predictions is an essential component of most validation methodologies, whether they are proposed as part of a philosophical argument or for pragmatic evaluation of numerical models used for the licensing of a nuclear waste repository [
1].
Evaluation activities and acceptance criteria will vary, as they are related to the demands imposed on the models by features of the engineering or scientific problem at hand. That said, it is self-evident that a good general system understanding is a pre-requisite for building models that are expected to provide reliable, quantitative predictions of previously unobserved system behavior. Similarly, following standards and best practices [
55,
56], checking the development of individual model components and undergoing independent review will increase the credibility of a model, regardless of its ultimate use. Nevertheless, assessing adequacy-for-purpose of a model includes additional considerations.
Pragmatic model evaluation helps to identify and correct flaws in the model by identifying and properly testing hypotheses, assumptions, and methods. It will also expose each proposed modeling approach to a test of its usefulness. It is apparent that the evaluation approach has to be adapted to fit the model, the question the model is expected to answer, and the overall goal of its use. The proposed account of pragmatic model evaluation can be conceptually divided into the following six phases [
22]:
Definition of the model purpose: The aim of pragmatic model-evaluation is to determine whether a model is adequate-for-purpose: does the model make a valuable contribution to the solution of the problem at hand? The model purpose must be clearly specified as it determines the benchmark, standards, and acceptance criteria for critical evaluation.
Determination of critical aspects: For reasons of pragmatism, effectiveness, and efficiency, it is essential to identify which aspects of the models will require particular attention and thus warrant targeted review and testing effort. These aspects are likely to be specific to the intended use and are those that have the greatest impact on critical model outcomes. Moreover, model evaluation should be focused on the subset of aspects that are uncertain or where the modelers lack confidence in their correct or accurate representation in the model.
Definition of performance measures and criteria: To be able to assess whether a model is adequate-for-purpose requires the definition of suitable performance measures and acceptance criteria. They must either be directly calculatable by the model or indirectly inferable from the modeling results. Most critically, they must be relevant to the end use. Information, observations, or testing data used for model assessment should be as close to the performance measures as possible, in terms of influential factors, processes, and scale. The accuracy of both the model output and data must be sufficiently high that they are discriminative in the evaluation of the acceptance criteria.
Sensitivity and uncertainty analysis of influential factors: Selecting influential factors is an important step during model development, but even more so for model evaluation. Influential factors are model-specific, although they may be common to several models. The difference between the influential factors identified during model development (specifically model calibration) and the factors identified as influential for the ultimate model use is an indication of the degree of extrapolation undertaken when using a model for a purpose that may not have been envisioned during model development, and for which no closely related calibration data were available.
Prediction-outcome exercises: An important aspect of pragmatic evaluation is the testing of model predictions [
1]. Whilst direct testing of the model predictions against the reality of interest is often not possible, the critical aspects and significant influential factors should be the basis for design and evaluation of prediction-outcome tests. Uncertainties in the influential factors need to be propagated through the model to the performance measures so that meaningful statements about system behaviors can be made that account for relevant uncertainty.
Model evaluation, documentation, and model audit: As all model predictions are extrapolations (spatially, temporally, parametric, and regarding the features and processes that need to be considered), and the testing data never fully correspond to the ultimate performance metrics, confidence in the model cannot solely rely on the comparison between model output and measurements. Instead, each model development step must be clearly documented. In particular, the conceptual models and their assumptions need to be reviewed as they often have the greatest potential to bias modelling results [
11]. It is also important to document and review the criteria used to reject a model or the criteria employed when calling for an update of the model. Any consensus—and in particular any disagreement—among model reviewers should be acknowledged.
6. Conclusions
This article presents our perspective on the need for critically evaluating numerical models used to support important policy decisions, specifically those related to the licensing of a radioactive waste repository. This need is deeply rooted in the fundamental nature of any conceptual and numerical model. While we acknowledge that models are inherently uncertain, if not erroneous, we reject the notion that any validation effort is futile. By contrast, we take this realization as a call for due diligence, which involves a careful evaluation of the model (or models), the simulation results, and their interpretation. Rather than resigning because it is impossible to know or verify the truth, we propose to assume a pragmatic view, which addresses the challenges of the actual situation in which models are employed.
Pragmatic validation aims at demonstrating that a model is fit for purpose. This may lower the expectations of what the model needs to accomplish: it is not anticipated that the model can make accurate statements or predictions of any type and under any conditions; the model needs to perform only within a limited domain of applicability. On the other hand, the model is expected to provide useful information to solve a specific problem, not just insights about a general system behavior.
Multiple models should be developed based on alternative conceptualizations. If these models yield consistent conclusions about the behavior of interest, confidence is gained that the performance metrics can be calculated in a robust manner [
41]. This indicates that the outcome does not greatly depend on uncertain factors, which may have been implemented differently in each of the models, but that the general system understanding, as well as the information provided by the site characterization data, are sufficient to constrain the predictions.
Conversely, model comparison may also point to conceptual aspects that need to be revised. When combining or comparing alternative conceptual models, the performance of each model during the calibration and validation phases is accounted for [
57]. Such a combined analysis does not state which (if any) of the alternative models is the best representation of the real system [
39]; instead, it evaluates the contribution each model makes in support of the overall goal, and pragmatically combines the insights gained from each approach.
While many computational toolsets exist that support certain steps of the validation process [
58], it is apparent that no single validation approach exists that is best regardless of the application area. Even within a specific domain, such as nuclear waste isolation, the approach must be adapted to fit the model, the question the model is expected to answer, and the overall goal of its use. While validation has fundamental and practical limitations, the exercise of trying to test a model in an attempt to find its weaknesses is a valuable, if not necessary, effort.