Operation Characteristics of Adjustable Field IPMSM Utilizing Magnetic Saturation
Abstract
:1. Introduction
- (1)
- Adjustable field capability with genuine electromagnetic operation;
- (2)
- Capability of the reluctance torque generation;
- (3)
- Independency of the field adjustment on the motor operation (vector control) and the rotating speed;
- (4)
- Higher anti-demagnetization capability of PMs;
- (5)
- Continuous magnetic field control;
- (6)
- Better productivity of the motor hardware;
- (7)
- Lower copper loss for magnetic field control.
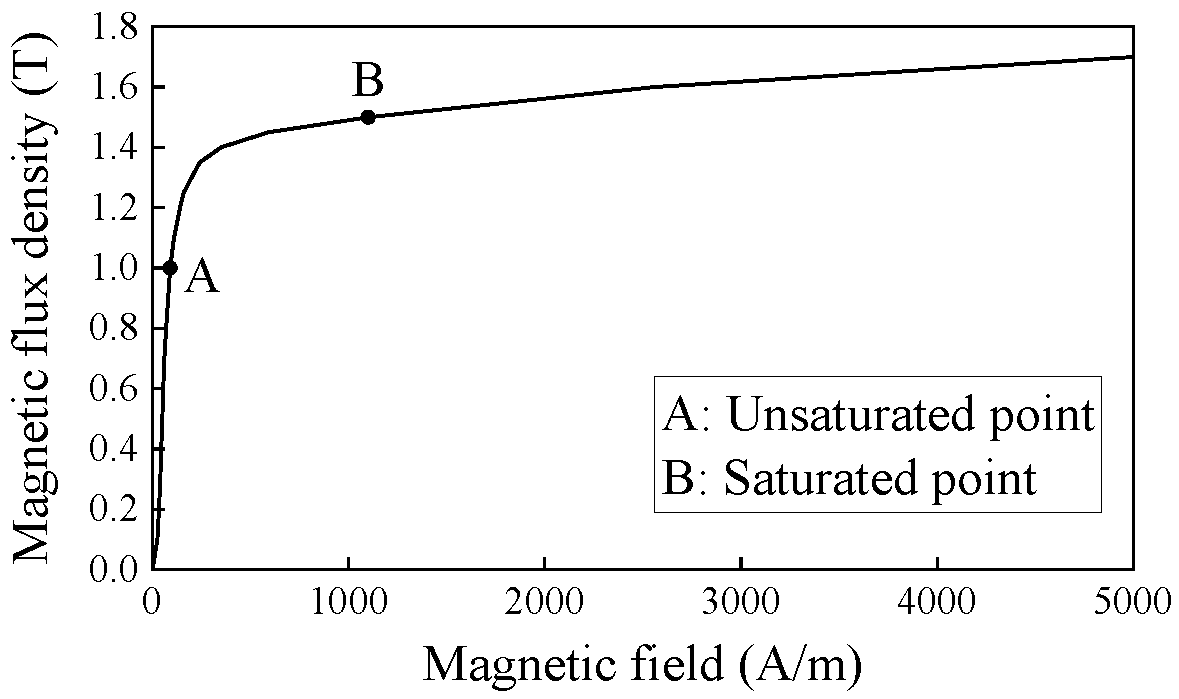
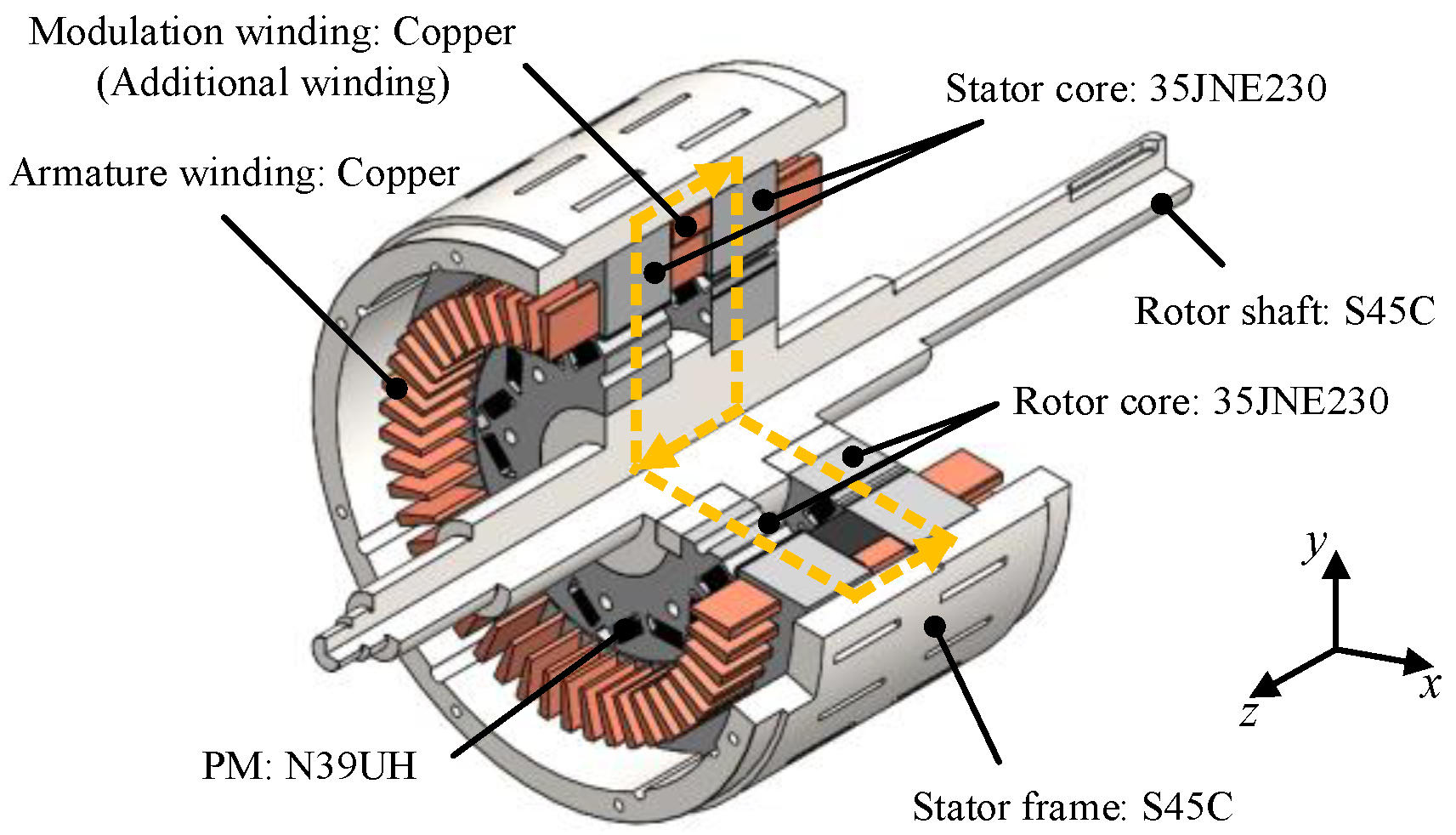
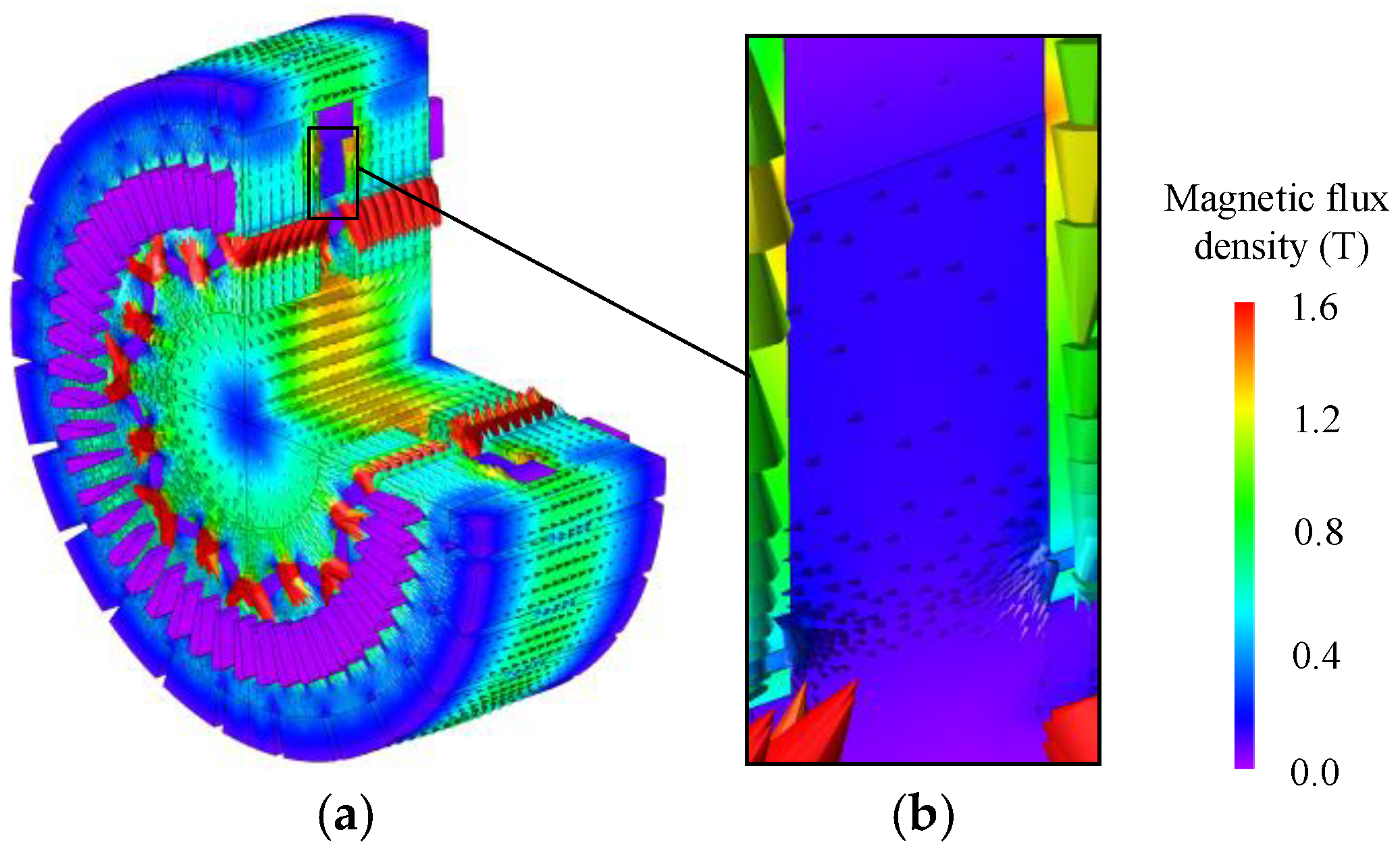
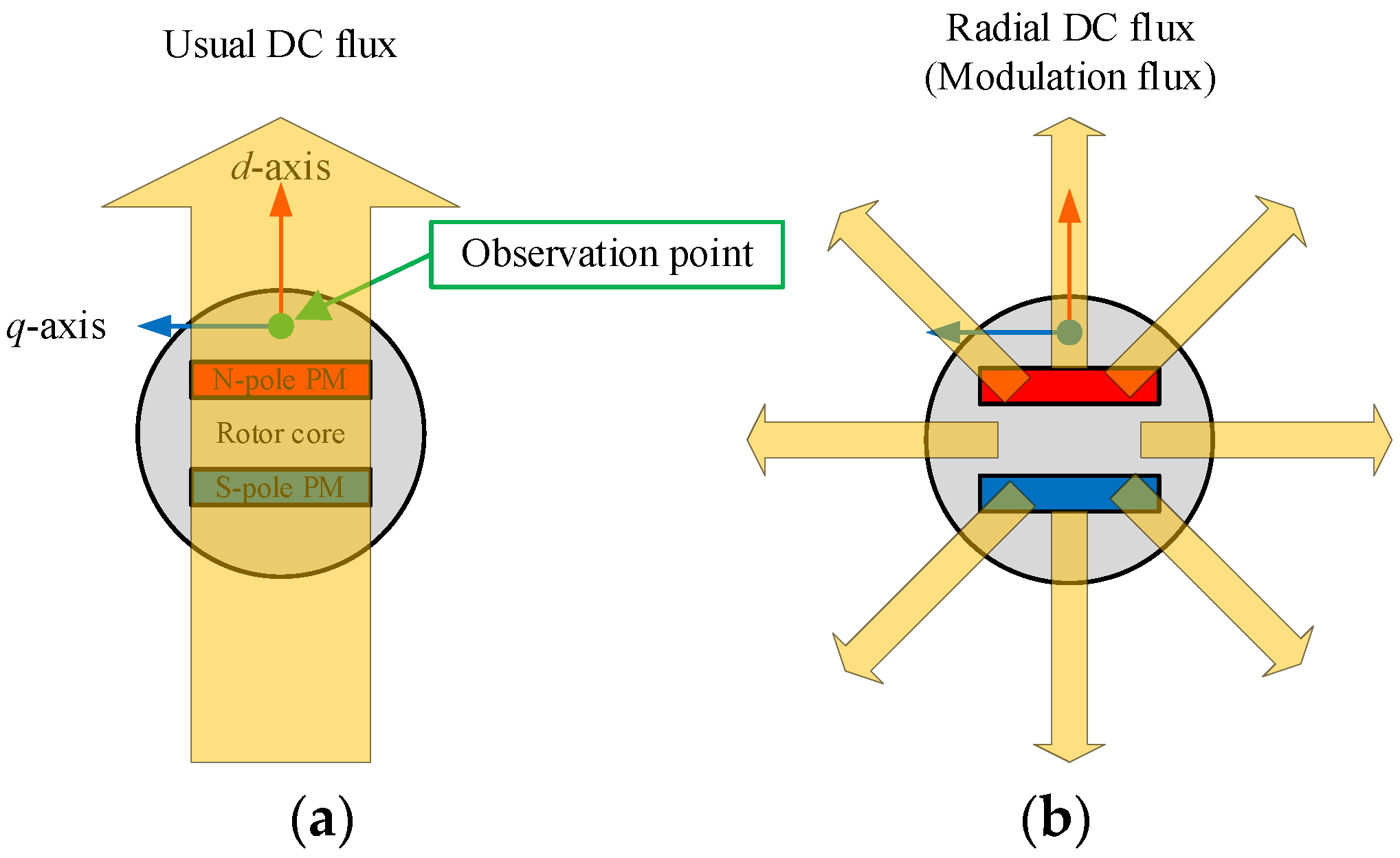
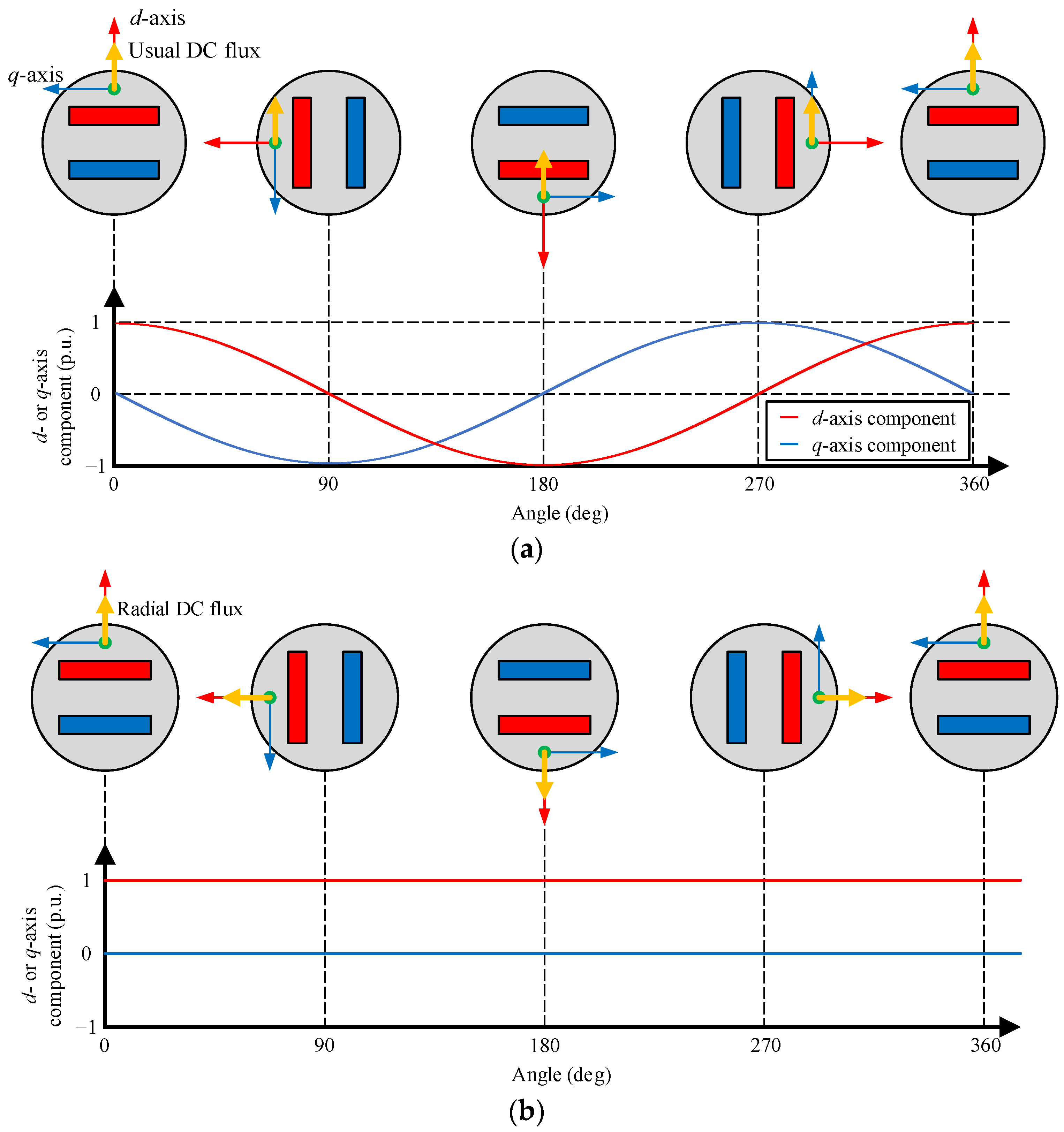
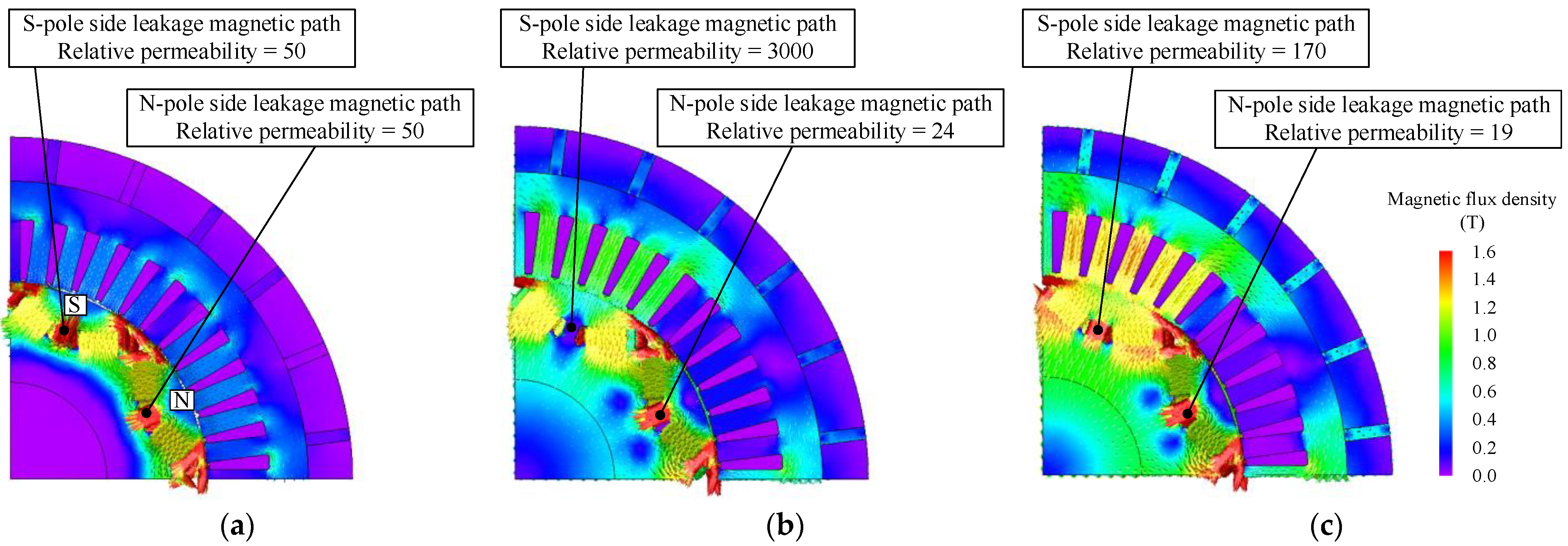
2. Principle of Adjustable Field Method Utilizing Magnetic Saturation
3. Back E.m.f. Characteristic
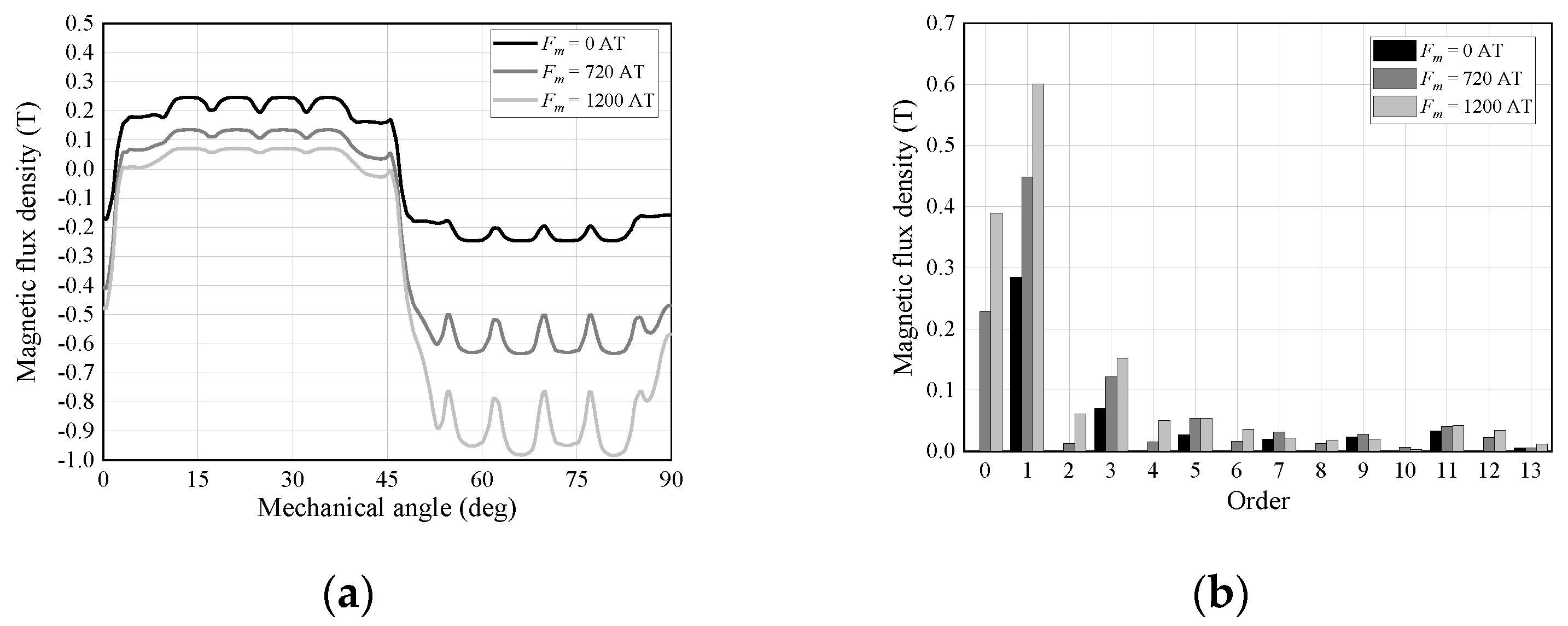
3.1. Analysis of Back E.m.f.
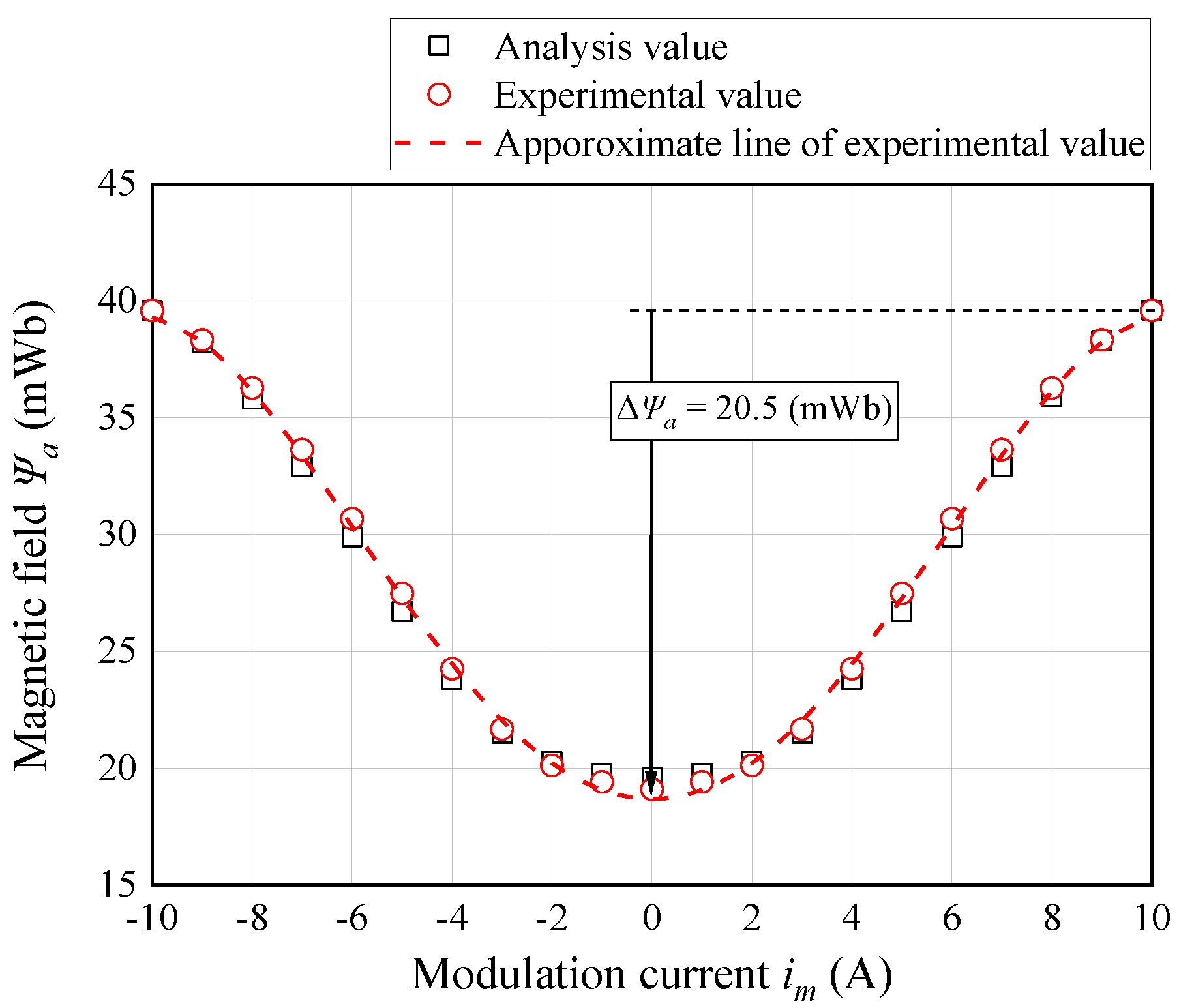
3.2. Back E.m.f. Measurement Test
3.3. Magnetic Field Control Performance Comparison with Other Methods
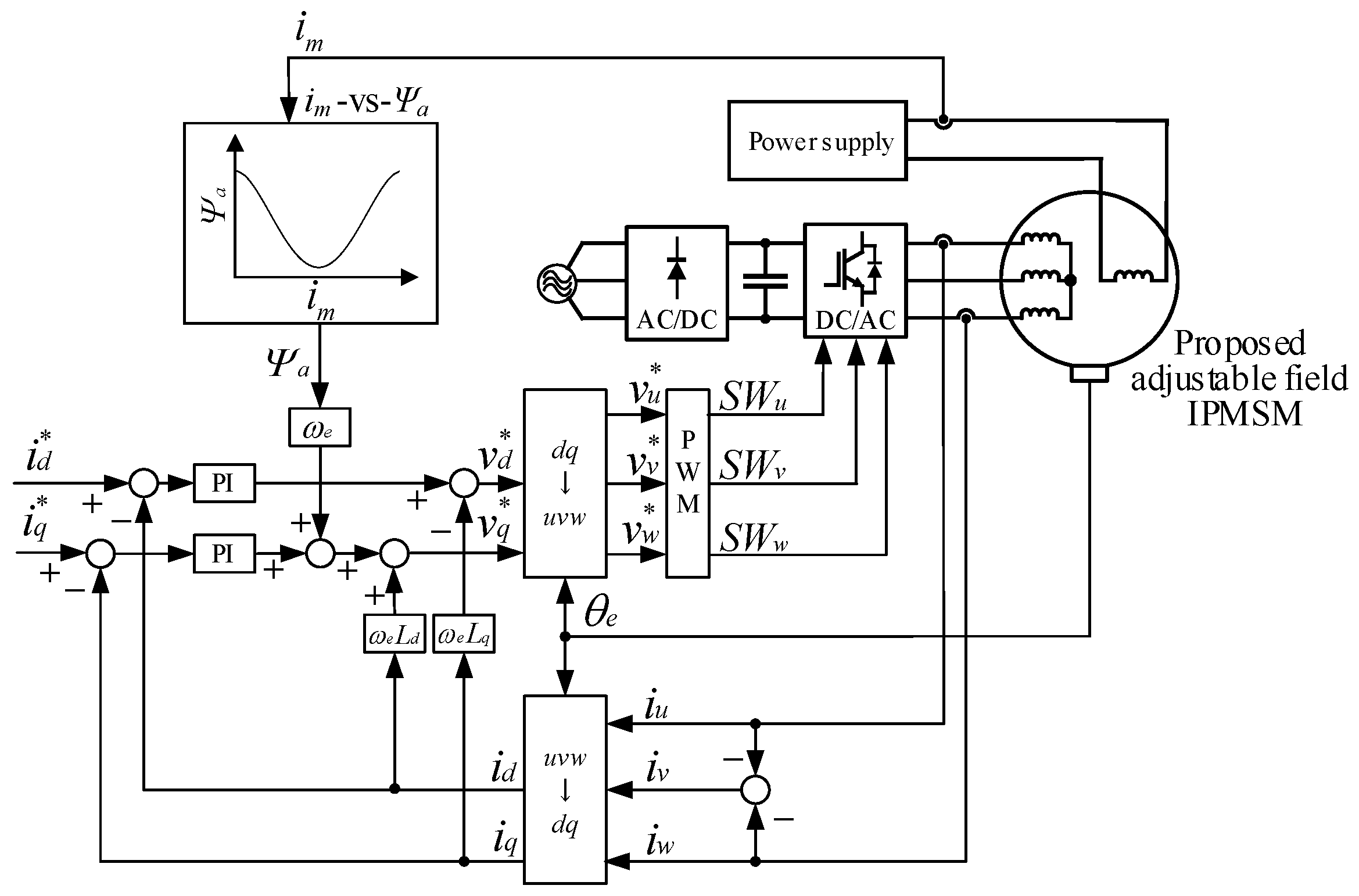
4. Drive System of Prototype Motor
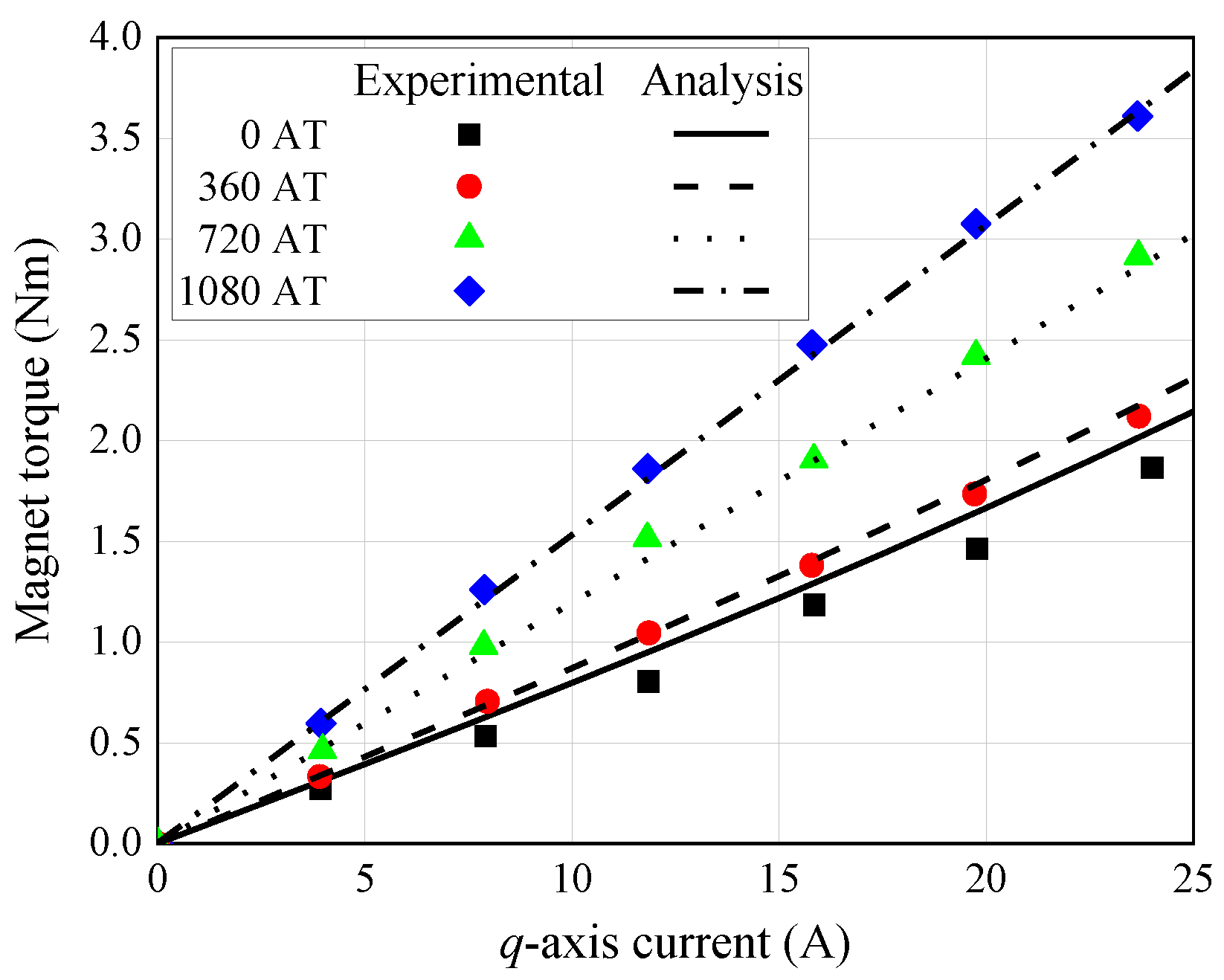
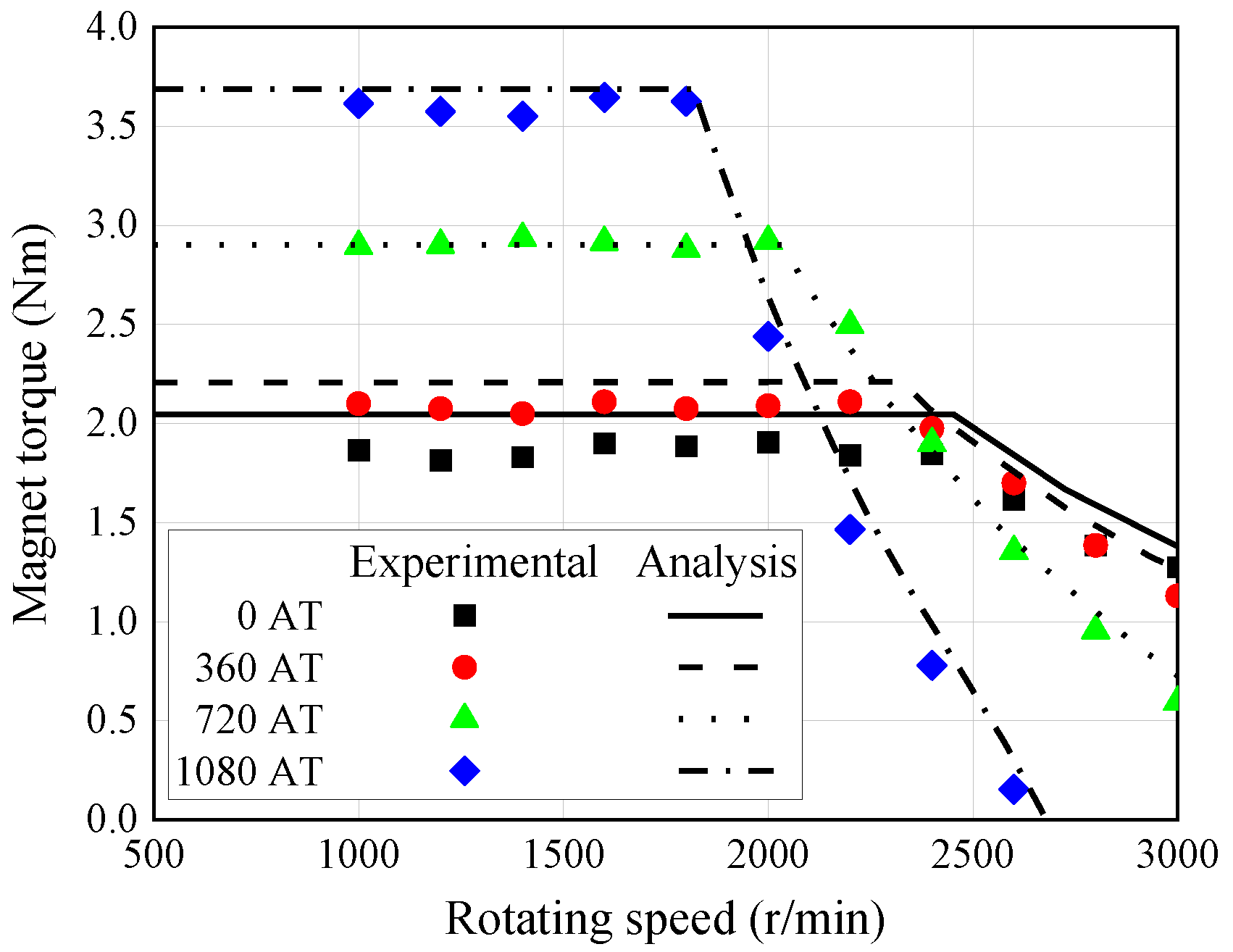
5. Load Characteristics
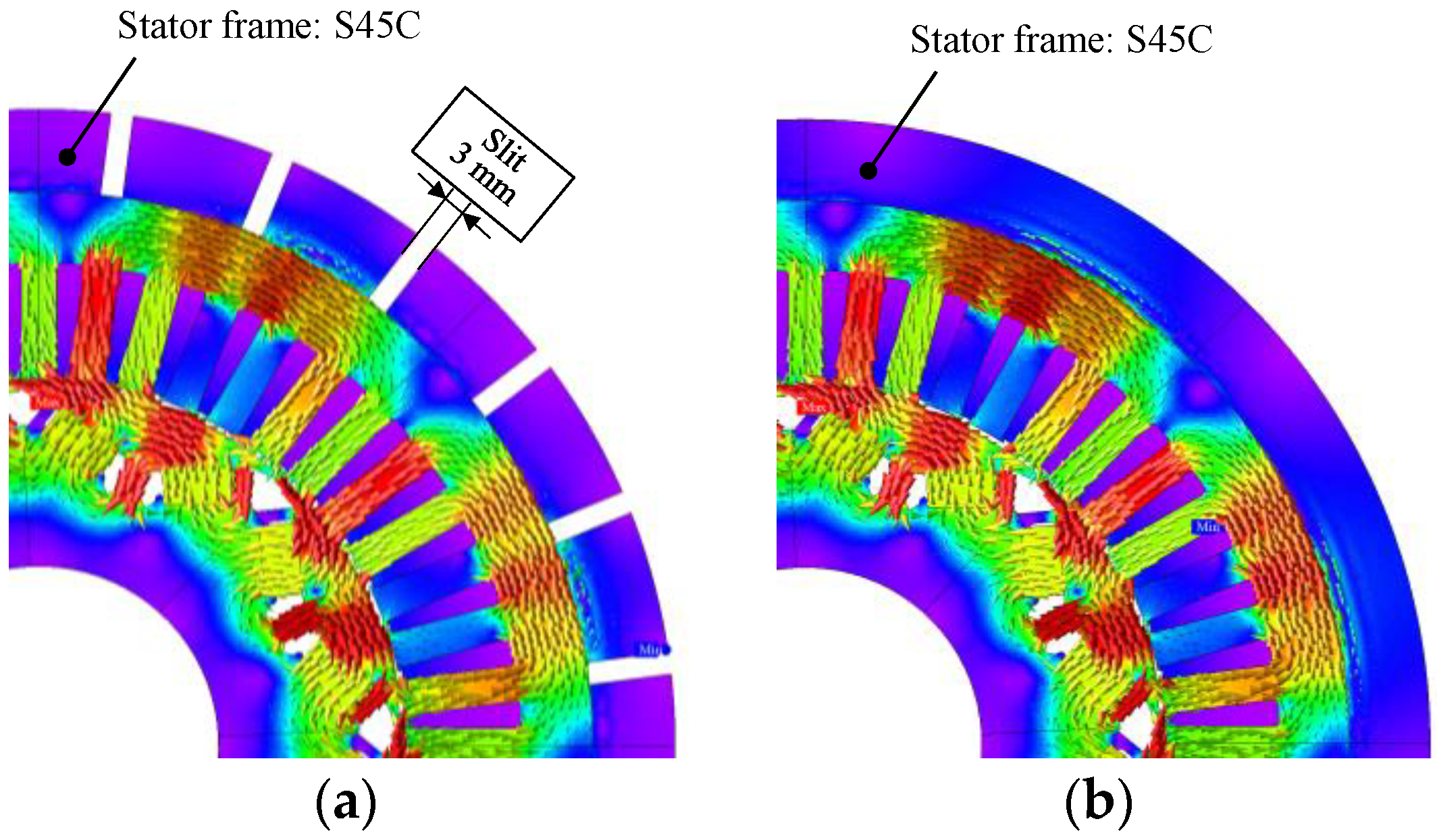
5.1. Load Analysis
5.2. Load Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pellegrino, G.; Vagati, A.; Guglielmi, P.; Boazzo, B. Performance Comparison between Surface-Mounted and Interior PM Motor Drives for Electric Vehicle Application. IEEE Trans. Ind. Appl. 2012, 59, 803–811. [Google Scholar] [CrossRef] [Green Version]
- Fatemi, A.; Ionel, D.M.; Popescu, M.; Chong, Y.C.; Demerdash, N.A.O. Design Optimization of a High Torque Density Spoke-Type PM Motor for a Fomula E Race Drive Cycle. IEEE Trans. Ind. Appl. 2018, 54, 4343–4354. [Google Scholar] [CrossRef]
- Jo, C.; Seol, J.Y.; Ha, I.J. Flux-Weakening Control of IPM Motors with Significant Effect of Magnetic Saturation and Stator Resistance. IEEE Trans. Ind. Electron. 2008, 55, 1330–1340. [Google Scholar]
- Sue, S.M.; Pan, C.T. Voltage-Constraint-Tracking-Based Field-Weakening Control of IPM Synchronous Motor Drives. IEEE Trans. Ind. Electron. 2008, 55, 340–347. [Google Scholar] [CrossRef]
- Mizuno, T.; Nagayama, K.; Ashikaga, T.; Kobayashi, T. Basic Principles and Characteristics of Hybrid Excitation Type Synchronous Machine. IEEJ Trans. Ind. Appl. 1995, 115, 1402–1411. [Google Scholar] [CrossRef] [Green Version]
- Tapia, J.A.; Leonardi, F.; Lipo, T.A. Consequent-Pole Permanent-Magnet Machine with Extended Field-Weakening Capability. IEEE Trans. Ind. Appl. 2003, 39, 1704–1709. [Google Scholar] [CrossRef] [Green Version]
- Kato, T.; Hijikata, H.; Minowa, M.; Akatsu, K.; Lorenz, R.D. Design Methodology for Variable Leakage Flux IPM for Automobile Traction Drives. In Proceedings of the 2014 Energy Conversion Congress and Exposition–ECCE, Pittsburgh, PA, USA, 14–18 September 2014; pp. 3548–3555. [Google Scholar]
- Aoyama, M.; Noguchi, T. Automatic Variable Magnetic Flux Technique in Consequent Pole Type PM-Motor Utilizing Space Harmonic. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation, and Motion–SPEEDAM, Amalfi, Italy, 20–22 June 2018; pp. 1315–1320. [Google Scholar]
- Hijikata, H.; Saka, Y.; Akatsu, K.; Miyama, Y.; Arita, H.; Daikoku, A. Multi-Phase Inverter-Fed MATRIX Motor for High Efficiency Driving. IEEJ Trans. Ind. Appl. 2018, 138, 257–264. [Google Scholar] [CrossRef]
- Sakai, K.; Hashimoto, H.; Kuramochi, S. Principle and Basic Characteristics of Variable-Magnetic-Force Memory Motors. IEEJ Trans. Ind. Appl. 2011, 131, 53–60. [Google Scholar] [CrossRef]
- Zhu, X.; Xiang, Z.; Quan, L.; Wu, W.; Du, Y. Multimode Optimization Design Methodology for a Flux-Controllable Stator Permanent Magnet Memory Motor Considering Driving Cycles. IEEE Trans. Ind. Electron. 2018, 65, 5353–5366. [Google Scholar] [CrossRef]
- Iwama, K.; Noguchi, T. Performance Comparison between Adjustable Field IPM Motor Based on Permeability Modulation Technique and Conventional IPM Motor. In Proceedings of the 23rd International Conference on Electrical Machines and Systems–ICEMS, Hamamatsu, Japan, 24–27 November 2020; pp. 1418–1423. [Google Scholar]
- Chen, X.; Wang, J.; Sen, B.; Lazari, P.; Sun, T. A High-Fidelity and Computationally Efficient Model for Interior Permanent-Magnet Machines Considering the Magnetic Saturation, Spatial Harmonics, and Iron Loss Effect. IEEE Trans. Ind. Electron. 2015, 62, 4044–4055. [Google Scholar] [CrossRef]
- Liang, P.; Chai, F.; Li, Y.; Pei, Y. Analytical prediction of magnetic field distribution in spoke-type permanent-magnet synchronous machines accounting for bridge saturation and magnet shape. IEEE Trans. Ind. Electron. 2017, 64, 3479–3488. [Google Scholar] [CrossRef]
- Hemeida, A.; Lehikoinen, A.; Rasilo, P.; Vansompel, H.; Belahcen, A.; Arkkio, A.; Sergeant, P. A Simple and Efficient Quasi-3-D Magnetic Equivalent Circuit for Surface Axial Flux Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2019, 66, 8318–8333. [Google Scholar] [CrossRef]
- Alipour-Sarabi, R.; Nasiri-Gheidari, Z.; Oraee, H. Development of a three-dimensional magnetic equivalent circuit model for axial flux machines. IEEE Trans. Ind. Electron. 2020, 67, 5758–5767. [Google Scholar] [CrossRef]
- Shokrollahi, H.; Janghorban, K. Soft magnetic composite materials (SMCs). J. Mater. Process. Technol. 2007, 189, 1–12. [Google Scholar] [CrossRef]
- Diao, N.; Sun, X.; Song, C.; Zhang, Q.; Zhang, Z. A Multi-modulation Times SVPWM for Dead Time Effect Elimination in Three-level Neutral Point Clamped Converters. IEEE Trans. Ind. Electron. 2021, 68, 5476–5485. [Google Scholar] [CrossRef]
- Oto, Y.; Noguchi, T.; Sasaya, T.; Yamada, T.; Kazaoka, R. Space Vector Modulation of Dual-Inverter System Focusing on Improvement of Multilevel Voltage Waveforms. IEEE Trans. Ind. Electron. 2019, 66, 9139–9148. [Google Scholar] [CrossRef]
- Mapelli, F.L.; Tarsitano, D.; Mauri, M. Plug-In Hybrid Electric Vehicle: Modeling, Prototype Realization, and Inverter Losses Reduction Analysis. IEEE Trans. Ind. Electron. 2009, 57, 598–607. [Google Scholar] [CrossRef]
- Caruso, M.; Tommaso, A.O.D.; Lisciandrello, G.; Mastromauro, R.A.; Miceli, R.; Nevoloso, C.; Spataro, C.; Trapanese, M. A General and Accurate Measurement Procedure for the Detection of Power Losses Variations in Permanent Magnet Synchronous Motor Drives. Energies 2020, 13, 5770. [Google Scholar] [CrossRef]

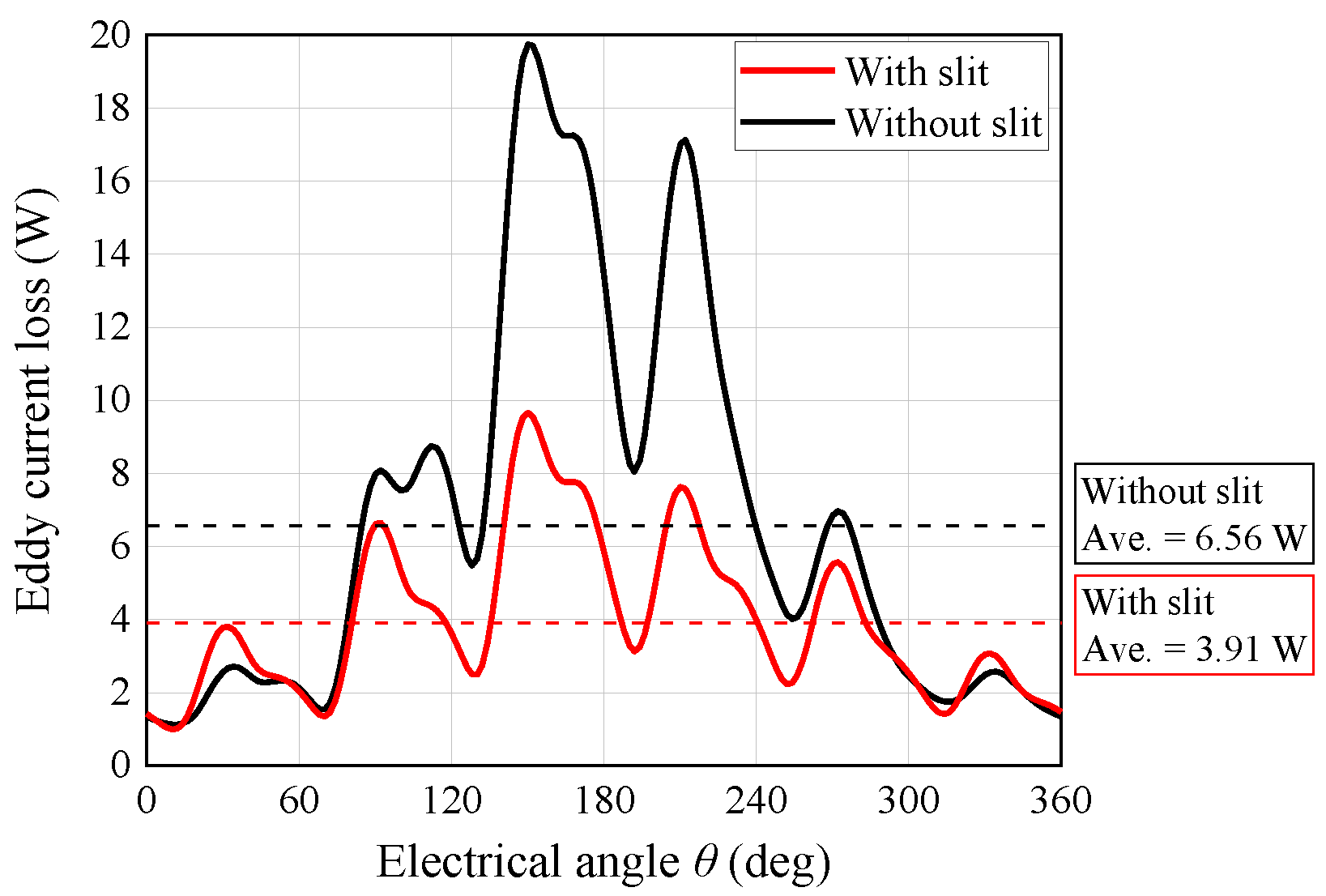
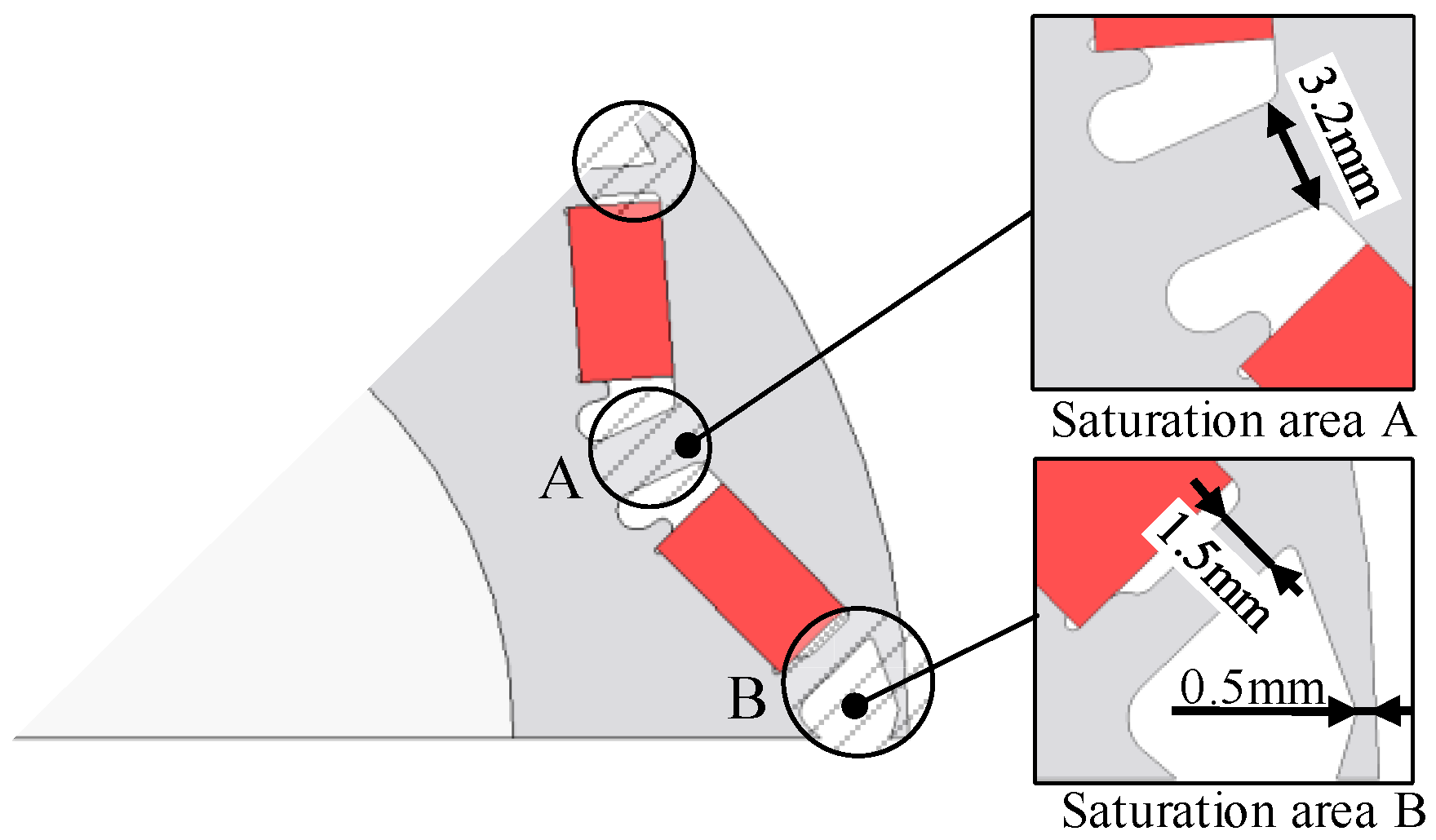
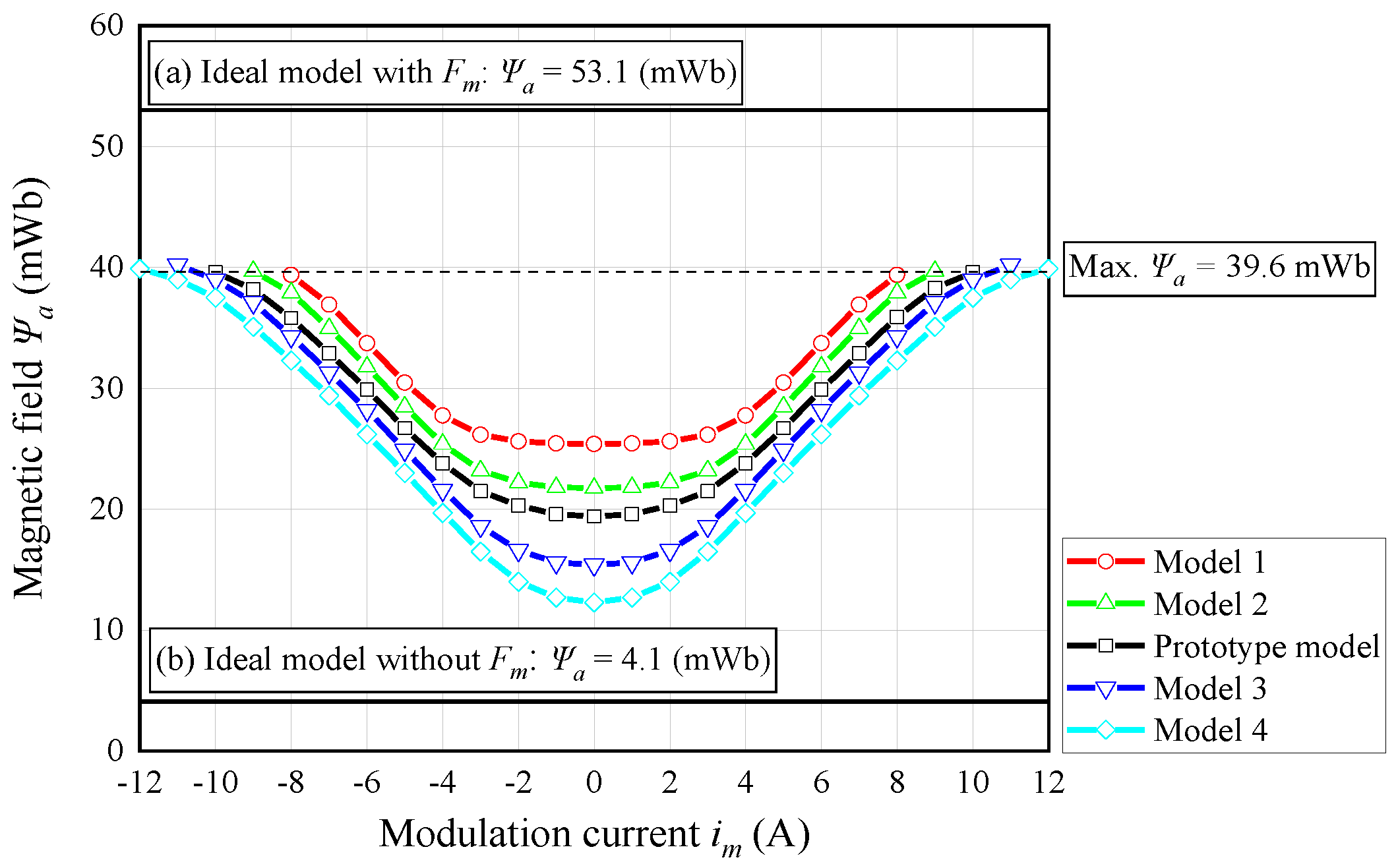

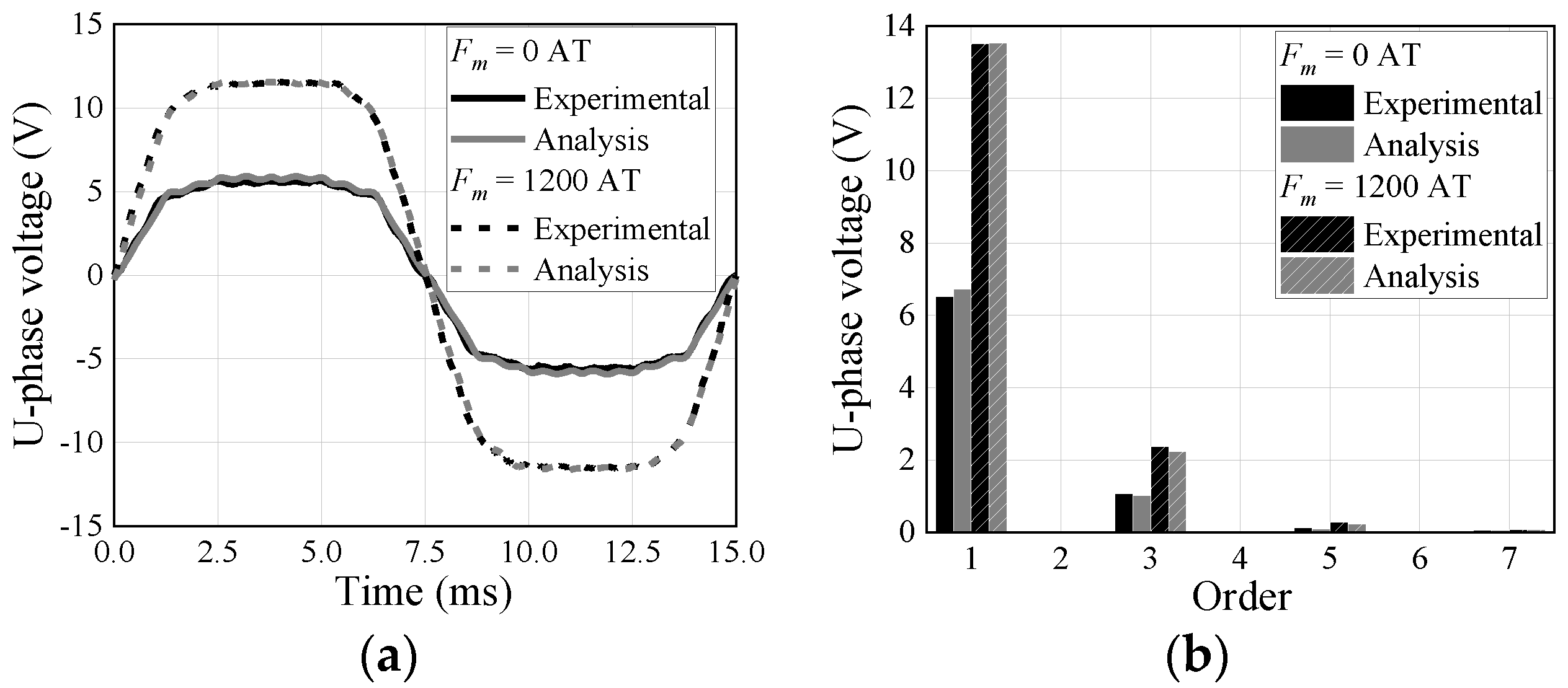
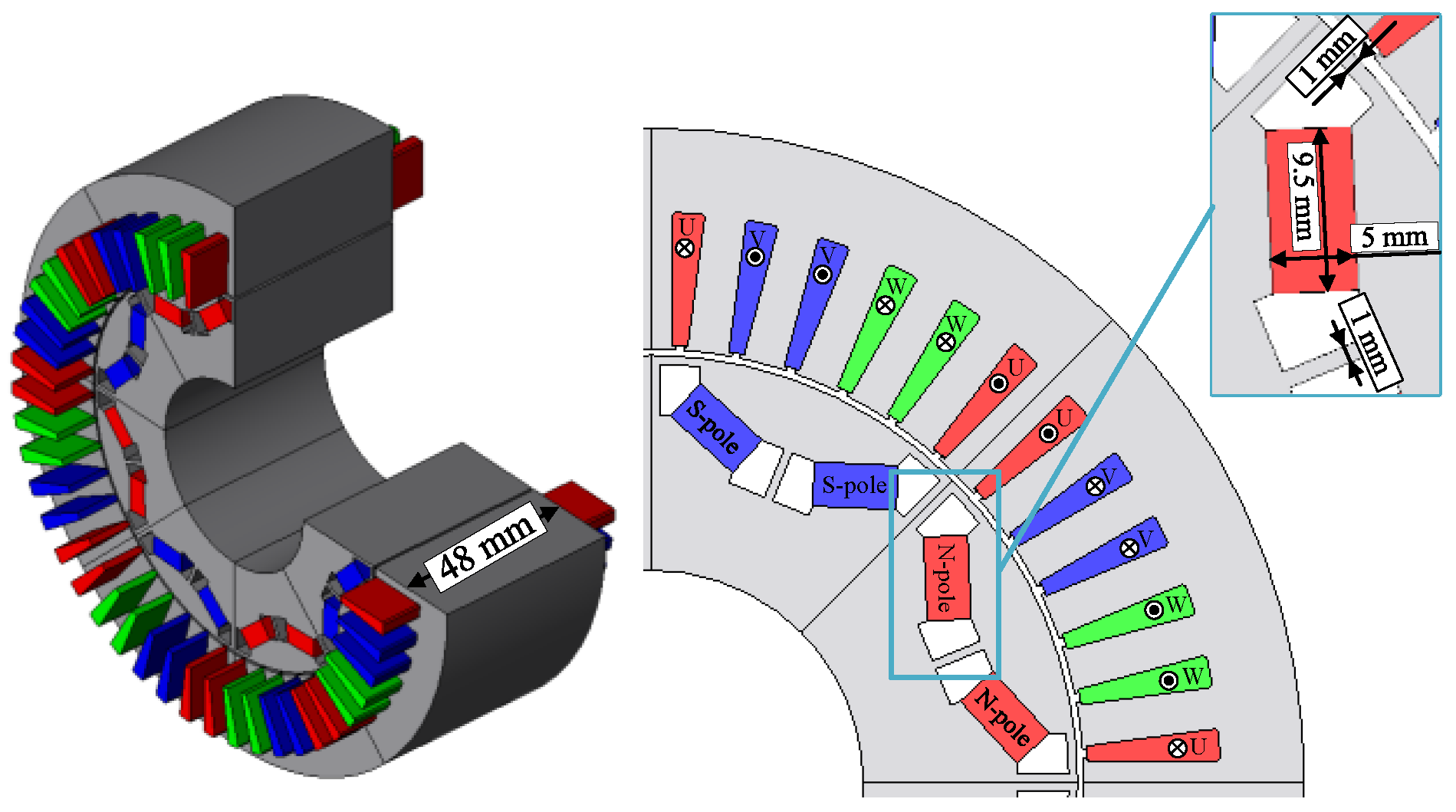

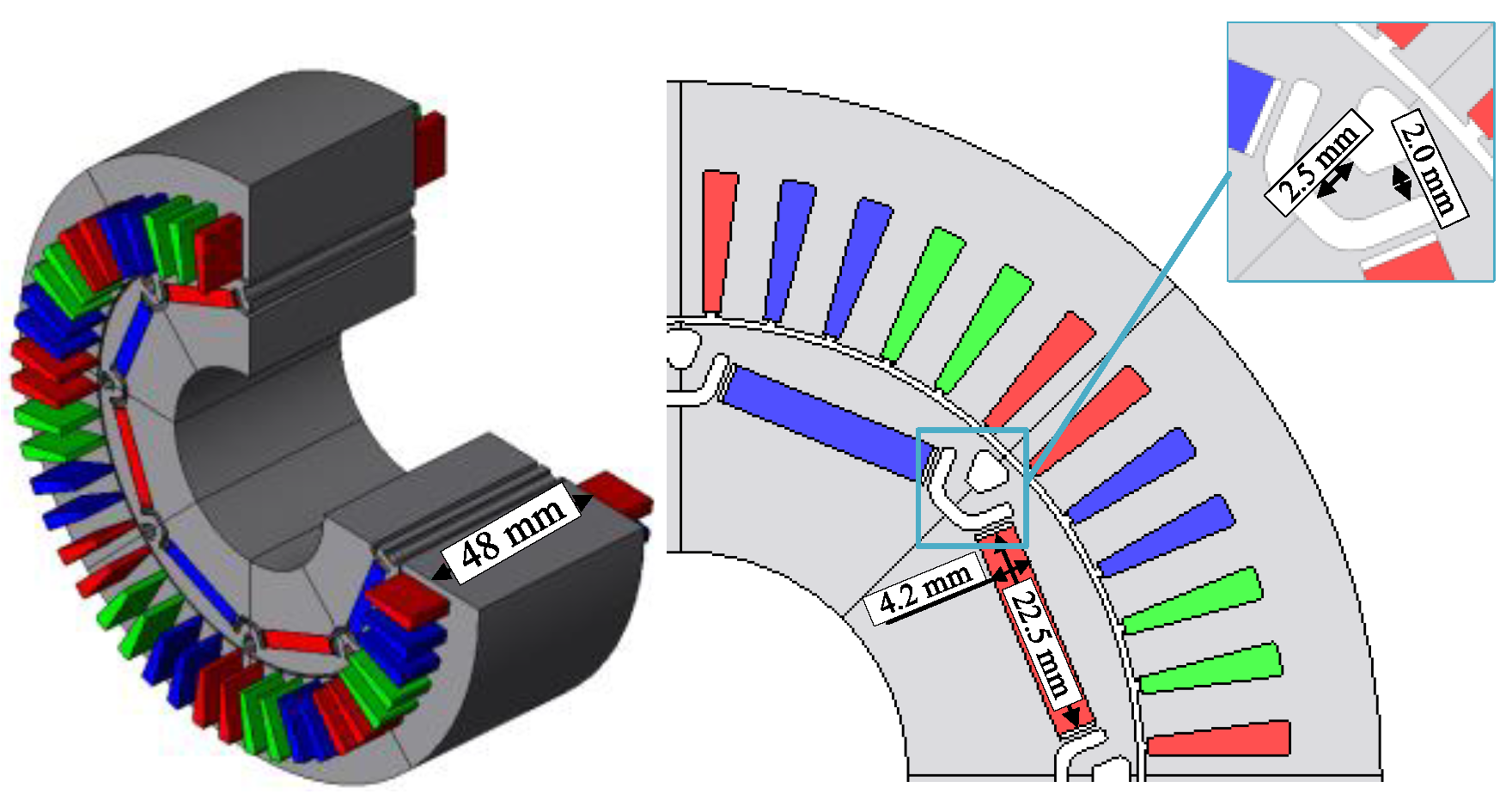



| Parameter | Value |
|---|---|
| Number of poles and slots | 8 poles, 48 slots |
| Armature winding | 6 turns/slot, 0.15 Ω |
| Modulation winding | 120 turns, 1.8 Ω |
| Stator diameter | ϕ148 mm |
| Rotor diameter | ϕ96.6 mm |
| Stack length | 63 mm |
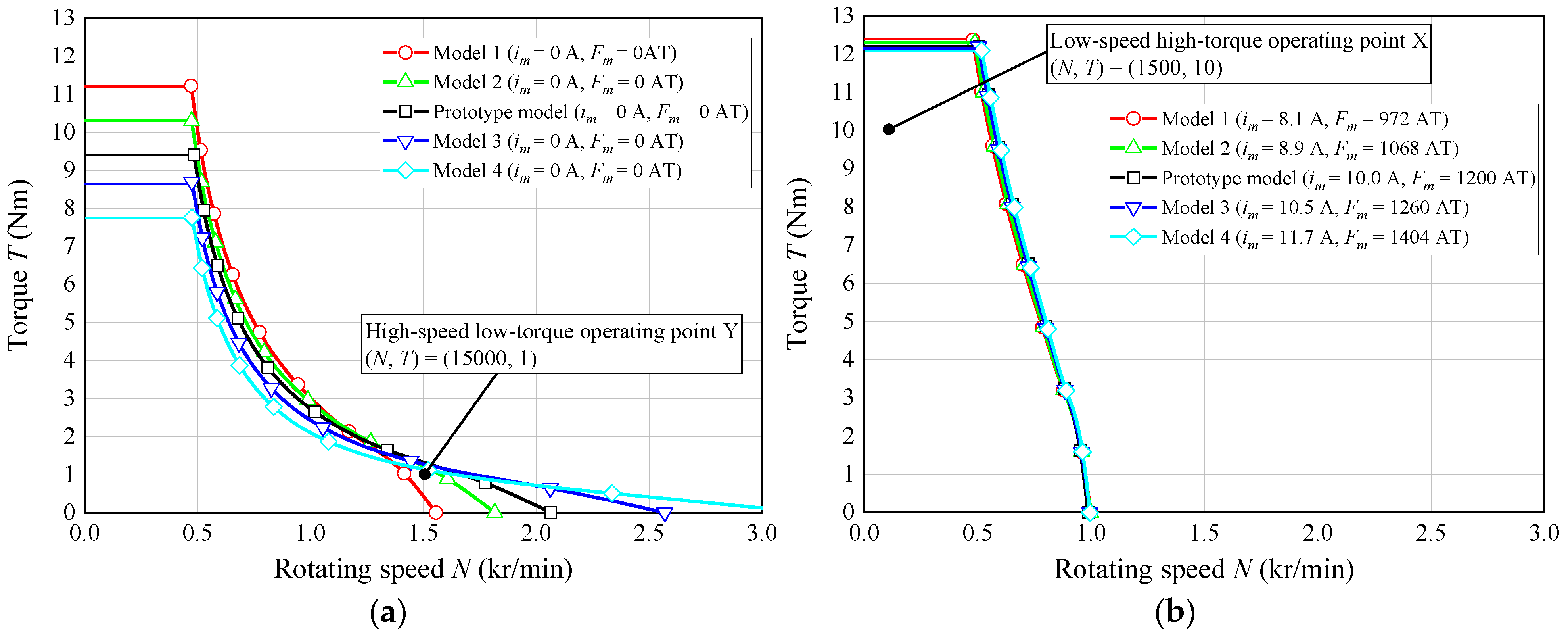
| Model | Saturation Area A | Saturation Area B |
|---|---|---|
| Model 1 | 2.1 mm | 1.00 mm, 0.5 mm |
| Model 2 | 2.7 mm | 1.25 mm, 0.5 mm |
| Model 3 | 3.7 mm | 1.75 mm, 0.5 mm |
| Model 4 | 4.3 mm | 2.00 mm, 0.5 mm |
| Parameter | Model 1 | Model 2 | Prototype Model | Model 3 | Model 4 | |
|---|---|---|---|---|---|---|
| Max. Ψa | im (A) | 8.1 | 8.9 | 10.0 | 10.5 | 11.7 |
| Ψa (mWb) | 39.6 | 39.6 | 39.6 | 39.6 | 39.6 | |
| Copper loss (W) | 118 | 143 | 180 | 198 | 246 | |
| Min. Ψa | im (A) | 0 | 0 | 0 | 0 | 0 |
| Ψa (mWb) | 25.4 | 21.7 | 19.4 | 15.4 | 12.3 | |
| Copper loss (W) | 0 | 0 | 0 | 0 | 0 | |
| Controllable range of Ψa (mWb) | 14.2 | 17.9 | 20.2 | 24.2 | 27.3 | |
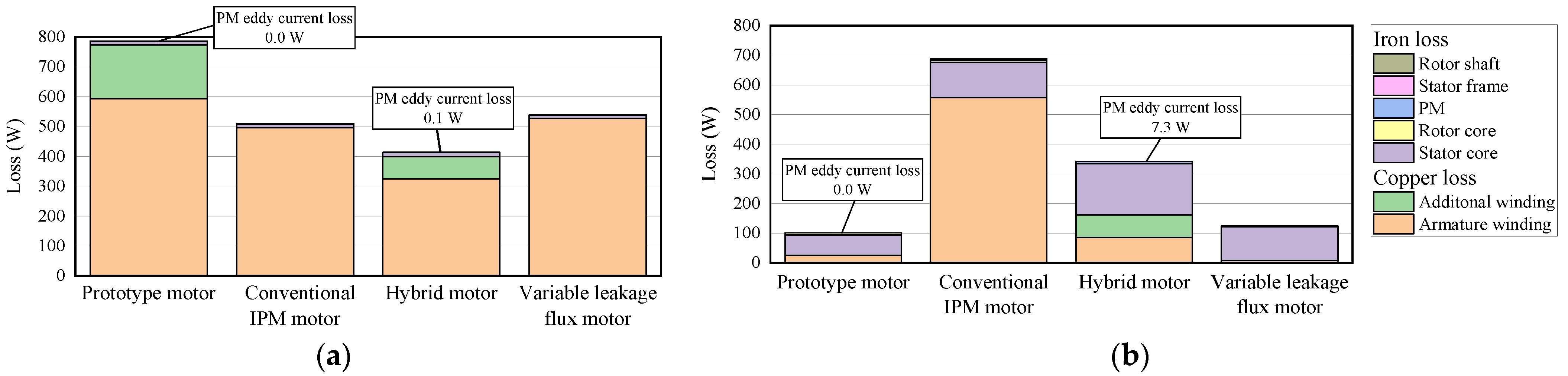
| Parameter | Prototype Motor | Conventional IPM Motor | Hybrid Motor | Variable Leakage Flux Motor | |
|---|---|---|---|---|---|
| Manipulating variable for magnetic field control | Modulation current | d-axis current | Field current | q-axis current | |
| im | id | if | iq | ||
| Stator core diameter (mm) | ϕ148 | ← | ← | ← | |
| Stack length (mm) | 63 | 48 | 55.8 | 48 | |
| (Core stack length: 48) | (Core stack length: 48) | ||||
| Number of turns | Armature winding | 6 turns/slot | ← | ← | ← |
| Additional winding | 120 turns | - | 120 turns | - | |
| Core volume (mm3) | 577,000 | 564,000 | 542,000 | 572,000 | |
| Copper volume (mm3) | Armature winding | 337,000 | 307,000 | 323,000 | 307,000 |
| Additional winding | 59,000 | - | 31,000 | - | |
| PM volume (mm3) | 36,000 | ← | ← | ← | |
| Magnetic circuit volume (mm3) | 1,440,000 | 908,000 | 1,370,000 | 915,000 | |
| Max. current density (Arms/mm2) | 20 | ← | ← | ← | |
| Resistance | Armature winding | 0.150 | 0.137 | 0.144 | 0.137 |
| (Ω) | Additional winding | 1.80 | - | 4.29 | - |
| Max. torque (Nm) | 12.2 (im = 10 A, iq = 80 A) | 14.4 (iq = 80 A) | 16.6 (if = 4.2 A, iq = 80 A) | 13.9 (iq = 80 A) | |
| Parameter | Prototype Motor | Conventional IPM Motor | Hybrid Motor | Variable Leakage Flux Motor | |
|---|---|---|---|---|---|
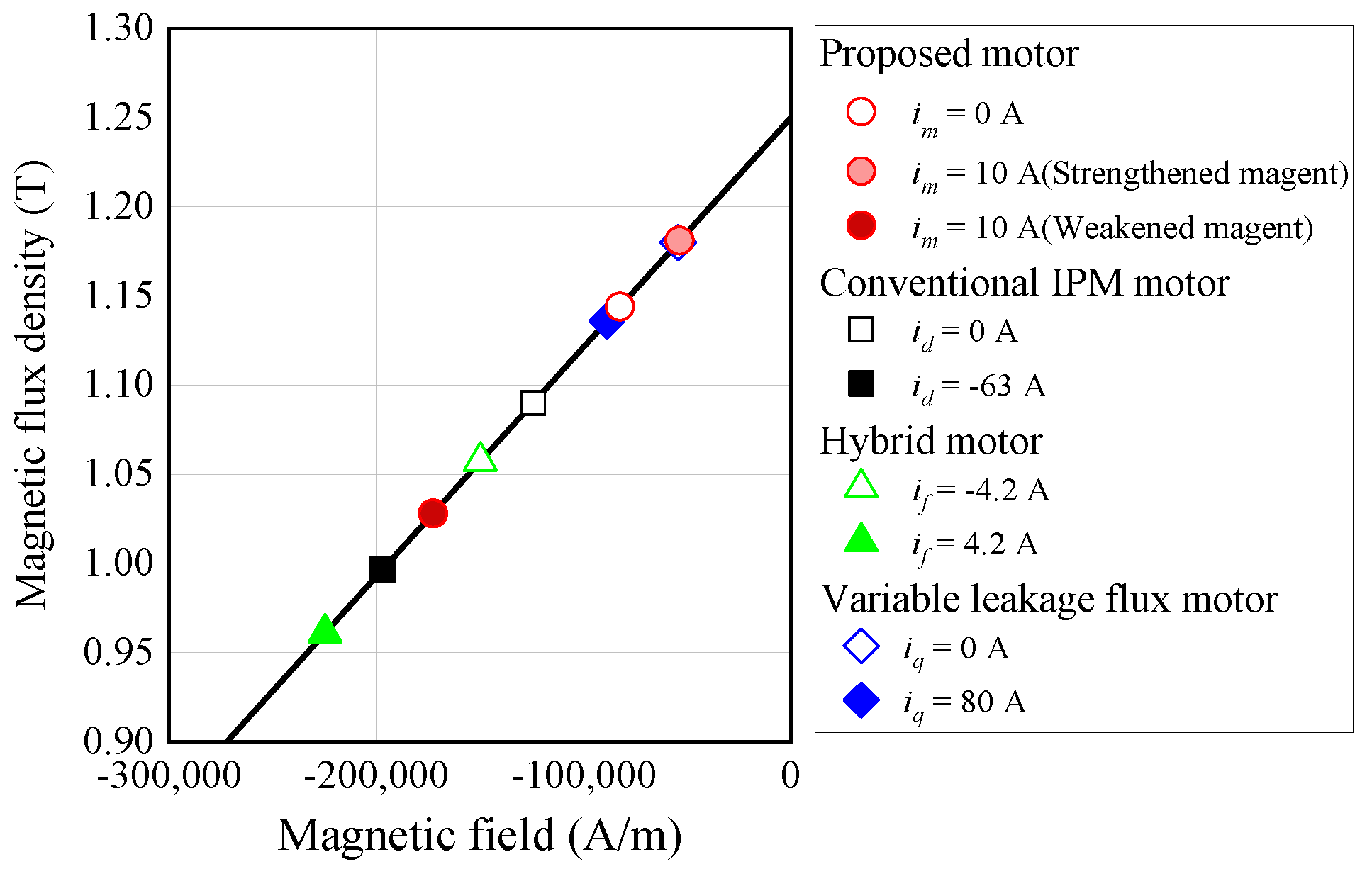
| Max. Ψa or Max. Ψd | Variable value (A) | im = 10 | id = 0 | if = 4.2 | iq = 80 |
| Ψa or Ψd (mWb) | Ψa = 39.6 | Ψd = 41.7 | Ψa =53.0 | Ψa = 43.5 | |
| Copper loss (W) | 180 | 0 | 75.7 | 877 | |
| Min. Ψa or Min. Ψd | Variable value (A) | im = 0 | id = −63 | if = −4.2 | iq = 0 |
| Ψa or Ψd (mWb) | Ψa = 19.1 | Ψd = 21.2 | Ψa =32.3 | Ψa = 33.3 | |
| Copper loss (W) | 0 | 544 | 75.7 | 0 | |
| Controllable range of Ψa or Ψd (mWb) | 20.5 | 20.5 | 20.7 | 10.1 | |
| Parameter | Symbol | Value |
|---|---|---|
| DC-bus voltage | Vdc | 270 V |
| Dead time | td | 4 μs |
| Switching frequency | fsw | 10 kHz |
| Crossover frequency of current control | ωc | 4000 rad/s |
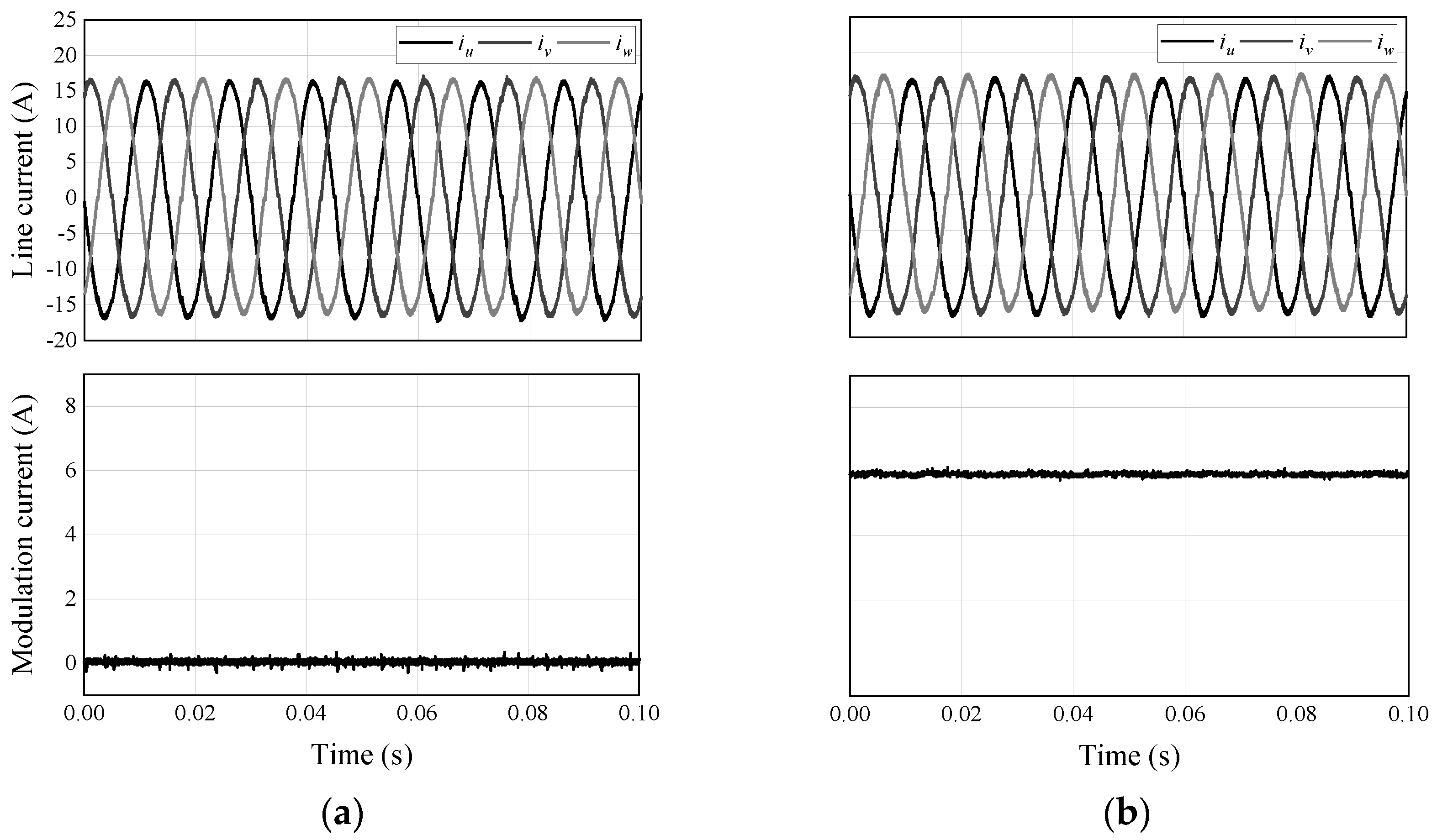
| Modulation Current | q-Axis Current | Output Torque |
|---|---|---|
| DC 0 Adc | 20 A | 1.49 Nm |
| DC 6 Adc | 20 A | 2.40 Nm |
| Operating Point | Prototype Motor | Conventional IPM Motor | Hybrid Motor | Variable Leakage Flux Motor |
|---|---|---|---|---|
| X | im = 10 A, iq = 63 A | id = 0.0 A, iq = 58 A | if = 4.2 A, iq = 47 A | iq = 62 A |
| Y | im = 0.0 A, iq = 13 A | id = −63 A, iq = 10 A | if = −4.2 A, iq = 7.7 A | iq = 7.5 A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwama, K.; Noguchi, T. Operation Characteristics of Adjustable Field IPMSM Utilizing Magnetic Saturation. Energies 2022, 15, 52. https://doi.org/10.3390/en15010052
Iwama K, Noguchi T. Operation Characteristics of Adjustable Field IPMSM Utilizing Magnetic Saturation. Energies. 2022; 15(1):52. https://doi.org/10.3390/en15010052
Chicago/Turabian StyleIwama, Kiyohiro, and Toshihiko Noguchi. 2022. "Operation Characteristics of Adjustable Field IPMSM Utilizing Magnetic Saturation" Energies 15, no. 1: 52. https://doi.org/10.3390/en15010052
APA StyleIwama, K., & Noguchi, T. (2022). Operation Characteristics of Adjustable Field IPMSM Utilizing Magnetic Saturation. Energies, 15(1), 52. https://doi.org/10.3390/en15010052






