Self-Balancing Supercapacitor Energy Storage System Based on a Modular Multilevel Converter
Abstract
:1. Introduction
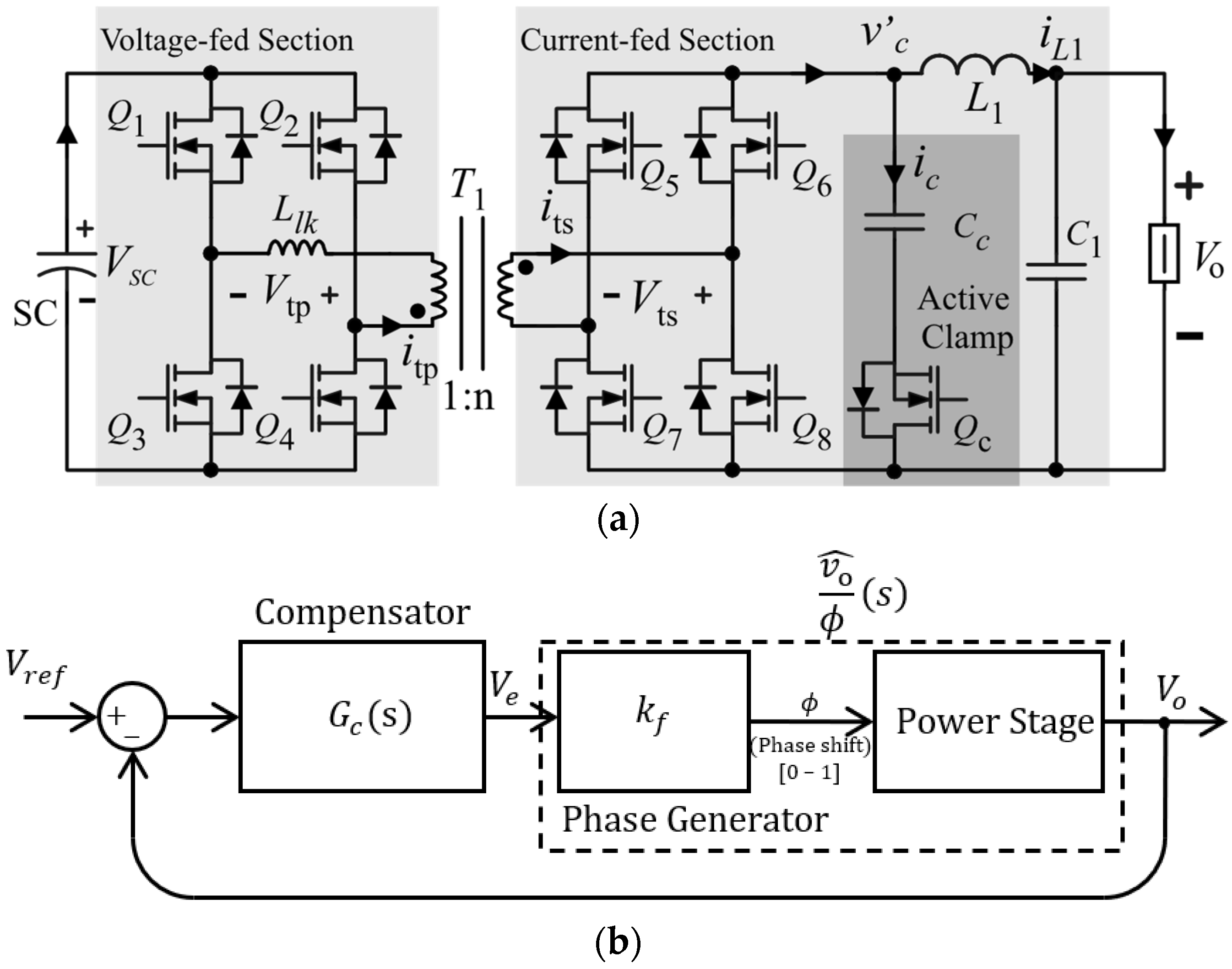
2. Submodule Operation
2.1. Buck-Mode (C → Vo)
2.2. Boost-Mode (Vo → )
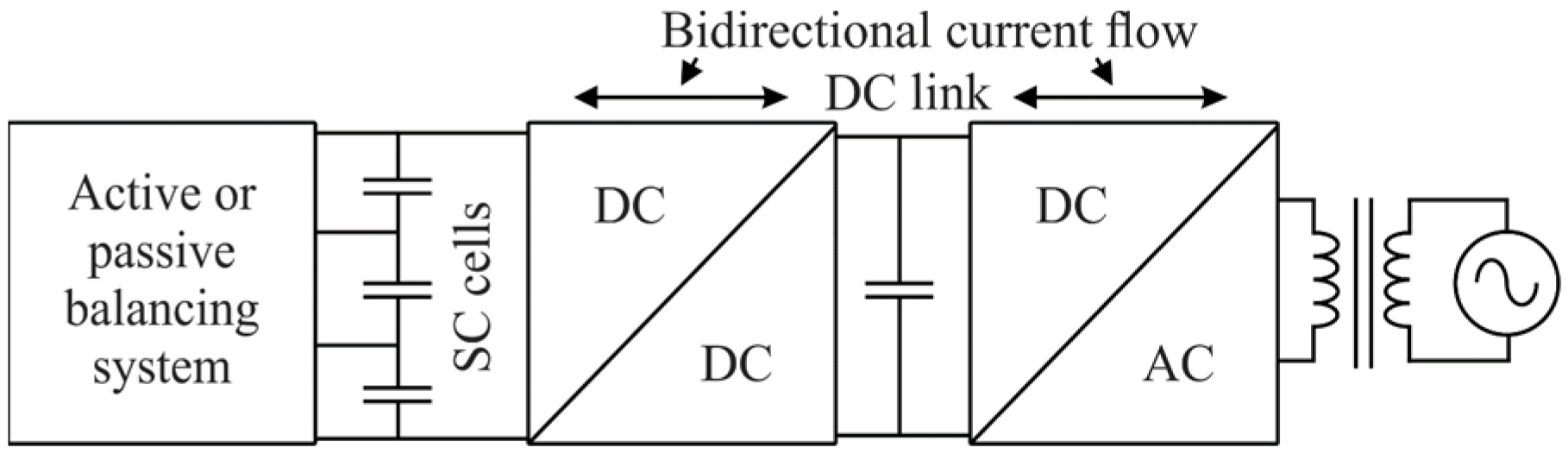
3. Modular Multilevel ESS
3.1. Energy Storage Device
3.2. DC/DC Conversion with Galvanic Isolation
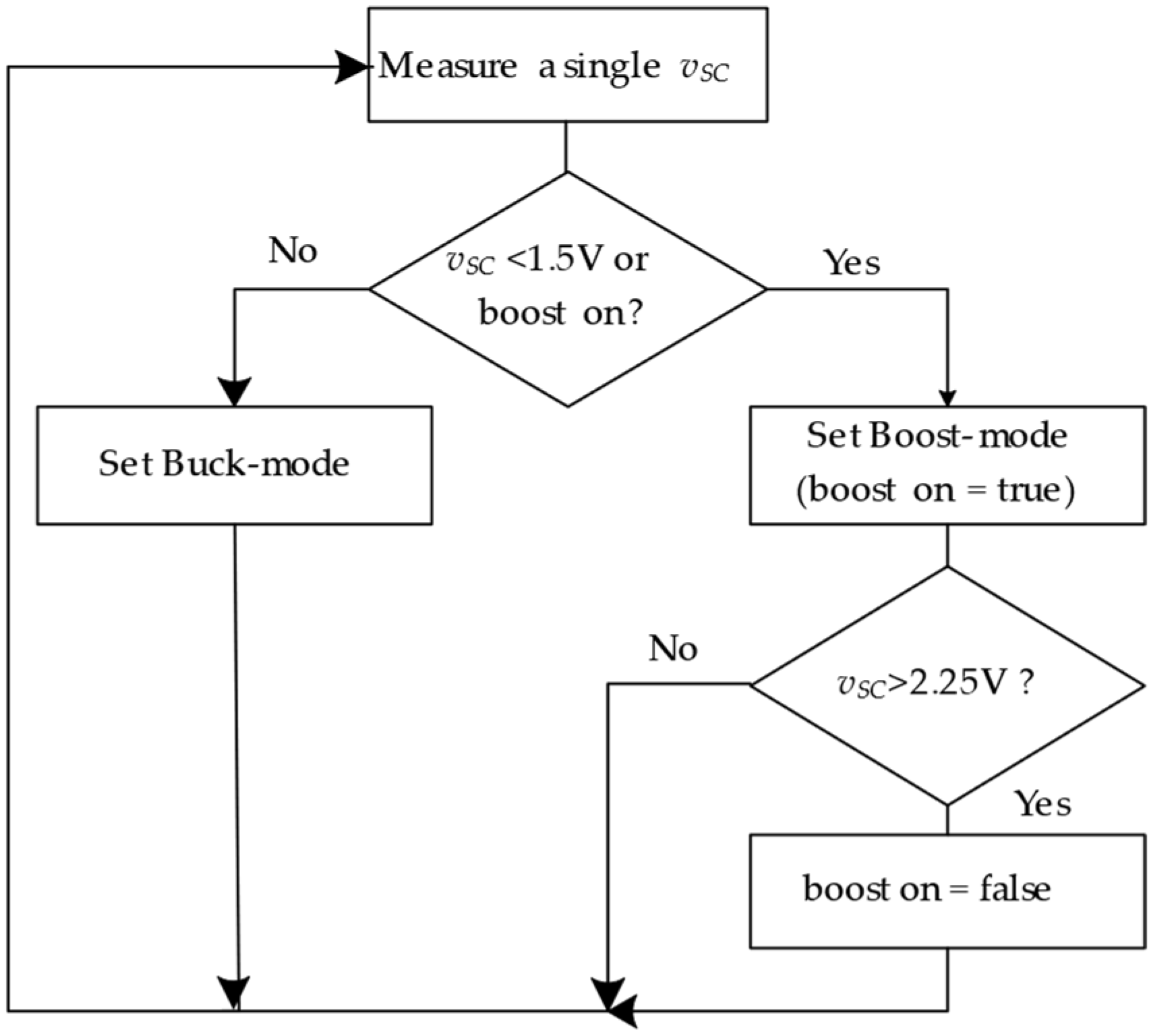
3.3. Balancing Method
3.4. DC/AC Conversion
3.5. Grid Connection with Bidirectional Power Flow
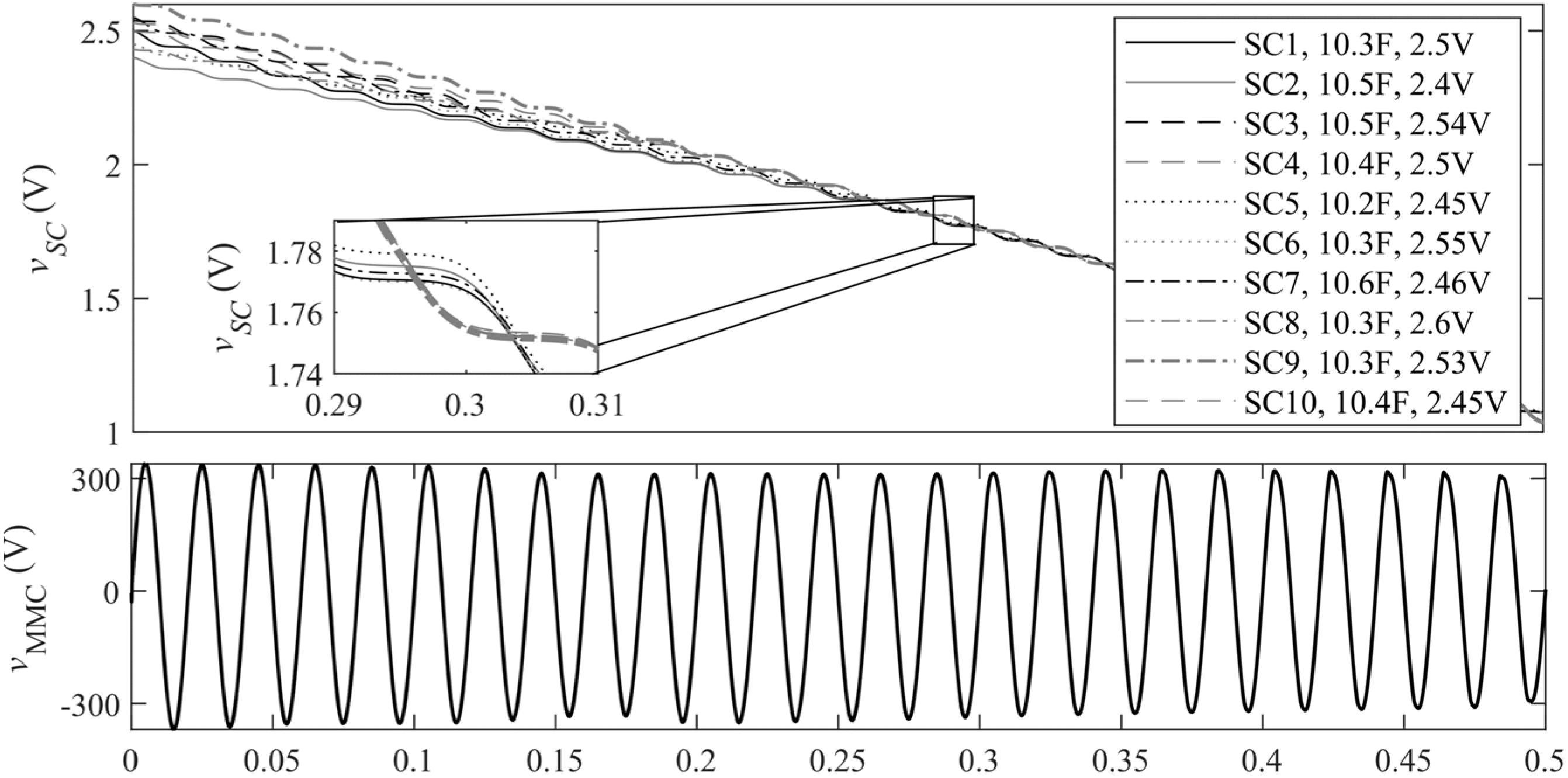
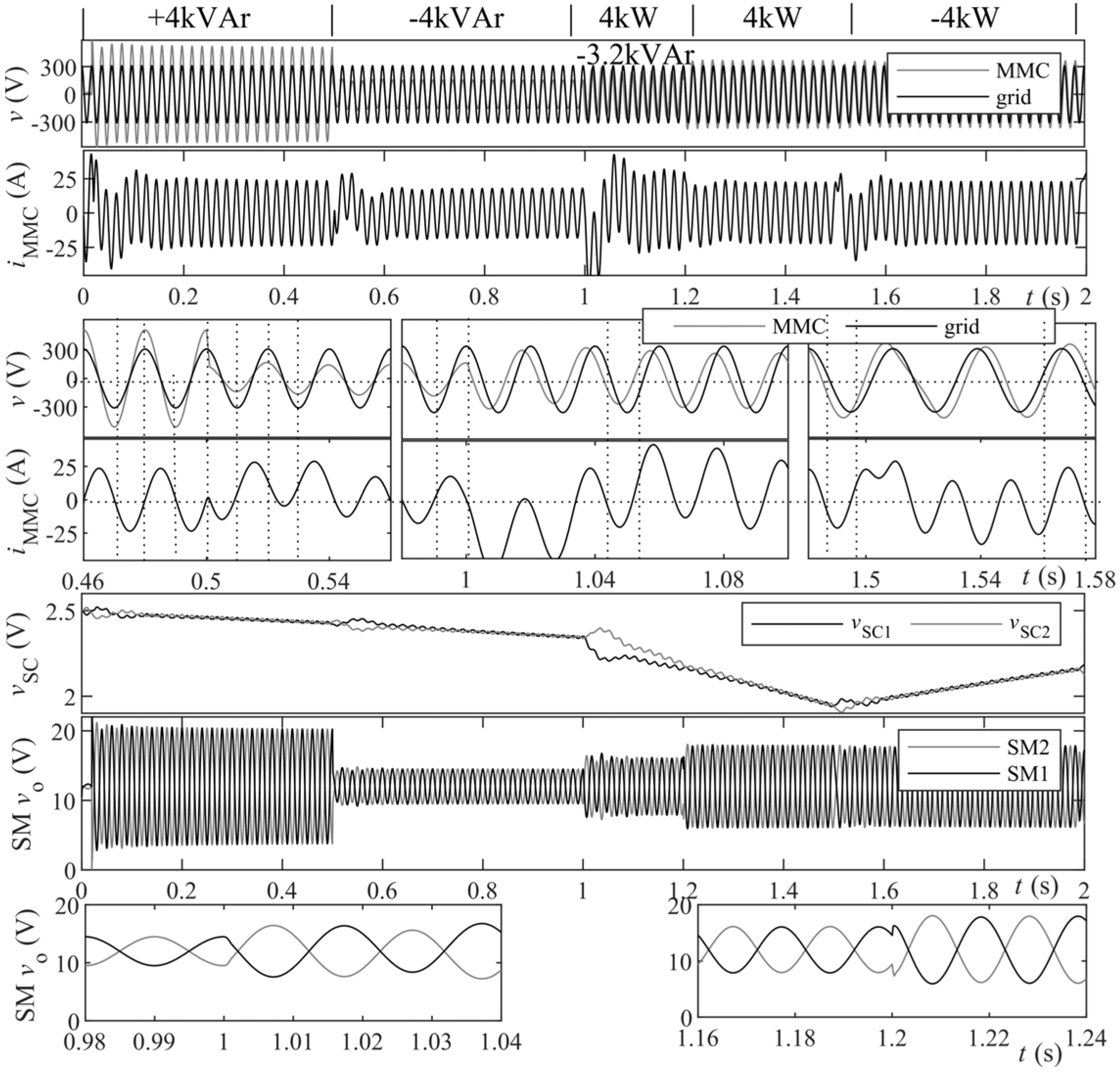
4. Simulation Results
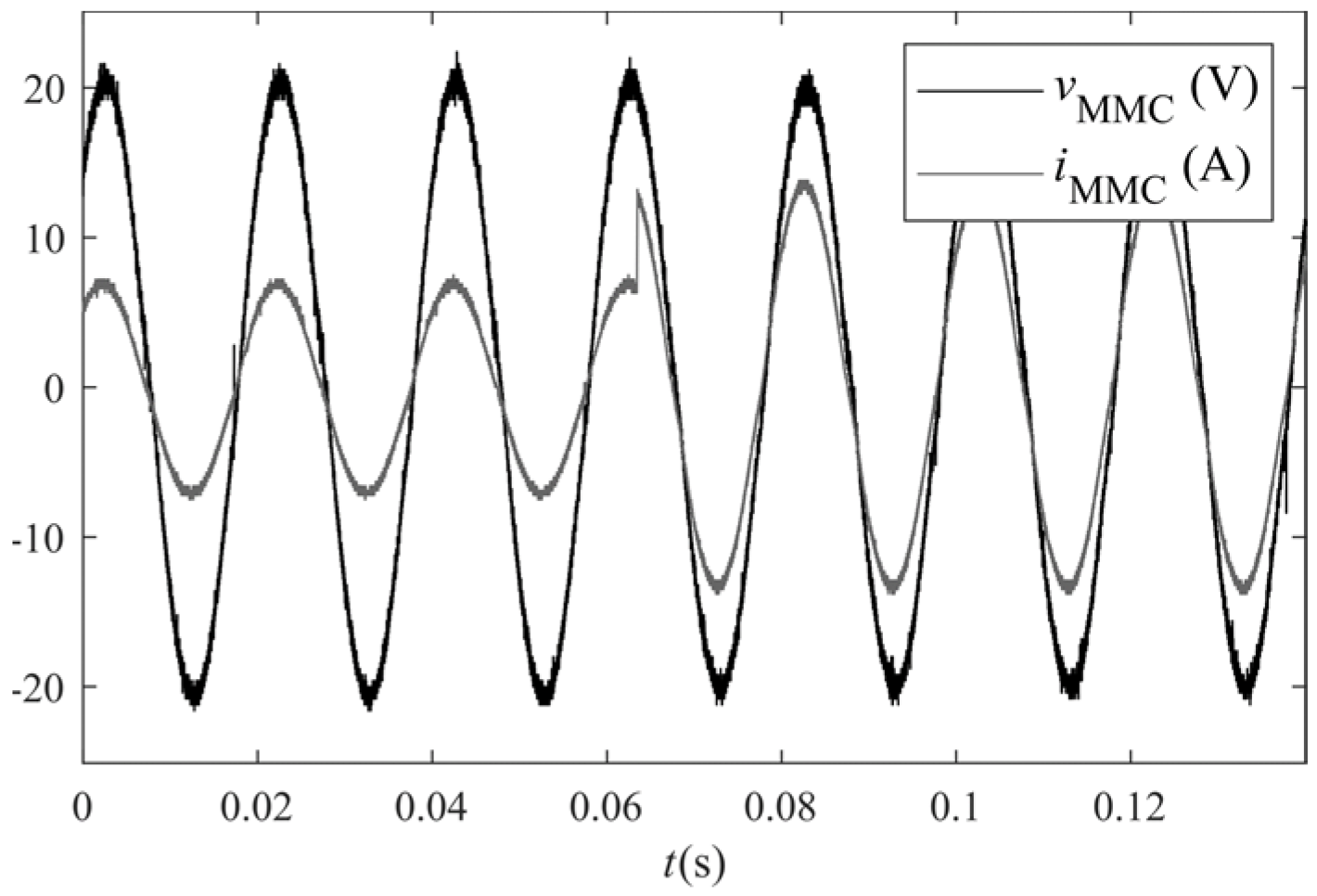
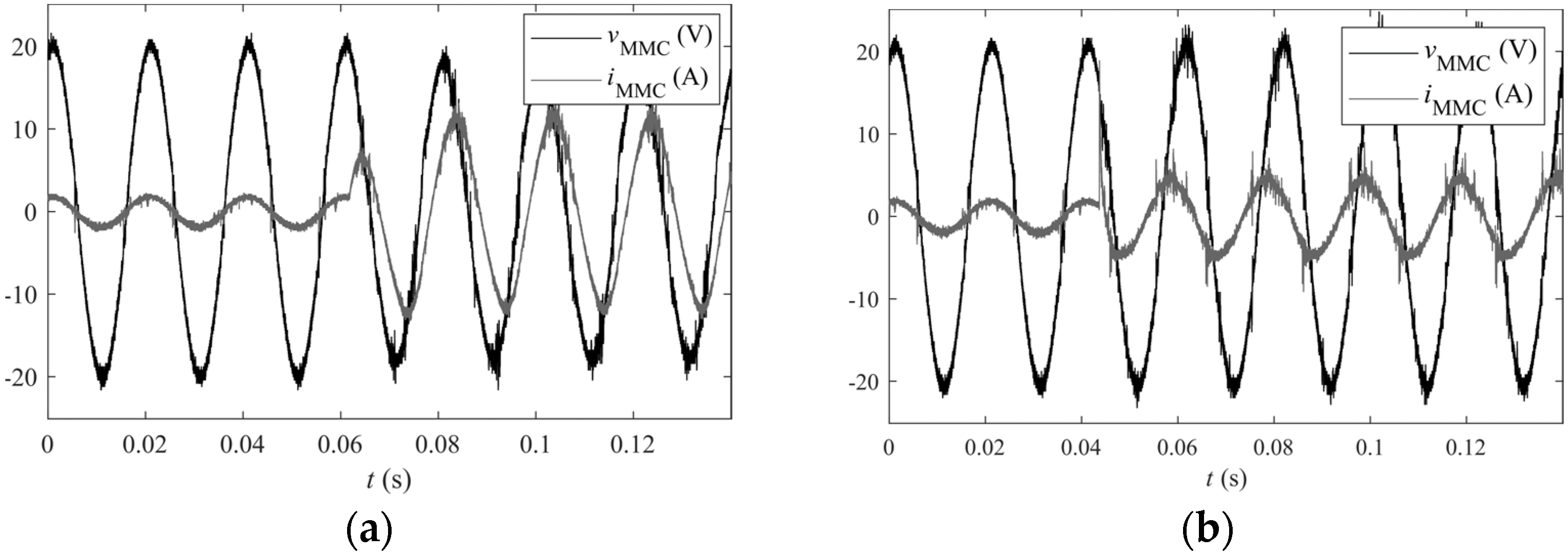
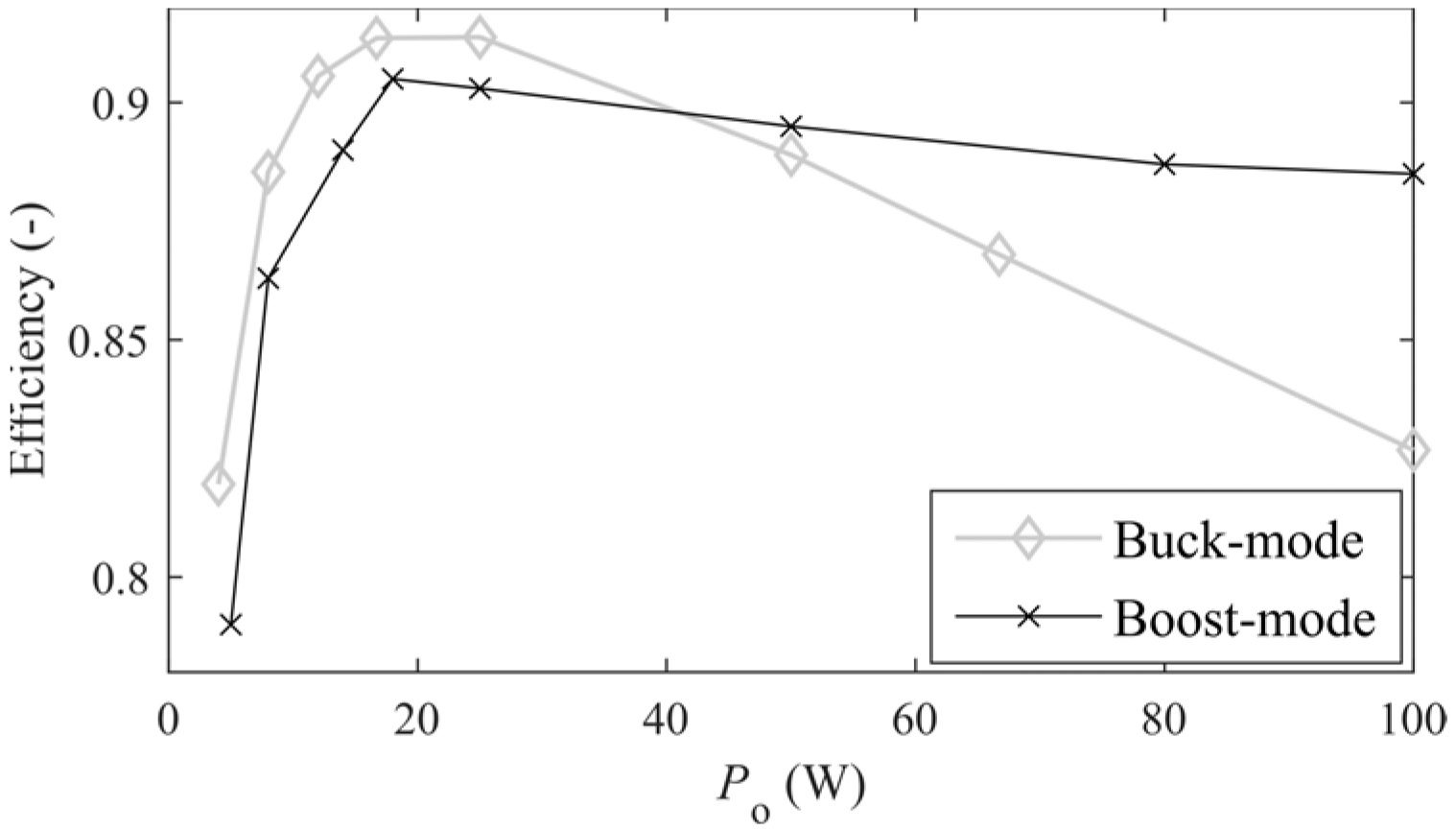
5. Experimental Results
Comparsion with Other ESSs
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ESS | Energy storage system |
| MMC | Modular multilevel converter |
| SM | Submodule |
| SC | Supercapacitor |
| THD | Total harmonic distortion |
| MCU | Microcontroller unit |
Nomenclature
| vMMC | Output voltage port of the MMC |
| LC | Coupling inductor |
| vgrid | Grid voltage |
| L1 | Output inductor at SM level |
| C1 | Output capacitor at SM level |
| VSC | Supercapacitor voltage at SM level |
| Vo | Output voltage at SM level |
| Cc | Clamp capacitor at SM level |
| Qc | Clamp switch at SM level |
| Q1 to Q4 | Full-bridge voltage-fed section switches at SM level |
| T1 | High-frequency transformer at SM level. |
| Q5 to Q8 | Full-bridge current-fed section switches at SM level. |
| t1 to t6 | time intervals for the DC/DC converter operation |
| Switching period | |
| Phase-shift angle | |
| Duty cycle at boost-mode | |
| Leakage inductance | |
| Lmag | Magnetizing inductance |
| vtp | Transformer’s primary voltage |
| vts | Transformer’s secondary voltage |
| Clamp voltage node | |
| n | Transformer’s turn-ratio |
| Clamp capacitor’s voltage | |
| Leakage inductor’s current | |
| Output inductor’s current | |
| Clamp capacitor’s current | |
| Leakage inductor’s voltage | |
| Resonant frequency between the capacitor’s clamp and the leakage inductance | |
| Io | Output current at SM level |
| M | Voltage transfer function at SM level |
| Switching frequency | |
| Type-III controller transfer function at SM level | |
| Lead-lag alfa parameter of the type-III controller | |
| Gain parameter of the type-III controller | |
| T | Time constant of the type-III controller |
| Lead-lag frequency parameter of the type-III controller | |
| Low pass filter frequency of the type-III controller | |
| Error signal for the supercapacitor balancing embedded controller at each SM | |
| Voltage reference for each SM at MMC level | |
| Current reference for each SM at MMC level | |
| MMC current |
References
- Farhadi, M.; Mohammed, O. Energy Storage Technologies for High-Power Applications. IEEE Trans. Ind. Appl. 2016, 52, 1953–1962. [Google Scholar] [CrossRef]
- Khaligh, A.; Li, Z. Battery, Ultracapacitor, Fuel Cell, and Hybrid Energy Storage Systems for Electric, Hybrid Electric, Fuel Cell, and Plug-in Hybrid Electric Vehicles: State of the Art. IEEE Trans. Veh. Technol. 2010, 59, 2806–2814. [Google Scholar] [CrossRef]
- Kotz, R.; Carlen, M. Principles and Applications of Electrochemical Capacitors. Electrochim. Acta 2000, 45, 2483–2498. [Google Scholar] [CrossRef]
- Ibanez, F.; Vadillo, J.; Echeverria, J.M.; Fontan, L. Design Methodology of a Balancing Network for Supercapacitors. In Proceedings of the 2013 4th IEEE/PES Innovative Smart Grid Technologies Europe (ISGT Europe 2013), Lyngby, Denmark, 6–9 October 2013; Volume 2, pp. 1–5. [Google Scholar]
- Li, L.; Huang, Z.; Li, H.; Peng, J. A Rapid Cell Voltage Balancing Scheme for Supercapacitor Based Energy Storage Systems for Urban Rail Vehicles. Electr. Power Syst. Res. 2017, 142, 329–340. [Google Scholar] [CrossRef]
- Falck, J.; Felgemacher, C.; Rojko, A.; Liserre, M.; Zacharias, P. Reliability of Power Electronic Systems. IEEE Ind. Electron. Mag. 2018, 12, 24–35. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An Industry-Based Survey of Reliability in Power Electronic Converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Lone, S.A.; Iqbal, S.J.; Ahmad, M.; Ismail, M. Super-Capacitor Based Energy Storage System for Improved Load Frequency Control. Electr. Power Syst. Res. 2009, 79, 226–233. [Google Scholar]
- Partridge, J.; Abouelamaimen, D.I. The Role of Supercapacitors in Regenerative Braking Systems. Energies 2019, 12, 2683. [Google Scholar] [CrossRef] [Green Version]
- Kerdphol, T.; Rahman, F.S.; Watanabe, M.; Mitani, Y. Robust Virtual Inertia Control of a Low Inertia Microgrid Considering Frequency Measurement Effects. IEEE Access 2019, 7, 57550–57560. [Google Scholar] [CrossRef]
- Khalid, M. A Review on the Selected Applications of Battery-Supercapacitor Hybrid Energy Storage Systems for Microgrids. Energies 2019, 12, 4559. [Google Scholar] [CrossRef] [Green Version]
- Ibañez, F.M.; Vadillo, J.; Echeverria, J.M.; Fontán, L. 100 kW Bidirectional DC/DC Converter for a Supercapacitor Stack. In Proceedings of the 2013 4th IEEE/PES Innovative Smart Grid Technologies Europe (ISGT Europe 2013), Lyngby, Denmark, 6–9 October 2013; pp. 1–5. [Google Scholar]
- Ibanez, F.M.; Echeverria, J.M.; Vadillo, J.; Fontan, L. Multimode Step-up Bidirectional Series Resonant DC/DC Converter Using Continuous Current Mode. IEEE Trans. Power Electron. 2015, 30, 1393–1402. [Google Scholar] [CrossRef]
- Luna, M.; Sferlazza, A.; Accetta, A.; Di Piazza, M.C.; La Tona, G.; Pucci, M. Modeling and Performance Assessment of the Split-Pi Used as a Storage Converter in All the Possible DC Microgrid Scenarios. Part I: Theoretical Analysis. Energies 2021, 14, 4902. [Google Scholar] [CrossRef]
- Luna, M.; Sferlazza, A.; Accetta, A.; Di Piazza, M.C.; La Tona, G.; Pucci, M. Modeling and Performance Assessment of the Split-Pi Used as a Storage Converter in All the Possible DC Microgrid Scenarios. Part II: Simulation and Experimental Results. Energies 2021, 14, 5616. [Google Scholar] [CrossRef]
- Wang, L.; Guo, J.; Xu, C.; Wu, T.; Lin, H. Article Hybrid Model Predictive Control Strategy of Supercapacitor Energy Storage System Based on Double Active Bridge. Energies 2019, 12, 2134. [Google Scholar] [CrossRef] [Green Version]
- Ibanez, F.M. Bidirectional Series Resonant DC/AC Converter for Energy Storage Systems. IEEE Trans. Power Electron. 2019, 34, 3429–3444. [Google Scholar] [CrossRef]
- Ertl, H.; Kolar, J.W.; Zach, F.C. A Novel Multicell DC-AC Converter for Applications in Renewable Energy Systems. IEEE Trans. Ind. Electron. 2002, 49, 1048–1057. [Google Scholar] [CrossRef]
- Allebrod, S.; Hamerski, R.; Marquardt, R. New Transformerless, Scalable Modular Multilevel Converters for HVDC-Transmission. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 174–179. [Google Scholar]
- Ferreira, J.A. The Multilevel Modular DC Converter. IEEE Trans. Power Electron. 2013, 28, 4460–4465. [Google Scholar] [CrossRef]
- Ibanez, F. Quasi-Resonant Multilevel Converter for Supercapacitor Energy Storage Systems. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Turin, Italy, 26–29 September 2017; pp. 1–6. [Google Scholar]
- Mukherjee, N.; Tricoli, P. Modular Multilevel Converter Based Supercapacitor Integration Strategies and Their Comparative Evaluation for Railway Traction Drive Systems. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar]
- Hernandez, F.D.; Ibanez, F.; Samanbakhsh, R.; Velazquez, R. A Comparative Study of Energy Storage Systems Based on Modular Multilevel Converters. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–5. [Google Scholar]
- Errigo, F.; Venet, P.; Chedot, L.; Sari, A. Optimal Supercapacitor Pack Sizing for Modular Multilevel Converter with Integrated Energy Storage System. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 20–22 February 2018; pp. 1760–1766. [Google Scholar]
- Coppola, M.; Del Pizzo, A.; Iannuzzi, D. A Power Traction Converter Based on Modular Multilevel Architecture Integrated with Energy Storage Devices. In Proceedings of the 2012 Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 16–18 October 2012; pp. 1–7. [Google Scholar]
- Montesinos-Miracle, D.; Massot-Campos, M.; Bergas-Jane, J.; Galceran-Arellano, S.; Rufer, A. Design and Control of a Modular Multilevel DC/DC Converter for Regenerative Applications. IEEE Trans. Power Electron. 2013, 28, 3970–3979. [Google Scholar] [CrossRef]
- Wang, K.; Lee, F.C.; Lai, J. Operation Principles of Bi-Directional Full-Bridge DC/DC Converter with Unified Soft-Switching Scheme and Soft-Starting Capability. In Proceedings of the Fifteenth Annual IEEE Applied Power Electronics Conference and Exposition (Cat. No.00CH37058), New Orleans, LA, USA, 6–10 February 2002; pp. 111–118. [Google Scholar]
- Prasanna, U.R.; Rathore, A.K. Extended Range ZVS Active-Clamped Current-Fed Full-Bridge Isolated DC/DC Converter for Fuel Cell Applications: Analysis, Design, and Experimental Results. IEEE Trans. Ind. Electron. 2013, 60, 2661–2672. [Google Scholar]
- Freijedo, F.D.; Doval-Gandoy, J.; Lopez, O.; Cabaleiro, J. Robust Phase Locked Loops Optimized for DSP Implementation in Power Quality Applications. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 3052–3057. [Google Scholar]
- Qin, Y.; Hua, H.; Cao, J. Stochastic Optimal Control Scheme for Battery Lifetime Extension in Islanded Microgrid via a Novel Modeling Approach. IEEE Trans. Smart Grid 2019, 10, 4467–4475. [Google Scholar] [CrossRef]
- Hua, H.; Qin, Y.; Cao, J. Coordinated Frequency Control for Multiple Microgrids in Energy Internet: A Stochastic H∞ Approach. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 810–815. [Google Scholar]











| Component | Value | Details |
|---|---|---|
| SC | 10F PSIM and 3000F prototype | ESR = 0.4 mΩ |
| Q1 to Q4 | 3 × BSC009NE2LS5 | rDS(on) = 0.9 mΩ |
| Q5 to Q8 and Qc | 2 × BSC022N04LS6 | rDS(on) = 2.2 mΩ |
| T1 core and LMAG | 5.7 µH | ELP32, N87 material |
| Turns ratio | 1:8 | - |
| CC | 6 × 0.068 µF in parallel | 0805 X7R |
| L1 | 10 µH | EPCOS B82559 |
| C1 | 2 × 100 µF in parallel | Solid tantalum |
| TS | 10 µS | 1/TS = Fsw = 100 kHz |
| LC | 1 mH | Coupling inductor |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernandez, F.D.; Samanbakhsh, R.; Ibanez, F.M.; Martin, F. Self-Balancing Supercapacitor Energy Storage System Based on a Modular Multilevel Converter. Energies 2022, 15, 338. https://doi.org/10.3390/en15010338
Hernandez FD, Samanbakhsh R, Ibanez FM, Martin F. Self-Balancing Supercapacitor Energy Storage System Based on a Modular Multilevel Converter. Energies. 2022; 15(1):338. https://doi.org/10.3390/en15010338
Chicago/Turabian StyleHernandez, Fernando Davalos, Rahim Samanbakhsh, Federico Martin Ibanez, and Fernando Martin. 2022. "Self-Balancing Supercapacitor Energy Storage System Based on a Modular Multilevel Converter" Energies 15, no. 1: 338. https://doi.org/10.3390/en15010338
APA StyleHernandez, F. D., Samanbakhsh, R., Ibanez, F. M., & Martin, F. (2022). Self-Balancing Supercapacitor Energy Storage System Based on a Modular Multilevel Converter. Energies, 15(1), 338. https://doi.org/10.3390/en15010338







