Numerical Assessment and Parametric Optimization of a Piezoelectric Wind Energy Harvester for IoT-Based Applications
Abstract
1. Introduction
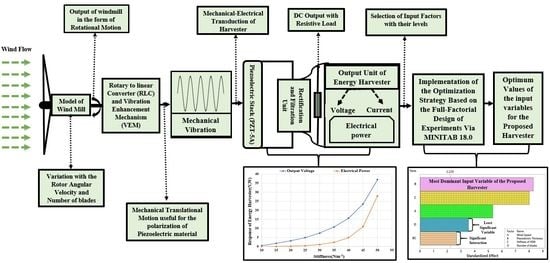
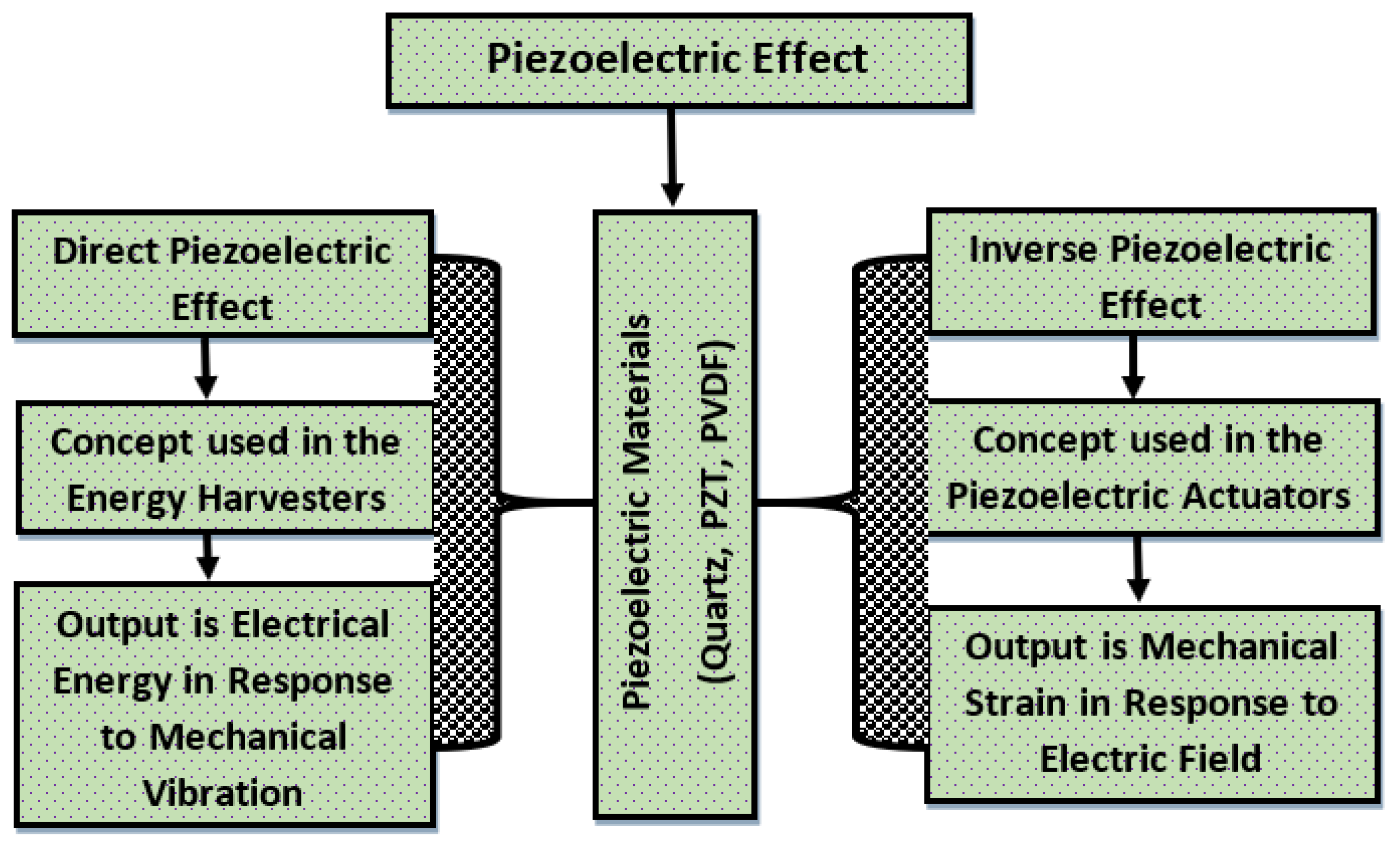
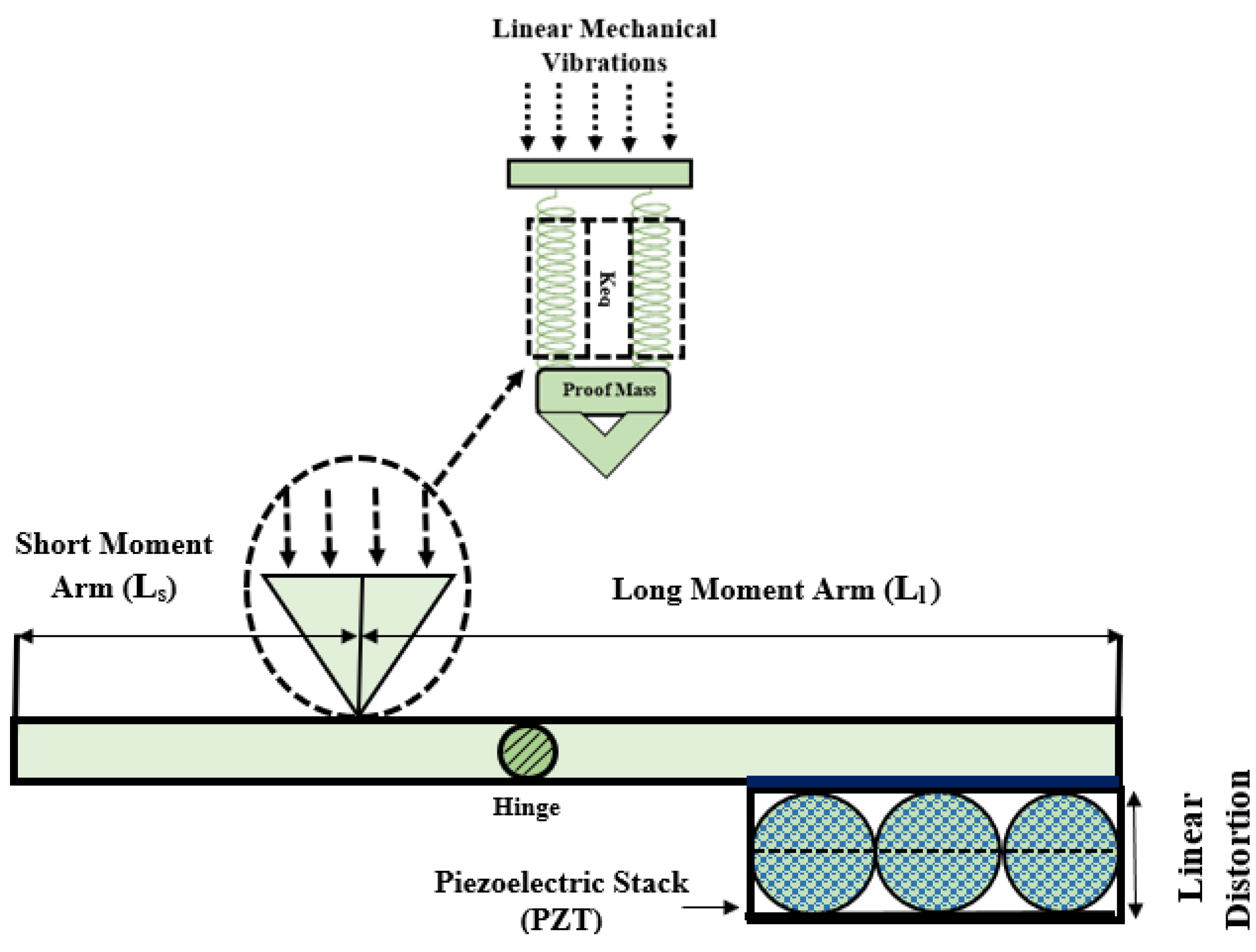
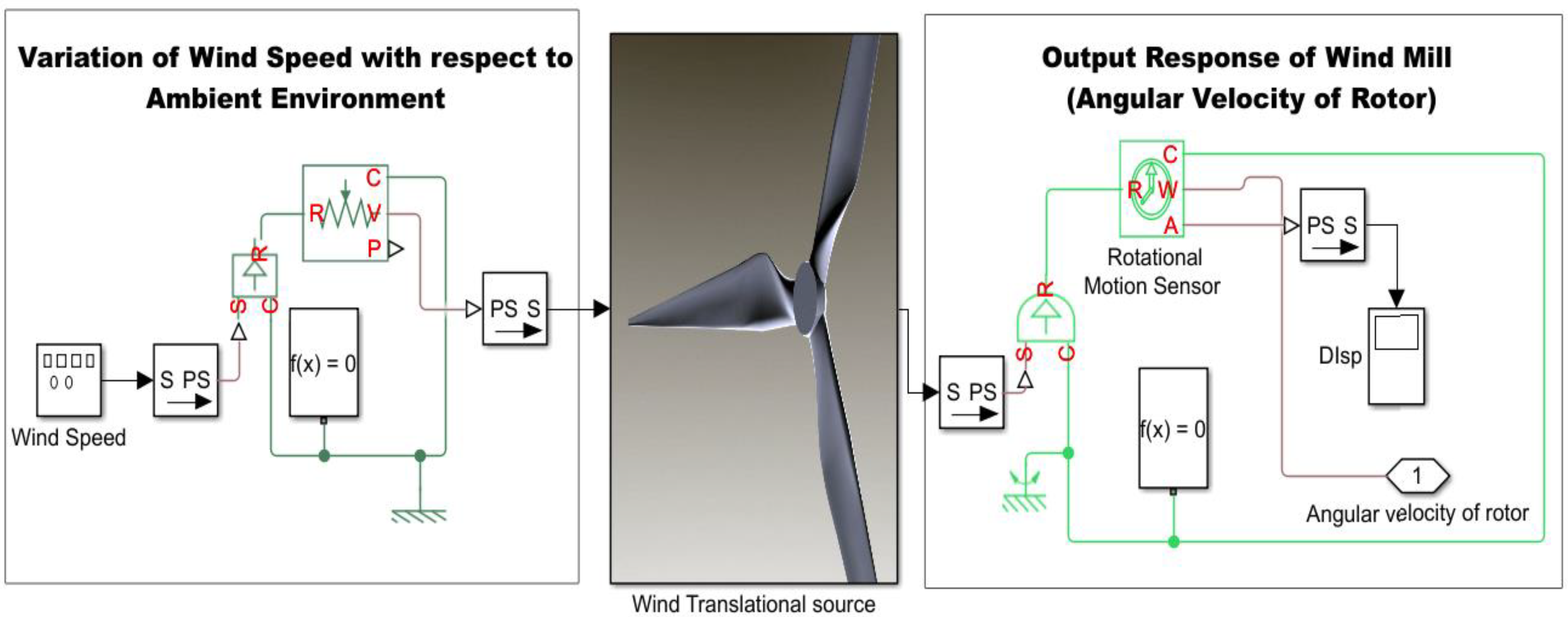
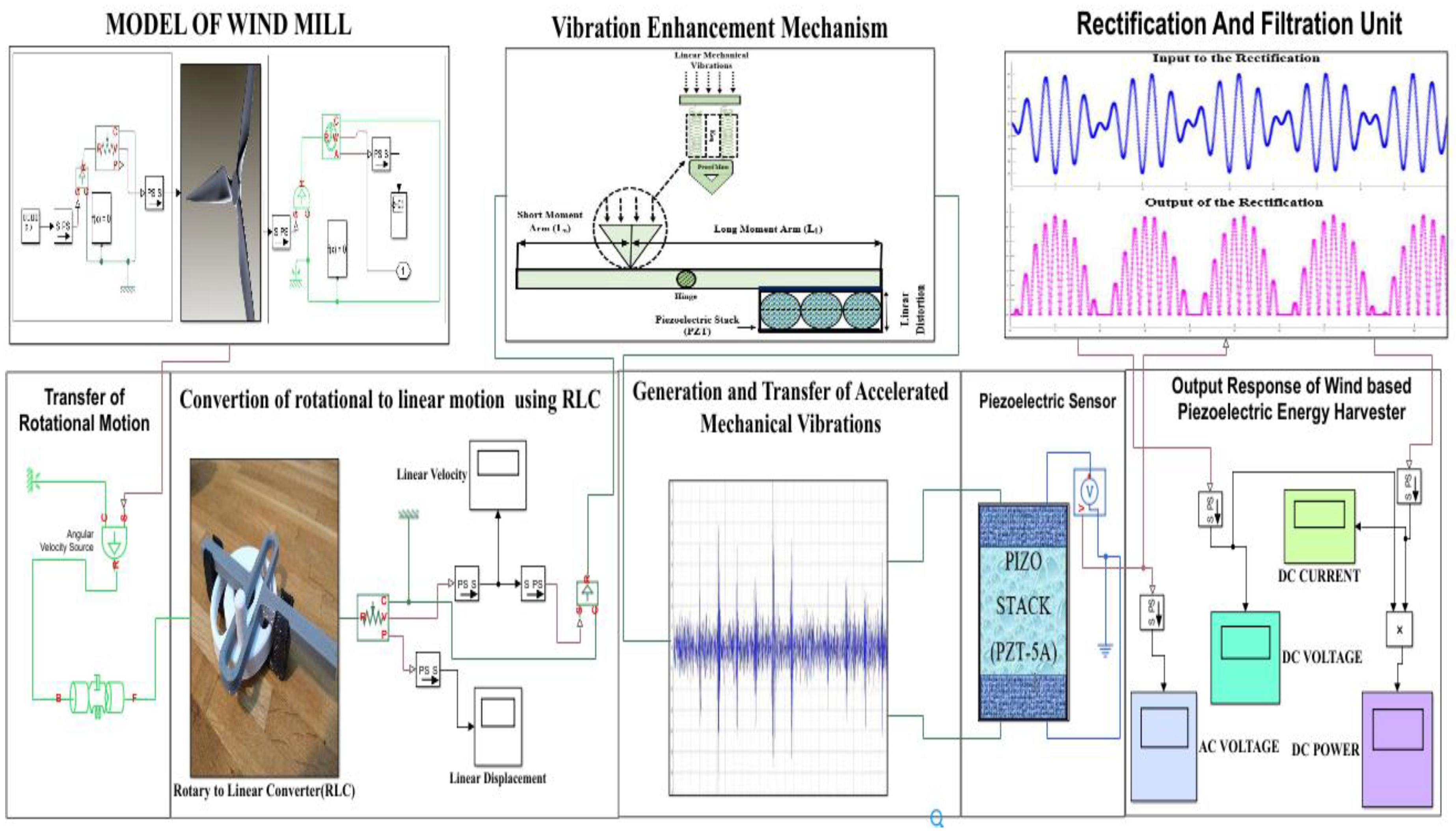
2. Analytical Model
3. Simulation and Analysis
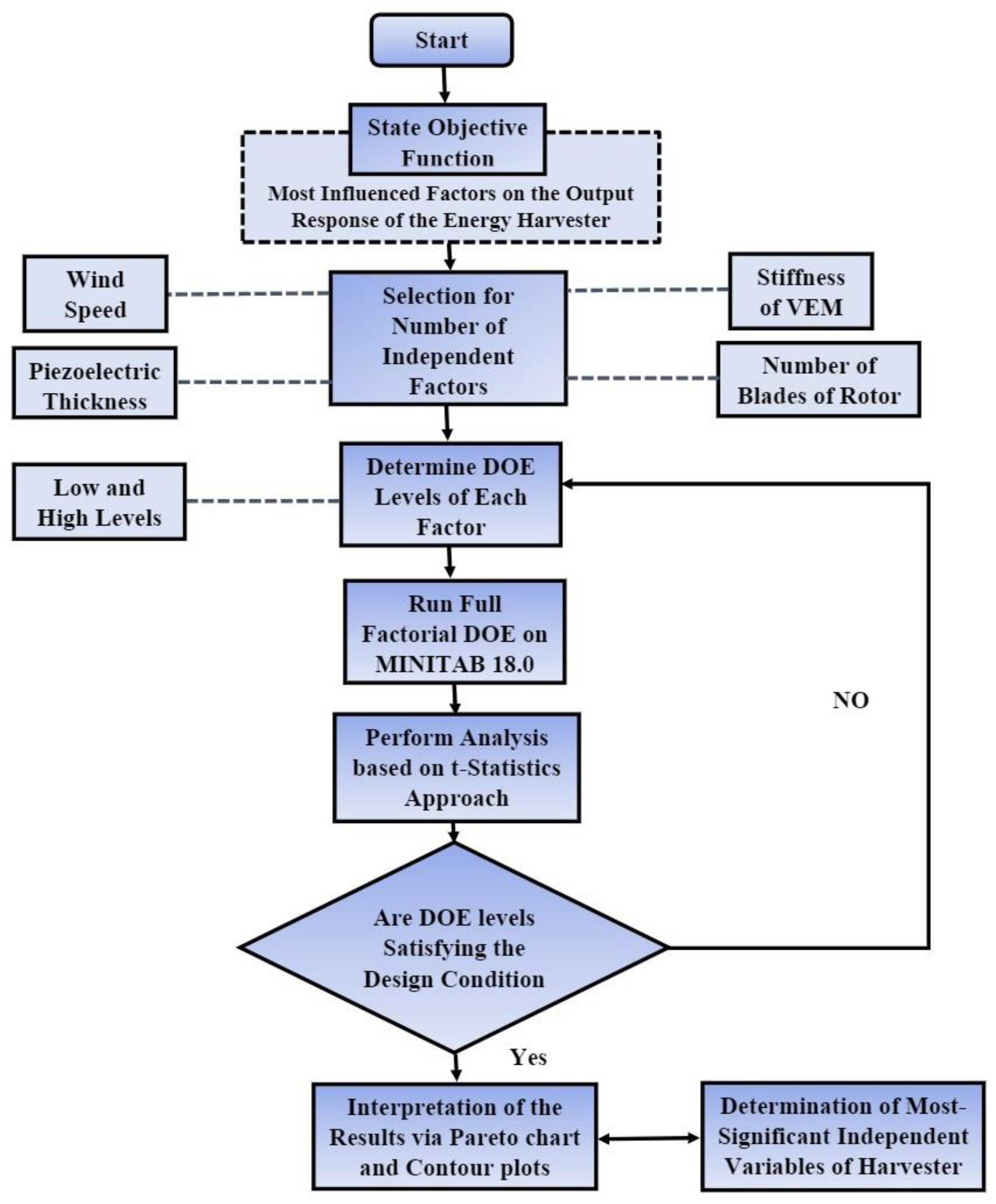
4. Optimization Strategy for the Proposed Energy Harvester
Factorial Design of Experiment
5. Results and Discussions
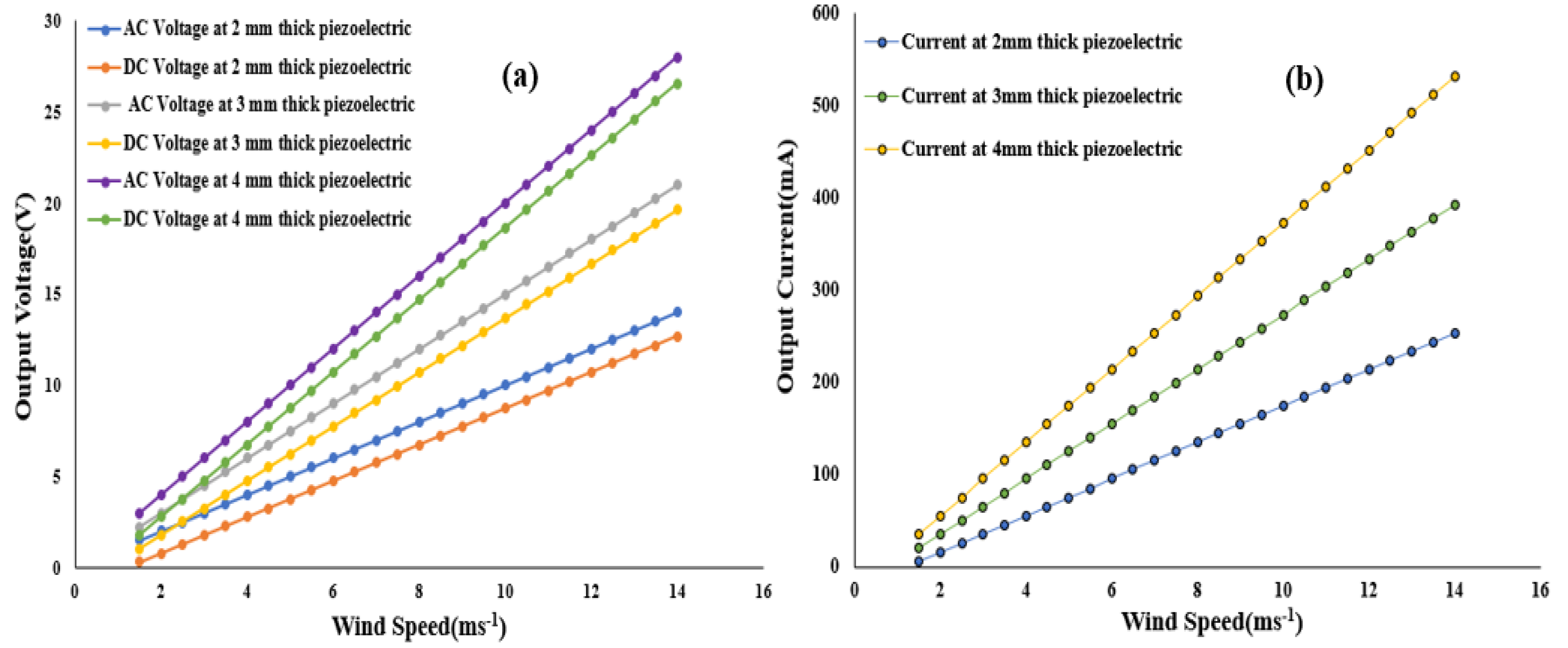
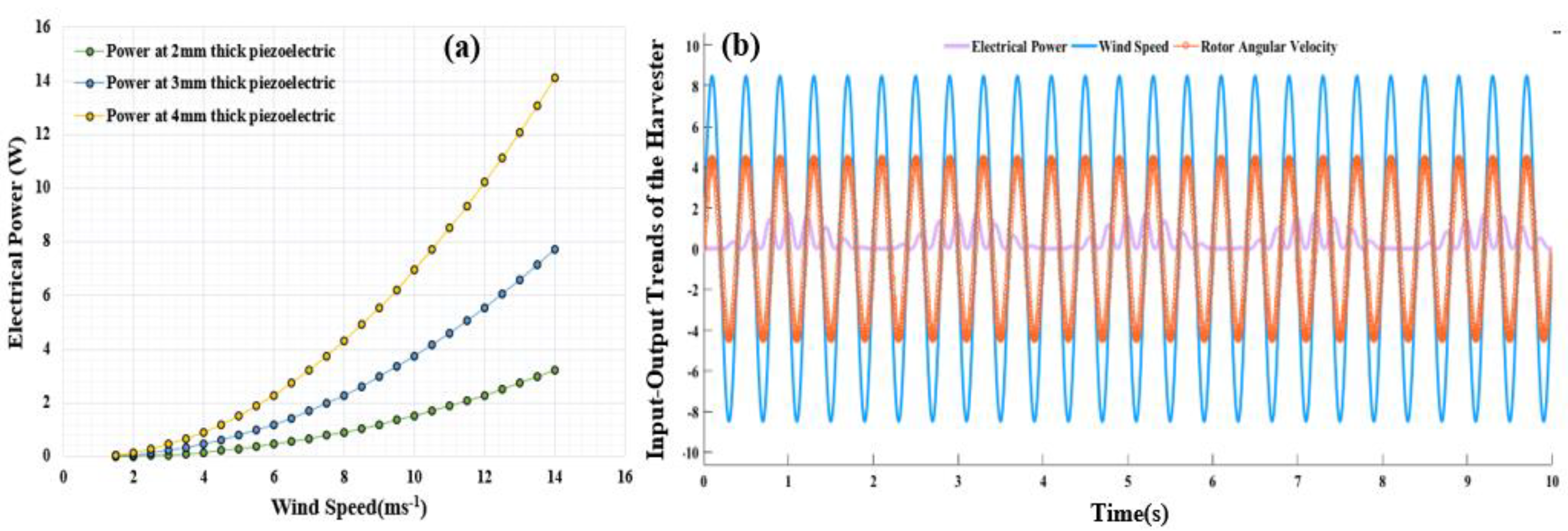
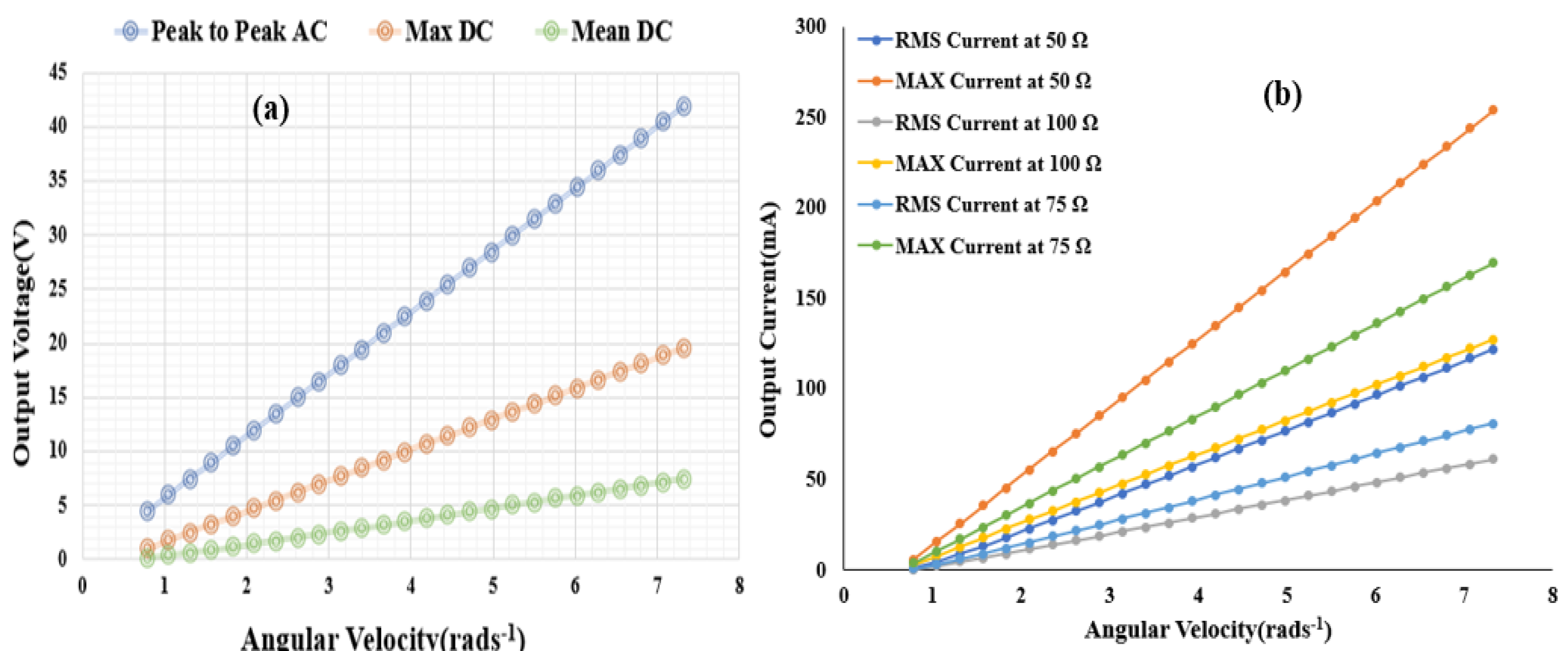
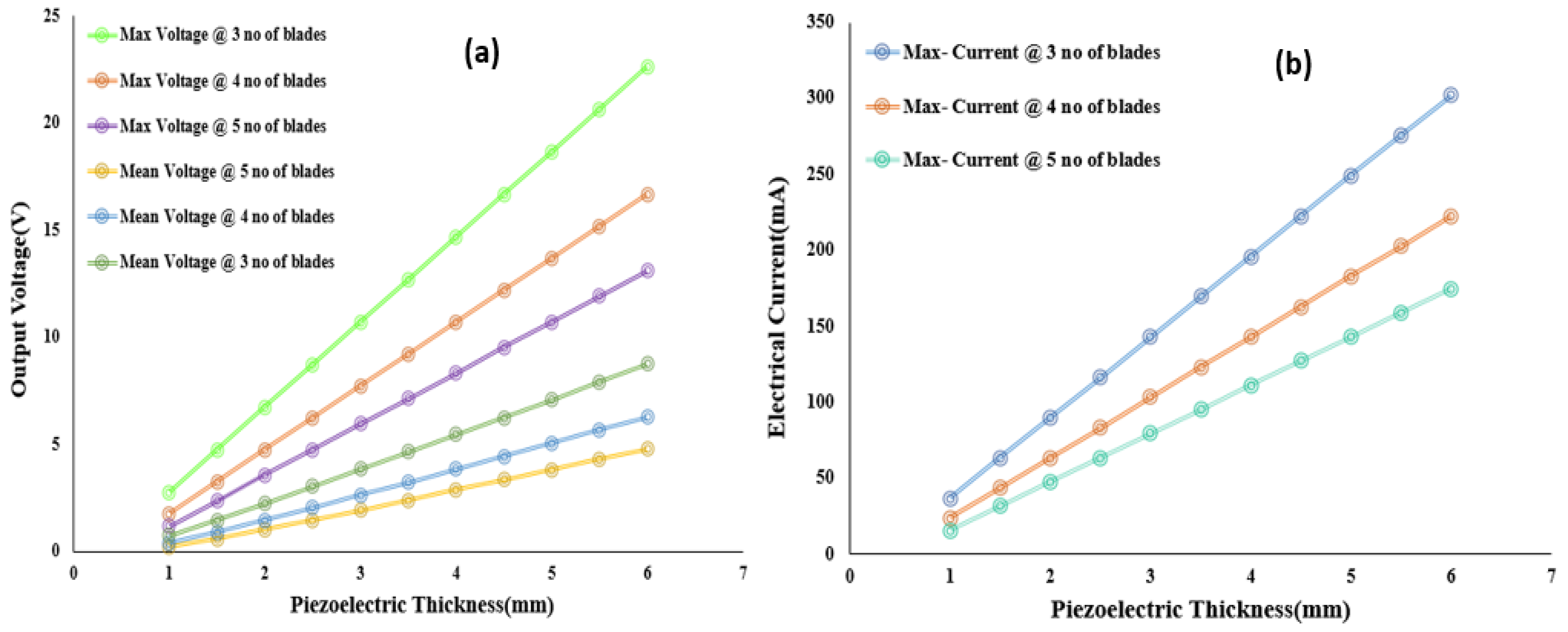
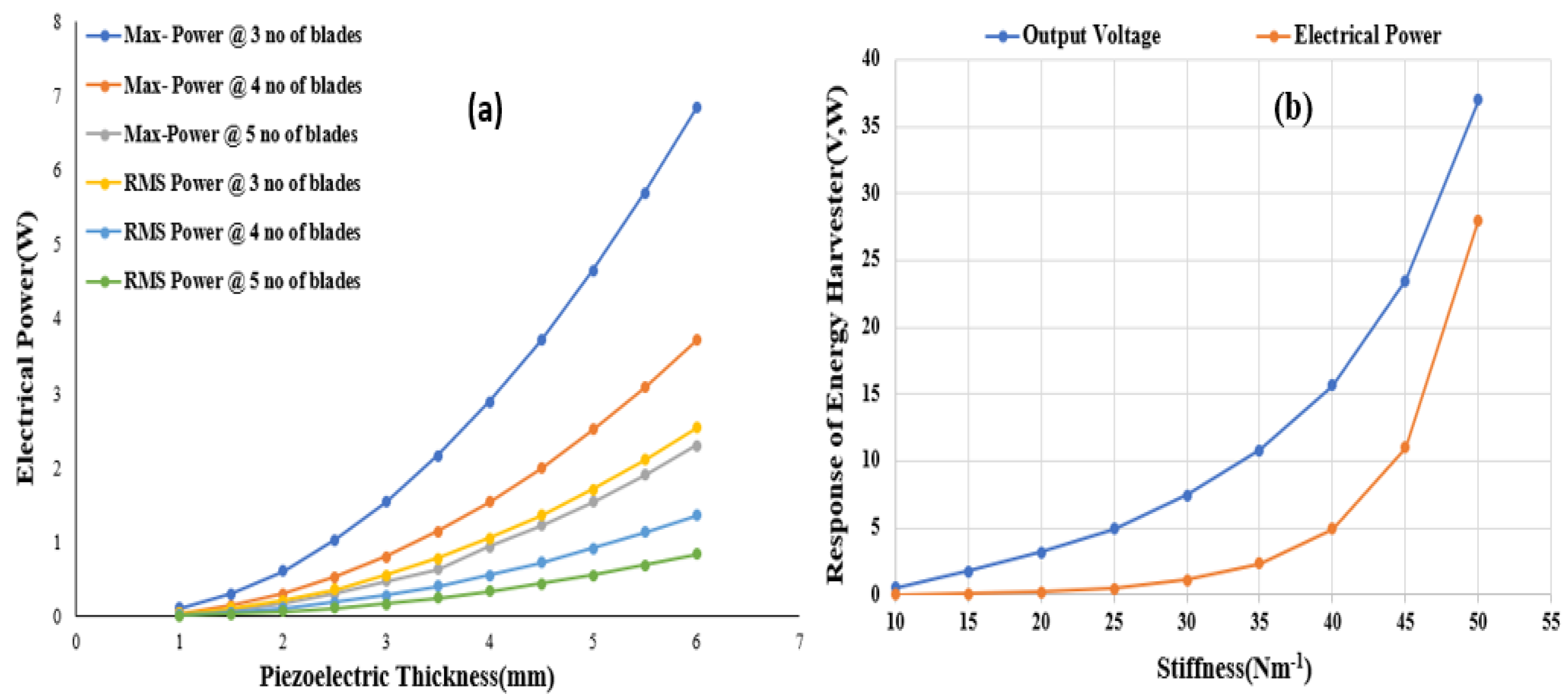
5.1. Outcomes of Simulation
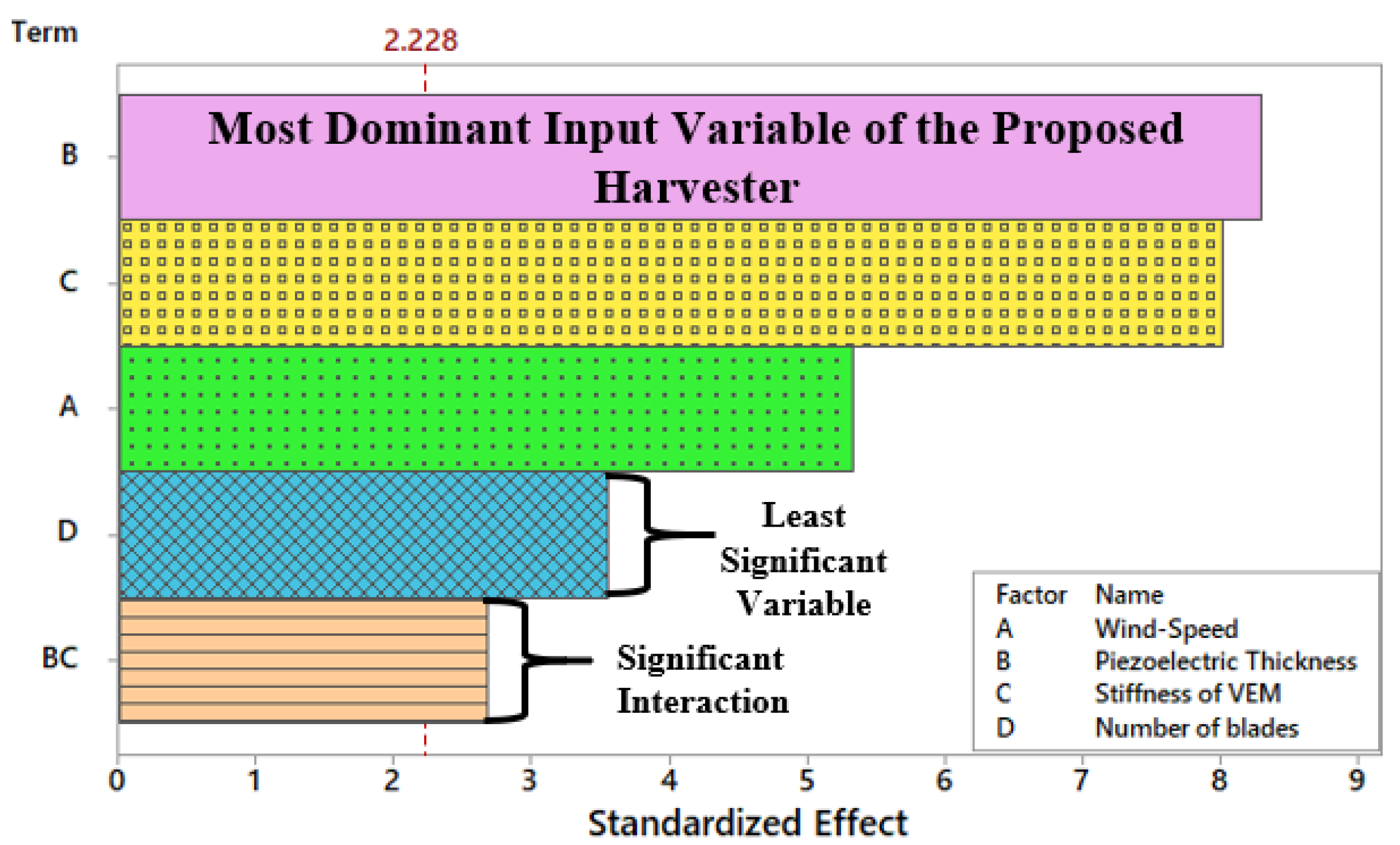
5.2. Outcomes of Optimization Strategy
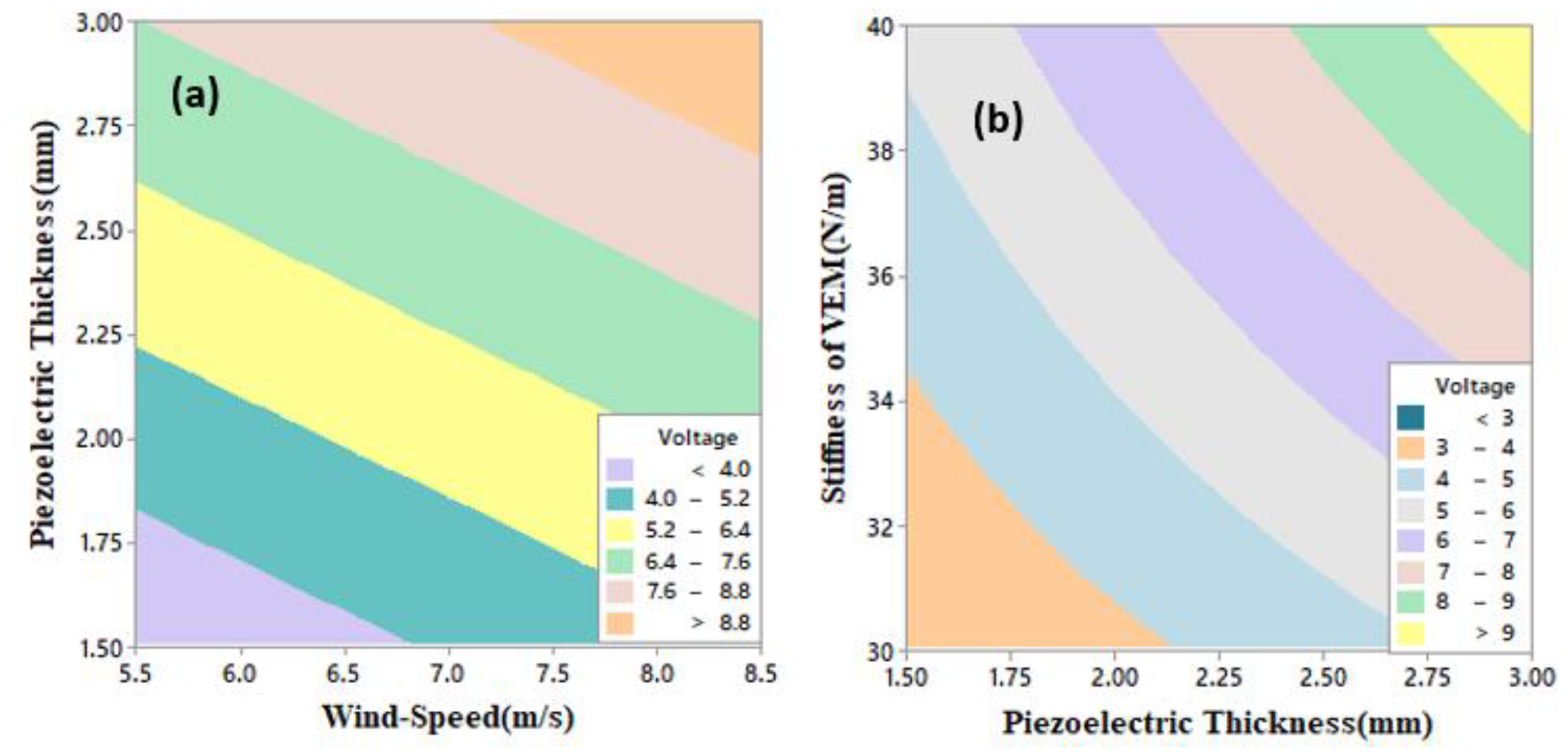
Pareto and Contour Charts for Dominant Factors
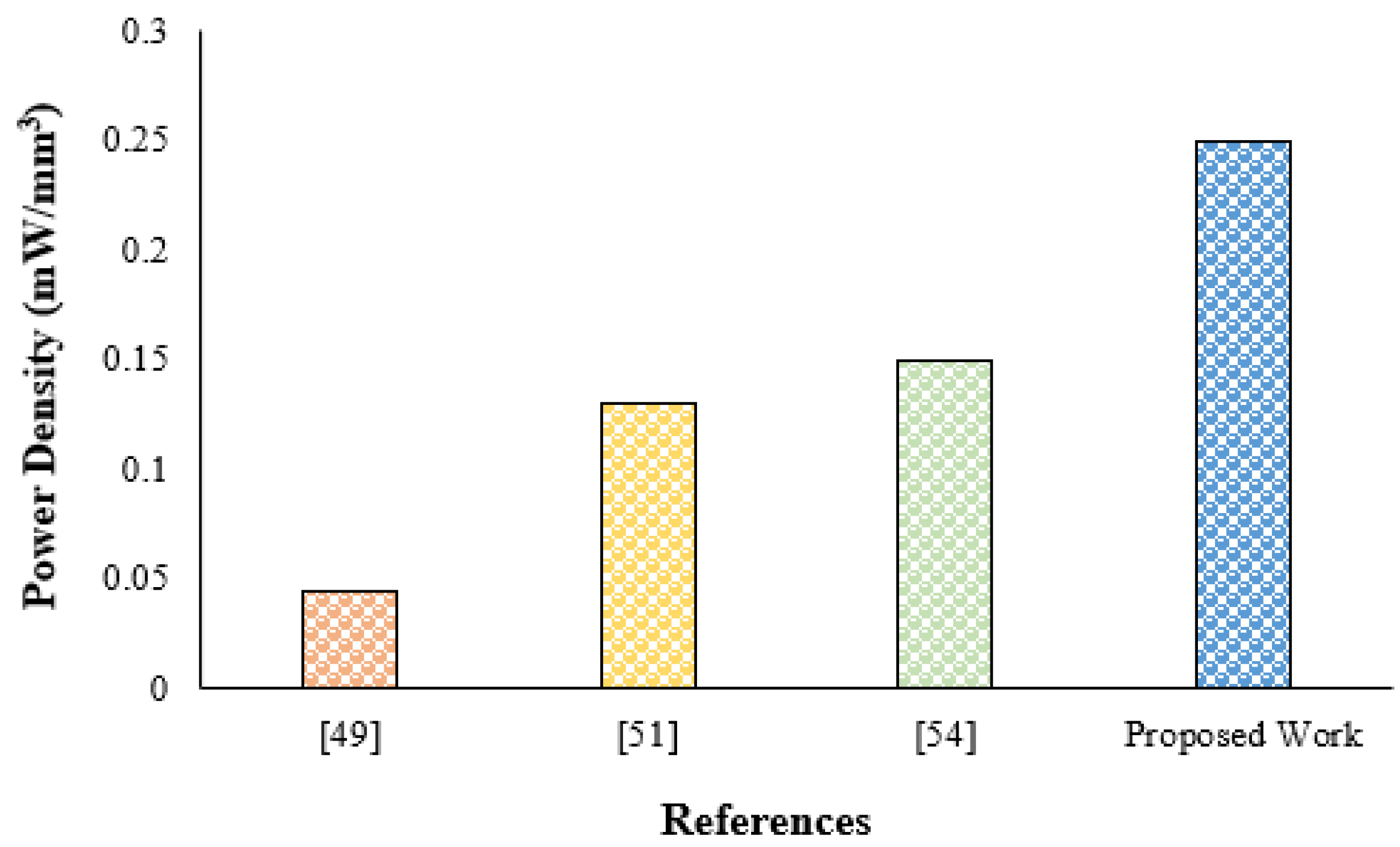
5.3. A State of the Art-Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Rotor Cross Sectional Area |
| C33 | Elastic Stiffness |
| Cp | Piezoelectric Capacitance |
| d33 | Piezoelectric Coefficient |
| E33 | Piezoelectric Constant |
| Fp | Equivalent Piezoelectric force |
| Kb | Stiffness of VEM |
| Kp | Stiffness of Piezoelectric layer |
| Lp | Piezoelectric Stack’s Length |
| Lb | Length of rotor blade |
| tp | Thickness of Piezoelectric Stack |
| wp | Piezoelectric Stack’s Width |
| Z | Distance between slider and slotted rod |
| Ze | Equivalent Displacement |
| Magnifying Ratio | |
| A | Level of Significance |
| Acronyms | |
| DOE | Design of Experiment |
| DOF | Degree of Freedom |
| FSI | Fluid Structure Interaction |
| LCO | Limit Cycle Oscillation |
| MATLAB | Matrix Laboratory |
| PZT | Lead Zirconate Titanate |
| RLC | Rotary to linear Converter |
| VEM | Vibration Enhancement Mechanism |
References
- Zeadally, S.; Shaikh, F.K.; Talpur, A.; Sheng, Q.Z. Design architectures for energy harvesting in the Internet of Things. Renew. Sustain. Energy Rev. 2020, 128, 109901. [Google Scholar] [CrossRef]
- Wei, C.; Jing, X. A comprehensive review on vibration energy harvesting: Modelling and realization. Renew. Sustain. Energy Rev. 2017, 74, 1–18. [Google Scholar] [CrossRef]
- Sarker, M.R.; Julai, S.; Sabri, M.F.M.; Said, S.M.; Islam, M.M.; Tahir, M. Review of piezoelectric energy harvesting system and application of optimization techniques to enhance the performance of the harvesting system. Sens. Actuators A Phys. 2019, 300, 111634. [Google Scholar] [CrossRef]
- Ahmad, I.; Ur Rehman, M.M.; Khan, M.; Abbas, A.; Ishfaq, S.; Malik, S. Flow-based electromagnetic-type energy harvester using microplanar coil for IoT sensors application. Int. J. Energy Res. 2019, 43, 5384–5391. [Google Scholar] [CrossRef]
- Shakeel, M.; Rehman, K.; Ahmad, S.; Amin, M.; Iqbal, N.; Khan, A. A low-cost printed organic thermoelectric generator for low-temperature energy harvesting. Renew. Energy 2021, 167, 853–860. [Google Scholar] [CrossRef]
- Watson, S.; Moro, A.; Reis, V.; Baniotopoulos, C.; Barth, S.; Bartoli, G.; Bauer, F.; Boelman, E.; Bosse, D.; Cherubini, A.; et al. Future emerging technologies in the wind power sector: A European perspective. Renew. Sustain. Energy Rev. 2019, 113, 109270. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L. A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings. Meas. J. Int. Meas. Confed. 2020, 149, 107002. [Google Scholar] [CrossRef]
- Wang, T.; Han, Q.; Chu, F.; Feng, Z. Vibration based condition monitoring and fault diagnosis of wind turbine planetary gearbox: A review. Mech. Syst. Signal Process. 2019, 126, 662–685. [Google Scholar] [CrossRef]
- Paulsamy, S. Reduction of cogging torque in dual rotor permanent magnet generator for direct coupled wind energy systems. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, Y.; Wang, J.; Huang, X.; Wei, X.; Liu, W. Structural failure test of a 52.5 m wind turbine blade under combined loading. Eng. Fail. Anal. 2019, 103, 286–293. [Google Scholar] [CrossRef]
- Mishnaevsky, L. Repair of wind turbine blades: Review of methods and related computational mechanics problems. Renew. Energy 2019, 140, 828–839. [Google Scholar] [CrossRef]
- Ilbahar, E.; Cebi, S.; Kahraman, C. A state-of-the-art review on multi-attribute renewable energy decision making. Energy Strateg. Rev. 2019, 25, 18–33. [Google Scholar] [CrossRef]
- Shahid, M.; Ullah, K.; Imran, K.; Mahmood, I.; Mahmood, A. Electricity supply pathways based on renewable resources: A sustainable energy future for Pakistan. J. Clean. Prod. 2020, 263, 121511. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, Y. An impact-based broadband aeroelastic energy harvester for concurrent wind and base vibration energy harvesting. Appl. Energy 2018, 212, 233–243. [Google Scholar] [CrossRef]
- Saadon, S.; Sidek, O. A review of vibration-based MEMS piezoelectric energy harvesters. Energy Convers. Manag. 2011, 52, 500–504. [Google Scholar] [CrossRef]
- Briscoe, J.; Dunn, S. Piezoelectric nanogenerators–A review of nanostructured piezoelectric energy harvesters. Nano Energy 2014, 14, 15–29. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Gaudenzi, P. A review on mechanisms for piezoelectric-based energy harvesters. Energies 2018, 11, 1850. [Google Scholar] [CrossRef]
- Covaci, C.; Gontean, A. Piezoelectric energy harvesting solutions: A review. Sensors 2020, 20, 3512. [Google Scholar] [CrossRef] [PubMed]
- Elahi, H.; Eugeni, M.; Gaudenzi, P.; Qayyum, F.; Swati, R.F.; Khan, H.M. Response of piezoelectric materials on thermomechanical shocking and electrical shocking for aerospace applications. Microsyst. Technol. 2018, 24, 3791–3798. [Google Scholar] [CrossRef]
- Ahmad, I.; Hassan, A.; Anjum, M.U.; Malik, S.; Ali, T. Ambient Acoustic Energy Harvesting using Two Connected Resonators with Piezoelement for Wireless Distributed Sensor Network. Acoust. Phys. 2019, 65, 471–477. [Google Scholar] [CrossRef]
- Pradeesh, E.L.; Udhayakumar, S. Effect of placement of piezoelectric material and proof mass on the performance of piezoelectric energy harvester. Mech. Syst. Signal Process. 2019, 130, 664–676. [Google Scholar] [CrossRef]
- Karafi, M.R.; Khorasani, F. Evaluation of mechanical and electric power losses in a typical piezoelectric ultrasonic transducer. Sensors Actuators A Phys. 2019, 288, 156–164. [Google Scholar] [CrossRef]
- Orrego, S.; Shoele, K.; Ruas, A.; Doran, K.; Caggiano, B.; Mittal, R.; Kang, S.H. Harvesting ambient wind energy with an inverted piezoelectric flag. Appl. Energy 2017, 194, 212–222. [Google Scholar] [CrossRef]
- Sheeraz, M.A.; Butt, Z.; Khan, A.M.; Mehmood, S.; Ali, A.; Azeem, M.; Nasir, A.; Imtiaz, T. Design and Optimization of Piezoelectric Transducer (PZT-5H Stack). J. Electron. Mater. 2019, 48, 6487–6502. [Google Scholar] [CrossRef]
- Wu, N.; Wang, Q.; Xie, X. Wind energy harvesting with a piezoelectric harvester. Smart Mater. Struct. 2013, 22. [Google Scholar] [CrossRef]
- Priya, S. Modeling of electric energy harvesting using piezoelectric windmill. Appl. Phys. Lett. 2005, 87, 1–3. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Gaudenzi, P. Design and performance evaluation of a piezoelectric aeroelastic energy harvester based on the limit cycle oscillation phenomenon. Acta Astronaut. 2019, 157, 233–240. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, S.; Zhang, Z.; Yurchenko, D. High-performance piezoelectric wind energy harvester with Y-shaped attachments. Energy Convers. Manag. 2019, 181, 645–652. [Google Scholar] [CrossRef]
- Zhang, L.B.; Abdelkefi, A.; Dai, H.L.; Naseer, R.; Wang, L. Design and experimental analysis of broadband energy harvesting from vortex-induced vibrations. J. Sound Vib. 2017, 408, 210–219. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, M. Effects of side ratio on energy harvesting from transverse galloping of a rectangular cylinder. Energy 2021, 120420. [Google Scholar] [CrossRef]
- Caracoglia, L. Modeling the coupled electro-mechanical response of a torsional-flutter-based wind harvester with a focus on energy efficiency examination. J. Wind Eng. Ind. Aerodyn. 2018, 174, 437–450. [Google Scholar] [CrossRef]
- Elahi, H. The investigation on structural health monitoring of aerospace structures via piezoelectric aeroelastic energy harvesting. Microsyst. Technol. 2020, 1–9. [Google Scholar] [CrossRef]
- Elahi, H.; Munir, K.; Eugeni, M.; Atek, S.; Gaudenzi, P. Energy Harvesting towards Self-Powered IoT Devices. Energies 2020, 13, 5528. [Google Scholar] [CrossRef]
- Elahi, H.; Eugeni, M.; Fune, F.; Lampani, L.; Mastroddi, F.; Paolo Romano, G.; Gaudenzi, P. Performance evaluation of a piezoelectric energy harvester based on flag-flutter. Micromachines 2020, 11, 933. [Google Scholar] [CrossRef] [PubMed]
- Chawdhury, S.; Milani, D.; Morgenthal, G. Modeling of pulsating incoming flow using vortex particle methods to investigate the performance of flutter-based energy harvesters. Comput. Struct. 2018, 209, 130–149. [Google Scholar] [CrossRef]
- Aquino, A.I.; Calautit, J.K.; Hughes, B.R. A Study on the Wind-Induced Flutter Energy Harvester (WIFEH) Integration into Buildings. Energy Procedia 2017, 142, 321–327. [Google Scholar] [CrossRef]
- Eugeni, M.; Elahi, H.; Fune, F.; Lampani, L.; Mastroddi, F.; Romano, G.P.; Gaudenzi, P. Numerical and experimental investigation of piezoelectric energy harvester based on flag-flutter. Aerosp. Sci. Technol. 2020, 97, 105634. [Google Scholar] [CrossRef]
- Elvin, N.G.; Elvin, A.A. The flutter response of a piezoelectrically damped cantilever pipe. J. Intell. Mater. Syst. Struct. 2009, 20, 2017–2026. [Google Scholar] [CrossRef]
- Bae, J.S.; Inman, D.J. Aeroelastic characteristics of linear and nonlinear piezo-aeroelastic energy harvester. J. Intell. Mater. Syst. Struct. 2014, 25, 401–416. [Google Scholar] [CrossRef]
- Kishore, R.A.; Vučković, D.; Priya, S. Ultra-low wind speed piezoelectric windmill. Ferroelectrics 2014, 460, 98–107. [Google Scholar] [CrossRef]
- Hsieh, J.C.; Lin, D.T.W.; Lin, C.L. The development and optimization of an innovative piezoelectric energy harvester on the basis of vapor-induced vibrations. Mech. Syst. Signal Process. 2019, 131, 649–658. [Google Scholar] [CrossRef]
- Lü, C.; Zhang, Y.; Zhang, H.; Zhang, Z.; Shen, M.; Chen, Y. Generalized optimization method for energy conversion and storage efficiency of nanoscale flexible piezoelectric energy harvesters. Energy Convers. Manag. 2019, 182, 34–40. [Google Scholar] [CrossRef]
- Schoeftner, J.; Buchberger, G. A contribution on the optimal design of a vibrating cantilever in a power harvesting application–Optimization of piezoelectric layer distributions in combination with advanced harvesting circuits. Eng. Struct. 2013, 53, 92–101. [Google Scholar] [CrossRef]
- Merabet Boulouiha, H.; Khodja, M.; Rahiel, D.; Allali, A.; Kaddour, F.; Denaï, M. Power quality enhancement in electricity grids with wind energy using multicell converters and energy storage. J. Renew. Sustain. Energy 2019, 11. [Google Scholar] [CrossRef]
- Morel, A.; Badel, A.; Grézaud, R.; Gasnier, P.; Despesse, G.; Pillonnet, G. Resistive and reactive loads’ influences on highly coupled piezoelectric generators for wideband vibrations energy harvesting. J. Intell. Mater. Syst. Struct. 2019, 30, 386–399. [Google Scholar] [CrossRef]
- Qian, F.; Xu, T.; Zuo, L. Design, optimization, modeling and testing of a piezoelectric footwear energy harvester. Energy Convers. Manag. 2018, 171, 1352–1364. [Google Scholar] [CrossRef]
- Wang, Q. Energy harvesting from wind by a piezoelectric harvester. Eng. Struct. 2017, 133, 74–80. [Google Scholar] [CrossRef]
- Tyagi, K.; Tyagi, K. A Comparative Analysis of Optimization Techniques. Int. J. Comput. Appl. 2015, 131, 6–12. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Palazoglu, A.; El-Farra, N.H.; Shah, N. Optimization and control of offshore wind systems with energy storage. Energy Convers. Manag. 2018, 173, 426–437. [Google Scholar] [CrossRef]
- Zhao, L.; Tang, L.; Yang, Y. Comparison of modeling methods and parametric study for a piezoelectric wind energy harvester. Smart Mater. Struct. 2013, 22. [Google Scholar] [CrossRef]
- Zhou, H.; Wei, K.; Liu, J. Enhanced performance of piezoelectric wind energy harvester by a curved plate. Smart Mater. Struct. 2020, 28. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L.; Gao, Y.; Zhou, J.Y. Nonlinear analysis of piezoelectric wind energy harvesters with different geometrical shapes. Arch. Appl. Mech. 2020, 90, 721–736. [Google Scholar] [CrossRef]
- Sitharthan, R.; Yuvaraj, S.; Padmanabhan, S.; Holm-Nielsen, J.B.; Sujith, M.; Rajesh, M.; Prabaharan, N.; Vengatesan, K. Piezoelectric energy harvester converting wind aerodynamic energy into electrical energy for microelectronic application. IET Renew. Power Gener. 2021. [Google Scholar] [CrossRef]
- Shi, T.; Hu, G.; Zou, L.; Song, J.; Kwok, K.C.S. Performance of an omnidirectional piezoelectric wind energy harvester. Wind Energy 2021, 1–13. [Google Scholar] [CrossRef]
- Pauloe Silva, A.G.; Basílio Sobrinho, J.M.; da Rocha Souto, C.; Ries, A.; de Castro, A.C. Design, modelling and experimental analysis of a piezoelectric wind energy generator for low-power applications. Sens. Actuators A Phys. 2021, 317. [Google Scholar] [CrossRef]


| Sr# | Parameters | Symbol | Unit | Values |
|---|---|---|---|---|
| 1 | Elastic Stiffness | C33 | Nm−2 | 11.09 × 1010 |
| 2 | Radius of Rotor | R | m | 0.25 |
| 3 | Swept Area | As | m2 | 0.19 |
| 4 | Number of Blades | - | - | 3–5 |
| 5 | VEM Stiffness | K | Nm−1 | 10–40 |
| 6 | Proof Mass | mp | kg | 0.5 |
| 7 | Piezoelectric Charge Constant | d33 | C/N | 450 × 10−12 |
| 8 | Piezoelectric Coefficient | g33 | m2C−1 | 24 × 10−3 |
| 9 | Permittivity | Ɛ33 | Fm−1 | 706 × 10−11 |
| 10 | Density | ρ | Kgm−3 | 7750 |
| 11 | Piezoelectric Stack’s Length | Lp | mm | 10 |
| 12 | Piezoelectric Stack’s Width | wp | mm | 20 |
| 13 | Piezoelectric Stack’s Thickness | tp | mm | 0.5–4 |
| Independent Factors | Unit | Low Level | High Level |
|---|---|---|---|
| Wind Speed | ms−1 | 5.5 | 8.5 |
| Piezoelectric Thickness | mm | 1.5 | 3.0 |
| Stiffness of VEM | Nm−1 | 30 | 40 |
| Number of Blades | - | 3 | 4 |
| Terms | Coefficient | SE Coeff. | t-Value | p-Value |
|---|---|---|---|---|
| Wind-Speed | 1.110 | 0.208 | 5.33 | 0.004 |
| Piezoelectric Thickness | 1.727 | 0.208 | 8.29 | 0.001 |
| Stiffness of VEM | 1.668 | 0.208 | 8.01 | 0.002 |
| Number of blades | −0.740 | 0.208 | −3.55 | 0.005 |
| Piezoelectric Thickness * Stiffness of VEM | 0.556 | 0.208 | 2.67 | 0.023 |
| References | Authors | Publication Year | Approach | Piezoelectric Dimensions | Cut-In Speed | Output Power |
|---|---|---|---|---|---|---|
| [25] | Wu. N et.al. | 2013 | Analytical | 0.12 × 0.15 × 0.0125 m3 | - | 1.02 W @ 9 ms−1 |
| [50] | Zhao. L et.al. | 2013 | Analytical | 61 × 30 × 0.5 mm3 | ~2.1 ms−1 | 40 mW @ 14 ms−1 |
| [28] | Zhou. S et.al. | 2019 | Analytical and Experimental | - | 1.3 ms−1 | 1.2 mW @ 2.2 ms−1 |
| [51] | Wei et.al. | 2020 | Analytical and Experimental | 46 × 10 × 1 mm3 | 2 ms−1 | 35.6 µW @ 5.45 ms−1 |
| [52] | Wang. K et.al. | 2020 | Analytical and Numerical | 100 × 30 × 0.3mm3 | 6 ms−1 | 0.12 W @ 17–18 ms−1 |
| [53] | Sitharthan. R et.al. | 2021 | Experimental | 0.00234 m3 | <3 ms−1 | 2.6 W @ 9–11 ms−1 |
| [54] | Shi.T et.al. | 2021 | Experimental | - | ~2.1 ms−1 | 3 mW @ 4 ms−1 |
| [55] | Silva et.al. | 2021 | Numerical and Experimental | 12.9 mm3 | - | 2.06 mW |
| Proposed work | Sheeraz et.al. | - | Numerical | 10 × 20 × 3 mm3 | ~1.5 ms−1 | 2.622 W @ 8.5 ms−1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheeraz, M.A.; Malik, M.S.; Rehman, K.; Elahi, H.; Butt, Z.; Ahmad, I.; Eugeni, M.; Gaudenzi, P. Numerical Assessment and Parametric Optimization of a Piezoelectric Wind Energy Harvester for IoT-Based Applications. Energies 2021, 14, 2498. https://doi.org/10.3390/en14092498
Sheeraz MA, Malik MS, Rehman K, Elahi H, Butt Z, Ahmad I, Eugeni M, Gaudenzi P. Numerical Assessment and Parametric Optimization of a Piezoelectric Wind Energy Harvester for IoT-Based Applications. Energies. 2021; 14(9):2498. https://doi.org/10.3390/en14092498
Chicago/Turabian StyleSheeraz, Muhammad Abdullah, Muhammad Sohail Malik, Khalid Rehman, Hassan Elahi, Zubair Butt, Iftikhar Ahmad, Marco Eugeni, and Paolo Gaudenzi. 2021. "Numerical Assessment and Parametric Optimization of a Piezoelectric Wind Energy Harvester for IoT-Based Applications" Energies 14, no. 9: 2498. https://doi.org/10.3390/en14092498
APA StyleSheeraz, M. A., Malik, M. S., Rehman, K., Elahi, H., Butt, Z., Ahmad, I., Eugeni, M., & Gaudenzi, P. (2021). Numerical Assessment and Parametric Optimization of a Piezoelectric Wind Energy Harvester for IoT-Based Applications. Energies, 14(9), 2498. https://doi.org/10.3390/en14092498