1. Introduction
Electric vehicles (EVs) have witnessed a quickening development in recent years [
1]. By improving their battery capacities and recharging technologies, EVs can circulate for long distances and be recharged in short periods of time (e.g., a Tesla Roadster can travel up to 340 km while recharging its battery takes no more than 20 min using fast-charging technology [
2]). This development is also accompanied by some challenges, since it can reshape the future of electric mobility and affect people’s lives on both social and economic levels [
3]. These challenges include: the efficient distribution of charging facilities; the need for new legislative proposals to accelerate EVs integration to mobility systems; the development of efficient frameworks for modeling and calculating EV energy consumption and measuring their potential impacts on existing electric grids [
4]; and the availability of optimized operational plans that can guarantee the quality of provided services and comply to people’s needs [
5].
With the increasing interest in using EVs in future transportation systems, the need for deploying fast-charging infrastructures, especially on highways and high-speed roads, becomes essential. To fulfill this need and determine its required investments, it is important to anticipate EV future charging demands and requirements and optimize their facility location taking into account the different mobility flows (i.e., small vehicles, heavy trucks, etc.) and the existing electric grid [
6]. In addition, integrating new sources of renewable energy (e.g., photovoltaic power) into power systems represents one promising opportunity to fulfill the increasing demand for energy related to EV charging. Together, vehicle electrification and renewable energy generation can help in providing a sustainable transportation service while reducing emissions of the road transportation sector [
7].
In this paper, we start by providing a comprehensive classification of the related literature and its different models and solution approaches. Then, we develop a data-driven modeling approach along with an optimization model to solve the problem of positioning fast charging stations for EVs on a highway network. The proposed model takes into account EV charging demands based on the different mobility flows, including those for small vehicles and heavy trucks, as well as the constraints imposed by the available electric grid. In addition, the model considers the availability of a local photovoltaic farm and integrates its generated power to the grid to supply EV charging. More precisely, the deployment of EV charging stations and the number of fast-chargers is based on the charging demand in the first place. Then, this deployment must respect the restrictions of the electric grid as well as the availability of parking places at charging stations. For this purpose, we provide a mathematical formulation for the problem aiming at maximizing the covered charging demand (i.e., for both small electric vehicles and heavy trucks) while respecting investment budget limits and the available capacities provided by the electric grid. The underlying optimization problem corresponds to the well-known facility location problem where our facilities are the charging stations [
8]. Through a case study on Paris-Saclay area, we provide locations for deploying EV charging stations as well as the number of fast chargers to be installed at each charging station. We also analyze the benefits of PV power integration and its productions costs and different charging capacities.
The paper is organized as follows. In
Section 2, we provide a thorough classification of related literature. In
Section 3, we describe the considered problem. The proposed modeling approach is then presented in
Section 4. In
Section 5, we present the computational study we have conducted. Finally, in
Section 6, the key findings are highlighted and research perspectives are suggested.
2. Literature Review
Research on locating EV charging stations can be classified into three main categories:
transportation-based,
electric-based and
hybrid approaches [
9].
Transportation-based approaches focus on the transportation perspective when designing EV charging networks (i.e., mobility flows and passengers demand), while ignoring power system constraints [
10]. Their main drawback is that they need to be readjusted according to the existing power system conditions. On the other hand,
electric-based approaches aim to locate EV charging stations in power systems such that their capacity and security requirements are satisfied and the investment costs needed to upgrade them are minimized [
11] (i.e., transportation constraints are ignored). These approaches also need to be readjusted according to the existing mobility conditions. Since both transportation and electric perspectives are important in our case, we develop a
hybrid approach in this paper, where both types of constraints are considered [
12]. We thus propose to deploy EV charging stations while taking into account both the actual transportation and power system conditions in the studied area.
From a transportation perspective, according to Zhang [
13], there are three main planning methodologies for locating EV charging stations:
nodal demand-based,
simulation-based and
traffic flow-based planning. In
nodal demand-based planning, charging stations are located to satisfy EV charging demands that appear at some geographical locations. The main drawback is that some transportation network issues (e.g., traffic congestion) are ignored in this methodology. On the other hand,
simulation-based and
traffic flow-based planning estimate EV charging demands based on real-life transportation surveys and origin-destination traffic flow (OD matrices), respectively. However, simulating EV charging demands is computationally expensive, while EV driving-range limit is not often considered when planning traffic flow-based methods. Relatively, EV charging demands can be represented in different ways [
9]. In
point-based representations, EV charging demands are concentrated at certain points. In addition,
polygon-based representations consider dividing the studied area into smaller sub-areas (e.g., polygons) where each charging demand is represented by the centroid of the sub-area where it is located. The spatial attributes of the demand are thus ignored. Unlike the first two cases,
network-based representations do not only consider the spatial attributes of the demand; they also reflect the existing highway network as well as the different travel patterns of travelers in the studied area (commute, transit, etc.). In this latter case, charging demands can appear during long-distance or short-distance trips (referred to as
inter-city and
intra-city, respectively). As such, we use a traffic flow-based methodology in order to estimate EV charging demands where a network-based approach is used to represent them. This choice is made as it complies with our problem description and takes into account the availability of traffic flow data for the studied area.
From an electric perspective, different types of chargers have been considered in the literature:
Level 1 chargers (referred to as
slow-charging, 110V/15A),
Level 2 chargers (220V/15-30A) and
Level 3 chargers (referred to as
fast-charging, 400-500V/50A) (
Table 1). These chargers have different features and requirements, such as power capacities, charging times, cabling and outlets, etc. Some studies considered only one type of chargers, while other studies integrated different types of chargers into their models. For example, in [
9], the distribution of
Level 2 charging stations among territory segments is considered, based on the potential use of EVs and the different parking behaviors. In [
12], the focus is on selecting locations for fast-charging stations (
Level 3) through a highway network for long-distance trips in the US. On the other hand, in [
6], the deployment of both
Level 2 and
Level 3 chargers is considered to fulfil EV charging requirements while respecting the specifications of the electric grid. In this paper, we consider the deployment of
Level 3 chargers as the aim is to satisfy charging demands on a highway network where EVs need to be recharged at short charging times.
Many decision models have been proposed in the literature for modeling the problem of deploying EV charging stations. These models represent the mathematical formulation used to model the underlying operational problem. For example, some studies suggested to use a
Facility Location Model (FLM) [
9] or a
set-covering model [
14], while others introduced a
Flow Refueling Location Model (FRLM) or one of its variants (e.g.,
Multi-period FRLM,
Capacitated FRLM, etc.) as they provide a better coverage of mobility flows [
10]. These different formulations share many features and constraints but can also vary depending on the problem setting and its application context. Different objectives can be assigned to these models, such as
minimizing investment costs [
15],
maximizing covered mobility flows or
the number recharged EVs [
6] and
minimizingemissions [
16]. The choice of which objective to use depends on the optimization problem itself and its overall aim.
Regarding modeling approaches, some studies assumed charging demands to be aggregated at certain nodes and aim to cover these demands by locating charging stations within a feasible distance or travel time of these nodes (
node-based modeling) (e.g., EV charging demand in residential areas) [
17]. Some other studies located charging demands through arcs linking different nodes (
arc-based modeling) (e.g., charging demand through a highway linking two residential areas) [
10]. Furthermore, more researchers are recently interested in modeling charging demands using sequences of nodes and arcs (
path-based modeling) [
18]. This combined approach has the advantage of modeling traffic flows where the aim is to locate charging stations so that the captured flow is maximized. In this paper, we consider a
facility location model (FLM) where a path-based modeling approach is used in order to maximize the charging demand covered by the proposed network of fast-charging stations. Once the decision model is built, most studies suggested solving it using a
mathematical solver (e.g.,
Cplex,
Gurobi or other solvers) so that the optimal deployment of EV charging stations can be found. However, due to the potential complexity of the underlying optimization problem, some studies developed more sophisticated methods for solving these models, such as
Branch-and-Bound (B&B) [
13],
Dynamic Programming (DA) [
15] and
Genetic Algorithms (GA) [
14]. In this paper, we provide a data-driven framework in which we solve the proposed model using
Cplex mathematical solver and analyze the obtained results. This is due to the limited number of variables in our model which allows finding solutions in feasible computational times (
Section 4). Solving such models requires input data regarding different mobility and electric aspects. These datasets can either be based on real-life case studies (
real datasets, as in our case) or on datasets that are generated randomly or using a simulation approach (
simulated datasets). A comprehensive summary of the reviewed literature is presented in
Table 2.
Finally, many recent studies focus on using green energy sources for supplying EV charging networks. In [
19], a review of photovoltaic energy systems along with their sizing strategies, optimization techniques and cost evaluation methodologies is provided. In addition, the main indices for analyzing energy costs and pricing schemes is presented. A relevant application of these indices can be found in [
20], where the investment of a photovoltaic energy system was evaluated through a case study in three different cities in Turkey. To model production uncertainty in photovoltaic energy systems, a scenario-based approach to evaluate the potential use of photovoltaic energy for charging EVs was introduced by Good [
21]. The results of testing the proposed approach on two Scandinavian cities demonstrate that PV energy yield can cover EV demands in most of the considered scenarios. The necessity of stochastic approaches to deal with uncertainty in PV production was also confirmed by Thomas [
22]. This was done by evaluating a set of case studies using a linear programming framework that takes into account PV uncertainty and stochastic EV driving schedules. In this paper, we consider the availability of local photovoltaic (PV) power station, study the use of its produced energy for supplying EV chargers and analyze their potential benefits as well as its different prices and production costs.
3. Problem Description
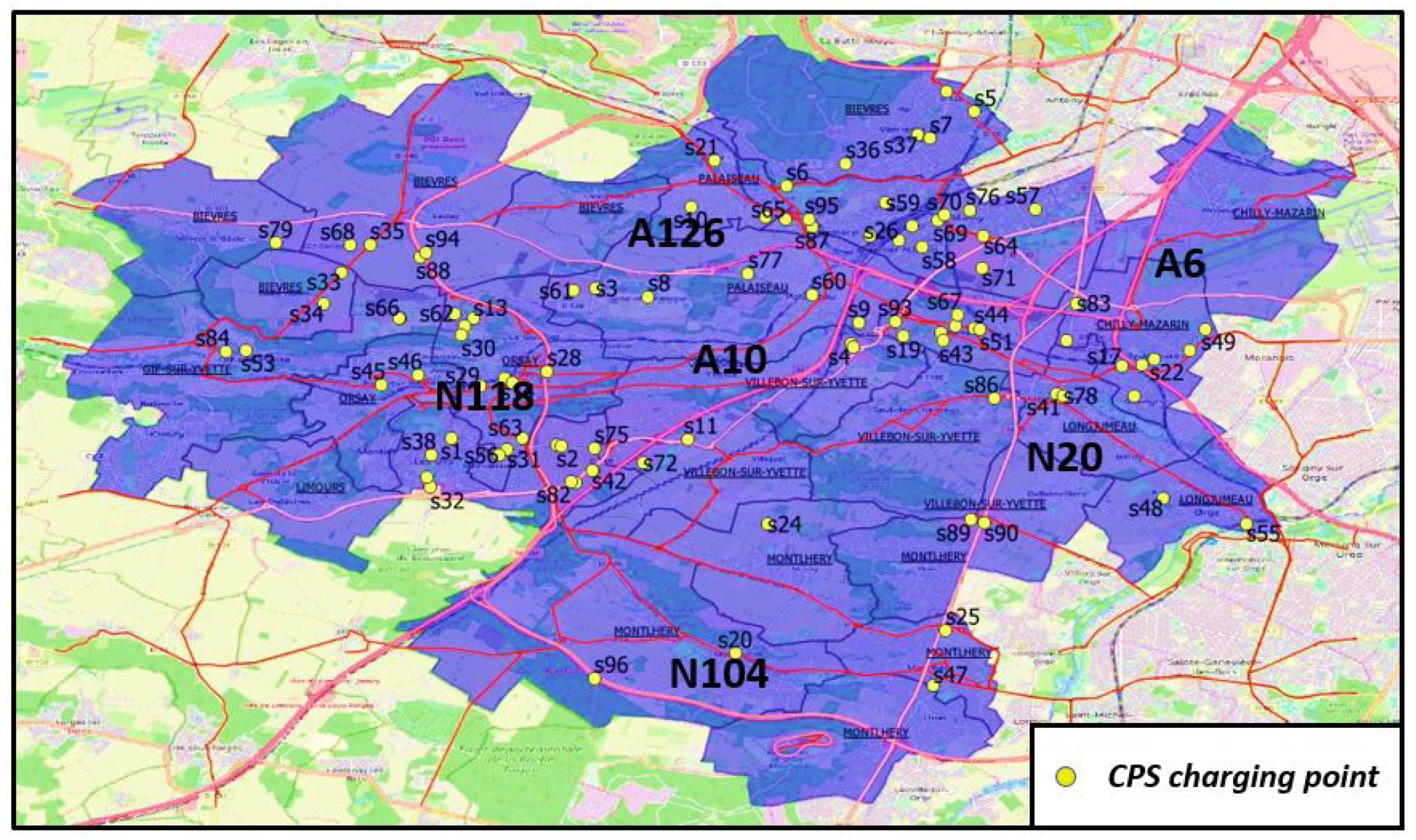
We introduce the considered operational problem and the modeling approach used to solve it using Paris-Saclay area as our case study. Paris-Saclay is an agglomeration community located at the south of Paris. As it is geographically close to the capital and to main economical activities, Paris-Saclay is traversed by many major mobility axes (e.g., A6, A10 and N20 in
Figure 1). These axes are used by personal vehicles and heavy trucks for short-distance trips (e.g., commuting) as well as international transit flows. In addition, a large photovoltaic (PV) farm is to be installed at Marcoussis district (next to the intersection of “A10” and “N104” highways,
Figure 1) with 76,500 PV panels and up to 24 GWh annual power production. The PV power will be raised to the voltage of the electric grid so that it can be injected into the distribution network. Thus, this farm has the potential of increasing charging power at nearby EV charging stations while reducing their reliance on the existing distribution network.
Based on these specifications, we provide a formal definition for the problem of locating EV fast-charging stations at Paris-Saclay area. First, we consider two types of fast chargers, one for charging small electric vehicles and the other for charging heavy electric trucks. In addition, We consider a set of potential charging locations
, where
includes locations that are powered by the distribution network and
includes those that are powered by a local PV station. Every charging location
is defined by a cost (
) indicating required investment to use this location as a charging station, and it has a maximum electric capacity and a max/min number of fast chargers that can be installed for small vehicles as well as heavy trucks (
and
, respectively). The investment cost (
) includes land cost (i.e., the cost required for purchasing the land where charging stations are to be installed) and cabling expenses (i.e., the extra expenses required to establish charging stations and connect them to the grid). For charging locations that are powered by the distribution network, the maximum electric capacity is fixed and depends on the distribution network itself. We refer to this fixed capacity as
(
). On the other hand, this capacity cannot be fixed for charging locations that are powered by PV energy as it highly depends on PV energy production which is stochastic (i.e., it depends on cloudiness index, season and solar irradiation). We thus refer to this varying electric capacity as
(
). To build mobility paths, we consider a set of coupling nodes
N representing different highway intersections. As such, we consider a set of paths
that link sequences of coupling nodes. Every path
is defined by its charging demands
and
, representing the number of electric vehicles and trucks, respectively, to be recharged per day. The set of charging locations that are associated with each path
p is denoted as
. The numbers of electric vehicles and trucks that can be recharged using a fast charger per day are defined as
and
respectively. Similarly, the amounts of electric power needed to recharge an electric vehicle or an electric truck using a fast charger are defined as
and
respectively. Moreover, installing a fast charger for electric vehicles or trucks implies extra costs (i.e., charger costs). These costs are defined as
and
, respectively. For the sake of simplicity, we assume all electric vehicles to be homogeneous, and, thus, their recharging time and energy are the same. We consider the same assumption for electric trucks (notations and variables are summarized in
Table 3).
Hence, the choice of deploying a charging station at location and the number of fast chargers to be installed is based on the recharging demand through the path where s is located. However, the number of chargers to be installed is limited by the available electric capacity and the availability of places and parking slots at location s. As such, we build a model to optimize this deployment by maximizing the satisfied demand while respecting the different constraints.
6. Conclusions
In this paper, a data-driven approach and an optimization model for the deployment of EV charging stations through a network of highways is introduced. The model was tested using a Cplex solver and a case study on Paris-Saclay area was performed. After selecting optimal locations for charging stations, the results highlight the benefits of integrating PV energy production on improving demand coverage rates. In addition, the economical benefits of this integration were quantified ( over 20 years lifetime).
The main perspectives of this research can be summarized in two levels. On the methodological level, the proposed approach can be extended to consider multiple renewable energy sources and integrate their power to the electric grid. Another interesting research direction is to consider EV battery states and the possibility of storing energy excess at charging stations during low-demand periods, so that it can be used later to charge EV at high-demand periods. This can lead to more realistic scenarios as both EV charging demand and PV production vary in different seasons and hours of the day. In addition, a stochastic programming approach can be developed for modeling uncertainty in PV production and better estimating its different scenarios. On the analytical level, besides analyzing the benefits of using PV energy for charging EVs, it is also important to study the impacts of this integration on the electric grid in terms of its infrastructure, as well as its effects on other sources of electric demands (e.g., transport, domestic, commerce, etc.). Finally, anticipating future charging demands and capacities represents a key passage for improving the obtained solution and adapting it to the future needs of EV charging networks. We thus believe that this study helps in better understanding the potential deployment of EV fast-charging stations in real-life applications and, thus, promoting more research towards studying this rising trend in the future.