Developing a Decision Tree Algorithm for Wind Power Plants Siting and Sizing in Distribution Networks
Abstract
:1. Introduction
- SCC: The amount of power that flows through a specified point when a short-circuit fault occurs at that point is expressed by SCC. The value of SCC depends on rated voltage (Vrated) and short-circuit impedance (Zsc) and is given as in (1) [4].
- SCR: The ratio between the grid’s SCC and the power injected by WPP is given by SCR. At the PCC bus of a distribution system connected to WPP, SCR quantifies the bus strength against the power quality issues caused by the wind power penetration. The value of SCR is calculated, as shown in (2) [4].
- X/RPCC: The grid impedance angle ratio seen at the PCC bus is defined by the X/RPCC. The value of the X/RPCC is determined by the ratio of Thevenin equivalent reactance and Thevenin equivalent resistance seen from that specified point [4]. The internal reactance of distribution lines is small, making the equivalent X/R value seen at the PCC small. The majority of existing approaches proposed for mitigating the voltage stability issues through reactive power compensation are applicable to power transmission networks where the X/R ratio is large [6]. Hence, these methods are not appropriate for distribution networks.
- Develop a novel voltage stability decision tree algorithm-based model predicting the key power quality components at a given PCC bus, i.e., VPCC and Pwind, based on the values of SCR and X/RPCC seen at that bus;
- Simplify the siting and sizing of IG- and DFIG-based WPPs in weak distribution network;
- Increase the prediction accuracy compared to the voltage stability mathematical model presented in [1].
2. Methodology
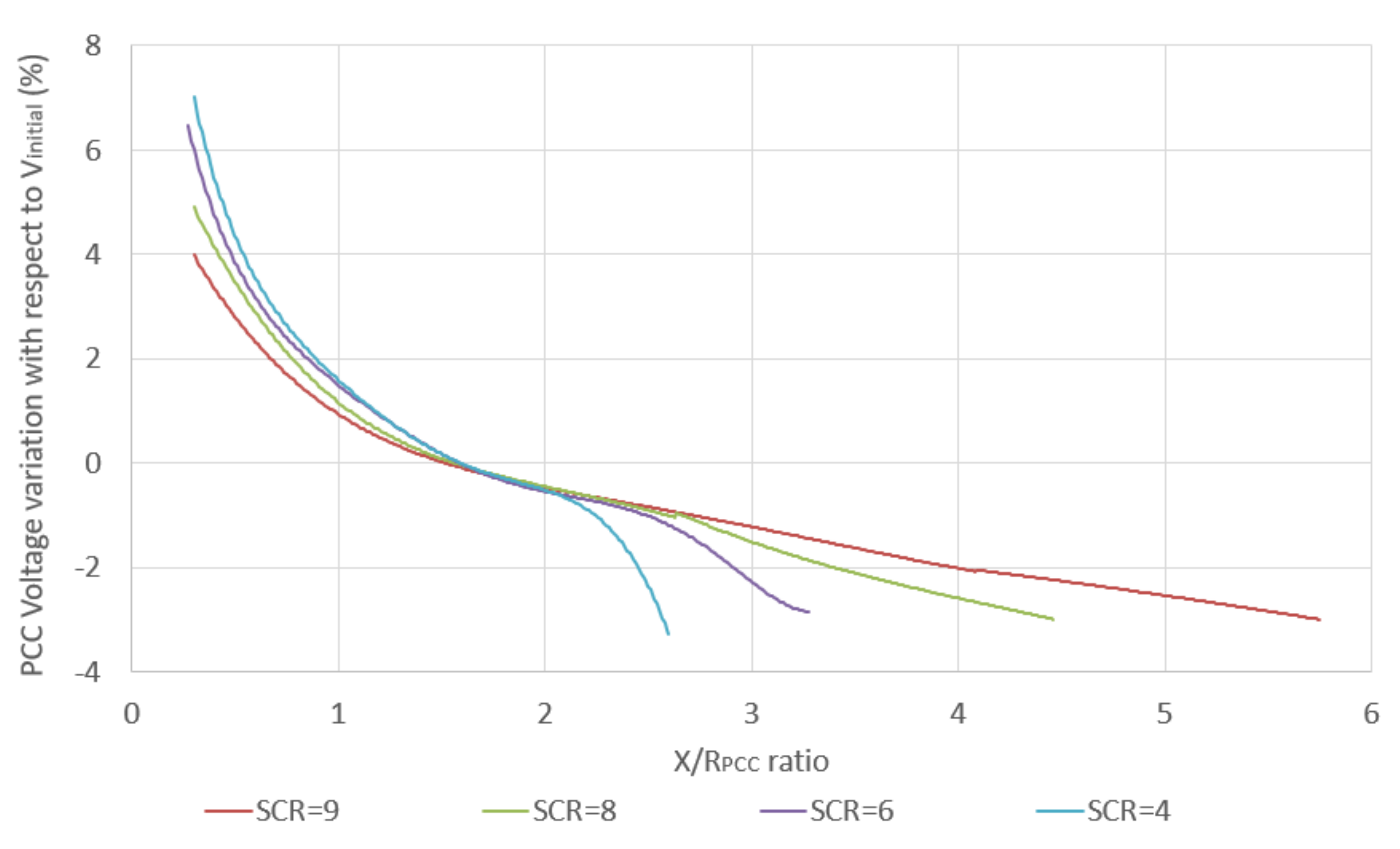
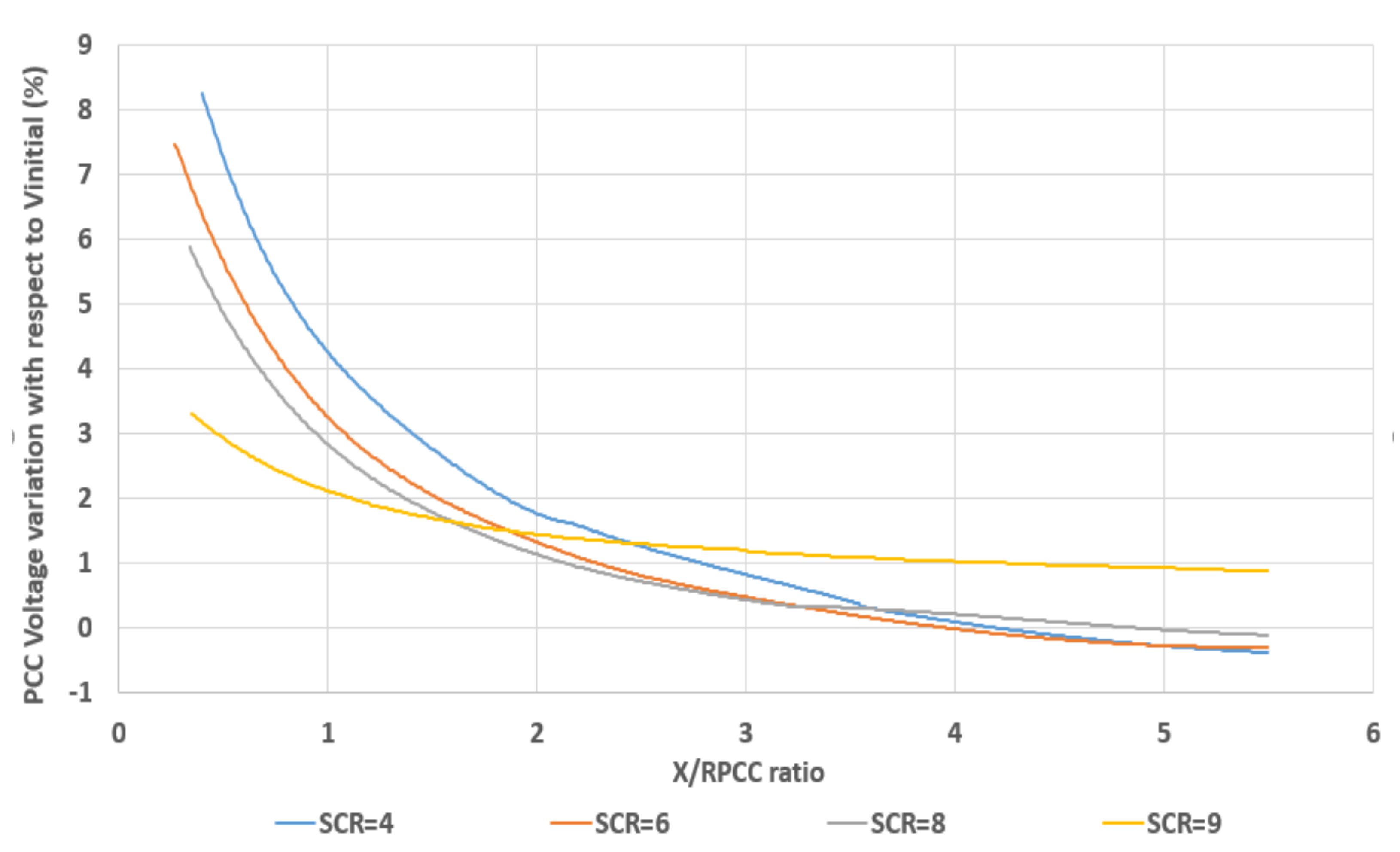
- Data collection and extension: In this study, the X/RPCC-dVPCC characteristics were required for test systems with different SCR ratios. For this purpose, the X/RPCC-dVPCC data points were obtained simulating the test systems from authors’ previous work presented in [1]. As discussed earlier, the higher accuracy of the prediction can be achieved by increasing the number of data points. However, the size of simulation data obtained by the test systems is small due to the limited capability of the MATLAB/Simulink solver in providing X/RPCC-dVPCC data points. Hence the obtained simulation data were then extended to obtain large training data set. In this work, the extension of simulation data was conducted using Microsoft Excel.
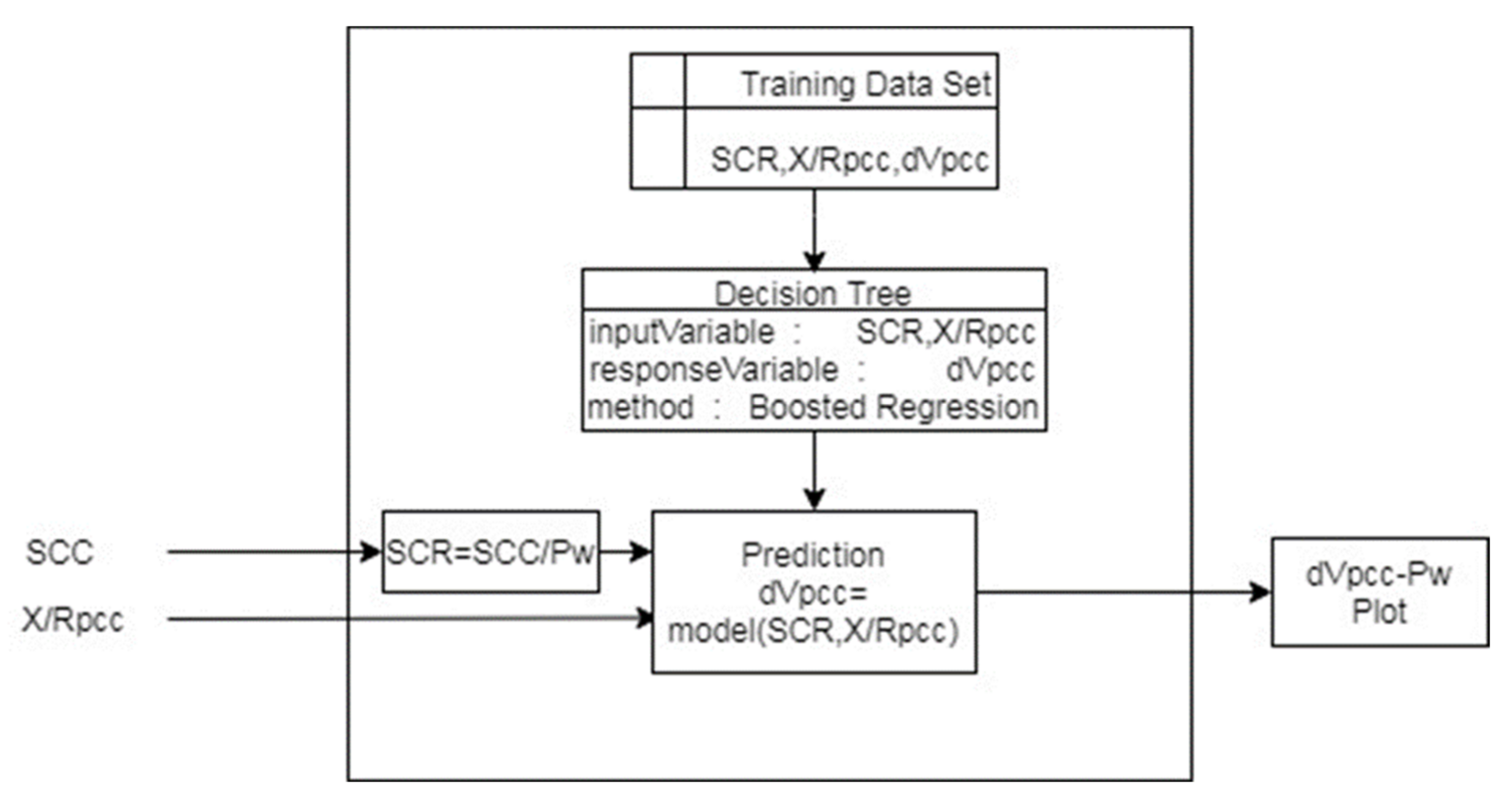
- Developing decision tree algorithm: The extended data were then trained in the decision tree in the MATLAB (version 2014a developed by MathWorks) to formulate a model for predicting dVPCC using the values of SCR and X/RPCC. Boosted regression decision tree was utilized to predict the voltage profile from given network parameters (SCR and X/RPCC).
2.1. Data Collection and Extension
2.2. Decision Tree Algorithm
3. Results and Discussion
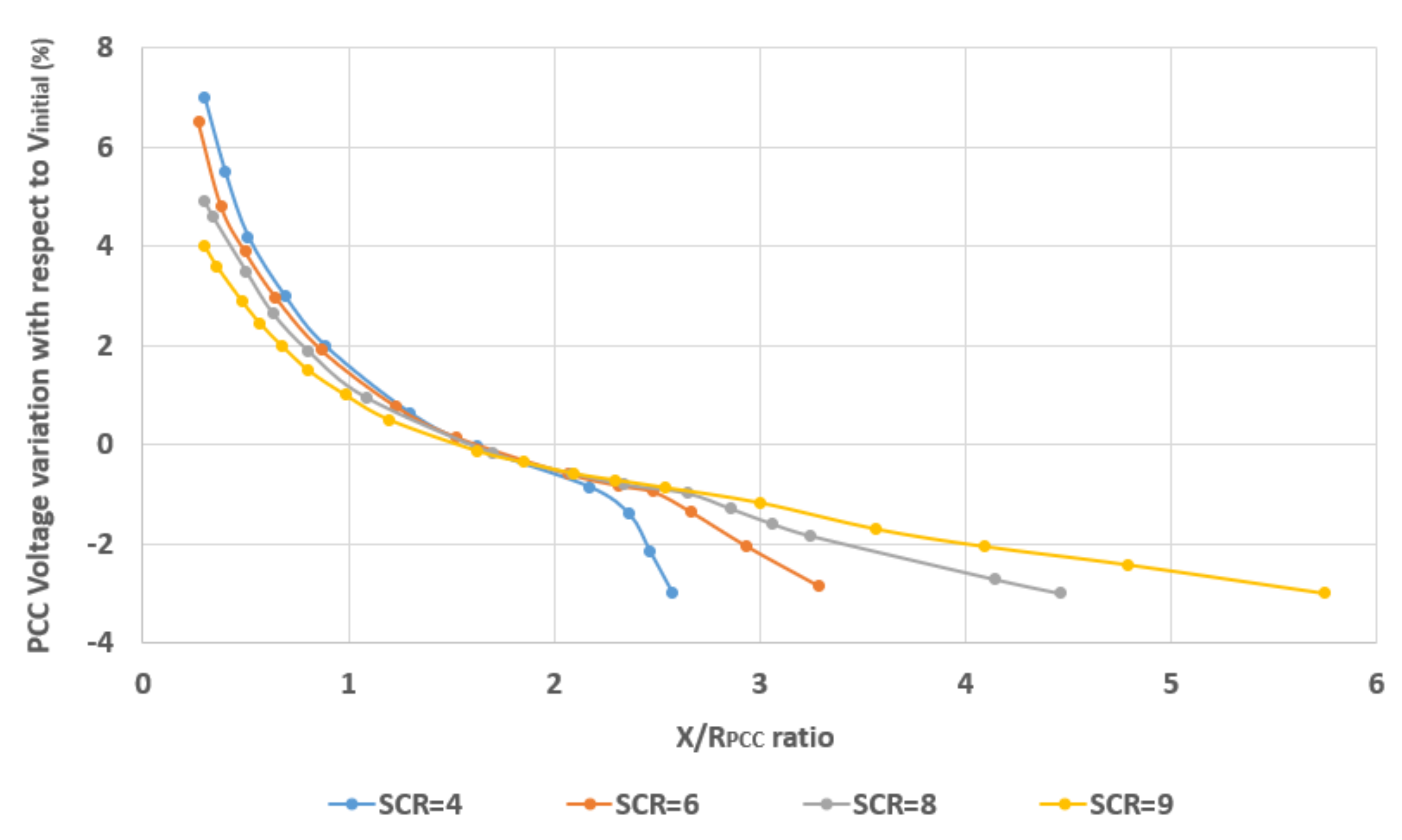
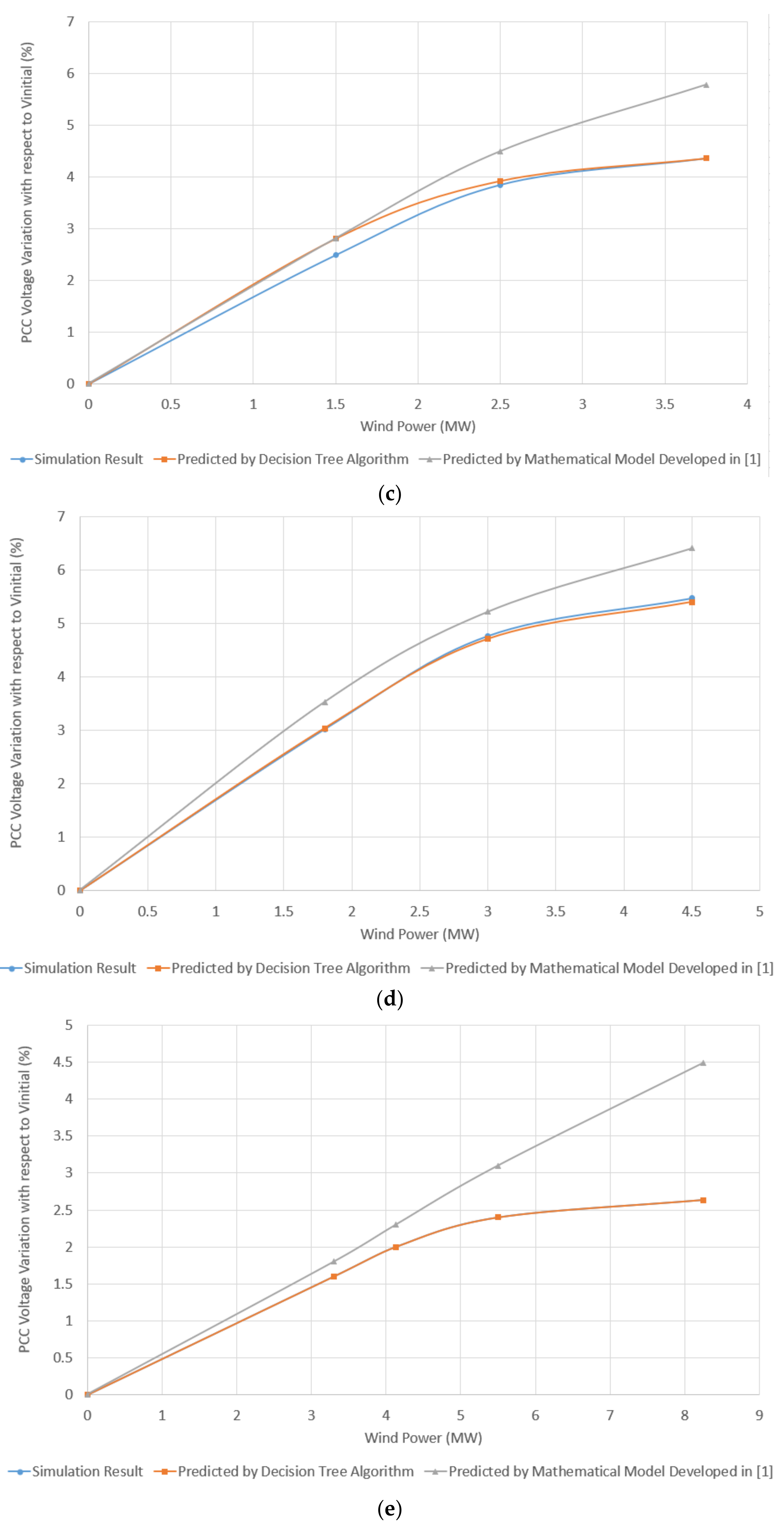
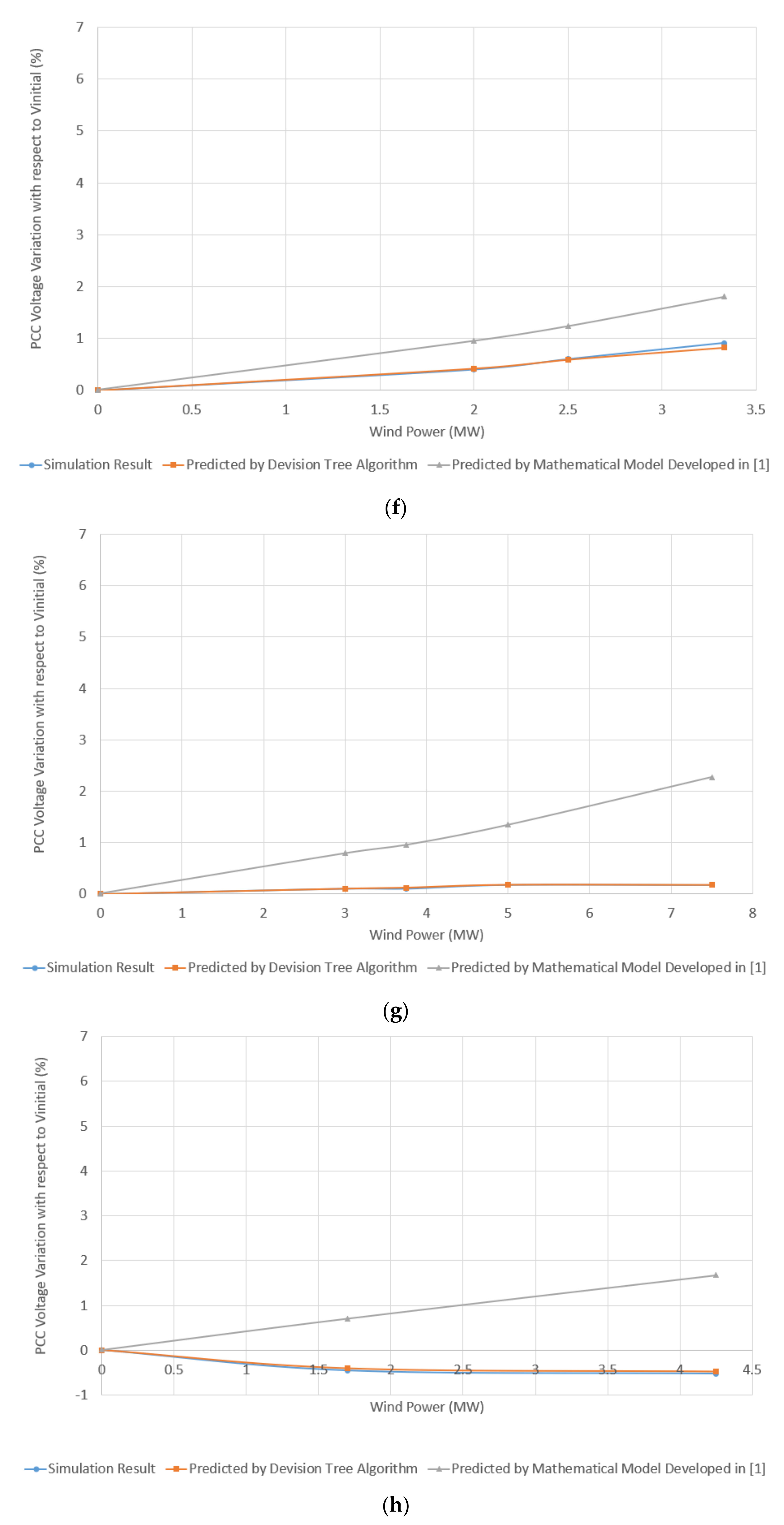
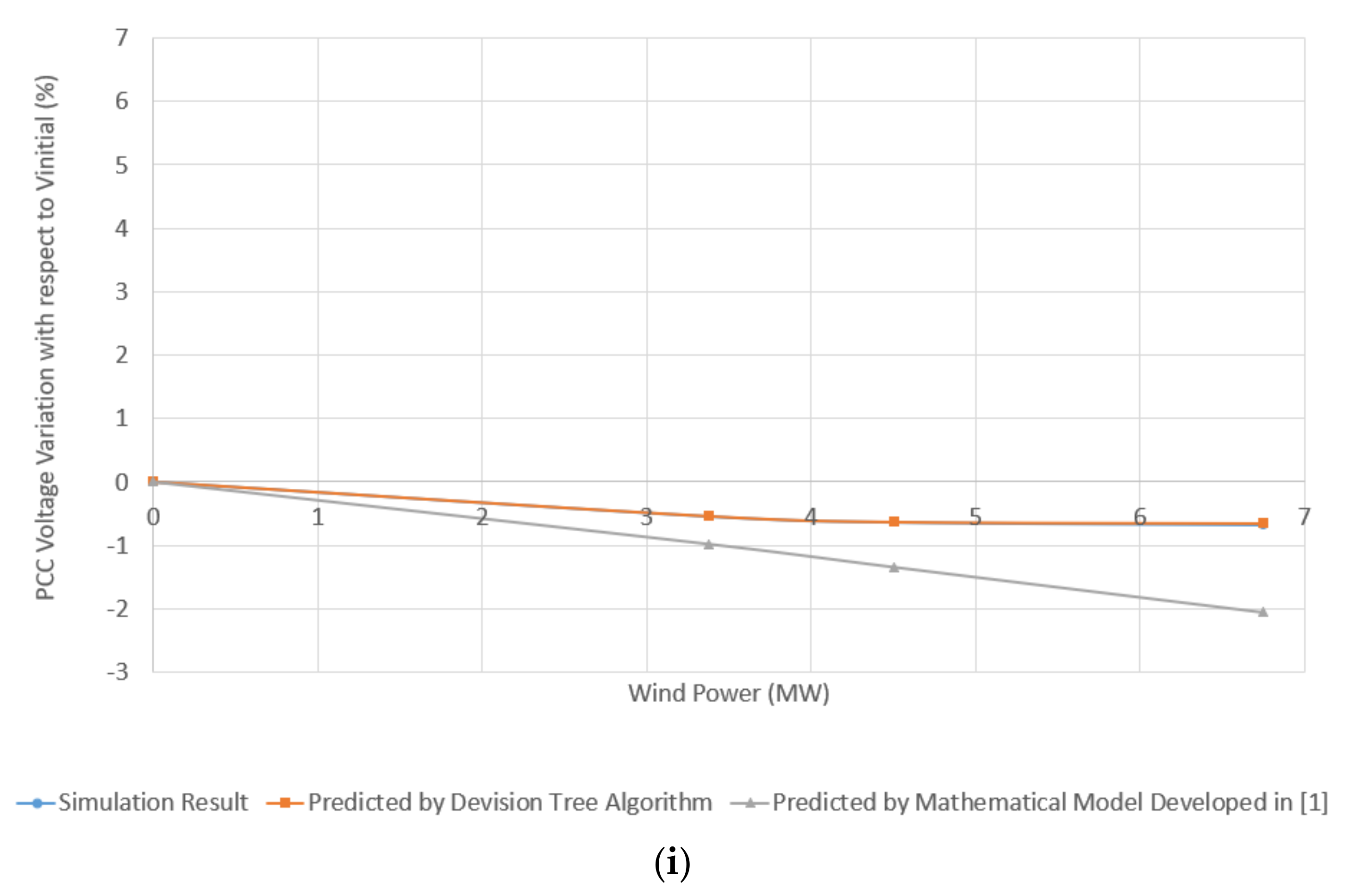
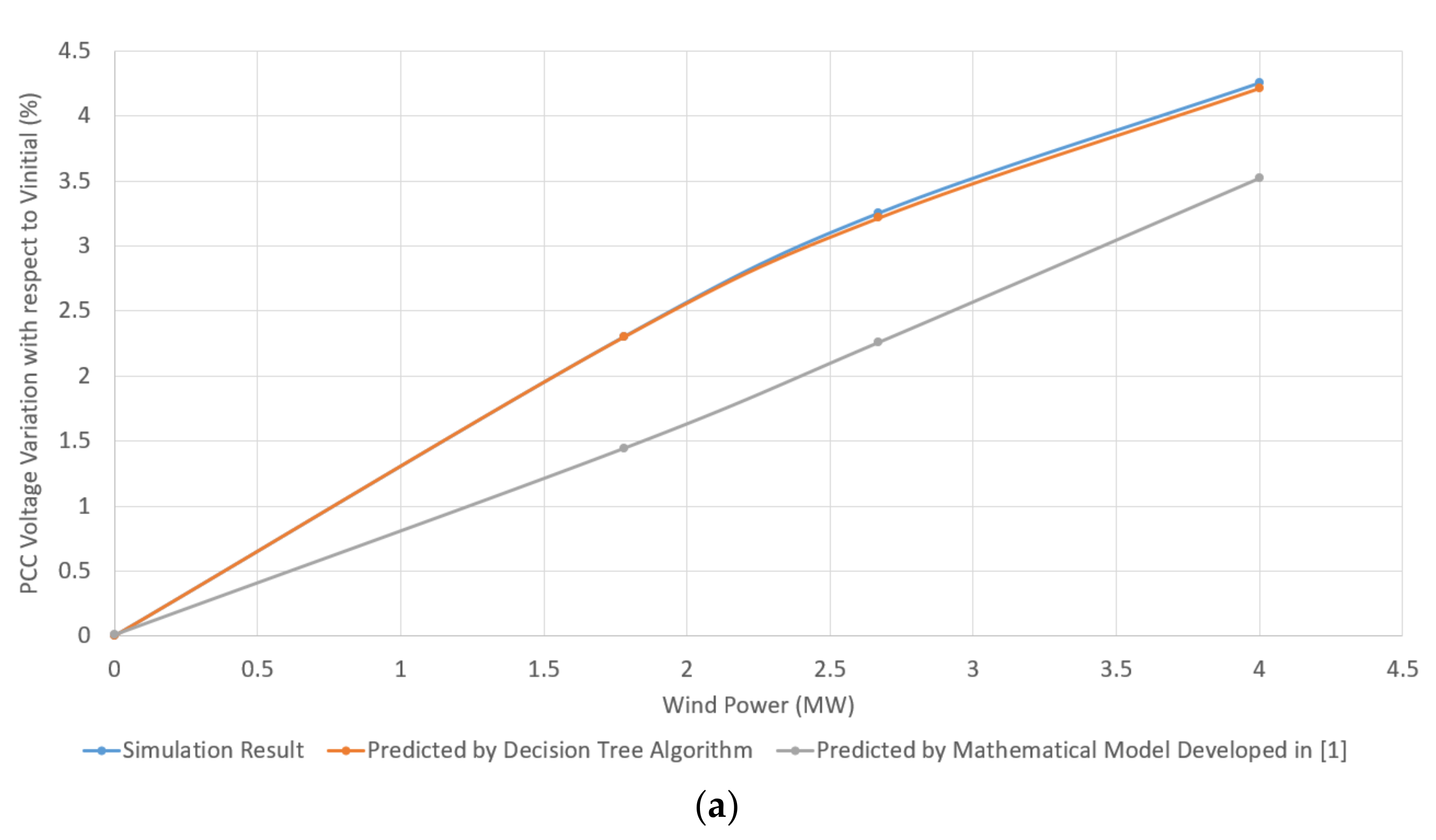
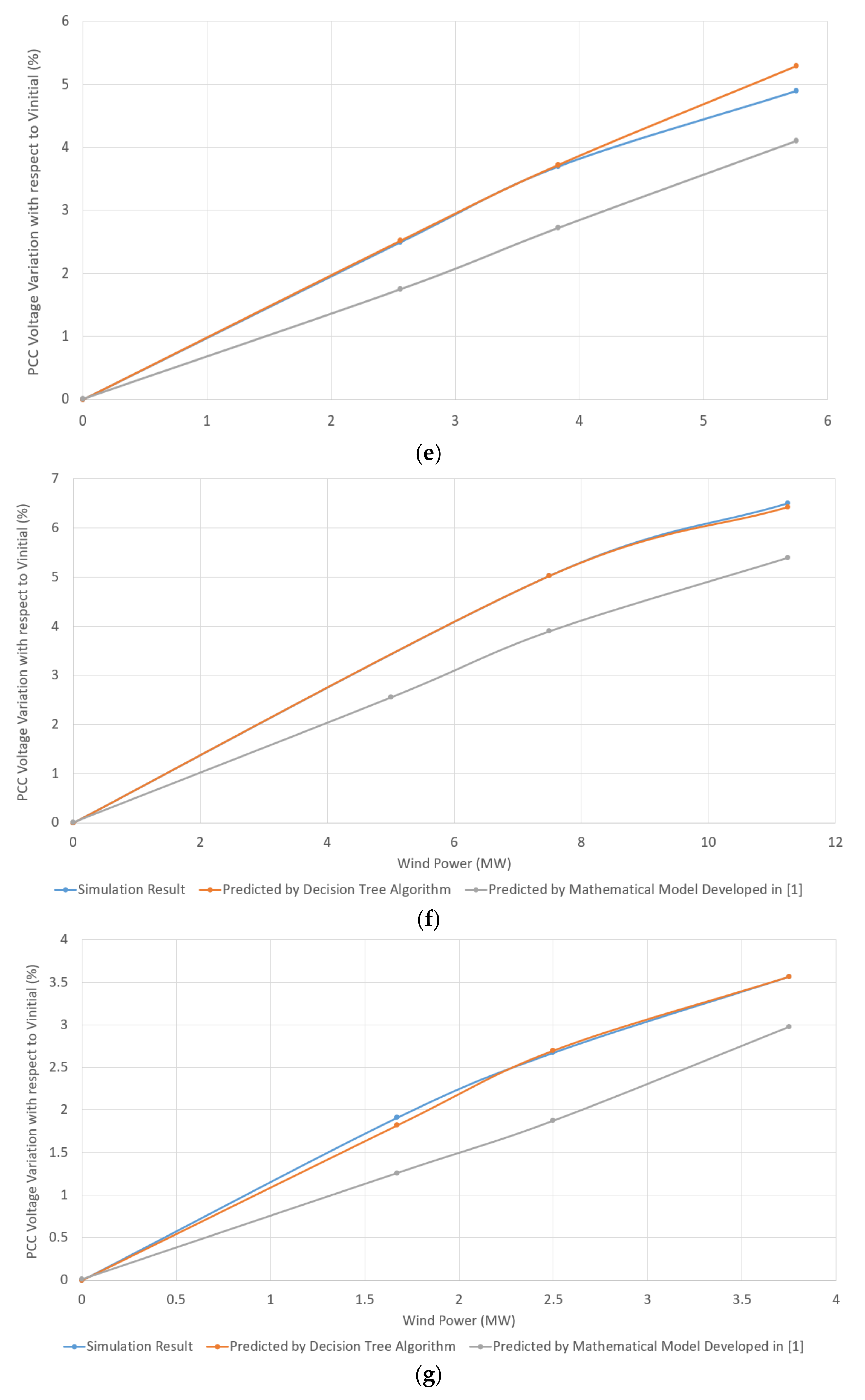
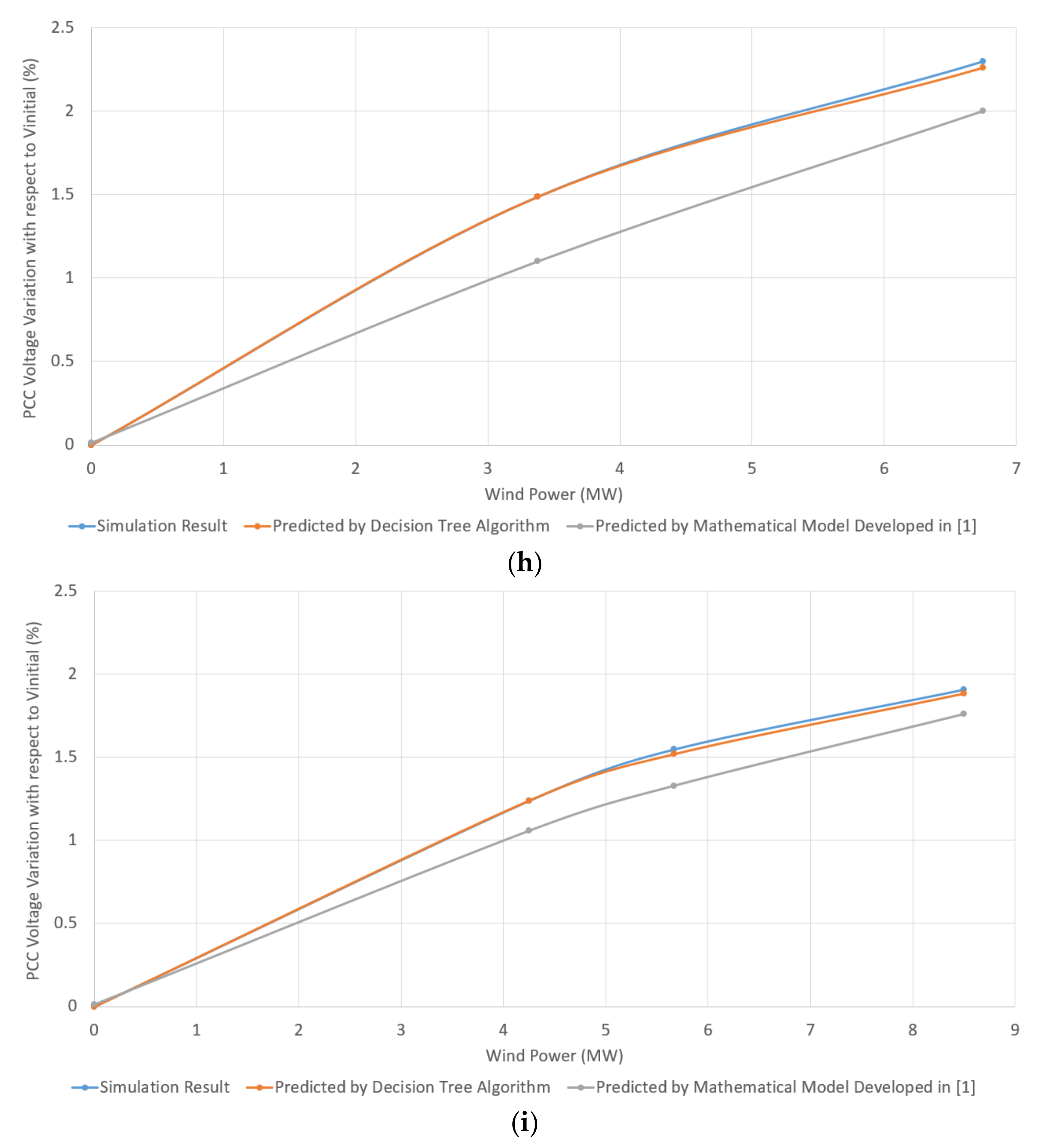
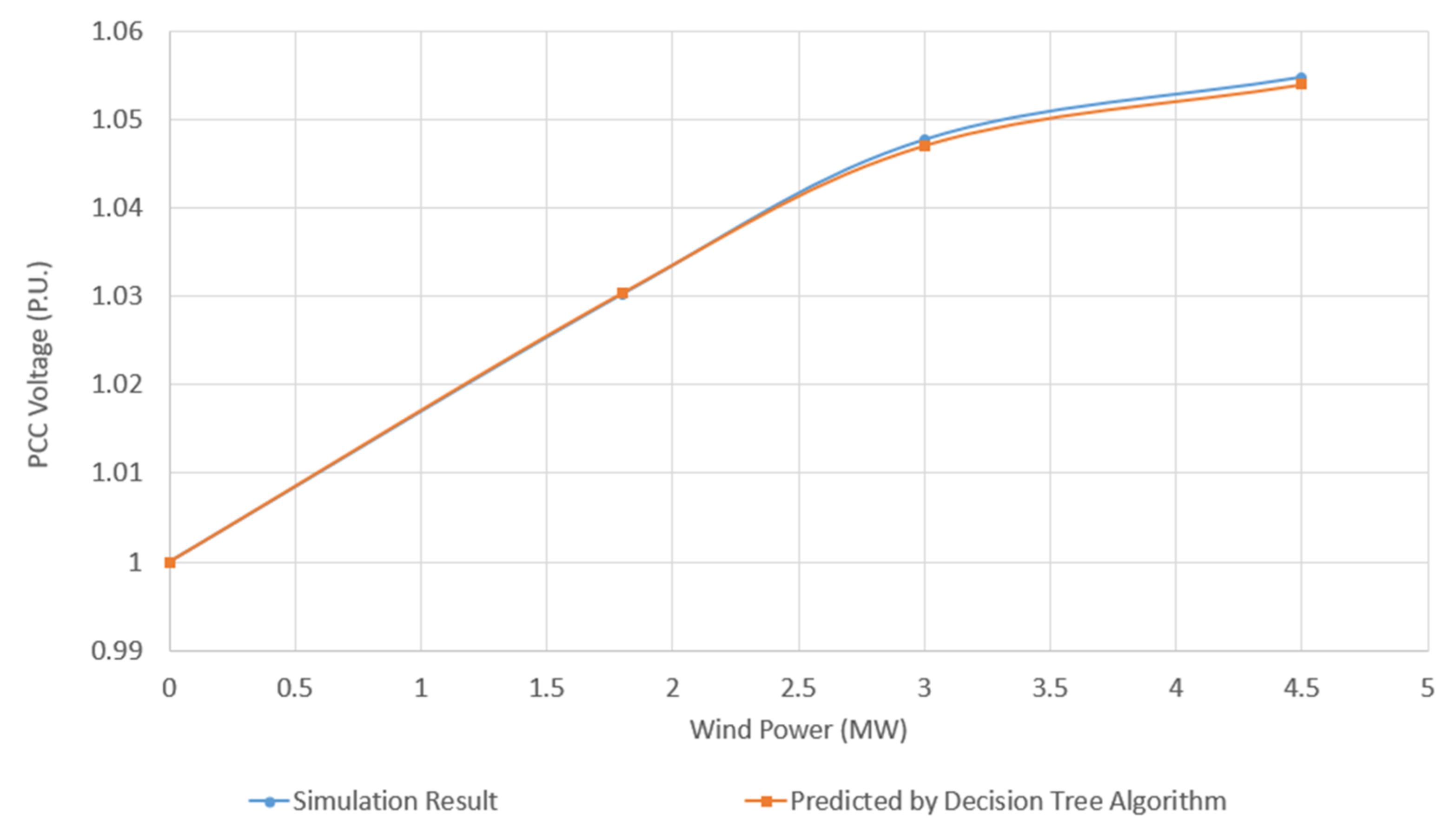
3.1. IG-Based WPPs
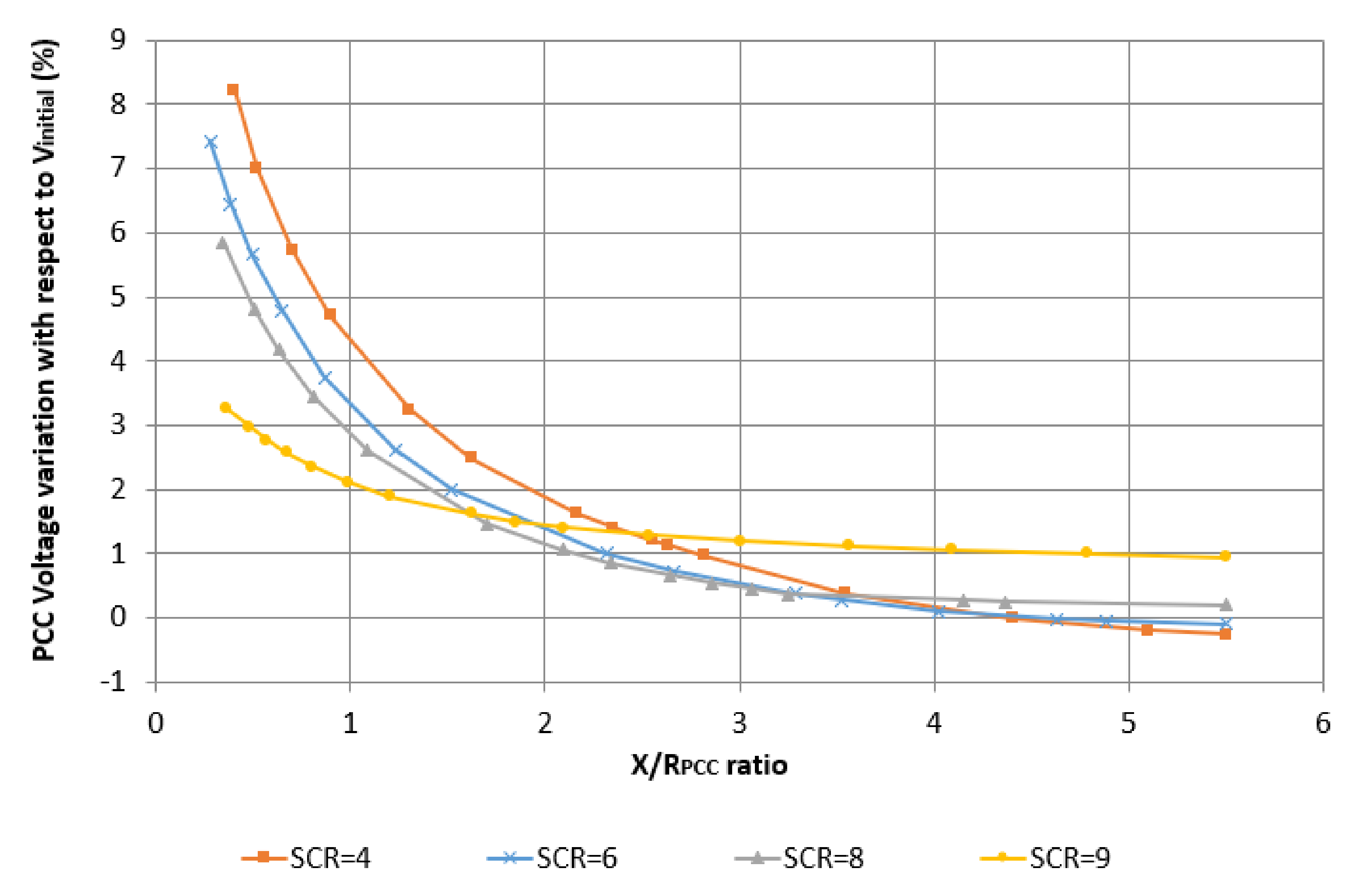
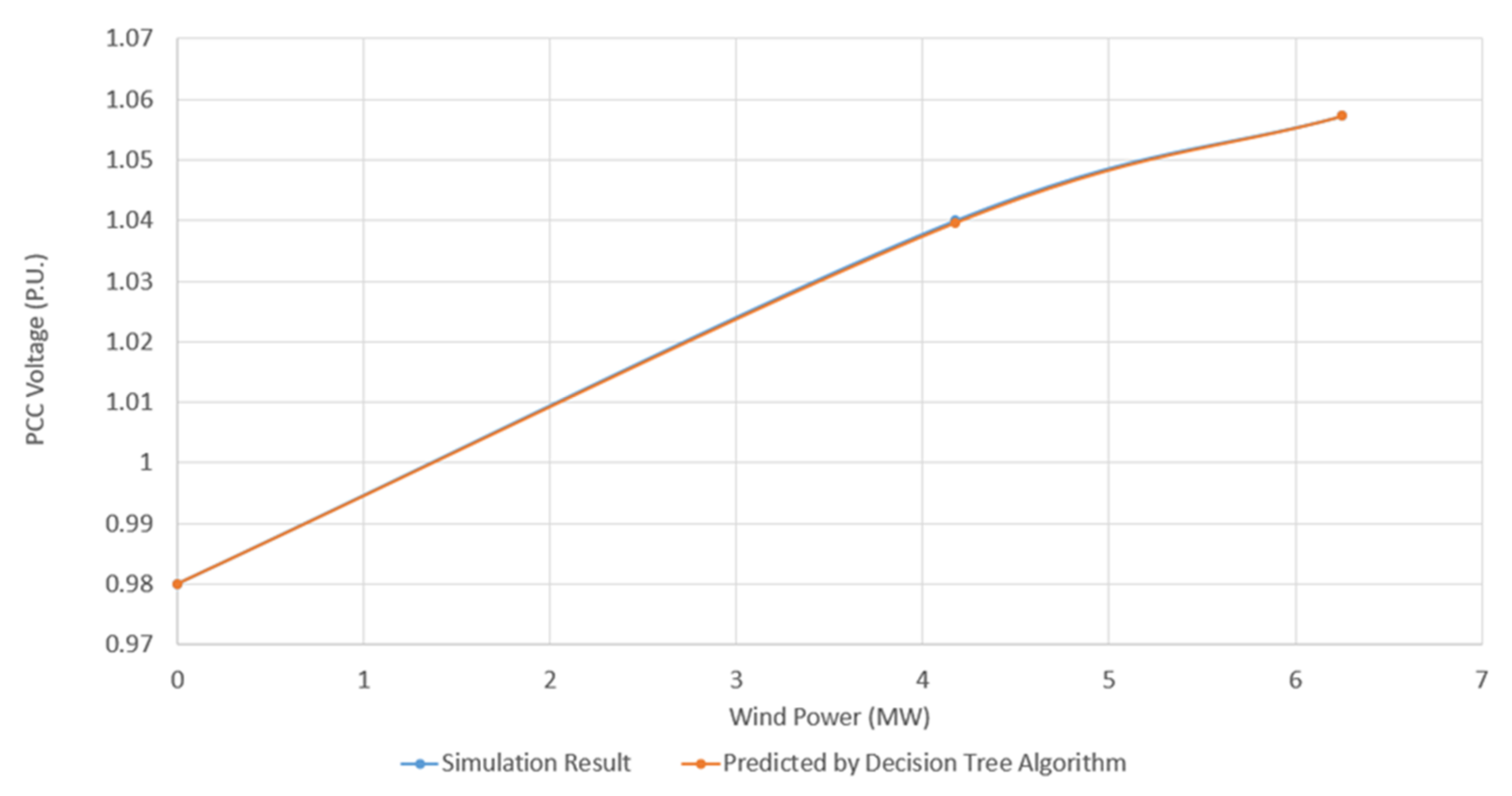
3.2. DFIG-Based WPPs
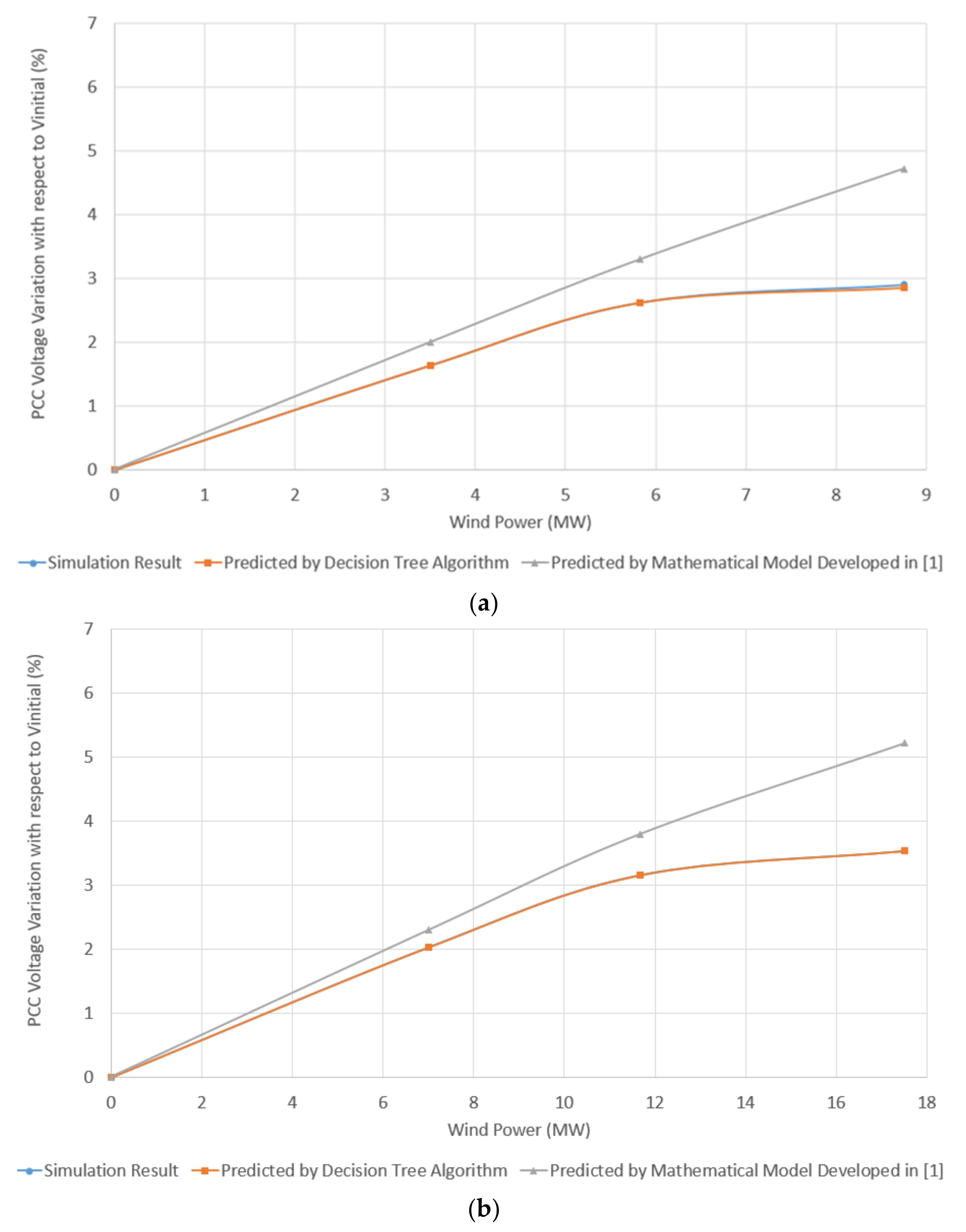
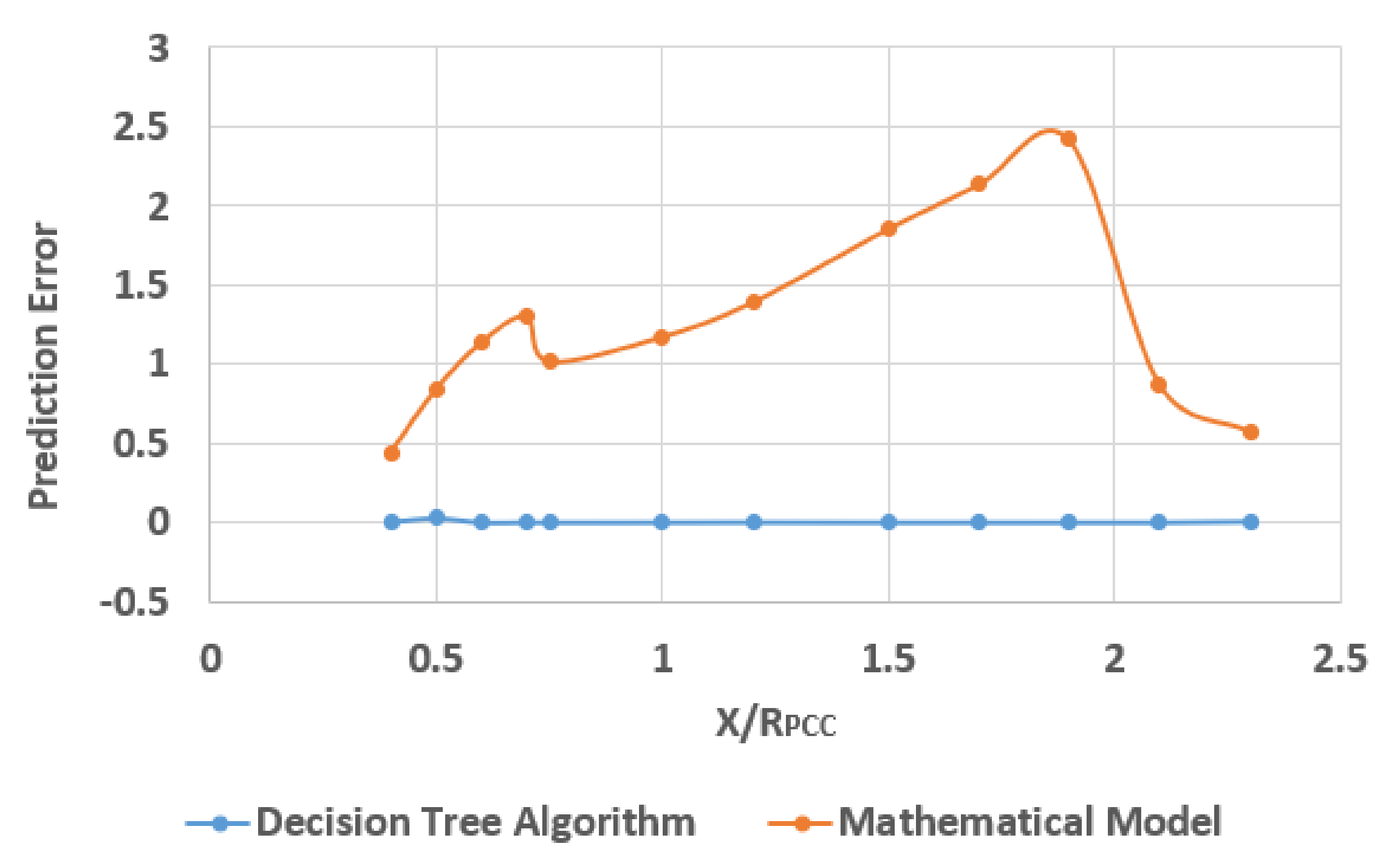
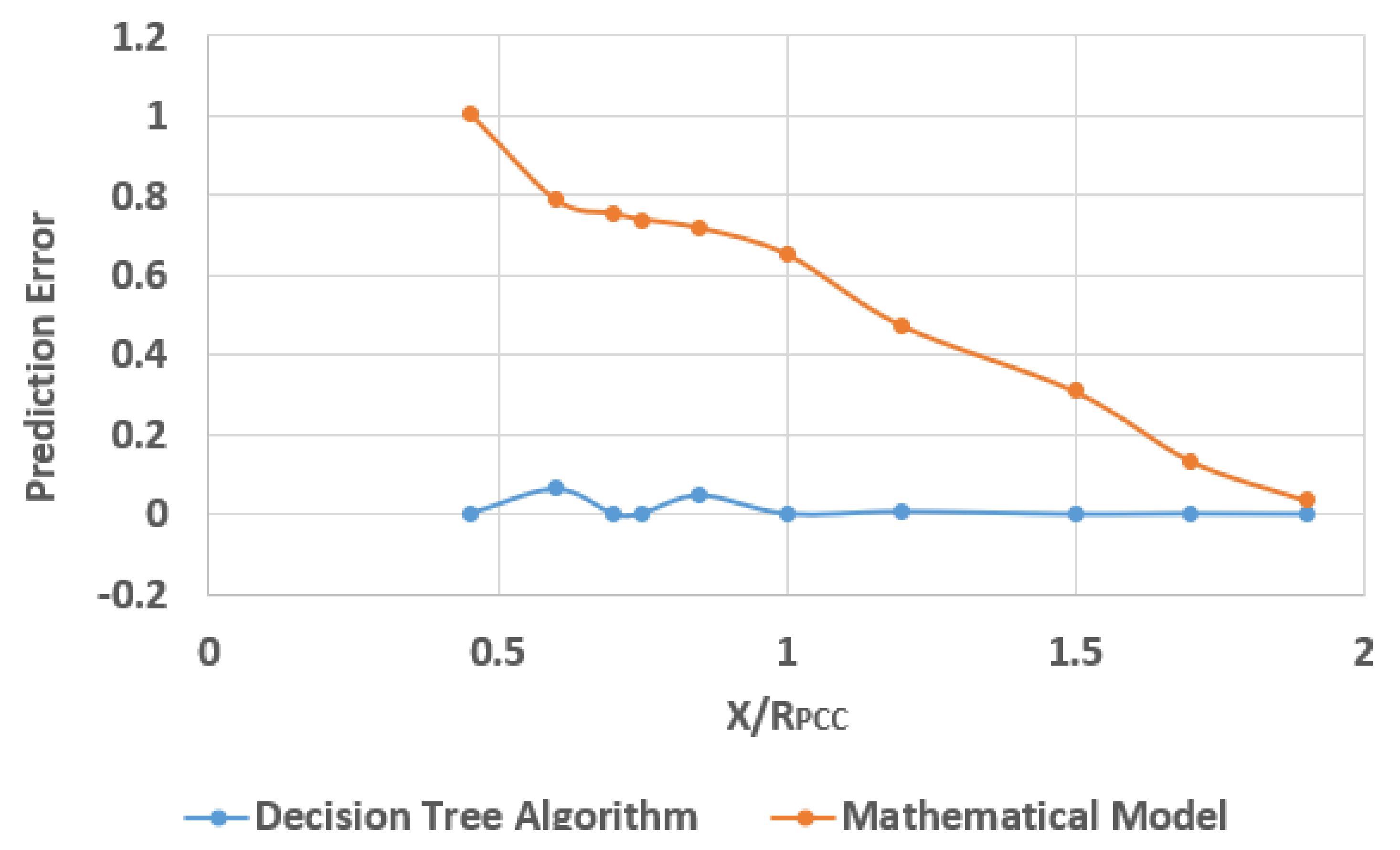
3.3. Comparison of Decision Tree Model and Mathematical Model for Different Ranges of X/RPCC
- N is the number of the Pwind-dVPCC data points;
- ∆Vp expresses the dVPCC value obtained by the predictive models, i.e., the decision tree-based model proposed in this paper and the mathematical model presented in [1], given the Pwind value;
- ∆Vr expresses the reference dVPCC obtained using the test simulation systems for each level of wind power penetration.
4. Significance of the Proposed Decision Tree-Based Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| IG | Induction generator |
| Isc | Short-circuit current |
| DFIG | Double-fed induction generator |
| dVPCC | Voltage variation concerning the voltage value before wind power plant connection at the point of common coupling |
| PE | Prediction error |
| PCC | Point of common coupling |
| Pwind | Power generated by wind power plant |
| SCC | Short-circuit capacity |
| SCR | Short-circuit ratio |
| Vinitial | Voltage at distribution feeder before the connection of wind power plant |
| WPP | Wind power plant |
| X/RPCC | Short-circuit impedance angle ratio seen at the point of common coupling |
| Zsc | Short-circuit impedance |
References
- Alizadeh, S.M.; Sadeghipour, S.; Ozansoy, C.; Kalam, A. Developing a Mathematical Model for Wind Power Plant Siting and Sizing in Distribution Networks. Energies 2020, 13, 3485. [Google Scholar] [CrossRef]
- Ahmed, S.D.; Al-Ismali, F.S.M.; Shafiullah, M.; Al-Sulaiman, F.A.; El-Amin, I.M. Grid Integration Challenges of Wind Energy: A Review. IEEE Access 2020, 8, 10857–10878. [Google Scholar] [CrossRef]
- Machado, I.; Arias, I. Grid Codes Comparison. Master’s Thesis, Chalmers University of Technology, Göteborg, Sweden, 2006. [Google Scholar]
- Alizadeh, S.M. An Analytical Voltage Stability Model for Wind Power Plant Sizing and Siting in Distribution Networks. Ph.D. Thesis, Victoria University, Footscray, Australia, 2017. [Google Scholar]
- Golieva, A. Low Short-Circuit Ratio Connection of Wind Power Plants. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2015. [Google Scholar]
- Alizadeh, S.M.; Ozansoy, C.; Alpcan, T. In The Impact of X/R Ratio on Voltage Stability in a Distribution Network Penetrated by Wind Farms. In Proceedings of the 2016 Australasian Universities Power Engineering Conference (AUPEC), Brisbane, Australia, 25–28 September 2016; pp. 1–6. [Google Scholar]
- Naik, S.G.; Khatod, D.; Sharma, M. In Sizing and Siting of Distributed Generation in Distribution Networks for Real Power Loss Minimization Using Analytical Approach. In Proceedings of the International Conference on Power, Energy and Control (ICPEC), Sri Rangalatchum Dindigul, India, 6–8 February 2013; pp. 740–745. [Google Scholar]
- Keane, A.; O’Malley, M. Optimal Utilization of Distribution Networks for Energy Harvesting. IEEE Trans. Power Syst. 2007, 22, 467–475. [Google Scholar] [CrossRef]
- Atwa, Y.M.; El-Saadany, E.F.; Salama, M.M.A.; Seethapathy, R. Optimal Renewable Resources Mix for Distribution System Energy Loss Minimization. IEEE Trans. Power Syst. 2010, 25, 360–370. [Google Scholar] [CrossRef]
- Khalesi, N.; Rezaei, N.; Haghifam, M.R. DG Allocation with Application of Dynamic Programming for Loss Reduction and Reliability Improvement. Int. J. Electr. Power Energy Syst. 2011, 33, 288–295. [Google Scholar] [CrossRef]
- Georgilakis, P.S.; Hatziargyriou, N.D. Optimal Distributed Generation Placement in Power Distribution Networks: Models, Methods, and Future Research. IEEE Trans. Power Syst. 2013, 28, 3420–3428. [Google Scholar] [CrossRef]
- Farhat, I.A. Ant Colony Optimization for Optimal Distributed Generation in Distribution Systems. Int. J. Comput. Inf. Eng. 2013, 7, 1094–1098. [Google Scholar]
- Ali, A.; Padmanaban, S.; Twala, B.; Marwala, T. Electric Power Grids Distribution Generation System for Optimal Location and Sizing–A Case Study Investigation by Various Optimization Algorithms. Energies 2017, 10, 960. [Google Scholar]
- Mohammadi, M.; Naseb, M.A. PSO Based Multiobjective Approach for Optimal Sizing and Placement of Distributed Generation. Res. J. Appl. Sci. Eng. Technol. 2011, 2, 832–837. [Google Scholar]
- Seker, A.A.; Hocaoglu, M.H. In Artificial Bee Colony Algorithm for Optimal Placement and Sizing of Distributed Generation. In Proceedings of the 8th International Conference on Electrical and Electronics Engineering, Bursa, Turkey, 28–30 November 2013; pp. 127–131. [Google Scholar]
- Australian Energy Market Operator. Modelling Requirements. Available online: https://www.aemo.com.au/Electricity/National-Electricity-Market-NEM/Network-connections/Modelling-requirements (accessed on 8 October 2018).
- Chauhan, N.S. Decision Tree Algorithm—Explained. Available online: https://www.kdnuggets.com/2020/01/decision-tree-algorithm-explained.html (accessed on 14 January 2020).
- Poojari, D. Machine Learning Basics: Decision Tree from Scratch. Towards Data Science. Available online: https://towardsdatascience.com/machine-learning-basics-descision-tree-from-scratch-part-ii-dee664d46831 (accessed on 2 August 2019).
- Reginato, R.; Zanchettin, M.G.; Tragueta, M. Analysis of Safe Integration Criteria for Wind Power with Induction Generators Based Wind Turbines. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar]
- Bluttman, K. Excel Formulas and Functions for Dummies, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA; pp. 1–400.
- Sayad, D.S. Decision Tree–Regression. Available online: https://www.saedsayad.com/decision_tree_reg.htm (accessed on 1 January 2010).
- Rokach, L.; Maimon, O. Decision Trees. In Data Mining and Knowledge Discovery Handbook; Springer: Boston, MA, USA, 2005; pp. 165–192. [Google Scholar]
- Rocca, J. Ensemble Methods: Bagging, Boosting and Stacking. Towards Data Science. Available online: https://towardsdatascience.com/ensemble-methods-bagging-boosting-and-stacking-c9214a10a205 (accessed on 23 April 2019).
- Glen, S. Prediction Error: Definition. Statistics How To. Available online: https://www.statisticshowto.com/prediction-error-definition (accessed on 2 October 2019).
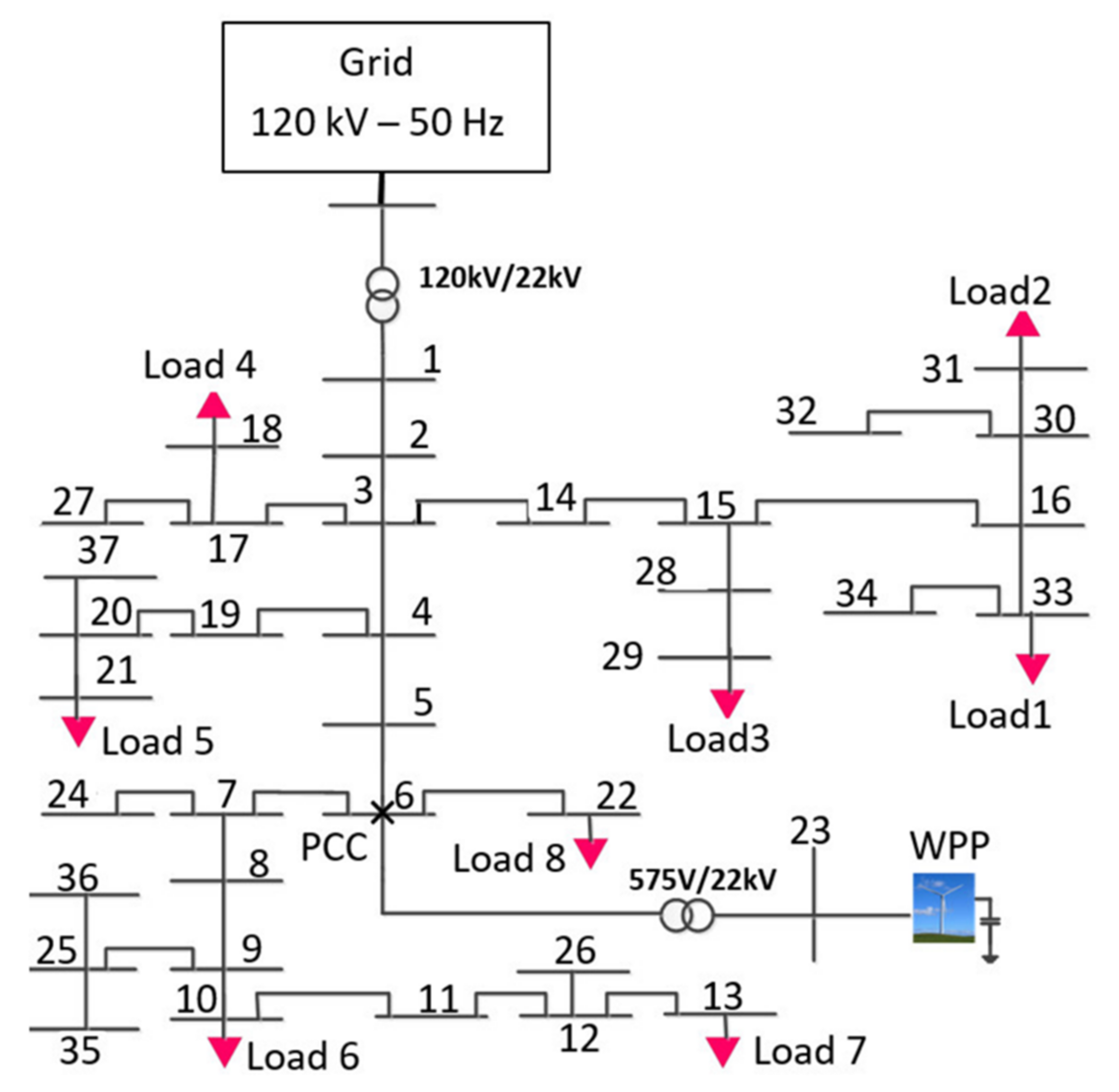
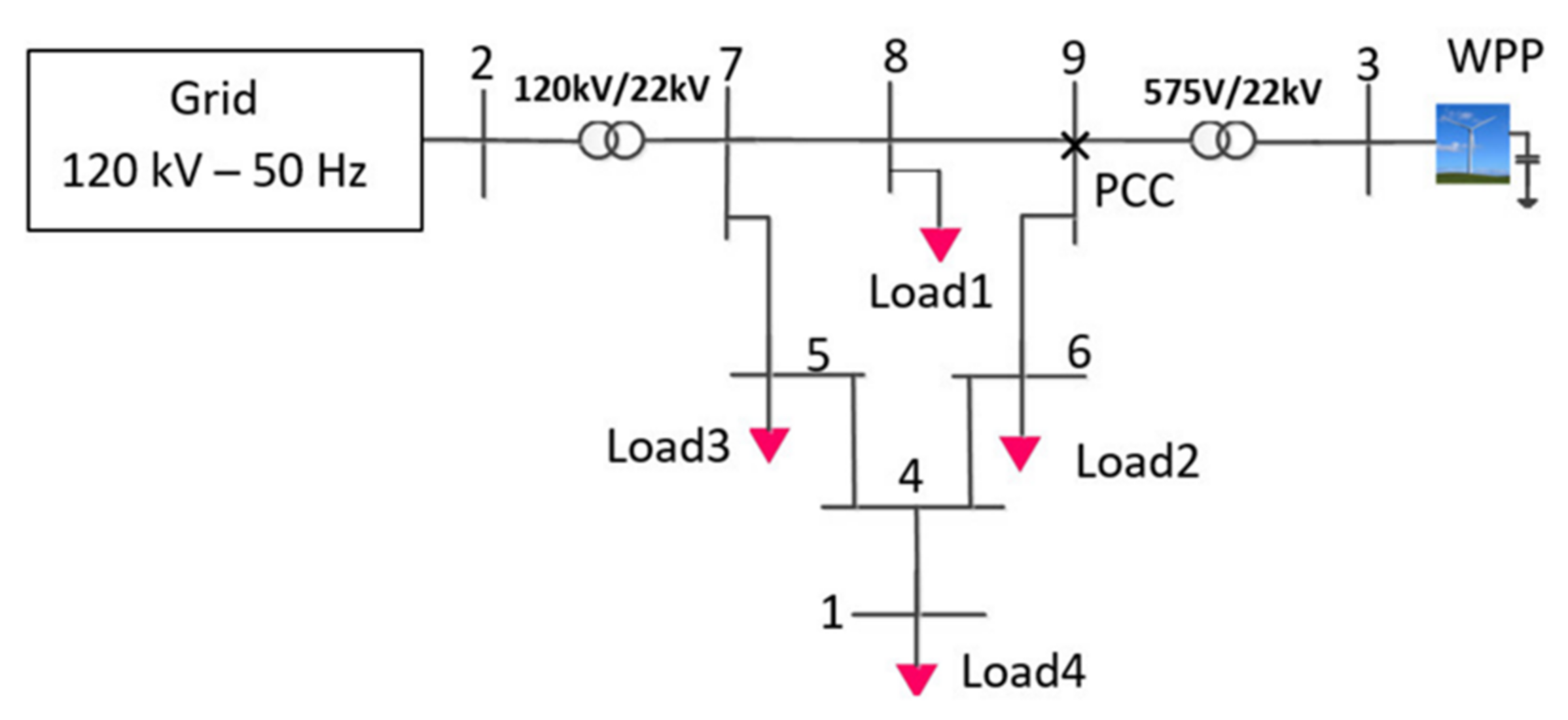

| Case Study | Topology | Isc (kA) | SCC (MVA) | Pwind (MW) | SCR |
|---|---|---|---|---|---|
| Test 1 | IEEE 37-bus system | 0.95 | 36 | 9 | 4 |
| Test 2 | IEEE 37-bus system | 1.42 | 54 | 9 | 6 |
| Test 3 | IEEE 37-bus system | 1.89 | 72 | 9 | 8 |
| Test 4 | IEEE 9-bus system | 0.71 | 27 | 3 | 9 |
| Step | Pseudo Code | Description |
|---|---|---|
| 1. | Load IG_data/DFIG_data (extended) | The table that contains extended data (SCR, X/RPCC, dVPCC) is loaded as training data set. |
| 2. | Feature variable (input) ← SCR,X/RPCC | Assign feature and response variable |
| response variable (output) ← dVPCC | ||
| 3. | T ← template tree (min leaf size = 5) | Create a template tree having a minimum number of data points in a leaf = 5 |
| 4. | model ← fit regression tree (SCC, X/RPCC, dVPCC) Method ← least square boosting number of learning cycles ← 100 | The ensemble tree is created from training data set using the least square boosting method and with 100 learning cycles |
| 5. | Prompt SCC, X/RPCC | Request input from the user |
| 6. | Pwind ← [SCC/SCR] Input = (SCR, X/RPCC) | Find power points for respective SCR values |
| 7. | [dVPCC] = predict (Igmodel, Input) | Predict the response variable (dVPCC) from features (SCR, X/RPCC) |
| 8. | Plot (Pwind, dVPCC) | Plot variation in voltage profile with the amount of penetrated power |
| Test No. | SCC | X/RPCC |
|---|---|---|
| 1 | 35 | 0.7 |
| 2 | 70 | 0.6 |
| 3 | 15 | 0.5 |
| 4 | 18 | 0.4 |
| 5 | 33 | 0.75 |
| 6 | 20 | 1.2 |
| 7 | 30 | 1.5 |
| 8 | 17 | 1.9 |
| 9 | 27 | 2.1 |
| Test No. | SCC | X/RPCC |
|---|---|---|
| 1 | 16 | 1 |
| 2 | 25 | 0.45 |
| 3 | 45 | 0.75 |
| 4 | 35 | 0.7 |
| 5 | 23 | 0.85 |
| 6 | 45 | 0.6 |
| 7 | 15 | 1.2 |
| 8 | 27 | 1.7 |
| 9 | 34 | 1.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghimire, S.; Alizadeh, S.M. Developing a Decision Tree Algorithm for Wind Power Plants Siting and Sizing in Distribution Networks. Energies 2021, 14, 2293. https://doi.org/10.3390/en14082293
Ghimire S, Alizadeh SM. Developing a Decision Tree Algorithm for Wind Power Plants Siting and Sizing in Distribution Networks. Energies. 2021; 14(8):2293. https://doi.org/10.3390/en14082293
Chicago/Turabian StyleGhimire, Santosh, and Seyed Morteza Alizadeh. 2021. "Developing a Decision Tree Algorithm for Wind Power Plants Siting and Sizing in Distribution Networks" Energies 14, no. 8: 2293. https://doi.org/10.3390/en14082293
APA StyleGhimire, S., & Alizadeh, S. M. (2021). Developing a Decision Tree Algorithm for Wind Power Plants Siting and Sizing in Distribution Networks. Energies, 14(8), 2293. https://doi.org/10.3390/en14082293







