A Simulation Model for Providing Analysis of Wind Farms Frequency and Voltage Regulation Services in an Electrical Power System †
Abstract
1. Introduction
2. Principles of Frequency and Voltage Regulation in the EPS
2.1. Frequency Control
2.2. Voltage Control
3. System under Study
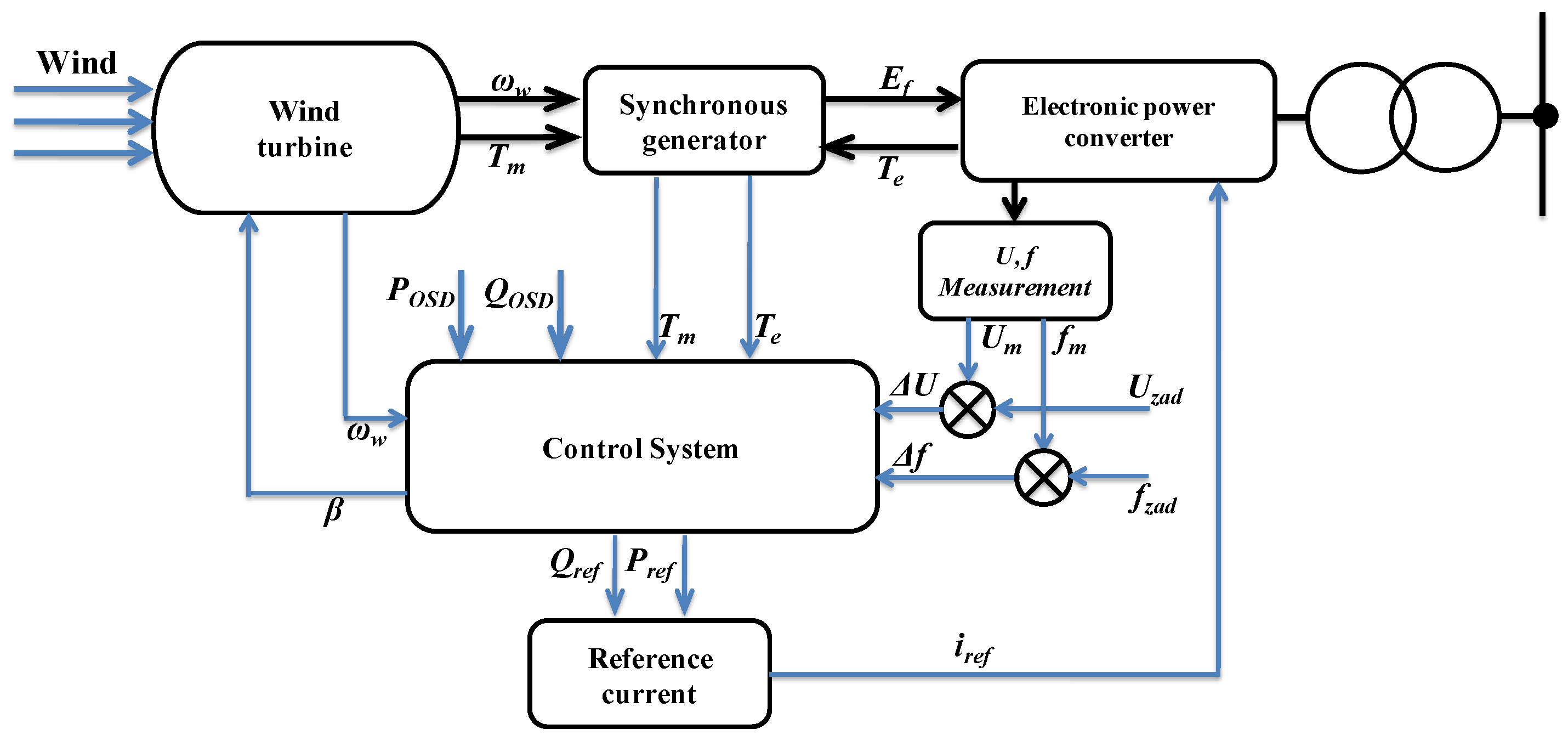
3.1. System Layout
3.2. Assumptions for WF Control
- Normal operation mode with available power or power limitations,
- Intervention mode, operation with performing voltage and/or frequency regulation services.
4. System Model
4.1. The Wind Farm Model
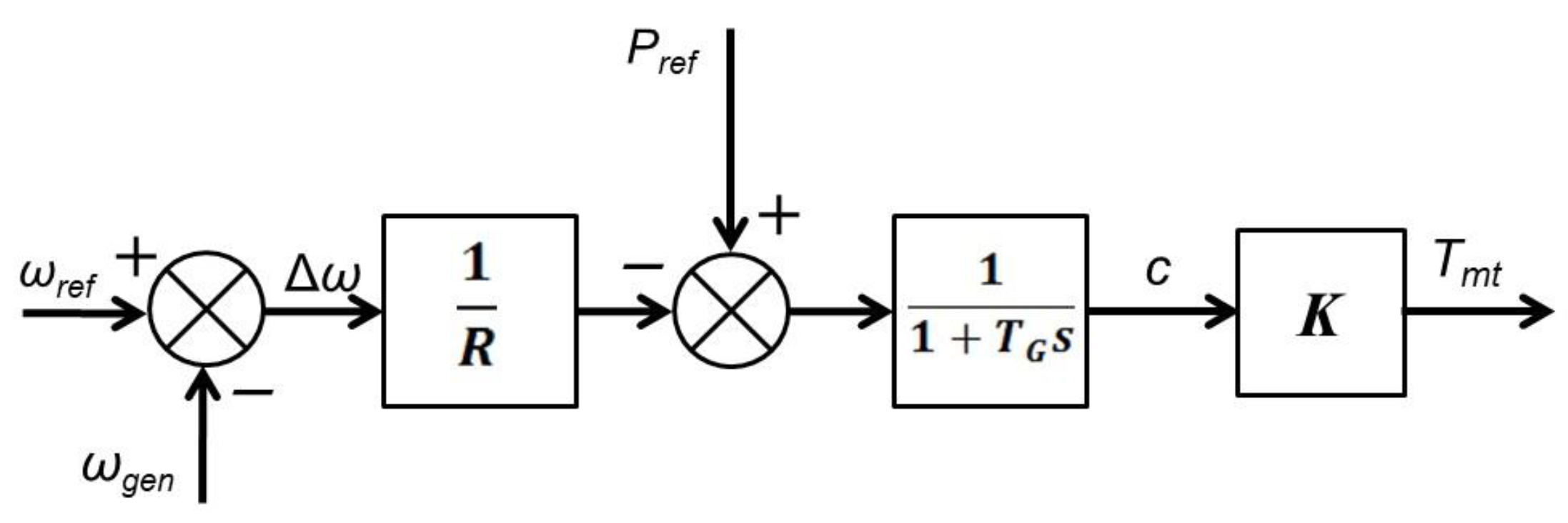
4.2. The Wind Farm Control
- The angle speed of the turbine-generator unit ωw,
- The values of the mechanical and electromagnetic torque Te, Tm,
- The values of active and reactive power set by the operator, divided equally between individual turbine-generator units POSD, QOSD,
- Measured active power Pm,
- Measured deviations of frequency and voltage Δf, ΔU.
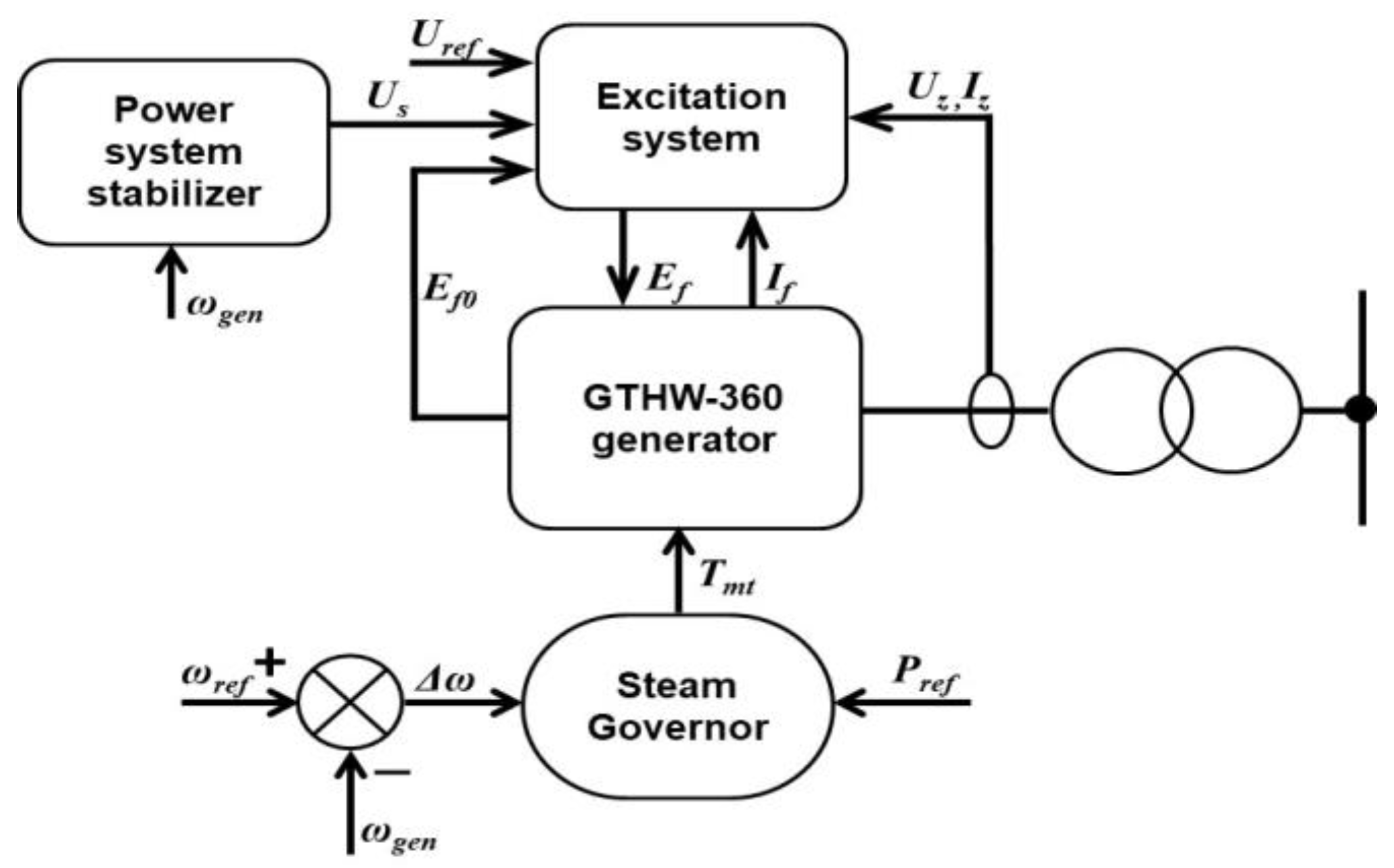
4.3. The Conventional Power Plant Model
4.4. The Load Model
5. System Model
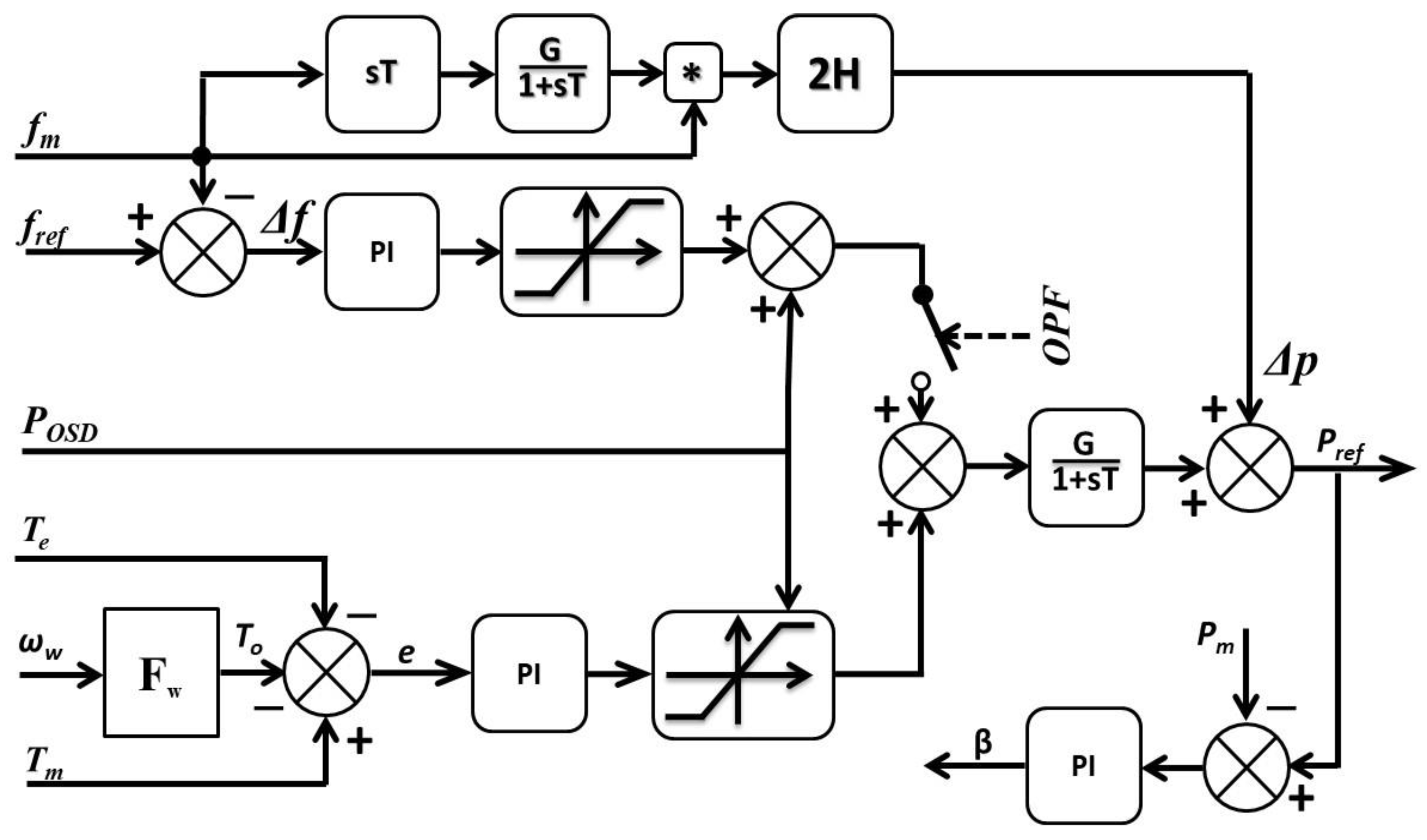
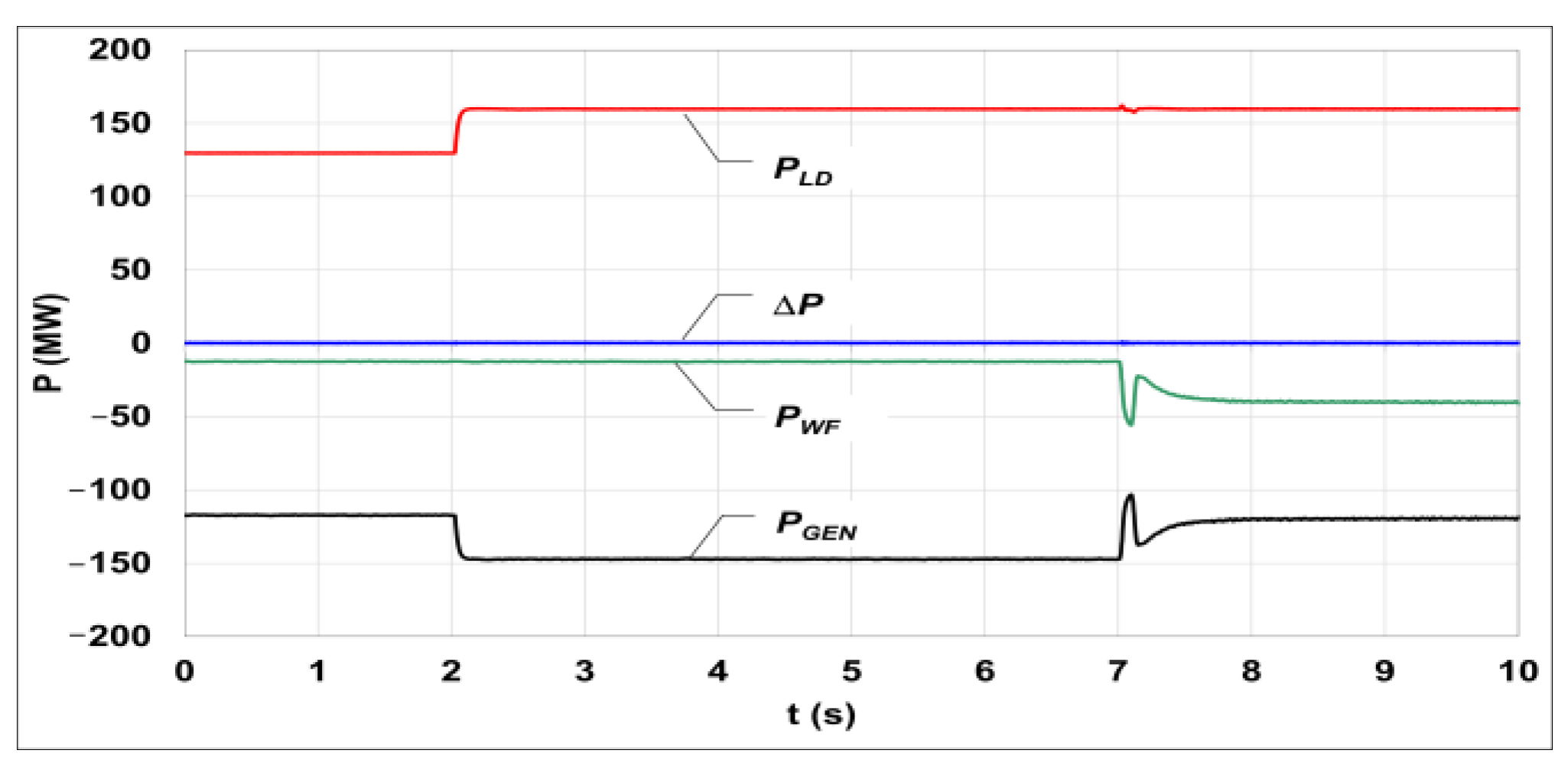
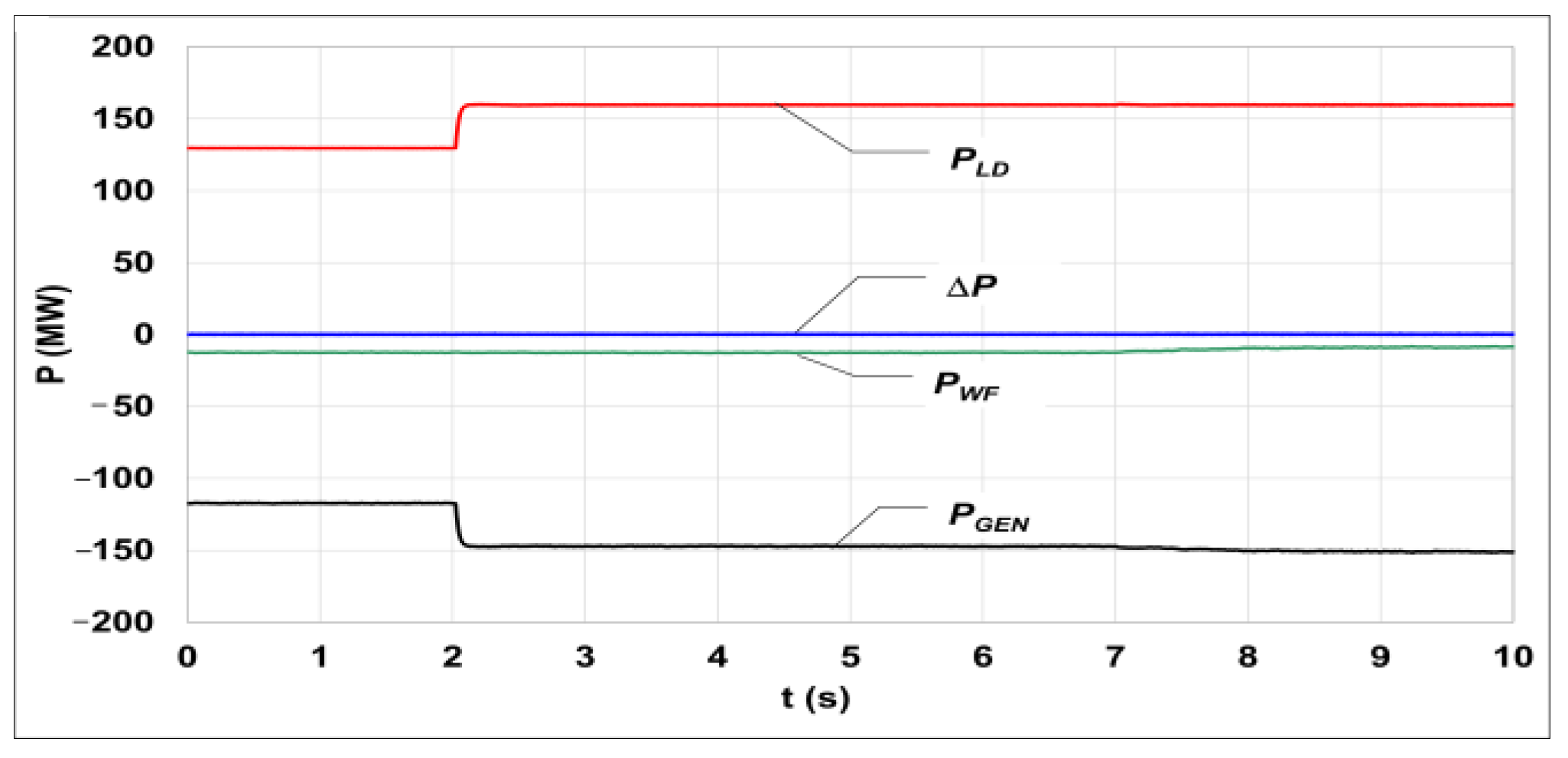
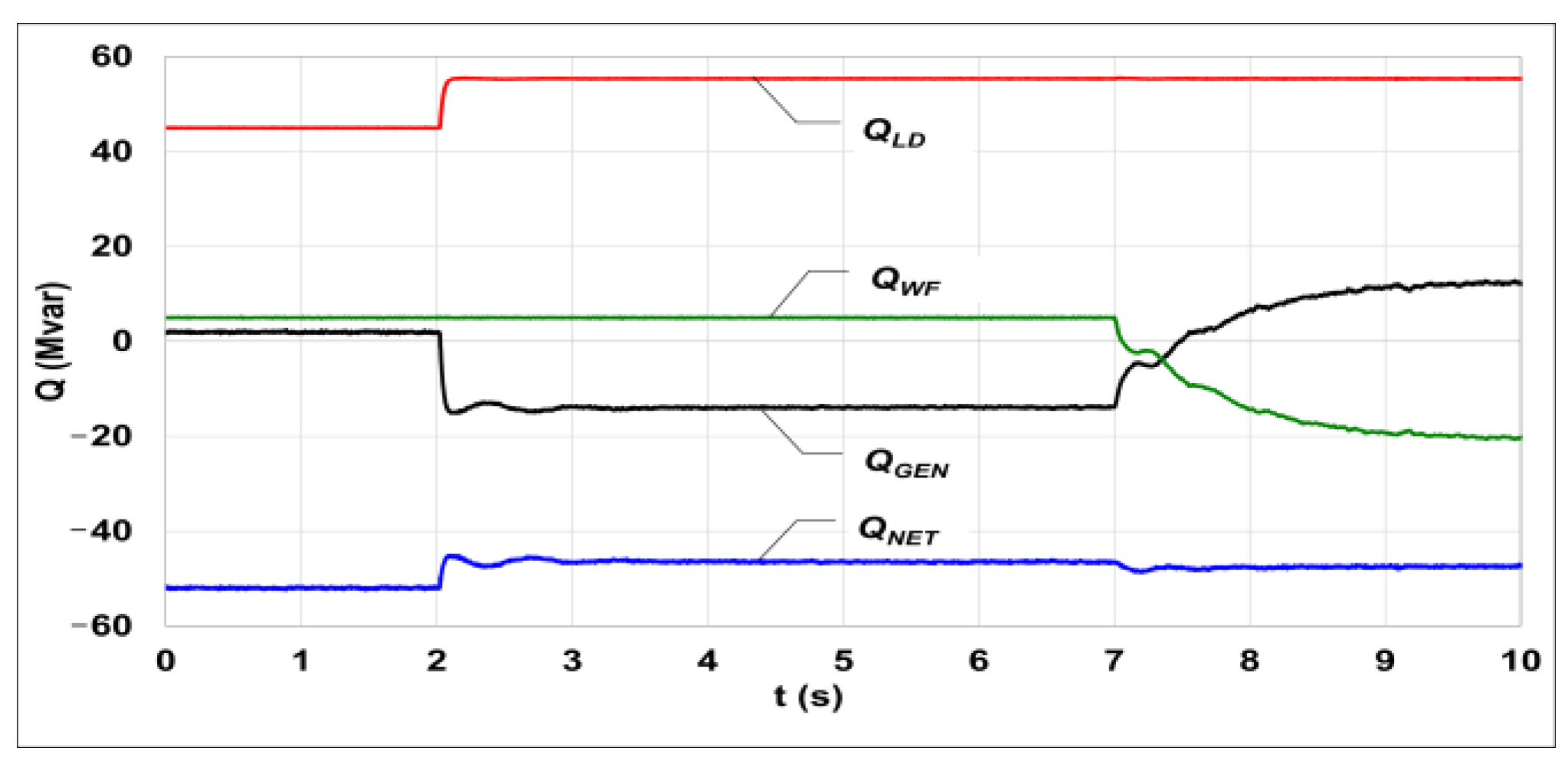
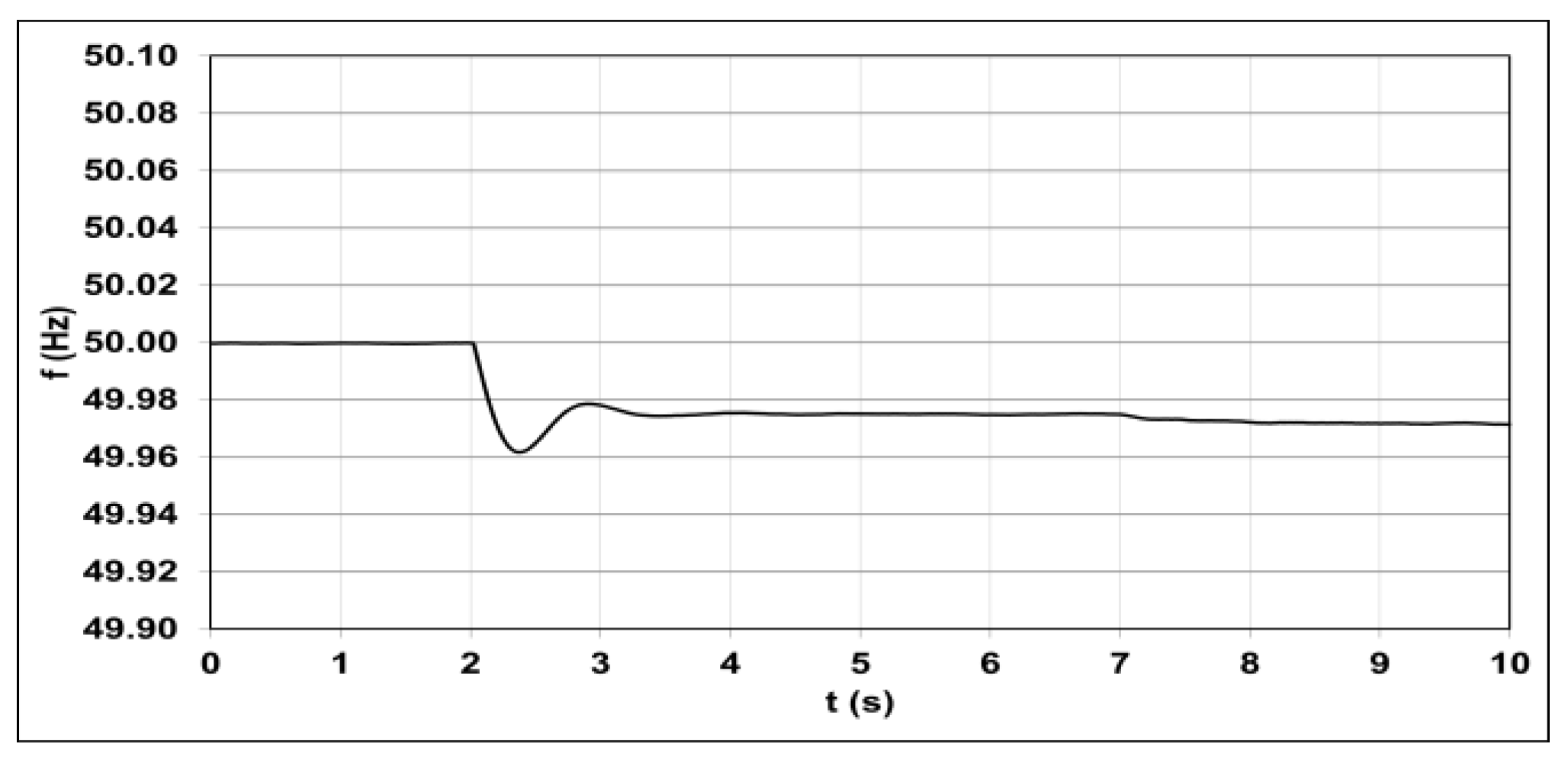
5.1. Participation of the WF in Frequency Regulation
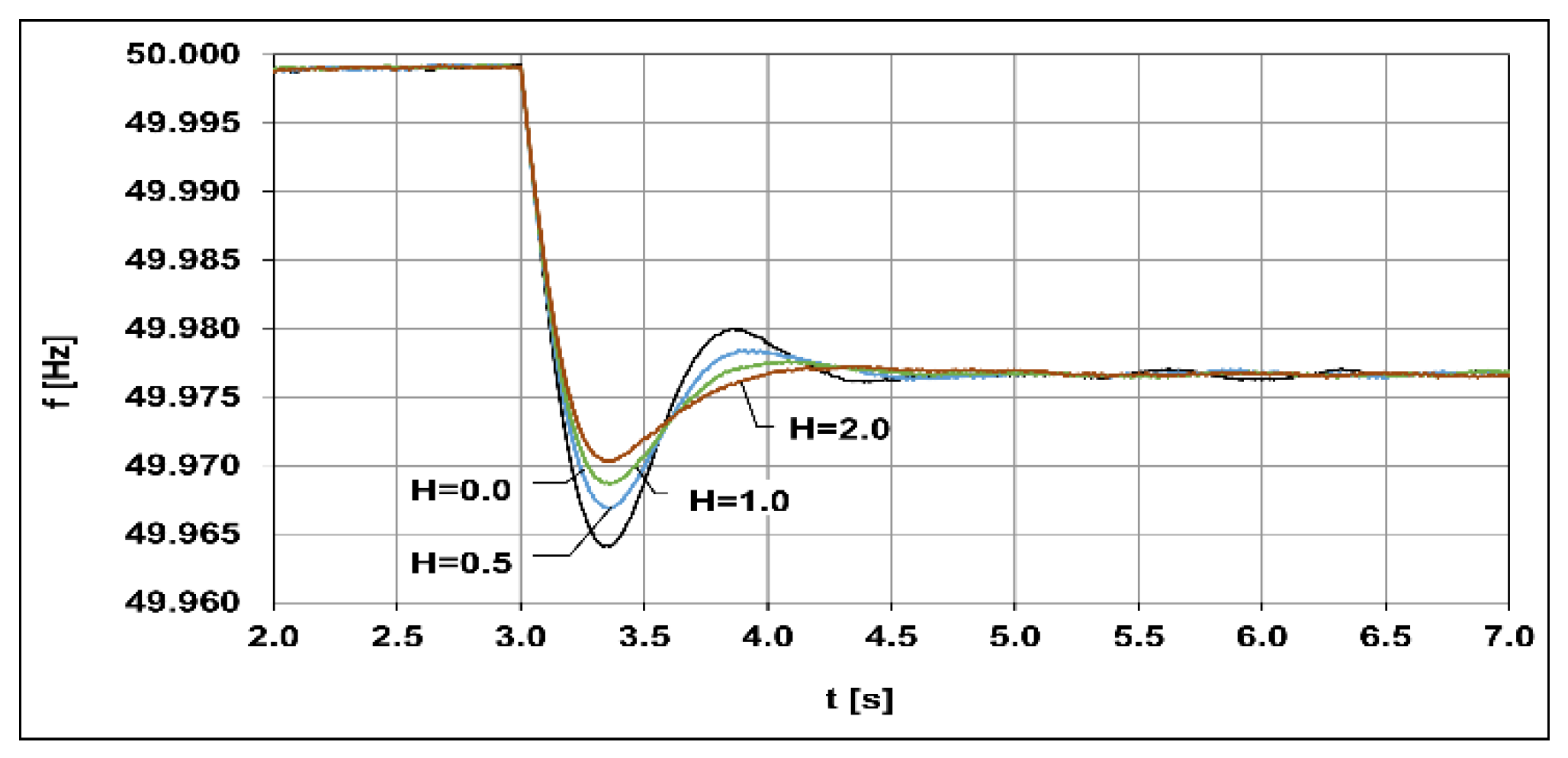
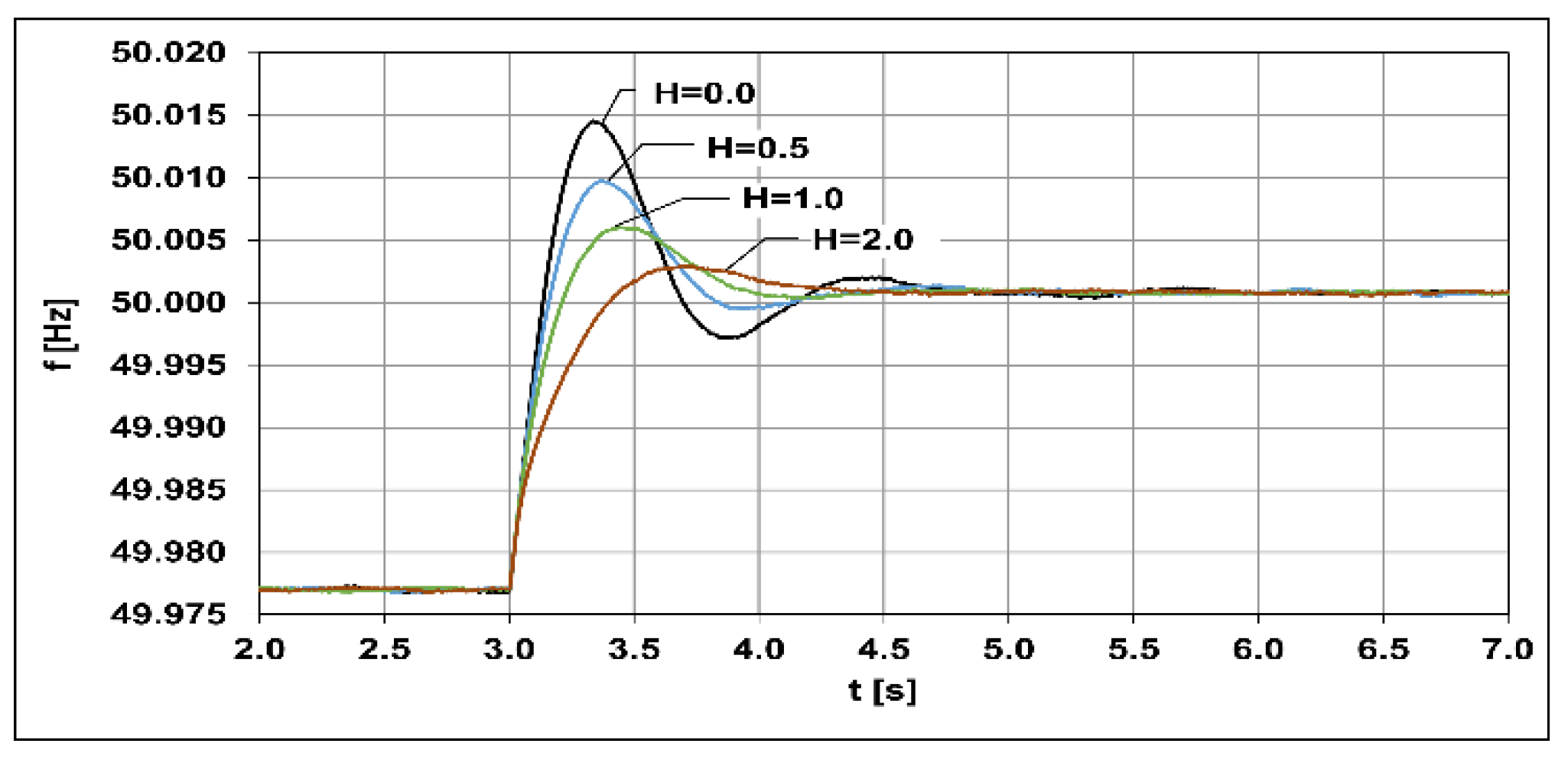
5.2. WF Frequency Response Using Virtual Inertia
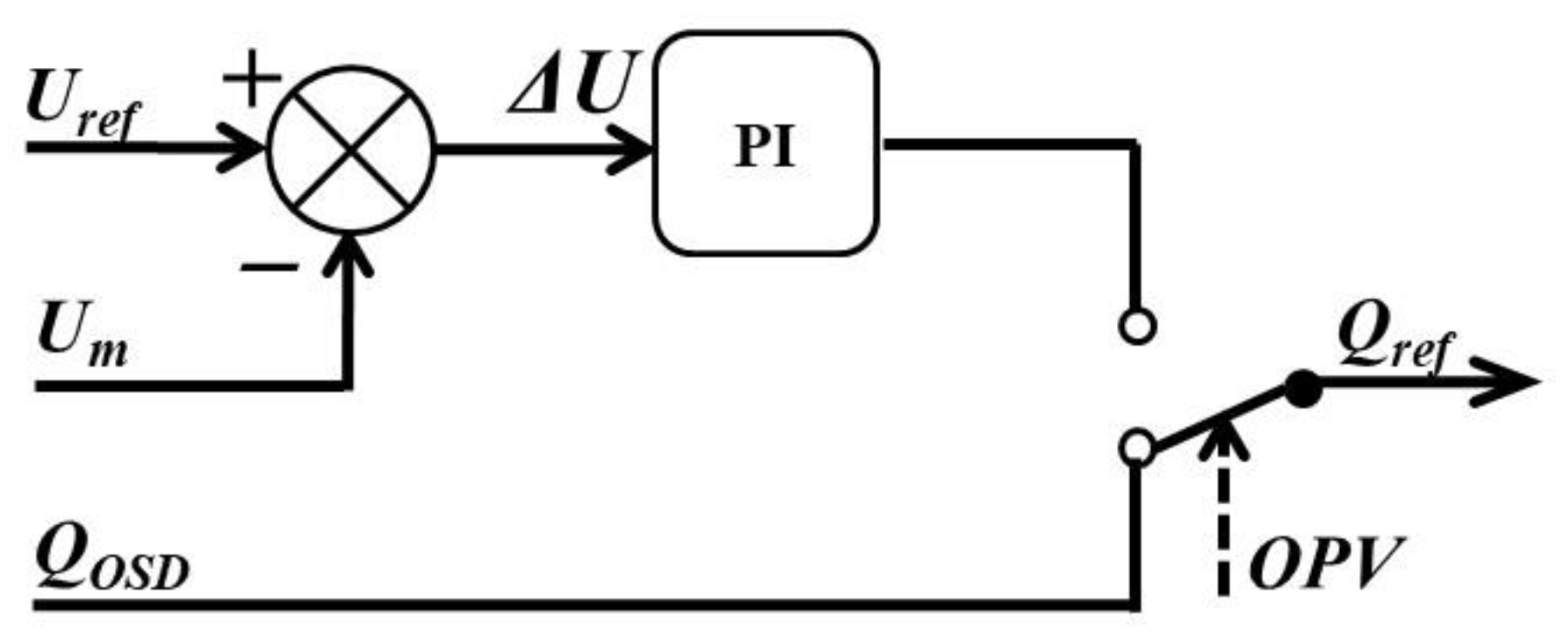
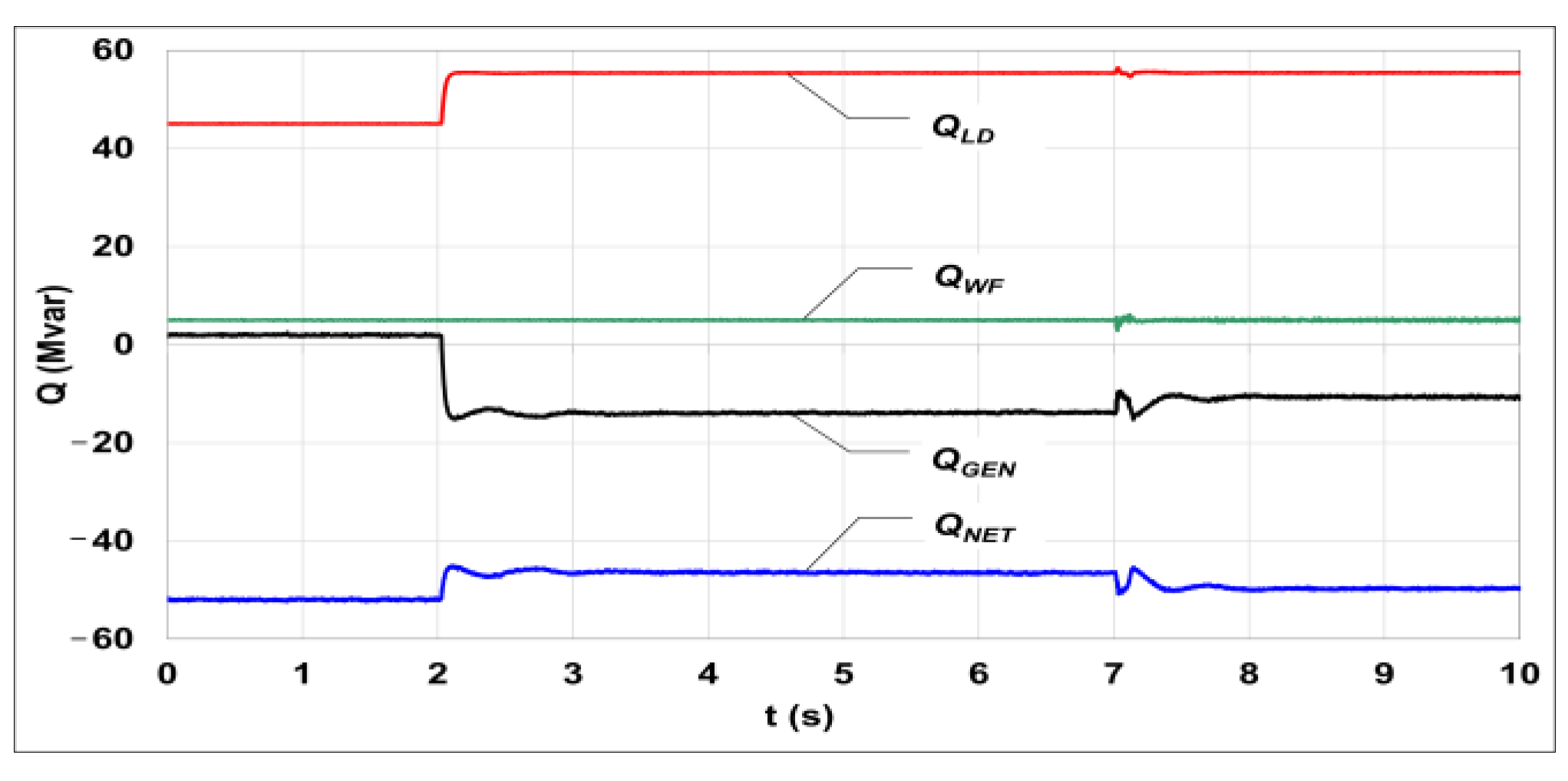
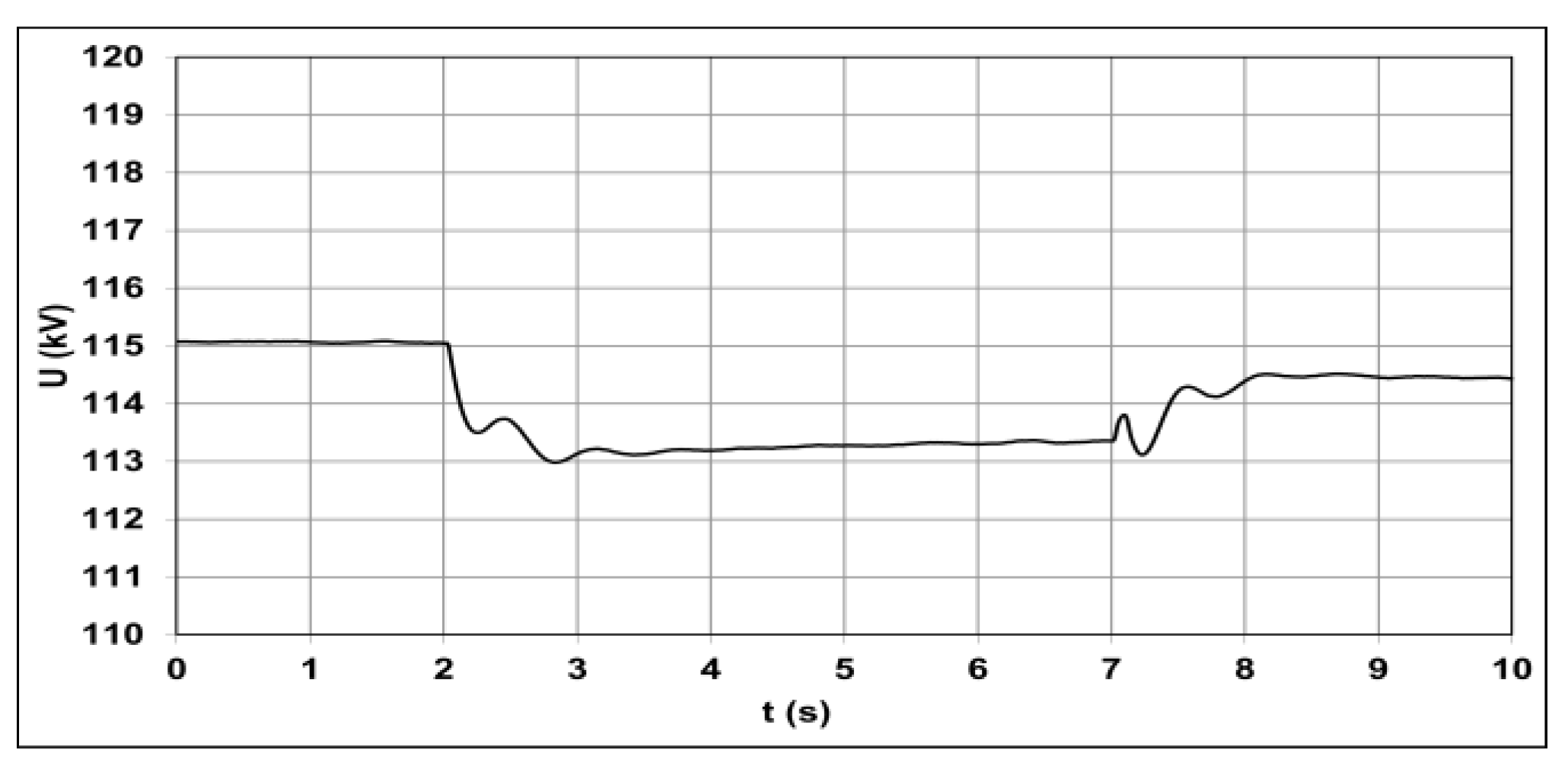
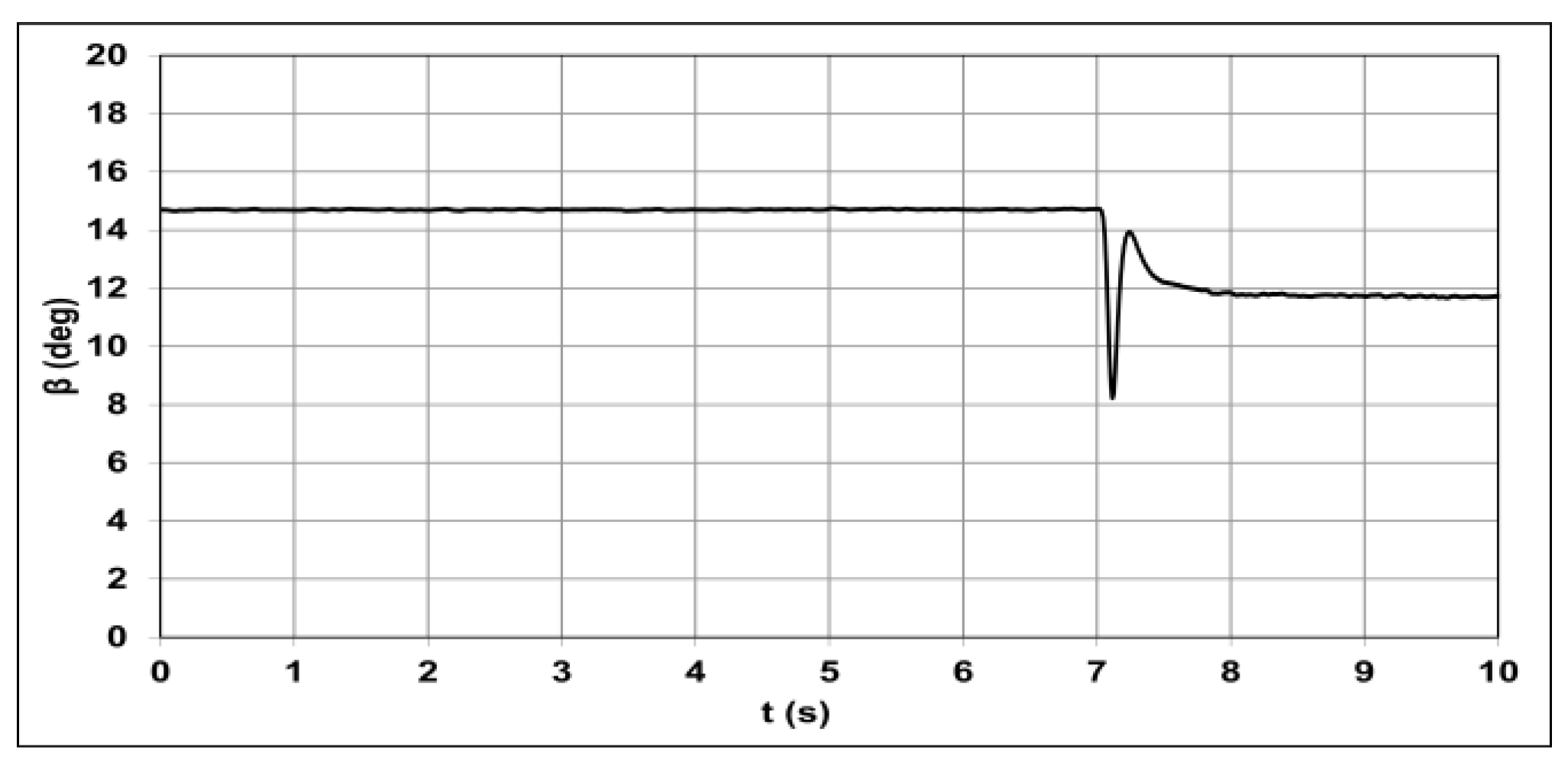
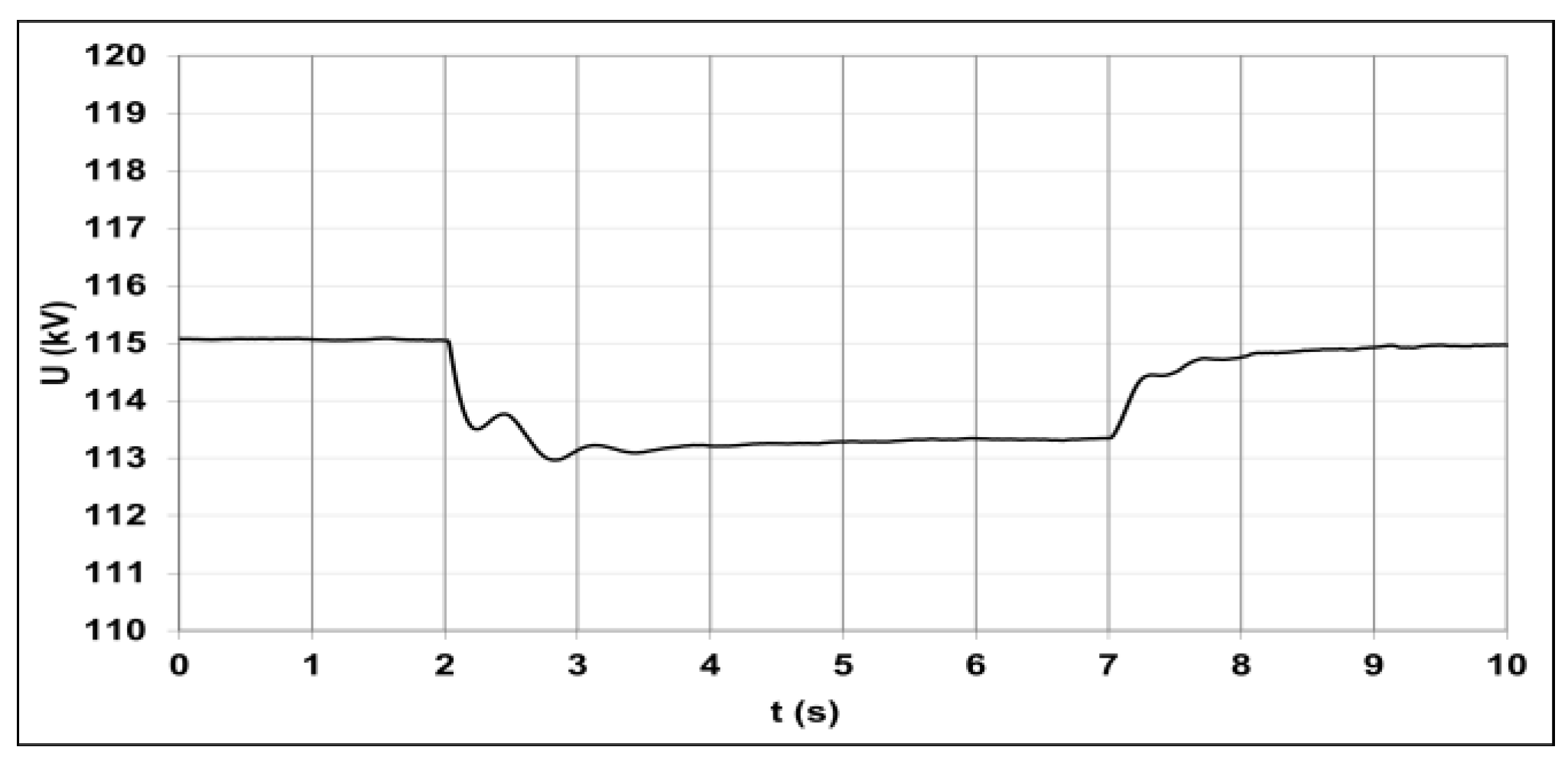
5.3. Participation of the WF in Voltage Regulation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Szablicki, M.; Rzepka, P. Analysis of technical possibilities of photovoltaic and wind sources playing in an ancillary service of frequency and power regulation. Acta Energetica 2016, 4, 112–119. [Google Scholar] [CrossRef]
- Czarnecki, B. Possibilities for regulation of wind farms in the context of ancillary services. Defined in PolishGridCode. In Proceedings of the XVIII Scientific Conference Advances in Power Engineering, Jastrzębia Góra, Poland, 7–9 July 2017. [Google Scholar]
- Klempke, H.; McCulloch, C.B.; Piekutowski, M.; Wong, A. Impact of high wind generation penetration on frequency control. In Proceedings of the 20th Australasian Universities Power Engineering Conference, Christchurch, New Zealand, 5–8 December 2010. [Google Scholar]
- Ulbig, A.; Borsche, T.; Andersson, G. Impact of low rotational inertia on power system stability and operation. In Proceedings of the IFAC, Cape Town, South Africa, 24–29 August 2014; pp. 7290–7297. [Google Scholar] [CrossRef]
- Muljadi, E.; Singh, M. Understanding inertial and frequency response of wind power plants. In Proceedings of the IEEE Conference: Power Electronics and Machines in Wind Applications (PEMWA), Denver, CO, USA, 16–18 July 2012. [Google Scholar] [CrossRef]
- Miller, N.W.; Clark, K.; Shao, M. Frequency responsive wind plant controls: Impacts on grid performance. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar] [CrossRef]
- Wasilewski, J.; Lubośny, Z. Analysis of annual rotational mass inertia variability in the synchronous power system of continental Europe in the context of RES development and operation. Electrotech. News 2017, 85, 8–14. [Google Scholar] [CrossRef]
- Keung, P.K.; Li, P.; Banakar, H.; Ooi, B.T. Kinetic Energy of Wind-Turbine Generators for System Frequency Support. IEEE Trans. Power Syst. 2009, 24, 279–287. [Google Scholar] [CrossRef]
- Ma, H.T.; Chowdhury, B.H. Working towards frequency regulation with wind plants: Combined control approaches. IET Renew. Power Gener. 2010, 4, 308–316. [Google Scholar] [CrossRef]
- Wang, D.; Gao, X.; Meng, K.; Qiu, J.; Lei Lai, L.; Gao, S. Utilisation of kinetic energy from wind turbine for grid connections: A review paper. IET Renew. Power Gener. 2018, 12, 615–624. [Google Scholar] [CrossRef]
- Akbari, M.; Madani, S.M. Analytical evaluation of control strategies for participation of doubly fed induction generator-based wind farms in power system short-term frequency regulation. IET Renew. Power Gener. 2014, 8, 324–333. [Google Scholar] [CrossRef]
- Mujcinagic, A.; Kusljugic, M.; Nukic, E. Wind inertial response based on the center of inertia frequency of a control area. Energies 2020, 13, 6177. [Google Scholar] [CrossRef]
- Morren, J.; Pierik, J.; de Haan, S.W.H. Inertial response of variable speed wind turbines. Electr. Power Syst. Res. 2006, 76, 980–987. [Google Scholar] [CrossRef]
- Polish Grid Code. Instruction of Transmission System operations and Maintenance Version 1.2; Polish Power System: Warsaw, Poland, 15 December 2011; Available online: https://www.pse.pl/web/pse-eng/documents (accessed on 23 February 2020).
- Regulation of the Minister of Economy of 4 May 2007 regarding detailed conditions for the functioning of the electrical energy system. Pol. J. Laws 2007, 93, 623.
- Tsili, M.; Papathanassiou, S. A review of grid code technical requirements for wind farms. IET Renew. Power Gener. 2009, 3, 308–332. [Google Scholar] [CrossRef]
- Van de Vyver, J.; Vandoorn, T.; De Kooning, J.; Meersman, B.; Vandevelde, L. Provision of ancillary services with variable speed wind turbines. In Proceedings of the IEEE Young Researchers Symposium, Ghent, Belgium, 24–25 April 2014; EESA: Ghent, Belgium, 2014; pp. 1–6. [Google Scholar]
- Anca, D.; Blaabjerg, F.; Iov, F.; Sorensen, P. Modeling of wind farm controllers. In Proceedings of the European Wind Energy Conference and Exhibition 2006, Athens, Greece, 27 February–2 March 2006; pp. 2377–2385. [Google Scholar]
- Bao, Y.Q.; Li, Y. On deloading control strategies of wind generators for system frequency regulation. Int. Trans. Electr. Energy Syst. 2015, 25, 623–635. [Google Scholar] [CrossRef]
- Fischer, M.; Mendonca, A.; Engelken, S.; Mihov, N. Operational experiences with inertial response provided by type 4 wind turbines. IET Renew. Power Gener. 2016, 10, 17–24. [Google Scholar] [CrossRef]
- Margaris, I.D.; Papathanassiou, S.A.; Hatziargyriou, N.D.; Hansen, A.D.; Sorensen, P. Frequency control in autonomous power systems with high wind power penetration. IEEE Trans. Power Syst. 2012, 32, 189–199. [Google Scholar] [CrossRef]
- Rebello, E.; Watson, D.; Rodgers, M. Performance analysis of a 10 MW wind farm in providing secondary frequency regulation: Experimental aspects. IEEE Trans. Power Syst. 2019, 34, 3090–3097. [Google Scholar] [CrossRef]
- Mullane, A.; Bryans, G.; O’Malley, M. Kinetic energy and frequency response comparison for renewable generation systems. In Proceedings of the International Conference on Future Power Systems, Amsterdam, The Netherlands, 18 November 2005. [Google Scholar] [CrossRef]
- Boersma, S.; Doekemeijer, B.M.; Siniscalchi-Minna, S.; Wingerden, J.W. A constrained wind farm controller providing secondary frequency regulation: An LES study. Renew. Energy 2019, 134, 639–652. [Google Scholar] [CrossRef]
- Shapiro, C.; Meyers, J.; Meneveau, C.; Dennice, G. Wind farms providing secondary frequency regulation: Evaluating the performance of model-based receding horizon control. Wind Energy Sci. 2008, 3, 11–24. [Google Scholar] [CrossRef]
- Rebello, E.; Watson, D.; Rodgers, M. Ancillary services from wind turbines: Automatic generation control (AGC) from a single Type 4 turbine. Wind Energy Sci. 2020, 5, 225–236. [Google Scholar] [CrossRef]
- EU. Horizon 2020 Project Closed Loop Wind Farm Control; Deliverable No. 4.1. Classification of Control-Oriented Models for Wind Farm Control Applications; EU: Stuttgart, Germany, 2018. [Google Scholar]
- Kanev, S.K.; Savenije, F.J.; Soleimanzadeh, M.; Wiggelinkhuizen, E. Wind Farm Modeling and Control: An Inventory ECN-E–13-058; ECN: Le Petten, The Netherlands, December 2013. [Google Scholar]
- Boersma, S.; Doekemeijer, B.; Vali, M.; Meyers, J.; van Wingerden, J.-W. A control-oriented dynamic wind farm model: WFSim. Wind Energy Sci. 2018, 3, 75–95. [Google Scholar] [CrossRef]
- Silva, J.E.; Danao, L.A.M. Varying VAWT cluster configuration and the effect on individual rotor and overall cluster performance. Energies 2021, 14, 1567. [Google Scholar] [CrossRef]
- Haces-Fernandez, F.; Li, H.; Ramirez, D. Improving wind farm power output through deactivating selected wind turbines. Energy Convers. Manag. 2019, 187, 407–422. [Google Scholar] [CrossRef]
- Liu, F.; Ju, X.; Wang, N.; Wang, L.; Lee, W.J. Wind farm macro-siting optimization with insightful bi-criteria identification and relocation mechanism in genetic algorithm. Energy Convers. Manag. 2020, 217. [Google Scholar] [CrossRef]
- Ju, H.; Liu, F.; Wang, L.; Lee, W.J. Wind farm layout optimization based on support vector regression guided genetic algorithm with consideration of participation among landowners. Energy Convers. Manag. 2019, 196, 1267–1281. [Google Scholar] [CrossRef]
- Ju, X.; Liu, F. Wind farm layout optimization using self-informed genetic algorithm with information guided exploitation. Appl. Energy 2019, 248, 429–445. [Google Scholar] [CrossRef]
- Chirapongsananurak, P.; Santoso, S.; Dugan, R.C.; Smith, J. Voltage regulation in distribution circuits with wind power. In Proceedings of the IEEE Power and Energy Society General Meeting 2012, San Diego, CA, USA, 22–26 July 2012. [Google Scholar] [CrossRef]
- Kłosowski, Z. The analysis of the possible use of wind turbines for voltage stabilization in the power node of MV Line with use of a real-time simulator. Przegląd Elektrotechniczny 2015, 91, 20–27. [Google Scholar] [CrossRef]
- Fandi, G.; Igbinovia, F.O.; Tlusty, J.; Mahmoud, R. Voltage regulation and power losses reduction in a wind farm integrated MV distribution network. J. Electr. Eng. 2018, 69, 85–92. [Google Scholar] [CrossRef]
- Josefsson, R.; Mehmedovic, H.; Wang-Hansen, M. Frequency controlling wind power modeling of control strategies. IEEE Trans. Sustain. Energy 2013, 4, 954–959. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, W.; Gao, T.; Yan, W.; Zhang, H.; Yan, S.; Wang, X. State-of-the-art review on frequency response of wind power plants in power systems. J. Mod. Power Syst. Clean Energy 2018, 6, 1–16. [Google Scholar] [CrossRef]
- Asmine, M.; Langlois, C.-E.; Aubut, N. Inertial response from wind power plants during a frequency disturbance on the Hydro-Quebec system—Event analysis and validation. IET Renew. Power Gener. 2018, 12, 515–522. [Google Scholar] [CrossRef]
- Vidyanandan, K.V.; Sneroy, N. Primary frequency regulation by deloaded wind turbines using variable droop. IEEE Trans. Power Syst. 2013, 28, 837–846. [Google Scholar] [CrossRef]
- Oshnoei, A.; Khezri, R.; Muyeen, S.; Blaabjerg, F. On the contribution of wind farms in automatic generation control: Review and new control approach. Appl. Sci. 2018, 8, 1848. [Google Scholar] [CrossRef]
- Wilches-Bernal, F.; Chow, J.H.; Sanchez-Gasca, J.J. A fundamental study of applying wind turbines for power system frequency control. IEEE Trans. Power Syst. 2016, 31, 1496–1505. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Hong, H. Active power control design for supporting grid frequency regulation in wind farms. Annu. Rev. Control. 2015, 40, 70–81. [Google Scholar] [CrossRef]
- Białas, H.; Pawełek, R.; Wasiak, J. A simulation model for the analysis of wind farm usage in frequency and voltage regulation in an electrical power system. In Proceedings of the 12th International Conference and Exhibition on Electrical Power Quality and Utilisation, Krakow, Poland, 14–15 September 2020; IEEE Publisher: New York, NY, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, A.; Matveev, A.; Nilssen, R.; Nysveen, A. High-power generators for offshore wind turbines. Energy Proc. 2013, 35, 52–61. [Google Scholar] [CrossRef]
- Attya, A.; Luis Dominguez-Garcia, J. Provision of ancillary services by wind power generators. In Advances in Modelling and Control of Wind and Hydrogenerators; Ebrahimi, A., Ed.; IntechOpen: London, UK, 2020; Available online: https://www.intechopen.com/books/advances-in-modelling-and-control-of-wind-and-hydrogenerators/provision-of-ancillary-services-by-wind-power-generators (accessed on 23 February 2020). [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y. Virtual inertia control application to enhance frequency stability of interconnected power systems with high renewable energy penetration. Energies 2018, 11, 981. [Google Scholar] [CrossRef]
- Yuan, T.; Wang, J.; Guan, Y.; Liu, Z.; Song, X.; Che, Y.; Cao, W. Virtual inertia adaptive control of a doubly fed induction generator (DFIG) wind power system with hydrogen energy storage. Energies 2018, 11, 904. [Google Scholar] [CrossRef]
- Díaz-González, F.; Sumper, A.; Gomis-Bellmunt, O.; Villafáfila-Robles, R. A review of energy storage technologies for wind power applications. Renew. Sustain. Energy Rev. 2012, 16, 2154–2171. [Google Scholar] [CrossRef]
- Zhaoxia, X.; Yu, H.; Guerrero, J.M.; Hongwei, F. Frequency participation by using virtual inertia in wind turbines including energy storage. In Proceedings of the 43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017. [Google Scholar] [CrossRef]
- Canbulat, S.; Balci, K.; Canbulat, O.; Bayram, I.S. Techno-economic analysis of on-site energy storage units to mitigate wind energy curtailment: A case study in scotland. Energies 2021, 14, 1691. [Google Scholar] [CrossRef]
- Ullah, N.; Thiringer, T.; Karlsson, D. Temporary primary frequency control support by variable speed wind turbines—Potential and applications. IEEE Trans. Power Syst. 2008, 23, 601–612. [Google Scholar] [CrossRef]
- Beltran, O.; Peña, R.; Segundo, J.; Esparza, A.; Muljadi, E.; Wenzhong, D. Inertia estimation of wind power plants based on the swing equation and phasor measurement units. Appl. Sci. 2018, 8, 2413. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Sun, Y.Z.; Lin, J.; Li, G.J. Coordinated frequency regulation by doubly fed induction generator-based wind power plants. IET Renew. Power Gener. 2012, 6, 38–47. [Google Scholar] [CrossRef]
- Eto, J.H.; Undrill, J.; Mackin, P.; Daschmans, R.; Williams, B.; Haney, B.; Hunt, R.; Ellis, J.; Illian, H.; Martinez, C.; et al. Use of Frequency Response Metrics to Asses the Planning and Operating Requirements for Reliable Integration of Variable Renewable Generation; The Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2010. [Google Scholar] [CrossRef]
- Matos, K.N.V.; Londero, R.R.; de M. Affonso, C.; Vieira, A.P.A. Secondary voltage control applied to DFIG-based wind park and its effect on long-term voltage stability. Electr. Power Syst. Res. 2019, 175. [Google Scholar] [CrossRef]
- Chiandone, M.; Campaner, R.; Arcidiacono, V.; Sulligoi, G.; Milano, F. Automatic voltage and reactive power regulator for wind farms participating to TSO voltage regulation. In Proceedings of the IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar] [CrossRef]
- Pathak, A.K.; Sharma, M.P.; Bundele, M. A critical review of voltage and reactive power managementof wind farms. Renew. Sustain. Energy Rev. 2015, 51, 460–471. [Google Scholar] [CrossRef]
- Bena, L.; Kut, P. Wind farms in the process of voltage regulation in the power system. Przegląd Elektrotechniczny 2019, 8, 20–27. [Google Scholar] [CrossRef]
- Al-Majed, S.I. Secondary voltage control: Enhancing power system voltage profile. In Proceedings of the 2nd IEEE International Conference on Power and Energy, Johor Baharu, Malaysia, 1–3 December 2008. [Google Scholar] [CrossRef]
- PSCAD—Power Systems Computer Aided Design. User’s Guide on the Use of PSCAD; Manitoba Research Centre: Winnipeg, MB, Canada, 2003; Available online: https://www.pscad.com/uploads/ck/files/reference_material/PSCAD_User_Guide_v4_3_1.pdf (accessed on 23 February 2020).
- ENERCON GmbH. ENERCON Wind Energy Converters. Technology & Service; ENERCON GmbH: Aurich, Germany, June 2015; Available online: https://www.enercon.de/fileadmin/Redakteur/Medien-Portal/broschueren/pdf/en/ENERCON_TuS_en_06_2015.pdf (accessed on 23 February 2020).
- Eriksson, R.; Modig, N.; Elkington, K. Synthetic inertia versus fast frequency response: A definition. IET Renew. Power Gener. 2018, 12, 507–514. [Google Scholar] [CrossRef]
- Dharmawardena, H.; Uhlen, K.; Gjerde, S. Modeling wind farm with synthetic inertia for power system dynamic studies. In Proceedings of the IEEE International Energy Conference, Leuven, Belgium, 4–8 April 2016. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.M. Effects of the synthetic inertia from wind power on the total system inertia: Simulation study. In Proceedings of the 2nd International Symposium on Environment Friendly Energies and Applications, Newcastle Upon Tyne, UK, 25–27 June 2012. [Google Scholar] [CrossRef]
- Wasilewski, J.; Karkoszka, K.; Lubośny, Z.; Rzepka, P.; Szablicki, M. Investigation of the impact of synthetic inertia coming from wind sources on the dynamics of a domestics power system working asynchronously in relation to the neighbouring transmission systems. Power Eng. 2018, 4, 209–213. [Google Scholar]
- Liu, Z.; Liu, F.; Shen, C.; Mei, S.; Yao, Y. Speed recovery strategy for the inertia response control of DFIGs: Extended state observer based approach. IET Renew. Power Gener. 2017, 11, 1110–1120. [Google Scholar] [CrossRef]
- Shang, L.; Hu, J.; Yuan, X.; Chi, Y. Understanding inertial response of variable-speed wind turbines by defined internal potential vector. Energies 2017, 10, 22. [Google Scholar] [CrossRef]
- Hu, J.; Sun, L.; Yuan, X.; Wang, S.; Chi, Y. Modeling of type 3 wind turbines with df/dt inertia control for system frequency response study. IEEE Trans. Power Syst. 2017, 32, 2799–2809. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control, 6th ed.; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Machowski, J.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control, 2nd ed.; John Wiley: Oxford, UK, 2008. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bialas, H.; Pawelek, R.; Wasiak, I. A Simulation Model for Providing Analysis of Wind Farms Frequency and Voltage Regulation Services in an Electrical Power System. Energies 2021, 14, 2250. https://doi.org/10.3390/en14082250
Bialas H, Pawelek R, Wasiak I. A Simulation Model for Providing Analysis of Wind Farms Frequency and Voltage Regulation Services in an Electrical Power System. Energies. 2021; 14(8):2250. https://doi.org/10.3390/en14082250
Chicago/Turabian StyleBialas, Hubert, Ryszard Pawelek, and Irena Wasiak. 2021. "A Simulation Model for Providing Analysis of Wind Farms Frequency and Voltage Regulation Services in an Electrical Power System" Energies 14, no. 8: 2250. https://doi.org/10.3390/en14082250
APA StyleBialas, H., Pawelek, R., & Wasiak, I. (2021). A Simulation Model for Providing Analysis of Wind Farms Frequency and Voltage Regulation Services in an Electrical Power System. Energies, 14(8), 2250. https://doi.org/10.3390/en14082250





