Simulative Investigation of Thermal Capacity Analysis Methods for Metallic Latent Thermal Energy Storage Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulated Specimen
2.2. Methods
- •
- Isothermal calorimeters can only be operated at a defined temperature, thus it is not possible to test the whole operating temperature range of the specimen system.
- •
- Isoperibol calorimeters with uncontrolled heat exchange cannot fulfill the criterion of controllable heat input and output.
- •
- Isoperibol flow calorimeters are only suitable for fluid specimens.
- •
- Calorimeters with linear or nonlinear temperature changes of the surroundings are called scanning calorimeters. An essential component in the operation of scanning calorimeters is the time needed for heat exchange between the furnace and specimen. Depending on the heat path from the sample to the surroundings, the calorimeter signal can show a thermal lag [28,29]. Therefore, scanning calorimeters are not recommended for use with large sample sizes [30] and inhomogeneous samples, which is how the THS specimen system can be classified [31].
2.2.1. Stepwise Adiabatic Procedure
2.2.2. Isoperibolic Procedure with Loss Correlation
2.2.3. Isoperibolic Procedure with Cooling Correlation
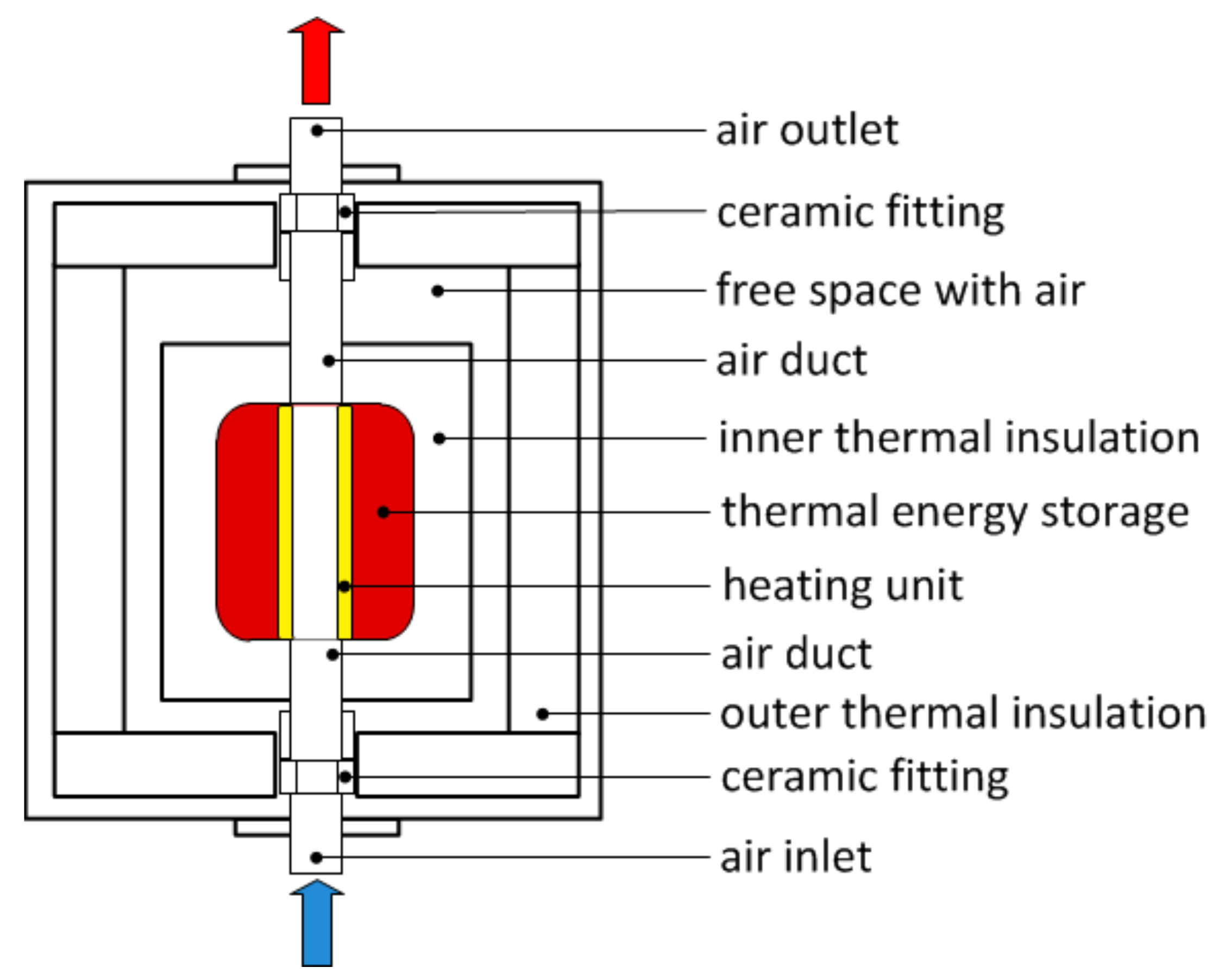
2.3. Experimental Setup
2.4. Simulation
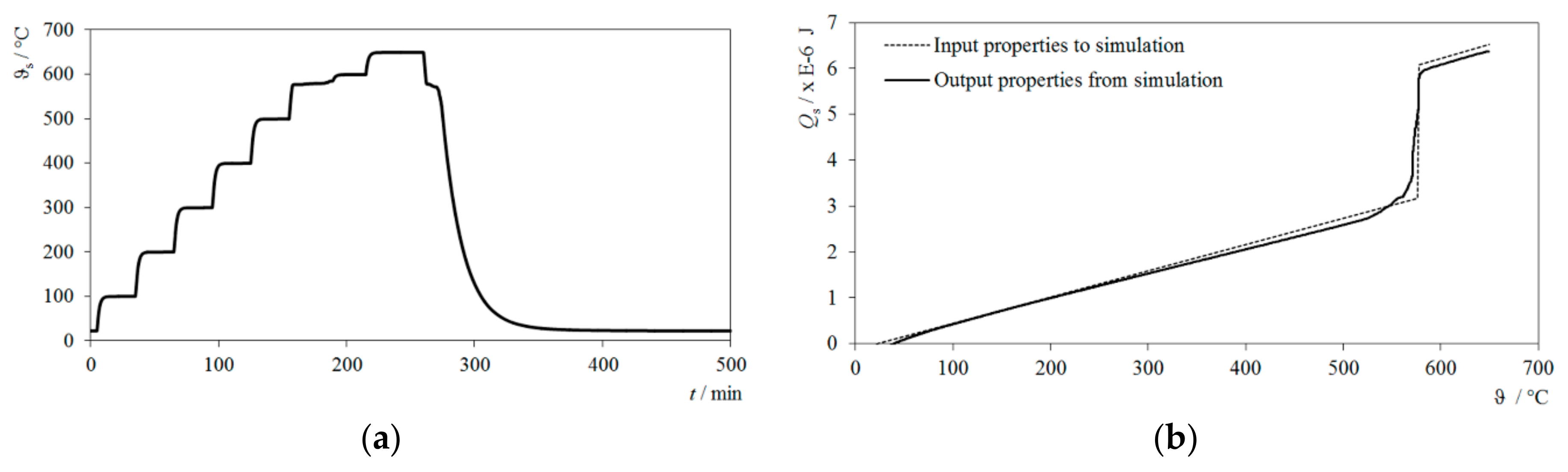
3. Results
3.1. Stepwise Adiabatic Procedure
3.2. Isoperibolic Procedure with Loss Correlation
3.3. Isoperibolic Procedure with Cooling Correlation
3.4. Deviation of Simulation Input Values
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Neubauer, J.; Wood, E. Thru-life impacts of driver aggression, climate, cabin thermal management, and battery thermal management on battery electric vehicle utility. J. Power Sources 2014, 259, 262–275. [Google Scholar] [CrossRef]
- Kambly, K.; Bradley, T.H. Geographical and temporal differences in electric vehicle range due to cabin conditioning energy consumption. J. Power Sources 2015, 275, 468–475. [Google Scholar] [CrossRef]
- Yuksel, T.; Michalek, J.J. Effects of regional temperature on electric vehicle efficiency, range, and emissions in the United States. Environ. Sci. Technol. 2015, 49, 3974–3980. [Google Scholar] [CrossRef]
- Kraft, W.; Altstedde, M.K. Use of metallic Phase Change Materials (mPCM) for heat storage in Electric- and Hybrid Vehicles. In Proceedings of the Tagungsband 6th Hybrid and Electric Vehicles Conference (HEVC 2016), London, UK, 2–3 November 2016; pp. 1–6. [Google Scholar]
- Kraft, W.; Jilg, V.; Klein Altstedde, M.; Lanz, T.; Vetter, P.; Schwarz, D. Thermal High Performance Storages for Use in Vehicle Applications; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Gasia, J.; Miró, L.; Cabeza, L.F. Materials and system requirements of high temperature thermal energy storage systems: A review. Part 2: Thermal conductivity enhancement techniques. Renew. Sustain. Energy Rev. 2016, 60, 1584–1601. [Google Scholar] [CrossRef]
- Ibrahim, N.I.; Al-Sulaiman, F.A.; Rahman, S.; Yilbas, B.S.; Sahin, A.Z. Heat transfer enhancement of phase change materials for thermal energy storage applications: A critical review. Renew. Sustain. Energy Rev. 2017, 74, 26–50. [Google Scholar] [CrossRef]
- Birchenall, C.E.; Riechman, A.F. Heat Storage in Eutectic Alloys. Metall. Trans. A 1980, 11, 1415–1420. [Google Scholar] [CrossRef]
- Khare, S.; Dell’Amico, M.; Knight, C.; McGarry, S. Selection of materials for high temperature latent heat energy storage. Sol. Energy Mater. Sol. Cells 2012, 107, 20–27. [Google Scholar] [CrossRef]
- Shamberger, P.J.; Bruno, N.M. Review of metallic phase change materials for high heat flux transient thermal management applications. Appl. Energy 2020, 258, 113955. [Google Scholar] [CrossRef]
- Kraft, W.; Stahl, V.; Vetter, P. Thermal Storage Using Metallic Phase Change Materials for Bus Heating—State of the Art of Electric Buses and Requirements for the Storage System. Energies 2020, 13, 3023. [Google Scholar] [CrossRef]
- Yinping, Z.; Yi, J. A simple method, the -history method, of determining the heat of fusion, specific heat and thermal conductivity of phase-change materials. Meas. Sci. Technol. 1999, 10, 201–205. [Google Scholar] [CrossRef]
- Solé, A.; Miró, L.; Barreneche, C.; Martorell, I.; Cabeza, L.F. Review of the T -history method to determine thermophysical properties of phase change materials (PCM). Renew. Sustain. Energy Rev. 2013, 26, 425–436. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Barreneche, C.; Martorell, I.; Miró, L.; Sari-Bey, S.; Fois, M.; Paksoy, H.O.; Sahan, N.; Weber, R.; Constantinescu, M.; et al. Unconventional experimental technologies available for phase change materials (PCM) characterization. Part 1. Thermophysical properties. Renew. Sustain. Energy Rev. 2015, 43, 1399–1414. [Google Scholar] [CrossRef]
- Navrotsky, A. New Developments in the Calorimetry of High-Temperature Materials. Engineering 2019, 5, 366–371. [Google Scholar] [CrossRef]
- Binder, S.; Haussener, S. Design guidelines for Al-12%Si latent heat storage encapsulations to optimize performance and mitigate degradation. Appl. Surf. Sci. 2020, 505, 143684. [Google Scholar] [CrossRef]
- Günther, E.; Hiebler, S.; Mehling, H. Determination of the Heat Storage Capacity of PCM and PCM-Objects as a Function of Temperature. In Proceedings of the ECOSTOCK 10th International Conference on Thermal Energy Storage, Stockton, NJ, USA, 31 May–2 June 2006. [Google Scholar]
- Rathgeber, C.; Schmit, H.; Miró, L.; Cabeza, L.F.; Gutierrez, A.; Ushak, S.N.; Hiebler, S. Enthalpy-temperature plots to compare calorimetric measurements of phase change materials at different sample scales. J. Energy Storage 2018, 15, 32–38. [Google Scholar] [CrossRef]
- Xu, T.; Gunasekara, S.N.; Chiu, J.N.; Palm, B.; Sawalha, S. Thermal behavior of a sodium acetate trihydrate-based PCM: T-history and full-scale tests. Appl. Energy 2020, 261, 114432. [Google Scholar] [CrossRef]
- Klimeš, L.; Charvát, P.; Mastani Joybari, M.; Zálešák, M.; Haghighat, F.; Panchabikesan, K.; El Mankibi, M.; Yuan, Y. Computer modelling and experimental investigation of phase change hysteresis of PCMs: The state-of-the-art review. Appl. Energy 2020, 263, 114572. [Google Scholar] [CrossRef]
- Zauner, C.; Hengstberger, F.; Mörzinger, B.; Hofmann, R.; Walter, H. Experimental characterization and simulation of a hybrid sensible-latent heat storage. Appl. Energy 2017, 189, 506–519. [Google Scholar] [CrossRef]
- Jansone, D.; Dzikevics, M.; Veidenbergs, I. Determination of thermophysical properties of phase change materials using T-History method. Energy Procedia 2018, 147, 488–494. [Google Scholar] [CrossRef]
- Waser, R.; Ghani, F.; Maranda, S.; O’Donovan, T.S.; Schuetz, P.; Zaglio, M.; Worlitschek, J. Fast and experimentally validated model of a latent thermal energy storage device for system level simulations. Appl. Energy 2018, 231, 116–126. [Google Scholar] [CrossRef]
- Pirasaci, T.; Wickramaratne, C.; Moloney, F.; Goswami, D.Y.; Stefanakos, E. Influence of design on performance of a latent heat storage system at high temperatures. Appl. Energy 2018, 224, 220–229. [Google Scholar] [CrossRef]
- Rea, J.E.; Oshman, C.J.; Singh, A.; Alleman, J.; Parilla, P.A.; Hardin, C.L.; Olsen, M.L.; Siegel, N.P.; Ginley, D.S.; Toberer, E.S. Experimental demonstration of a dispatchable latent heat storage system with aluminum-silicon as a phase change material. Appl. Energy 2018, 230, 1218–1229. [Google Scholar] [CrossRef]
- Rea, J.E.; Oshman, C.J.; Singh, A.; Alleman, J.; Buchholz, G.; Parilla, P.A.; Adamczyk, J.M.; Fujishin, H.-N.; Ortiz, B.R.; Braden, T.; et al. Prototype latent heat storage system with aluminum-silicon as a phase change material and a Stirling engine for electricity generation. Energy Convers. Manag. 2019, 199, 111992. [Google Scholar] [CrossRef]
- Blanco-Rodríguez, P.; Rodríguez-Aseguinolaza, J.; Gil, A.; Risueño, E.; D’Aguanno, B.; Loroño, I.; Martín, L. Experiments on a Lab Scale TES Unit using Eutectic Metal Alloy as PCM. Energy Procedia 2015, 69, 769–778. [Google Scholar] [CrossRef]
- Sarge, S.M.; Höhne, G.W.H.; Hemminger, W. Calorimetry. Fundamentals, Instrumentation and Applications, 2nd ed.; Wiley-VCH Verlag: Weinheim, Germany, 2014; ISBN 978-3-527-32761-4. [Google Scholar]
- Mathis, D.; Blanchet, P.; Landry, V.; Lagière, P. Thermal characterization of bio-based phase changing materials in decorative wood-based panels for thermal energy storage. Green Energy Environ. 2019, 4, 56–65. [Google Scholar] [CrossRef]
- Quick, C.R.; Schawe, J.E.K.; Uggowitzer, P.J.; Pogatscher, S. Measurement of specific heat capacity via fast scanning calorimetry—Accuracy and loss corrections. Thermochim. Acta 2019, 677, 12–20. [Google Scholar] [CrossRef]
- Shukla, N.; Kosny, J. DHFMA Method for Dynamic Thermal Property Measurement of PCM-integrated Building Materials. Curr. Sustain. Renew. Energy Rep. 2015, 2, 41–46. [Google Scholar] [CrossRef][Green Version]
- Bessergenev, V.G.; Kovalevskaya, Y.A.; Paukov, I.E.; Shkredov, Y.A. Heat capacity measurements under continuous heating and cooling using vacuum adiabatic calorimetry. Thermochim. Acta 1989, 139, 245–256. [Google Scholar] [CrossRef]
- Kværnø, A. Singly Diagonally Implicit Runge–Kutta Methods with an Explicit First Stage. BIT Numer. Math. 2004, 44, 489–502. [Google Scholar] [CrossRef]
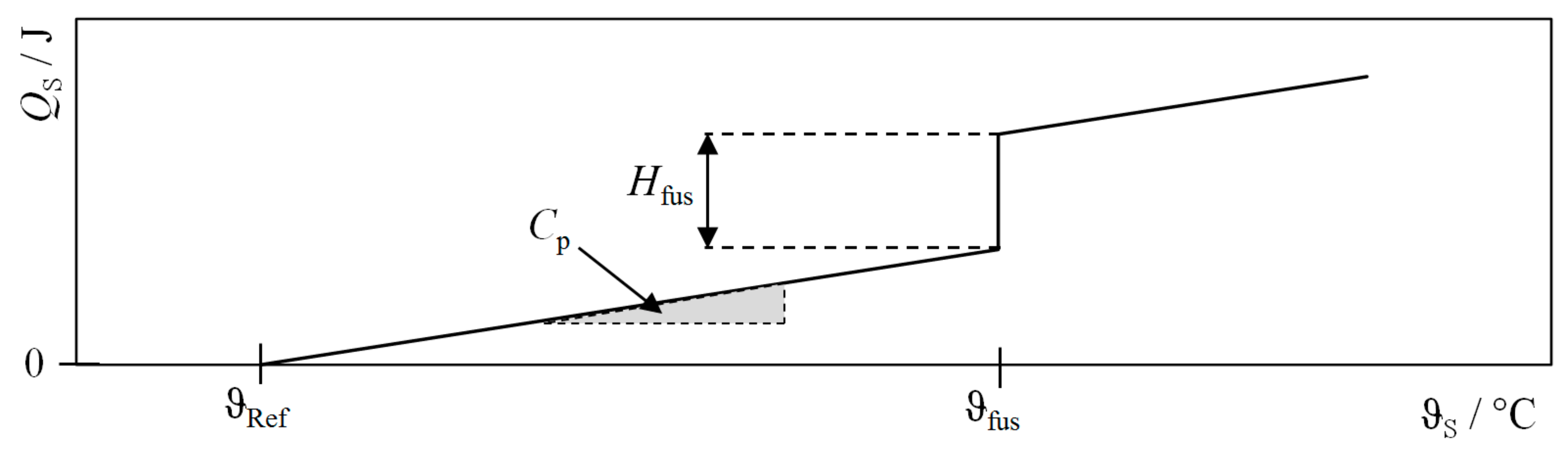
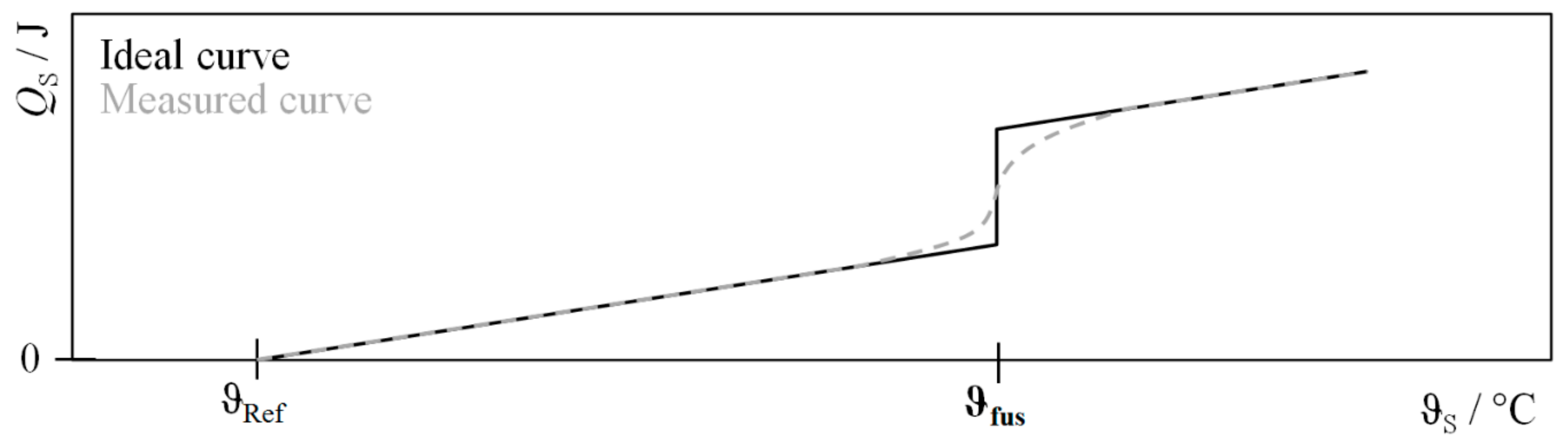
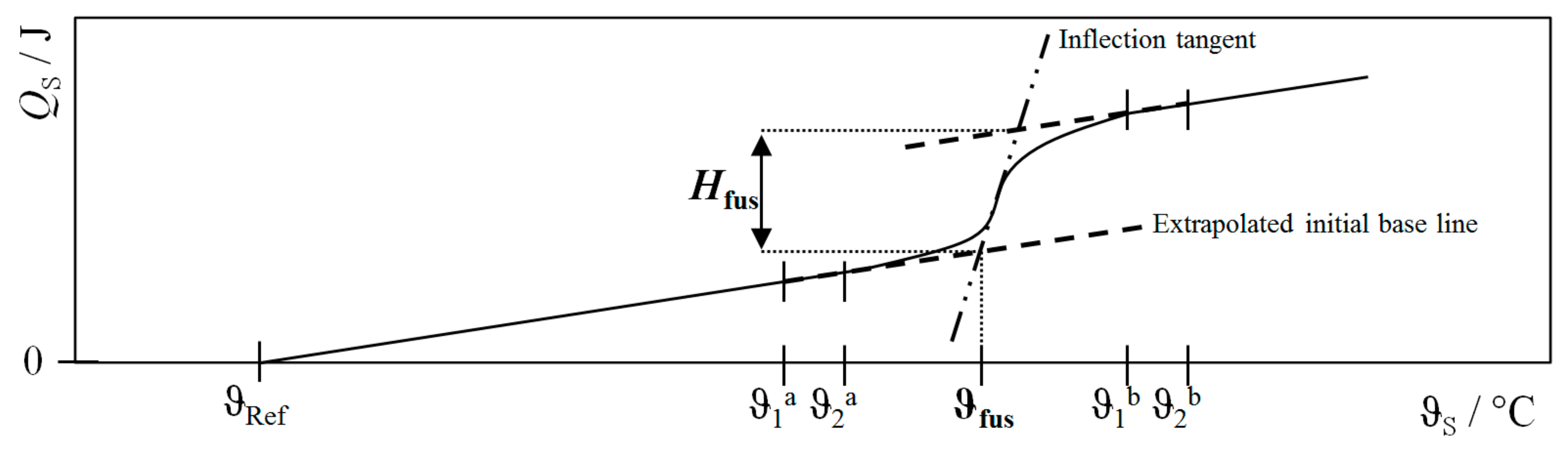
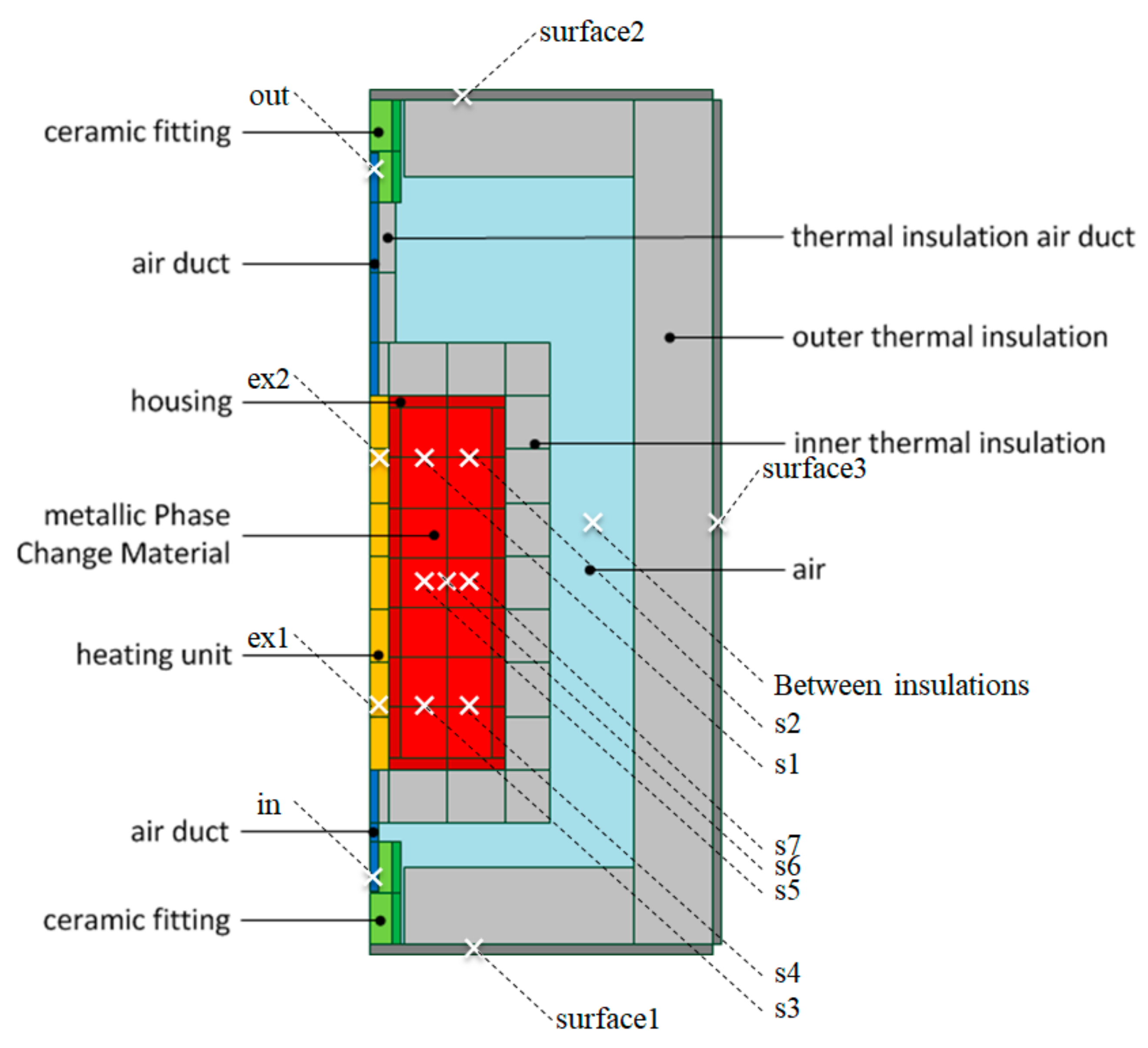



| Procedure | QH | QC | QLoss | QWF |
|---|---|---|---|---|
| Stepwise adiabatic | Measure PH | Measure (ϑC − ϑC,0) | Correlate to ϑSurface | Zero |
| Isoperibolic with loss correlation | Zero | Measure (ϑC − ϑC,0) | Correlate to ϑSurface | Measure (ϑout − ϑin) and |
| Isoperibolic with cooling correlation | Zero | Measure (ϑC − ϑC,0) | Correlate QCool to ϑex | |
| Measure | Sensors |
|---|---|
| ϑs | Average of seven temperature sensors located in mPCM (s1–s7) |
| ϑsurface | Weighted average from three temperature sensors at the bottom, one side and top sheet (surface1–surface3) |
| ϑout | One temperature sensor (out) |
| ϑin | One temperature sensor (in) |
| ϑex | Average of two temperature sensors located at top and bottom of copper cylinder (ex1 and ex2) |
| ϑC | Components of test bench were divided into: Copper cylinder: ϑex Inner insulation: Average of ϑS and temperature sensor between insulations Outer insulation: Average of temperature sensor between insulations and ϑSurface Outer sheets: ϑSurface Containment: ϑS |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stahl, V.; Kraft, W.; Vetter, P.; Feder, F. Simulative Investigation of Thermal Capacity Analysis Methods for Metallic Latent Thermal Energy Storage Systems. Energies 2021, 14, 2241. https://doi.org/10.3390/en14082241
Stahl V, Kraft W, Vetter P, Feder F. Simulative Investigation of Thermal Capacity Analysis Methods for Metallic Latent Thermal Energy Storage Systems. Energies. 2021; 14(8):2241. https://doi.org/10.3390/en14082241
Chicago/Turabian StyleStahl, Veronika, Werner Kraft, Peter Vetter, and Florian Feder. 2021. "Simulative Investigation of Thermal Capacity Analysis Methods for Metallic Latent Thermal Energy Storage Systems" Energies 14, no. 8: 2241. https://doi.org/10.3390/en14082241
APA StyleStahl, V., Kraft, W., Vetter, P., & Feder, F. (2021). Simulative Investigation of Thermal Capacity Analysis Methods for Metallic Latent Thermal Energy Storage Systems. Energies, 14(8), 2241. https://doi.org/10.3390/en14082241






