Transition Prediction in Incompressible Boundary Layer with Finite-Amplitude Streaks
Abstract
1. Introduction
2. Theory
2.1. Streaky Base Flow Formulation
2.2. Stability Analysis
Plane-Marching PSE
3. Results and Discussion
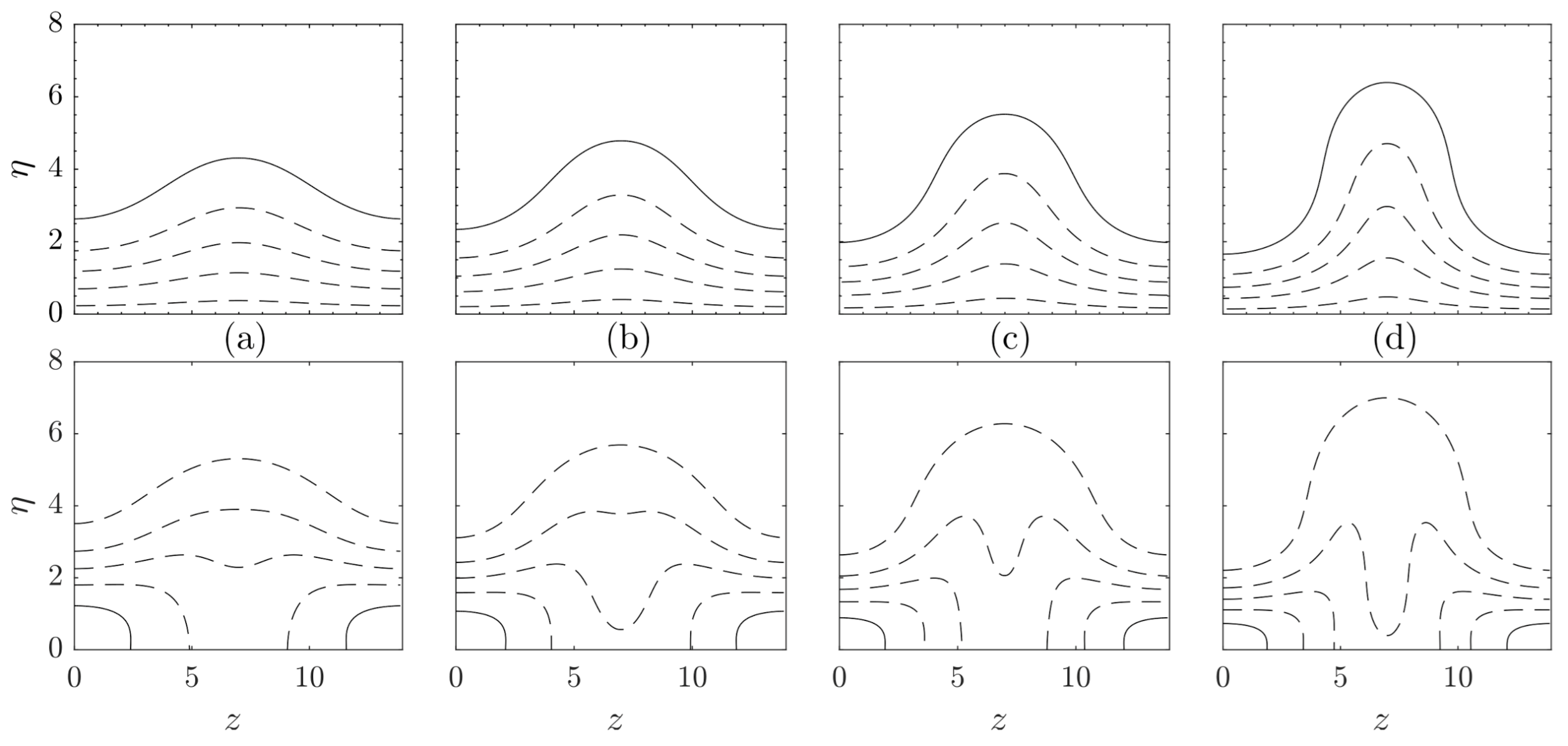
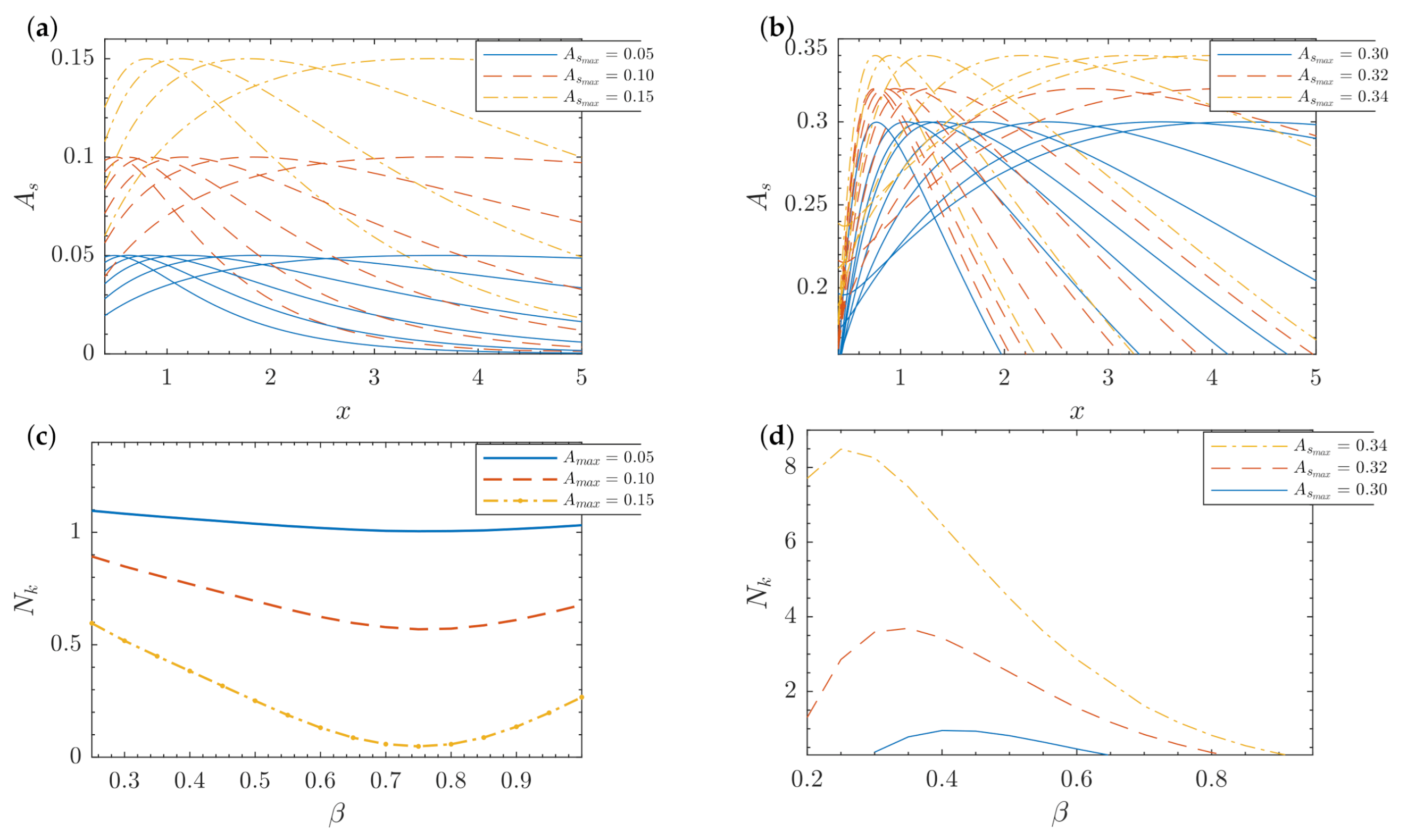
3.1. Optimal Streaks
3.2. Suboptimal Streaks
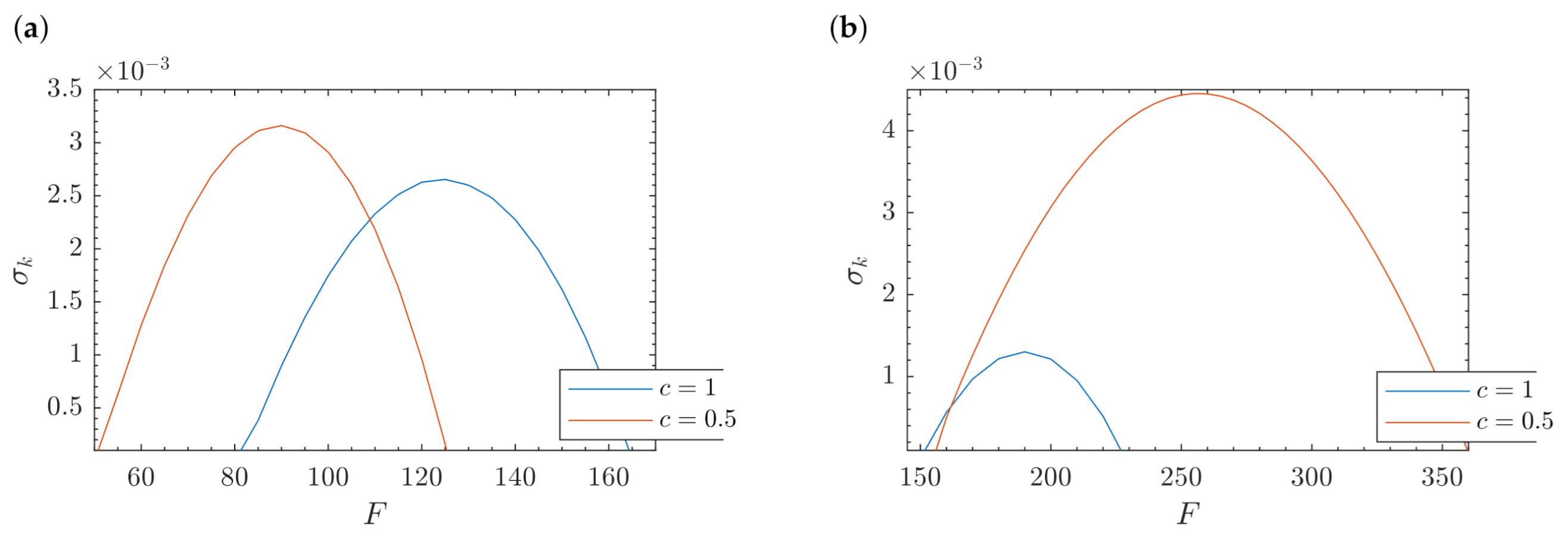
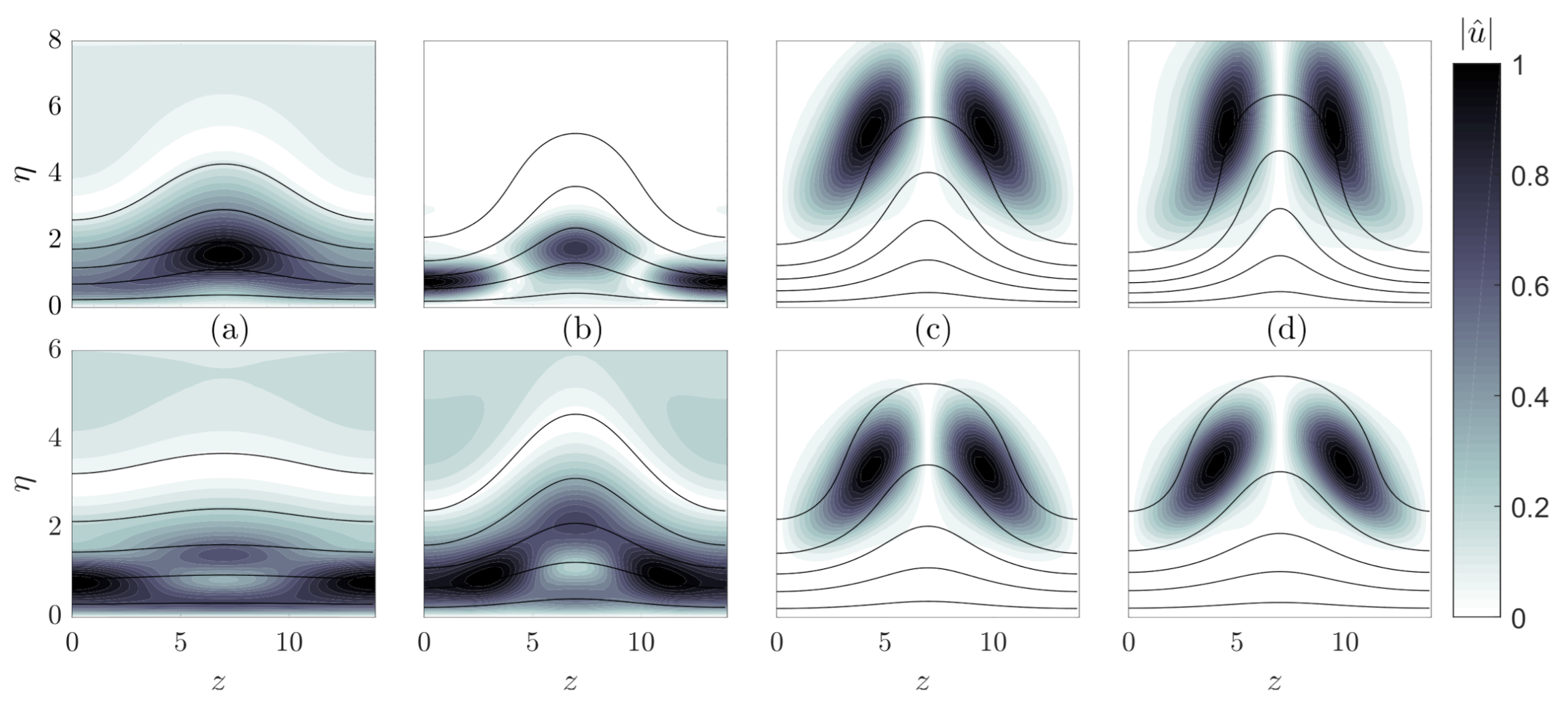
3.3. Stability of Optimal Streaks
3.4. Analysis of the Spanwise Wavenumber of Streaks
3.5. Efficiency of Streaks to Delay Transition
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Matsubara, M.; Alfredsson, P. Disturbance growth in boundary layers subjected to free-stream turbulence. J. Fluid Mech. 2001, 430, 149–168. [Google Scholar] [CrossRef]
- Brandt, L.; Henningson, D. Transition of streamwise streaks in zero-pressure-gradient boundary layers. J. Fluid Mech. 2002, 472, 229–261. [Google Scholar] [CrossRef]
- Brandt, L. Numerical studies of the instability and breakdown of a boundary-layer low-speed streak. Eur. J. Mech. B Fluids 2007, 26, 64–82. [Google Scholar] [CrossRef]
- Cossu, C.; Brandt, L. Stabilization of Tollmien-Schlichting waves by finite amplitude optimal streaks in the Blasius boundary layer. Phys. Fluids 2002, 14, L57–L60. [Google Scholar] [CrossRef]
- Cossu, C.; Brandt, L. On Tollmien-Schlichting-like waves in streaky boundary layers. Eur. J. Mech. B Fluids 2004, 23, 815–833. [Google Scholar] [CrossRef]
- Bagheri, S.; Hanifi, A. The stabilizing effect of streaks on Tollmien-Schlichting and oblique waves: A parametric study. Phys. Fluids 2007, 19, 078103. [Google Scholar] [CrossRef]
- Fransson, J.H.M.; Brandt, L.; Talamelli, A.; Cossu, C. Experimental and theoretical investigation of the nonmodal growth of steady streaks in a flat plate boundary layer. Phys. Fluids 2004, 16, 3627–3638. [Google Scholar] [CrossRef]
- Fransson, J.H.M.; Brandt, L.; Talamelli, A.; Cossu, C. Experimental study of the stabilization of Tollmien-Schlichting waves by finite amplitude streaks. Phys. Fluids 2005, 17, 054110. [Google Scholar] [CrossRef]
- Fransson, J.H.M.; Talamelli, A.; Brandt, L.; Cossu, C. Delaying transition to turbulence by a passive mechanism. Phys. Rev. Lett. 2006, 96, 064501. [Google Scholar] [CrossRef]
- Tani, I.; Komoda, H. Boundary-Layer transition in the presence of streamwise vortices. J. Aerosp. Sci. 1962, 29, 440–444. [Google Scholar] [CrossRef]
- Fransson, J.H.M.; Talamelli, A. On the generation of steady streamwise streaks in flat-plate boundary layers. J. Fluid Mech. 2012, 698, 211–234. [Google Scholar] [CrossRef]
- Shahinfar, S.; Sattarzadeh, S.S.; Fransson, J.H.M.; Talamelli, A. Revival of Classical Vortex Generators Now for Transition Delay. Phys. Rev. Lett. 2012, 109, 074501. [Google Scholar] [CrossRef]
- Shahinfar, S.; Fransson, J.H.M.; Sattarzadeh, S.S.; Talamelli, A. Scaling of streamwise boundary layer streaks and their ability to reduce skin-friction drag. J. Fluid Mech. 2013, 733, 1–32. [Google Scholar] [CrossRef]
- Sattarzadeh, S.S.; Fransson, J.H.M.; Talamelli, A.; Fallenius, B.E.G. Consecutive turbulence transition delay with reinforced passive control. Phys. Rev. E 2014, 89, 061001. [Google Scholar] [CrossRef]
- Shahinfar, S.; Sattarzadeh, S.S.; Fransson, J.H.M. Passive boundary layer control of oblique disturbances by finite-amplitude streaks. J. Fluid Mech. 2014, 749, 1–36. [Google Scholar] [CrossRef]
- Siconolfi, L.; Camarri, S.; Fransson, J.H.M. Stability analysis of boundary layers controlled by miniature vortex generators. J. Fluid Mech. 2015, 784, 596–618. [Google Scholar] [CrossRef]
- Downs, R.S.; Fransson, J.H.M. Tollmien-Schlichting wave growth over spanwise-periodic surface patterns. J. Fluid Mech. 2014, 754, 39–74. [Google Scholar] [CrossRef]
- Doerr, P.C.; Kloker, M.J. Numerical Investigations on Tollmien-Schlichting Wave Attenuation Using Plasma-Actuator Vortex Generators. AIAA J. 2018, 56, 1305–1309. [Google Scholar] [CrossRef]
- Sattarzadeh, S.S.; Fransson, J.H.M. Spanwise boundary layer modulations using finite discrete suction for transition delay. Exp. Fluids 2017, 58, 14. [Google Scholar] [CrossRef]
- Kemp, N. The Laminar Three-Dimensional Boundary Layer and a Study of the Flow Past a Side Edge. Ph.D. Thesis, Cornell University, Ithaca, NY, USA, 1951. [Google Scholar]
- Martin, J.A.; Martel, C. Nonlinear streak computation using boundary region equations. Fluid Dyn. Res. 2012, 44, 045503. [Google Scholar] [CrossRef]
- Paredes, P.; Rodriguez, D.; Theofilis, V. Three-Dimensional Solutions of Trailing-Vortex Flows Using Parabolized Equations. AIAA J. 2013, 51, 2763–2770. [Google Scholar] [CrossRef]
- Paredes, P. Advances in Global Instability Computations: From Incompressible to Hypersonic Flow. Ph.D. Thesis, Technical University of Madrid, Madrid, Spain, 2014. [Google Scholar]
- Paredes, P.; Hanifi, A.; Theofilis, V.; Henningson, D. The nonlinear PSE-3D concept for transition prediction in flows with a single slowly-varying spatial direction. Procedia IUTAM 2015, 14C, 35–44. [Google Scholar] [CrossRef]
- Martín, J.A.; Paredes, P. Three-dimensional instability analysis of boundary layers perturbed by streamwise vortices. Theor. Comp. Fluid Dyn. 2017, 31, 505–517. [Google Scholar] [CrossRef]
- Rubin, S.G.; Tannehill, J.C. Parabolized Reduced Navier-Stokes Computational Techniques. Annu. Rev. Fluid Mech. 1992, 24, 117–144. [Google Scholar] [CrossRef]
- Hall, P. The Nonlinear Development of Görtler Vortices in Growing Boundary-Layers. J. Fluid Mech. 1988, 193, 243–266. [Google Scholar] [CrossRef]
- Hall, P.; Smith, F.T. On Strongly Nonlinear Vortex Wave Interactions in Boundary-Layer-Transition. J. Fluid Mech. 1991, 227, 641–666. [Google Scholar] [CrossRef]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics; Springer: Berlin, Germany, 1988; Volume II, p. 411. [Google Scholar]
- Chen, C.S. Numerical method for predicting three-dimensional steady compressible flow in long microchannels. J. Micromech. Microeng. 2004, 14, 1091–1100. [Google Scholar] [CrossRef]
- Chen, C.S. Reduced Navier-Stokes simulation of incompressible microchannel flows. Numer. Heat Transf. Part A 2008, 53, 71–87. [Google Scholar] [CrossRef]
- Goldstein, M.; Wundrow, D. On the environmental realizability of algebraically growing disturbances and their relation to Klebanoff modes. Theoret. Comput. Fluid Dyn. 1998, 10, 171–186. [Google Scholar] [CrossRef]
- Wundrow, D.; Goldstein, M. Effect on a laminar boundary layer of small-amplitude streamwise vorticity in the upstream flow. J. Fluid Mech. 2001, 426, 229–262. [Google Scholar] [CrossRef]
- Leib, S.; Wundrow, D.; Goldstein, M. Effect of free-stream turbulence and other vortical disturbances on a laminar boundary layer. J. Fluid Mech. 1999, 380, 169–203. [Google Scholar] [CrossRef]
- Goldstein, M.; Sescu, A. Boundary-layer transition at high free-stream disturbance levels – beyond Klebanoff modes. J. Fluid Mech. 2008, 613, 95–124. [Google Scholar] [CrossRef]
- Ricco, P. The pre-transitional Klebanoff modes and other boundary-layer disturbances induced by small-wavelength free stream vorticity. J. Fluid Mech. 2009, 638, 267–303. [Google Scholar] [CrossRef]
- Ricco, P.; Luo, J.; Wu, X. Evolution and instability of unsteady nonlinear streaks generated by free-stream vortical disturbances. J. Fluid Mech. 2011, 677, 1–38. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, D.; Luo, J. Excitation of steady and unsteady Görtler vortices by free-stream vortical disturbances. J. Fluid Mech. 2011, 682, 66–100. [Google Scholar] [CrossRef]
- Herbert, T. Parabolized stability equations. Annu. Rev. Fluid Mech. 1997, 29, 245–283. [Google Scholar] [CrossRef]
- Bridges, T.; Morris, P. Differential eigenvalue problems in which the parameter appears nonlinearly. J. Comp. Phys. 1984, 55, 437–460. [Google Scholar] [CrossRef]
- Theofilis, V. Spatial stability of incompressible attachment line flow. Theor. Comput. Fluid Dyn. 1995, 7, 159–171. [Google Scholar] [CrossRef]
- Paredes, P.; Hermanns, M.; Le Clainche, S.; Theofilis, V. Order 104 speedup in global linear instability analysis using matrix formation. CMAME 2013, 253, 287–304. [Google Scholar] [CrossRef]
- Andersson, P.; Berggren, M.; Henningson, D.S. Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 1999, 11, 134–150. [Google Scholar] [CrossRef]
- Andersson, P.; Brandt, L.; Bottaro, A.; Henningson, D. On the breakdown of boundary layer streaks. J. Fluid Mech. 2001, 428, 29–60. [Google Scholar] [CrossRef]
- Denissen, N.A.; White, E.B. Secondary instability of roughness-induced transient growth. Phys. Fluids 2013, 25, 114108. [Google Scholar] [CrossRef]
- White, E.B. Transient growth of stationary disturbances in a flat plate boundary layer. Phys. Fluids 2002, 14, 4429–4439. [Google Scholar] [CrossRef]
- White, E.B.; Rice, J.M.; Ergin, F.K. Receptivity of stationary transient disturbances to surface roughness. Phys. Fluids 2005, 17, 064109. [Google Scholar] [CrossRef]
- Ingen, J.L.V. The eN method for transition prediction. Historical review of work at TU Delft. In Proceedings of the AIAA 38th Fluid Dynamics Conference and Exhibit, Seattle, WA, USA, 23–26 June 2008; p. 3830. [Google Scholar]
- Moralev, I.A.; Firsov, A.A.; Preobrazhensky, D.; Selivonin, I. Damping of the low velocity streak by adaptive plasma actuator. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences (EUCASS), Milan, Italy, 3–6 July 2017; p. 270. [Google Scholar]


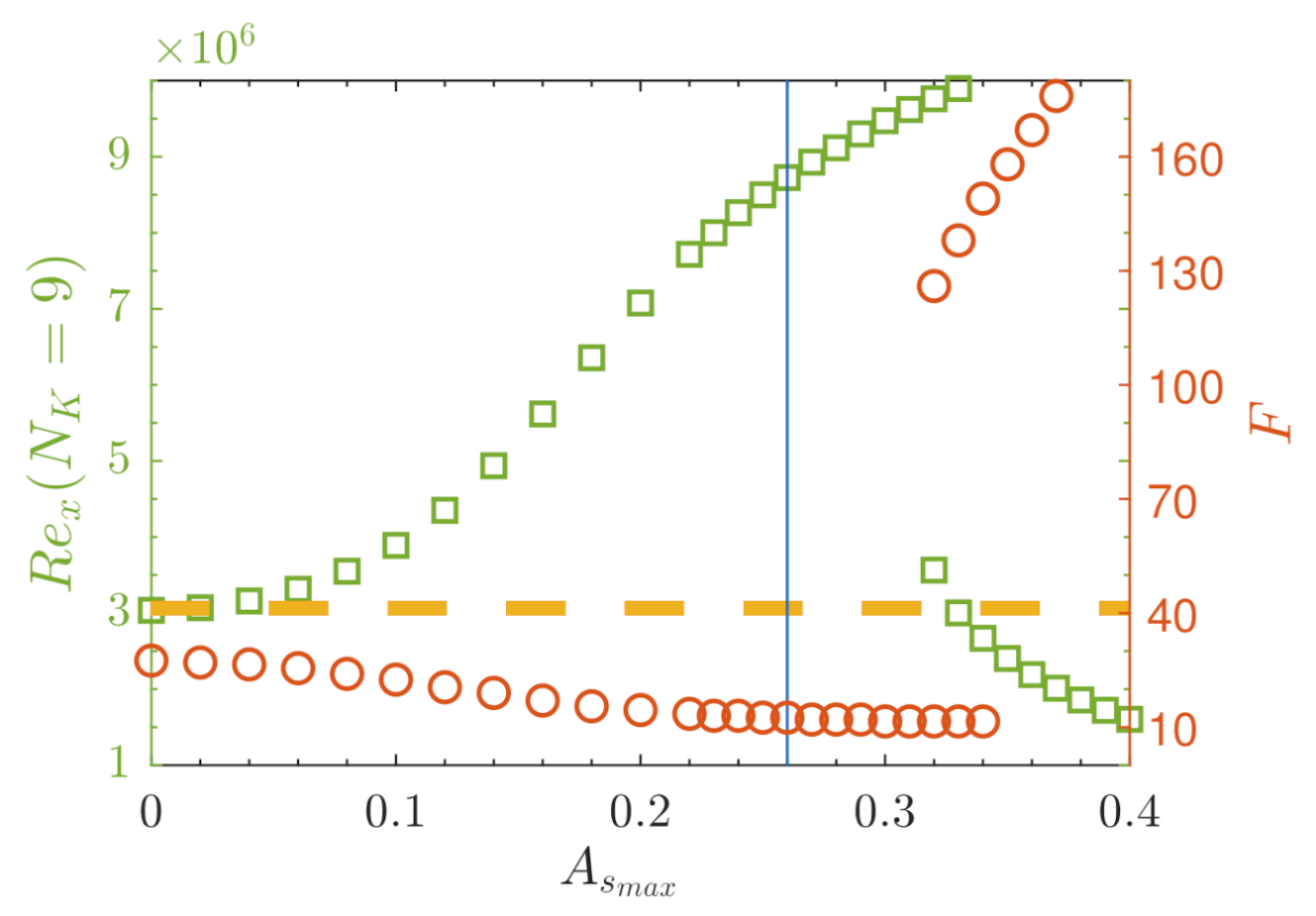
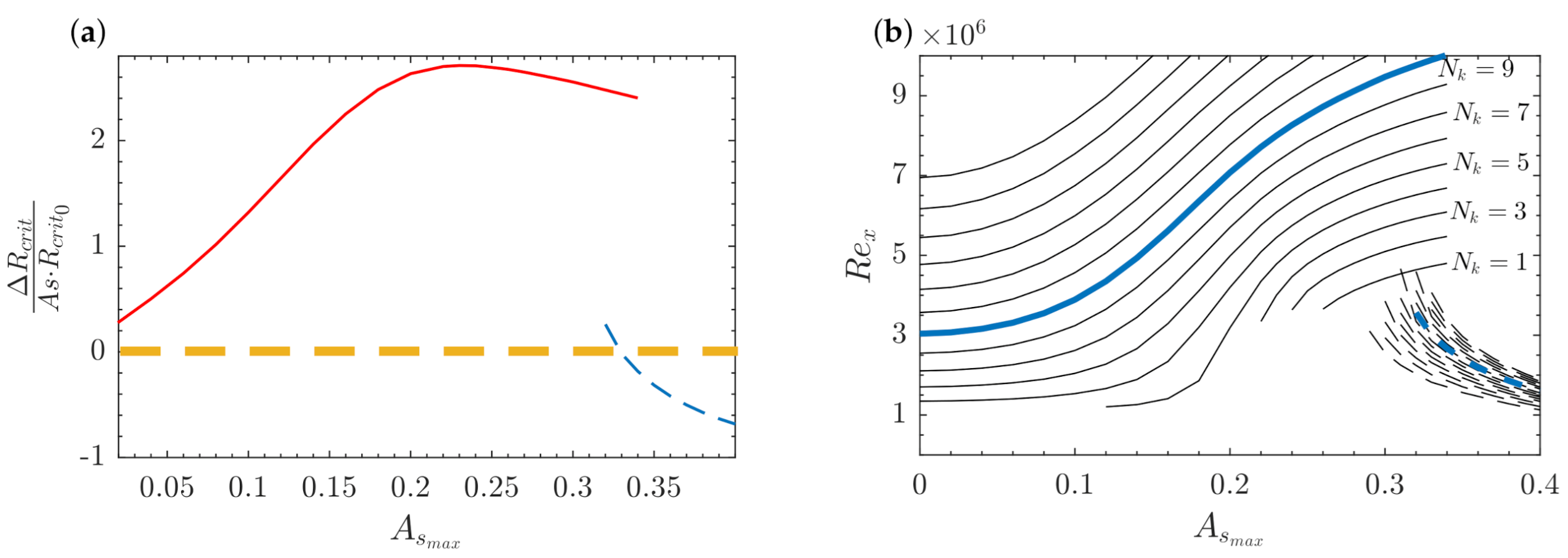
| where | F for | ||
|---|---|---|---|
| 0.00 | 5.3 | 1251 | 48 |
| 0.14 | 3.5 | 1236 | 48 |
| 0.20 | 2.1 | 1225 | 48 |
| 0.25 | 0.01 | 332 | 220 |
| 0.28 | 0.1 | 759 | 190 |
| 0.30 | 1.1 | 843 | 240 |
| 0.32 | 4.0 | 901 | 295 |
| 0.34 | 8.1 | 943 | 340 |
| 0.36 | 13.0 | 976 | 380 |
| 0.38 | 18.2 | 1004 | 415 |
| 0.40 | 23.2 | 1025 | 445 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín, J.Á.; Paredes, P. Transition Prediction in Incompressible Boundary Layer with Finite-Amplitude Streaks. Energies 2021, 14, 2147. https://doi.org/10.3390/en14082147
Martín JÁ, Paredes P. Transition Prediction in Incompressible Boundary Layer with Finite-Amplitude Streaks. Energies. 2021; 14(8):2147. https://doi.org/10.3390/en14082147
Chicago/Turabian StyleMartín, Juan Ángel, and Pedro Paredes. 2021. "Transition Prediction in Incompressible Boundary Layer with Finite-Amplitude Streaks" Energies 14, no. 8: 2147. https://doi.org/10.3390/en14082147
APA StyleMartín, J. Á., & Paredes, P. (2021). Transition Prediction in Incompressible Boundary Layer with Finite-Amplitude Streaks. Energies, 14(8), 2147. https://doi.org/10.3390/en14082147






