Abstract
A stand-alone machine learned turbulence model is developed and applied for the solution of steady and unsteady boundary layer equations, and issues and constraints associated with the model are investigated. The results demonstrate that an accurately trained machine learned model can provide grid convergent, smooth solutions, work in extrapolation mode, and converge to a correct solution from ill-posed flow conditions. The accuracy of the machine learned response surface depends on the choice of flow variables, and training approach to minimize the overlap in the datasets. For the former, grouping flow variables into a problem relevant parameter for input features is desirable. For the latter, incorporation of physics-based constraints during training is helpful. Data clustering is also identified to be a useful tool as it avoids skewness of the model towards a dominant flow feature.
1. Introduction
Engineering applications encounter complex flow regimes involving turbulent and transition (from laminar to turbulent) flows, which encompass a wide range of length and time scales that increase with the Reynolds number (Re). Direct Numerical Simulations (DNS) require grid resolutions small enough to resolve the entire range of turbulent scales and are beyond the current computational capability. Availability of high-fidelity DNS and experimental datasets is fueling the emergence of machine learning tools to improve accuracy, convergence and speed-up of turbulent flow predictions [1,2]. Machine learning tools depend on neural networks to identify the correlation between input and output features, and have been used in different ways for turbulent flow predictions, such as direct field estimation, estimation of turbulence modeling uncertainty, or advance turbulence modeling.
In the direct field estimation approach, the entire flow field is predicted using a ML approach, i.e., the flow field is the desired output feature. For example, Milano and Koumoutsakos [3] estimated mean flow profile in the turbulent buffer-layer region using Burger’s equation and channel flow DNS results as training datasets. Hocevar et al. [4] predicted the scalar concentration spectra in an airfoil wake using experimental datasets as training datasets. Jin et al. [5] estimated unsteady velocity distribution in the near wake (within four diameters) of a 2D circular cylinder using laminar solutions as training datasets and surface pressure distribution as input feature. Obiols-Sales et al. [6] developed Computational Fluid Dynamics (CFD) Network CFDNet—a physical simulation and deep learning coupled framework to speed-up the convergence of CFD simulations. For this purpose, a convolution neural network was trained to predict the primary variables of the flow. The neural network was used as intermediate step in the flow prediction, i.e., CFD simulations are solved as a warmup preprocessing step, then the neural network is used to infer the steady state solution, and following that CFD simulations are performed to correct the solution to satisfy the desired convergence constraints. The method was applied for range of canonical flows such as channel flow, flow over ellipse, airfoil, cylinder, where the results were encouraging.
For the turbulence model uncertainty assessment, the desired output feature is the error in a CFD solution due to turbulence modeling. For example, Edeling et al. [7] used velocity data from several boundary layer flow experiments with variable pressure gradients to evaluate the k-ε model coefficient ranges. Then, the variation in model coefficients were used to estimate the uncertainty in Reynolds averaged Navier Stokes (RANS) solution. Ling and Tempelton [8] compared several flow features predicted by k-ε RANS with DNS/LES results for canonical flows (e.g., duct flow, flow over a wavy wall, square cylinder etc.) and estimated errors in RANS predictions due to νT < 0, νT isotropy, and stress non-linearity.
Simulations on coarser grids require a model for the turbulent stresses (τ). The stress terms account for the effect of unresolved (or subgrid) turbulent flow on the mean (or resolved) flow for RANS (or LES) computations. The primary question for turbulence modeling is how turbulent stresses are correlated with flow parameters or variables? A review of the literature as summarized in Appendix A Table A1 and Table A2 shows that machine learning has been used to either augment physics-based models to improve their predictive capability [9,10,11,12,13,14,15,16,17,18,19,20,21,22] or develop standalone turbulence models [23,24,25,26,27,28,29,30]. The details of the input and output features and test and validation cases used in the studies are listed in the Tables, and the salient points of the studies are discussed below.
Parish and Duraisamy [9] analyzed DNS of plane channel flow to estimate the response surface of TKE production multiplier (β) as a function of four turbulent flow variables. The model was used to argument k-ω model. In a follow-on study [10] experimental data for wind turbine airfoils was used to adjust the Spalart–Allmaras (SA) RANS model νT production as a function of five turbulent flow parameters. The β function was reconstructed using an artificial neural network to minimize the difference between the experimental data and SA model results. The models were used for aposteriori tests, where it showed significant improvement over the standard RANS models and was found to be robust even for unseen geometries and flow conditions. He et al. [11] developed a similar approach, wherein adjoint equations were derived for SA model solution error due to νT production. The SA model predictions were compared with the experimental data at selected locations during runtime. Then, a solution of β was obtained using the adjoint equation to minimize discrepancy between the predictions and experimental data. The approach was applied for several canonical test cases and encouraging results were reported. Yang and Xiao [12] extended the work of Duraisamy et al. [9,10] to train a correction term for the transition model time-scale. Their model was trained using DNS datasets for flow over an airfoil at different angle of attack using both random forest and artificial neural network and using six different flow variables as input features. The trained correction term was implemented in a 4-Equation transition model, and applied for aposteriori tests involving unseen flow conditions (both interpolation and extrapolation mode) and geometry. The study reported good agreement for the transition location, validating the efficacy of such models.
Ling et al. [13] used six different DNS/LES canonical flow results to obtain coefficients of a non-linear stress formulation consisting of ten (10) terms involving non-linear combinations of the of rate-of-strain (S) and rotation tensors (Ω). The model coefficients were trained using a deep neural network as a function of five invariants of S and Ω tensors. The trained model coefficient map was applied for both apriori and aposteriori tests, including unseen geometry. The study reported that the ML model performs better than both the linear and non-linear physics-based models and performed reasonably well for unseen geometries and flow conditions.
Xiao and coworkers [14,15] trained a response surface of the errors in k-ε RANS turbulent stress predictions as a function of ten flow features using random forest regression. The model was validated for apriori tests for two sets of cases, one where the test flow and training flow were similar, and second for unseen geometry and flow conditions. It was reported that the model performed better for the former case. Wu et al. [15] investigated metrics to quantify the similarity between the training flows and the test flow that can be used to provide guidelines for selecting suitable training flows to improve the prediction of such models. Wang et al. [16] extended the above approach for compressible flows. A model was trained using DNS datasets with 47 flow features obtained using combination of S, Ω, ∇k, and ∇T, inspired by Ling et al. [13]. The model was validated for apriori tests for flat-plate boundary layer simulations. The study identified that the machine learned model predictions depend significantly on the closeness to the training dataset.
Wu et al. [17] developed a model to address the ill-conditioned solutions predicted by machine learned model during aposteriori tests (i.e., small errors in the modeled Reynolds stresses results in large errors in velocity predictions). For this purpose, a model was trained to account for the errors in k-ε RANS model stress predictions (both linear and non-linear terms) using seven turbulent flow features. The model was applied as an aposteriori test for flows involving slightly different geometry than the training case. Yin et al. [18] investigated the role of the feature selection and grid topology on the unsmoothness of the solution and large prediction errors reported in the above [17] study. They trained a model using 47 input features, inspired by Ling et al. [13]. The model was applied for apriori and aposteriori tests, wherein for the latter machine learned turbulent stresses were frozen. The study concluded that unsmoothness of the solution was primarily due to grid topology issues which results in discontinuities in the input features.
Yang et al. [19] used neural networks to train a wall-model for LES. The model was trained using three sets of input features: (1) wall parallel velocity (u||) and d; (2) u||, d and grid aspect ratio; and (3) u||, d, grid aspect ratio and ∇p. The model was coupled with a Lagrangian dynamic Smagorinsky model and applied for channel flow over a wide range of flow conditions Reτ = 103 to 1010. The study reported that inclusion of additional flow features such as grid aspect ratio and pressure gradient does not show significant improvement in the predictions.
Weatheritt and Sandberg [20] used symbolic regression to derive an analytic formulation for turbulent stress anisotropy. The model was trained using hybrid RANS/LES solutions and a regression map for the model coefficients were obtained as a function of rate-of-strain and rotation tensor magnitudes. The anisotropy formulation was used along with the k-ω model, and the model showed very encouraging results for both apriori and aposteriori tests including unseen geometries. Jian et al. [21] used a deep neural network to train a regression map of the model coefficients for an algebraic RANS model. The model was trained using a single parameter |S|k/ε as the input feature. The model was validated for both apriori and aposteriori tests, including extrapolation mode, i.e., Reτ larger than those in the training dataset. The study reported that the ML model performed better than the non-linear physics-based models due to its capability to better capture the large stress-strain misalignment and strong stress anisotropy in the near-wall region. Xie et al. [22] used neural networks to train model coefficients of a mixed subgrid stress/thermal flux model. The model trained compressible isotropic turbulence flow using six flow features, and it was reported that the machine learned model performs better than the physics-based models.
Comparatively limited efforts have been made to develop standalone machine learned turbulence models. Schmelzer et al. [23] used a symbolic regression approach to infer the model coefficients of an algebraic RANS model. The model was trained using DNS datasets using invariants of S and Ω tensors. The model was applied for unseen flow conditions, where the machine learned model performed better than the k-ω RANS. Fang et al. [24] developed a model for turbulent shear stress using DNS of channel flow. The model used a deep neural network trained using mean flow gradients and Reτ as key input parameters, and non-slip boundary condition and spatial non-locality were enforced during training. The model was applied for aposteriori tests involving unseen flow conditions, and it was reported that the model worked better than the model proposed by Ling et al. [16] due to the use of Reτ and boundary condition enforcement. Zhu et al. [25] developed a regression map of RANS turbulent eddy viscosity using a radial basis function network using SA RANS solutions for flow over NACA 0012 and RAE2822 airfoils at different angles of attack using eight input features based on flow, gradient and wall distance. The flow domain was separated into near-wall, wake, and far-field regions, and a different model was trained in each region. The study reported that using wall-distance as weights helped during training, but training using log-transformation of dataset did not help. The model was applied for aposteriori tests for the training geometry but for unseen angles of attack (flow condition), and good predictions were reported for the lift/drag coefficients, and skin friction distributions.
King et al. [26] developed a subgrid stress model using DNS of isotropic and sheared turbulence using velocity, pressure, S and grid parameters as input features. The model was applied for apriori tests for the isotropic and sheared turbulence test cases on coarse grid, where it performed better than the dynamic LES model. Gamahara and Hattori [27] used a feed-forward neural network to train a regression map of LES turbulent stresses. For this purpose, DNS results for plane channel flow for Reτ = 180 to 800 were filtered on up to four times (in each direction) coarser grids, and the filtered flow field was used as input features. The study used four different sets of input features involving S, Ω, wall-distance, and velocity gradients, and models were validated for apriori tests for unseen flow conditions. The study reported that the best model was predicted when u and d were used as input features. Further, it was reported that the machine learned models are more accurate than the similarity models, because of their ability to learn the non-linear functional relation between the resolved flow field and the subgrid stresses better than those prescribed in the physics-based model. Zhou et al. [28] used a similar approach to develop LES subgrid-scale model. The model was trained for isotropic decaying turbulence using gradients of filtered velocity and filter width (Δ). Yuan et al. [29] also developed an LES model using deconvolution neural network with isotropic decaying turbulence datasets for training. The model was trained using filtered velocity as the input parameter and validated for both apriori and aposteriori tests. Maulik et al. [30] used an artificial neural network to train a regression map of subgrid term for 2D turbulence using primary variables and its gradients as input features. The model was validated for both apriori and aposteriori tests. The ML model provided good predictions; however, it was reported that some measure of aposteriori error must be considered during optimal model selection for greater accuracy.
Some recent studies [31,32,33] have investigated the development of machine learning models for turbulent flow predictions by incorporating physics-based constrained during the training. These models provide an important direction to the applicability of the machine learning approach, but thus far they have used only for direct field estimation.
Overall, a review of the literature shows that
- (1)
- Machine learning has been primarily used for RANS model augmentation, where either turbulence production is adjusted, or nonlinear stress components are added to linear eddy viscosity term. Limited effort has been made to develop a stand-alone model, except for some recent effort focusing on modeling of subgrid stresses for LES.
- (2)
- Studies have used wide range input flow features for machine learned model training. There is a consensus that combining flow features into physically relevant flow feature is desirable, as this helps incorporate physics in machine-learning. Use of a large numbers of input features have been found to be helpful to some extent as it allows output features to be uniquely identified in the different flow regimes. However, they introduce additional sources of inaccuracy. For example, unsmooth solutions have been reported due to inaccurate calculation in the input features involving higher-order formulations of the derivative terms.
- (3)
- Machine learned models have been applied for both apriori and aposteriori tests for both unseen geometry and flow conditions, including Re extrapolation mode. The model in general perform well for unseen flow conditions, but issues have been reported for unseen geometries. In general, the machine learned models are most accurate when the test flow has similar complexity to the training flow.
- (4)
- Studies have reported issues during training due to overlap in the output features in different flow regimes. It has been tacked by using more input features, as discussed above, and by segregating the flow domain into regions with similar flow characteristics, such as near-wall, wake and far-field regions, and train separate models in each region.
In summary, there are open issues such as, “What is the best way to use machine learning for turbulence model development?” Should machine learning be used to augment an existing model or to develop a stand-alone model. The model augmentation approach builds on a baseline physics-based model; thus, it has some inherent robustness, especially when the model is used in extrapolation mode or for unseen geometry. However, this approach undercuts the advantage of machine learning. If it is expected that neural networks can accurately learn the errors in a RANS model and provide a universal model for the errors, then there is no reason to believe that same approach cannot provide a model for Reynolds stresses. Second, none of the studies in the literature have validated the machine learned model in a similar fashion as the physics-based model, i.e., how does it perform when started from ill-posed flow conditions, i.e., when simulation is started from an arbitrary initial condition, or does it provide grid convergence, or can independently query output in contiguous regions result in kinks in the solution. Apart from the above questions, there are additional issues regarding the best practices for optimizing machine learning approach itself [31].
The objective of this paper is to investigate the predictive capability of a stand-alone machine learned turbulence model and shed light on some of the above issues and constraints. To achieve these objectives, a DNS/LES database is curated for incompressible boundary layer solution available in the literature (i.e., channel flow and flat-plate boundary layer solution at zero pressure gradient), and a DNS database has been generated for oscillating channel flow. The datasets are used to train a ML response surface for the turbulent stress. The model is validated for apriori and aposteriori tests, and predictions are compared with DNS and RANS model results. The preliminary results for the channel flow case have been presented in ASME conference paper [32], and those of oscillating channel flow case has been presented in SC20 conference paper [33]. The results from the above publications have been further refined and are presented herein.
The novel aspects of this study include: development of a stand-alone RANS model, which has not received same level of attention as the RANS model augmentation; the effect of physics-based constraints during the training of a model is investigated, which has not been done before; the machine learned model is applied for an unsteady flow, thus far none of the studies have applied and tested machine learned model for unsteady flows; and the ability of the machine learned model to adapt to ill-posed initial flow conditions, as expected in a typical CFD simulation, and their ability to provide grid independent solution as expected for a RANS model are investigated.
The following section provides an overview of the DNS/LES datasets curated or procured in this research. Section 2 provides an overview of the machine learning approach. Section 3 and Section 4 focuses on development and validation of the machine learned model for boundary layer flows and oscillating channel flow case, respectively. Finally, some key conclusions and future work are discussed in Section 5.
2. Machine Learning Approach
The basic framework of the deep learning neural network is described in Figure 1, inspired from LeCun et al. [34]. The network consists of various layers, including the first input layer comprising of input features, the last output layer comprising of the required output features, and multiple hidden layers comprising of features units obtained using linear combination of feature units from the previous layer. Each layer, excluding the input layer, has input features (z) and output features (y). Let’s say for the pth layer with m feature units, the input and output features are z1 to zm and y1 to ym, respectively. The input feature units for the pth layer is obtained from the linear combination of the n output feature units in the layer above or (p − 1)th layer, as below:
where superscript (p) is used to represent the pth layer, i varies from 1 to m and j varies from 1 to n, and are the unknown weights that need to be estimated. Thus, there are m neurons that connect the (p − 1)th and pth layer. Note that for the first hidden layer z vector are the input features, and for the last output layer y vector are the output features. Also note that some of the features in the hidden layers can be dropped depending on the threshold of weights permitted. Usually in deep learning applications, the input features in the input layer are scaled to vary in-between 0 and 1, and similarly the weights are positive and normalized such that . For each hidden and output layers, the output features are obtained from the input features on that layer as
where is a pre-defined non-linear analytic activation function. The most common functions are
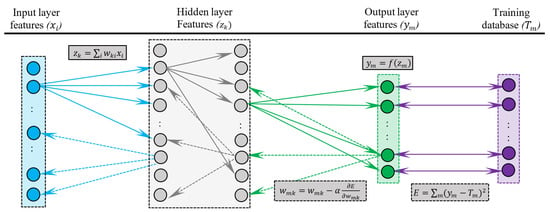
Figure 1.
Block diagram summarizing machine learning approach inspired from LeCun et al. [34]. The above example shows a neural network with one input, two hidden and output layers. Each of the circles represent a feature in a layer, let’s say i features in the input layer, k features in the hidden layer and m features in the output layer. The variable “x” are the input parameters, and “z” and “y” are the inputs and outputs, respectively, of both hidden and output layers. The features on the extreme right are the true values (T) used for training the network. The forward arrows represent the calculation of the features on the next layer based on linear combination of features on previous layer using the (positive) weight matrix (). Broken arrows show backpropagation of the network prediction error to readjust the weights. The network prediction error (E) is computed using a predefined cost function comparing the network output with the true values. The derivatives of the errors are computed to adjust the weight matrix, where α is learning rate.
Rectilinear Linear Units (ReLU) function provides a linear dependency on the input features, exponential Linear Units (ELU) are same as ReLU for non-negative inputs, but use exponential modulation for negative inputs, hyperbolic tangent and logistic functions modulate both the positive and negative inputs. As pointed out by Lee et al. [35], ReLU is the most commonly used function for training deep neural networks because they do not suffer from vanishing gradients and they are fast to train. However, they ignore the negative values and hence lose information, which is referred to as “dying ReLU”. ELU on the other hand can capture information for the negative inputs, so they used ELU for training their physics-informed neural network.
The unknown weight matrix in each layer is estimated using backpropagation approach, as described below. The network is first initialized with constant zero weight for each layer and the error in the network prediction are obtained by comparing them with training dataset or true values (T) using a user specified analytic cost function, such as L2 norm
For the above defined analytic cost function, the derivatives of the errors in the output layer with respect to the output feature is
and the derivative of the errors with respect to the input features is
where, is a known analytic function from Equation (3). Since the input features of a layer are linearly related to the output features of the previous layer as shown in Equation (1), the derivative of the errors with respect to the weights are computed as
Lastly, the weights in each layer are adjusted as
where α is learning rate, and subscript it represents the iteration level. Commonly available ML softwares provide optimizers which dictate the learning rate. For example, adaptive moment estimation (ADAM) optimizer [36] available in Keras application programming interface (API) requires a user specified initial learning rate, but the rate is adaptively adjusted during training. Note that in deep neural networks “iterations” refer to running a subset of the data (batch) forward and backwards through the network, whereas “epoch” refers to running all the training data forward and backward through the network. Thus, epochs are not same as iterations, unless the entire dataset is the batch size. Further note that the terms on RHS is known from Equations (5) and (6) for the output layer. For the hidden layers a backpropagation approach is used, where the derivative information is computed based on information from the layer ahead starting from the output layer, Equation (5), as below:
and then Equations (6) and (7) are used to obtain .
In the physics-informed machine learning (PIML) approach [37] the cost function is modified to include the residual in the governing equations (); thus, Equation (4) is modified to
Note that Equation (5) remains changed.
3. Test Cases and Database for Model Training
Two different text cases have been considered in this study, steady and unsteady channel flow. For the former, the mean flow solution describes the inner layer of a flat-plate boundary layer (with zero pressure gradient) at a fixed location on the plate. This case is a fundament test case for turbulence model development and several DNS studies are available for a range of flow conditions. The flow pattern for this case reduces to a one-dimensional (1D) problem. For the second test case, the inner boundary layer undergoes unsteadiness due to prescribed pressure gradient pulse. The mean flow pattern for this case reduces to an unsteady 1D problem, which adds another level of complexity to the first test case.
3.1. Plane Channel Flow
3.1.1. Governing Equation
This test case focuses on the simulation of the inner layer of the turbulent boundary layer under zero-pressure gradient at a fixed location on a flat-plate. The governing equations for such flow condition can be derived from the incompressible Navier–Stokes equations under the assumption that the flow is 2D and steady, and streamwise gradients are negligible compared to those along the wall normal direction (refer to Appendix B for derivation) as below:
where y is the coordinate direction normal to the wall and u is the ensembled averaged streamwise velocity. Note that the correlation between streamwise and wall-normal turbulent velocity fluctuations (, which are the shear stresses) is the only unknown quantity that needs to be modeled. Also note that although the above equations are valid for flows with zero pressure gradient, the above equation includes a body force term (), which can be misconstrued as pressure-gradient term. This term is added because the simulations are performed for flow between two flat-plates; thus, a body force is required to balance the momentum loss due to wall friction and achieve a steady state. The body force term is a function of wall shear stress expected at the simulated flat-plate location. The wall shear stress can be expressed in terms of friction velocity , and is a fixed input parameter:
and
where is the half channel height. Note that the simulated flow conditions in a channel flow case can be changed simply by changing the wall friction value (or the applied body force term). Further note that a time-derivative term in the governing equation is a pseudo time derivative, and used as a residual term and provides a measure of the solution convergence. A steady state solution is achieved as the time derivative term approaches zero.
Commonly used linear URANS models express the turbulent shear stress as [38]
where, is an unknown turbulent eddy viscosity. The one-equation URANS model requires solution of an additional transport equation for turbulent kinetic energy (k)
and turbulent eddy viscosity is obtained as
The turbulent length scale is prescribed as
where von-Karman constant and d is distance from the wall. Refer to Warsi [38] for details for the modeling. Similar to the streamwise velocity equation (Equation (11)), the time derivative can be perceived as a residual term for steady simulations, and a steady state is achieved as term approaches zero. The time derivate term provides the time-accurate solution for URANS simulations.
3.1.2. DNS/LES Database
A DNS/LES database is curated to train a ML response surface for . As summarized in Table A3, the database includes, 21 channel flow DNS cases with Reynolds numbers ranging from Reτ = 109 to 5200 [39,40,41,42,43,44,45]; 18 flat-plate boundary layer with zero-pressure gradient DNS cases with Reynolds numbers ranging from Reθ = 670 to 6500 [46,47,48]; and 14 flat-plate boundary layer with zero-pressure gradient LES cases with Reθ = 670 to 11,000 [49,50]. The database contained around 20,000 data points of which 3.4% were in the sub-layer, 5.7% in buffer layer and 90.9% in the log-layer or the outer layer. Note that all the datasets are for flat-plate boundary layer with zero-pressure gradient, where the channel flow cases represent only the inner-layer.
3.1.3. ML Model Training and Refinement Using Apriori Tests
ML model is developed using the cost function in Equation (4), which is referred to as data-driven machine learned (DDML) model, and cost function including the residual in the governing equations, i.e., Equation (10), which is referred to as physics-informed machine learned (PIML) model. For the PIML model training, the residual of the governing equation is obtained using the integral form of the governing equation (Equation (11)) at steady state as below:
where subscript ‘i’ denotes the solution at the epoch level.
The DDML model is trained used a multilayer perceptron (MLP) neural network consisting of two dense hidden layers, each with 512 neurons with ReLU activations, and a linear activation on the output layer. ADAM optimizer is used during training with a mean absolute error loss function, generating 276,000 trainable parameters. To mitigate over-fitting during training, each layer has a 20% dropout [51]. The PIML model is trained using an eight-layer deep neural network with each hidden layer having 20 neurons and a hyperbolic tangent activation function. The model is optimized using an L-BFGS quasi-Newton full-batch gradient-based optimization method and iterated for 2400 epochs. For the model training, the dataset is not separated into training and test sets; but rather 70% of the dataset is chosen randomly. Thus, it is possible that there could be an overlap in the datasets used for training and apriori tests. A parametric study was also performed by choosing 80% and 100% of datasets, which did not show much effect on the model predictions in apriori tests. Further note that the number of layers and neurons used for training DDML and PIML are different. For DDML training, a parametric study was performed using more layers and different number of neurons. The tests revealed that increasing the number of layers increases the training time, but does not necessarily improve the training accuracy. Increasing the number of neurons in lieu of layers was found to be computationally efficient and helped in reducing the training error. The numbers of layers and neurons used in the study are found to provide optimal model in terms of computational cost and accuracy. The optimal width and depth of neural network architecture also depends on the amount of data available for training the networks [52]. A shallow depth network is partially due to comparable small training dataset. For the PIML training a similar test was not performed and the training set-up was same as that used by [37]. Overall, although the numbers of layers and neurons differed between the PIML and DDML model training, but the neural network architecture for both provided the needed accuracy.
The machine learned turbulence model seeks to obtain a response surface of the shear stress , which is the output feature. The input features are the flow parameters. Referring to Figure 1, if a training batch uses N number of data points and each data point has M flow parameters, then the total number of input features , and total number of output features . The batch size was 128 for this case. Note that even though the M flow parameters at each data point are related; however, during the training they are considered independent of each other. The PIML model may leverage the correlation between the input features at a datapoint, as the feature set is expected to satisfy the governing equations.
Considering all the possible flow variables; the response surface of the shear stress is expected to have following functional form:
Instead of providing the flow features independently, they are grouped or non-dimensionalized into physically relevant parameter. The velocity derivative is a key term, which captures the rate-of-strain in the flow. It is commonly accepted that turbulent stresses can be modeled by extending Stokes’ law of friction (for viscous stresses), except that the linear assumption is debatable [38]. Thus, the velocity derivative normalized by the centerline velocity and channel height H is used as an input parameter. Figure 2 provides an overview of the correlation of with respect to key input features . As evident, the dataset shows quite an overlap especially for . Thus, it is clear that this parameter alone is not sufficient to train a reliable regression map.
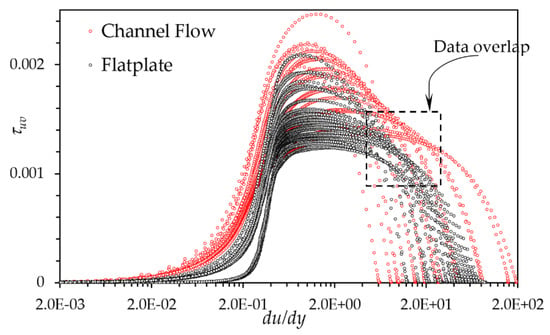
Figure 2.
Correlation of shear stress () with mean velocity gradient for channel and flat-plate boundary later DNS/LES dataset. The dataset shows significant overlap for du/dy between 5 and 20 (within the box region).
The flow viscosity ν is one of the fundamental bulk fluid property and dictates one of the key non-dimensional parameters for the boundary layer flow, which is the Reynolds number (Re). Re is usually defined based on global properties, such as channel height H and centerline velocity , Re = H/ν. This bulk flow parameter has little significance to the local stresses; thus, is not a suitable input parameter for machine learning. Rather, Reynolds number based on wall distance or based on local velocity and wall distance seem to be better choice, as they also incorporate local parameters. Note that for channel flow datasets, both the global parameters and are related via near-wall velocity gradient, and do not provide any additional information about the flow. Thus, when training a model just using the channel flow datasets is not required. However, when the datasets include both flat-plate boundary layer and channel flow datasets, then provides additional identifying information (as discussed below).
A preliminary apriori analysis is performed using just the channel flow DNS datasets to evaluate which Re formulation ( or ) is better, and also to investigated how inclusion of higher-order terms of rate-of-strain affects the model. For this purpose, the DDML model was trained using the following four sets of input parameters:
As shown in Figure 3a, the stresses obtained using input feature set is around 8% under predictive whereas those using obtained using compare very well and is only 2% over predictive. An accurate prediction by the latter is not surprising, as local Reynolds number is a physical quantity that separates the flow regime, i.e., is sub-layer; is buffer-layer; and is log-layer. The advantage of over is also evident in Figure 3b,c, where the former shows a better collapse in dataset in the buffer layer. Further, including as an input feature deteriorates the model performance and the stresses are overpredicted by 9%. However, using as a weighting parameter improves the results and the L2 norm error for this case is estimated to be 2.9 × 10−4, slightly better than the L2 norm error of 5.2 × 10−4 obtained using the feature set .
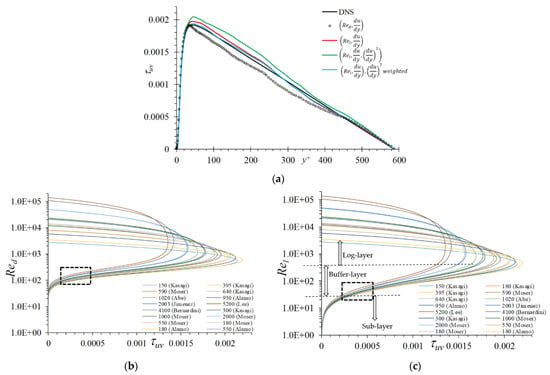
Figure 3.
(a) Apriori predictions using data-driven machine learned (DDML) using different sets of input parameters in Equation (20) for channel flow datasets. Variation of shear stress () for channel flow dataset with respect to (b) and (c). The latter shows better collapse in the DNS dataset in the buffer-layer region (within the box region).
When the entire channel and flat-plate database is considered, we need an additional parameter to demarcate between the inner and outer boundary layer. The inner and outer layer demarcation can be achieved by using a combination of and , where large and corresponds to the start of the outer layer. Thus, a model was trained using the following set of input parameters:
In addition, different weighting functions, ML-1 through ML-4 as shown below, were used during training of the DDML response surface as the data show significant overlap (as pointed out in Figure 2) at the intersection of the inner and outer layers:
- ML-1: No weighting
- ML-2: Weighted using curvature of the profiles
- ML-3: levels were expanded to separate out the curves
- ML-4: Not-weighted for but weighted for
Note that was also considered. But, similar to the earlier test this weighting did not show significant improvement over ML-1. This is expected as neural networks should be able to learn the dependency on higher-order forms of the input parameters all by itself. Thus, such weighting is not considered further.
An apriori analysis for a range of channel flow conditions in Figure 4 shows that the DDML response surface obtained without any weighting (ML-1) is consistently under predictive. Those obtained using profile curvature as a weighting function (ML-2) results in a waviness in the profile and is not recommended. DDML using weighting improves the results, and ML-4 provides somewhat better results than ML-3. The model shows some limitations for the prediction of peak stress for Reτ = 1000, which needs to be further investigated. The PIML model shows the best predictions among all the models for the entire range of Reτ, and compares very well with DNS, including those for Reτ = 1000. In addition, PIML removes the trial-and-error approach to train the model.
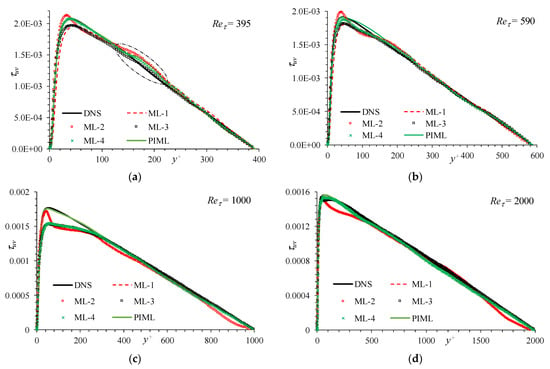
Figure 4.
Apriori DDML and physics-informed machine learning (PIML) stress predictions trained using channel and flat-plate datasets for channel flows at Reτ = (a) 395, (b) 590, (c) 1000, and (d) 2000 using different weighting functions and PIML are compared with DNS results.
3.2. Oscillating Plane Channel Flow
Oscillating channel flow is a canonical test case used in the literature to understand turbulence flow physics and validate the predictive capability of LES models. Scotti and Piomelli [53] performed DNS and LES of oscillating channel flow to study the effect of pressure gradients on the modulation of the viscous sublayer, turbulent stresses and the topology of the coherent structures. In this test case, an unsteady pressure pulse (body force term) is applied along the streamwise direction, which introduces periodic unsteadiness in the flow.
3.2.1. Governing Equation
The governing equation for the mean flow for this case can be obtained similar to the inner boundary layer equations as discussed in Appendix B as below:
where
is the prescribed pressure pulse. The above equation is derived under the assumption that mean flow is 2D in nature and wall-normal gradient is more dominant than the streamwise gradients. Both of these assumptions are valid for this case. Because DNS is performed using periodic domain, the mean flow variation along the streamwise direction is assumed negligible, and the velocity changes occur in time. Thus, this test case represents how boundary layer flow, at a fixed location on a flat plate, varies in time as the free-stream pressure gradient in varied. Further, note that the term corresponds to the forcing required to obtain steady state solution for flow between two flat-plates, which is the baseline flow. The term accounts for the variation of the free-stream pressure gradients. Similar to the steady inner-boundary layer case, the closure of the above equation requires modeling of shear stress . The physics-based one-equation URANS model described in Section 3.1.1 is valid for this case as well.
3.2.2. DNS Database
The DNS for this case is performed using an in-house parallel pseudo-spectral solver, which discretizes the incompressible Navier–Stokes equations using Fast Fourier Transform (FFT) along the homogenous streamwise and spanwise directions and Chebyshev polynomials in the wall-normal direction. The solver is parallelized using a hybrid OpenMP/MPI approach, scales up to 16K processors on up to 1 billion grid points, and has been extensively validated for LES and DNS studies [54,55].
DNS were performed for three different (high, medium, and low) streamwise pressure pulses, as used in [53]. The simulations were performed using as domain size of 3π × 2 × π along the streamwise, wall normal and spanwise directions, respectively, on a grid consisting of 192 × 129 × 192 points. The domain size is consistent with those used in [52], but the grids are finer. The details of the simulation set-up are provided in Table A4. The simulations were performed using periodic boundary condition along streamwise and spanwise directions, and no-slip wall at y = ±1.
The DNS results were validated in a previous study [56] for the prediction of the alternating (AC) and mean (DC) components of the mean flow against results presented in [53]. The AC components were obtained by decomposing normalized-planar-averaged velocity profile at every one-eight cycle using Fast Fourier Transform at each wall normal location. The DNS results were found to be in good agreement with the available benchmark results. The low frequency pulse resulted in re-laminarization and transition behavior, which is a challenging case for RANS predictions. The high frequency case was primarily driven by the pressure gradient, and turbulence levels were small. The medium frequency case provides a compromise between the two extremes and is used in this study.
The variation of the wall shear stress and streamwise and wall-normal velocities for the medium frequency case is shown in Figure 5. The positive pressure gradient generates adverse flow conditions and decelerates the flow (and decreases wall shear stress magnitude) and the negative pressure gradient generates favorable flow conditions which accelerates the flow (and increases wall shear stress). The peak wall shear (and velocity) is observed around 3/4th cycle (t = 0.75). The wall normal velocity shows that the ejection events are subdued during the first part of the oscillation cycle (descending leg), i.e., at t = 0.25 the ejection events are limited within the quarter channel and diminished at the mid-cycle (t = 0.5). The ejection events are enhanced during the ascending leg of the pressure pulse. The ejection events are very prominent for t = 0. Thus, shear stress is expected to be generated during the last part of the oscillation cycle.
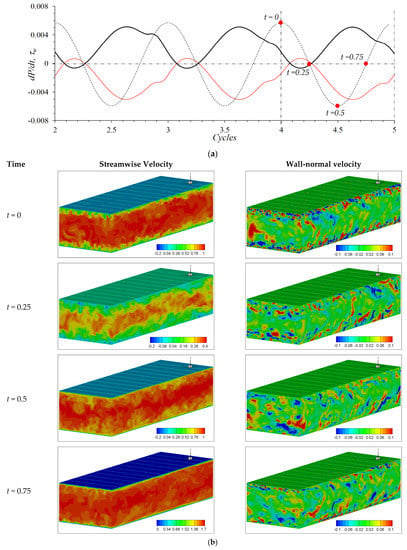
Figure 5.
(a) Pressure pulse, (broken black line), and variation of wall shear stress (solid red line: top wall, solid black line: bottom wall) over five pressure oscillation cycles, and (b) instantaneous streamwise and wall-normal velocity profiles at quarter cycle obtained from DNS for the medium frequency case. As marked in subfigure (a), t = 0 and 0.5 corresponds to the peak and trough of the pressure gradient pulse, respectively. Results are shown for the medium frequency case.
3.2.3. ML Model Training Using Apriori Tests
For training of the ML turbulence model, the 3D DNS dataset was processed to obtain an unsteady 1D dataset. Due to the use of a periodic boundary condition along the streamwise direction, the simulation domain is expected to move in time [57], and as demonstrated in Figure 6a. Further, the results at any time step represents multiple (every grid point in the streamwise-spanwise plane or 192 × 192) realizations of the turbulent flow field expected at that oscillation phase. The solutions were averaged over these realizations to obtain mean 1D flow along the wall normal (y) direction. The 1D solutions every 100th time step or 1/400th pressure oscillation cycle were used to generate a 2D y-time map of the mean flow as shown in Figure 6b. Solutions were collected over three pressure oscillation cycles resulting in 129 × 1201 (or around 155,000) data points.
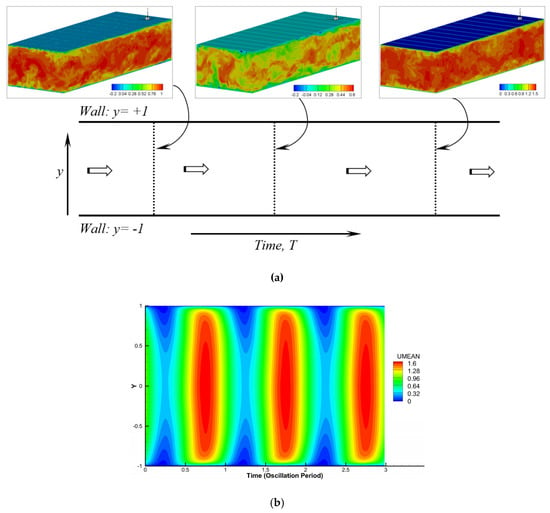
Figure 6.
(a) Schematic diagram demonstrating the post-processing of the 3D DNS data to obtain 1D unsteady mean flow. (b) Variation of the mean velocity over three oscillation period.
For this case, k is also added as an unknown turbulence quantity, and the machine learned model seeks to obtain regression map with two outputs (). Based on the experience of the boundary layer case, the input flow parameters for this case are identified to be the time varying and steady mean flow quantities as below:
where is the local friction velocity and is the baseline wall friction corresponding to .
Only the DDML model is trained for this case, as temporal derivatives could not be computed during training. The model was trained using a three-layer-deep neural network with 512 neurons in each hidden layer with ReLU activation functions. The final layer was a linear fully connected layer. The model was trained for 200 epochs using an ADAM optimizer with a batch size of 128 and a learning rate of 0.01. During the training, the L2 norm error dropped by an order of magnitude in the first 25 epochs, and the error drop stalled thereafter.
The oscillating channel flow involves a wide range of turbulence regimes unlike the boundary layer case which only has sub-, buffer- and log-layer regimes. As shown in Figure 7 in this case, the turbulence is most prominent toward the end of the pressure-oscillation cycle, and varies significantly along the wall-normal direction. Thus, training a ML model using the entire dataset may be skewed toward the more prominent features. For example, for the boundary layer case the models perform much better in log-layer than in the buffer-layer, as 91% of the datasets were in log-layer region. The Birch clustering algorithm sklearn was used to cluster the datapoints into unique flow regimes. The clusters were automatically determined using a non-dimensional threshold of 0.3, which resulted in 412 clusters with (min, max, mean, std) of points to be (1, 10,700, 376, 937), as shown in Figure 7. Note that the clustering preserves the periodicity of data.
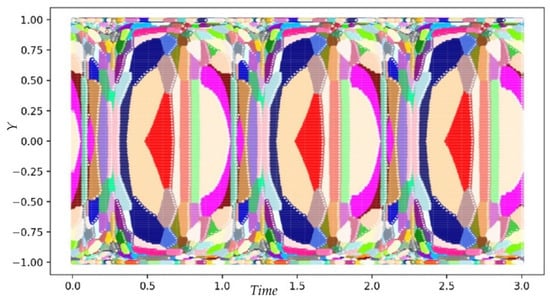
Figure 7.
Clustering of the shear stress () DNS data using sklearn. The different colored regions represent unique turbulence feature.
Several ML models were trained by randomly sampling various percentage of points within each cluster from 0.25% to 100% of the total dataset. As shown in Figure 8b–d, training using just one datapoint per cluster (0.25% of total) results in errors of 35%. The error level reduced to 28% when four points are used per cluster (or 1% of total). The error levels were around 12% when 10% of the datasets (either 10 points or 10% of each cluster) was used. A similar error levels were obtained when model was trained using all the datapoints. In addition, training using 10% of the data points required around eight times smaller computational cost compared to those using all of the datapoints. This indicates that an intelligently sampled dataset can generate reliable machine learned models at a lower computational cost.
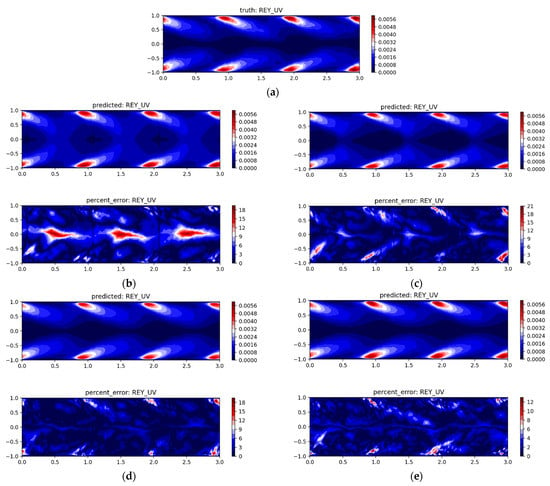
Figure 8.
(a) magnitude predicted by DNS. regression map (top) and error in the ML model (bottom) trained using (b) 0.25%, (c) 1%, (d) 10% and (e) 100% of datapoints.
4. Aposteriori Tests of the ML Model
For aposteriori tests, the machine learned turbulent shear stress (and TKE) regression map obtained in the pre-processing step above was coupled with the parallel pseudo-spectral solver used for DNS of oscillating channel flow (discussed in Section 3.2.2). Figure 9 provides a schematic diagram demonstrating the coupling of machine learned turbulence model with the CFD solver. As shown, the stress (or TKE) regression map is queried every time step using the flow predictions at that iteration level, and the stresses are used to advance the solution to the next time step. Both the test cases considered in this study are 1D in nature, i.e., mean streamwise velocity varies only along the wall-normal direction; thus, the simulations were performed using only two points in the streamwise and spanwise direction.
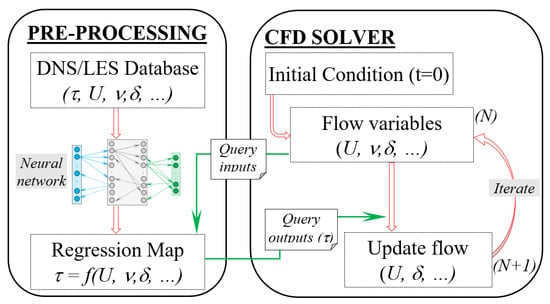
Figure 9.
Schematic diagram demonstrating coupling between machine learning turbulence model with a CFD solver.
4.1. Steady Plane Channel Flow
The ML trained turbulent shear stress response surface (generated in previous section) was used in the solution of the boundary layer equation (Equation (11)). The equations were solved using a domain y = [−1,1] with no-slip boundary condition (u = 0) at y = ±1. The simulations were performed using 49 (coarse), 65 (medium), and 97 (fine) grid points. Two sets of simulations were performed for this case. For the first set, the simulations were started from a converged channel flow RANS solution obtained using one-equation model, and the second set of simulations were started from an ill-conditioned velocity field. The DDML and PIML model simulations were performed using input feature set (as shown in Equation (21)). Further for the DDML simulations ML-3 and ML-4 weighting which provided the best predictions for apriori tests were considered.
Figure 10a shows solution convergence on all the three grids obtained using DDML when solution is started from RANS solution. The convergence time history shows a kink in residual early-on in the simulation, but eventually solution shows steady convergence. The convergence is faster for the fine grid and slowest for the coarse grid. On the coarse grid the residual converges to around 2 × 10−6. Whereas for both medium and fine grid simulations, the residual keep dropping even below 1.2 × 10−6 after 30 thousand (K) pseudo timestep iterations. The PIML results in Figure 10b shows a similar convergence.
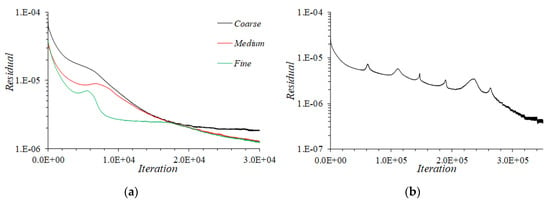
Figure 10.
(a) Convergence of DDML (input feature set and ML-3 weighting) turbulence model simulation on coarse, medium, and fine grids for simulations started from converged one-equation RANS results. (b) Convergence of PIML turbulence model simulation on coarse grid for simulation started from ill-conditioned initial condition . The abscissa title “iterations” refers to pseudo timestep level during the solution of the governing equations.
Figure 11 compares the results obtained using DDML and PIML (after 30K pseudo timesteps) with DNS and RANS results. Among the DDML models, the model obtained using ML-4 weighting performed better than those obtained using ML-3. This is in contrast to the apriori tests, where ML-3 performed better than ML-4. Note that the one-equation model underpredicts the velocity at the center compared to the DNS, and both the DDML and PIML models resolve the issue. The DDML model predictions improve with grid refinement, whereas the largest improvement is obtained in between coarse and medium grids. However, the results show oscillation near the peak, which is clearly evident in the turbulent and shear stress predictions and more prominent for the fine grid predictions. The oscillations suggest that the “query output” jumps between the database curves. For the boundary layer equations, one of the physical constraints is the shear stress must satisfy C1 continuity, i.e., both stress and its derivative are continuous in space (i.e., along y direction). Node/point-based queries are definitely not satisfying this constraint, which is probably the cause of the oscillations.
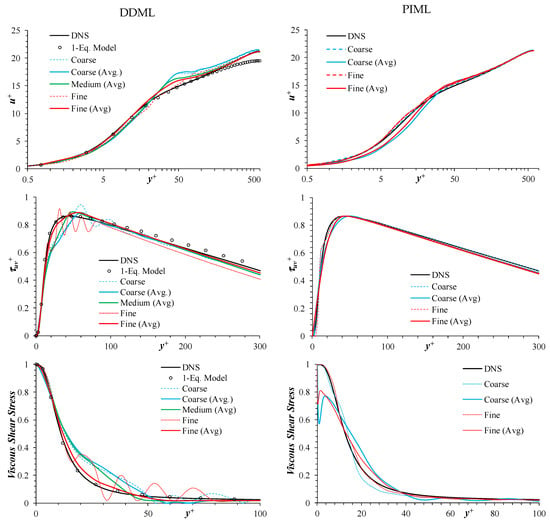
Figure 11.
Predictions of mean velocity (top row), turbulent (middle row) and viscous (bottom row) shear stresses for Reτ = 590 obtained using DDML (left column) and PIML (right column) using input feature set . The DDML used ML-3 weighting. Simulations were started from an initial velocity profile obtained from one-equation RANS model. Results are compared with DNS and one-equation RANS (1-Equation Model) results.
To resolve the stress oscillation issue in the DDML model predictions, solution smoothness was enforced by implementing region-based query, i.e., use averaged output for the input parameter sets at the node and its two neighboring nodes, i.e.,
As shown in Figure 11, the above averaging approach helps get rid of oscillations, and the results improve with grid refinement consistent with grid convergence.
The PIML model predictions show only marginal improvement with grid refinement, and the results do not show oscillations similar to the DDML model. Further, when averaging was applied it significantly deteriorated the performance of the model. In general, the PIML model performs better than the DDML especially in the lower log-layer region, i.e., y+ ~ 30 to 40.
In the next test set, the simulations were started from ill-conditioned initial condition profile:
This profile is much steeper than that of the turbulent boundary layer, as shown in Figure 12 (It = 0 plot), and the associated set of input features are not expected to be present in the DNS/LES database. Thus, the model operates in extrapolation mode. As shown in Figure 12a, the DDML model predictions converge to the correct sub-layer and log-layer profiles, but shows significant differences in the buffer- and lower log-layer (20 ≤ y+ < 80). A good prediction of the sub- and log-layer is very encouraging, and suggests that the extrapolation issue can be addressed by incorporating physics constraints during query process, such that the query recognizes that the inputs are out of bound of the database and provides a better educated guess of the output. As shown in Figure 12b, the PIML model converges slowly (as shown in the convergence plot in Figure 10b) to the DNS profile. This suggest that a well-trained machine learned model can converge to the correct solution.
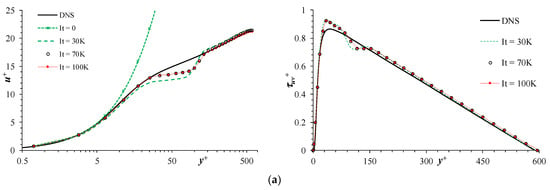
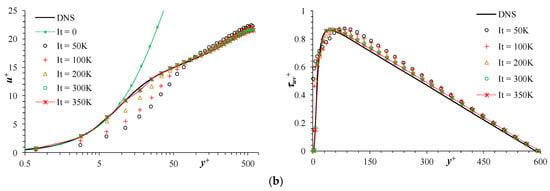
Figure 12.
Predictions of mean velocity (left panel) and turbulent shear stress (right column) for Reτ = 590 obtained using (a) DDML and (b) PIML turbulence models. The simulations were started from ill-posed initial flow condition.
4.2. Oscillating Plane Channel Flow
Three sets of simulations were performed for this case using 65 grid points in the wall-normal direction. The simulations were performed using the DDML model trained using input feature set shown in Equation (24), and using 10% of the datasets (i.e., either 10 points or 10% of each cluster). For set #1, the DDML model was used in apriori mode, i.e., simulations were performed using one-equation URANS model, and the local flow predictions were used to query the regression map. For set #2, the DDML model was used in aposteriori mode, where the simulations were started from fully converged channel flow velocity profile corresponding to Reτ = 350 obtained using RANS. For set #3, both URANS and DDML simulations were started from an ill-posed initial flow condition i.e.,
The DDML model predictions from set #1 and #2 are compared with DNS and URANS predictions in Figure 13. The URANS model performs quite well for the mean flow, but predicts significantly diffused shear stress and the peak values are 9% under predicted. The largest error is obtained for the turbulent kinetic energy for which the peak values are underpredicted by 60%. The DDML model predictions (in apriori mode) show significantly better shear stress predictions than the URANS model. The predictions have errors on the order of 3–5% for the mean velocity and shear-stress, and peak TKE are overpredicted by 15%. Since the DDML model uses the velocities and derivatives predicted by the URANS model, the improved prediction by the former can be attributed to its ability to learn the non-linear correlation between the turbulent stresses and rate-of-strain. The DDML model also works very well in the aposteriori mode, and both the mean velocity, shear stress and k compare within 8% of the DNS. Note that the simulations used a (wall-normal) grid and time step size two times smaller and 10 times larger, respectively, compared to those of DNS, thus the predictions are considered reasonably accurate.
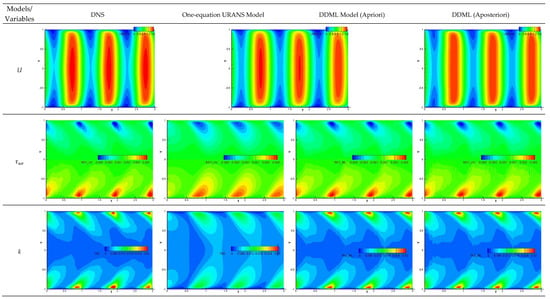
Figure 13.
Predictions of mean velocity (top row), turbulent shear stress (middle row) and turbulent kinetic energy (bottom row) for oscillating channel flow case over three pressure oscillation cycles. Results obtained using DNS (leftmost column), one-equation URANS (second column), apriori DDML predictions (third column), and aposteriori DDML (rightmost column). The URANS and DDML simulations were started from channel flow velocity profile corresponding to Reτ = 350.
As shown in Figure 14, for the simulations started from ill-posed initial flow conditions, the URANS solutions show large differences with the DNS during the early part of the simulations, but the solution slowly recovers, and the solutions for the second and third cycles are very similar to those for the earlier case. This is because the flow is primarily driven by the pressure gradient, and the flow adapts to the pressure variations. The DDML model adjusts to ill-posed initial flow condition much faster than the URANS model, and results compare very well with the DNS, and the predictions errors are similar to those of set #2.
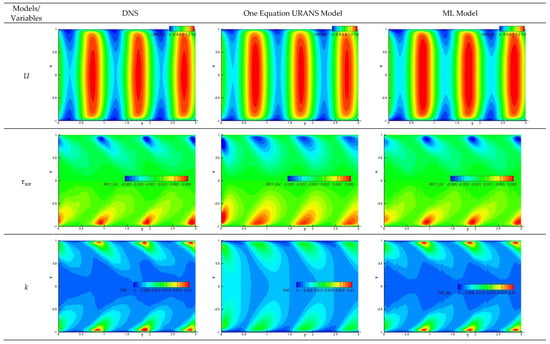
Figure 14.
Predictions of mean velocity (top row), turbulent shear stress (middle row), and turbulent kinetic energy (bottom row) for oscillating channel flow case over three pressure oscillation cycles. Results obtained using DNS (leftmost column), one-equation RANS (middle column), and aposteriori DDML (rightmost column). The URANS and DDML simulations are started from an ill-posed initial flow condition.
5. Conclusions and Future Work
This study investigates the ability of neural networks to train a stand-alone turbulence model and the effects of input parameter selection and training approach on the accuracy of the machine learned regression map. To achieve these objectives, a DNS/LES database is curated and/or developed for steady and unsteady boundary layer flows, for which the mean flow simplifies to a 1D steady and unsteady problem, respectively, and closure of the governing equations require modeling of turbulent shear stress. The database was used to train data driven and physics-informed machine learned turbulence model. For the latter, the residual in the governing equation solution was incorporated in the cost function during the model training. The model was validated for apriori and aposteriori tests, including ill-posed flow condition.
Overall, the results demonstrate that machine learning can help develop a stand-alone turbulence model. Moreover, an accurately trained model can provide grid convergent, smooth solutions, which works well in extrapolation mode, and converge to a correct solution from ill-posed flow conditions. The accuracy of the machine learned response surface depends on
- The choice of input parameters. Feature engineering was used to find the optimal input features for the neural network training. It was identified that grouping flow variables into a problem relevant parameter improves the accuracy of the model. For example, a model trained using Re based on local flow velocity and wall distance is more accurate compared to the model trained using Re based on global flow. Furthermore, higher order functions of an input variable, such as square of the rate-of-strain along with rate-of-strain, does not help in improving the accuracy of the map. However, they may be used as weighting function to reduce the overlap in the datasets; and
- How the database is weighted to minimize the overlap between the datasets. This requires a trial-and-error method to come up with an appropriate weighting function. A better way to improve the accuracy of the regression surface is to include physical constraints to the loss function during training, which is referred to as the PIML approach. However, it is not straightforward to incorporate physical constrains during the training due to issues in calculation of the derivates, such as temporal derivatives, for unsteady problem. Data clustering is also identified to be a useful tool to improve accuracy of the machine learned model and reduce computational cost, as it avoids skewness of the model towards a dominant flow feature.
Herein, machine learning was applied for cases which are very similar to the training datasets, which limits the applicability of the model, as well as does not sufficiently challenge the robustness of the machine learning approach. The ongoing work is focusing on generation of a larger database encompassing steady and unsteady boundary layer flows, including separated flow regimes. A model trained using such a database will help in development of a more generic turbulence model for boundary layer flows. It is expected that data clustering will be very helpful for training such as model due to the presence of wide range of turbulence characteristics. On a final note, the machine learned models were found to be extremely computationally expensive compared to the physics-based model (the former was around two order of magnitude more expensive). This was because of the added cost associated with ML query every iteration for every grid point. This research primarily focused on the accuracy of the model and efforts were not made to improve the efficiency of the ML model query. However, practical application of ML model would require investigation of approaches to improve the computational efficiency of run-time ML query.
Author Contributions
Conceptualization, S.B.; methodology, S.B., G.W.B., W.B. and I.D.D.; software, S.B., G.W.B. and W.B.; validation, S.B. and G.W.B.; formal analysis, S.B.; investigation, S.B. and G.W.B.; resources, I.D.D.; data curation, S.B.; writing—original draft preparation, S.B.; writing—review and editing, G.W.B., W.B. and I.D.D.; visualization, S.B. and G.W.B.; supervision, I.D.D.; project administration, I.D.D.; funding acquisition, S.B., G.W.B. and W.B. All authors have read and agreed to the published version of the manuscript.
Funding
Effort at Mississippi State University was sponsored by the Engineering Research & Development Center under Cooperative Agreement number W912HZ-17-2-0014. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the Engineering Research & Development Center or the US Government. This material is also based upon work supported by, or in part by, the Department of Defense (DoD) High Performance Computing Modernization Program (HPCMP) under User Productivity Enhancement, Technology Transfer, and Training (PET) contract #47QFSA18K0111, TO# ID04180146.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbols | |
| Q | Second invariant of rate-of-strain tensor |
| u | Local flow velocity vector |
| u′ | Turbulent velocity fluctuation vector |
| Free-stream (global) velocity (or centerline channel velocity) | |
| H | Half channel height |
| uτ | Friction velocity |
| p | Pressure |
| k | Turbulent kinetic energy |
| ε | Dissipation |
| ν | Kinematic molecular viscosity |
| νT | Turbulent eddy viscosity |
| d | Distance from the wall |
| ω | Specific dissipation, ε/k |
| y+ | Wall distance normalized by friction velocity, d |
| τw | Wall shear stress |
| ∇ | Gradient operator |
| S | Rate-of-strain tensor |
| Ω | Rotation tensor |
| |S| | Magnitude of rate-of-strain tensor, |
| |Ω| | Magnitude of rotation tensor, |
| P | Production of turbulent kinetic energy |
| Re | Reynolds number based on global flow variables, such as and geometry length |
| Ret | Turbulent Re based on distance from the wall, |
| Red | Re based on distance from wall, d/ν |
| Rel | Reynolds number based on the local velocity and distance from the wall, |
| Shear stress tensor | |
| τuv | Turbulent shear stress component in x-y plane, |
| ML | Machine Learning |
| Dot product | |
| Double dot product | |
| Terminology | |
| Database | Curated DNS/LES datasets for ML training |
| Response surface | Output from ML training |
| Input features | Input flow variables for ML |
| Output features | Flow variable for which the response surface is generated |
| Query inputs | Input variables to query the response surface |
| Query output | Output variables obtained from the query of the response surface |
| Unseen case (flow) | Geometry (or flow condition) not used during ML training |
| Apriori test | ML model is applied as a post-processing step |
| Aposteriori test | ML model is coupled with CFD solver and its prediction is used during runtime |
Appendix A

Table A1.
Literature review of machine learning approach for turbulence model augmentation.
Table A1.
Literature review of machine learning approach for turbulence model augmentation.
| Reference | Response Surface | Turbulence Model | Input Features | Training Flows | Validation Case | Comments |
|---|---|---|---|---|---|---|
| Parish and Duraisamy [9] | TKE production multiplier: (ηi) (Neural network) | k-ω RANS: | 4 features: ηi = | DNS: Plane channel flow, Reτ = 180, 550, 950, 4200 | Plane channel flow, Reτ = 2000 |
|
| Singh et al. [10] | Turbulence production multiplier: (ηi). (Neural network) | Spalart-Allmaras RANS: | 5 features: ηi = | Experiment: lift coefficient (CL) and surface pressure (CP) for wind turbine airfoils S805, S809, S814, Re = 106, 2 × 106, 3 × 106 | CL and CP for S809, α = 14°, Re = 2 × 106 | |
| He et al. [11] | Adjoint equations for solution error. β distribution to minimize error. | Velocities | Experiment: At several cross-sections in the flow. | Cylinder flow, Re = 2 × 104; Round jet, Re = 6000; Hump flow, Re = 9.4 × 105, Wall mounted cube, Re = 105 |
| |
| Yang and Xiao [12] | Correction term for the Transition time-scale correction, β; (Random forest, Neural Network) | Transition model timescale for first mode: τnt1= βτnt1 | d, streamline curvature, , Q, ∇p | DNS: NLF(1)-0416 airfoil, α = 0° and 4° | NLF(1)-0416 airfoil, α = 2° and 6°; NACA 0012, α = 3° |
|
| Ling et al. [13] | Coefficients of non-linear stress terms: (Deep Neural Network) | ; ;;;;;;; ; *Anisotropic component | Invariants of S and Ω: | DNS/LES: Duct flow, Re = 3500; Channel flow, Reτ = 590; normal (Re = 5000) and inclined (Re = 3000) jet in crossflow; Square cylinder, Re = 2000; converging-diverging channel, Reτ = 600 | Duct flow Re = 2000 Wavy channel, Re = 6850 |
|
| Wang et al. [14] | Stress prediction error: ; Δτ = τRANS − τDNS/LES (Random forest regression) | k-ε RANS model: τRANS + Δτ() | 10 features : Q, k, , , , k/ε, , , streamline curvature etc. | DNS: Duct flow, Re = 2200, 2600 and 2900 | Duct flow, Re = 3500 |
|
| DNS: Periodic hill, Re = 1400, 5600 | Periodic hill, Re = 10,595 | |||||
| DNS: Wavy channel Re = 360 LES: Curved backward facing step, Re = 13,200 | ||||||
| Wu et al. [15] | DNS: Periodic hill, Re = 1400, 2800, 5600; Curved backward facing step, Re = 13200; Converging-diverging channel, Re = 11,300; Backward facing step, Re = 4900; Wavy channel, Re = 360 | Periodic hill, Re = 10,595 | ||||
| Wang et al. [16] | k-ω RANS model: τRANS + Δτ() | 47 features based on combination of S, Ω, ∇k and ∇T | DNS: Flat-plate boundary layer for Ma = 2.5, 6 and 7.8, Reτ ~ 400 | Flat-plate boundary layer, Ma = 8 |
| |
| Wu et al. [17] | Eddy viscosity for linear stress: ; Non-linear anisotropic stress: (Random forest regression) | S,Ω, ∇k,∇p, , k, k/ε | DNS and RANS: Duct flow, Re = 2200 LES and RANS: Periodic hill—Re = 5600 | Duct flow, Re = 3500, 1.25 × 105 (Shallower) Periodic hill, Re = 5600 |
| |
| Yin et al. [18] | Stress prediction error: ; Δτ = τRANS − τDNS(Neural Network) | k-ω RANS model: τRANS + Δτ() | 47 features based on combination of S, Ω, ∇p and ∇k | DNS: Periodic hill with different steepness, L = 3.858 α +5.142, α = 0.8, 1.2, Re = 5600 | Periodic hill, α = 0.5, 1, 1.5 (Re = 5600) |
|
| Yang et al. [19] | τw = f(ηi) (Fastforward Neural Network) | Wall-modeling for Lagrangian dynamic Smagorinsky (LES) model | ηi: wall parallel velocity (u||), d, grid aspect ratio and ∇p | DNS: Channel flow Reτ = 1000 | Channel flow Re = 1000 to 1010 |
|
| Weatheritt and Sandberg [20] | Analytic function of anisotropic stress coefficients: βi; (Symbolic regression) | σ = −2νTS+2k; k-ω model | Hybrid RANS/LES: Duct flows (Re = 104, Ar = 3.3), and diffuser flow (Re = 104, Ar = 1) | Duct (Re = 104, Ar = 3.3 to 1), and diffuser (Re = 5000, 104, Ar = 1.7) |
| |
| Jian et al. [21] | Model coefficients: Cμ, bmn, Cmn, dmn (Deep neural network) | RANS: | DNS: Plane channel flow, Reτ = 1000, 1990, 2020, 4100 | Plane channel flow, Reτ = 650, 1000, 5200 |
| |
| Xie et al. [22] | Model coefficients C1 and C2 for mixed SGS model (Neural networks) | LES, subgrid stresses and heat flux | Vorticity magnitude, velocity divergence, , |S|, ∇T | DNS: Compressible isotropic turbulence, Reλ = 260, Ma = 0.4, 0.6, 0.8, 1.02 | Compressible isotropic turbulence, coarser grids |
|

Table A2.
Literature review of machine learning approach for stand-alone turbulence model.
Table A2.
Literature review of machine learning approach for stand-alone turbulence model.
| Reference | Response Surface | Turbulence Model | Input Features | Training Flows | Validation Case | Comments |
|---|---|---|---|---|---|---|
| Schmelzer et al. [23] | Analytic formulation of anisotropic stress; (Symbolic regression) | RANS: = f (S, , , , ) | S, Ω, k,τ | DNS: Periodic hill, Re = 1.1 × 104; Converging-diverging channel, 1.26 × 104; Curved backward-facing step 1.37 × 104 | Periodic hill, Re = 3.7 × 104 |
|
| Fang et al. [24] | Shear stress: τuv (Deep neural network) | RANS, τuv | du/dy, Reτ, near-wall van-Driest damping, spatial non-locality | DNS: Channel flow, Reτ = 550, 1000, 2000, 5200 | Channel flow (unseen data) |
|
| Zhu et al. [25] | Turbulent eddy viscosity: νT; (Radial basis function neural network) | RANS: τ = νT S | U, ρ, d, d2 |Ω|, velocity direction, vorticity, Entropy, strain-rate | SA RANS: NACA0012 α = 0, 10, 15, Ma = 0.15, Re = 3 × 106; RAE2822 α = 2.8, Ma = 0.73 and 0.75, Re = 6.2–6.5 × 106 | Airfoil flow different α |
|
| King et al. [26] | Stress tensor τ | LES, subgrid stresses τ | U, p, filter width, resolved rate-of-strain | DNS: Isotropic and sheared turbulence | Isotropic and sheared turbulence on coarse grids |
|
| Gambara and Hattori [27] | Stress tensor τ (Feedforward neural network) | LES, subgrid stresses τ | Different sets: S, d; S, Ω, d; ∇u, d; ∇u | DNS: Channel flow, Reτ = 180, 400, 600 and 800 | Channel flows for unseen flow conditions. |
|
| Zhou et al. [28] | ∇u, Δ (filter width) | DNS: Isotropic decaying turbulence, Reλ = 129 and 302 | Isotropic decaying turbulence, Reλ = 205 |
| ||
| Yuan et al. [29] | Stress tensor τ (Deconvolutional neural network) | LES, subgrid stresses τ | Filtered velocity | DNS: Isotropic decaying turbulence, Reλ = 252 | Isotropic decaying turbulence, Reλ = 252 |
|
| Maulik et al. [30] | Subgrid term π (Artificial neural network) | LES, Subgrid term π | Vorticity, streamfunction, rate-of-strain, vorticity gradient | DNS: Decaying 2D turbulence, Re = 3.2 × 104, 6.4 × 104 | Decaying 2D turbulence |
|

Table A3.
Channel and flat-plate boundary layer database curated for ML model training.
Table A3.
Channel and flat-plate boundary layer database curated for ML model training.
| Case | Reference | Flow Conditions | #Points | Distribution of Data Points | |||
|---|---|---|---|---|---|---|---|
| Reτ | Rec | Sublayer, y+ < 6 | Buffer Layer, 6 ≤ y+ ≤ 40 | Log-Layer, y+ > 40 | |||
| Channel Flow (DNS) | |||||||
| 1 | Iwamoto et al. [39] | 109.4 | 1918 | 65 | 13 | 22 | 29 |
| 2 | 191.8 | 3345.5 | 65 | 6 | 19 | 39 | |
| 3 | 150.18 | 2681.082 | 73 | 13 | 21 | 38 | |
| 4 | 297.9 | 5788.15 | 193 | 24 | 40 | 128 | |
| 5 | 395.76 | 7988.02 | 257 | 28 | 45 | 183 | |
| 6 | 642.54 | 13843.3 | 193 | 16 | 27 | 149 | |
| 7 | Alamo and Jimenez [40] | 186.34 | 3406.97 | 49 | 7 | 13 | 28 |
| 8 | Moser et al. [41] | 180.56 | 3298.5 | 96 | 17 | 25 | 53 |
| 9 | 392.24 | 7896.97 | 129 | 14 | 23 | 91 | |
| 10 | 587.19 | 12,485.42 | 129 | 11 | 19 | 98 | |
| 11 | Lee and Moser [42] | 541.232 | 11,365.96 | 192 | 8 | 41 | 142 |
| 12 | Alamo and Jimenez [40] | 546.74 | 11,476.1 | 129 | 12 | 19 | 97 |
| 13 | 933.96 | 20,962.51 | 193 | 13 | 22 | 157 | |
| 14 | Abe et al. [43] | 1016.36 | 23,433.9 | 224 | 15 | 30 | 179 |
| 15 | Lee and Moser [42] | 997.4 | 22,534.1 | 256 | 20 | 28 | 207 |
| 16 | 1990.64 | 48,563.2 | 384 | 21 | 30 | 332 | |
| 17 | Hoyas and Jimenez [44] | 2004.3 | 48,683.87 | 317 | 8 | 17 | 291 |
| 18 | Bernardini et al. [45] | 994.7 | 22,292.1 | 192 | 13 | 22 | 157 |
| 19 | 2017.4 | 48621.8 | 384 | 19 | 30 | 335 | |
| 20 | 4072.6 | 105,702.4 | 512 | 18 | 28 | 466 | |
| 21 | Lee and Moser [42] | 5180.73 | 137,679.2 | 768 | 13 | 32 | 722 |
| Flat-plate (DNS) | |||||||
| Schlatter and Orlu [46] | Reθ | Reτ | #Points | Sublayer, y+ < 6 | Buffer layer, 6 ≤ y+ ≤ 40 | Log-layer, y+ > 40 | |
| 22 | 670 | 252.2550 | 513 | 13 | 19 | 481 | |
| 23 | 1000 | 359.3794 | 13 | 20 | 480 | ||
| 24 | 1410 | 492.2115 | 13 | 20 | 480 | ||
| 25 | 2000 | 671.1240 | 513 | 13 | 21 | 479 | |
| 26 | 3030 | 974.1849 | 14 | 21 | 478 | ||
| 27 | 3270 | 1043.4272 | 14 | 21 | 478 | ||
| 28 | 3630 | 1145.1699 | 14 | 21 | 478 | ||
| 29 | 3970 | 1244.7742 | 14 | 22 | 477 | ||
| 30 | 4060 | 1271.5350 | 14 | 22 | 478 | ||
| 31 | Jimenesz et al. [47] | 1100 | 445.4685 | 345 | 10 | 19 | 316 |
| 32 | 1551 | 577.7820 | 10 | 20 | 315 | ||
| 33 | 1968 | 690.4122 | 10 | 21 | 314 | ||
| 34 | Sillero et al. [48] | 4000 | 1306.9373 | 535 | 10 | 19 | 506 |
| 35 | 4060 | 1271.5350 | 14 | 22 | 499 | ||
| 36 | 4500 | 1437.0660 | 10 | 19 | 506 | ||
| 37 | 5000 | 1571.1952 | 14 | 19 | 502 | ||
| 38 | 6000 | 1847.6544 | 10 | 19 | 502 | ||
| 39 | 6500 | 1989.4720 | 10 | 19 | 502 | ||
| Flat-plate (LES) | |||||||
| Reθ | Reτ | #Points | Sublayer, y+ ≤ 6 | Buffer layer, 7 ≤ y+ ≤ 40 | Log-layer, y+ >40 | ||
| 40 | Schlatter et al. [49] | 670 | 257.1964 | 385 | 10 | 14 | 361 |
| 41 | 1000 | 359.5164 | 9 | 14 | 362 | ||
| 42 | 1410 | 491.7486 | 10 | 15 | 360 | ||
| 43 | 2150 | 721.5341 | 10 | 14 | 361 | ||
| 44 | 2560 | 839.5576 | 10 | 16 | 359 | ||
| 45 | 3660 | 1162.2723 | 11 | 16 | 358 | ||
| 46 | 4100 | 1286.7014 | 11 | 16 | 358 | ||
| 47 | Eitel-Amor et al. [50] | 5000 | 1367.3586 | 512 | 10 | 15 | 487 |
| 48 | 6000 | 1561.062 | 10 | 15 | 487 | ||
| 49 | 7000 | 1750.5198 | 10 | 16 | 486 | ||
| 50 | 8000 | 1937.3113 | 10 | 16 | 486 | ||
| 51 | 9000 | 2118.0861 | 10 | 16 | 486 | ||
| 52 | 10000 | 2299.2119 | 10 | 16 | 486 | ||
| 53 | 11000 | 2478.9901 | 10 | 18 | 486 | ||
| Total | 19,919 | 670 (3.4%) | 1134 (5.7%) | 18,115 (90.9%) | |||

Table A4.
Flow parameters for oscillating channel flow DNS. The non-dimensional quantities are highlighted in yellow.
Table A4.
Flow parameters for oscillating channel flow DNS. The non-dimensional quantities are highlighted in yellow.
| Flow Parameters | High Frequency | Med. Frequency | Low Frequency |
|---|---|---|---|
| Baseline flow Reτ,0 | 350 | ||
| Baseline flow Rec,0 | 7250 | ||
| Baseline flow centerline velocity Uc | 1 | ||
| Half channel height H | 1 | ||
| Kinematic viscosity ν | 1.38 × 10−4 | ||
| Domain size | 3π × 2 × π | ||
| Grid | 192 × 129 × 192 | ||
| Baseline flow | = 0.002331 | ||
| Density ρ | 1 | ||
| Baseline flow uτ,0 | 0.048276 | ||
| α | 200 | 50 | 8 |
| 0.4662 | 0.11655 | 0.01865 | |
| Non-dimensional pulse frequency | 0.04 | 0.01 | 0.0016 |
| Pulse frequency ω | 0.67565 | 0.16891 | 0.02703 |
| Boundary layer thickness | 0.2021 | 0.4042 | 1.0106 |
| 7.071 | 14.142 | 35.355 | |
| 100 | 200 | 500 | |
| 0.03296 | |||
| Time step size (Δt) | 0.0002325 | 0.00093 | 0.000969 |
| Timesteps per period (2π/ωΔt) | 40000 | 40,000 | 240,000 |
| Pressure pulse | |||
References
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence Modeling in the Age of Data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Milano, M.; Koumoutsakos, P. Neural network modeling for near wall turbulent flow. J. Comput. Phys. 2002, 182, 1–26. [Google Scholar] [CrossRef]
- Hocevar, M.; Sirok, B.; Grabec, I. A turbulent wake estimation using radial basis function neural networks. Flow Turbul. Combust. 2005, 74, 291–308. [Google Scholar] [CrossRef]
- Jin, X.W.; Cheng, P.; Chen, W.L.; Li, H. Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder. Phys. Fluids 2018, 30, 047105. [Google Scholar] [CrossRef]
- Obiols-Sales, O.; Vishnu, A.; Chandramowlishwaran, A. CFDNet: A Deep Learning-Based Accelerator for Fluid Simulations. In Proceedings of the 34th ACM International Conference on Supercomputing, Barcelona, Spain, 29 June–2 July 2020. [Google Scholar]
- Edeling, W.N.; Cinnella, P.; Dwight, R.P.; Bijl, H. Bayesian estimates of parameter variability in the k-ε turbulence model. J. Comput. Phys. 2014, 258, 73–94. [Google Scholar] [CrossRef]
- Ling, J.; Templeton, J. Evaluation of machine learning algorithms for prediction of regions of high Reynolds averaged Navier Stokes uncertainty. Phys. Fluids 2015, 27, 085103. [Google Scholar] [CrossRef]
- Parish, E.J.; Duraisamy, K. A paradigm for data-driven predictive modeling using field inversion and machine learning. J. Comput. Phys. 2016, 305, 758–774. [Google Scholar] [CrossRef]
- Singh, A.P.; Medida, S.; Duraisamy, K. Machine-learning-augmented predictive modeling of turbulent separated flows over airfoils. AIAA J. 2017, 55, 2215–2227. [Google Scholar] [CrossRef]
- He, C.X.; Liu, Y.; Gan, L. A data assimilation model for turbulent flows using continuous adjoint formulation. Phys. Fluids 2018, 30, 105108. [Google Scholar] [CrossRef]
- Yang, M.; Xiao, Z. Improving the k-ω-γ-Ar transition model by the field inversion and machine learning framework. Phys. Fluids 2020, 32, 064101. [Google Scholar]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Wang, J.X.; Wu, J.L.; Xiao, H. Physics informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Phys. Rev. Fluids 2017, 2, 034603. [Google Scholar] [CrossRef]
- Wu, J.L.; Wang, J.X.; Xiao, H.; Ling, L. A priori assessment of prediction confidence for data-driven turbulence modeling. Flow, Turbul. Combust. 2017, 99, 25–46. [Google Scholar] [CrossRef]
- Wang, J.X.; Huang, J.; Duan, L.; Xiao, H. Prediction of Reynolds stresses in high-Mach-number turbulent boundary layers using physics-informed machine learning. Theor. Comput. Fluid Dyn. 2019, 33, 1–19. [Google Scholar] [CrossRef]
- Wu, J.L.; Xiao, H.; Paterson, E. Physics-Informed Machine Learning Approach for Augmenting Turbulence Models: A Comprehensive Framework. Phys. Rev. Fluids 2018, 3, 074602. [Google Scholar] [CrossRef]
- Yin, Y.; Yang, P.; Zhang, Y.; Chen, H.; Fu, S. Feature selection and processing of turbulence modeling based on an artificial neural network. Phys. Fluids 2020, 32, 105117. [Google Scholar] [CrossRef]
- Yang, X.I.A.; Zafar, S.; Wang, J.X.; Xiao, H. Predictive large-eddy-simulation wall modeling via physics-informed neural networks. Phys. Rev. Fluids 2019, 4, 034602. [Google Scholar] [CrossRef]
- Weatheritt, J.; Sandberg, R.D. The development of algebraic stress models using a novel evolutionary algorithm. Int. J. Heat Fluid Flow 2017, 68, 298–318. [Google Scholar] [CrossRef]
- Jiang, C.; Mi, J.; Laima, S.; Li, H. A Novel Algebraic Stress Model with Machine-Learning-Assisted Parameterization Energies. Energies 2020, 13, 258. [Google Scholar] [CrossRef]
- Xie, C.; Wang, J.; Li, H.; Wan, M.; Chen, S. Artificial neural network mixed model for large eddy simulation of compressible isotropic turbulence. Phys. Fluids 2019, 31, 085112. [Google Scholar]
- Schmelzer, M.; Dwight, R.P.; Cinnella, P. Discovery of algebraic Reynolds stress models using sparse symbolic regression. Flow Turbul. Combust. 2020, 104, 579–603. [Google Scholar] [CrossRef]
- Fang, R.; Sondak, D.; Protopapas, P.; Succi, S. Neural network models for the anisotropic Reynolds stress tensor in turbulent channel flow. J. Turbul. 2020, 21, 9–10. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, W.; Kou, J.; Liu, Y. Machine learning methods for turbulence modeling in subsonic flows around airfoils. Phys. Fluids 2019, 31, 015105. [Google Scholar] [CrossRef]
- King, R.N.; Hamlington, P.E.; Dahm, W.J.A. Autonomic closure for turbulence simulations. Phys. Rev. E 2016, 93, 031301. [Google Scholar] [CrossRef] [PubMed]
- Gamabara, M.; Hattori, Y. Searching for turbulence models by artificial neural network. Phys. Rev. Fluids 2017, 2, 054604. [Google Scholar] [CrossRef]
- Zhou, G.; He, G.; Wang, S.; Jin, G. Subgrid-scale model for large-eddy simulation of isotropic turbulent flows using an artificial neural network. Comput. Fluids 2019, 195, 104319. [Google Scholar] [CrossRef]
- Yuan, Z.; Xie, C.; Wang, J. Deconvolutional artificial neural network models for large eddy simulation of turbulence. Phys. Fluids 2020, 32, 115106. [Google Scholar] [CrossRef]
- Maulik, R.; San, O.; Rasheed, A.; Vedula, P. Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 2019, 858, 122–144. [Google Scholar] [CrossRef]
- Nathan, K.J. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar]
- Bhushan, S.; Burgreen, G.W.; Martinez, D.; Brewer, W. Machine Learning for Turbulence Modeling and Predictions. In Proceedings of the ASME 2020 Fluids Engineering Division Summer Meeting FEDSM2020, Orlando, FL, USA, 12–16 July 2020. [Google Scholar]
- Bhushan, S.; Burgreen, G.W.; Bowman, J.; Dettwiller, I.; Brewer, W. Predictions of Steady and Unsteady Flows using Machine Learned Surrogate Models. In Proceedings of the 2020 IEEE/ACM Workshop on Machine Learning in High Performance Computing Environments (MLHPC) and Workshop on Artificial Intelligence and Machine Learning for Scientific Applications (AI4S), Supercomputing 2020, Online Conference, 12 November 2020. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.; Kim, H.; Joe, H.; Kim, H.-G. Multi-channel PINN: Investigating scalable and transferable neural networks for drug discovery. J. Cheminform. 2019, 11, 46. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Maziar, R.; Paris Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar]
- Warsi, Z.U.A. Fluid Dynamics: Theoretical and Computational Approaches; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Iwamoto, K.; Kasagi, N.; Suzuki, Y. Direct Numerical Simulation of Turbulent channel Flow at Reτ = 2320. In Proceedings of the 6th Symposium Smart Control of Turbulence, Tokyo, Japan, 6–9 March 2005. [Google Scholar]
- Alamo, J.C.; Jimenez, J.; Zandonade, P.; Moser, R.D. Scaling of the Energy Spectra of Turbulent Channels. J. Fluid Mech. 2004, 500, 135–144. [Google Scholar]
- Moser, R.D.; Kim, J.; Mansour, N.N. Direct Numerical Simulation of Turbulent Channel Flow Up to Reτ = 590. Phys. Fluids 1999, 11, 943–945. [Google Scholar] [CrossRef]
- Lee, M.; Moser, R.D. Direct numerical simulation of turbulent channel flow up to Reτ = 5200. J. Fluid Mech. 2015, 744, 395–415. [Google Scholar] [CrossRef]
- Abe, H.; Kawamura, H.; Matsuo, Y. Surface heat-flux fluctuations in a turbulent channel flow up to Reτ = 1020 with Pr = 0.025 and 0.71. Int. J. Heat Fluid Flow 2004, 25, 404–419. [Google Scholar] [CrossRef]
- Hoyas, S.; Jimenez, J. Scaling of the Velocity Fluctuations in Turbulent Channels up to Reτ = 2003. Phys. Fluids 2006, 18, 011702. [Google Scholar] [CrossRef]
- Bernardini, M.; Pirozzoli, S.; Orlandi, P. Velocity statistics in turbulent channel flow up to Reτ = 4000. J. Fluid Mech. 2014, 742, 171–191. [Google Scholar] [CrossRef]
- Schlatter, P.; Orlu, R. Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 2010, 659, 116–126. [Google Scholar] [CrossRef]
- Jimenez, J.; Hoyas, S.; Simens, M.P.; Mizuno, Y. Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 2010, 657, 335–360. [Google Scholar] [CrossRef]
- Sillero, J.A.; Jimenez, J.; Moser, R.D. One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to Re~2000. Phys. Fluids 2013, 25, 105102. [Google Scholar] [CrossRef]
- Schlatter, P.; Li, Q.; Brethouwer, G.; Johansson, A.V.; Henningson, D.S. Simulations of spatially evolving turbulent boundary layers up to Reθ = 4300. Int. J. Heat Fluid Flow 2010, 31, 251–261. [Google Scholar] [CrossRef]
- Eitel-Amor, G.; Örlü, R.; Schlatter, P. Simulation and validation of a spatially evolving turbulent boundary layer up to Reθ = 8300. Int. J. Heat Fluid Flow 2014, 47, 57–69. [Google Scholar] [CrossRef]
- Martinez, D.; Brewer, W.; Strelzoff, A.; Wilson, A.; Wade, D. Rotorcraft virtual sensors via deep regression. J. Parallel Distrib. Comput. 2020, 135, 114–126. [Google Scholar] [CrossRef]
- Rolnick, D.; Tegmark, M. The power of deeper networks for expressing natural functions. arXiv 2018, arXiv:1705.05502. [Google Scholar]
- Scotti, A.; Piomelli, U. Numerical Simulation of Pulsating Turbulent Channel Flow. Phys. Fluids 2001, 13, 1367–1384. [Google Scholar] [CrossRef]
- Bhushan, S.; Walters, D.K. Development of a Parallel Pseudo-Spectral Solver Using the Influence Matrix Method and Application to Boundary Layer Transition. Eng. Appl. Comput. Fluid Mech. 2014, 8, 158–177. [Google Scholar] [CrossRef]
- Bhushan, S.; Muthu, S. Performance and Error Assessment of Parallel Pseudo-Spectra Methods for Direct Numerical Simulations. Eng. Appl. Comput. Fluid Dyn. 2019, 13, 763–781. [Google Scholar]
- Jamal, T.; Bhushan, S.; Walters, D.K. Numerical Simulation of Non-Stationary Turbulent Flows using Double Exponential Dynamic Time Filtering Technique. In Proceedings of the ASME 2020 Fluids Engineering Division Summer Meeting FEDSM 2020, Orlando, FL, USA, 12–16 July 2020. [Google Scholar]
- Muthu, S.; Bhushan, S. Temporal Direct Numerical Simulation for Flat-Plate Boundary Layer Bypass Transition. J. Turbul. 2020, 21, 311–354. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).