An Integrated Approach to Adaptive Control and Supervisory Optimisation of HVAC Control Systems for Demand Response Applications
Abstract
1. Introduction
1.1. Motivation
1.2. Previous Work
1.3. Current Contributions
1.4. Structure
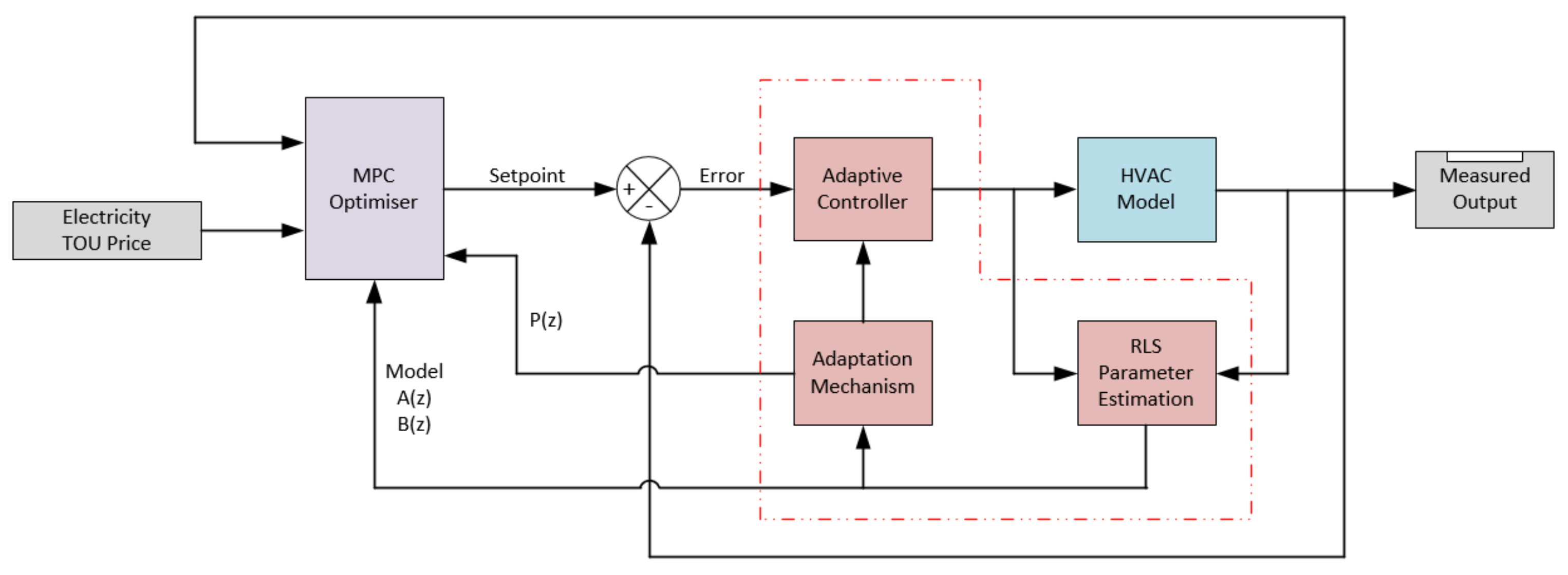
2. System Description
2.1. HVAC Process Models
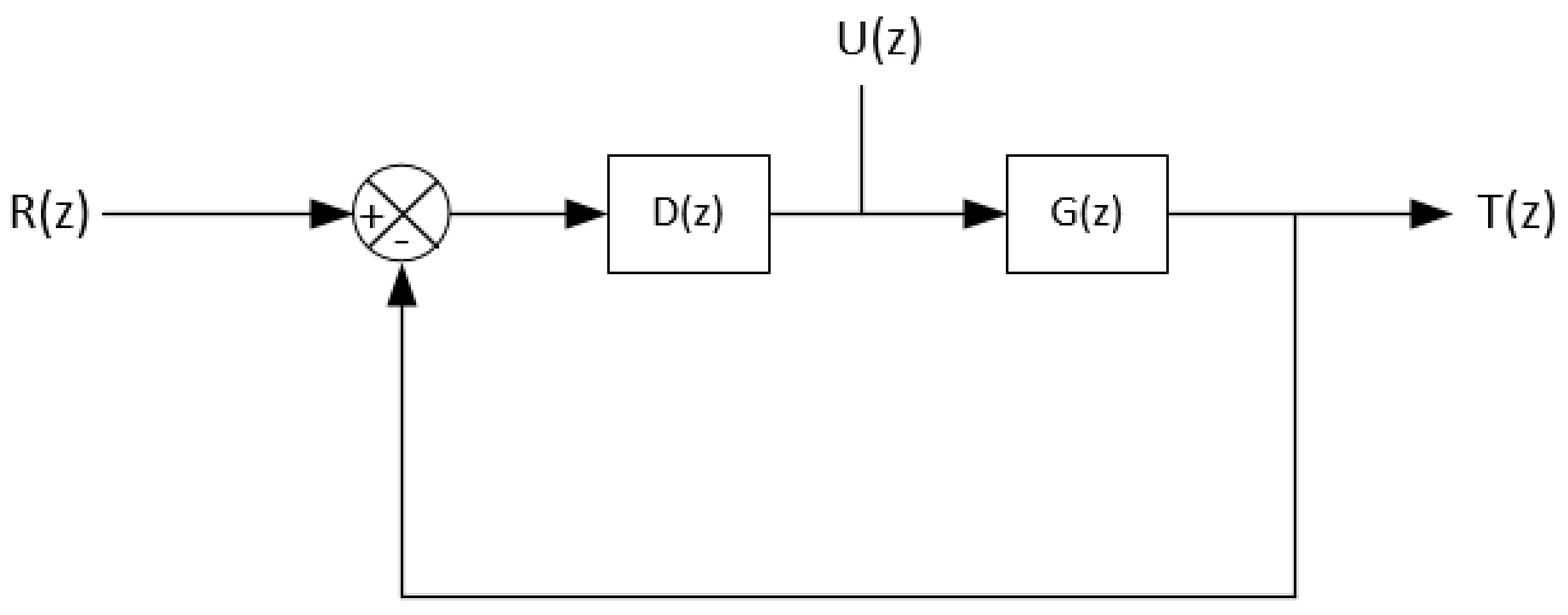
2.2. Digital Adaptive Controller
2.3. MPC Objective Function
2.4. Simplified Case
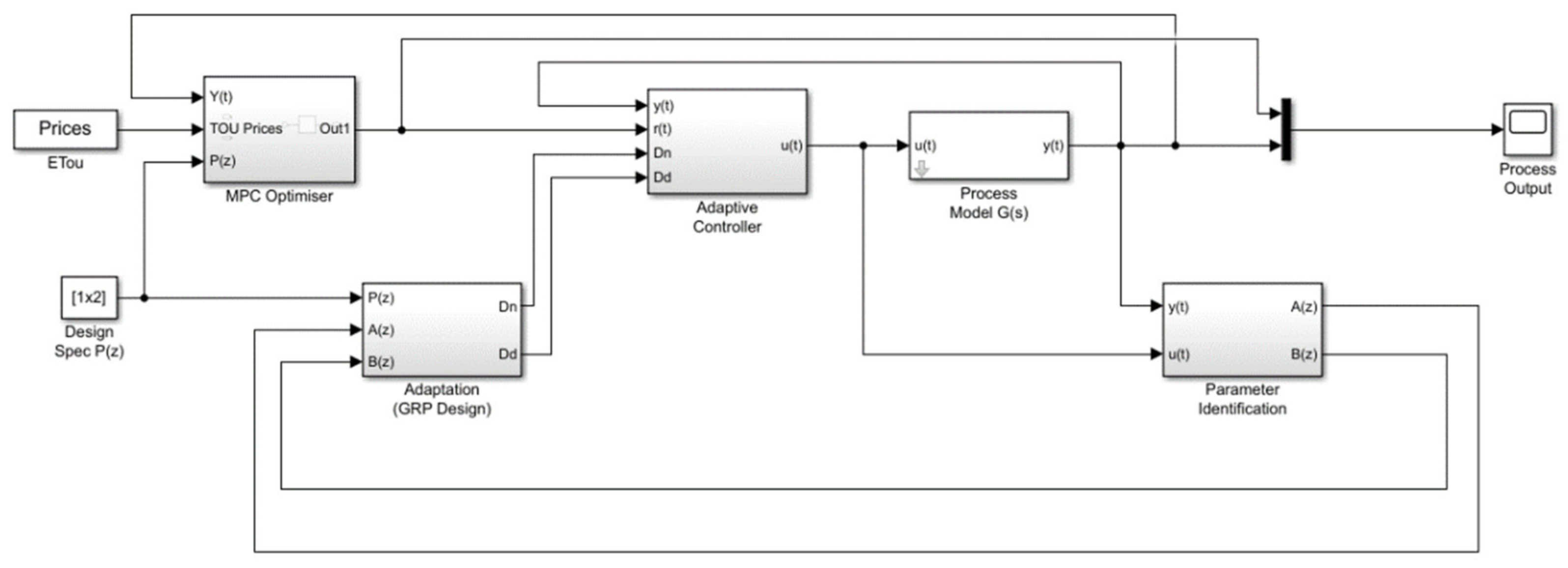
3. Implementation
Simulation Cases
4. Results and Analysis
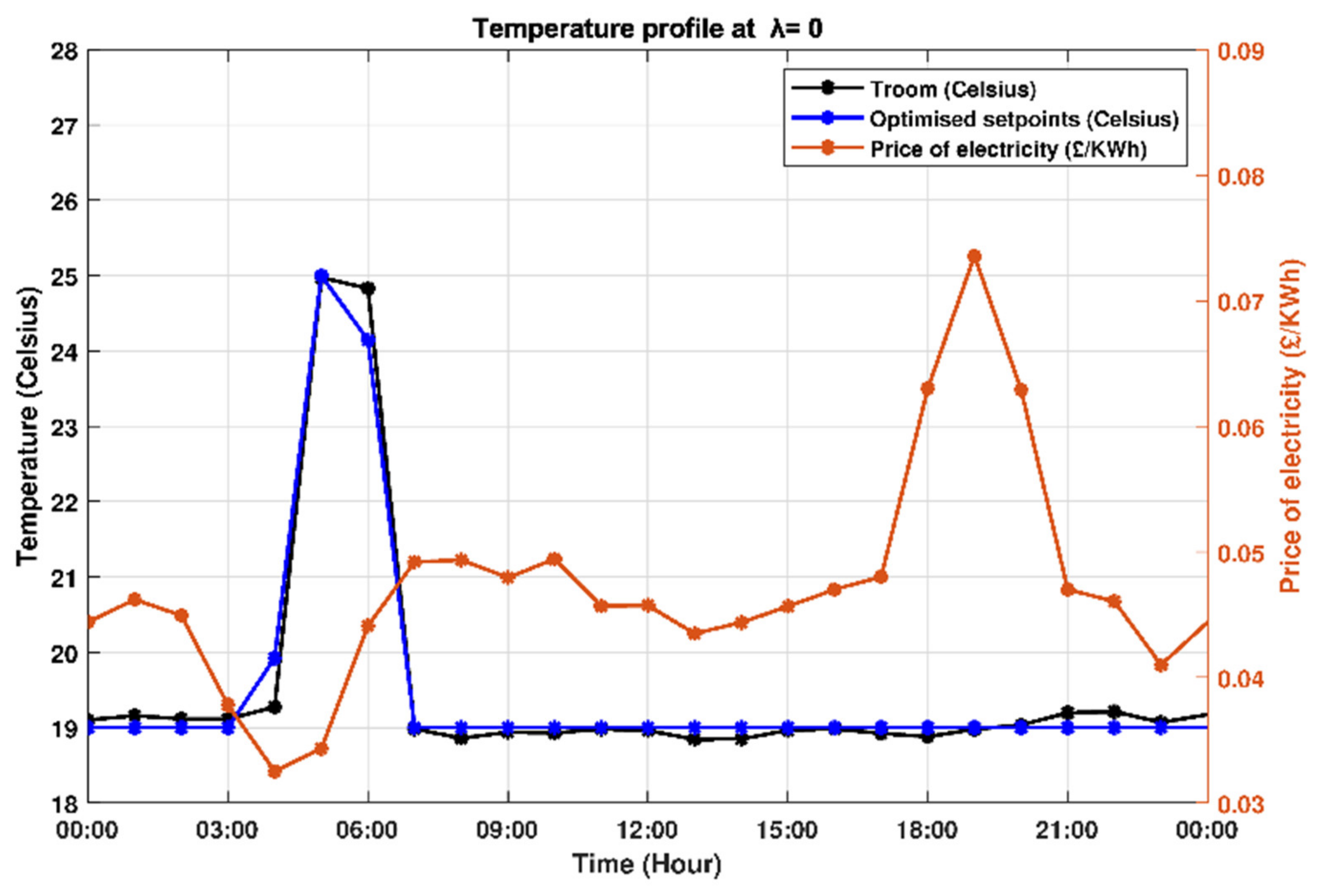
4.1. Maximum Economic Cost Saving (λ = 0)
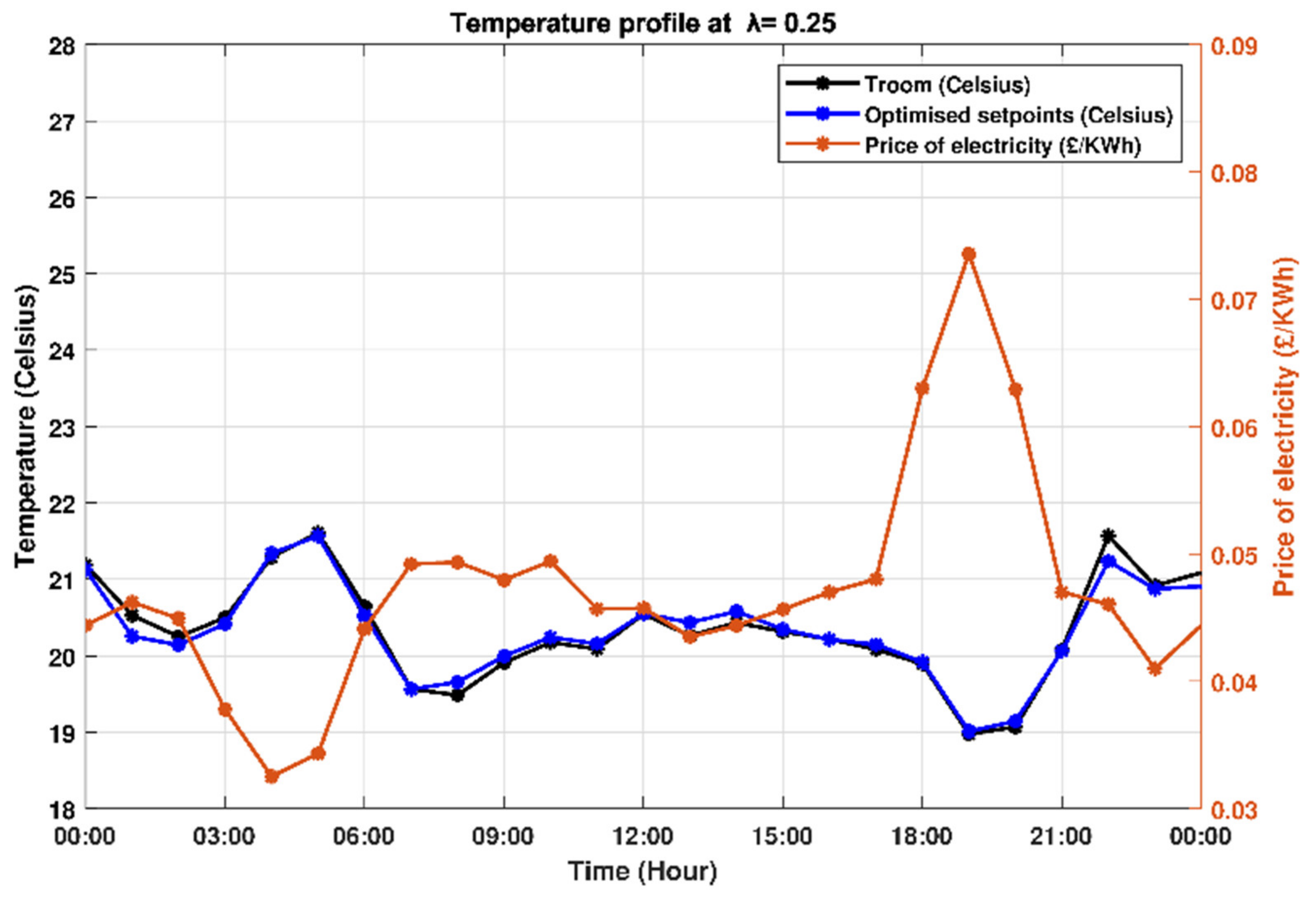
4.2. Higher Preference for Economic Cost Saving (λ = 0.25)
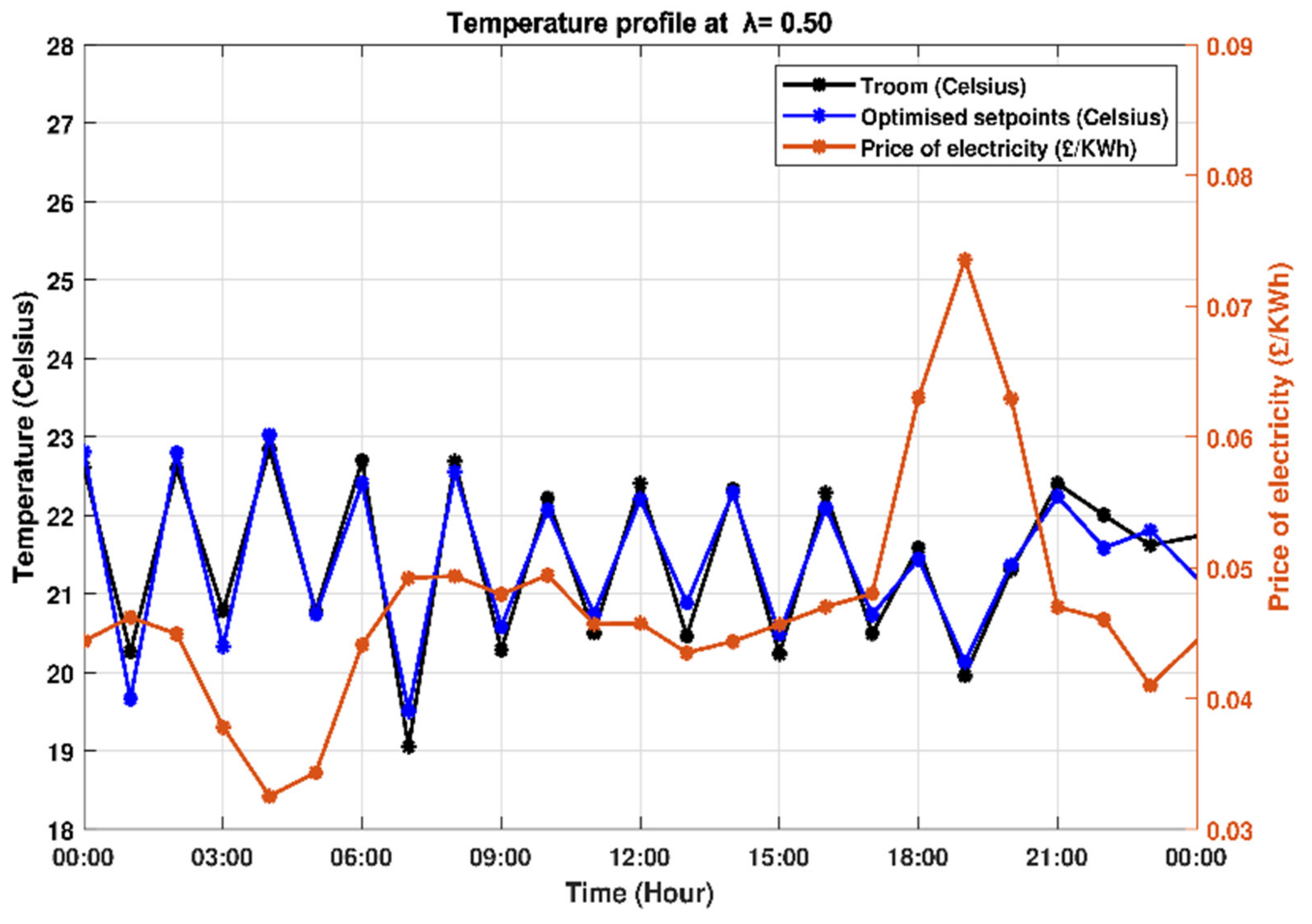
4.3. Equal Preference for Thermal Comfort and Energy Cost (λ = 0.50)
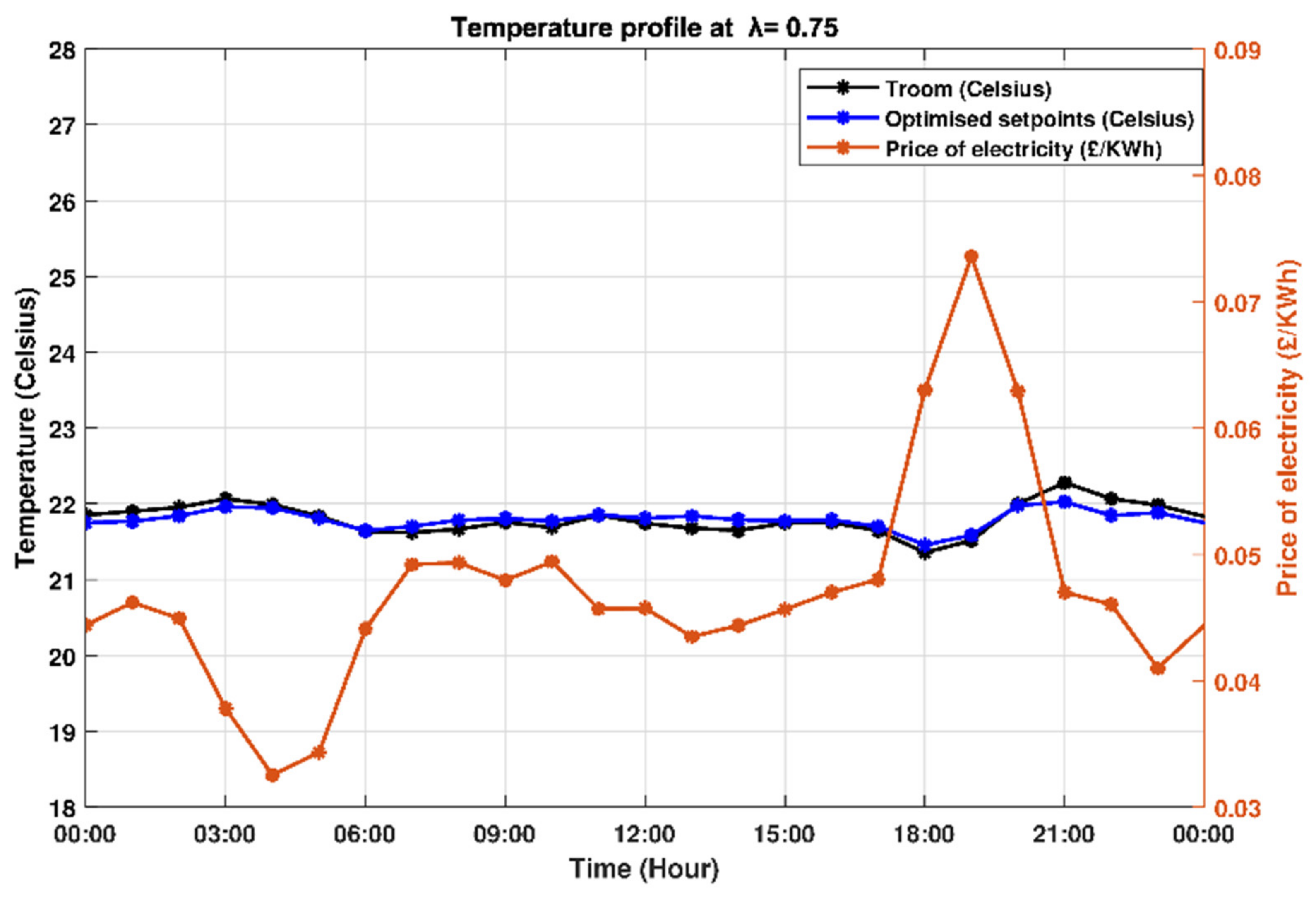
4.4. Higher Preference for Thermal Comfort (λ = 0.75)
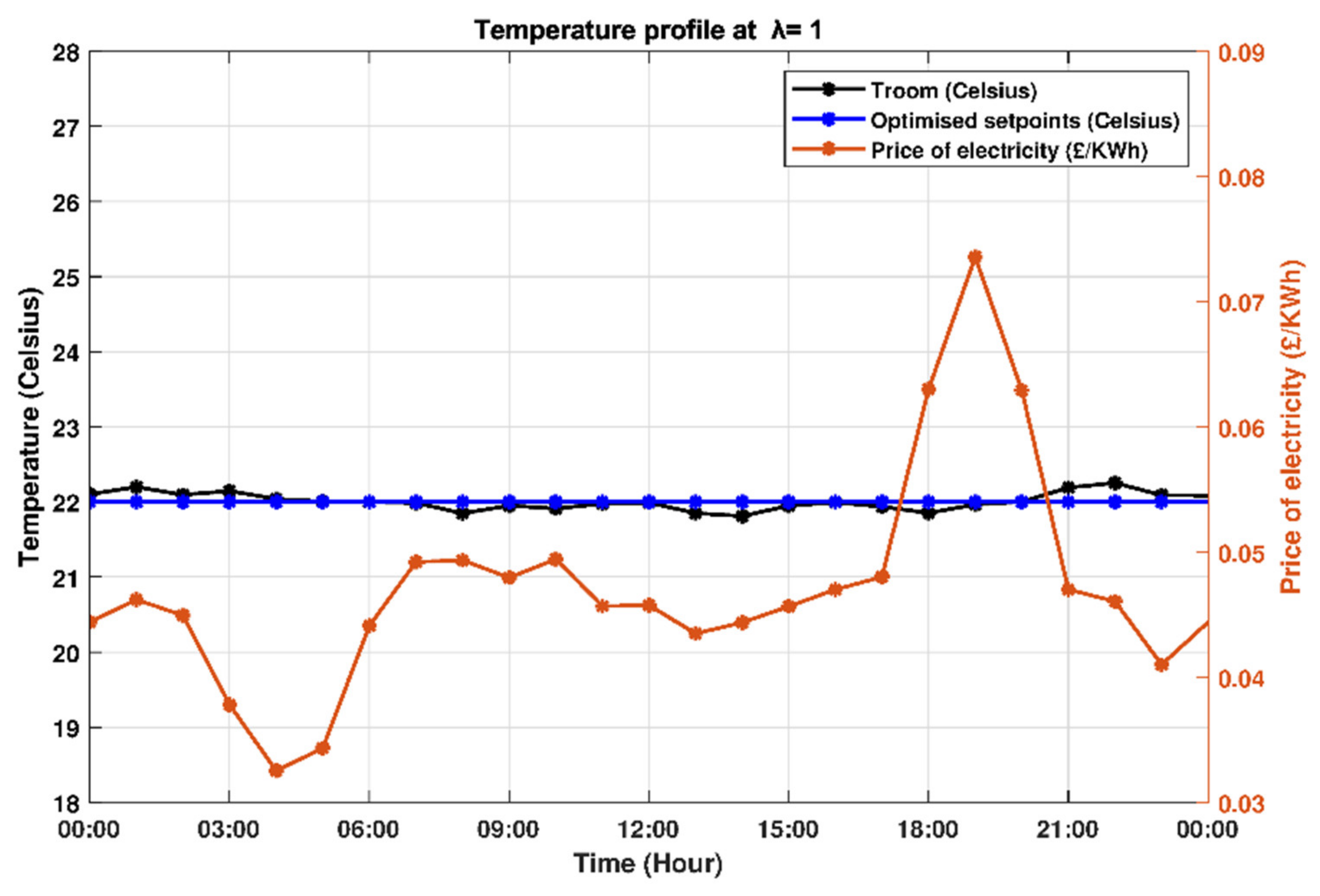
4.5. Maximum Thermal Deviation Saving (λ = 1)
5. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crosbie, T.; Short, M.; Dawood, M.; Charlesworth, R. Demand response in blocks of buildings: Opportunities and requirements. Entrep. Sustain. Issues 2017, 4, 271–281. [Google Scholar] [CrossRef]
- Pérez-Lombard, L.; Ortiz, J.; Pout, C. A review on buildings energy consumption information. Energy Build. 2008, 40, 394–398. [Google Scholar] [CrossRef]
- Costa, A.; Keane, M.M.; Torrens, J.I.; Corry, E. Building operation and energy performance: Monitoring, analysis and optimisation toolkit. Appl. Energy 2013, 101, 310–316. [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Supervisory model predictive controller (MPC) for residential HVAC systems: Implementation and experimentation on archetype sustainable house in Toronto. Energy Build. 2017, 154, 268–282. [Google Scholar] [CrossRef]
- Kang, H.J. Development of an Nearly Zero Emission Building (nZEB) Life Cycle Cost Assessment Tool for Fast Decision Making in the Early Design Phase. Energies 2017, 10, 59. [Google Scholar] [CrossRef]
- Afram, A.; Janadi-Sharaf, F. Review of modeling methods for HVAC systems. Appl. Therm. Eng. 2014, 67, 507–519. [Google Scholar] [CrossRef]
- Short, M. Control and Informatics for Demand Response and Renewables Integration. In Handbook of Smart Materials, Technologies, and Devices: Applications of Industry 4.0; Springer Nature: Basingstoke, UK, 2021. (in press)
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control systems—A review of model predictive control (MPC). Build. Environ. 2014. [Google Scholar] [CrossRef]
- Underwood, C. HVAC Control Systems: Modelling, Analysis and Design; Taylor & Francis/Spon: London, UK, 1999. [Google Scholar]
- Moradi, H.; Saffar-Avval, M.; Bakhtiari-Nejad, F. Nonlinear multivariable control and performance analysis of an air-handling unit. Energy Build. 2011. [Google Scholar] [CrossRef]
- Al-Assadi, S.A.K.; Patel, R.V.; Zaheer-uddin, M.; Verma, M.S.; Breitinger, J. Robust decentralized control of HVAC systems using -performance measures. J. Franklin Inst. 2004. [Google Scholar] [CrossRef]
- Soyguder, S.; Karakose, M.; Alli, H. Design and simulation of self-tuning PID-type fuzzy adaptive control for an expert HVAC system. Expert Syst. Appl. 2009, 36, 4566–4573. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Artificial neural networks and genetic algorithms in energy applications in buildings. Adv. Build. Energy Res. 2009, 3, 83–120. [Google Scholar] [CrossRef]
- Favre, B.; Peuportier, B. Application of dynamic programming to study load shifting in buildings. Energy Build. 2014, 82, 57–64. [Google Scholar] [CrossRef]
- Péan, T.Q.; Salom, J.; Costa-Castelló, R. Review of control strategies for improving the energy flexibility provided by heat pump systems in buildings. J. Process Control 2019, 74, 35–49. [Google Scholar] [CrossRef]
- Yoon, J.H.; Bladick, R.; Novoselac, A. Demand response for residential buildings based on dynamic price of electricity. Energy Build. 2014, 80, 531–541. [Google Scholar] [CrossRef]
- Carvalho, A.D.; Moura, P.; Vaz, G.C.; de Almeida, A.T. Ground source heat pumps as high efficient solutions for building space conditioning and for integration in smart grids. Energy Convers. Manag. 2015, 103, 991–1007. [Google Scholar] [CrossRef]
- Schibuola, L.; Scarpa, M.; Tambani, C. Demand response management by means of heat pumps controlled via real time pricing. Energy Build. 2015, 90, 15–28. [Google Scholar] [CrossRef]
- Avci, M.; Erkoc, M.; Rahmani, A.; Asfour, S. Model predictive HVAC load control in buildings using real-time electricity pricing. Energy Build. 2013, 60, 199–209. [Google Scholar] [CrossRef]
- Kajgaard, M.U.; Mogensen, J.; Wittendorff, A.; Veress, A.T.; Biegel, B. Model predictive control of domestic heat pump. In Proceedings of the 2013 American Control Conference, IEEE, Washington, DC, USA, 17–19 June 2013; pp. 2013–2018. [Google Scholar] [CrossRef]
- Široký, J.; Oldewurtel, F.; Cigler, J.; Prívara, S. Experimental analysis of model predictive control for an energy efficient building heating system. Appl. Energy 2011, 88, 3079–3087. [Google Scholar] [CrossRef]
- West, S.R.; Ward, J.K.; Wall, J. Trial results from a model predictive control and optimisation system for commercial building HVAC. Energy Build. 2014, 72, 271–279. [Google Scholar] [CrossRef]
- Short, M.; Abugchem, F. On the Jitter Sensitivity of an Adaptive Digital Controller: A Computational Simulation Study. Int. J. Eng. Technol. Innov. 2019, 9, 241–256. [Google Scholar]
- Adegbenro, A.; Short, M.; Williams, S. Development of a Digital PID-like Adaptive Controller and its Application in HVAC systems. In Proceedings of the International Conference on Innovative Applied Energy, Oxford, UK, 14–15 March 2019; Available online: https://www.researchgate.net/publication/331952706_Development_of_a_Digital_PID-like_Adaptive_Controller_and_its_Application_in_HVAC_systems (accessed on 6 April 2021).
- De Wit, C.C.; Carrillo, J. A modified EW-RLS algorithm for systems with bounded disturbances. Automatica 1990, 26, 599–606. [Google Scholar] [CrossRef]
- Cochrane, C.J.; Lenahan, P.M. Real time exponentially weighted recursive least squares adaptive signal averaging for enhancing the sensitivity of continuous wave magnetic resonance. J. Magn. Reson. 2008, 295, 17–22. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control, 2nd ed.; Springer: London, UK, 2007. [Google Scholar]
- Angione, C.; Conway, M.; Lió, P. Multiplex methods provide effective integration of multi-omic data in genome-scale models. BMC Bioinform. 2016, 17, 257–269. [Google Scholar]
- Short, M.; Rodriguez, S.; Charlesworth, R.; Crosbie, T.; Dawood, N. Optimal Dispatch of Aggregated HVAC Units for Demand Response: An Industry 4.0 Approach. Energies 2019, 12, 4320. [Google Scholar] [CrossRef]
- Bai, J.; Zhang, X. A new adaptive PI controller and its application in HVAC systems. Energy Convers. Manag. 2007, 48, 1043–1054. [Google Scholar] [CrossRef]
| Simulation Case Type | Description | Setpoint |
|---|---|---|
| Base | Fixed setpoint control | 22 °C |
| Case 1 | Rule-based thermostatic control | 22 °C or 0 °C, depending on ETOU |
| Case 2 | Supervisory MPC (at λ = 0, 0.25, 0.5, 0.75 and 1) | Varied, depending on λ |
| Case 3 | Supervisory MPC (at λ = 0.25) for different seasons | Varied, depending on λ |
| Thermal Deviation Range | Thermal Comfort |
|---|---|
| 0–1000 | Very comfortable |
| 1000–1999 | Comfortable |
| 2000–2499 | Slightly comfortable |
| 2500–2999 | Uncomfortable |
| 3000+ | Very uncomfortable |
| Simulation Case Type | Energy Consumption (KWh) | Economic Cost (£) | Thermal Deviation | Average Room Temp. (°C) | Comfortability |
|---|---|---|---|---|---|
| Base (Fixed setpoint control) | 533 | 21.87 | 75 | 21.90 | Very comfortable |
| Case 1 (RBC strategy) | 326 | 13.40 | 12,467 | 13.50 | Very uncomfortable |
| Case 2 (MPC strategy) | |||||
| λ = 0.00 | 473 | 19.43 | 4123 | 19.50 | Very uncomfortable |
| λ = 0.25 | 490 | 20.13 | 2565 | 20.20 | Uncomfortable |
| λ = 0.50 | 516 | 21.20 | 1237 | 21.30 | Comfortable |
| λ = 0.75 | 527 | 21.62 | 527 | 21.70 | Very comfortable |
| λ = 1.00 | 533 | 21.87 | 75 | 21.90 | Very comfortable |
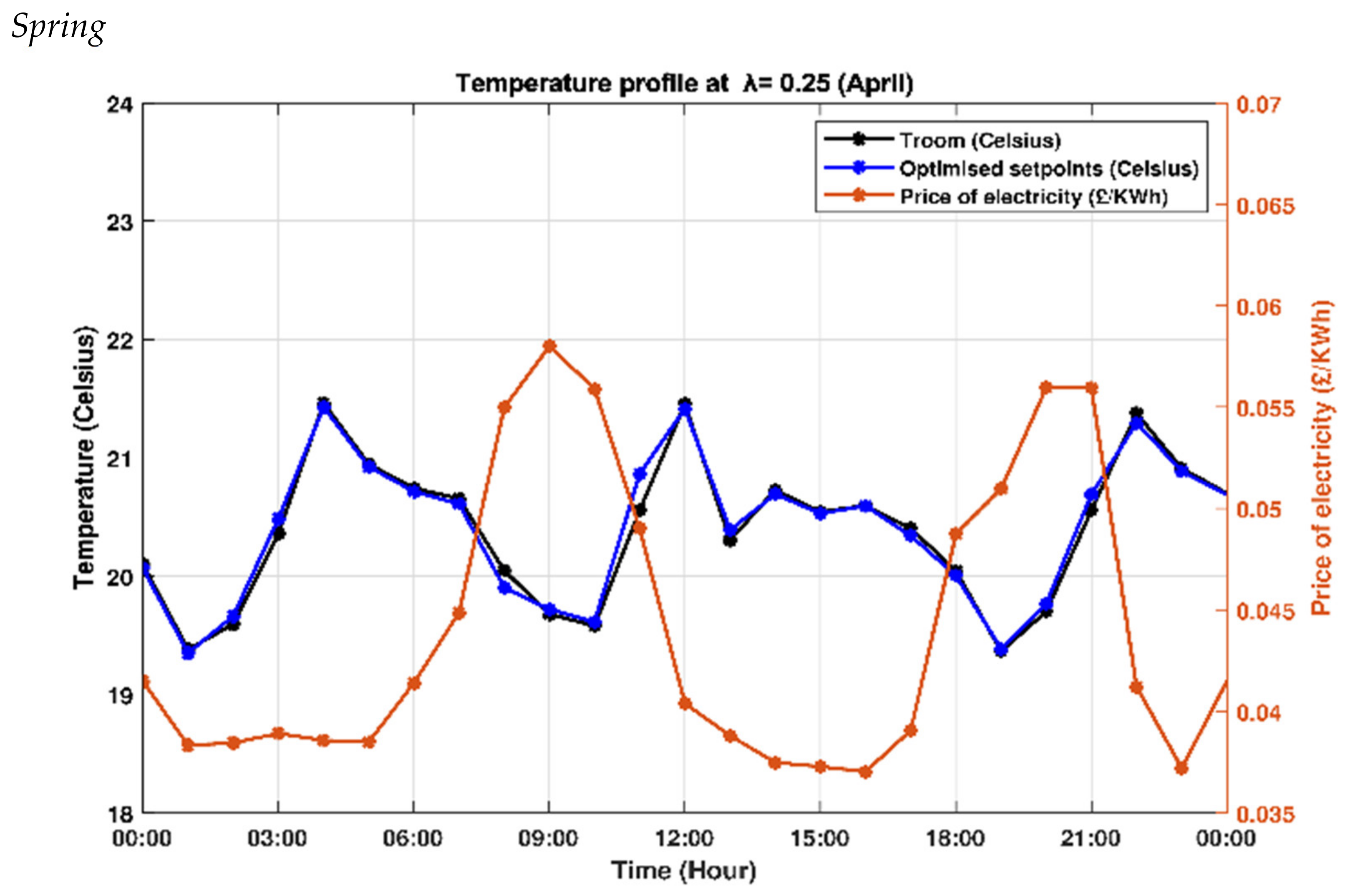
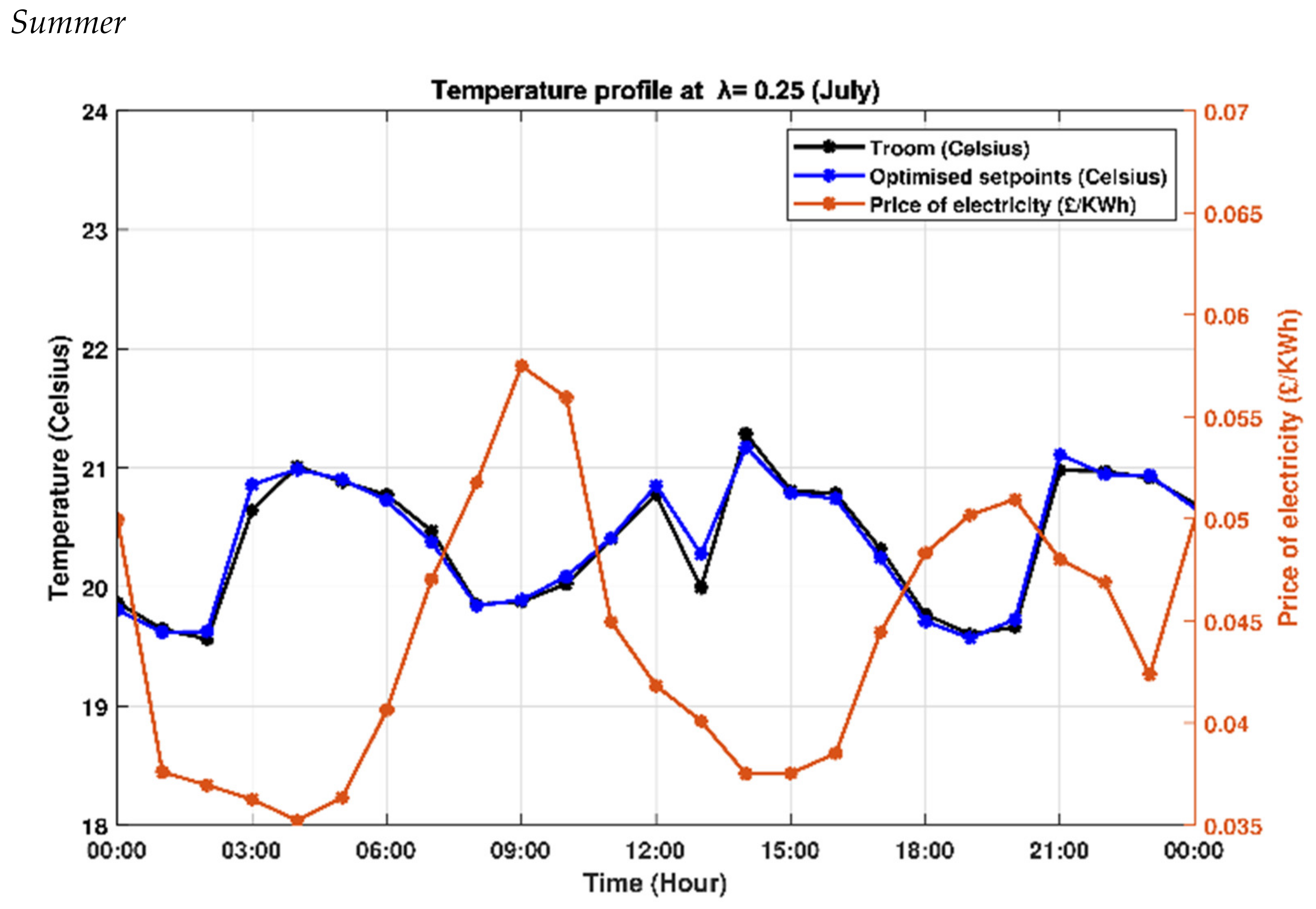
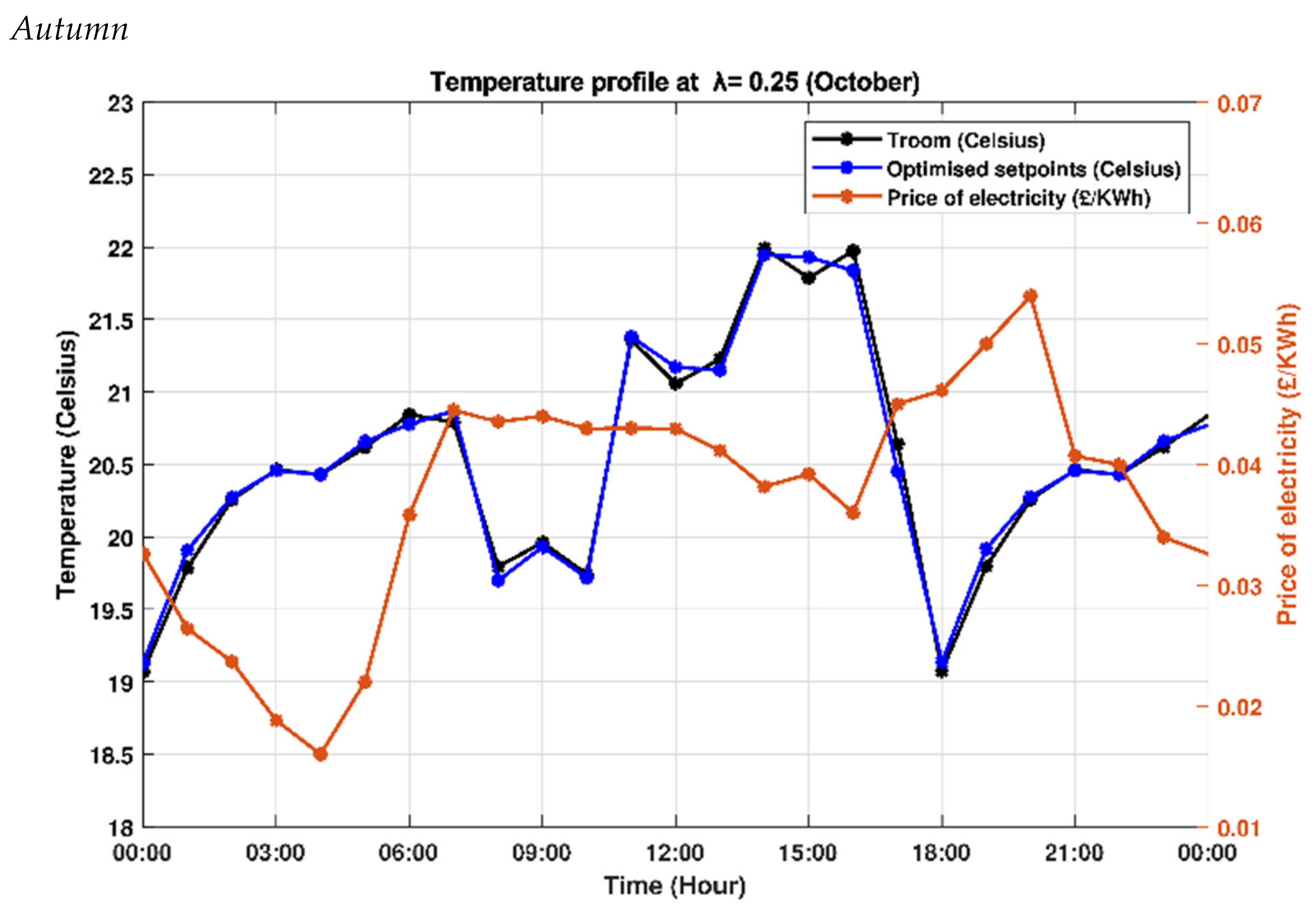
| Season | Energy Consumption (KWh) | Economic Cost (£) | Thermal Deviation | Average Room Temp. (°C) | Comfortability |
|---|---|---|---|---|---|
| Winter | 490 | 20.13 | 2565 | 20.20 | Uncomfortable |
| Spring | 492 | 18.30 | 2494 | 20.24 | Slightly comfortable |
| Summer | 492 | 20.86 | 2458 | 20.86 | Slightly comfortable |
| Autumn | 497 | 16.90 | 2172 | 20.48 | Slightly comfortable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adegbenro, A.; Short, M.; Angione, C. An Integrated Approach to Adaptive Control and Supervisory Optimisation of HVAC Control Systems for Demand Response Applications. Energies 2021, 14, 2078. https://doi.org/10.3390/en14082078
Adegbenro A, Short M, Angione C. An Integrated Approach to Adaptive Control and Supervisory Optimisation of HVAC Control Systems for Demand Response Applications. Energies. 2021; 14(8):2078. https://doi.org/10.3390/en14082078
Chicago/Turabian StyleAdegbenro, Akinkunmi, Michael Short, and Claudio Angione. 2021. "An Integrated Approach to Adaptive Control and Supervisory Optimisation of HVAC Control Systems for Demand Response Applications" Energies 14, no. 8: 2078. https://doi.org/10.3390/en14082078
APA StyleAdegbenro, A., Short, M., & Angione, C. (2021). An Integrated Approach to Adaptive Control and Supervisory Optimisation of HVAC Control Systems for Demand Response Applications. Energies, 14(8), 2078. https://doi.org/10.3390/en14082078








