Two-Step Finite Element Model Tuning Strategy of a Bridge Subjected to Mining-Triggered Tremors of Various Intensities Based on Experimental Modal Identification
Abstract
1. Introduction
- First step: calibration of the FE model, i.e., estimation of the elastic microslip parameter of the Coulomb friction-regularized model based on matching the results of the numerical and experimental modal identification of the bridge, carried out via low-energy operational modal analysis (OMA),
- Second step: modification of the FE model for mining-induced seismic performance assessment of higher energy level, i.e., implementation of the frictional contact based on elastoplasticity with the associated sliding rule as the constitutive model for bearing connectors.
2. Materials and Methods
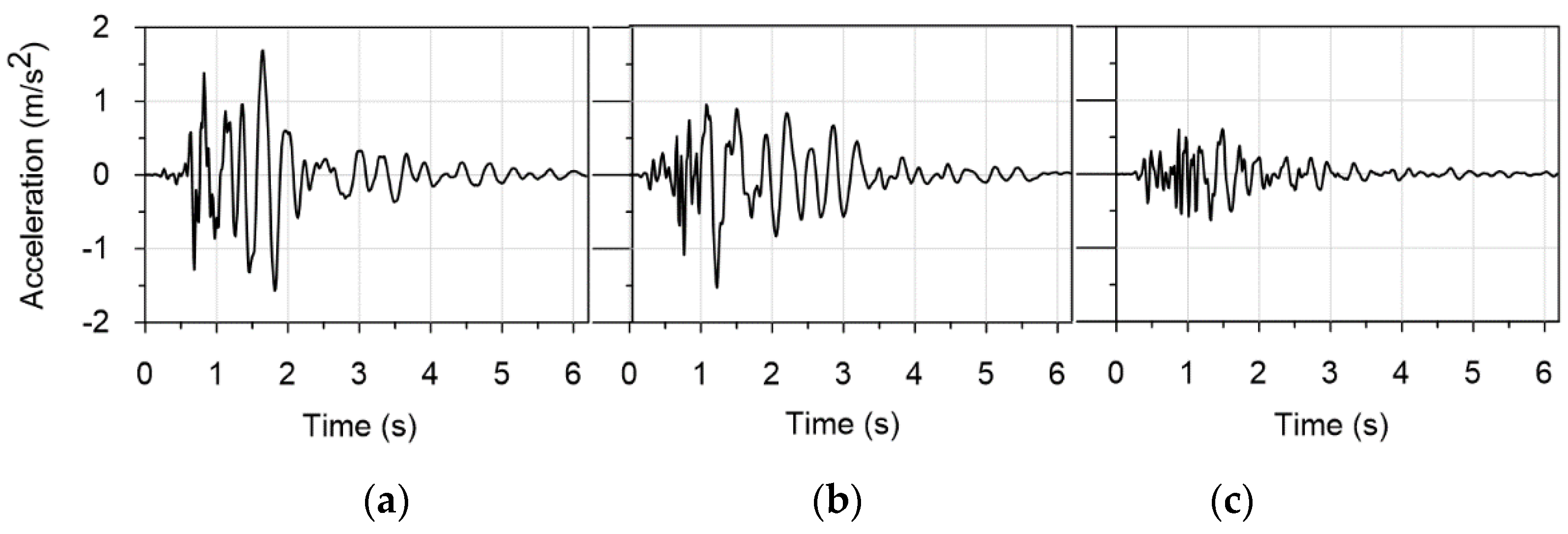
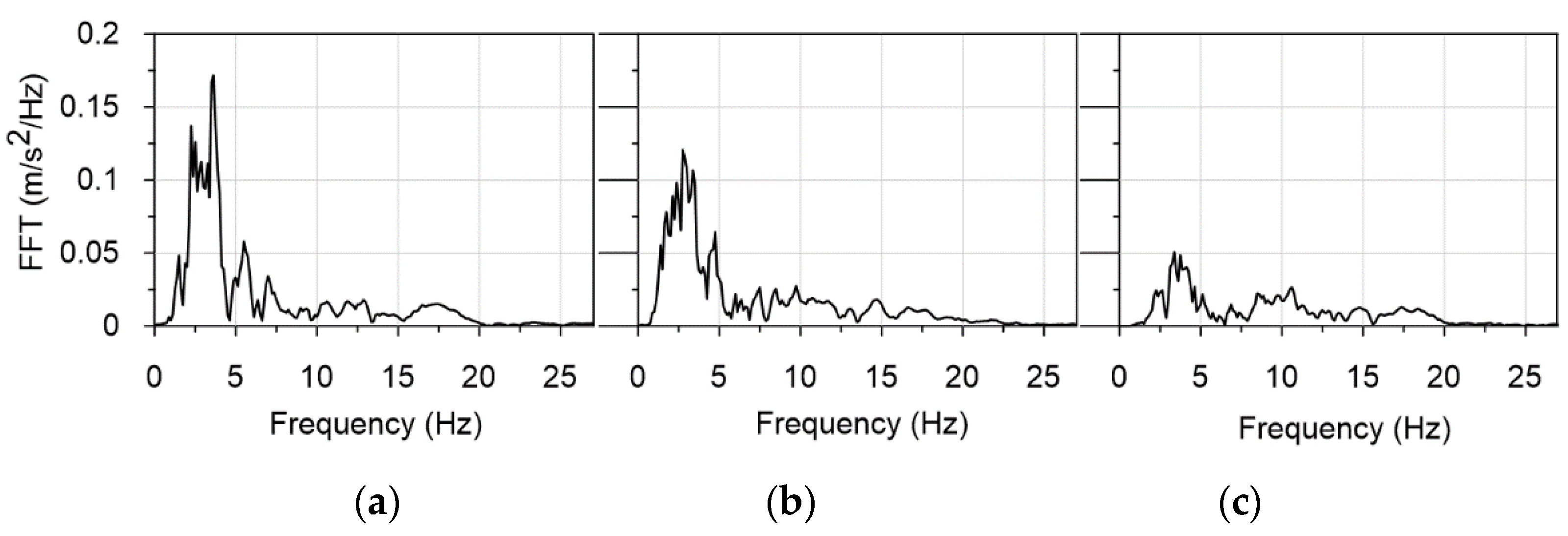
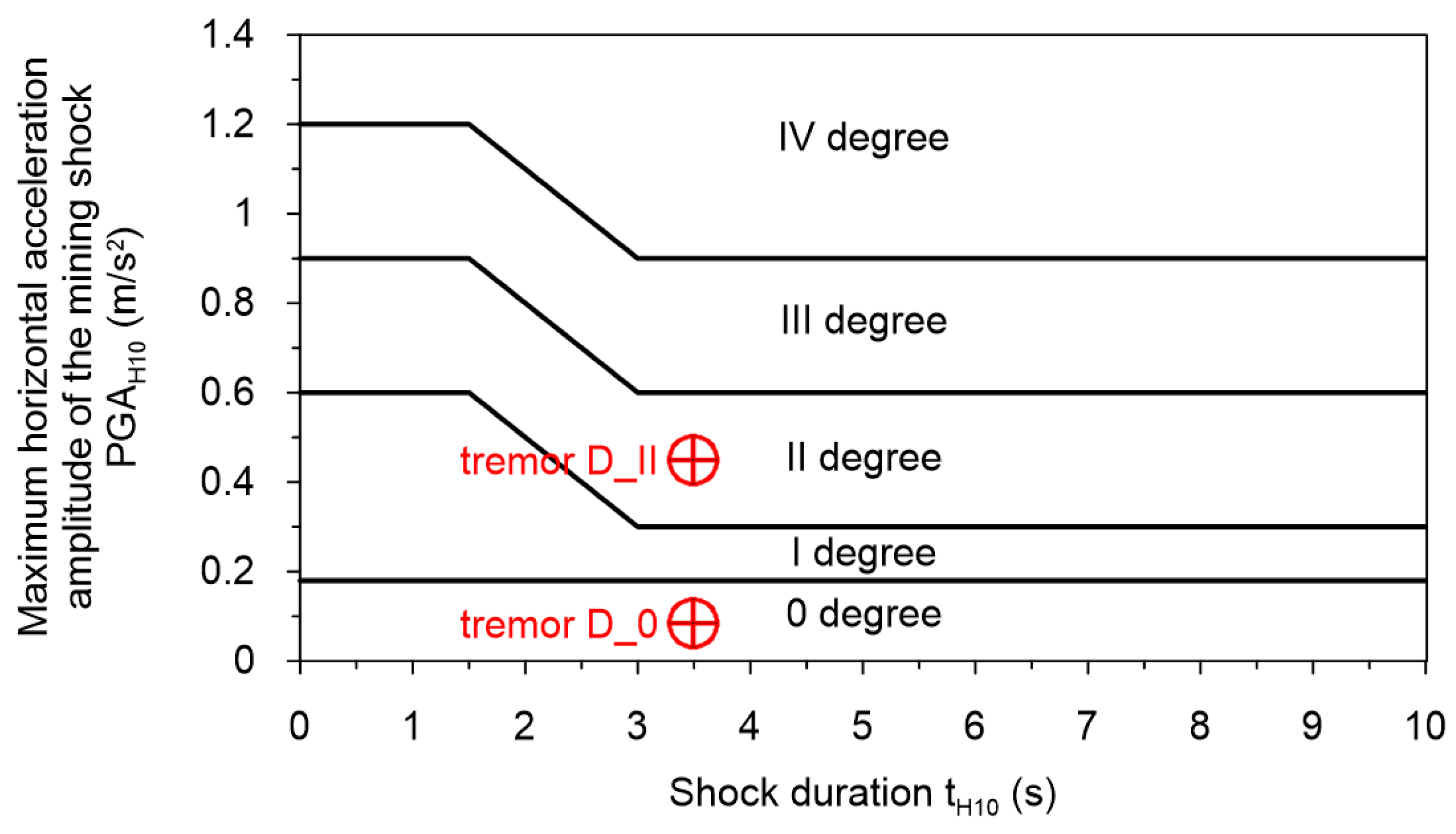
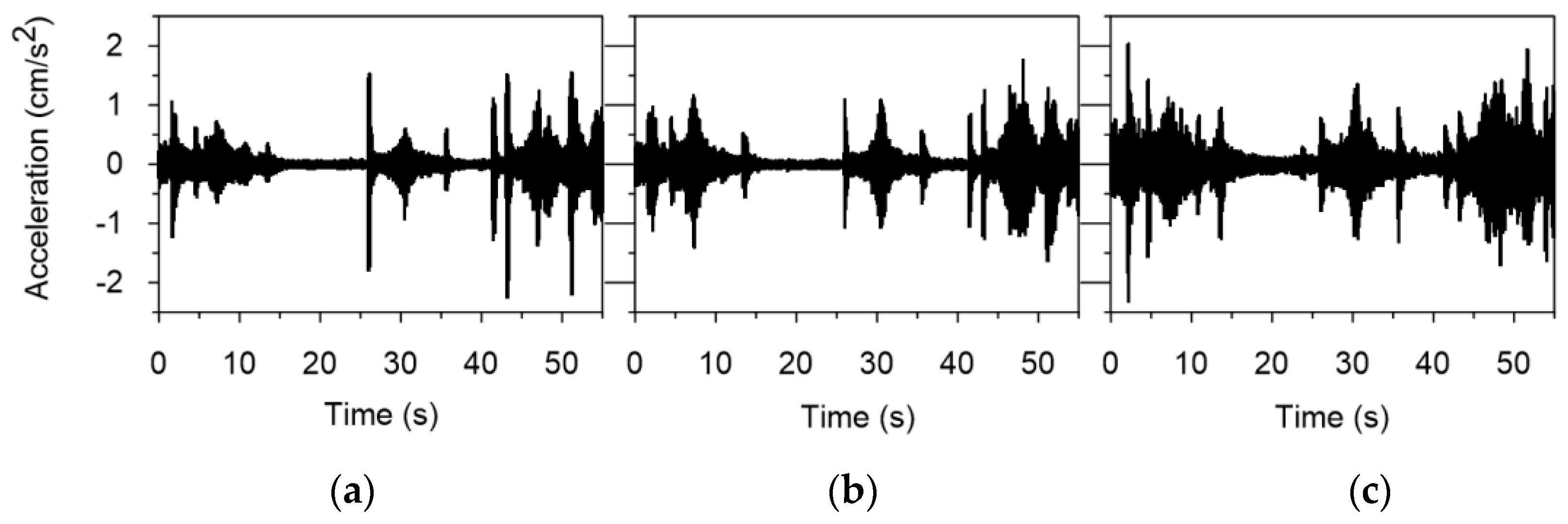
2.1. Data of the Mining-Triggered Tremor Registered in the Upper Silesian Basin, Poland
- (a)
- The maximum value of the resultant horizontal acceleration in the free field PGAH10 obtained based on filtered components of the recorded horizontal vibrations in the band up to 10 Hz (the subscript H10 means: H-horizontal accelerations, 10–maximal frequency in the filtered vibrations in (Hz)),
- (b)
- The duration of the intense vibration phase tHa (tHa is the time interval between moments where the Arias intensity [38] measure of horizontal acceleration reaches 5 and 95% of its maximum value).
- 0.1 m/s2, which corresponds to the tremor representing the zeroth degree of intensity (tremor D_0);
- 0.46 m/s2, which refers to the second degree of vibration intensity D_II (originally recorded tremor).
2.2. Description, Material Data and Numerical Model of the Bridge
2.2.1. Structural Layout and Material Data
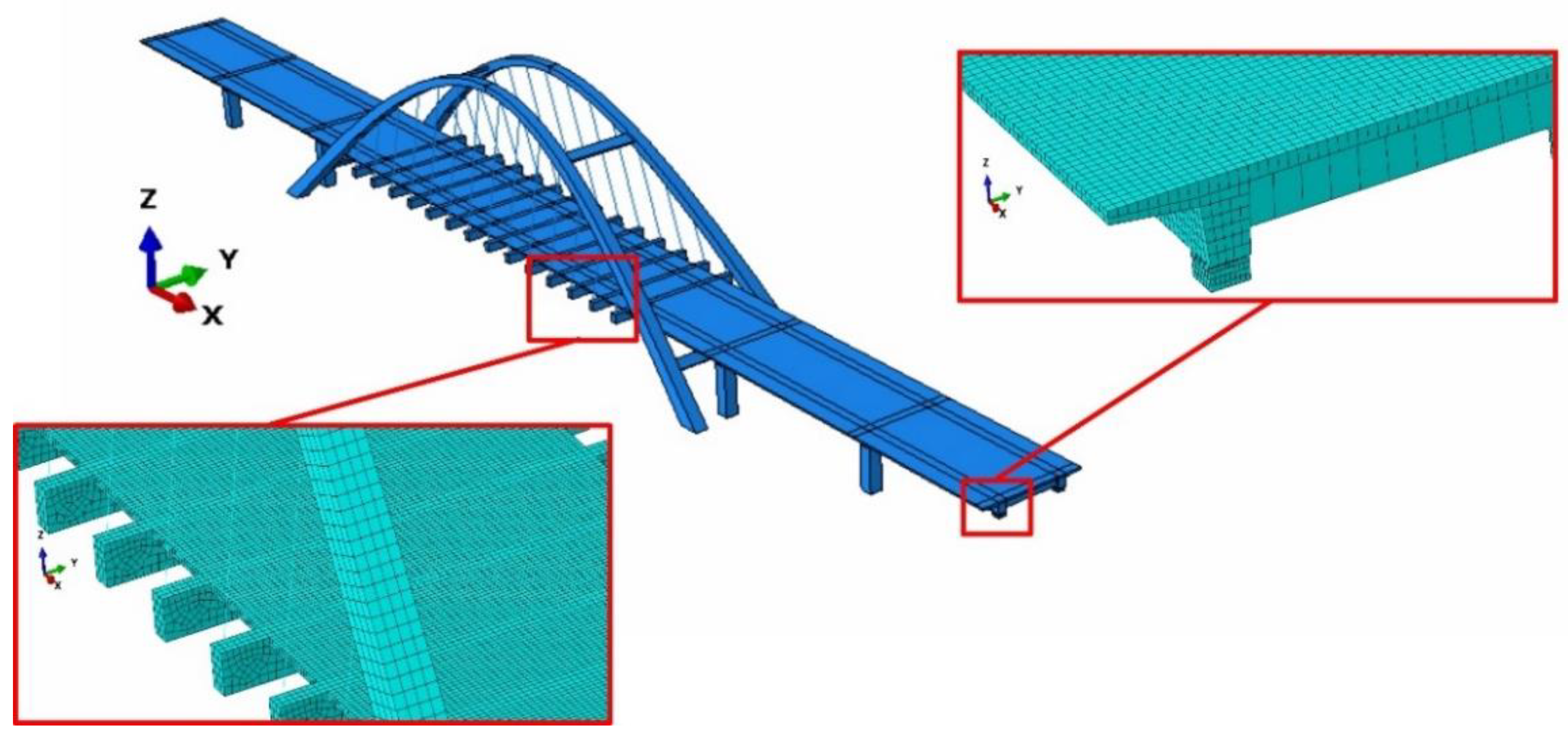
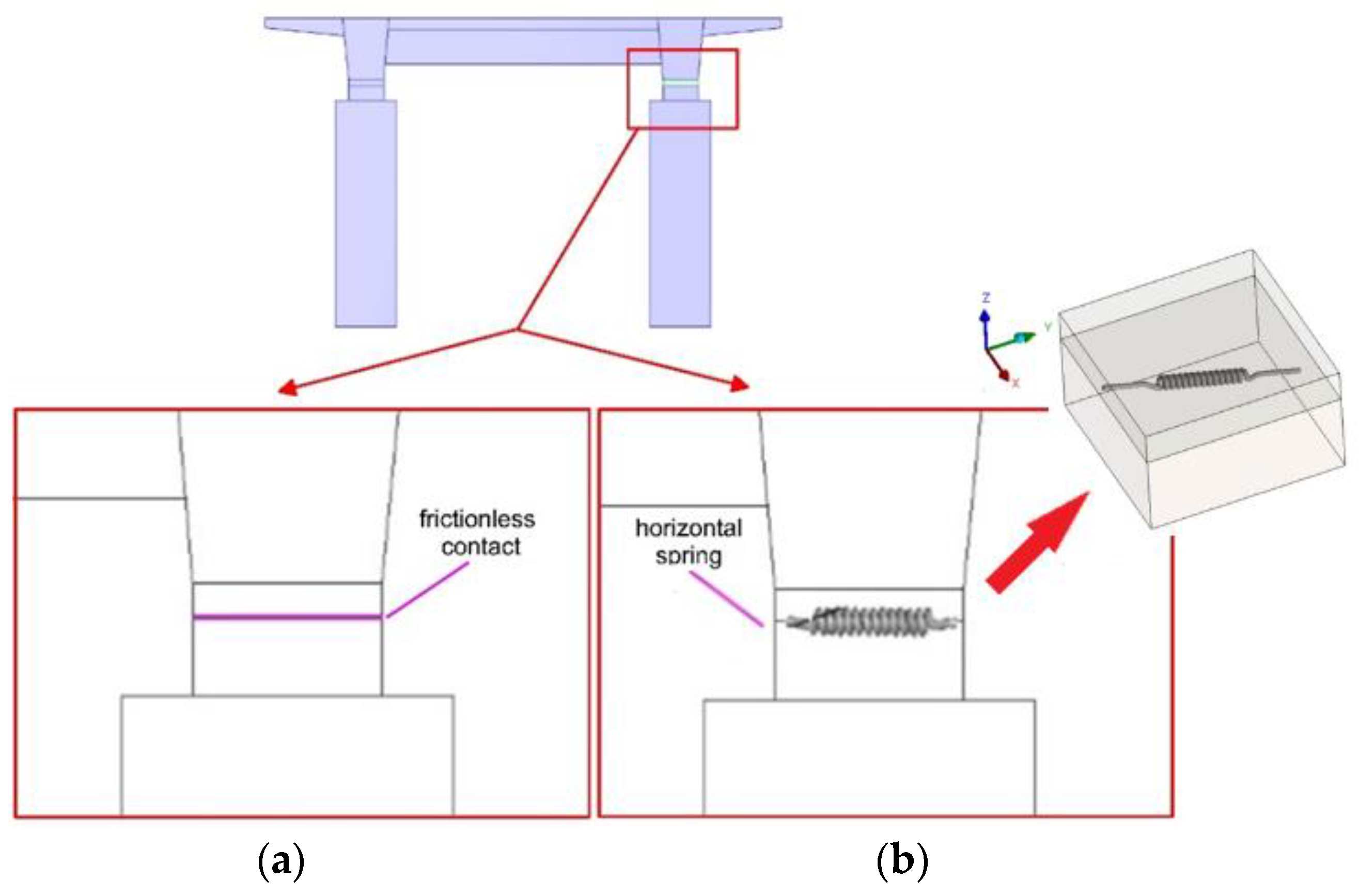
2.2.2. The Initial FE Model of the Bridge
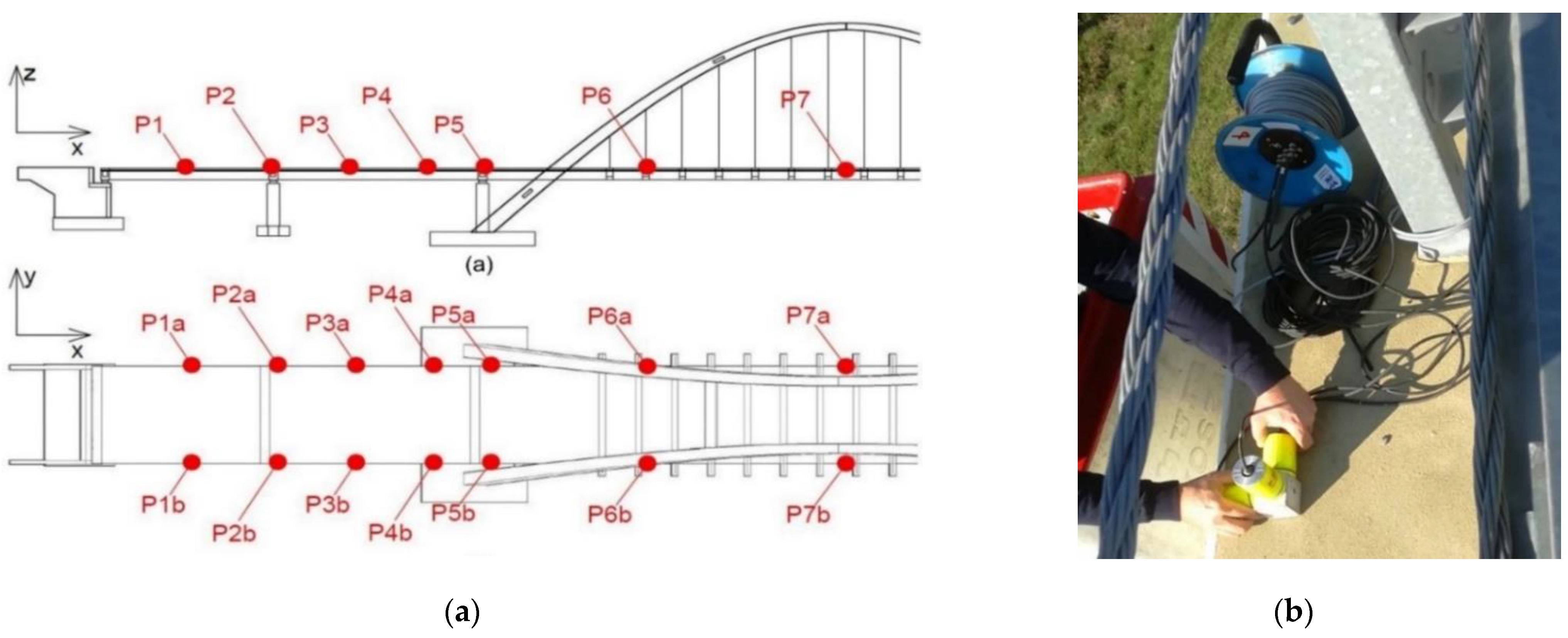
2.3. Experimental Setup for Nondestructive Testing
2.4. Theoretical Background for the In Situ Tests
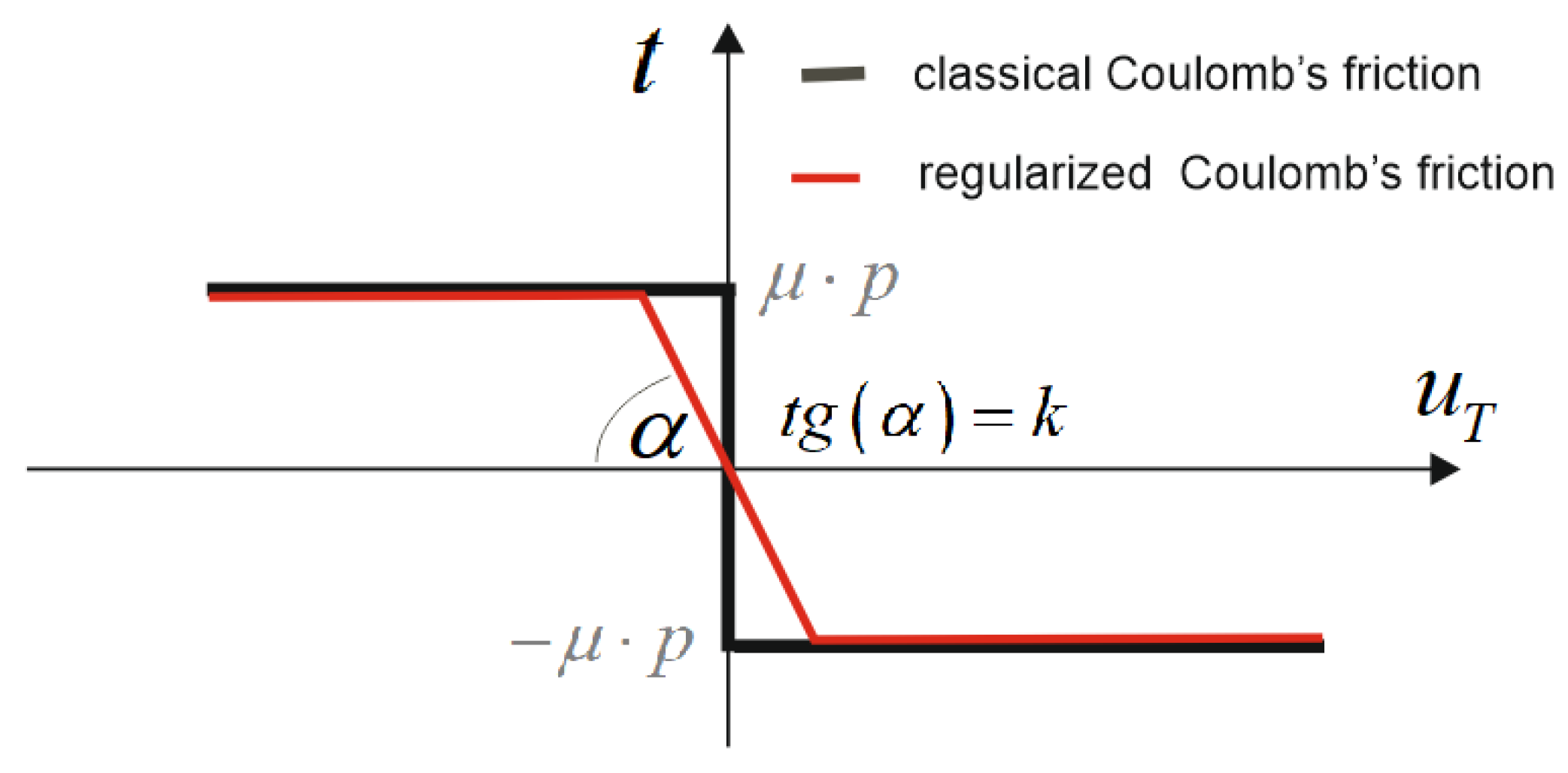
2.5. Theoretical Background for Frictional Contact Based on Elasto-Plasticity with Associated Sliding Rule
3. Results
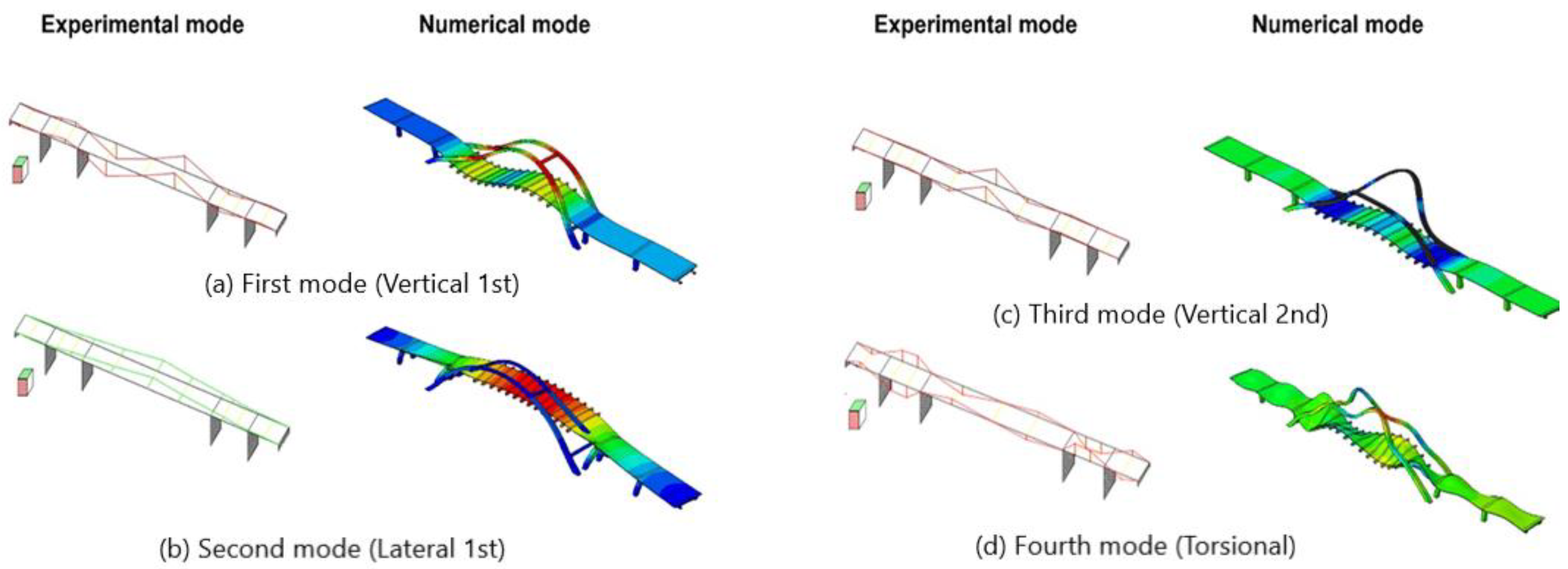
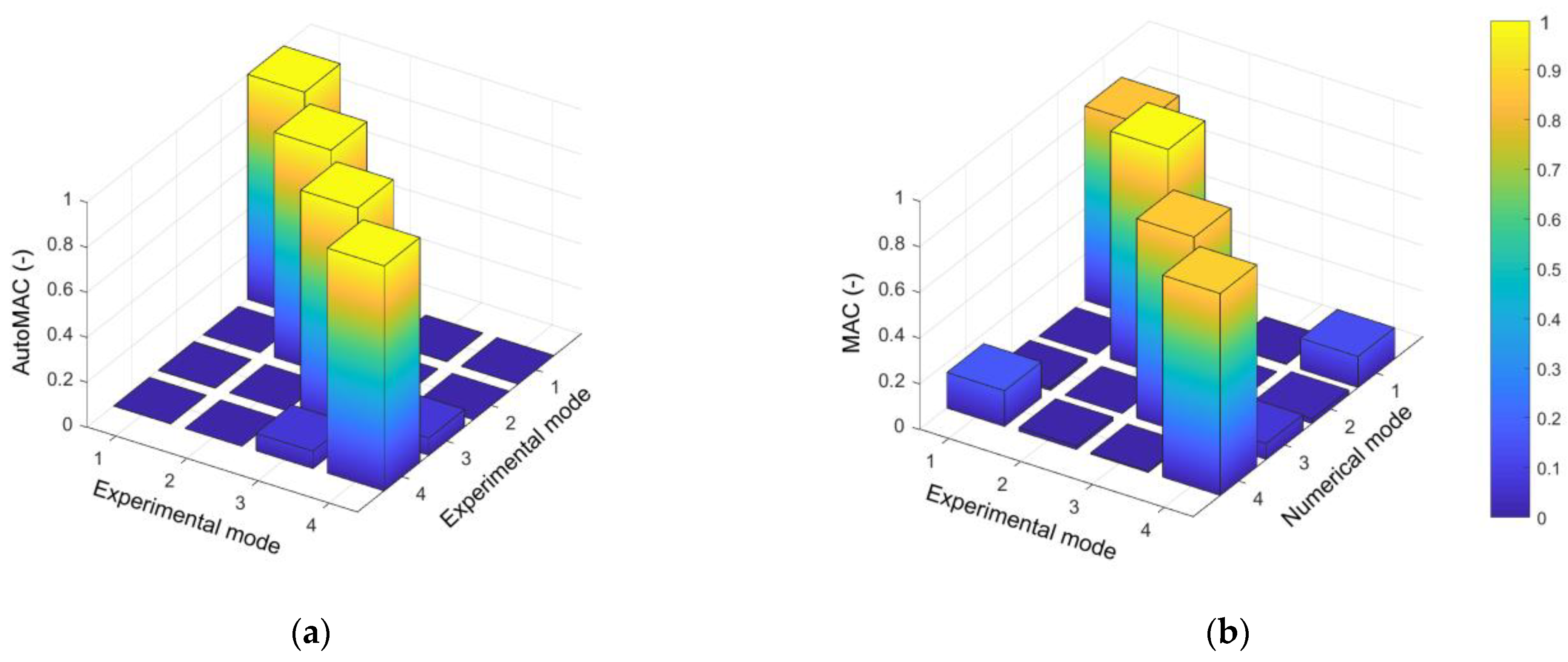
3.1. Experimental and Numerical Evaluation of Natural Frequencies and Modes of Vibration of the Bridge
3.2. Experimental Evaluation of Damping Properties
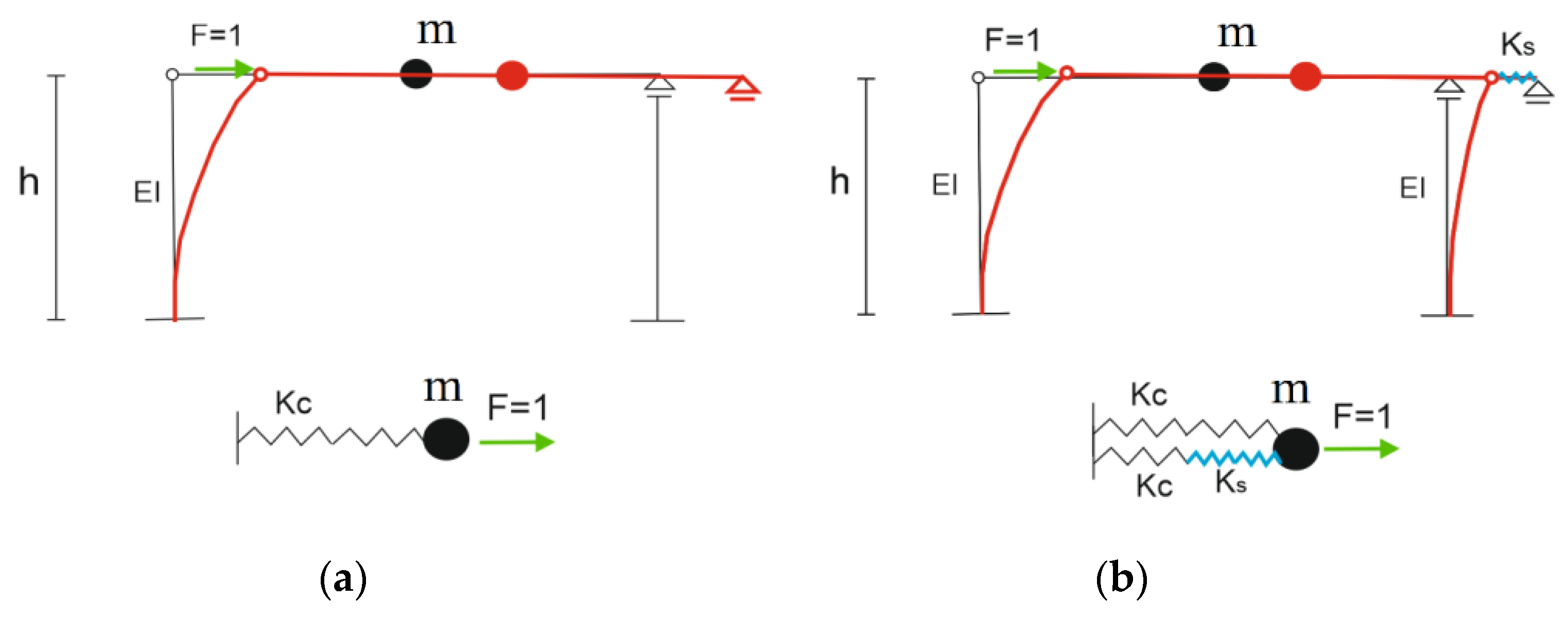
3.3. First Step of the Tuning Strategy: Calibration of the FE Model Based on the Experimental Modal Identification
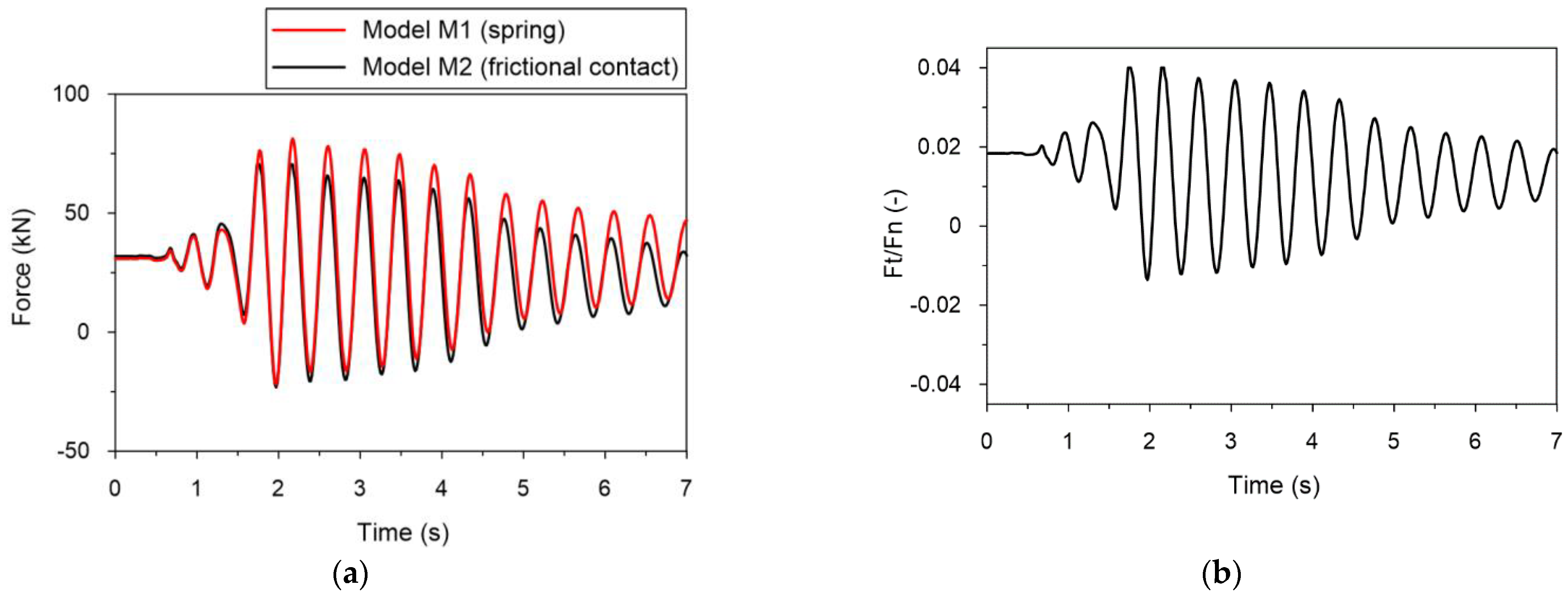
3.4. Second Step of the Tuning Strategy: Modification of the FE Model for Mining-Induced Seismic Performance Assessment
4. Discussion
4.1. Comparative Analysis of Dynamic Performance of the Bridge under Mining-Induced Shocks of Various Intensity: Untuned vs. Tuned FE Models
4.1.1. The General Framework of the Comparative Analyses
- M0—the untuned FE model, in which the sliding between bearing surfaces was assumed as a frictionless connection (see Section 2.2.2);
- M1—the “half” tuned FE model, after the first step of the tuning strategy, with the horizontal linear springs attached to the sliding bearings (see Section 3.3);
- M2—the fully tuned FE model, after the second step of the tuning strategy, with frictional regularized contact, applied as the constitutive model for bearing connectors (see Section 2.5 and Section 3.4).
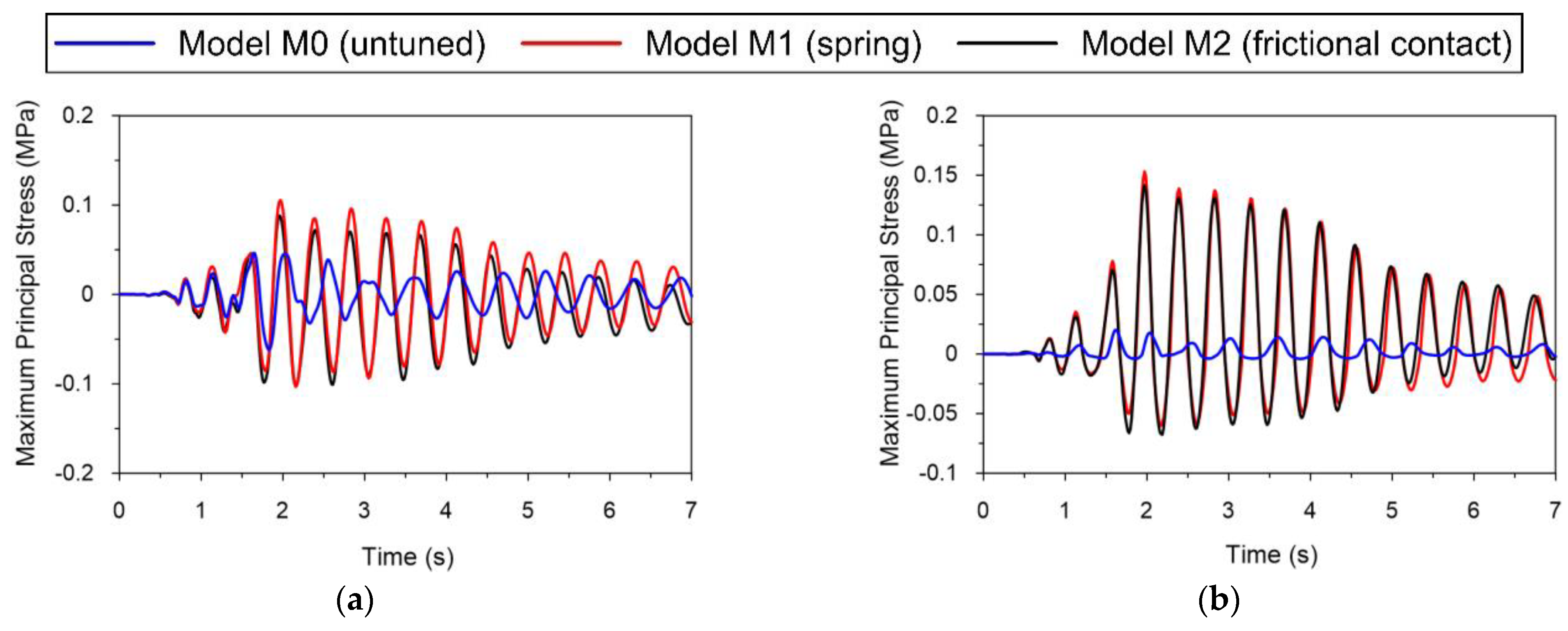
4.1.2. Dynamic Performance of the Bridge under the Tremor of the Zeroth Degree of Intensity (D_0)
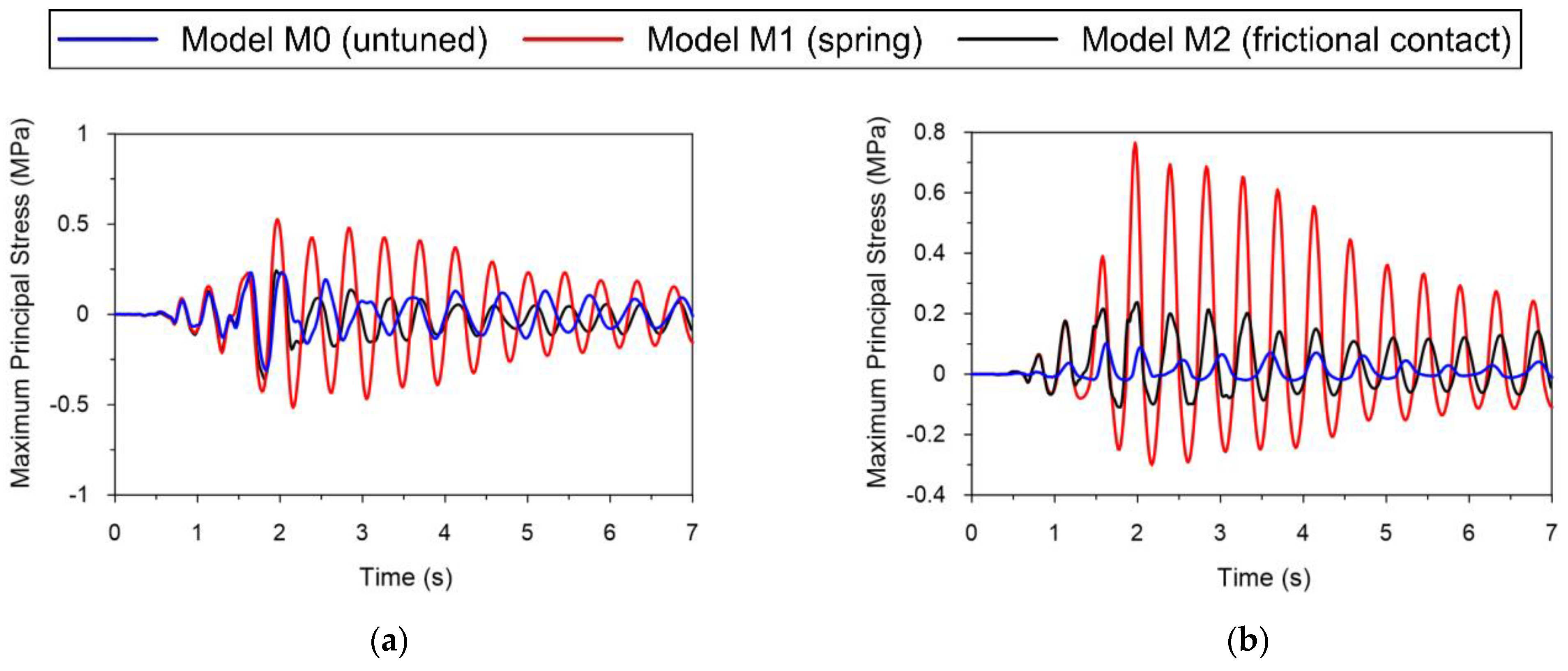
4.1.3. Dynamic Performance of the Bridge under the Tremor of the Second Degree of Intensity (D_II)
5. Conclusions
- The comparison of experimentally and numerically obtained natural frequencies indicated a poor level of consistency between the values of the second natural frequency corresponding to the transverse mode shape. The reason for such a discrepancy lies in the primary, untuned numerical model, with assumed frictionless sliding in bearings. Such simplification is not appropriate since, due to the low level of ambient vibration, sliding in the pot bearings was prevented by frictional forces;
- The proposed two-step tuning strategy of the FE bridge model significantly improved the consistency of the experimental and numerical values of the second natural frequency. In the proposed approach, the free bearing sliding was replaced with the Coulomb friction-regularized model, based on elastoplasticity with the associated sliding rule;
- The comparative analysis of the dynamic responses of the bridge models to mining-triggered tremors of various intensities (from 0 to IV degree) proved that the untuned model is not suitable for structure dynamic assessment in the case of low-energy tremors (0 degrees of intensity). The stresses obtained for this model turned out to be strongly underestimated. For shocks of higher intensity, frictionless sliding at bearings gave a relatively good global estimation of structure performance but undervalued its local response. On the other hand, the model tuned with linear springs proved to be applicable only for low-intensity tremors. In case of stronger shocks (from I to IV degree of intensity), the springs applied in bearings generated unrealistically large horizontal forces, resulting in a considerable overestimation of the structural dynamic response;
- The analysis revealed that only the fully tuned Coulomb friction-regularized model allows for the accurate simulation of sliding bearings under both low-energy and high-energy mining-induced tremors. However, it must be pointed out that this tuning strategy is valid for a particular type of bridge only, i.e., for those who benefitted from pot bearings (fixed and sliding).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Gunning, A.P.; Lasocki, S.; Capuano, P. Assessing environmental footprints induced by geo-energy exploitation: The shale gas case. Acta Geophys. 2019, 67, 279–290. [Google Scholar] [CrossRef]
- Foulger, G.; Wilson, M.; Gluyas, J.; Julian, B.; Davies, R. Global review of human-induced earthquakes. Earth Sci. Rev. 2018, 178, 438–514. [Google Scholar] [CrossRef]
- Peng, P.; Jiang, Y.; Wang, L.; He, Z.; Tu, S. A Fast ray-tracing method for locating mining-induced seismicity by considering underground voids. Appl. Sci. 2020, 10, 6763. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, X.; Chen, X.; Qin, D.; Chang, Z. Evolution of interior and exterior bearing structures of the deep-soft-rock roadway: From theory to field test in the Pingdingshan Mining Area. Energies 2020, 13, 4357. [Google Scholar] [CrossRef]
- Vižintin, G.; Kocjančič, M.; Vulić, M. Study of coal burst source locations in the Velenje Colliery. Energies 2016, 9, 507. [Google Scholar] [CrossRef]
- Tatara, T. Mining activity in Poland: Challenges. Brick and Block Masonry-From Historical to Sustainable Masonry. In Proceedings of the 17th International Brick/Block Masonry Conference (17thIB2MaC 2020), Krakow, Poland, 5–8 July 2020. [Google Scholar] [CrossRef]
- Olszewska, D.; Lasocki, S.; Leptokaropoulos, K. Non-stationarity and internal correlations of the occurrence process of mining-induced seismic events. Acta Geophys. 2017, 65, 507–515. [Google Scholar] [CrossRef]
- Kuzniar, K.; Tatara, T. The ratio of response spectra from seismic-type free-field and building foundation vibrations: The influence of rockburst parameters and simple models of kinematic soil-structure interaction. Bull. Earthq. Eng 2020, 18, 907–924. [Google Scholar] [CrossRef]
- Fuławka, K.; Pytel, W.; Pałac-Walko, B. Near-field measurement of six degrees of freedom mining-induced tremors in Lower Silesian Copper Basin. Sensors 2020, 20, 6801. [Google Scholar] [CrossRef]
- Boron, P.; Dulinska, J.; Jasinska, D. Impact of High Energy Mining-Induced Seismic Shocks from Different Mining Activity Regions on a Multiple-Support Road Viaduct. Energies 2020, 13, 4045. [Google Scholar] [CrossRef]
- Tatara, T. Dynamic Resistance of Building under Mining Tremors; The Cracow University of Technology Press: Krakow, Poland, 2002. (In Polish) [Google Scholar]
- Pachla, F.; Kowalska-Koczwara, A.; Tatara, T.; Stypula, K. The influence of vibration duration on the structure of irregular RC buildings. Bull. Earthq. Eng. 2019, 17, 3119–3138. [Google Scholar] [CrossRef]
- Fuławka, K.; Stolecki, L.; Jaśkiewicz-Proć, I.; Pytel, W.; Mertuszka, P. The analysis of seismic load characteristic observed in the Lower Silesian Copper Basin. SWS J. Earth Planet. Sci. 2020, 2, 35–49. [Google Scholar] [CrossRef]
- Dubinski, J.; Mutke, G.; Chodacki, J. Distribution of peak ground vibration caused by mining induced seismic events in the Upper Silesian Coal Basin in Poland. Arch. Min. Sci. 2020, 3, 419–432. [Google Scholar] [CrossRef]
- Furumura, T.; Takemura, S.; Noguchi, S.; Takemoto, T.; Maeda, T.; Iwai, K.; Padhy, S. Strong ground motions from 2011 off-the Pacyfic-Coast-of-Tohoku, Japan, (Mw = 9.0) earthquake obtained fram a dense nationwide seismic network. Landslides 2011, 8, 333–338. [Google Scholar] [CrossRef]
- Bayraktar, A.; Altunişik, A.; Sevim, B.; Türker, T. Modal testing, finite-element model updating, and dynamic analysis of an arch-type steel footbridge. J. Perform. Constr. Fac. 2009, 23. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calçada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite element model updating of a bowstring-arch railway bridge based on experimental modal parameters. Eng. Struct. 2012, 40, 413–435. [Google Scholar] [CrossRef]
- Chen, X.; Omenzetter, P.; Beskhyroun, S. Ambient vibration testing, system identification and model updating of a multiple-span elevated bridge. In Proceedings of the 9th International Conference on Structural Dynamics, EURODYN 2014, Porto, Portugal, 30 June–2 July 2014; pp. 2377–2384. [Google Scholar] [CrossRef]
- Banas, A.; Jankowski, R. Experimental and numerical study on dynamics of two footbridges with different shapes of girders. Appl. Sci. 2020, 10, 4505. [Google Scholar] [CrossRef]
- Zenunovic, D.; Topalovic, M.; Folic, R. Identification of modal parameters of bridges using ambient vibration measurements. Shock. Vib. 2015, 957841. [Google Scholar] [CrossRef][Green Version]
- Drygala, I.; Dulinska, J.M.; Polak, M.A. Seismic assessment of footbridges under spatial variation of earthquake ground motion (SVEGM): Experimental testing and finite element analyses. Sensors 2020, 20, 1227. [Google Scholar] [CrossRef]
- Cunha, A.; Caetano, E.; Magalhães, F.; Moutinho, C. Recent perspectives in dynamic testing and monitoring of bridges. Struct. Control. Health 2013, 20, 853–877. [Google Scholar] [CrossRef]
- Chen, G. Dynamic Testing and Model Updating of an Eleven-Span Concrete Motorway Bridge. Ph.D. Thesis, Department of Civil and Environmental Engineering, The University of Auckland, Auckland, New Zealand, October 2015. [Google Scholar]
- D’Amato, M.; Laterza, M.; Casamassima, V.M. Seismic performance evaluation of a multi-span existing masonry arch bridge. Open Civ. Eng. J. 2017, 11, 1191–1207. [Google Scholar] [CrossRef]
- Rota, M.; Pecker, A.; Bolognini, D.; Pinho, R. A methodology for seismic vulnerability of masonry arch bridge walls. J. Earthq. Eng. 2005, 9, 331–353. [Google Scholar] [CrossRef]
- Marcheggiani, L.; Clementi, F.; Formisano, A. Static and dynamic testing of highway bridges: A best practice example. J. Civ. Struct. Health Monit. 2020, 10, 43–56. [Google Scholar] [CrossRef]
- Hester, D.; Koo, K.; Xu, Y.; Brownjohn, J.; Bocian, M. Boundary condition focused finite element model updating for bridges. Eng. Struct. 2019, 198. [Google Scholar] [CrossRef]
- Brownjohn, J.; Dumanoglu, A.; Taylor, C. Dynamic investigation of a suspension footbridge. Eng. Struct. 1994, 16, 395–406. [Google Scholar] [CrossRef]
- Živanović, S.; Pavic, A.; Reynolds, P. Modal testing and FE model tuning of a lively footbridge structure. Eng. Struct. 2006, 28, 857–868. [Google Scholar] [CrossRef]
- Živanović, S.; Pavic, A.; Reynolds, P. Finite element modelling and updating of a lively footbridge: The complete process. J. Sound. Vib. 2007, 301, 126–145. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á.; Caetano, E.; Fonseca, A.; Bastos, R. Evaluation of dynamic properties of Infante D. Henrique Bridge. In Proceedings of the Third International Conference on Bridge Maintenance, Safety and Management, Porto, Portugal, 16–19 July 2006. [Google Scholar] [CrossRef]
- Zong, Z.; Jaishi, B.; Ge, J.; Ren, W. Dynamic analysis of a half-through concrete-filled steel tubular arch bridge. Eng. Struct. 2005, 27, 3–15. [Google Scholar] [CrossRef]
- Asgari, B.; Osman, S.; Adnan, A. Sensitivity analysis of the influence of structural parameters on the dynamic behaviour of highly redundant cable-stayed bridges. Adv. Mater. Res. 2013, 2013, 426932. [Google Scholar] [CrossRef]
- Athanatopoulou, A.; Ekmektsoglou, K.; Panetsos, P. Calibration of the dynamic model of a long concrete Ravine Bridge based on ambient vibration measurements. In Proceedings of the 16th World Conference on Earthquake, 16WCEE 2017, Santiago, Chile, 9–13 January 2017. Paper No 221. [Google Scholar]
- Biessikirski, A. Evaluation of paraseismic vibrations on a housing construction according to Polish and international regulation. Przegląd Górniczy 2014, 70, 1–6. [Google Scholar]
- Kuźniar, K.; Tatara, T. Application of mine-induced free-field and building foundation vibrations for evaluation of their harmfulness using mining scales. Procedia Eng. 2017, 199, 2378–2383. [Google Scholar] [CrossRef]
- Dubiński, J.; Mutke, G.; Tatara, T.; Muszyński, L.; Barański, A.; Kowal, T. Zasady Stosowania Zweryfikowanej Górniczej Skali Intensywności Drgań GSI-GZWKW-2012 do Prognozy i Oceny Skutków Wstrząsów Indukowanych Eksploatacją Złóż Węgla Kamiennego w Zakładach Górniczych Kompanii Węglowej S.A. na Obiekty Budowlane i na Ludzi; Kompania Węglowa: Katowice, Poland, 2013; unpublished report. (In Polish) [Google Scholar]
- Arias, A. A measure of earthquake intensity. In Seismic Design for Nuclear Power Plants; Hansen, R.J., Ed.; MIT Press: Cambridge MA, USA, 1970; pp. 438–483. [Google Scholar]
- Kuzniar, K.; Stec, K.; Tatara, T. Approximate classification of mining tremors harmfulness based on free-field and building foundation vibrations. E3S Web. Conf. 2018, 36, 01006. [Google Scholar] [CrossRef]
- Abaqus/Standard User’s Manual; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2020.
- Bednarski, Ł.; Sieńko, R.; Howiacki, T. Estimation of the value and variability of elastic modulus of concrete in the existing structures on the basis of continuous in situ measurements. Cem. Wapno. Beton. 2014, 6, 396–404. [Google Scholar]
- Ghalishooyan, M.; Shooshtari, A. Operational modal analysis techniques and their theoretical and practical aspects: A comprehensive review and introduction. In Proceedings of the 6th International Operational Modal Analysis Conference, Gijon, Spain, 12–14 May 2015. [Google Scholar]
- Van Overschee, P.; De Moor, B. Subspace Identification for Linear Systems: Theory—Implementation—Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Peeters, B.; De Roeck, G. Stochastic system identification for operational modal analysis: A review. J. Dyn. Syst. T ASME 2001, 123, 659–666. [Google Scholar] [CrossRef]
- Kim, B.; Stubbs, N.; Park, T. A new method to extract modal parameters using output-only responses. J. Sound Vib. 2005, 282, 215–230. [Google Scholar] [CrossRef]
- Hoa, L.T.; Tamura, Y.; Yoshida, A. Frequency domain versus time domain modal identification for ambient excited structures. In Proceedings of the International Conference on Engineering Mechanics and Automation (ICEMA 2010), Hanoi, Vietnam, 1–2 July 2010. [Google Scholar]
- De Moor, B.; van Overshee, P.; Suykens, J. Subspace Algorithms for System Identification and Stochastic Realization; ESAT/SISTA Report 1990-28; ESAT: Heverlee, Belgium, 1990. [Google Scholar]
- Avitable, P. Modal Space—In our own little world. Exp. Tech. 2013, 37, 3–5. [Google Scholar] [CrossRef]
- Allemang, R.J.; Brown, D.L. A Complete review of the Complex Mode Indicator Function (CMIF) with applications. In Proceedings of the ISMA 2006: International Conference on Noise and Vibration Engineering, Leuven, Belgium, 18–20 September 2006; p. 6. [Google Scholar]
- Shih, C.; Tsuei, Y.; Allemang, R.; Brown, D. Complex Mode Indication Function and its applications to spatial domain parameter estimation. Mech. Syst. Signal Pract. 1988, Z, 367–377. [Google Scholar] [CrossRef]
- Wilkie, J.; Johnson, M.; Katebi, R. Poles, zeros and system stability. In Control Engineering; Red Globe Press: London, UK, 2002. [Google Scholar]
- Trumper, D. Analysis and Design of Feedback Control Systems. Materials of MIT. 2014. Available online: https://ocw.mit.edu/courses/mechanical-engineering/2-14-analysis-and-design-of-feedback-control-systems-spring-2014/ (accessed on 5 February 2021).
- Mayes, R.; Rohe, D.; Brink, A.; Freymiller, J. The Complex Mode Indicator Function for Identifying Unit-to-Unit Variability; Report no SAND2016-5910C of Sandia Corporation, a Lockheed Martin Company for the United States Department of Energy’s National Nuclear Security Administration under contract DE-AC04-94AL85000; Sandia Corporation: Albuquerque, NM, USA, 2016. [Google Scholar]
- Karbhari, V.; Ansari, F. Structural Health Monitoring of Civil Infrastructures; Woodhead Publishing Series in Civil and Structural Engineering; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Avitabile, P. Modal Testing: A Practitioner’s Guide, Wiley/SEM Series on Experimental Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Li, D.; Ren, W.-X.; Hu, Y.-D.; Yang, D. Operational modal analysis of structures by stochastic subspace identification with a delay index. Struct. Eng. Mech. 2016, 59, 187–207. [Google Scholar] [CrossRef]
- Bayraktar, A.; Turker, T.; Altunisik, A.C.; Sevim, C.; Sahin, A.; Oscan, D.M. Determination of dynamic parameters of buildings by operational modal analysis. Tek. Dergi. 2010, 21, 5185–5205. [Google Scholar]
- Clough, R.W.; Penzien, J. Dynamics of Structures; McGraw Hill: New York, NY, USA, 1975. [Google Scholar]
- Michałowski, R.; Mróz, Z. Associated and nonassociated sliding rules in contact friction problems. Arch. Mech. 1978, 30, 259–276. [Google Scholar]
- Cournier, A. A theory of friction. Int. J. Solids Struct. 1984, 20, 637–647. [Google Scholar] [CrossRef]
- Anand, L. A constitutive model for interface friction. Comput. Mech. 1993, 12, 197–213. [Google Scholar] [CrossRef]
- Wriggers, P. Computational Contact Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Sung, Y.-C.; Lin, T.; Chiu, Y.; Chang, K.; Chen, K.; Chang, C. A bridge safety monitoring system for prestressed composite box-girder bridges with corrugated steel webs based on in-situ loading experiments and a long-term monitoring database. Eng. Struct. 2016, 126, 571–585. [Google Scholar] [CrossRef]
- Janas, L.; Jarominiak, A.; Michalak, E. Guidelines for Conducting Periodic Inspections of Road Engineering Structures; Stowarzyszenie Inżynierów i Techników Komunikacji RP Oddział Rzeszów: Warsaw, Poland, 2005. (In Polish) [Google Scholar]
- Protocol of Five Year Periodic Inspection—Extended Examination; NR 1/JNI/2018; Lehmann & Partner: Chrzanów, Poland, 2018. (In Polish)
- Protocol of Yearly Periodic Inspection—Basic Examination; NR 1/JNI/2020; Lehmann & Partner: Chrzanów, Poland, 2020. (In Polish)
- Gou, H.; He, Y.; Zhou, W.; Bao, Y.; Chen, G. Experimental and numerical investigations of the dynamic responses of an asymmetrical arch railway bridge. J. Rail Rapid Transit. 2018, 1–15. [Google Scholar] [CrossRef]
- Ding, Y.L.; Li, A.Q.; Du, D.S.; Liu, T. Multi-scale damage analysis for a steel box girder of a long-span cable-stayed bridge. Struct. Infrastruct. E 2014, 6, 725–739. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practise, and Application, 2nd ed.; Research Studies Press Ltd.: Philadelphia, PA, USA, 2000. [Google Scholar]
- Pot Bearing Allows Rotations by Shear Deformation. Available online: https://www.bridgebearing.org/bridgebearing/pot-bearing.html (accessed on 12 November 2020).
- Chopra, A.K. Dynamics of Structures, 4th ed.; University of California at Berkeley: Pearson, CA, USA, 2012. [Google Scholar]
- EN 1998-1:2004: Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; CEN: Brussels, Belgium, 2005.

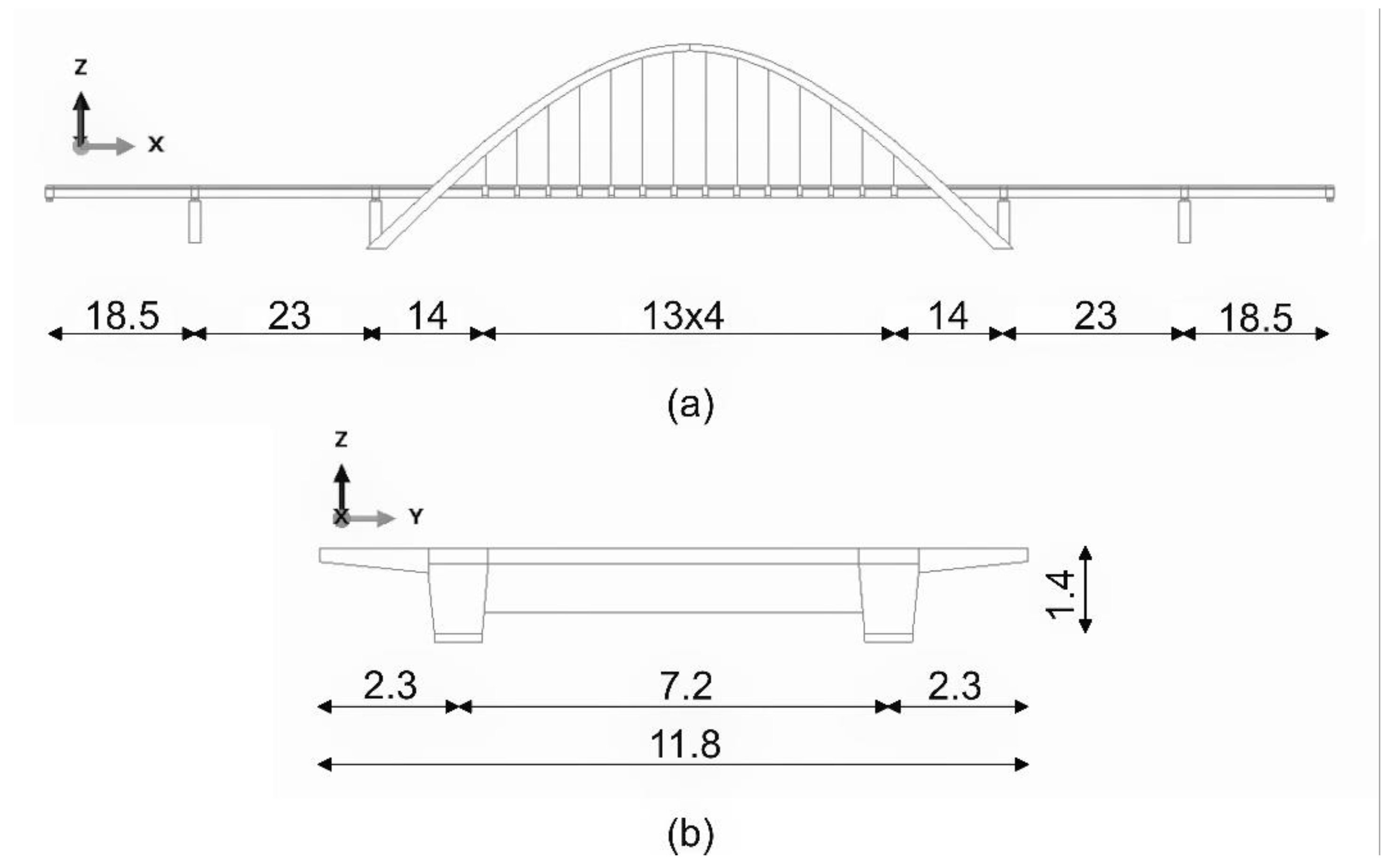



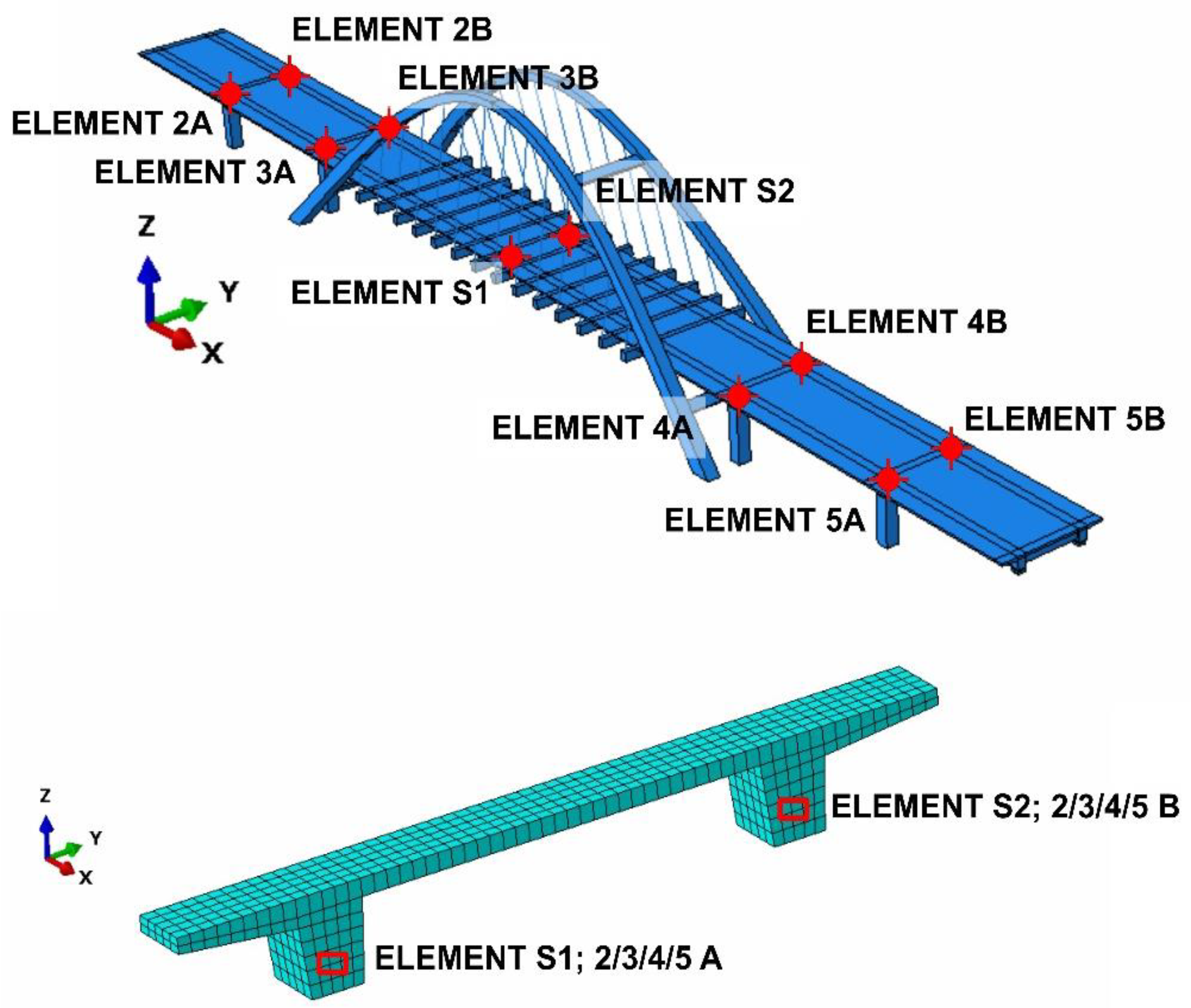

| Bridge Element | Material | Building Class |
|---|---|---|
| Girder beams, deck slab | Concrete | C40/50 |
| Pillars | Concrete | C30/37 |
| Arches | Concrete | C50-60 |
| Prestressing tendons | Steel | Y1860 |
| Hangers | Steel | S460 |
| Mode | Natural Frequency (Hz) | Natural Mode Shape | Relative Error (%) | |
|---|---|---|---|---|
| FE analysis Model no.1 | OMA | |||
| 1 | 1.57 | 1.50 | 1st Vertical | 4.6 |
| 2 | 1.87 | 2.48 | 1st Lateral | 24.6 |
| 3 | 3.48 | 3.36 | 2nd Vertical | 3.6 |
| 4 | 14.30 | 14.26 | 1st Torsional | 0.3 |
| Mode | Natural Frequency (Hz) | Natural Mode Shape | Relative Error (%) | |
|---|---|---|---|---|
| FE with Tuned Model | OMA | |||
| 1 | 1.60 | 1.50 | 1st vertical | 6.6 |
| 2 | 2.30 | 2.48 | 1st lateral | 7.2 |
| 3 | 3.48 | 3.36 | 2nd vertical | 3.6 |
| 4 | 14.31 | 14.26 | 1st torsional | 0.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boroń, P.; Dulińska, J.M.; Jasińska, D. Two-Step Finite Element Model Tuning Strategy of a Bridge Subjected to Mining-Triggered Tremors of Various Intensities Based on Experimental Modal Identification. Energies 2021, 14, 2062. https://doi.org/10.3390/en14082062
Boroń P, Dulińska JM, Jasińska D. Two-Step Finite Element Model Tuning Strategy of a Bridge Subjected to Mining-Triggered Tremors of Various Intensities Based on Experimental Modal Identification. Energies. 2021; 14(8):2062. https://doi.org/10.3390/en14082062
Chicago/Turabian StyleBoroń, Paweł, Joanna Maria Dulińska, and Dorota Jasińska. 2021. "Two-Step Finite Element Model Tuning Strategy of a Bridge Subjected to Mining-Triggered Tremors of Various Intensities Based on Experimental Modal Identification" Energies 14, no. 8: 2062. https://doi.org/10.3390/en14082062
APA StyleBoroń, P., Dulińska, J. M., & Jasińska, D. (2021). Two-Step Finite Element Model Tuning Strategy of a Bridge Subjected to Mining-Triggered Tremors of Various Intensities Based on Experimental Modal Identification. Energies, 14(8), 2062. https://doi.org/10.3390/en14082062






