Novel Intelligent Control Technology for Enhanced Stability Performance of an Ocean Wave Energy Conversion System
Abstract
1. Introduction
2. Modeling of the Studied System
2.1. Structure of the System
2.2. Wave Energy Characteristics
2.3. Wells Turbine Modeling
2.4. DFIG Modeling
3. Design of the Novel FLWRBFN with DEPSO Control System
3.1. Function-Link Based Wilcoxon Radial Basis Function Network (FLWRBFN)
3.2. Learning and Training Procedures of FLWRBFN
3.3. DEPSO Online Adjusts Learning Rate
4. Analysis of Convergence
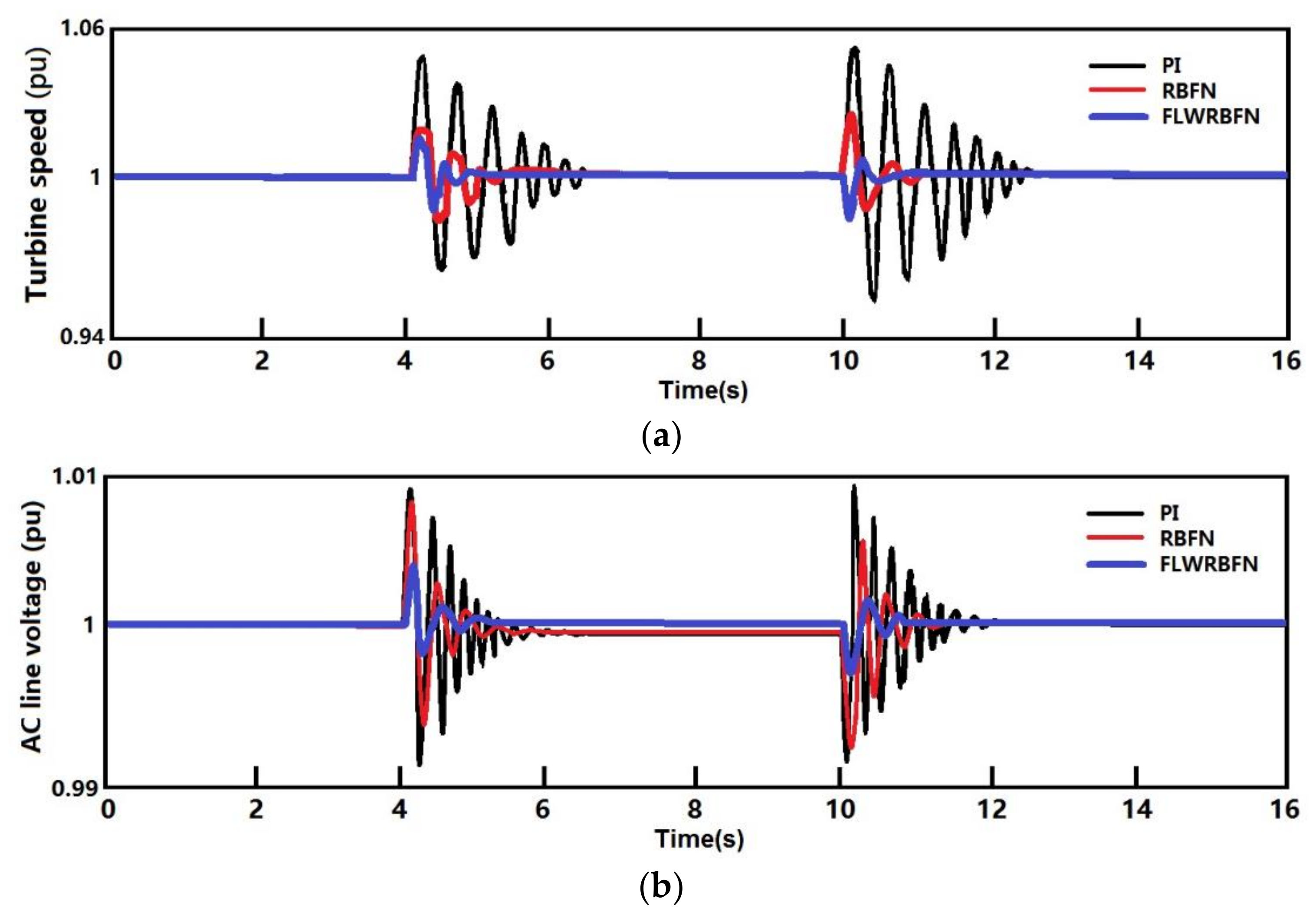
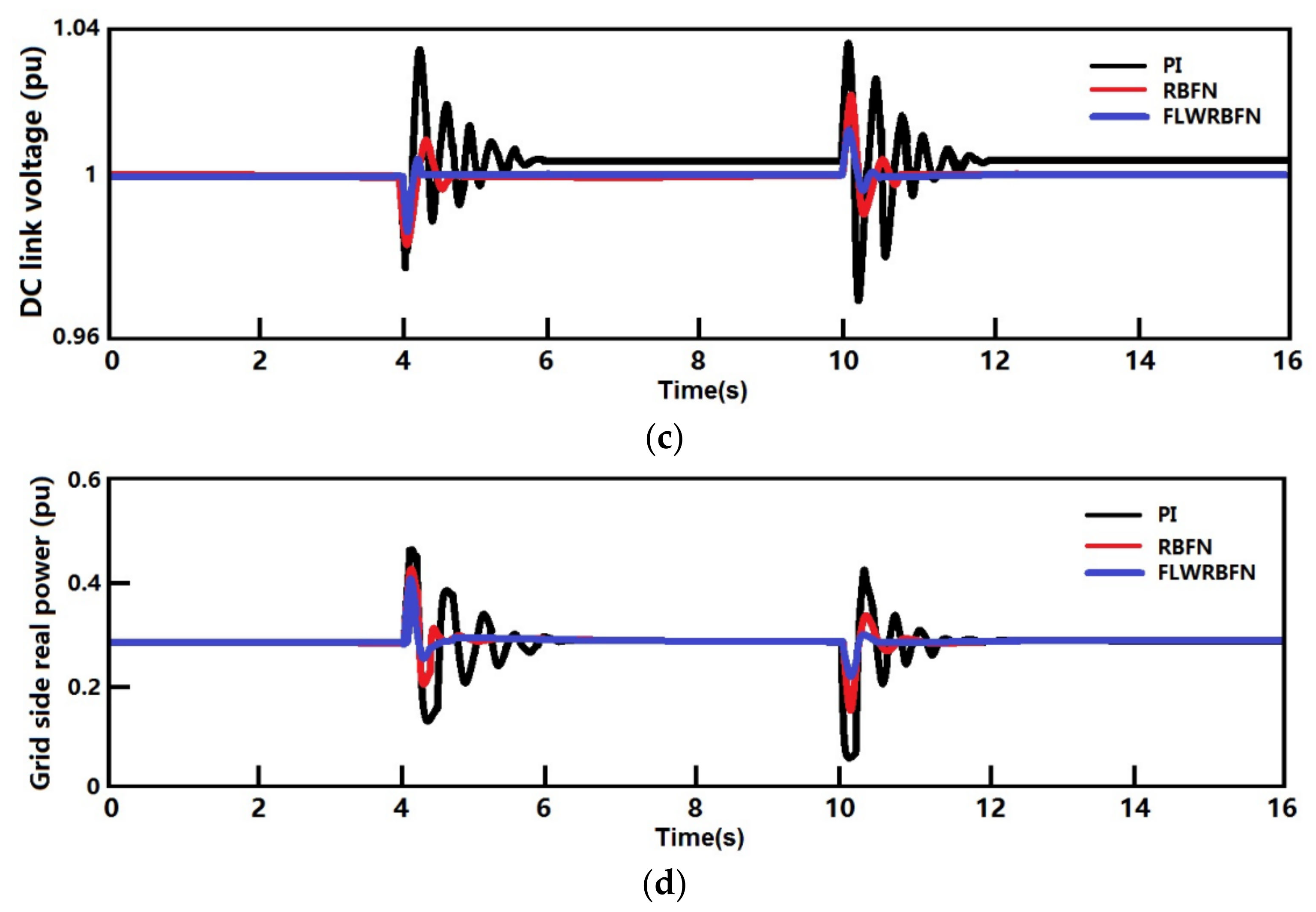
5. Simulation Results and Case Studies
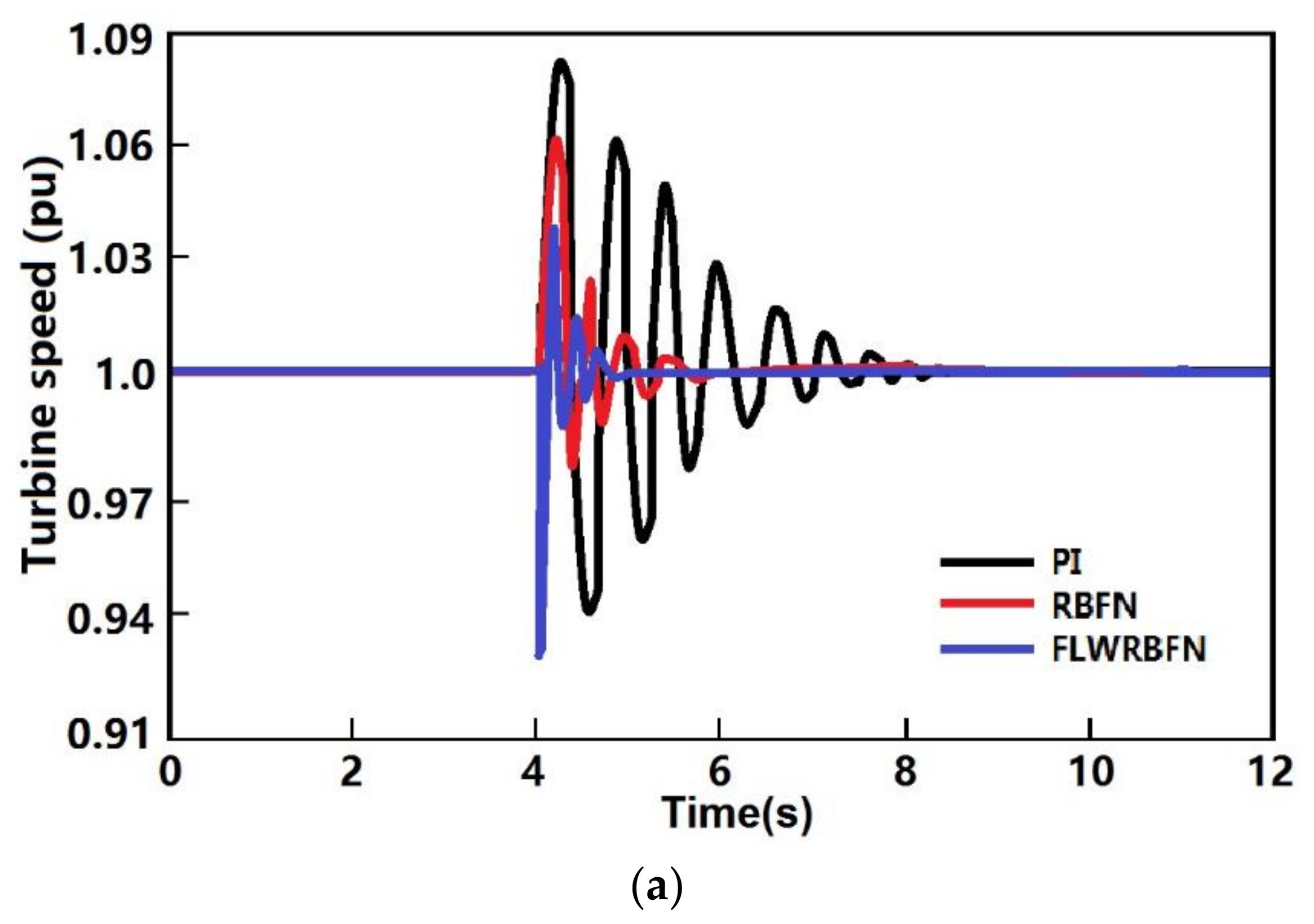
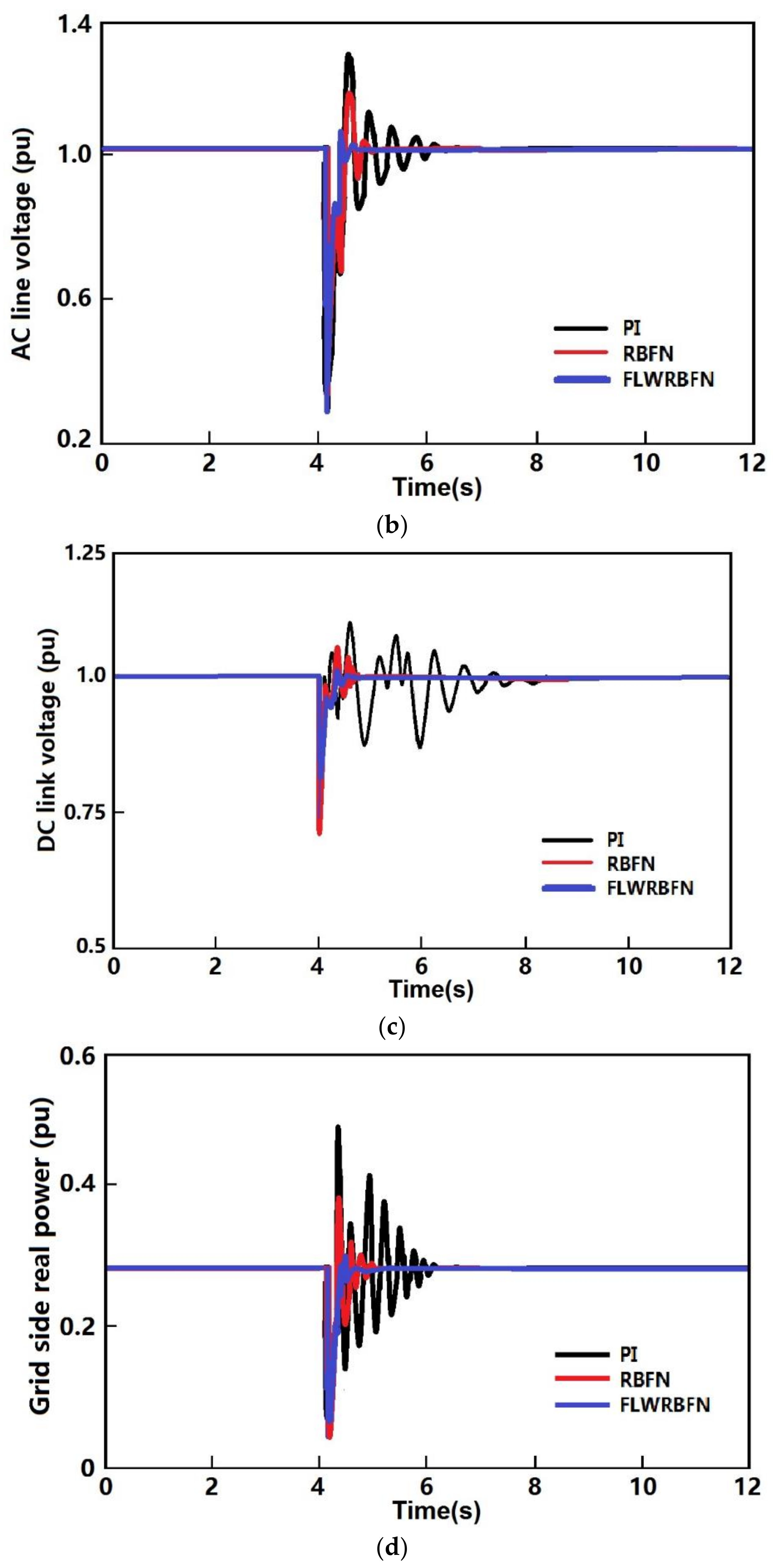
5.1. Load Change
5.2. Short Circuit Fault
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Halamay, D.A.; Simmons, A.; McArthur, S.; Brekken, T.K.A. Reserve requirement impacts of large-scale integration of wind, solar, and ocean wave power generation. IEEE Trans. Sustain. Energy 2011, 2, 321–328. [Google Scholar] [CrossRef]
- Zhao, X.; Yan, Z.; Zhang, X.-P. A wind-wave farm system with self-energy storage and smoothed power output. IEEE Access 2016, 4, 8634–8642. [Google Scholar] [CrossRef]
- Linda, S.; Rachel, S.; Thomas, D. What drives energy consumers: Engaging people in a sustainable energy transition. IEEE Power Energy Mag. 2018, 16, 20–28. [Google Scholar]
- Romain, G.; Josh, D.; John, V.R. Adaptive control of a wave energy converter. IEEE Trans. on Sustain. Energy 2018, 1, 1. [Google Scholar]
- Nicola, D.; Davide, B.; Francesco, G.; Paolo, C.; Giampaolo, B. Review of oscillating water column converters. IEEE Trans. Indust. Appl. 2016, 52, 1698–1710. [Google Scholar]
- Sunil, K.M.; Aradhna, P. Wells turbine modeling and PI control scheme for OWC plant using Xilinx system generator. In Proceedings of the International Conference on Power, Control & Embedded Systems (ICPCES), Allahabad, India, 9–11 March 2017; pp. 1–6. [Google Scholar]
- Francesco, F.; Ringwood, J.V. A simple and effective real-time controller for wave energy converters. IEEE Trans. Sustain. Energy 2013, 4, 21–30. [Google Scholar]
- Bacelli, G.; Nevarez, V.; Coe, R.G.; Wilson, D.G. Feedback Resonating Control for a Wave Energy Converter. IEEE Trans. Ind. Appl. 2019, 56, 1862–1868. [Google Scholar] [CrossRef]
- Foster, S.; Xu, L.; Fox, B. Coordinated reactive power control for facilitating fault ride through of doubly fed induction generator- and fixed speed induction generator-based wind farms. IET Renew. Power Gener. 2010, 4, 128–138. [Google Scholar] [CrossRef]
- López, J.; Gubía, E.; Olea, E.; Ruiz, J.; Marroyo, L. Ride through of wind turbines with doubly fed induction generator under sym-metrical voltage dips. IEEE Trans. Ind. Electron. 2009, 56, 4246–4254. [Google Scholar] [CrossRef]
- Meegahapola, L.G.; Littler, T.; Flynn, D. Decoupled-DFIG fault ride-through strategy for enhanced stability performance during grid faults. IEEE Trans. Sustain. Energy 2010, 1, 152–162. [Google Scholar] [CrossRef]
- Yang, L.; Xu, Z.; Ostergaard, J.; Dong, Z.Y.; Wong, K.P. Advanced control strategy of DFIG wind turbines for power system fault ride through. IEEE Trans. Power Syst. 2012, 27, 713–722. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimisation. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution-A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; Technical Report TR-95-012; International Computer Science Institute: Berkley, CA, USA, 1995. [Google Scholar]
- Mohammadmehdi, S.; Rasoul, R.; Saad, M.; Amanullah, M.T.O.; Alex, S.; Tey, K.S.; Alireza, S.G. Simulation and hardware im-plementation of new maximum power point tracking technique for partially shaded PV system using hybrid depso method. IEEE Trans. Sustain. Energy 2015, 6, 850–862. [Google Scholar]
- Huo, J.; Ma, L.; Yu, Y.; Wang, J. Hybrid algorithm based mobile robot localization using DE and PSO. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 5955–5959. [Google Scholar]
- Wang, P.; Liang, L.; Ji, Y.; Liu, X.; Chen, S.; Xie, G.; Fan, L. Parameter identification of steam turbine governor system based on DEPSO algorithm. In Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE); Institute of Electrical and Electronics Engineers (IEEE), Beijing, China, 17–19 August 2017; pp. 228–232. [Google Scholar]
- Elgammal, A.A.A. Adaptive fuzzy sliding mode controller for grid interface ocean wave energy conversion. J. Intell. Learn. Syst. Appl. 2014, 6, 53–69. [Google Scholar] [CrossRef]
- Hong, Y.; Waters, R.; Bostrom, C.; Eriksson, M.; Engstrom, J.; Leijon, M. Review on electrical control strategies for wave energy conversion systems. Renew. Sustain. Energy Rev. 2014, 31, 329–342. [Google Scholar] [CrossRef]
- Lin, W.-M.; Hong, C.-M.; Huang, C.-H.; Ou, T.-C. Hybrid control of a wind induction generator based on grey-elman neural network. IEEE Trans. Control. Syst. Technol. 2013, 21, 2367–2373. [Google Scholar] [CrossRef]
- Patra, J.C.; Pal, R.N. A functional link artificial neural network for adaptive channel equalization. Signal Process. 1995, 43, 181–195. [Google Scholar] [CrossRef]
- Ou, T.-C.; Lu, K.-H.; Huang, C.-J. Improvement of transient stability in a hybrid power multi-system using a designed NIDC (novel intelligent damping controller). Energies 2017, 10, 488. [Google Scholar] [CrossRef]
- Lin, W.; Lu, K.; Ou, T. Design of a novel intelligent damping controller for unified power flow controller in power system connected offshore power applications. IET Gener. Transm. Distrib. 2015, 9, 1708–1717. [Google Scholar] [CrossRef]
- Vinal, P.; Vaibhav, G.; Shashank, H.; Nithin, V.G. Design of adaptive exponential functional link network-based nonlinear filters. IEEE Trans. Circ. Syst. I. Regular Papers 2016, 63, 1434–1442. [Google Scholar]
- Brekken, T.K.A.; Ozkan-Haller, H.T.; Simmons, A. A methodology for large-scale ocean wave power time-series generation. IEEE J. Ocean. Eng. 2012, 37, 294–300. [Google Scholar] [CrossRef]
- Cashman, D.P. Electrical Machine Characterisation and Analysis for Renewable Energy Applications. Ph.D. Thesis, University College Cork, Cork, Ireland, 2010. [Google Scholar]
- Wang, L.; Chen, Z.-J. Stability analysis of a wave-energy conversion system containing a grid-connected induction generator driven by a wells turbine. IEEE Trans. Energy Convers. 2009, 25, 555–563. [Google Scholar] [CrossRef]
- Kiran, D.R.; Palani, A.; Muthukumar, S.; Jayashankar, V. Steady grid power from wave energy. IEEE Trans. Energy Convers. 2007, 22, 539–540. [Google Scholar] [CrossRef]
- Hogg, R.V.; McKean, J.W.; Craig, A.T. Introduction to Mathematical Statistics, 6th ed.; Prentice-Hall: New Jersey, NJ, USA, 2005. [Google Scholar]
- Lin, W.M.; Hong, C.M. Intelligent approach to maximum power point tracking control strategy for variable-speed wind turbine generation system. Energy 2010, 35, 2440–2447. [Google Scholar] [CrossRef]
- Lin, C.T.; Lee, G.C.S. Neural Fuzzy Systems; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Elsayed, S.M.; Sarker, R.A.; Essam, D.L. An improved self-adaptive differential evolution algorithm for optimization problems. IEEE Trans. Ind. Inform. 2012, 9, 89–99. [Google Scholar] [CrossRef]
- Xin, B.; Chen, J.; Zhang, J.; Fang, H.; Peng, Z.-H. Hybridizing differential evolution and particle swarm optimization to design powerful optimizers: A review and taxonomy. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2011, 42, 744–767. [Google Scholar] [CrossRef]
- Ben, N.; Li, L. A novel PSO-DE-based hybrid algorithm for global optimization. Comp. Sci. 2008, 5227, 156–163. [Google Scholar]
- Wu, Y.C.; Lee, W.P.; Chien, C.W. Modified the performance of differential evolution algorithm with dual evolution strategy. Int. Conf. Machine Learn. Comp. 2011, 3, 57–63. [Google Scholar]
- Yoo, S.J.; Choi, Y.H.; Park, J.B. Generalized predictive control based on self-recurrent wavelet neural network for stable path tracking of mobile robots: Adaptive learning rates approach. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 1381–1394. [Google Scholar] [CrossRef]
- Wai, R.J.; Li, C.M. Design of dynamic petri recurrent fuzzy neural network and its application to path-tracking control of nonho-lonomic mobile robot. IEEE Trans. Indust. Electron. 2009, 56, 2667–2683. [Google Scholar]
- Lin, W.-M.; Hong, C.-M. A new Elman neural network-based control algorithm for adjustable-pitch variable-speed wind-energy conversion systems. IEEE Trans. Power Electron. 2010, 26, 473–481. [Google Scholar] [CrossRef]
- Lu, K.-H.; Hong, C.-M.; Han, Z.; Yu, L. New Intelligent Control Strategy Hybrid Grey–RCMAC Algorithm for Ocean Wave Power Generation Systems. Energies 2020, 13, 241. [Google Scholar] [CrossRef]


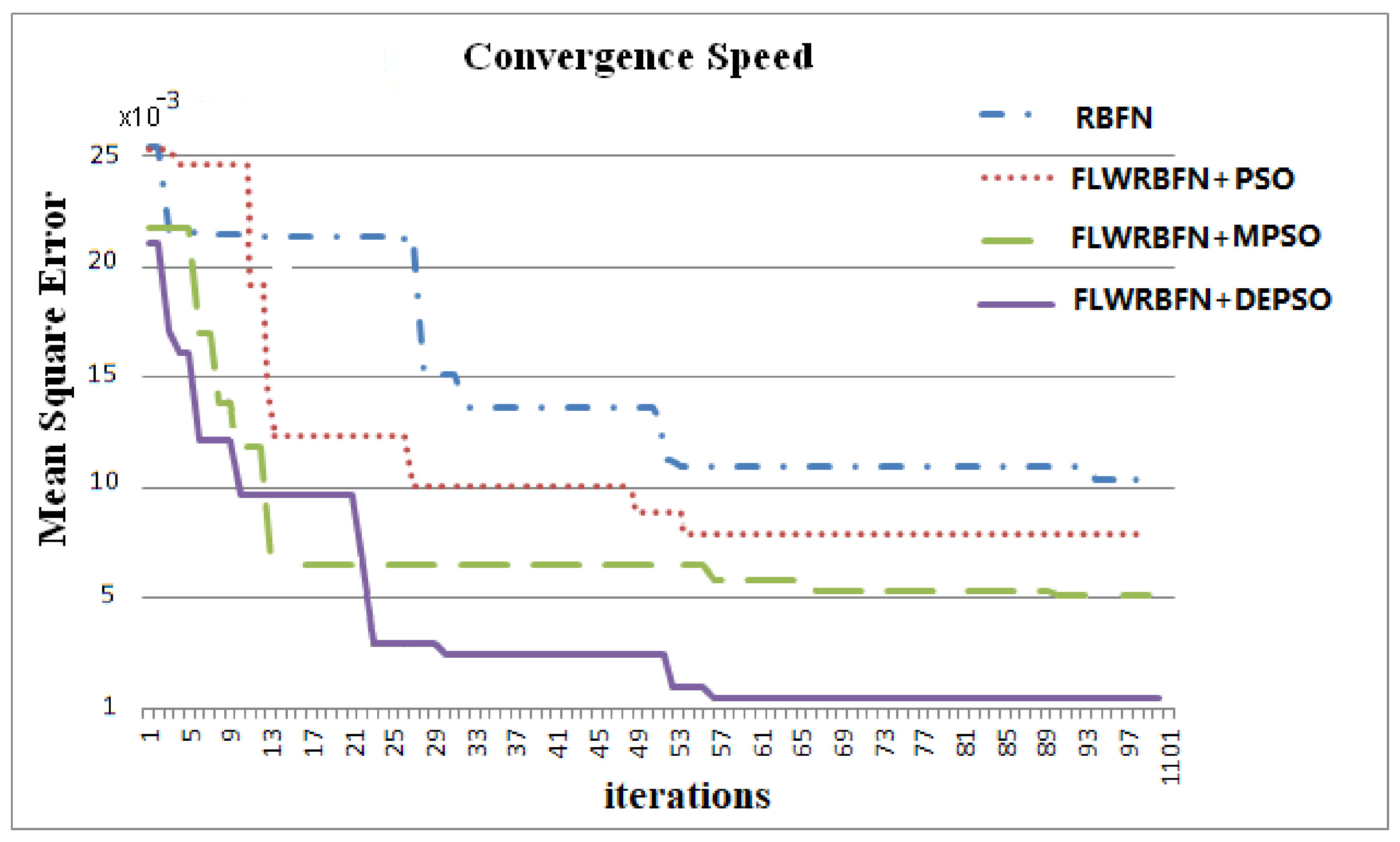
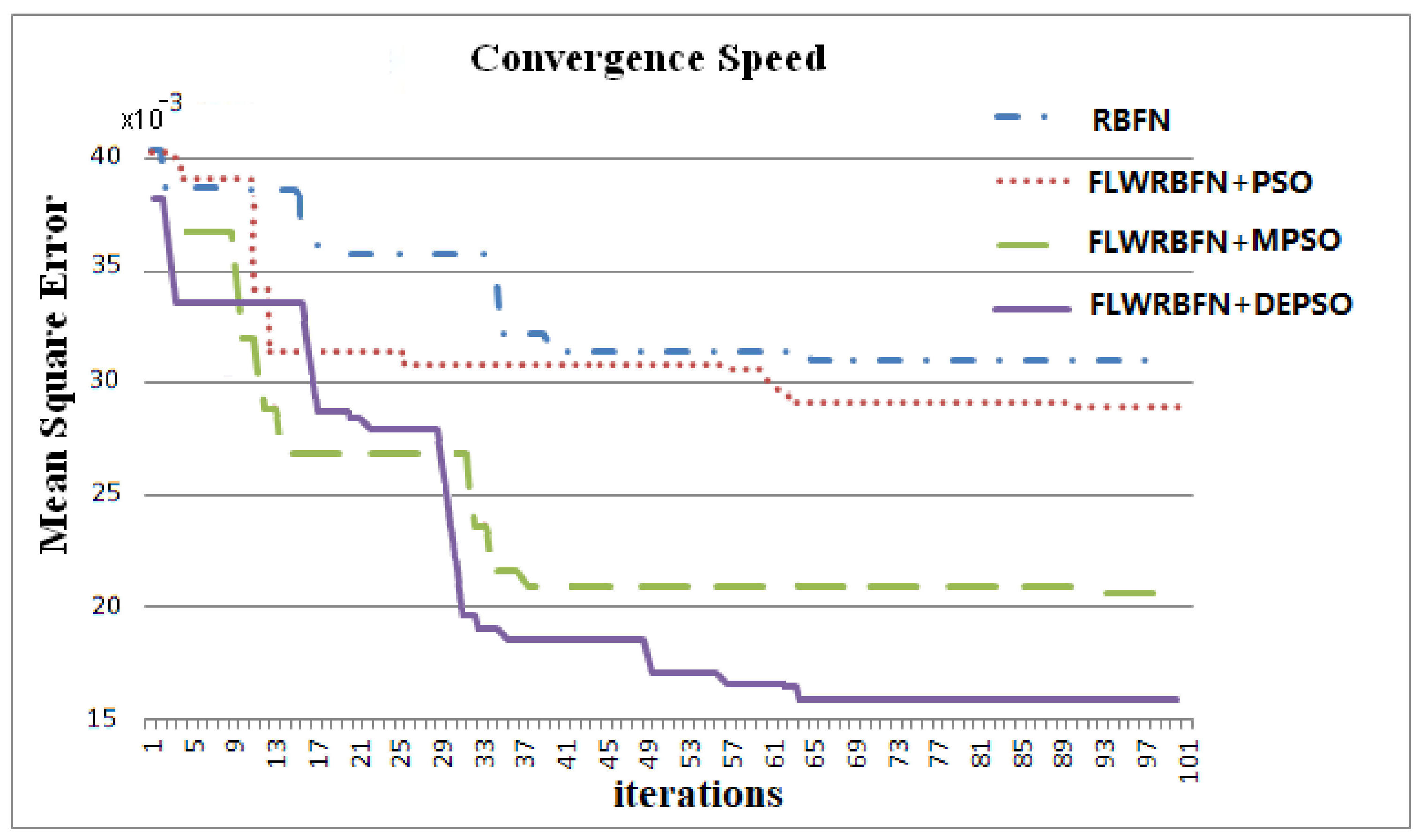
| Method | Iterative Number | CPU Run Time (102 s) | Mean Square Error (10−3) | Accuracy (%) |
|---|---|---|---|---|
| FLWRBFN + DEPSO | 57 | 1.48 | 1.235 | 98.76 |
| FLWRBFN + MPSO | 90 | 2.34 | 5.017 | 94.98 |
| FLWRBFN + PSO | 54 | 1.40 | 7.581 | 92.42 |
| RBFN | 94 | 2.44 | 10.051 | 89.95 |
| Methods | Interative Number | CPU Run Time (102 s) | Mean Square Error (10−3) | Accuracy (%) |
|---|---|---|---|---|
| FLWRBFN + DEPSO | 64 | 1.66 | 15.965 | 84.03 |
| FLWRBFN + MPSO | 94 | 2.44 | 20.071 | 79.93 |
| FLWRBFN + PSO | 91 | 2.36 | 29.057 | 70.94 |
| Method | FLWRBFN + DEPSO | FLWRBFN + MPSO | FLWRBFN + PSO | RBFN |
|---|---|---|---|---|
| Grid-Side Voltage | 1.0003125 | 1.0005316 | 1.0004338 | 0.9976911 |
| DC-Side Voltage | 1.0012123 | 1.0026557 | 1.0013670 | 0.9896110 |
| Max. Transient Over Shoot Voltage | 1.0043437 | 1.0060341 | 1.0071922 | 1.0085975 |
| Max. Transient Under Shoot Voltage | 0.9965313 | 0.9954371 | 0.9957687 | 0.991125 |
| Method | FLWRBFN + DEPSO | FLWRBFN + MPSO | FLWRBFN + PSO | RBFN |
|---|---|---|---|---|
| Grid-Side Voltage | 1.0204878 | 1.0257873 | 1.0310922 | 1.0214457 |
| DC-Side Voltage | 1.006251 | 1.0069122 | 1.0052166 | 1.0071458 |
| Max. Transient Over Shoot Voltage | 1.0780488 | 1.0993411 | 1.1477012 | 1.1931707 |
| Max. Transient Under Shoot Voltage | 0.9609756 | 0.0922378 | 0.0912409 | 0.0902439 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.-H.; Hong, C.-M.; Tan, X.; Cheng, F.-S. Novel Intelligent Control Technology for Enhanced Stability Performance of an Ocean Wave Energy Conversion System. Energies 2021, 14, 2027. https://doi.org/10.3390/en14072027
Lu K-H, Hong C-M, Tan X, Cheng F-S. Novel Intelligent Control Technology for Enhanced Stability Performance of an Ocean Wave Energy Conversion System. Energies. 2021; 14(7):2027. https://doi.org/10.3390/en14072027
Chicago/Turabian StyleLu, Kai-Hung, Chih-Ming Hong, Xiaojing Tan, and Fu-Sheng Cheng. 2021. "Novel Intelligent Control Technology for Enhanced Stability Performance of an Ocean Wave Energy Conversion System" Energies 14, no. 7: 2027. https://doi.org/10.3390/en14072027
APA StyleLu, K.-H., Hong, C.-M., Tan, X., & Cheng, F.-S. (2021). Novel Intelligent Control Technology for Enhanced Stability Performance of an Ocean Wave Energy Conversion System. Energies, 14(7), 2027. https://doi.org/10.3390/en14072027







