Component-in-the-Loop Testing of Automotive Powertrains Featuring All-Wheel-Drive
Abstract
1. Introduction
2. Component-in-the-Loop System Concepts
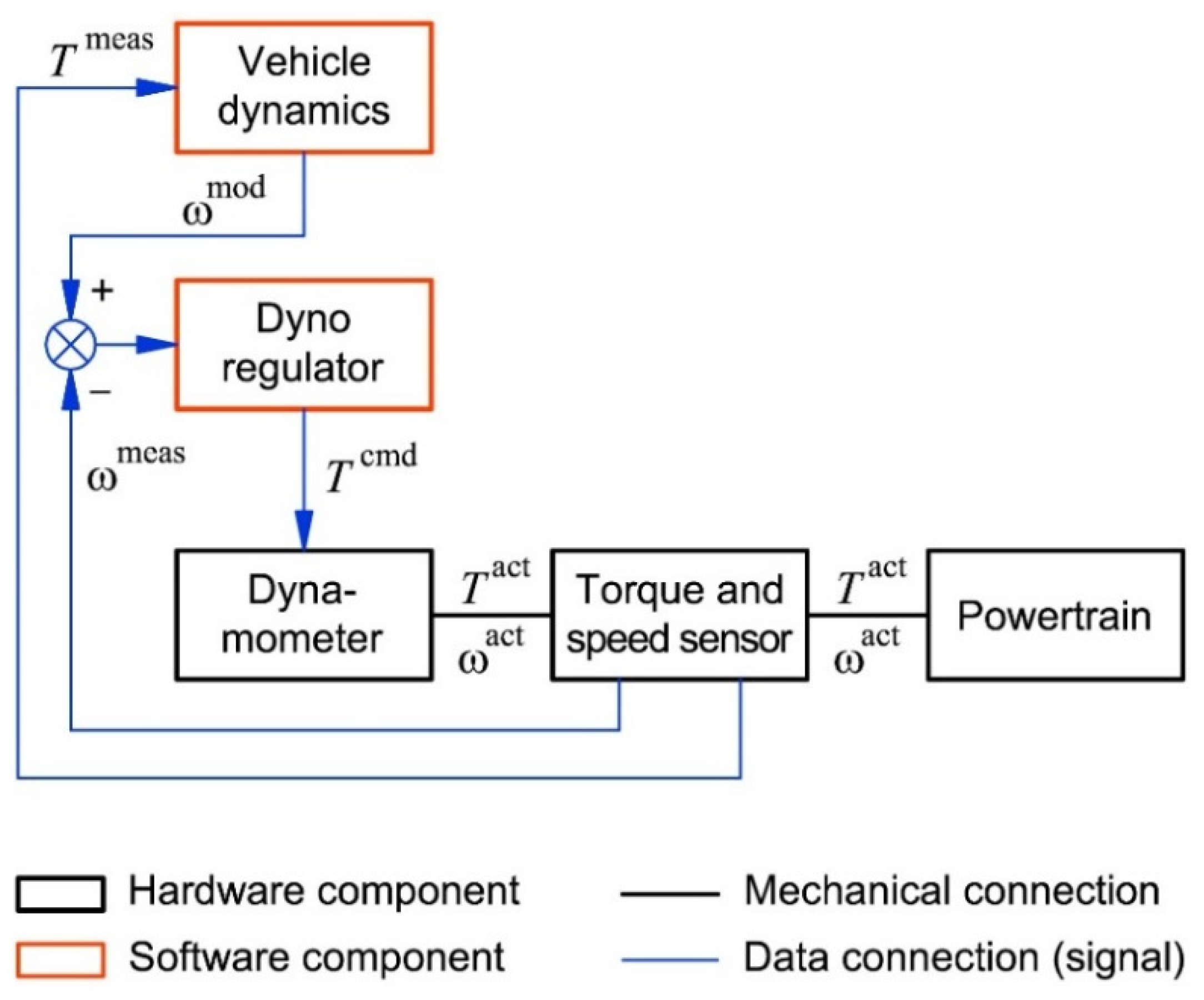
2.1. Operating and Control Loops
2.2. Virtual Inertia
3. Mathematical Models of Vehicle Dynamics for CiL Systems
3.1. “Simple” Model
3.2. “Complex” Model
4. Case Study
4.1. The Object and the Tasks
4.2. Component-in-the-Loop System Design and Implementation
4.2.1. Design Concept
4.2.2. Implementation
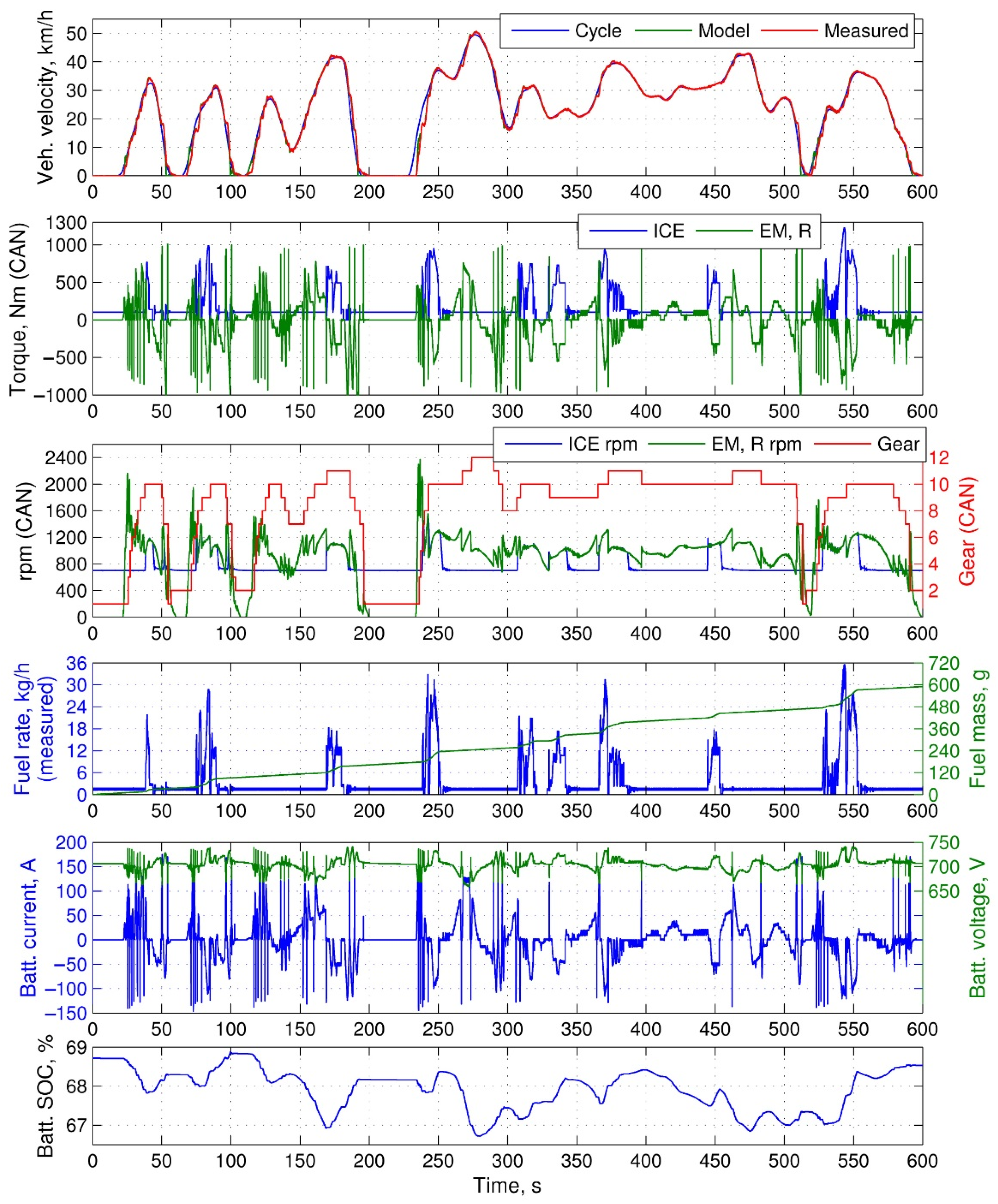
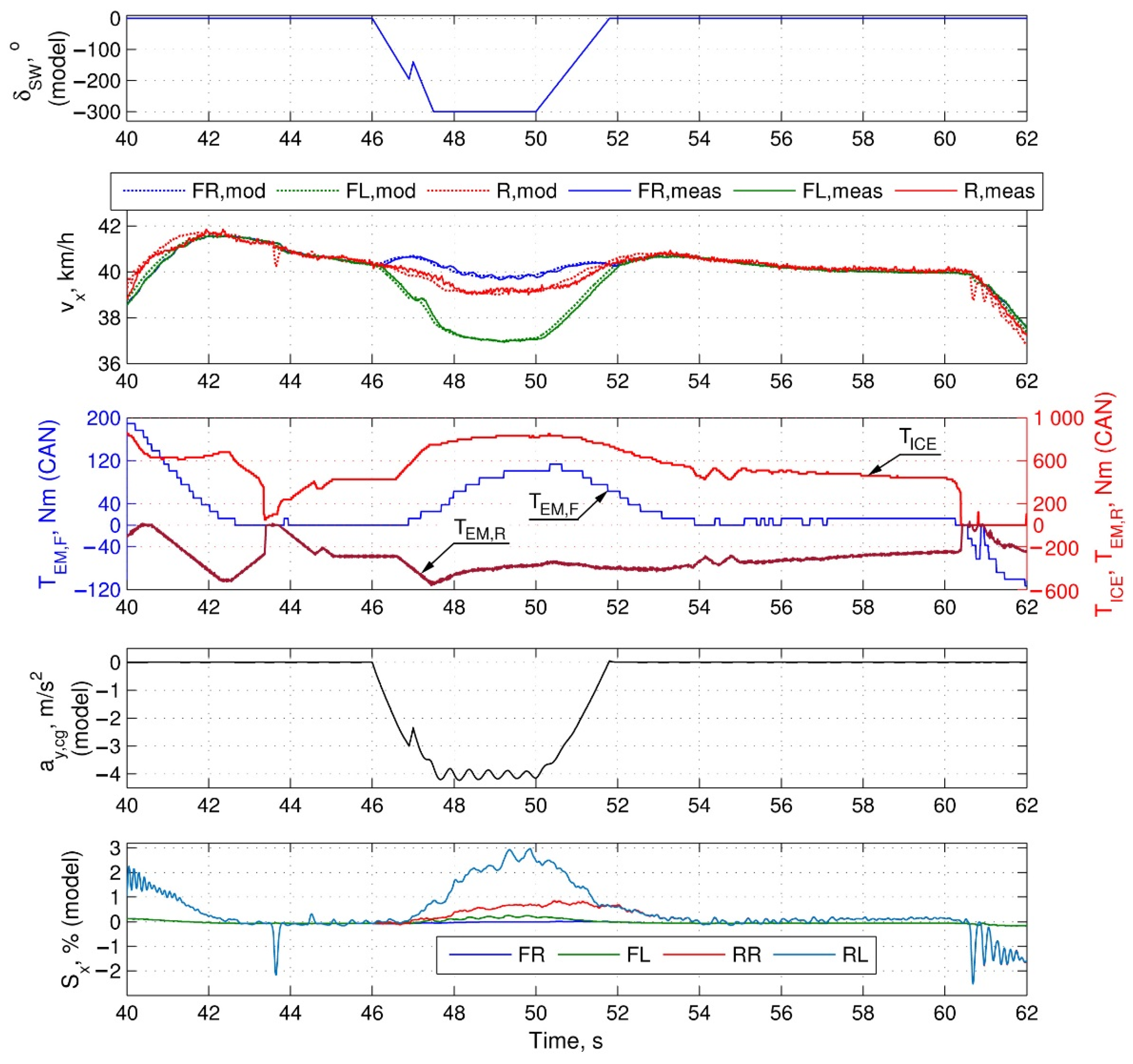
4.3. Component-in-the-Loop Testing Results
5. Conclusions
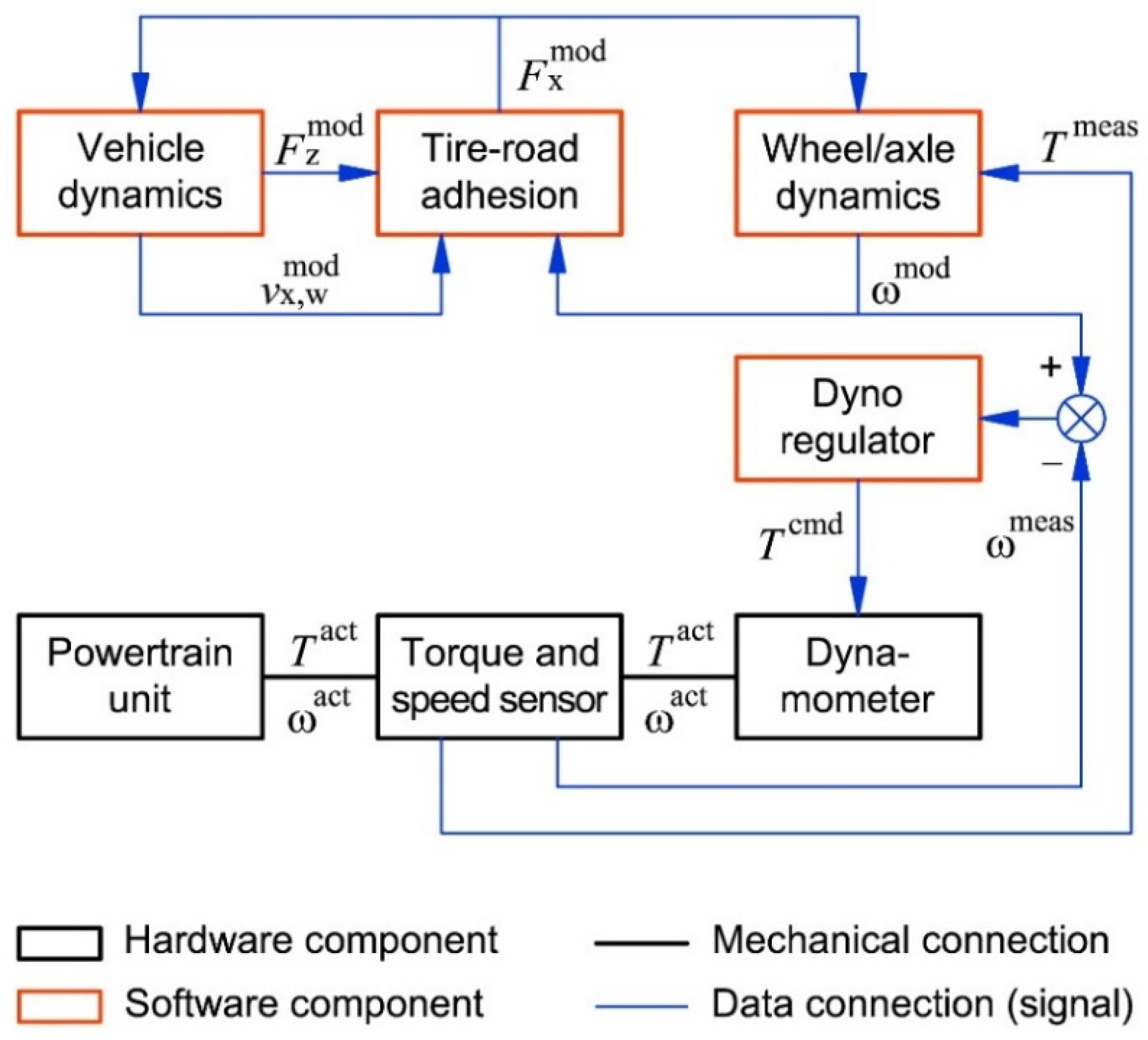
- When considering all-wheel-drive powertrains having functions that deal with vehicle active safety and dynamics, the CiL system is supposed to simulate vehicle maneuvers at road surfaces with a limited tire adhesion. In that case, one can use the described principle of synchronizing the operating loads between different drivelines of the powertrain taking into account their independent rotation due to tire slip or/and kinematics of trajectory motion. The principle is based on the cyclic relations between the vehicle velocity and the wheel speed stemming from the tire slip and the longitudinal tire force. The latter is a function of the slip, and simultaneously, the common acting factor for both the vehicle- and wheel dynamics. Therefore, the simulating loops sharing the common vehicle velocity and the individual angular speeds of the wheels generate the rpm commands for the dynamometers connected to the physical drivelines resulting in their synchronization in accordance with the simulated driving mode. The model of vehicle dynamics serves as a synchronizing “pivot” for the speed regimes of the modeled wheels (or axles) and the loading regimes of the hardware drivelines associated with those wheels.
- The analysis and clarification of the “virtual inertia” principle allows concluding that when an inertia is simulated by means of a closed loop control of the drivetrain’s shaft angular speed, it does not need to be taken into account or compensated in any additional way—neither in the vehicle model, nor in the CiL control system. If the virtual inertia is intended to simulate the vehicle mass then, in the virtual model, the vehicle should have the same mass as in an actual road test (i.e., no mass correction is required). The torque feedback signal provided by the shaft-mounted sensor “drives” the virtual vehicle, while the shaft angular speed feedback makes the dynamometer exert an operating load corresponding to the sum of the resistance forces including the inertial one.
- If the laboratory equipment employed in the CiL system is limited in terms of precision and time response, one can resort to the described method of tire slip simulation having low sensitivity to errors of measurement equipment and actuating mechanisms. The method implies that the slip is estimated using the calculated value of the wheel angular speed rather than that derived from the measured shaft rpm. This makes calculation of the tire force less dependent on hardware inaccuracies, therefore avoiding errors in the loading torque exerted by the dynamometer. When using the calculated quantity of the angular speed, the hardware equipment of a CiL system will simulate tire slip to the extent of accuracy allowed by its construction, hardware errors will not have a significant influence on this process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CAD | Computer aided design |
| CAN | Controller area network |
| CiL | Component-in-the-Loop |
| EM | Electric machine |
| FL, FR | Front left, front right |
| HCU | Hybrid Control Unit |
| ICE | Internal combustion engine |
| R | Rear (index) |
| SOC | State of charge |
| UNECE | United Nations Economic Commission for Europe |
References
- Isermann, R. Fahrdynamik-Regelung. Modellbildung, Fahrerassistenzsysteme, Mechatronik; Friedr. Vieweg & Sohn Verlag|GWV Fachverlage GmbH: Wiesbaden, Germany, 2006; pp. 169–211. [Google Scholar]
- Bakhmutov, S.V.; Ivanov, V.G.; Karpukhin, K.E.; Umnitsyn, A.A. Creation of operation algorithms for combined operation of anti-lock braking system (ABS) and electric machine included in the combined power plant. IOP Conf. Ser. Mater. Sci. Eng. 2018, 012003. [Google Scholar] [CrossRef]
- Shorin, A.A.; Karpukhin, K.E.; Terenchenko, A.S.; Kondrashov, V.N. Traction module of cabless unmanned cargo vehicles with electric drive. Int. J. Mech. Eng. Technol. 2018, 9, 1903–1909. [Google Scholar]
- Herring, J.A.; Burnham, K.J.; Oleksowicz, S. Review and Simulation of Torque Vectoring Yaw Rate Control. In Proceedings of the International Conference on Systems Engineering (ICSE), Coventry, UK, 11–13 September 2012. [Google Scholar]
- Goggia, T.; Sorniotti, A.; De Novellis, L.; Ferrara, A.; Pennycott, A.; Gruber, P.; Yunus, I. Integral Sliding Mode for the Yaw moment Control of Four-Wheel-Drive Fully Electric Vehicles with In-Wheel Motors. Int. J. Powertrains 2015, 4, 388–419. [Google Scholar] [CrossRef]
- Albers, A.; Düser, T. Implementation of a Vehicle-in-the-Loop Development and Validation Platform. Automobiles and sustainable mobility. In Proceedings of the FISITA 2010 World Automotive Congress, Budapest, Hungary, 30 May–4 June 2010. [Google Scholar]
- Tibba, G.; Malz, C.; Stoermer, C.; Nagarajan, N.; Zhang, L.; Chakraborty, S. Testing Automotive Embedded Systems under X-in-the-loop Setups. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD ’16), Austin, TX, USA, 7–10 November 2016. [Google Scholar] [CrossRef]
- Ivanov, V.; Augsburg, K.; Bernad, C.; Dhaens, M.; Dutré, M.; Gramstat, S.; Magnin, P.; Schreiber, V.; Skrt, U.; van Kelecom, N. Connected and Shared X-in-the-Loop Technologies for Electric Vehicle Design. World Electr. Veh. J. 2019, 10, 83. [Google Scholar] [CrossRef]
- Fegraus, C.E.; D’Angelo, S. Inertia and Road Load Simulation for Vehicle Testing. Patent US 4,161,116, 21 September 1977. [Google Scholar]
- Henry, K.J.; Kotwicki, A.J. Emulation System for a Motor Vehicle Drivetrain. Patent US 4,680,959, 23 April 1986. [Google Scholar]
- Lang, T.; Schyr, C. Simulation Aided Process for Developing Powertrains. In Proceedings of the SAE Brazil Convention 2000 (International Mobility Technology Conference and Exhibit), Sao Paulo, Brazil, 2–4 October 2000. [Google Scholar]
- Scordia, J.; Trigui, R.; Desbois-Renaudin, M.; Jeanneret, B.; Badin, F. Global Approach for Hybrid Vehicle Optimal Control. J. Asian Electr. Veh. 2009, 7, 1221–1230. [Google Scholar] [CrossRef]
- Trigui, R.; Jeanneret, B.; Malaquin, B.; Plasse, C. Performance Comparison of Three Storage Systems for Mild PHEVs Using PHIL Simulation. IEEE Trans. Veh. Technol. 2009, 58, 3959–3969. [Google Scholar] [CrossRef]
- Wu, J.; Dufour, C.; Sun, L. Hardware-in-the-Loop Testing of hybrid vehicle motor drives at Ford Motor Company. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010. [Google Scholar] [CrossRef]
- Kaup, C.; Pels, T.; Ebner, P.; Ellinger, R.; Gschweitl, K.; Loibner, E.; Schneider, R.; Walter, L. Systematic Development of Hybrid Systems for Commercial Vehicles; SAE Technical Paper 2011-28-0064; SAE: Warrendale, PA, USA, 2011. [Google Scholar] [CrossRef]
- Sheng-bing, Y.; Zhen-zhen, L.; Feng, X.; Guo-guang, Z.; Yuan-fa, D.; Jun, W. A Electric Vehicle Powertrain Simulation and Test of Driving Cycle Based on AC Electric Dynamometer Test Bench. In Proceedings of the 2012 International Conference on Mechanical Engineering and Material Science (MEMS 2012), Yangzhou, China, 16–18 December 2012; pp. 273–276. [Google Scholar] [CrossRef]
- Li, W.; Shi, X.; Guo, D.; Yi, P. A Test Technology of a Vehicle Driveline Test Bench with Electric Drive Dynamometer for Dynamic Emulation; SAE Technical Paper 2015-01-1303; SAE: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Klein, S.; Xia, F.; Etzold, K.; Andert, J.; Amringer, N.; Walter, S.; Blochwitz, T.; Bellanger, C. Electric-Motor-in-the-Loop: Efficient Testing and Calibration of Hybrid Power Trains. IFAC-PapersOnLine 2018, 51, 240–245. [Google Scholar] [CrossRef]
- Vafaeipour, M.; El Baghdadi, M.; Verbelen, F.; Sergeant, P.; Van Mierlo, J.; Hegazy, O. Experimental Implementation of Power-Split Control Strategies in a Versatile Hardware-in-the-Loop Laboratory Test Bench for Hybrid Electric Vehicles Equipped with Electrical Variable Transmission. Appl. Sci. 2020, 10, 4253. [Google Scholar] [CrossRef]
- Jiang, S.; Smith, M.; Kitchen, J.; Ogawa, A. Development of an Engine-in-the-Loop Vehicle Simulation System in Engine Dynamometer Test Cell; SAE Technical Paper 2009-01-1039; SAE: Warrendale, PA, USA, 2009. [Google Scholar] [CrossRef]
- Klein, S.; Savelsberg, R.; Xia, F.; Guse, D.; Andert, J.; Blochwitz, T.; Bellanger, C.; Walter, S.; Beringer, S.; Jochheim, J.; et al. Engine in the Loop: Closed Loop Test Bench Control with Real-Time Simulation. SAE Int. J. Commer. Veh. 2017, 10, 95–105. [Google Scholar] [CrossRef]
- Jung, T.; Kötter, M.; Schaub, J.; Quérel, C.; Thewes, S.; Hadj-amor, H.; Picard, M.; Lee, S.-Y. Engine-in-the-Loop: A Method for Efficient Calibration and Virtual Testing of Advanced Diesel Powertrains. In Simulation und Test 2018. Antriebsentwicklung im Digitalen Zeitalter 20. MTZ-Fachtagung; Springer Fachmedien GmbH: Wiesbaden, Germany, 2019. [Google Scholar] [CrossRef]
- Ersal, T.; Brudnak, M.; Stein, J.L.; Fathy, H.K. Variation-based transparency analysis of an internet-distributed hardware-in-the-loop simulation platform for vehicle powertrain systems. In Proceedings of the ASME Dynamic Systems and Control Conference, Hollywood, CA, USA, 12–14 October 2009; part B ed.. pp. 1217–1224. [Google Scholar] [CrossRef]
- Andert, J.; Klein, S.; Savelsberg, R.; Pischinger, S.; Hameyer, K. Virtual Shaft: Synchronized Motion Control for Real Time Testing of Automotive Powertrains. Control Eng. Pract. 2016, 56, 101–110. [Google Scholar] [CrossRef]
- Johnson, D.B.; Newberger, N.M.; Anselmo, I.C. Wheel Slip Simulation Systems and Methods. Patent US 8,631,693 B2, 23 December 2010. [Google Scholar]
- Germann, S.; Nonn, H.; Kopecky, W.; Abler, G.; Abler, G.; Witte, L.; Xuan, H.T.; Pfeiffer, M.; Brodbeck, P. Method of Simulating the Performance of a Vehicle on a Road Surface. Patent US 6,754,615 B1, 9 March 2000. [Google Scholar]
- Milliken, W.F.; Milliken, D.L. Race Car Vehicle Dynamics; SAE International: Warrendale, PA, USA, 1995; pp. 36–41. [Google Scholar]
- Pacejka, H.B.; Besselink, I. Tire and Vehicle Dynamics, 3rd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2012; pp. 4, 81–85, 165–183. [Google Scholar]
- Rill, G. Road Vehicle Dynamics. Fundamentals and Modeling; Taylor & Francis Group, LLC: Abingdon, UK, 2012; pp. 260, 303–309. [Google Scholar]
- Kulikov, I.A.; Bickel, J. Performance analysis of the vehicle electronic stability control in emergency maneuvers at low-adhesion surfaces. IOP Conf. Ser. Mater. Sci. Eng. 2019, 534, 012009. [Google Scholar] [CrossRef]
- Genta, G. Motor Vehicle Dynamics. In Modeling and Simulation; World Scientific: Singapore, 2006; pp. 43–44, 96. [Google Scholar]
- Hoffmann, J.; Kimmig, K.-L.; Baumgartner, A.; Erdmann, K.; Haas, W.; Wagner, P. The Top 3 of P2. Space, Space, Space. Mobility for Tomorrow. In Proceedings of the Schaeffler Symposium 2018, Baden-Baden, Germany, 11–13 April 2018; pp. 315–330. [Google Scholar]
- ZF Driveline Components–Hybrid Module. Available online: https://www.zf.com/products/en/cars/products_29311.html (accessed on 24 February 2021).
- United Nations Economic Commission for Europe (UNECE). Regulation No 49. In Uniform Provisions Concerning the Measures to Be Taken against the Emission of Gaseous and Particulate Pollutants from Compression Ignition Engines and Positive Ignition Engines for Use in Vehicles; United Nations Economic Commission for Europe: Geneva, Switzerland, 2013. [Google Scholar]
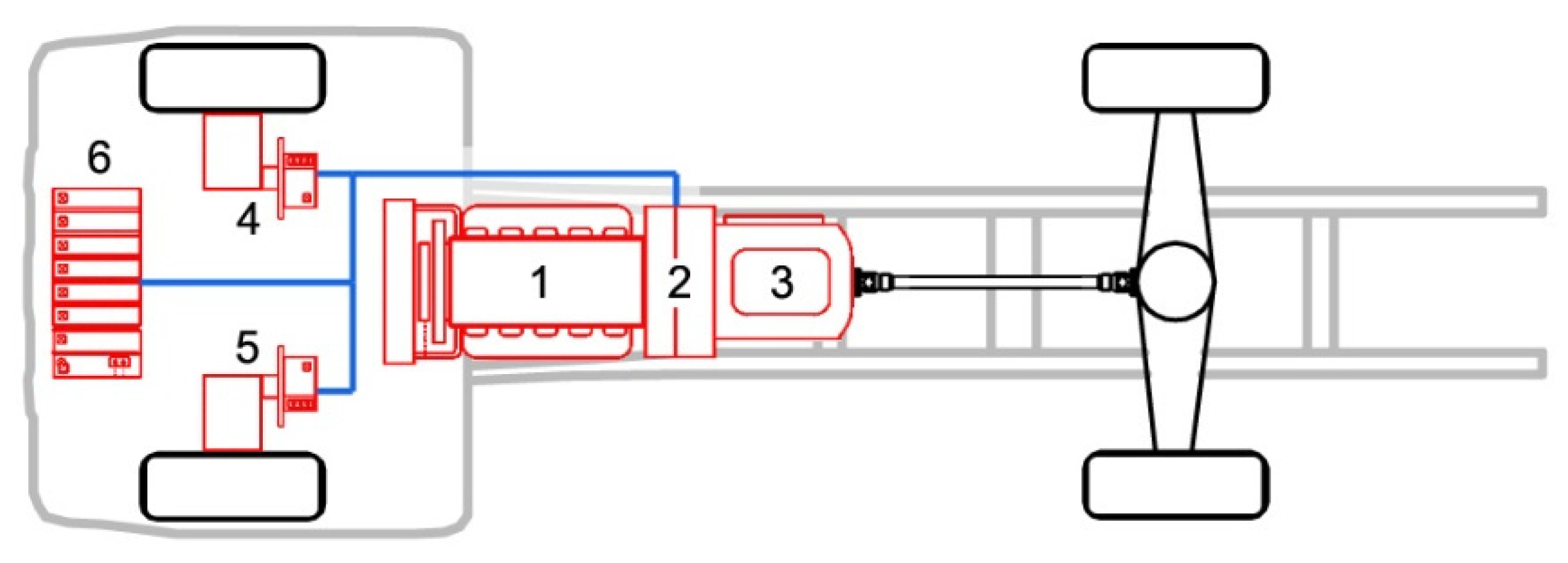
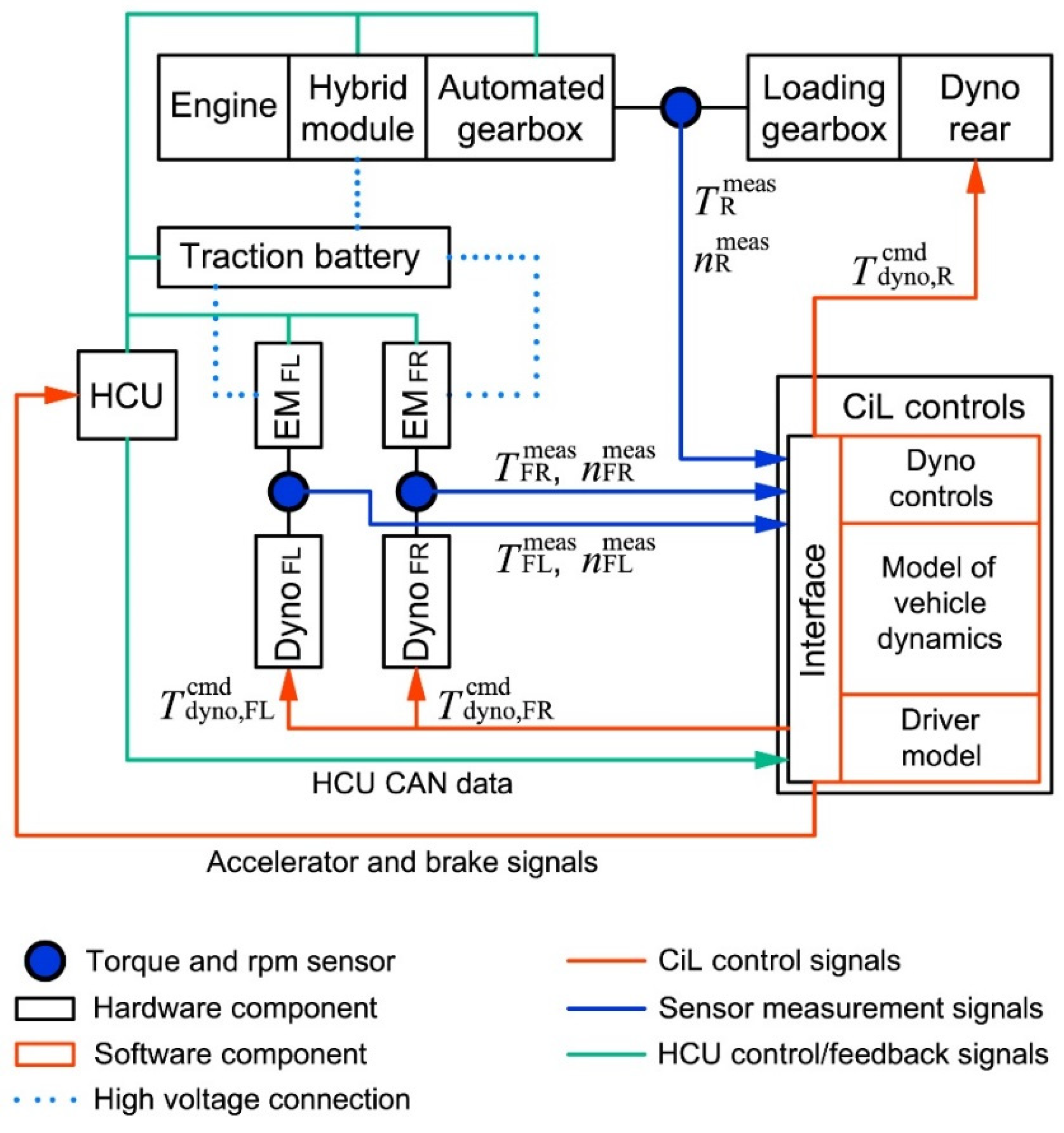

| Component | Type and/or Parameters |
|---|---|
| Internal combustion engine | diesel |
| Volume, L | 8.9 |
| Rated power, kW | 280 |
| Maximum torque, Nm | 1700 |
| Gearbox | automated mechanical, 12-speed |
| Hybrid module | three-phase, permanent magnet electric drive + automatic dry clutch |
| Maximum power of the electric drive, kW | 150 |
| Maximum torque of the electric drive, Nm | 1100 |
| Front electric drive (two units) | three-phase, permanent magnet |
| Unit’s maximum power, kW | 75 |
| Unit’s maximum torque, Nm | 250 |
| Reduction gear ratio | 12.6 |
| Traction battery | lithium-ion |
| Energy content, kWh | 14 |
| Nominal voltage, V | 700 |
| 9225 | 1.1 | 0.62 | 6.85 | 0.0045 | 2 × 10−6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulikov, I.; Korkin, S.; Kozlov, A.; Terenchenko, A.; Karpukhin, K.; Azimov, U. Component-in-the-Loop Testing of Automotive Powertrains Featuring All-Wheel-Drive. Energies 2021, 14, 2017. https://doi.org/10.3390/en14072017
Kulikov I, Korkin S, Kozlov A, Terenchenko A, Karpukhin K, Azimov U. Component-in-the-Loop Testing of Automotive Powertrains Featuring All-Wheel-Drive. Energies. 2021; 14(7):2017. https://doi.org/10.3390/en14072017
Chicago/Turabian StyleKulikov, Ilya, Sergey Korkin, Andrey Kozlov, Alexey Terenchenko, Kirill Karpukhin, and Ulugbek Azimov. 2021. "Component-in-the-Loop Testing of Automotive Powertrains Featuring All-Wheel-Drive" Energies 14, no. 7: 2017. https://doi.org/10.3390/en14072017
APA StyleKulikov, I., Korkin, S., Kozlov, A., Terenchenko, A., Karpukhin, K., & Azimov, U. (2021). Component-in-the-Loop Testing of Automotive Powertrains Featuring All-Wheel-Drive. Energies, 14(7), 2017. https://doi.org/10.3390/en14072017







