Optimal Siting and Sizing of Distributed Generators by Strawberry Plant Propagation Algorithm
Abstract
1. Introduction
- Type 1:
- Injects active power into the system;
- Type 2:
- Injects both active and reactive power into the system;
- Type 3:
- Injects active power but absorbs reactive power;
- Type 4:
- Injects reactive power only.
2. Power Loss Reduction and Cost Analysis Formulation
2.1. Power Loss Reduction
2.2. Cost Analysis
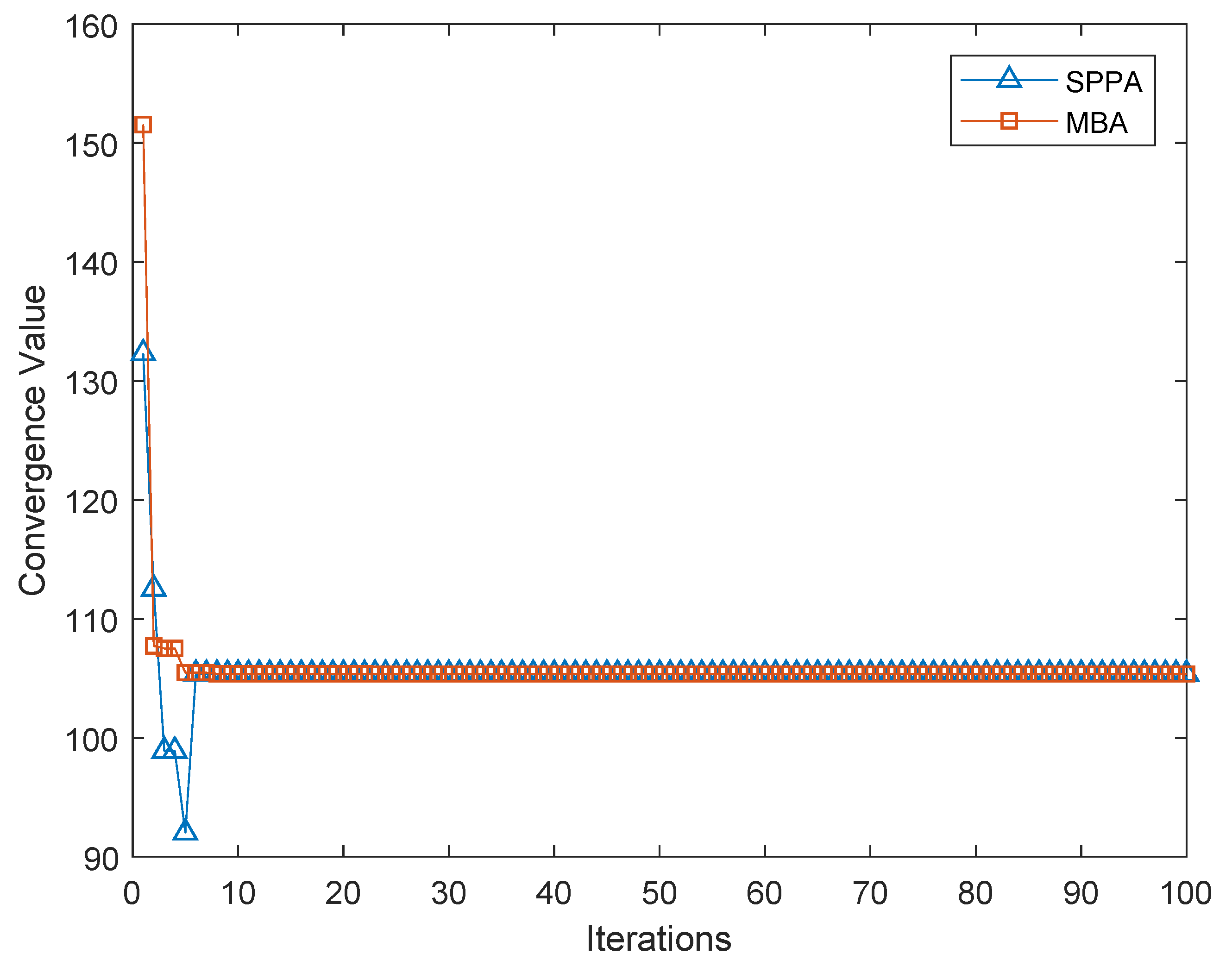
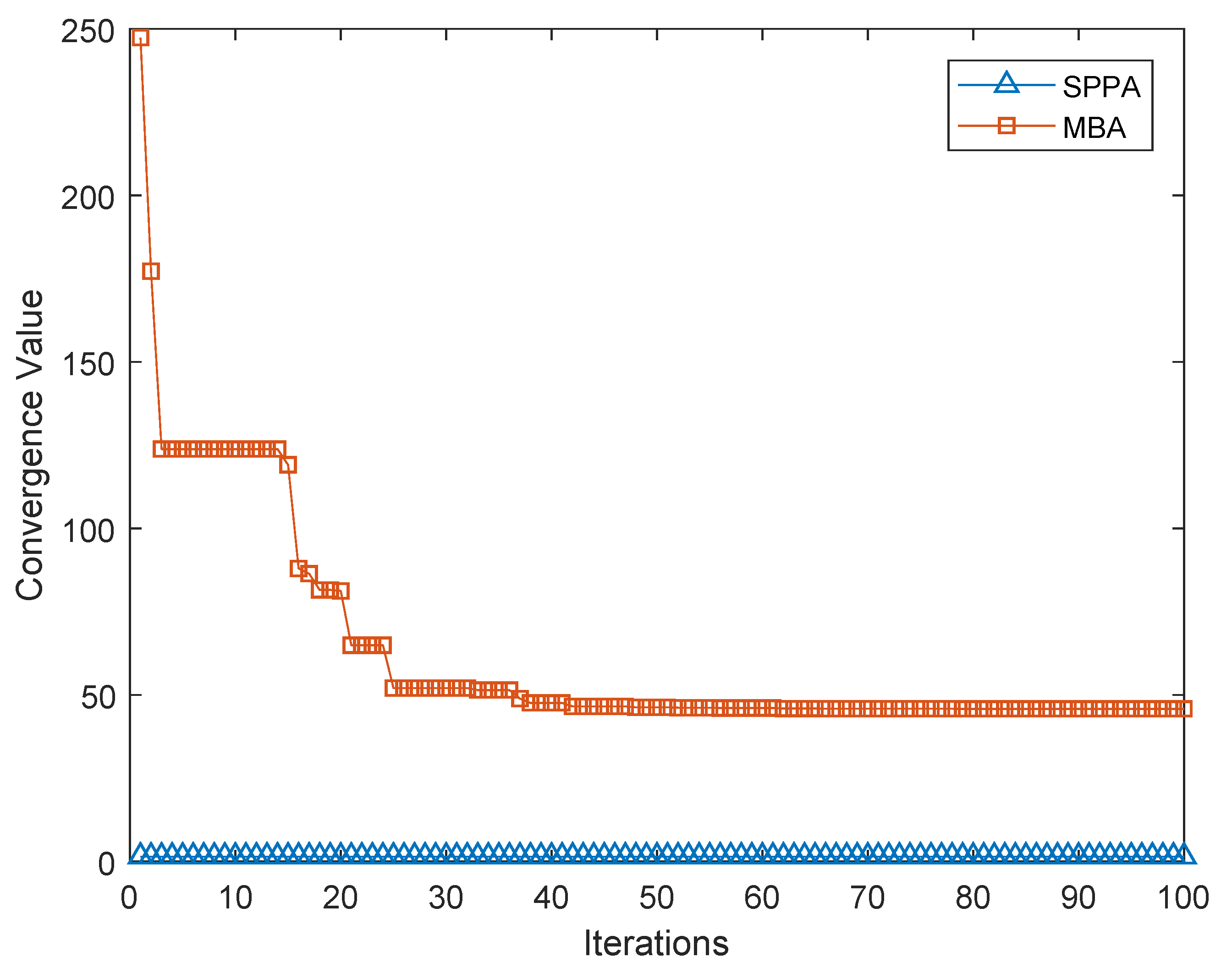
3. Optimization Using Strawberry Plant Propagation Algorithm
Optimal Placement of DGs Using SPPA
- Take network input from user and read system data.
- Initialize the algorithm parameters (, , population size , network size, DG type, and variable I to store the results of each iteration).
- Calculate P, Q, V, , and .
- Rank nodes with respect to power losses in descending order.
- Randomly, the number of runners, (i.e., DG Size) generated by a solution should be proportional to its fitness, given as:where is the maximum number of runners that can be generated, r is the binary variable, and is the mapped fitness of the solution.
- Distance covered (Loss) by each runner—i.e., —will be given as:
- The placement of DG is performed through an equation, given as:The values are then adjusted to ensure that new points generated are within the bounds and ; the distance calculated will be used to update the solution i based on the bounds in .
- Calculate and .
- Compare if is less than the previous iteration.
- Update the results stored in variable I (step 2).
- Else existing placement of DG will be remaining stored in variable I.
- Check if , then go to step 13; otherwise, go to step 3.
- Print results, the global optima is found.
4. Results and Discussion
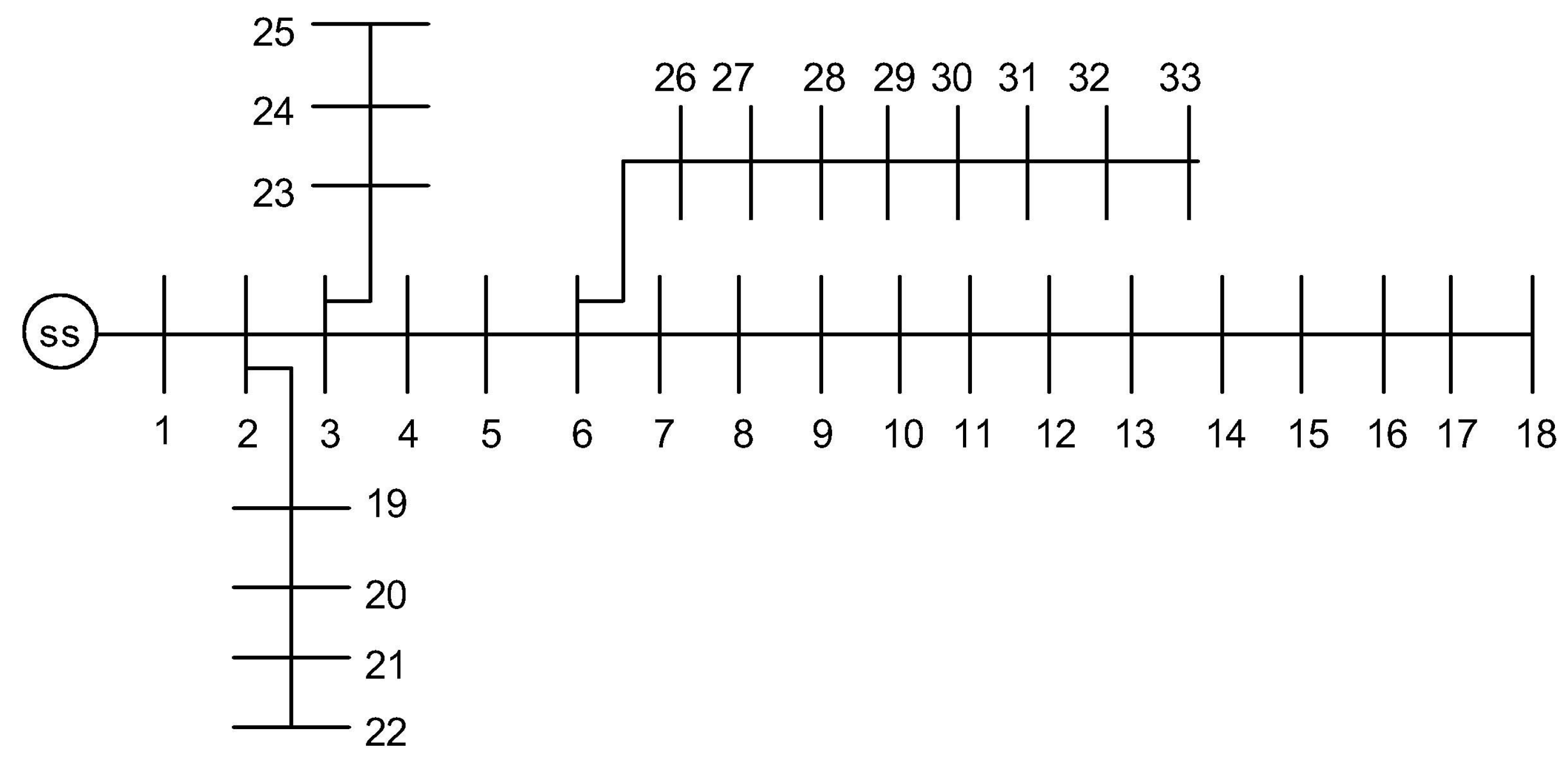
4.1. 33-Node System
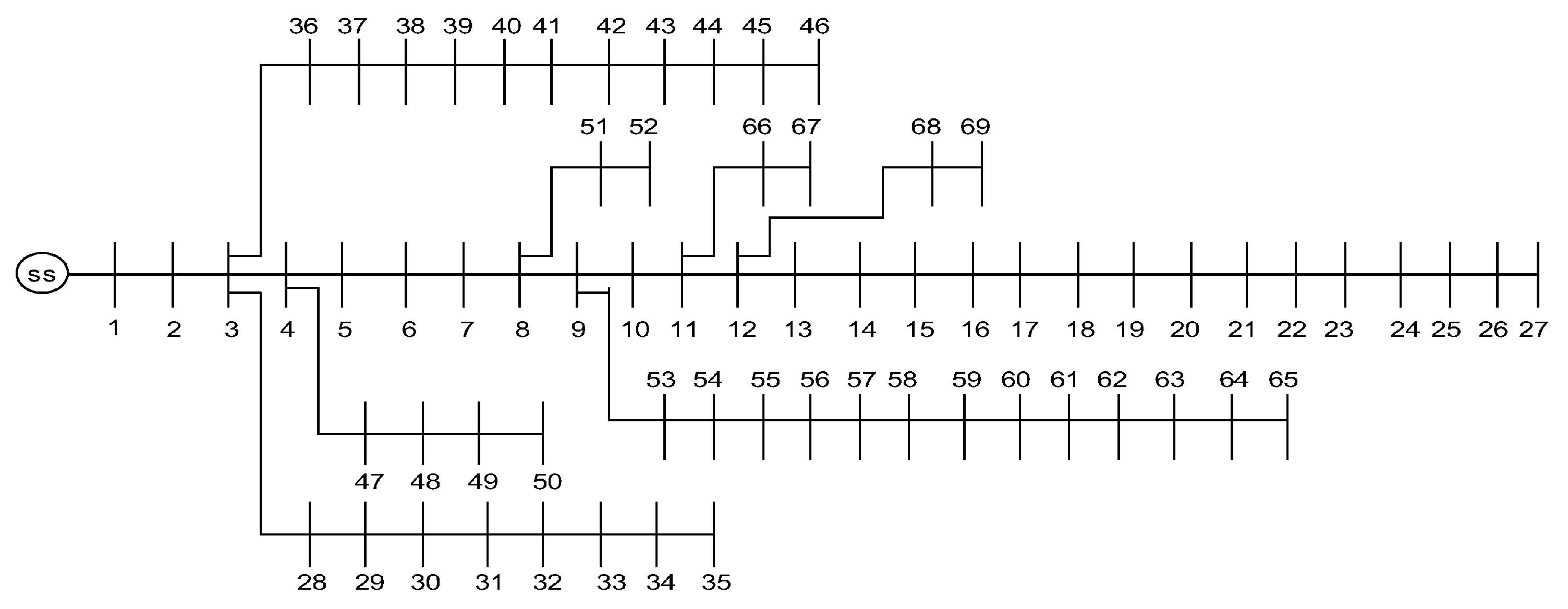
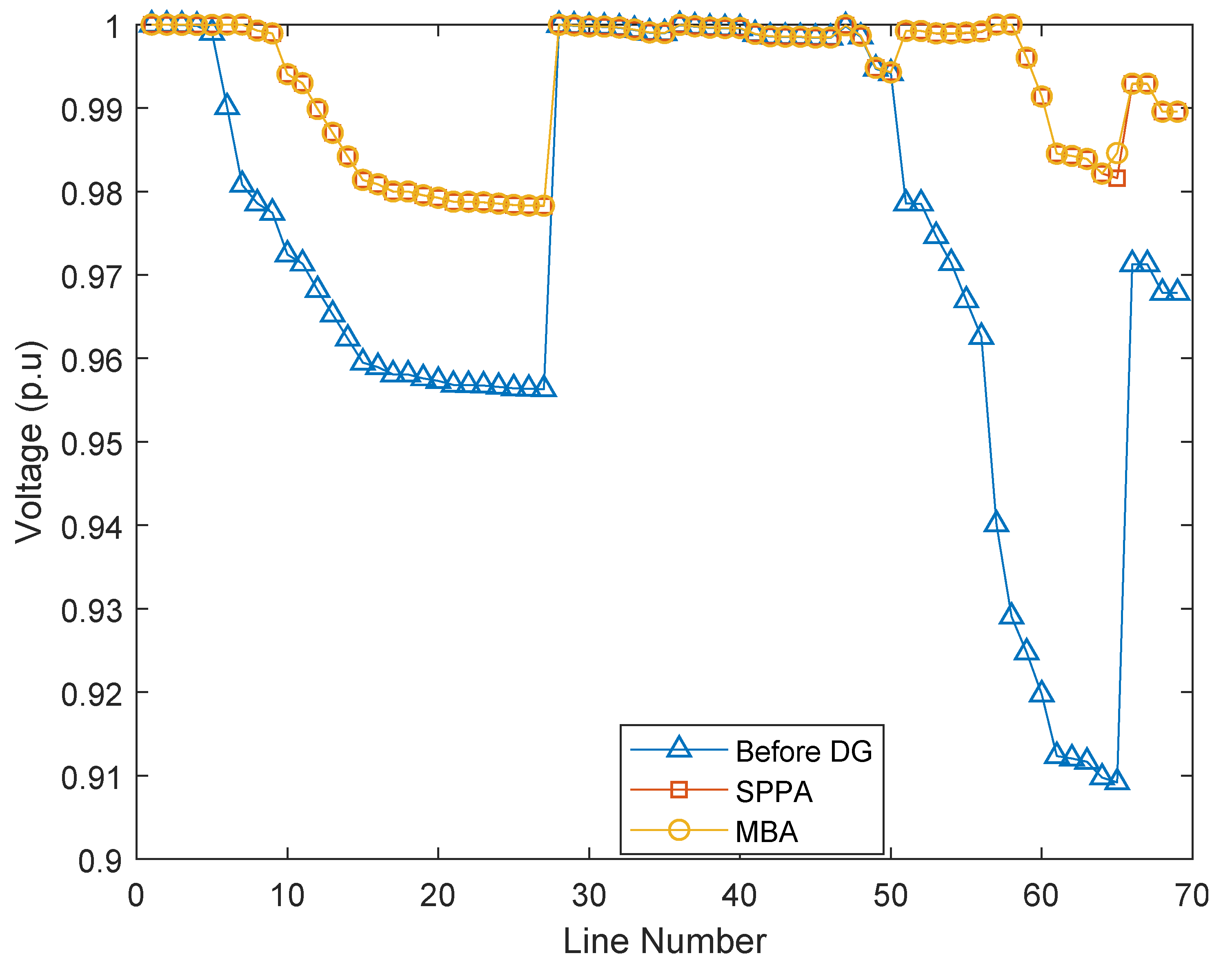
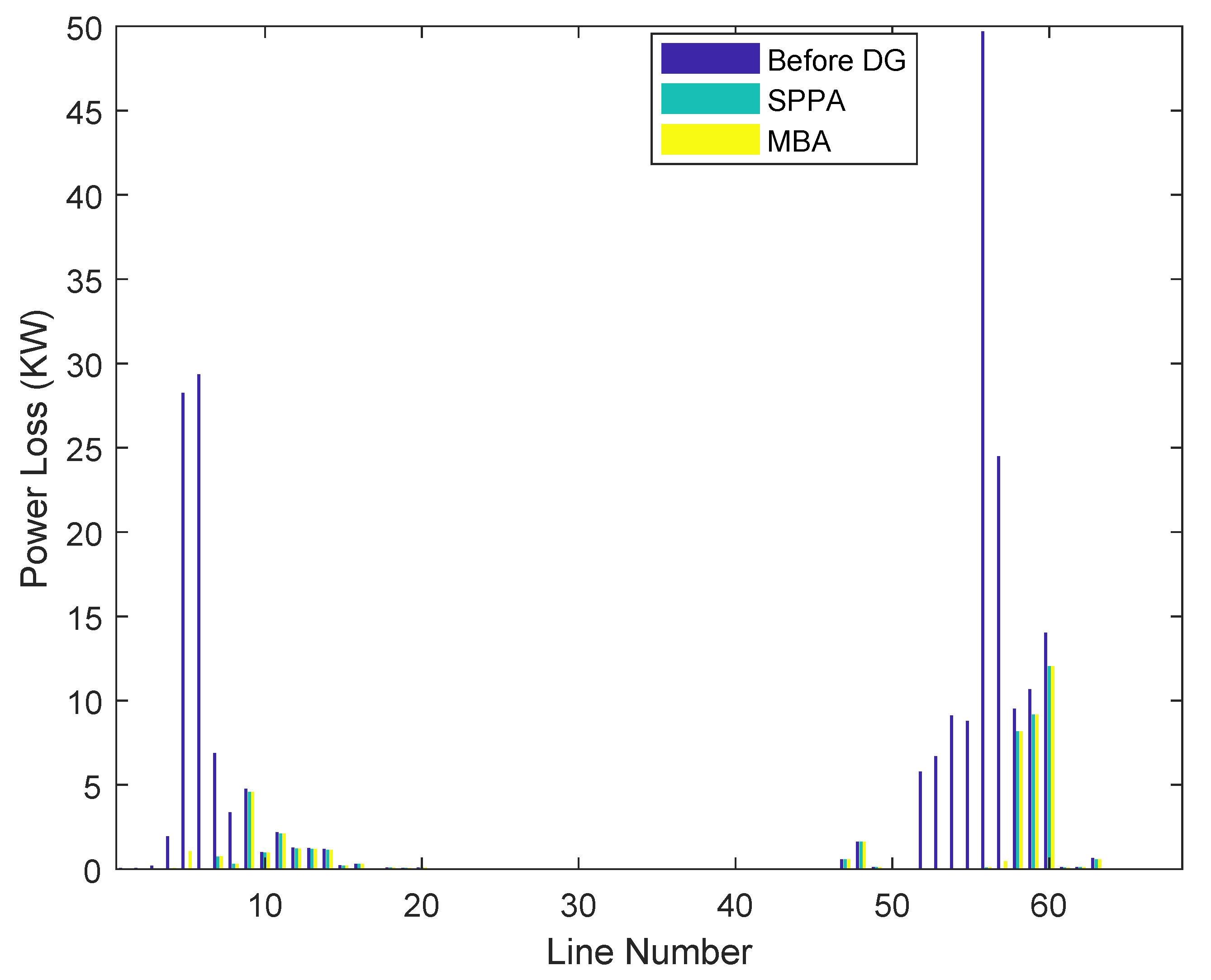
4.2. 69-Node System
4.3. Results Comparison with Other Optimization Techniques
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van Bavel, J. The world population explosion: Causes, backgrounds and projections for the future. Facts Views Vis. ObGyn 2013, 5, 281. [Google Scholar] [PubMed]
- Shahzad, M. Power system planning with multiple distributed generators. Ph.D. Thesis, TU Wien, Vienna, Austria, 2016. [Google Scholar]
- Aboli, R.; Ramezani, M.; Falaghi, H. A hybrid robust distributed model for short-term operation of multi-microgrid distribution networks. Electr. Power Syst. Res. 2019, 177, 106011. [Google Scholar] [CrossRef]
- Chiu, W.Y.; Sun, H.; Poor, H.V. A multiobjective approach to multimicrogrid system design. IEEE Trans. Smart Grid 2015, 6, 2263–2272. [Google Scholar] [CrossRef]
- Lin, Y.; Dong, P.; Sun, X.; Liu, M. Two-level game algorithm for multi-microgrid in electricity market. IET Renew. Power Gener. 2017, 11, 1733–1740. [Google Scholar] [CrossRef]
- Perpinias, I.I.; Papanikolaou, N.P.; Tatakis, E.C. Optimum design of low-voltage distributed photovoltaic systems oriented to enhanced fault ride through capability. IET Gener. Transm. Distrib. 2015, 9, 903–910. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Kinawy, A.M.; Mouwafi, M.T. Optimal capacitor placement in distribution systems for power loss reduction and voltage profile improvement. IET Gener. Transm. Distrib. 2016, 10, 1209–1221. [Google Scholar] [CrossRef]
- Suresh, M.; Edward, J.B. A hybrid algorithm based optimal placement of DG units for loss reduction in the distribution system. Appl. Soft Comput. 2020, 91, 106191. [Google Scholar] [CrossRef]
- Shahzad, M.; Ahmad, I.; Gawlik, W.; Palensky, P. Active power loss minimization in radial distribution networks with analytical method of simultaneous optimal DG sizing. In Proceedings of the 2016 IEEE International Conference on Industrial Technology (ICIT), Taipei, Taiwan, 14–17 March 2016; pp. 470–475. [Google Scholar]
- Shahzad, M.; Ahmad, I.; Gawlik, W.; Palensky, P. Load concentration factor based analytical method for optimal placement of multiple distribution generators for loss minimization and voltage profile improvement. Energies 2016, 9, 287. [Google Scholar] [CrossRef]
- Almabsout, E.A.; El-Sehiemy, R.A.; An, O.N.U.; Bayat, O. A hybrid local Search-Genetic algorithm for simultaneous placement of DG units and shunt capacitors in radial distribution systems. IEEE Access 2020, 8, 54465–54481. [Google Scholar] [CrossRef]
- Acharya, N.; Mahat, P.; Mithulananthan, N. An analytical approach for DG allocation in primary distribution network. Int. J. Electr. Power Energy Syst. 2006, 28, 669–678. [Google Scholar] [CrossRef]
- Alarcon-Rodriguez, A.; Ault, G.; Galloway, S. Multi-objective planning of distributed energy resources: A review of the state-of-the-art. Renew. Sustain. Energy Rev. 2010, 14, 1353–1366. [Google Scholar] [CrossRef]
- Coello, C.A.C. A comprehensive survey of evolutionary-based multiobjective optimization techniques. Knowl. Inf. Syst. 1999, 1, 269–308. [Google Scholar] [CrossRef]
- Merrikh-Bayat, F. A numerical optimization algorithm inspired by the strawberry plant. arXiv 2014, arXiv:1407.7399. [Google Scholar]
- Sultana, U.; Khairuddin, A.B.; Aman, M.; Mokhtar, A.; Zareen, N. A review of optimum DG placement based on minimization of power losses and voltage stability enhancement of distribution system. Renew. Sustain. Energy Rev. 2016, 63, 363–378. [Google Scholar] [CrossRef]
- Prakash, P.; Khatod, D.K. Optimal sizing and siting techniques for distributed generation in distribution systems: A review. Renew. Sustain. Energy Rev. 2016, 57, 111–130. [Google Scholar] [CrossRef]
- Paliwal, P.; Patidar, N.; Nema, R. Planning of grid integrated distributed generators: A review of technology, objectives and techniques. Renew. Sustain. Energy Rev. 2014, 40, 557–570. [Google Scholar] [CrossRef]
- Viral, R.; Khatod, D.K. An analytical approach for sizing and siting of DGs in balanced radial distribution networks for loss minimization. Int. J. Electr. Power Energy Syst. 2015, 67, 191–201. [Google Scholar] [CrossRef]
- Crossland, A.; Jones, D.; Wade, N. Planning the location and rating of distributed energy storage in LV networks using a genetic algorithm with simulated annealing. Int. J. Electr. Power Energy Syst. 2014, 59, 103–110. [Google Scholar] [CrossRef]
- Hassan, A.A.; Fahmy, F.H.; Nafeh, A.E.S.A.; Abu-elmagd, M.A. Genetic single objective optimisation for sizing and allocation of renewable DG systems. Int. J. Sustain. Energy 2017, 36, 545–562. [Google Scholar] [CrossRef]
- Zeb, M.Z.; Imran, K.; Janjua, A.K.; Nadeem, M.; Amin, A. Optimal allocation and sizing of solar panels generation via particle swarm optimization algorithm. In Proceedings of the 2019 2nd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 30–31 January 2019; pp. 1–5. [Google Scholar]
- Othman, M.; El-Khattam, W.; Hegazy, Y.; Abdelaziz, A.Y. Optimal placement and sizing of voltage controlled distributed generators in unbalanced distribution networks using supervised firefly algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 105–113. [Google Scholar] [CrossRef]
- Sudabattula, S.; Kowsalya, M. Optimal allocation of wind based distributed generators in distribution system using Cuckoo Search Algorithm. Procedia Comput. Sci. 2016, 92, 298–304. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, K.; Ravi, K. Optimal allocation of DG in the radial distribution network using bat optimization algorithm. In Advances in Power Systems and Energy Management; Springer: Berlin/Heidelberg, Germany, 2018; pp. 563–569. [Google Scholar]
- Oda, E.S.; Abdelsalam, A.A. Optimal DGs allocation in distribution networks using modified flower pollination algorithm. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 1424–1429. [Google Scholar]
- Devabalaji, K.; Ravi, K. Optimal size and siting of multiple DG and DSTATCOM in radial distribution system using Bacterial Foraging Optimization Algorithm. Ain Shams Eng. J. 2016, 7, 959–971. [Google Scholar] [CrossRef]
- Ali, A.H.; Youssef, A.R.; George, T.; Kamel, S. Optimal DG allocation in distribution systems using Ant lion optimizer. In Proceedings of the 2018 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 19–21 February 2018; pp. 324–331. [Google Scholar]
- George, T.; Youssef, A.R.; Kamel, S. Optimal Allocation of DGs and TCSC in Radial Networks Using Ant Lion Optimizer. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 1092–1097. [Google Scholar]
- Sanjay, R.; Jayabarathi, T.; Raghunathan, T.; Ramesh, V.; Mithulananthan, N. Optimal allocation of distributed generation using hybrid grey wolf optimizer. IEEE Access 2017, 5, 14807–14818. [Google Scholar] [CrossRef]
- Prakash, D.; Lakshminarayana, C. Multiple DG placements in radial distribution system for multi objectives using whale optimization algorithm. Alex. Eng. J. 2018, 57, 2797–2806. [Google Scholar] [CrossRef]
- Sabarinath, G.; Manohar, T.G. Optimal sitting and sizing of renewable energy resources for power loss reduction in radial distribution systems using whale optimization algorithm. In Proceedings of the 2018 International Conference on Emerging Trends and Innovations In Engineering And Technological Research (ICETIETR), Ernakulam, India, 11–13 July 2018; pp. 1–5. [Google Scholar]
- Nekooei, K.; Farsangi, M.M.; Nezamabadi-Pour, H.; Lee, K.Y. An improved multi-objective harmony search for optimal placement of DGs in distribution systems. IEEE Trans. Smart Grid 2013, 4, 557–567. [Google Scholar] [CrossRef]
- El-Fergany, A. Optimal allocation of multi-type distributed generators using backtracking search optimization algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 1197–1205. [Google Scholar] [CrossRef]
- Mena, A.J.G.; García, J.A.M. An efficient approach for the siting and sizing problem of distributed generation. Int. J. Electr. Power Energy Syst. 2015, 69, 167–172. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Gonzalez Montoya, D.; Ramos-Paja, C.A. Optimal sizing and location of distributed generators based on PBIL and PSO techniques. Energies 2018, 11, 1018. [Google Scholar] [CrossRef]
- Montoya, O.D.; Molina-Cabrera, A.; Chamorro, H.R.; Alvarado-Barrios, L.; Rivas-Trujillo, E. A Hybrid Approach Based on SOCP and the Discrete Version of the SCA for Optimal Placement and Sizing DGs in AC Distribution Networks. Electronics 2021, 10, 26. [Google Scholar] [CrossRef]
- Salhi, A.; Fraga, E. Nature-Inspired Optimisation Approaches and the New Plant Propagation Algorithm. In Proceedings of the The International Conference on Numerical Analysis and Optimization (ICeMATH’11), Yogyakarta, Indonesia, 6–8 June 2011. [Google Scholar]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Power Eng. Rev. 1989, 9, 101–102. [Google Scholar] [CrossRef]
- Aalen, O.O.; Husebye, E. Statistical analysis of repeated events forming renewal processes. Stat. Med. 1991, 10, 1227–1240. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, N.; Prasad, K. A fuzzy genetic approach for network reconfiguration to enhance voltage stability in radial distribution systems. Energy Convers. Manag. 2006, 47, 3288–3306. [Google Scholar] [CrossRef]
- Sarfaraz; Bansal, A.; Singh, S. Optimal allocation and sizing of distributed generation for power loss reduction. IET Conf. Proc. 2016, 6. [Google Scholar] [CrossRef]
- Ali, E.; Abd Elazim, S.; Abdelaziz, A. Ant Lion Optimization Algorithm for optimal location and sizing of renewable distributed generations. Renew. Energy 2017, 101, 1311–1324. [Google Scholar] [CrossRef]
- Oda, E.S.; Abdelsalam, A.A.; Abdel-Wahab, M.N.; El-Saadawi, M.M. Distributed generations planning using flower pollination algorithm for enhancing distribution system voltage stability. Ain Shams Eng. J. 2017, 8, 593–603. [Google Scholar] [CrossRef]
- Vatani, M.; Alkaran, D.S.; Sanjari, M.J.; Gharehpetian, G.B. Multiple distributed generation units allocation in distribution network for loss reduction based on a combination of analytical and genetic algorithm methods. IET Gener. Transm. Distrib. 2016, 10, 66–72. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Alghamdi, A.S.; Jurado, F. Optimal Placement of DGs in Distribution System Using an Improved Harris Hawks Optimizer Based on Single-and Multi-Objective Approaches. IEEE Access 2020, 8, 52815–52829. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L. An exact MINLP model for optimal location and sizing of DGs in distribution networks: A general algebraic modeling system approach. Ain Shams Eng. J. 2020, 11, 409–418. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Orozco-Henao, C. Vortex search and Chu-Beasley genetic algorithms for optimal location and sizing of distributed generators in distribution networks: A novel hybrid approach. Eng. Sci. Technol. Int. J. 2020, 23, 1351–1363. [Google Scholar]
- Musa, H.; Adamu, S.S. Optimal allocation and sizing of distributed generation for power loss reduction using modified PSO for radial distribution systems. J. Energy Technol. Policy 2013, 3, 1–8. [Google Scholar]
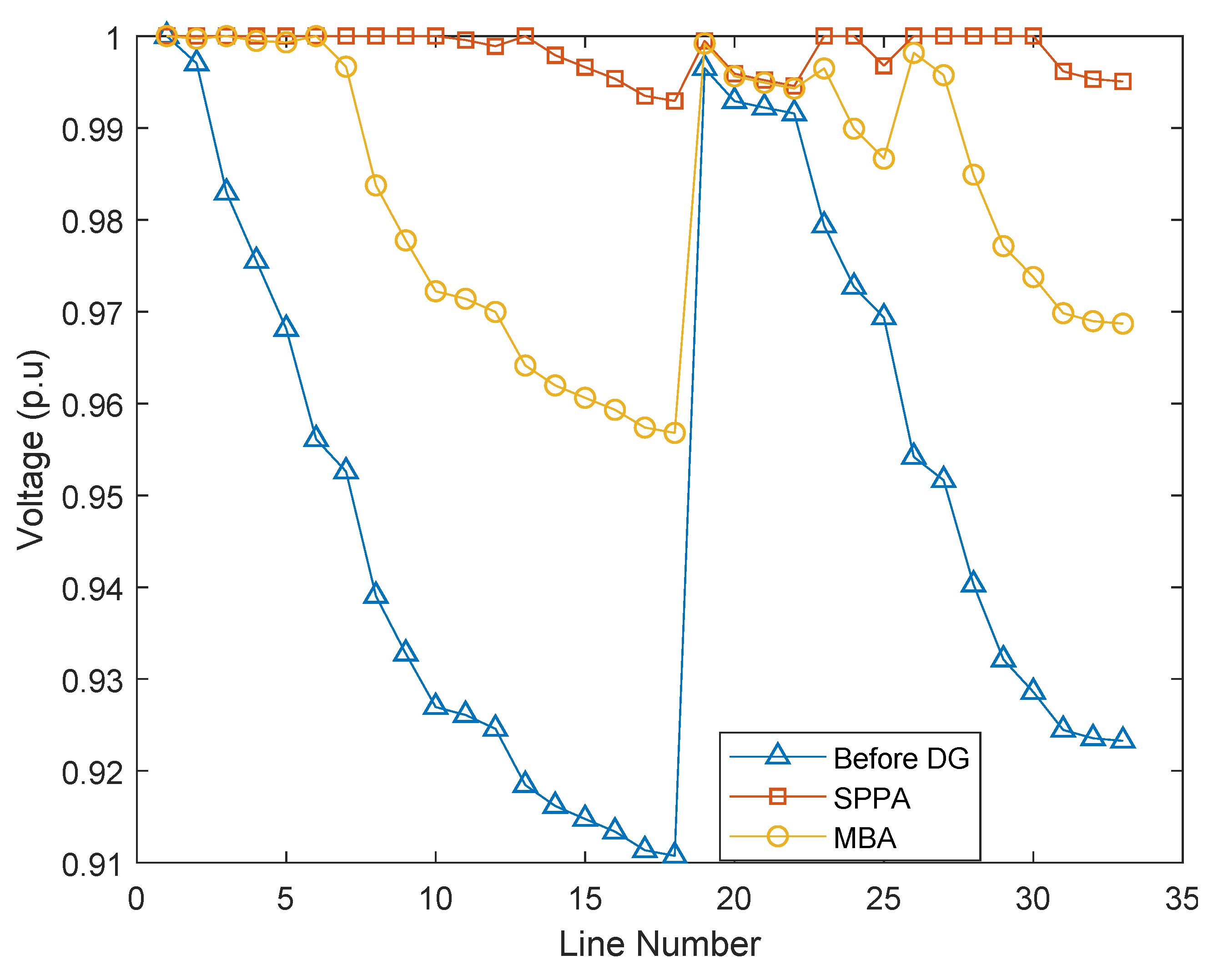
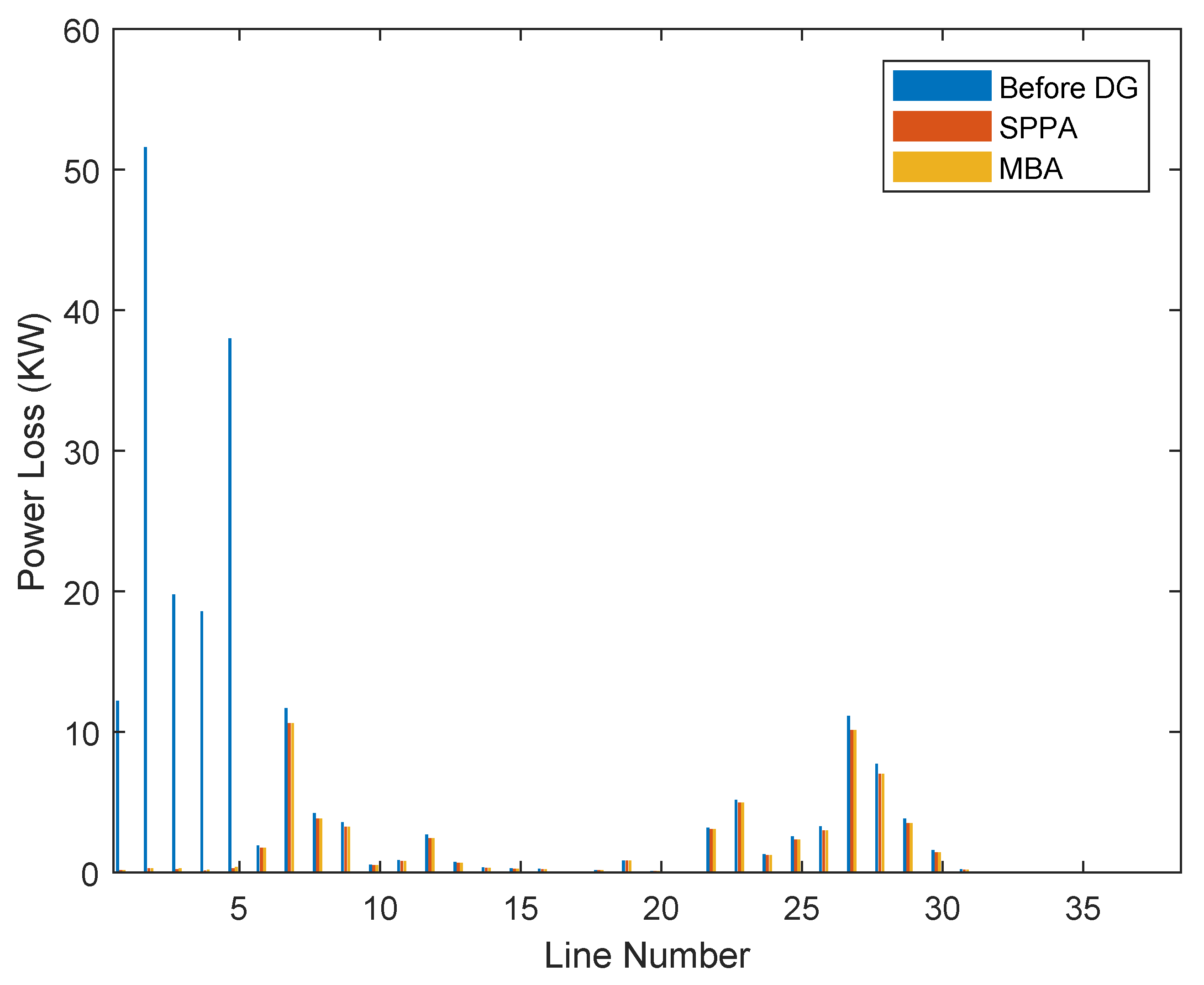
| Technique | Optimal Size (kW) | Optimal Location | (kW) | (kW) | (%) | (pu) | Ref. |
|---|---|---|---|---|---|---|---|
| BFOA | 779, 880, 1083 | 14, 25, 30 | 2742 | 73.53 | 65.1 | – | [27] |
| WOA | 1072.8, 772.5, 856.7 | 30, 25, 13 | 2702 | 73.75 | 65.1 | 0.97 | [31] |
| PPBIL& PSO | 403, 524, 642 | 12, 15, 31 | 1569 | 91.5 | 56.6 | 0.96 | [36] |
| DSCA-SOCP | 801, 1091, 1053 | 13, 24, 30 | 2945 | 72.8 | 65.5 | – | [37] |
| SPSO | 640, 740, 420 | 16, 30, 32 | 1800 | 74 | 64.5 | 0.97 | [42] |
| ALO | 850, 1191 | 13, 30 | 2041 | 82.6 | 60.8 | 0.97 | [43] |
| FPA | 1039, 1086 | 12, 30 | 2125 | 89.2 | 57.7 | 0.97 | [44] |
| GA | 1323, 867 | 30, 13 | 2190 | 81.75 | 61.1 | 0.97 | [45] |
| IHHO | 775.5, 1080.8, 1066.7 | 14, 24, 30 | 2923 | 72.8 | 65.5 | – | [46] |
| GAMS | 770, 1096, 1065 | 14, 24, 30 | 2931 | 72.8 | 65.5 | – | [47] |
| CBGA-VSA | 801, 1091, 1053 | 13, 24, 30 | 2945 | 72.8 | 65.5 | 0.97 | [48] |
| SPPA | 1270, 2225 | 3, 6 | 3495 | 63.74 | 69.4 | 0.99 | Proposed |
| Technique | Optimal Size (kW) | Optimal Location | (kW) | (kW) | (%) | (pu) | Ref. |
|---|---|---|---|---|---|---|---|
| WOA | 489, 476, 1680 | 11, 18, 61 | 2645 | 69.72 | 69 | 0.98 | [31] |
| PPBIL& PSO | 178, 1053, 420 | 26, 61, 66 | 1651 | 86.9 | 64.1 | 0.96 | [36] |
| DSCA-SOCP | 526, 380, 1719 | 11, 18, 61 | 2625 | 69.41 | 69.2 | – | [37] |
| SPSO | 1360, 520 | 61, 64 | 1880 | 81 | 64 | 0.98 | [42] |
| ALO | 538, 1700 | 17, 61 | 2238 | 70.75 | 68.6 | 0.98 | [43] |
| FPA | 463, 1771 | 17, 61 | 2234 | 71.7 | 68.1 | 0.97 | [44] |
| IHHO | 527.2, 382.5, 1719.4 | 11, 17, 61 | 2629.1 | 69.41 | 69.2 | – | [46] |
| GAMS | 813, 1444, 289 | 12, 61, 64 | 2546 | 72.09 | 68 | – | [47] |
| CBGA-VSA | 526, 380, 1719 | 11, 18, 61 | 2625 | 69.41 | 69.2 | 0.98 | [48] |
| PSO | 1293, 673, 868 | 61, 17, 50 | 2834 | 87.48 | 61.1 | 0.98 | [49] |
| SPPA | 42.8, 995, 102.1, 1768 | 57, 7, 6, 58 | 2907.9 | 46.89 | 79.2 | 0.98 | Proposed |
| Technique | (kW) | (kW) | (kW) | (kWh) | (kWh) | Cost Reduction | Ref. |
|---|---|---|---|---|---|---|---|
| BFOA | 73.53 | 2742 | 1046.5 | 9,167,603 | 1,672,171 | 73.1 | [27] |
| WOA | 73.75 | 2702 | 1086.8 | 9,520,315 | 1,736,505 | 72.3 | [31] |
| PPBIL& PSO | 91.5 | 1569 | 2237.5 | 19,600,500 | 3,575,131 | 42.9 | [36] |
| DSCA-SOCP | 72.8 | 2945 | 842.8 | 7,382,799 | 1,346,623 | 78.5 | [37] |
| SPSO | 74 | 1800 | 1989 | 17,423,640 | 3,178,072 | 49.3 | [42] |
| ALO | 82.6 | 2041 | 1756.6 | 15,387,816 | 2,806,738 | 55.2 | [43] |
| FPA | 89.2 | 2125 | 1679.2 | 14,709,792 | 2,683,066 | 57.2 | [44] |
| GA | 81.75 | 2190 | 1606.7 | 14,075,130 | 2,567,304 | 59.0 | [45] |
| IHHO | 72.79 | 2923 | 864.7 | 7,575,035 | 1,381,686 | 77.9 | [46] |
| GAMS | 72.01 | 2931 | 856.0 | 7,498,648 | 1,367,753 | 78.1 | [47] |
| CBGA-VSA | 72.09 | 2945 | 842.1 | 7,376,708 | 1,345,512 | 78.5 | [48] |
| SPPA | 63.74 | 3495 | 251.7 | 2,205,242 | 402,236 | 93.5 | Proposed |
| WITHOUT | 208.5 | 0 | 3923.5 | 34,369,503 | 6,268,997 |
| Technique | (kW) | (kW) | (kW) | (kWh) | (kWh) | Cost Reduction | Ref. |
|---|---|---|---|---|---|---|---|
| WOA | 69.7 | 2645 | 1226.7 | 10,746,067 | 1,960,083 | 69.5 | [31] |
| PPBIL& PSO | 86.9 | 2028 | 1860.9 | 16,301,484 | 2,973,391 | 53.8 | [36] |
| DSCA-SOCP | 69.4 | 2625 | 1246.4 | 10,918,552 | 1,991,544 | 69.1 | [37] |
| SPSO | 36 | 1880 | 1958 | 17,152,080 | 3,128,539 | 51.3 | [42] |
| ALO | 70.8 | 2238 | 1634.8 | 14,320,410 | 2,612,048 | 59.4 | [43] |
| FPA | 71.7 | 2234 | 1639.7 | 14,363,772 | 2,619,952 | 59.2 | [44] |
| IHHO | 69.4 | 2629 | 1242.3 | 10,882,636 | 1,984,993 | 69.1 | [46] |
| GAMS | 72.1 | 2546 | 1328.1 | 11,634,068 | 2,122,054 | 67.0 | [47] |
| CBGA-VSA | 69.4 | 2625 | 1246.4 | 10,918,464 | 1,991,528 | 69.0 | [48] |
| PSO | 87.5 | 2835 | 1054.5 | 9,237,245 | 1,684,873 | 73.8 | [49] |
| SPPA | 46.9 | 2907 | 941.9 | 8,250,956 | 1,504,974 | 76.6 | Proposed |
| WITHOUT | 225 | 0 | 4026.9 | 35,275,644 | 6,434,277 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahzad, M.; Akram, W.; Arif, M.; Khan, U.; Ullah, B. Optimal Siting and Sizing of Distributed Generators by Strawberry Plant Propagation Algorithm. Energies 2021, 14, 1744. https://doi.org/10.3390/en14061744
Shahzad M, Akram W, Arif M, Khan U, Ullah B. Optimal Siting and Sizing of Distributed Generators by Strawberry Plant Propagation Algorithm. Energies. 2021; 14(6):1744. https://doi.org/10.3390/en14061744
Chicago/Turabian StyleShahzad, Mohsin, Waseem Akram, Muhammad Arif, Uzair Khan, and Barkat Ullah. 2021. "Optimal Siting and Sizing of Distributed Generators by Strawberry Plant Propagation Algorithm" Energies 14, no. 6: 1744. https://doi.org/10.3390/en14061744
APA StyleShahzad, M., Akram, W., Arif, M., Khan, U., & Ullah, B. (2021). Optimal Siting and Sizing of Distributed Generators by Strawberry Plant Propagation Algorithm. Energies, 14(6), 1744. https://doi.org/10.3390/en14061744







