Real-Time Implementation of the Predictive-Based Control with Bacterial Foraging Optimization Technique for Power Management in Standalone Microgrid Application
Abstract
1. Introduction
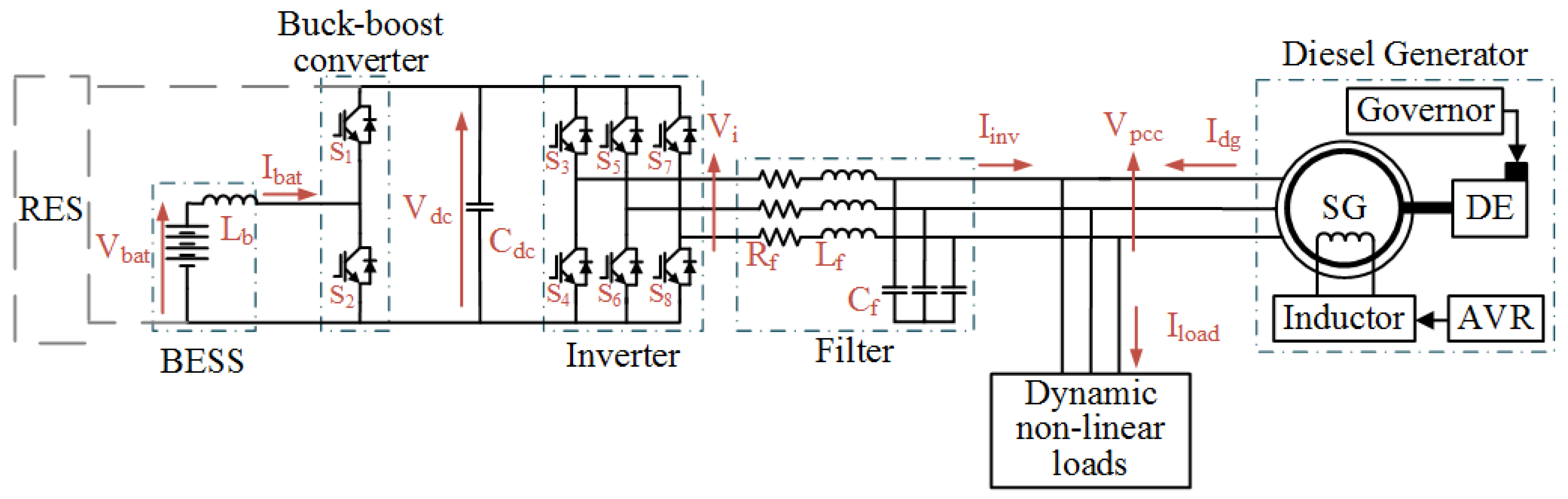
2. Microgrid Description
3. Control Strategies
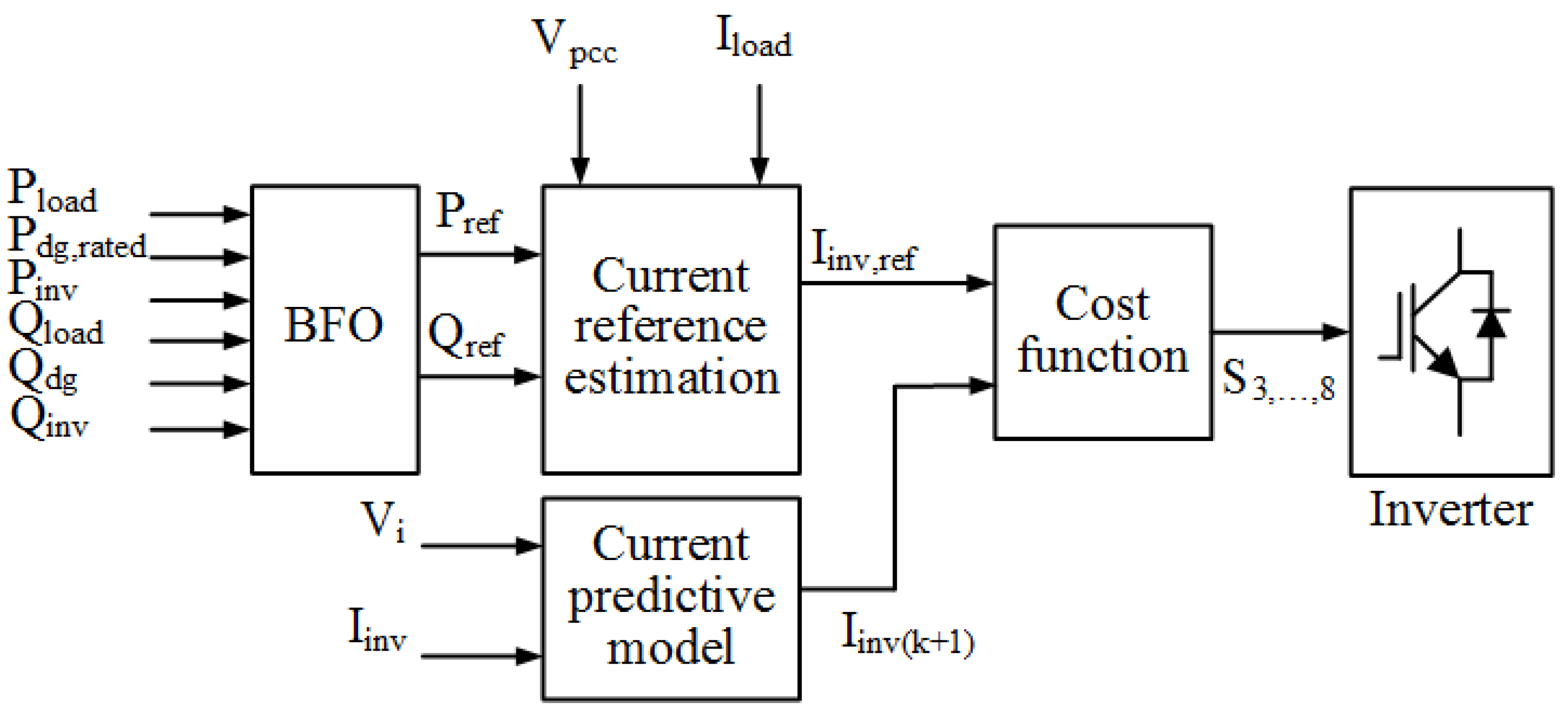
3.1. Inverter Predictive Control
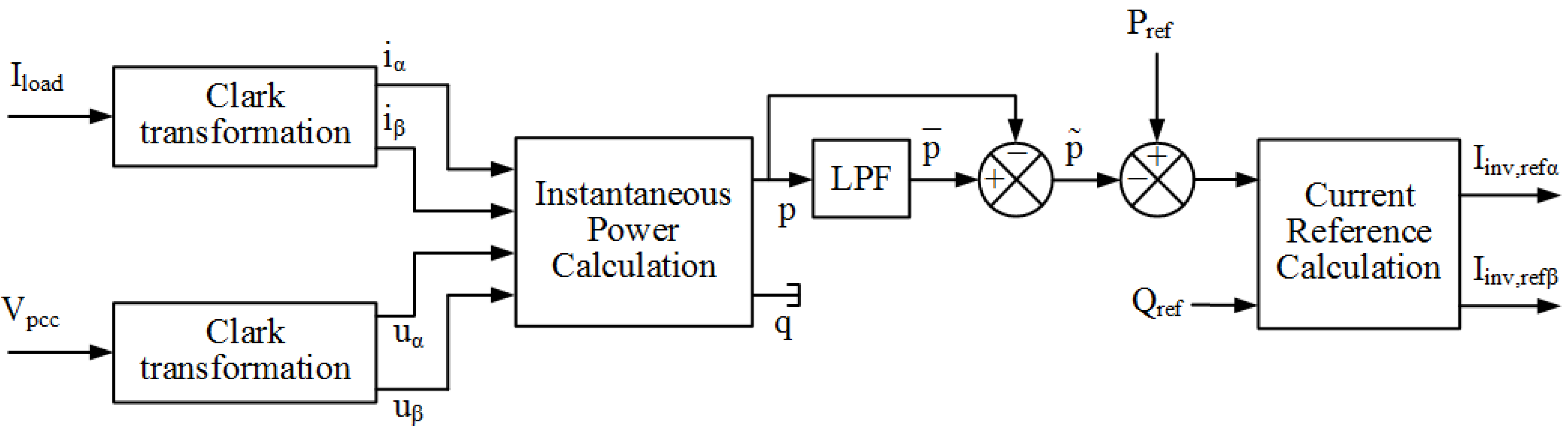
3.1.1. Inverter Reference Current Estimation
3.1.2. Current Predictive Model
3.1.3. Cost Function
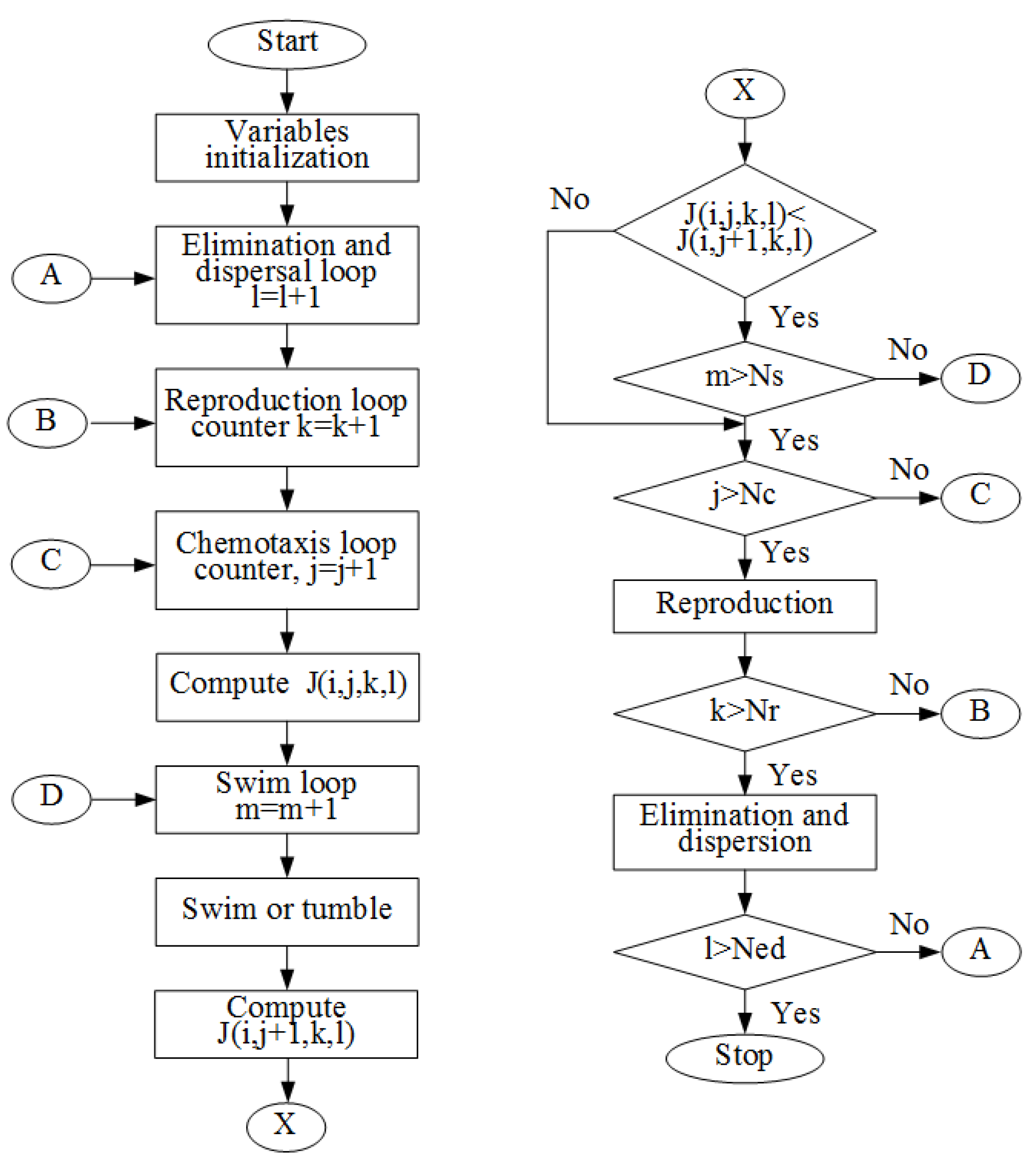
3.2. Bacterial Foraging Optimization Technique
3.2.1. Initialization
3.2.2. Chemotaxis
3.2.3. Swarming
3.2.4. Reproduction
3.2.5. Elimination and Dispersal
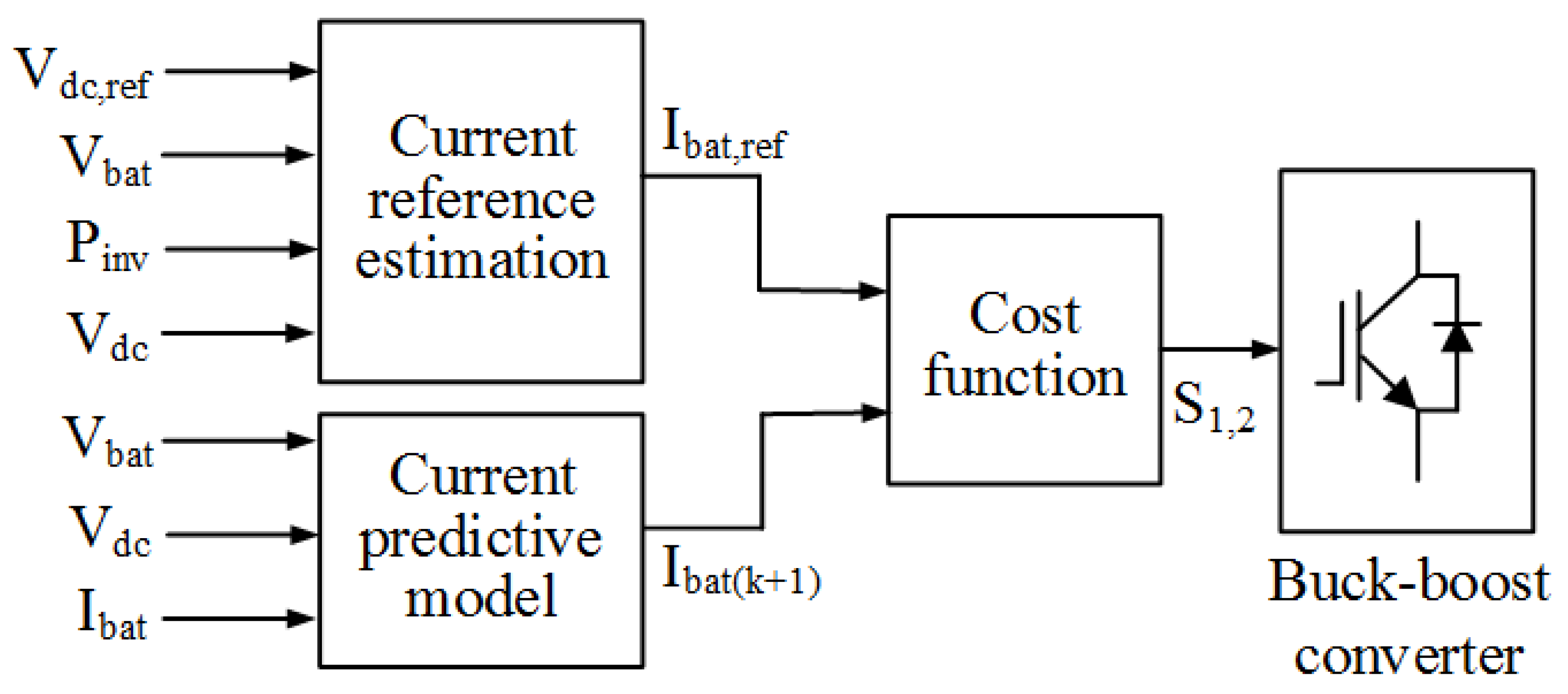
3.3. DC-DC Buck-Boost Converter Predictive Control
3.3.1. Current Predictive Model
3.3.2. BES Reference Current Estimation
3.3.3. Cost Function
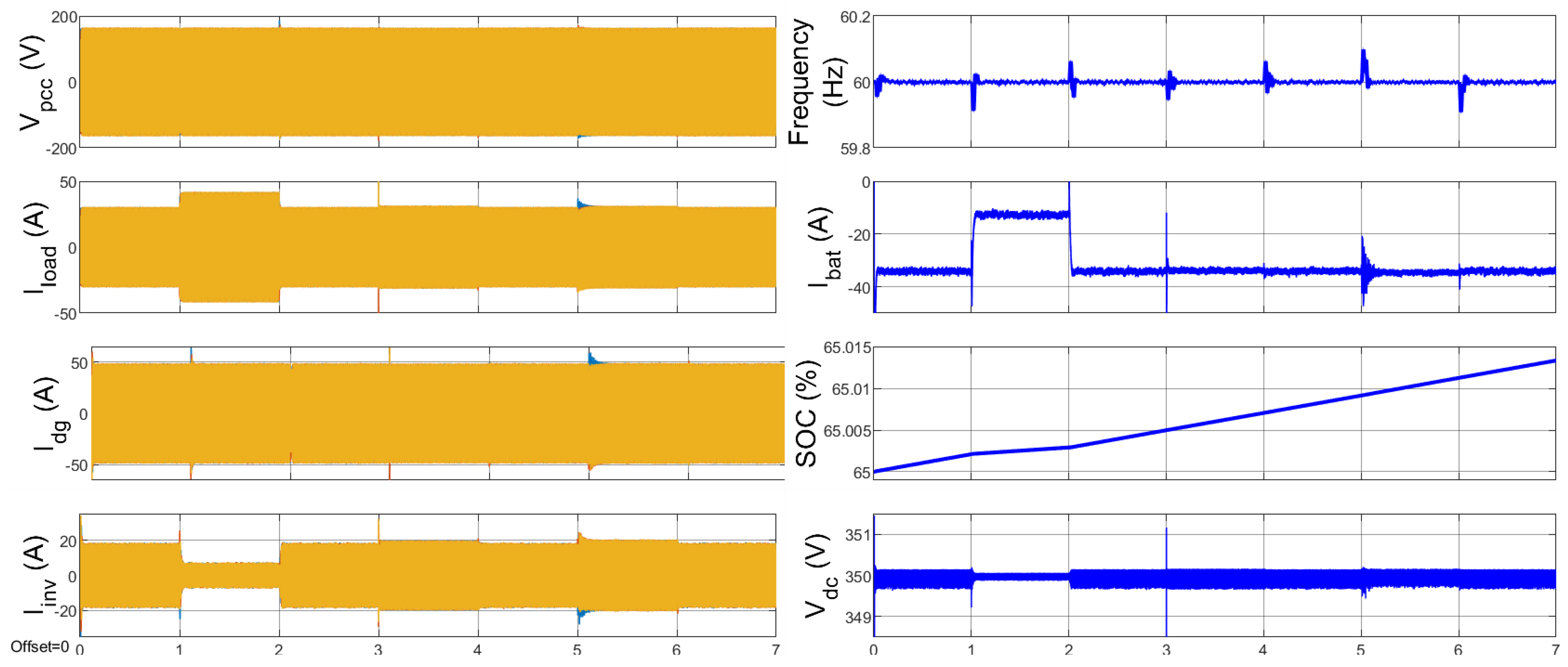
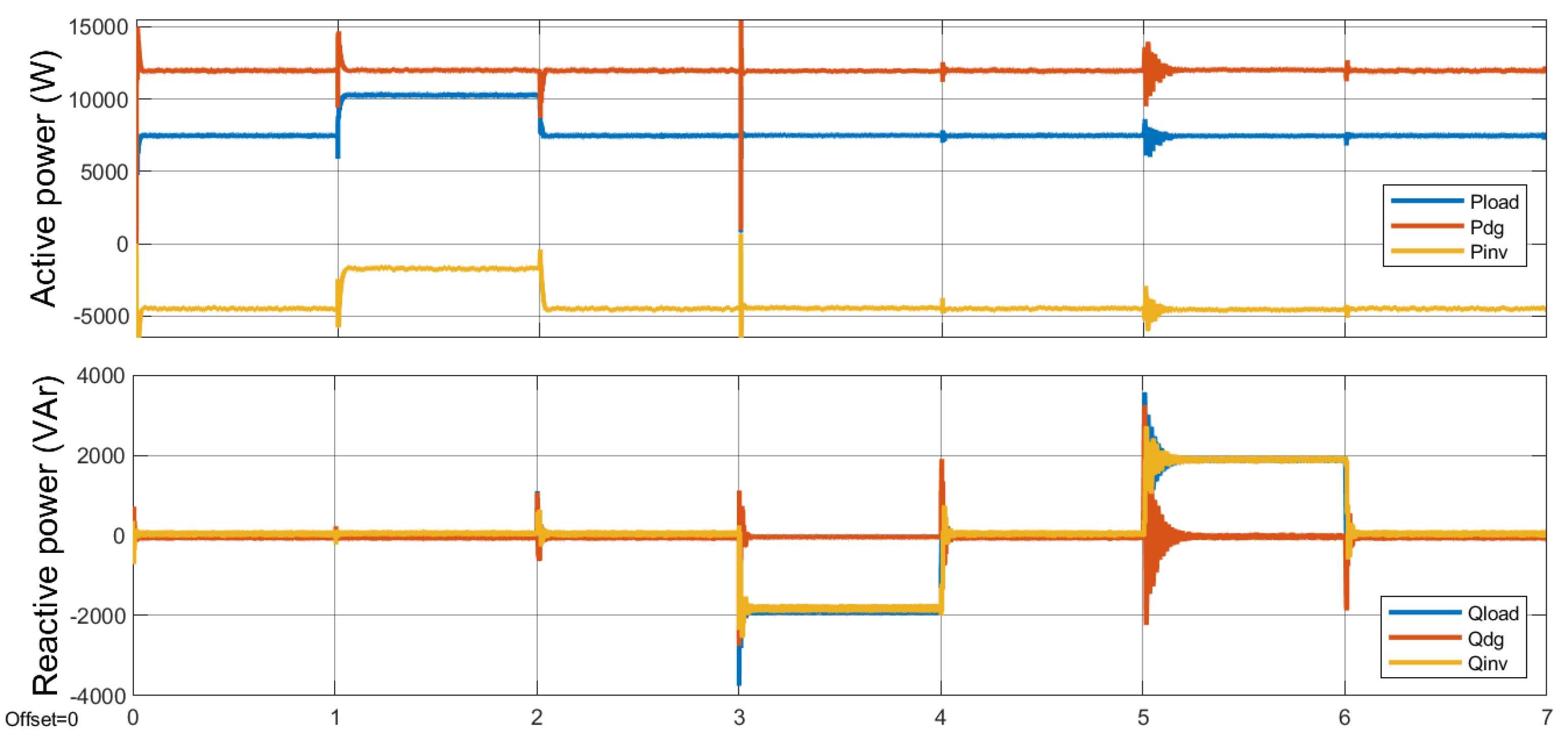
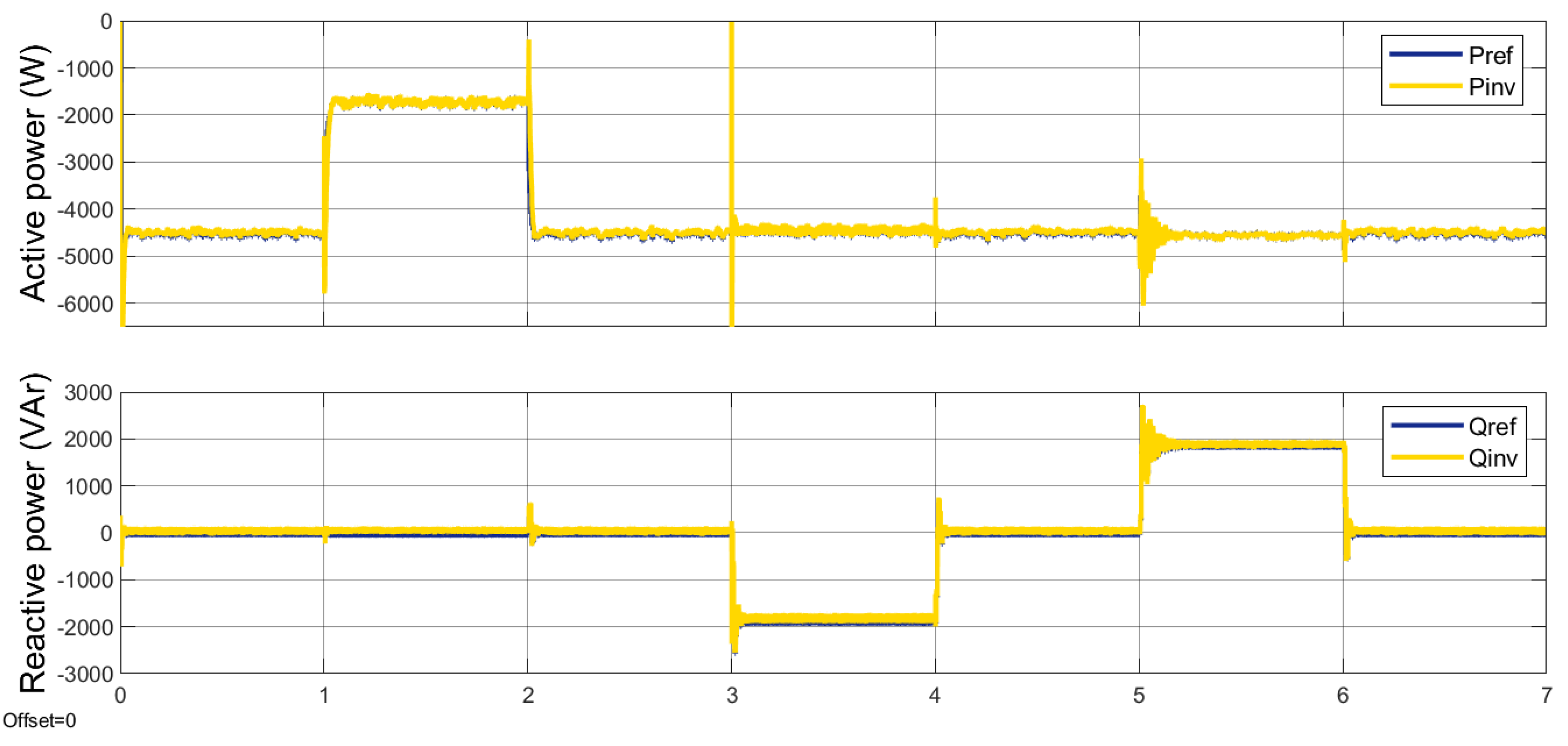
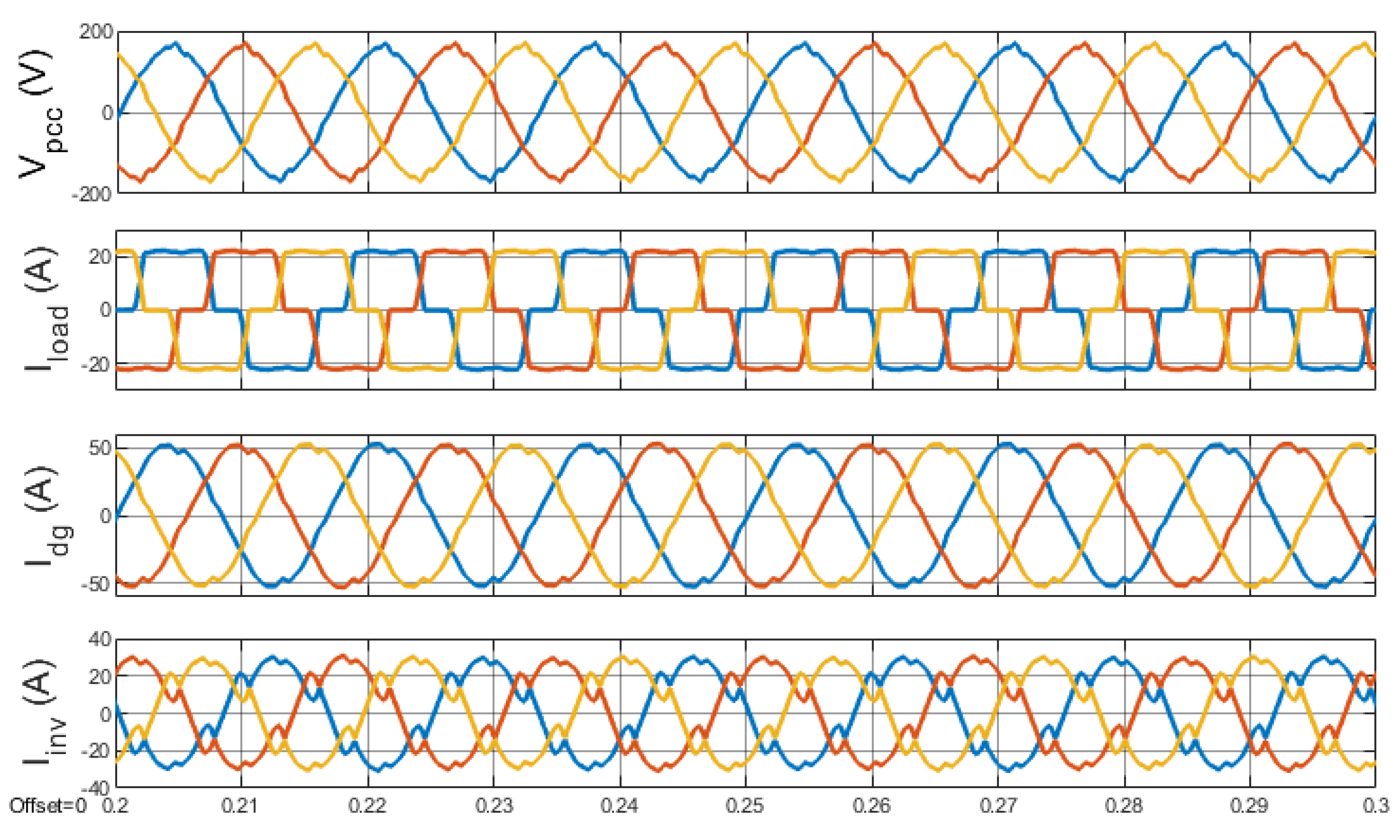
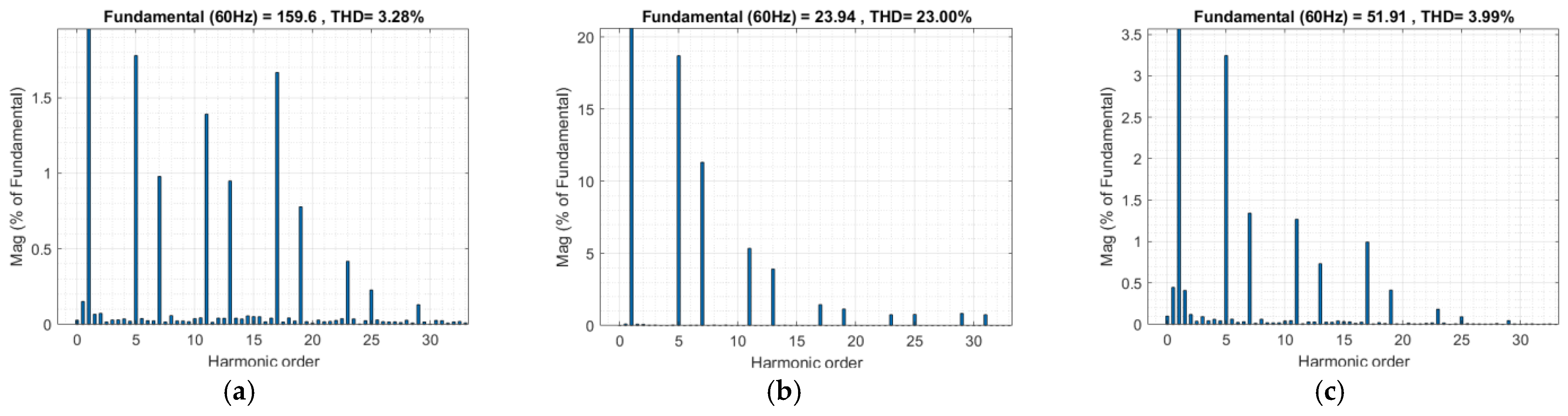
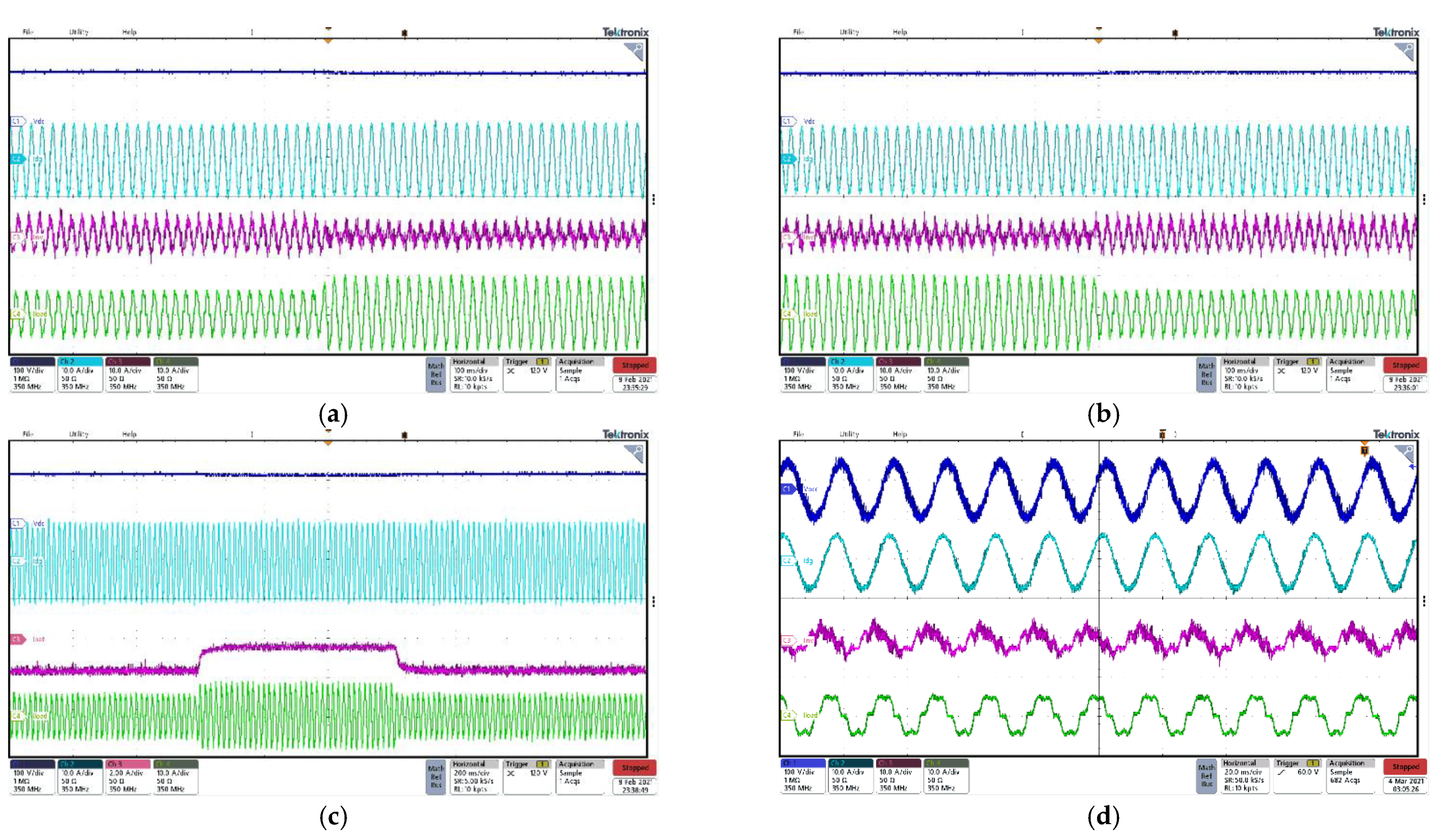
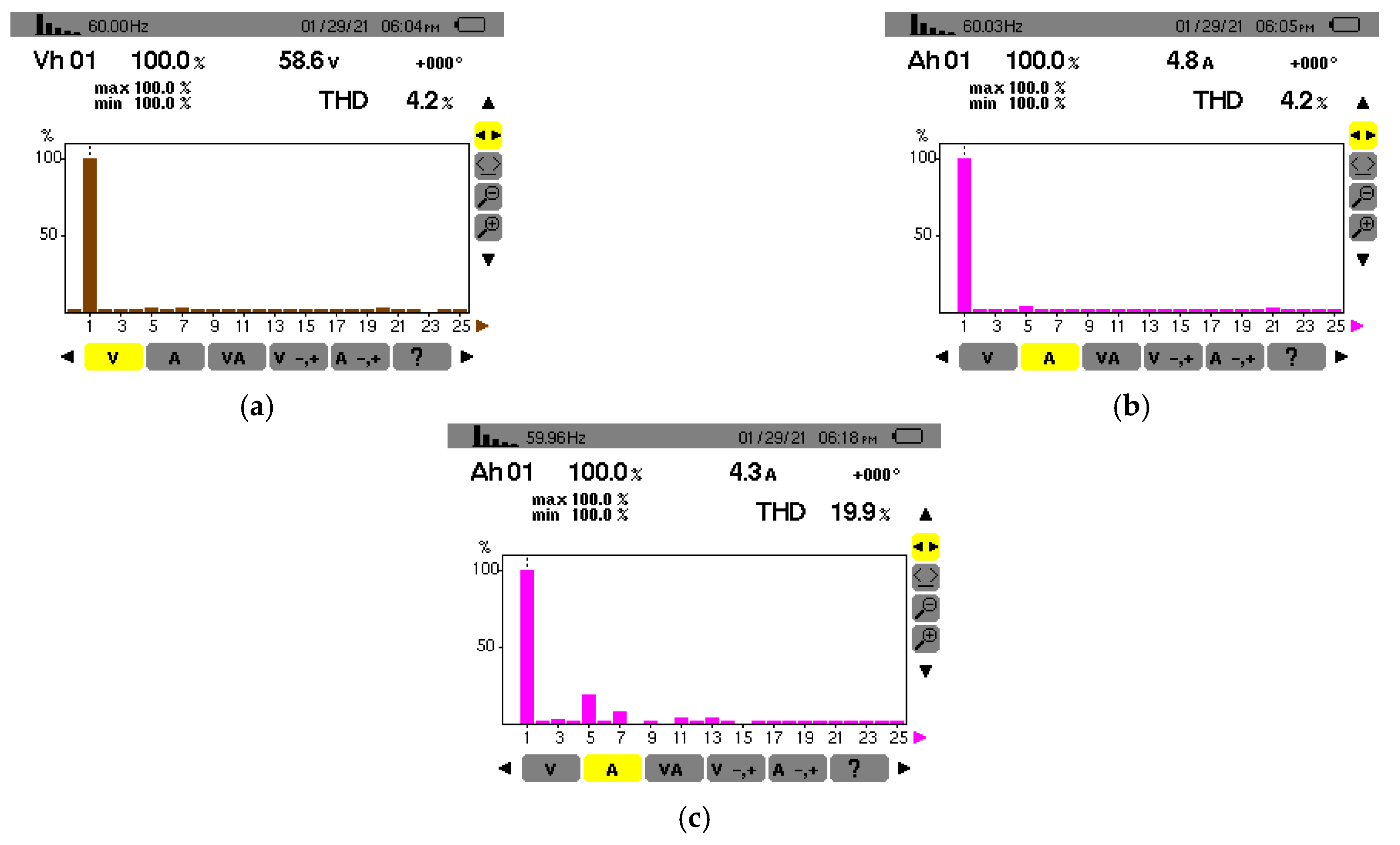
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Elements | Parameters |
|---|---|
| Synchronous Generator | Sn = 12 kVA, Vn = 208 V, fs = 60 Hz, 2 P = 4, Rinternal impedance = 0.8160 Ω, Linternal impedance = 0.8104 × 10−3 H, J = 3.895 × 106 kg.m2 |
| BES | Vn = 120 V, Rated capacity: 400 Ah, Vcut-off = 90 V, VFully-charge = 137.3 V, Idischarge-nom = 8 A, rinternal =0.0625 Ω, Lbat = 0.25 mH |
| Loads | Pconstant = 8 kW, Pdynamic = 3 kW, QdynamicC = 2 kVAr, QdynamicL = 2 kVAr Rsnl = 1 Ω, Lsnl = 0.5 ×10−3 H, Rnl = 10 Ω, Lnl = 10 × 10−3 H |
| Filter | Lf = 8.5 × 10−3 H, Cf = 40 × 10−6 F, Rf = 0.2 Ω |
| BFO | S = 20; Nc = 8; Ns = 12; Nre= 4; Ned= 2; Ped = 0.3 |
References
- Rezkallah, M.; Singh, S.; Singh, B.; Chandra, A.; Ibrahim, H.; Ghandour, M. Implementation of Two-Level Coordinated Control for Seamless Transfer in Standalone Microgrid. IEEE Trans. Ind. Appl. 2021, 57, 1057–1068. [Google Scholar] [CrossRef]
- Dubuisson, F.; Rezkallah, M.; Chandra, A.; Saad, M.; Tremblay, M.; Ibrahim, H. Control of Hybrid Wind–Diesel Standalone Microgrid for Water Treatment System Application. IEEE Trans. Ind. Appl. 2019, 55, 6499–6507. [Google Scholar] [CrossRef]
- Sidorov, D.; Panasetsky, D.; Tomin, N.; Karamov, D.; Zhukov, A.; Muftahov, I.; Dreglea, A.; Liu, F.; Li, Y. Toward Zero-Emission Hybrid AC/DC Power Systems with Renewable Energy Sources and Storages: A Case Study from Lake Baikal Region. Energies 2020, 13, 1226. [Google Scholar] [CrossRef]
- Dubuisson, F.; Chandra, A.; Rezkallah, M.; Ibrahim, H.; Singh, B. Predictive Based Control Algorithm for Hybrid Diesel-Battery Standalone Power Generation System. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar]
- Chishti, F.; Murshid, S.; Singh, B. PCC Voltage Quality Restoration Strategy of an Isolated Microgrid Based on Adjustable Step Adaptive Control. IEEE Trans. Ind. Appl. 2020, 56, 6206–6215. [Google Scholar] [CrossRef]
- Dogra, R.; Rajpurohit, B.S.; Tummuru, N.R.; Marinova, I.; Mateev, V. Fault Detection Scheme for Grid-Connected PV Based Multi-Terminal DC Microgrid. In Proceedings of the 2020 21st National Power Systems Conference (NPSC), Gujarat, India, 17–19 December 2020; pp. 1–6. [Google Scholar]
- Mohd, A.; Ortjohann, E.; Morton, D.; Omari, O. Review of Control Techniques for Inverters Parallel Operation. Electr. Power Syst. Res. 2010, 80, 1477–1487. [Google Scholar] [CrossRef]
- Mohan, A.M.; Meskin, N.; Mehrjerdi, H. A Comprehensive Review of the Cyber-Attacks and Cyber-Security on Load Frequency Control of Power Systems. Energies 2020, 13, 3860. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in Microgrid Control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Agelidis, V.G. Control Strategies for Microgrids with Distributed Energy Storage Systems: An Overview. IEEE Trans. Smart Grid 2018, 9, 3652–3666. [Google Scholar] [CrossRef]
- Pippia, T.; Sijs, J.; Schutter, B.D. A Single-Level Rule-Based Model Predictive Control Approach for Energy Management of Grid-Connected Microgrids. IEEE Trans. Control Syst. Technol. 2020, 28, 2364–2376. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Li, Z.; Guerrero, J.M. A Model Predictive Control for Renewable Energy Based AC Microgrids without Any PID Regulators. IEEE Trans. Power Electron. 2018, 33, 9122–9126. [Google Scholar] [CrossRef]
- Acuña, P.; Morán, L.; Rivera, M.; Dixon, J.; Rodriguez, J. Improved Active Power Filter Performance for Renewable Power Generation Systems. IEEE Trans. Power Electron. 2014, 29, 687–694. [Google Scholar] [CrossRef]
- Ikaouassen, H.; Raddaoui, A.; Rezkallah, M.; Chandra, A. Real-Time Implementation of Improved Predictive Model Control for Standalone Power Generation System Based PV Renewable Energy. IET Gener. Transm. Distrib. 2019, 13, 1068–1077. [Google Scholar] [CrossRef]
- Han, J.; Solanki, S.K.; Solanki, J. Coordinated Predictive Control of a Wind/Battery Microgrid System. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 296–305. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Guerrero, J.M.; Ioinovici, A.; Chan, K.W.; Rodriguez, J. Model Predictive Control of Microgrids—An Overview. Renew. Sustain. Energy Rev. 2021, 136, 110422. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A New Optimizer Using Particle Swarm Theory. In Proceedings of the MHS’95 Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant Colony Optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Haider, W.; Hassan, S.J.U.; Mehdi, A.; Hussain, A.; Adjayeng, G.O.M.; Kim, C.-H. Voltage Profile Enhancement and Loss Minimization Using Optimal Placement and Sizing of Distributed Generation in Reconfigured Network. Machines 2021, 9, 20. [Google Scholar] [CrossRef]
- Passino, K.M. Biomimicry of Bacterial Foraging for Distributed Optimization and Control. IEEE Control Syst. Mag. 2002, 22, 52–67. [Google Scholar] [CrossRef]
- Mishra, S.; Bhende, C.N. Bacterial Foraging Technique-Based Optimized Active Power Filter for Load Compensation. IEEE Trans. Power Deliv. 2007, 22, 457–465. [Google Scholar] [CrossRef]
- Ali, E.S.; Abd-Elazim, S.M. Bacteria Foraging Optimization Algorithm Based Load Frequency Controller for Interconnected Power System. Int. J. Electr. Power Energy Syst. 2011, 33, 633–638. [Google Scholar] [CrossRef]
- Sathish Kumar, K.; Jayabarathi, T. Power System Reconfiguration and Loss Minimization for an Distribution Systems Using Bacterial Foraging Optimization Algorithm. Int. J. Electr. Power Energy Syst. 2012, 36, 13–17. [Google Scholar] [CrossRef]
- Rajasekar, N.; Krishna Kumar, N.; Venugopalan, R. Bacterial Foraging Algorithm Based Solar PV Parameter Estimation. Sol. Energy 2013, 97, 255–265. [Google Scholar] [CrossRef]
- Te-Jen, S.; Chien-Fang, L.; Chun-Sheng, C.; Jui-Chuan, C. Solar Tracking Control System Based on a Hydrid BFO/PSO. In Proceedings of the 2013 International Symposium on Next-Generation Electronics, Taoyuan, Taiwan, 7–10 February 2013; pp. 482–485. [Google Scholar]
- Jiaqi, L.; Xianlin, H.; Xiaojun, B.; Gao, X.Z.; Zenger, K. An Intelligent Hybrid BFO-PSO Algorithm for Multi-Loop Robust Controller Design in Discrete-Time Networked Control Systems. In Proceedings of the 2014 International Conference on Mechatronics and Control (ICMC), Jinzhou, China, 3–5 July 2014; pp. 510–515. [Google Scholar]
- Niu, B.; Wang, H.; Wang, J.; Tan, L. Multi-Objective Bacterial Foraging Optimization. Neurocomputing 2013, 116, 336–345. [Google Scholar] [CrossRef]
- Nanda, J.; Mishra, S.; Saikia, L.C. Maiden Application of Bacterial Foraging-Based Optimization Technique in Multiarea Automatic Generation Control. IEEE Trans. Power Syst. 2009, 24, 602–609. [Google Scholar] [CrossRef]
- Imran, A.M.; Kowsalya, M. Optimal Size and Siting of Multiple Distributed Generators in Distribution System Using Bacterial Foraging Optimization. Swarm Evol. Comput. 2014, 15, 58–65. [Google Scholar] [CrossRef]
- Javaid, N.; Javaid, S.; Abdul, W.; Ahmed, I.; Almogren, A.; Alamri, A.; Niaz, I.A. A Hybrid Genetic Wind Driven Heuristic Optimization Algorithm for Demand Side Management in Smart Grid. Energies 2017, 10, 319. [Google Scholar] [CrossRef]
- Dubuisson, F.; Chandra, A.; Rezkallah, M.; Ibrahim, H. A Bacterial Foraging Optimization Technique and Predictive Control Approach for Power Management in a Standalone Microgrid. In Proceedings of the 2020 IEEE Electric Power and Energy Conference (EPEC), Edmonton, AB, Canada, 9–10 November 2020; pp. 1–7. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dubuisson, F.; Rezkallah, M.; Ibrahim, H.; Chandra, A. Real-Time Implementation of the Predictive-Based Control with Bacterial Foraging Optimization Technique for Power Management in Standalone Microgrid Application. Energies 2021, 14, 1723. https://doi.org/10.3390/en14061723
Dubuisson F, Rezkallah M, Ibrahim H, Chandra A. Real-Time Implementation of the Predictive-Based Control with Bacterial Foraging Optimization Technique for Power Management in Standalone Microgrid Application. Energies. 2021; 14(6):1723. https://doi.org/10.3390/en14061723
Chicago/Turabian StyleDubuisson, Félix, Miloud Rezkallah, Hussein Ibrahim, and Ambrish Chandra. 2021. "Real-Time Implementation of the Predictive-Based Control with Bacterial Foraging Optimization Technique for Power Management in Standalone Microgrid Application" Energies 14, no. 6: 1723. https://doi.org/10.3390/en14061723
APA StyleDubuisson, F., Rezkallah, M., Ibrahim, H., & Chandra, A. (2021). Real-Time Implementation of the Predictive-Based Control with Bacterial Foraging Optimization Technique for Power Management in Standalone Microgrid Application. Energies, 14(6), 1723. https://doi.org/10.3390/en14061723






