Ocean Energy Systems Wave Energy Modeling Task 10.4: Numerical Modeling of a Fixed Oscillating Water Column
Abstract
1. Introduction
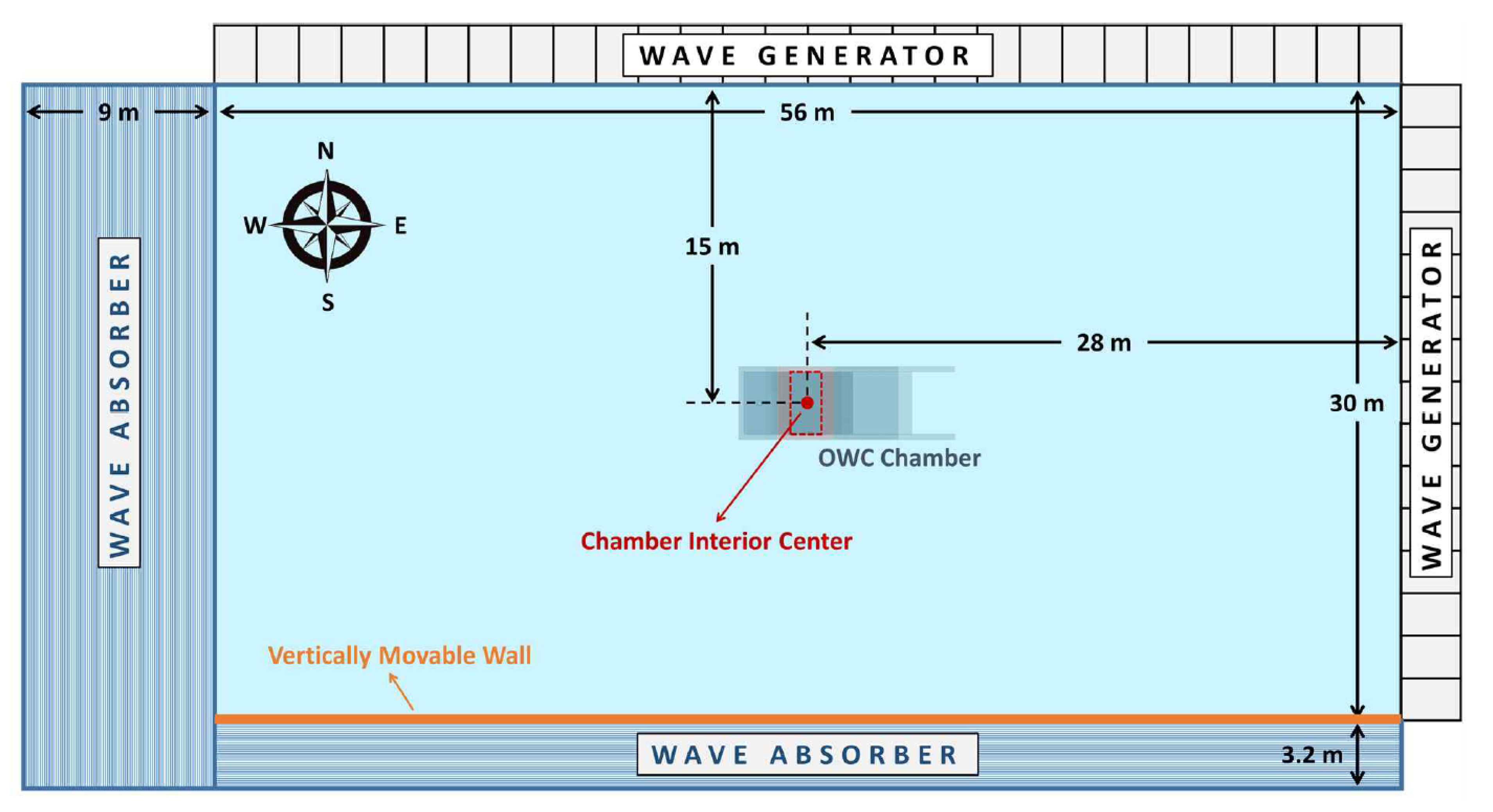
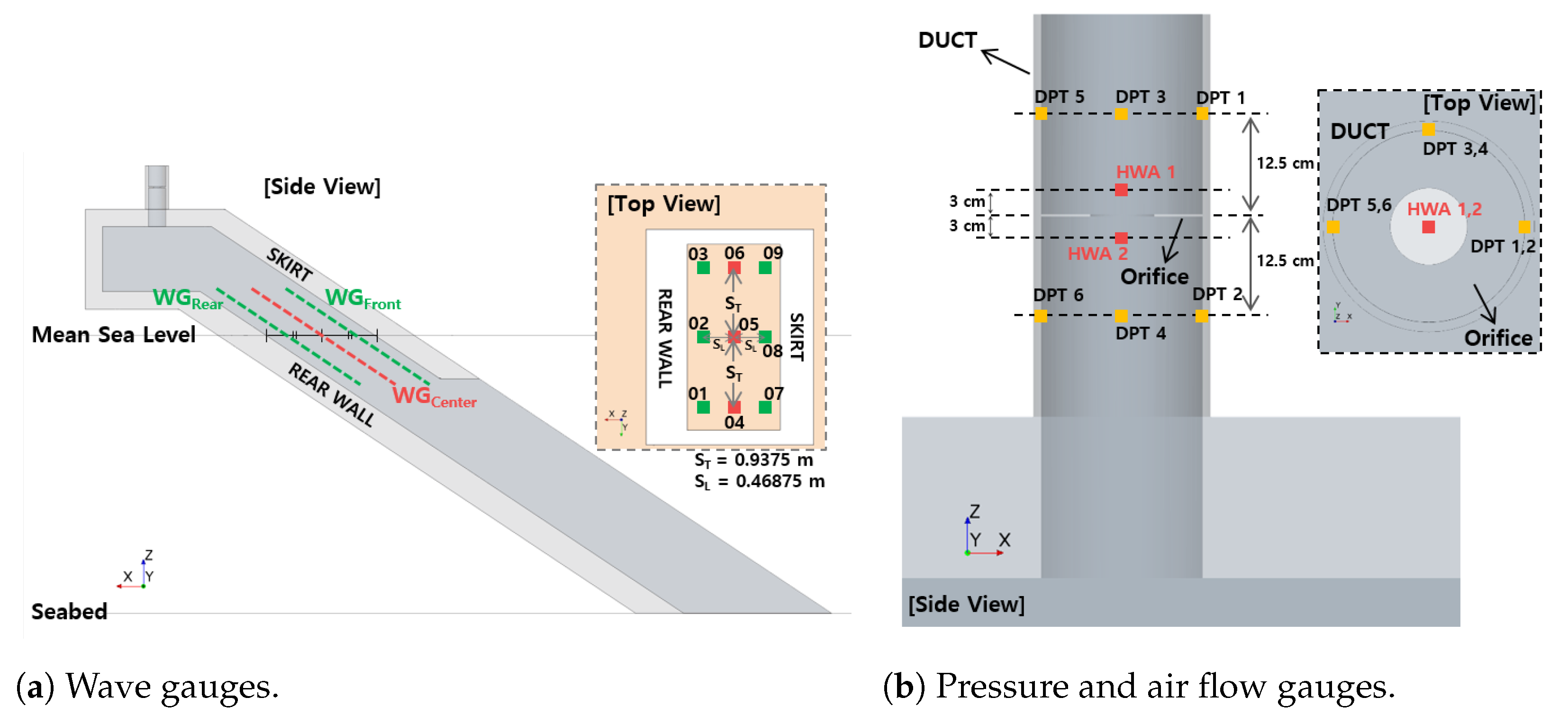
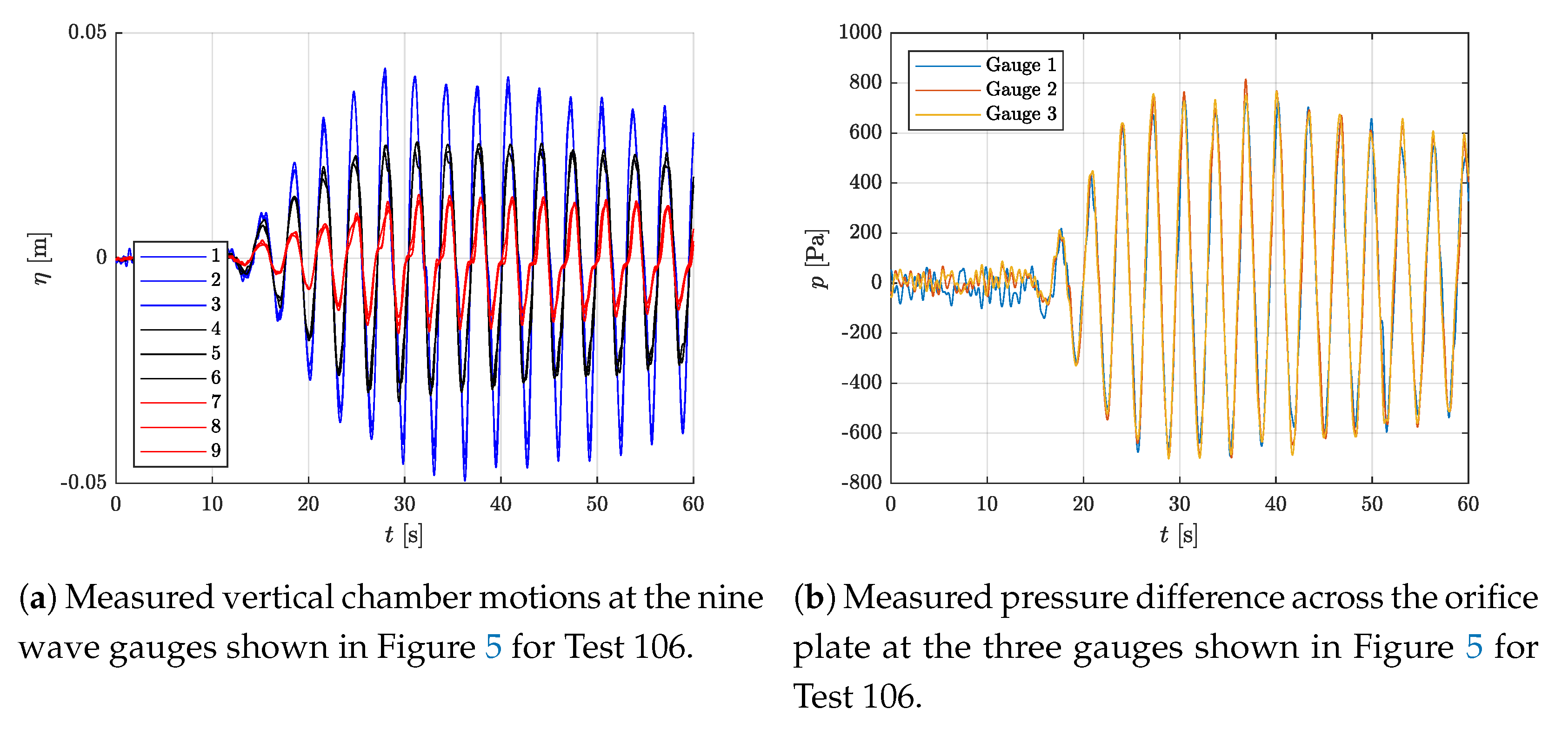
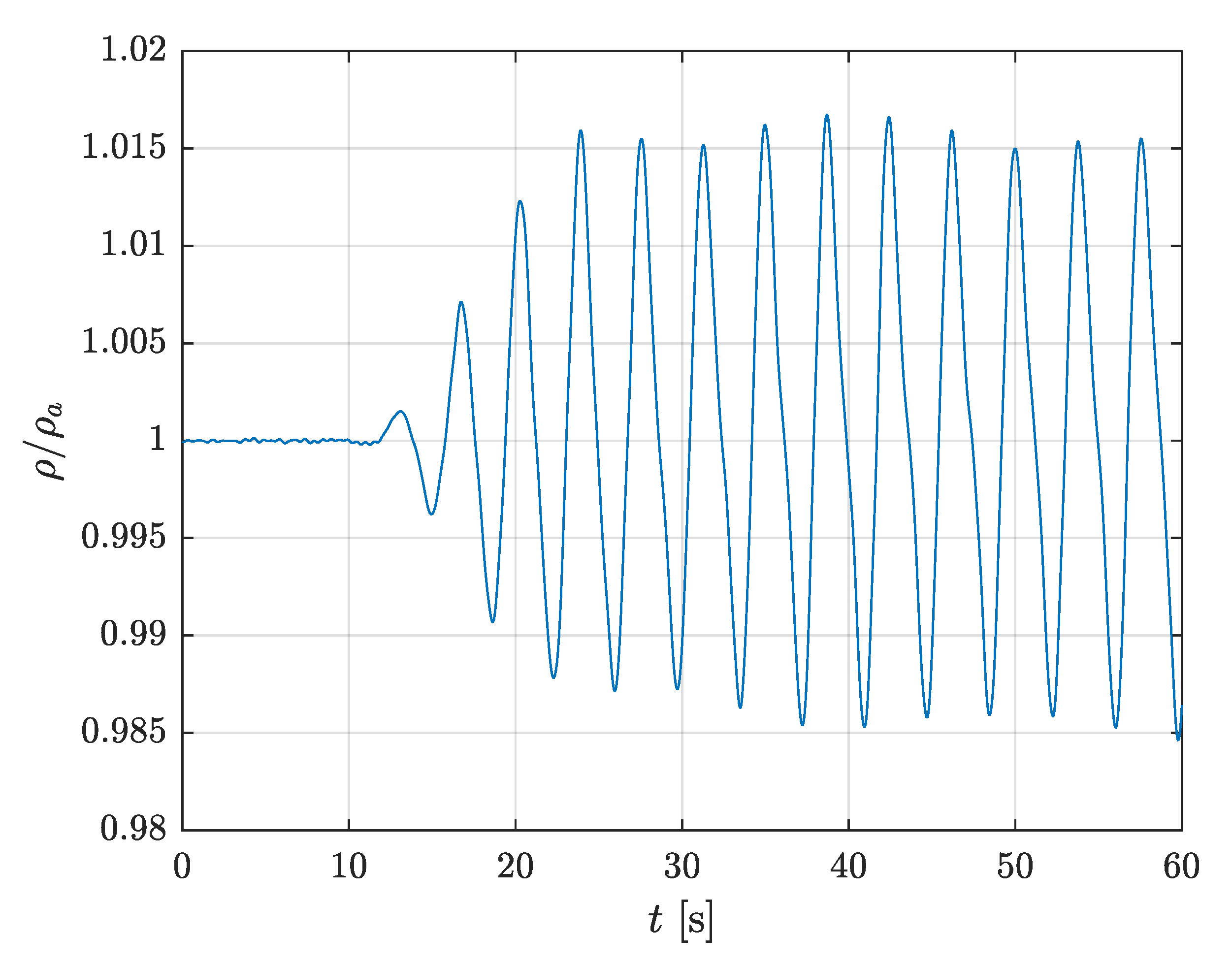
2. Experimental Measurements
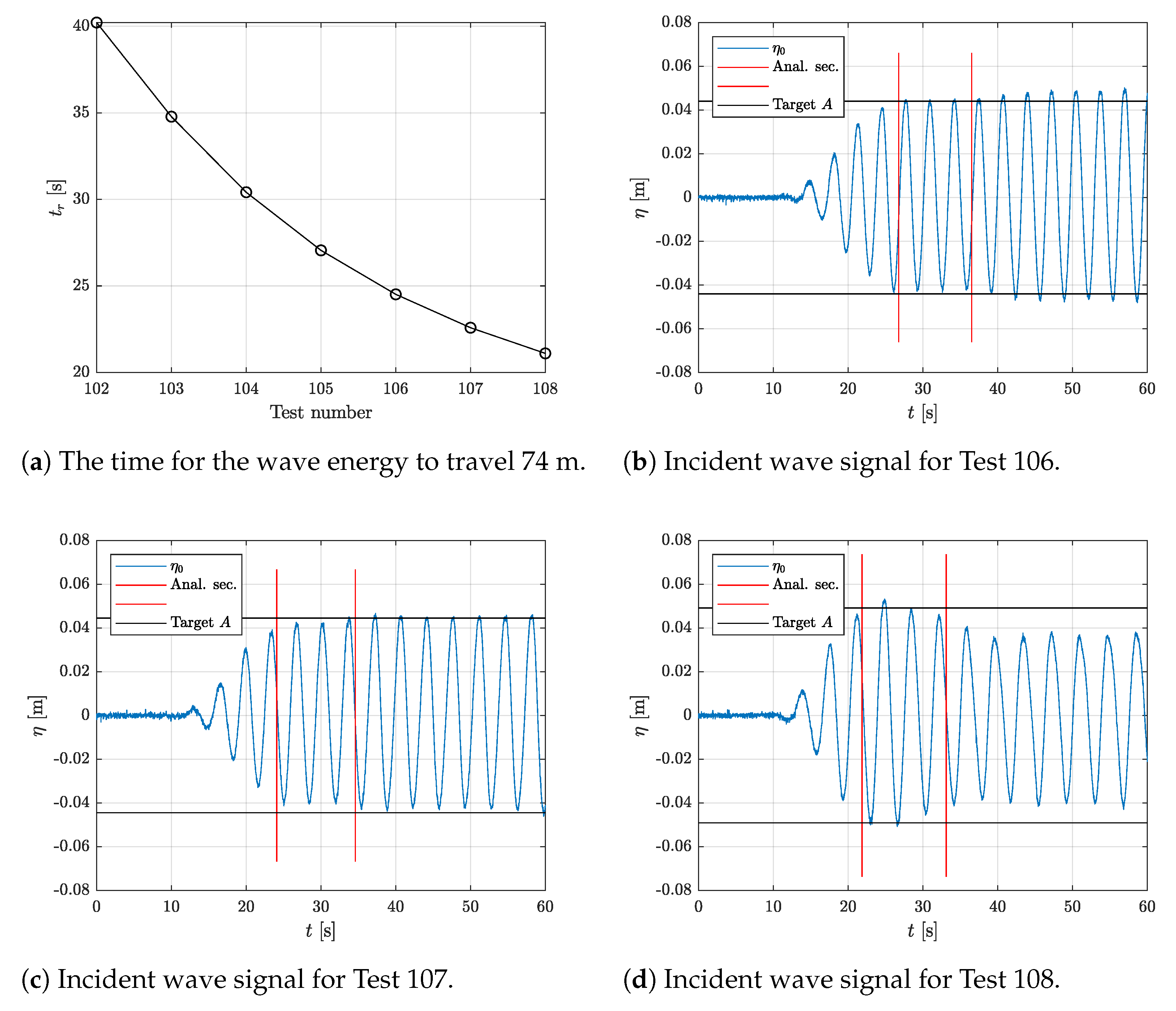
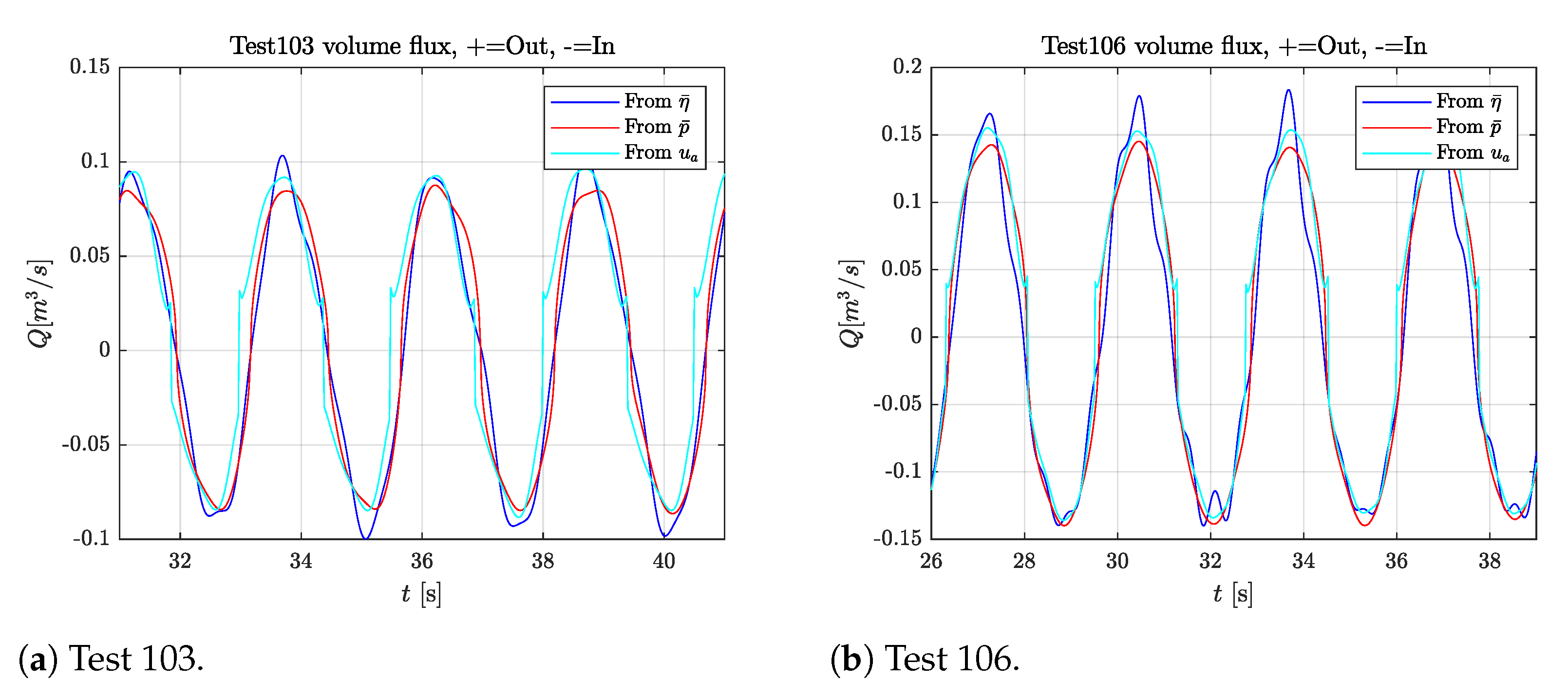
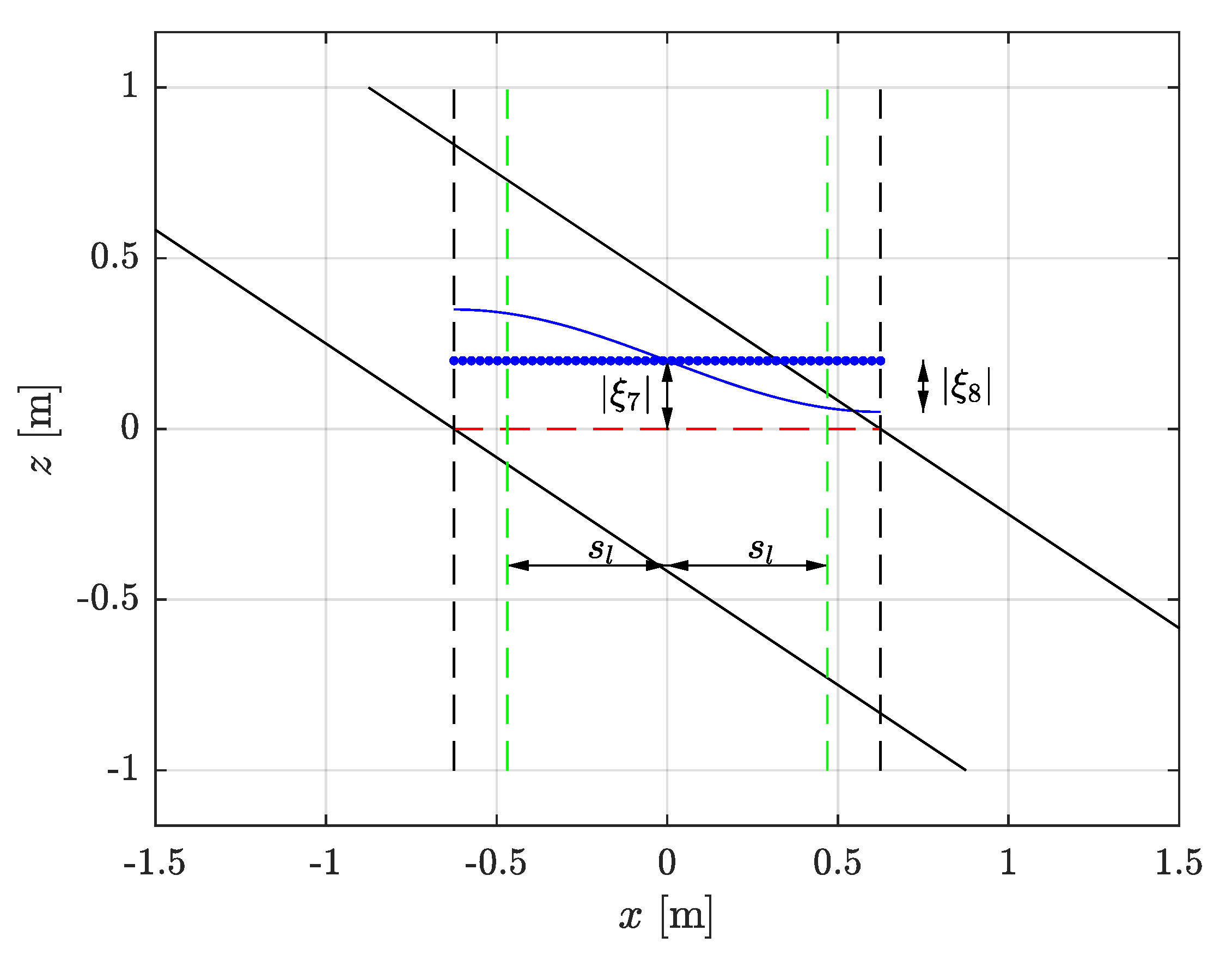
2.1. Analysis of the Experimental Data
- , where , with the mean of the nine internal wave gauge measurements and the time derivative (here taken by a fourth-order finite-difference scheme).
- , where is the measured air flow velocity through the orifice. Here, it was determined that the most accurate result was found by taking the value from the upper gauge for the outflow and from the lower gauge for the inflow.
- From Equation (6), we can write , where is the mean of the three pressure difference measurements.
3. Numerical Modeling of OWC Chambers
3.1. Weakly-Nonlinear Potential Flow Theory in the Frequency Domain
3.2. Weakly-Nonlinear Potential Flow Theory in the Time Domain
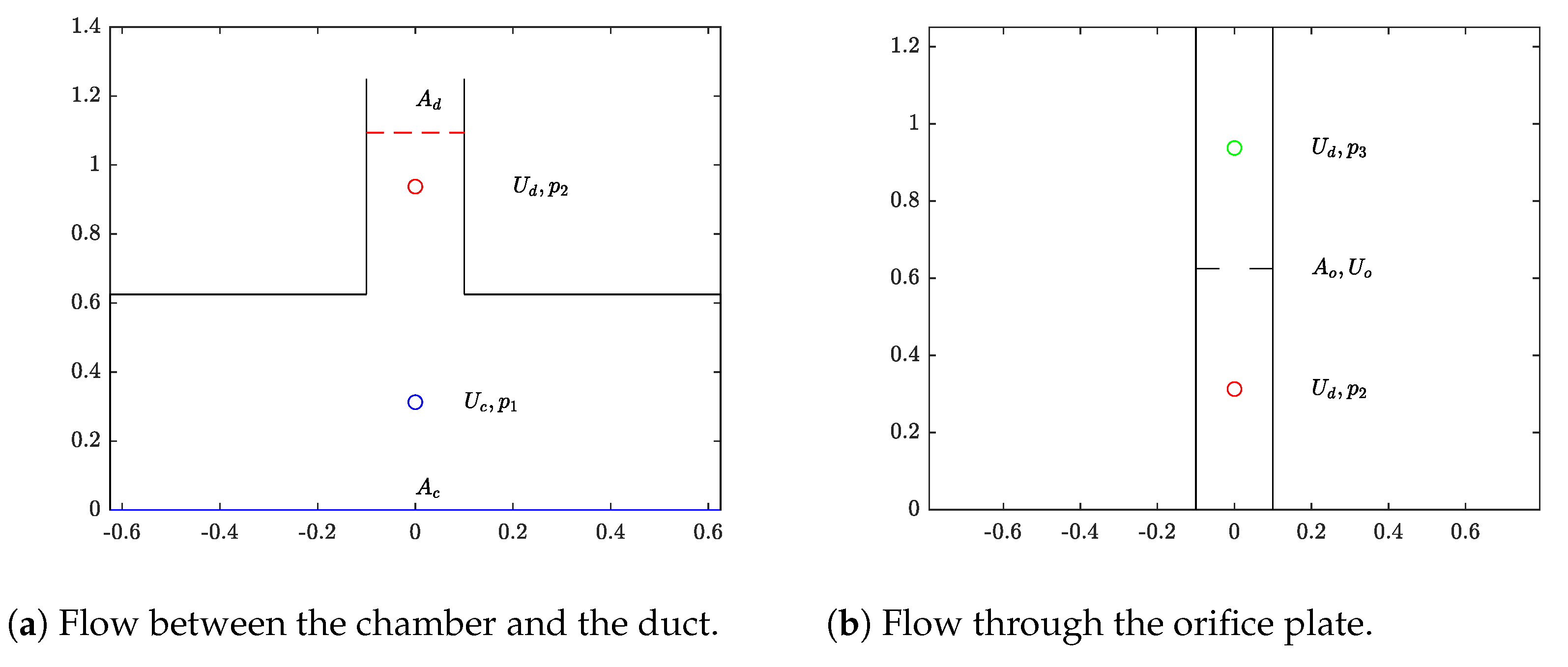
3.3. Potential Flow Modeling of the Orifice Plate Damping—Incompressible Flow
3.4. Potential Flow Modeling of the Orifice Plate Damping—Compressible Air Volume with Incompressible Orifice Flow
3.5. Potential Flow Modeling of the Orifice Plate Damping—Compressible Air Volume with Compressible Orifice Flow
3.6. Numerical Potential Flow Solutions
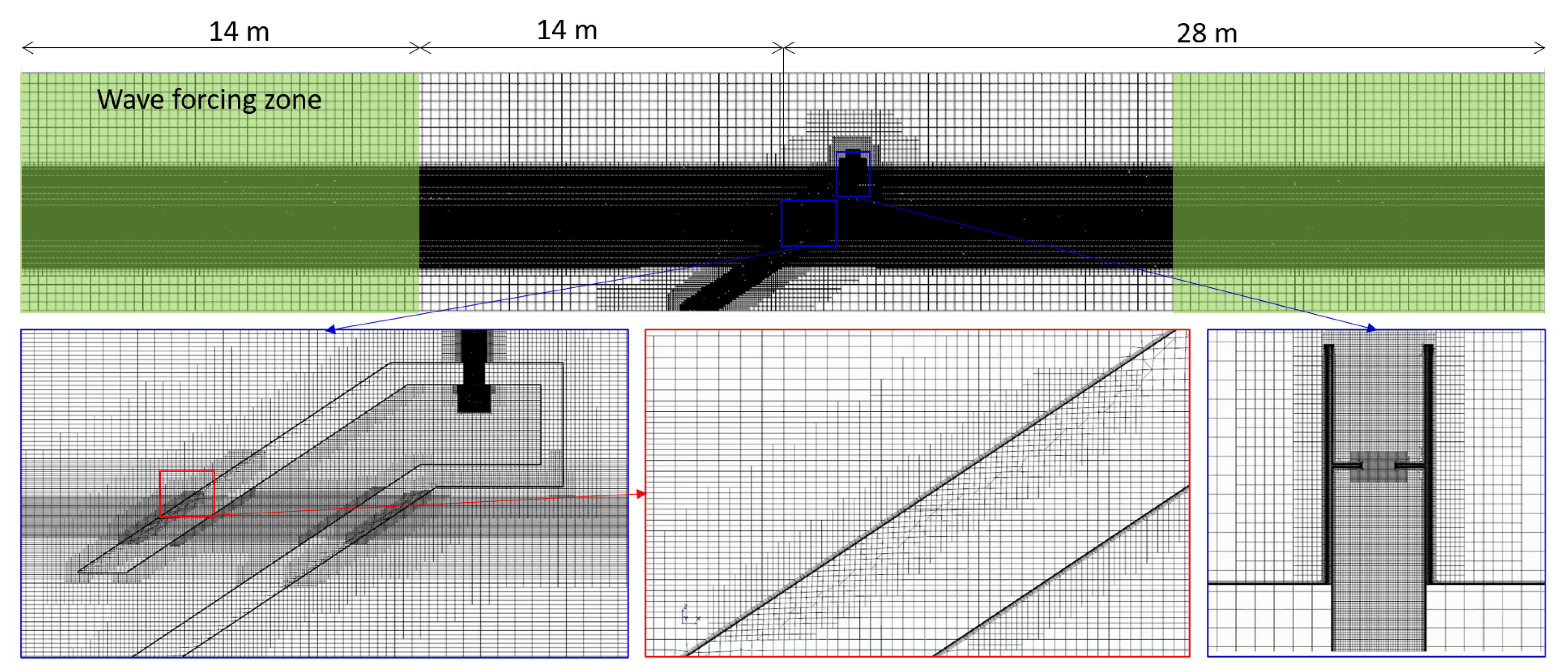
3.7. CFD Solutions
4. Description of the Participating Teams Solution Strategies
4.1. The Technical University of Denmark Team
4.2. The National Renewable Energy Laboratory Team
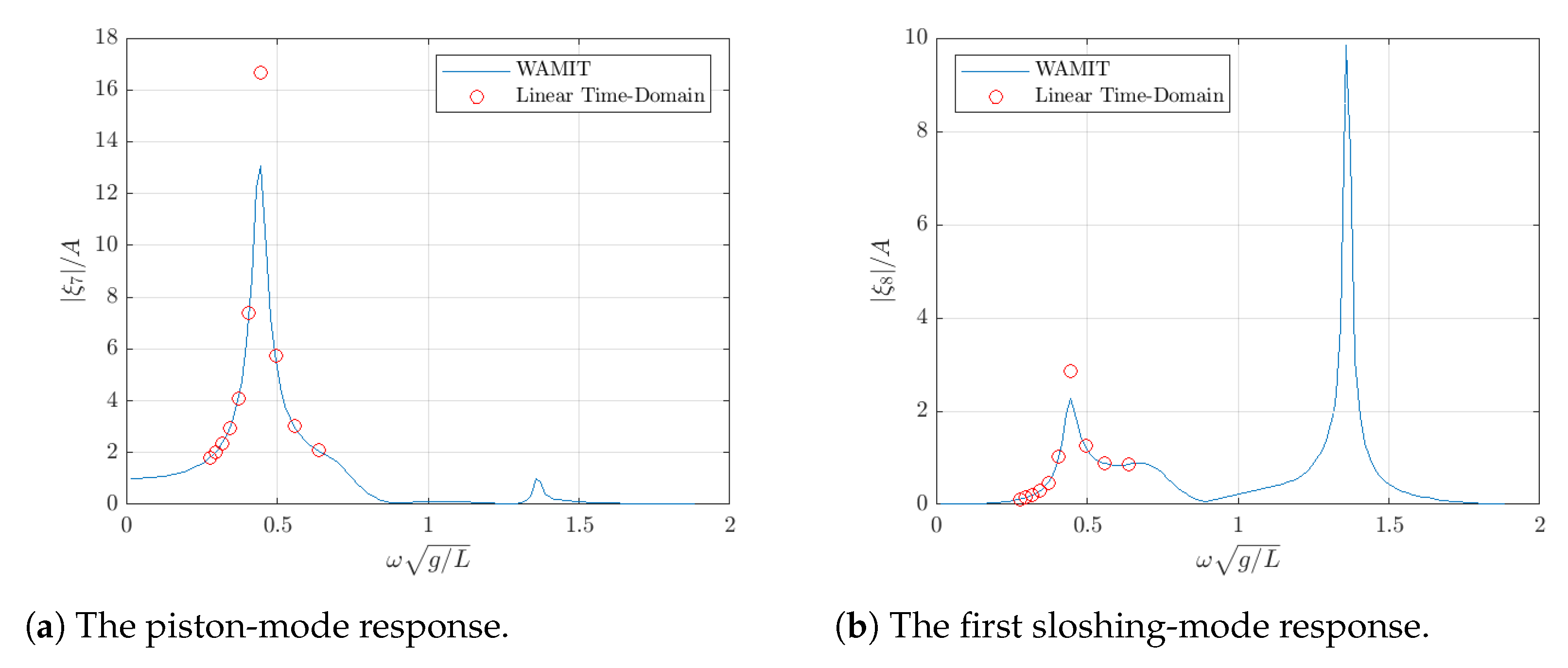
4.3. The Maynooth University/Dundalk IT Team
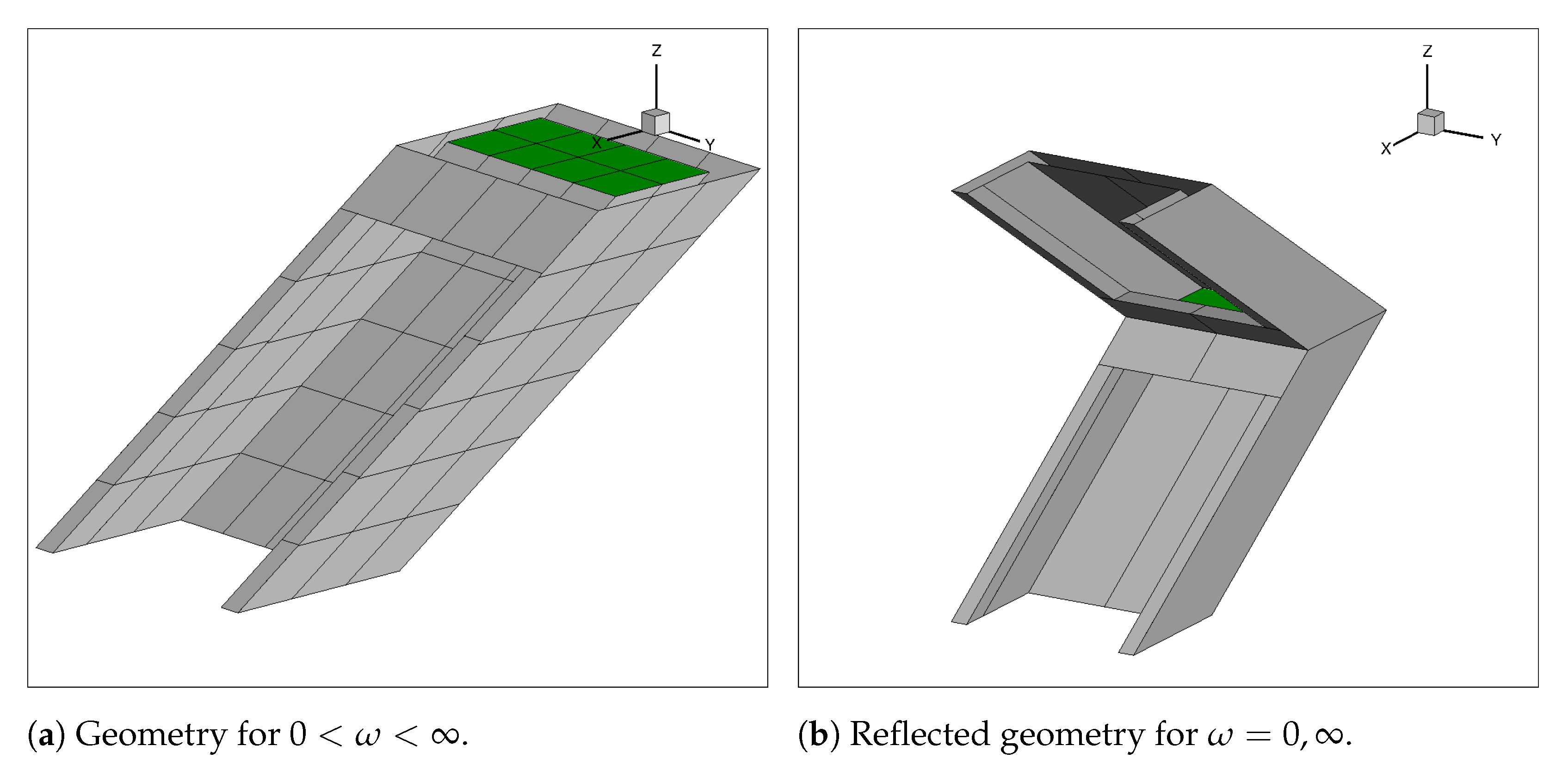
- The sloshing mode (mode 8) and the coupling modes (mode 78 and mode 87) are waveless (i.e., the convolution integrals for these modes can be set to zero).
- The coupling added masses, and , are independent of frequency and equal to their infinite frequency values, and , respectively.
4.4. The University of Plymouth Team
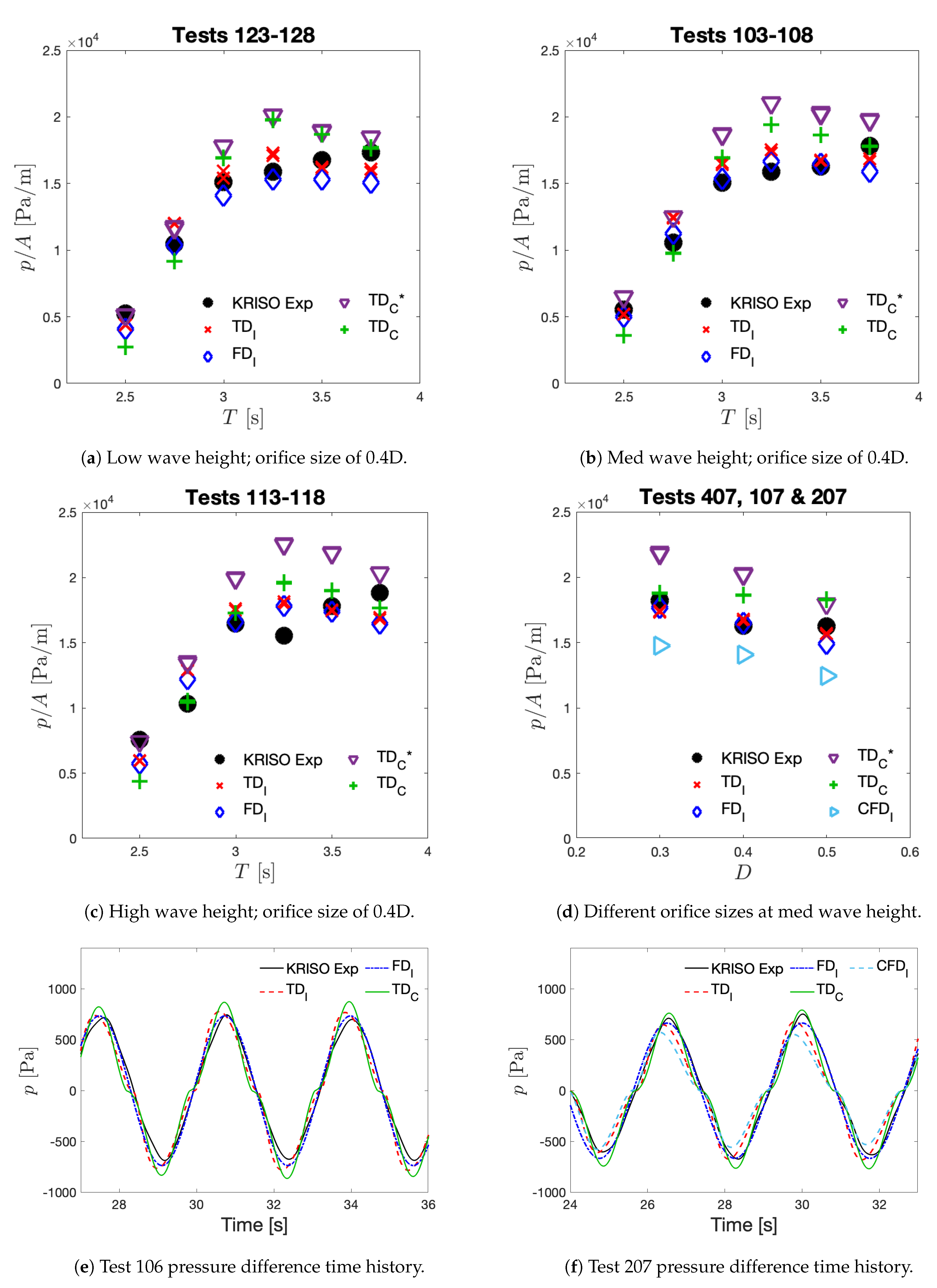
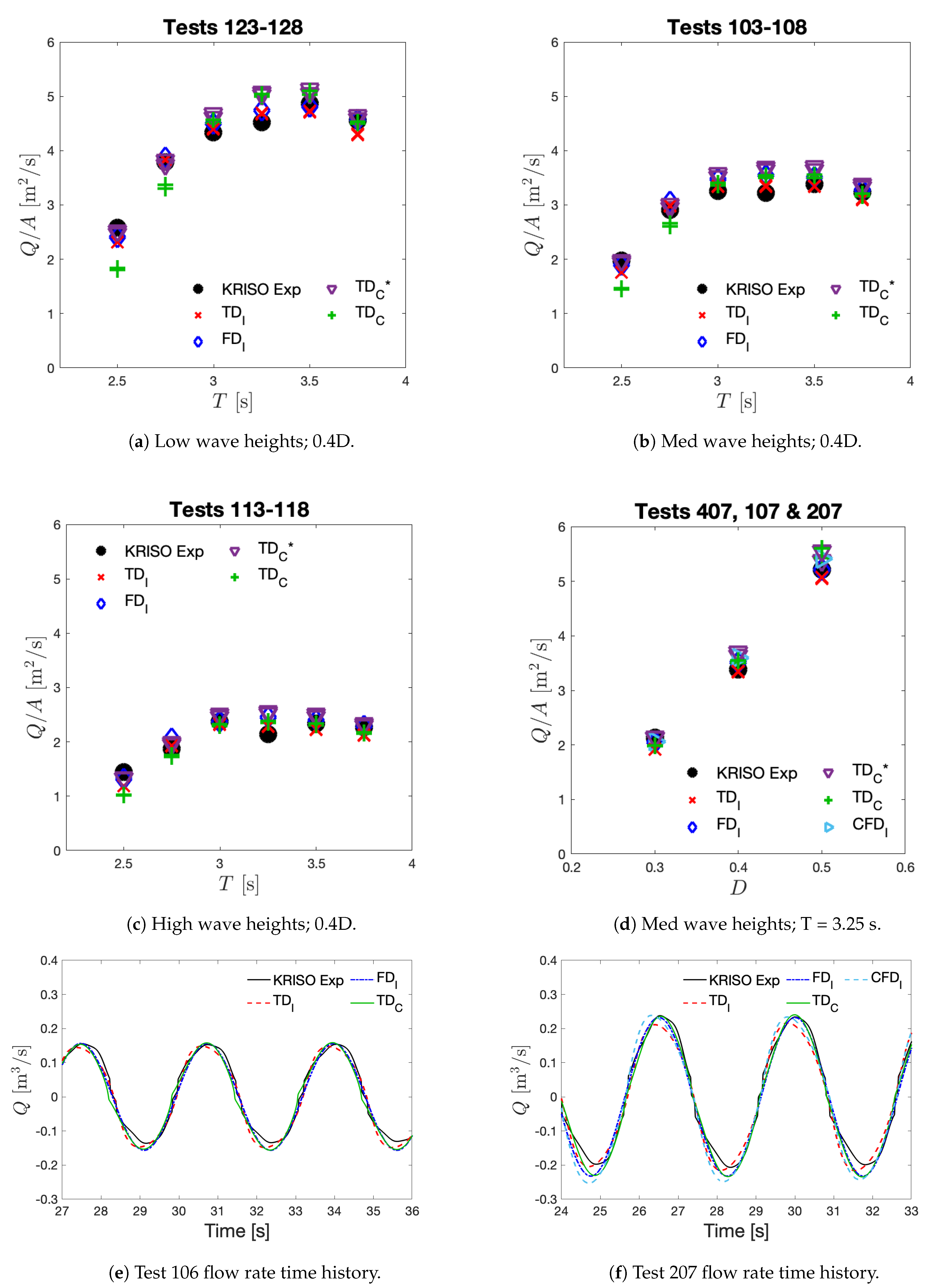
5. Comparison of Results
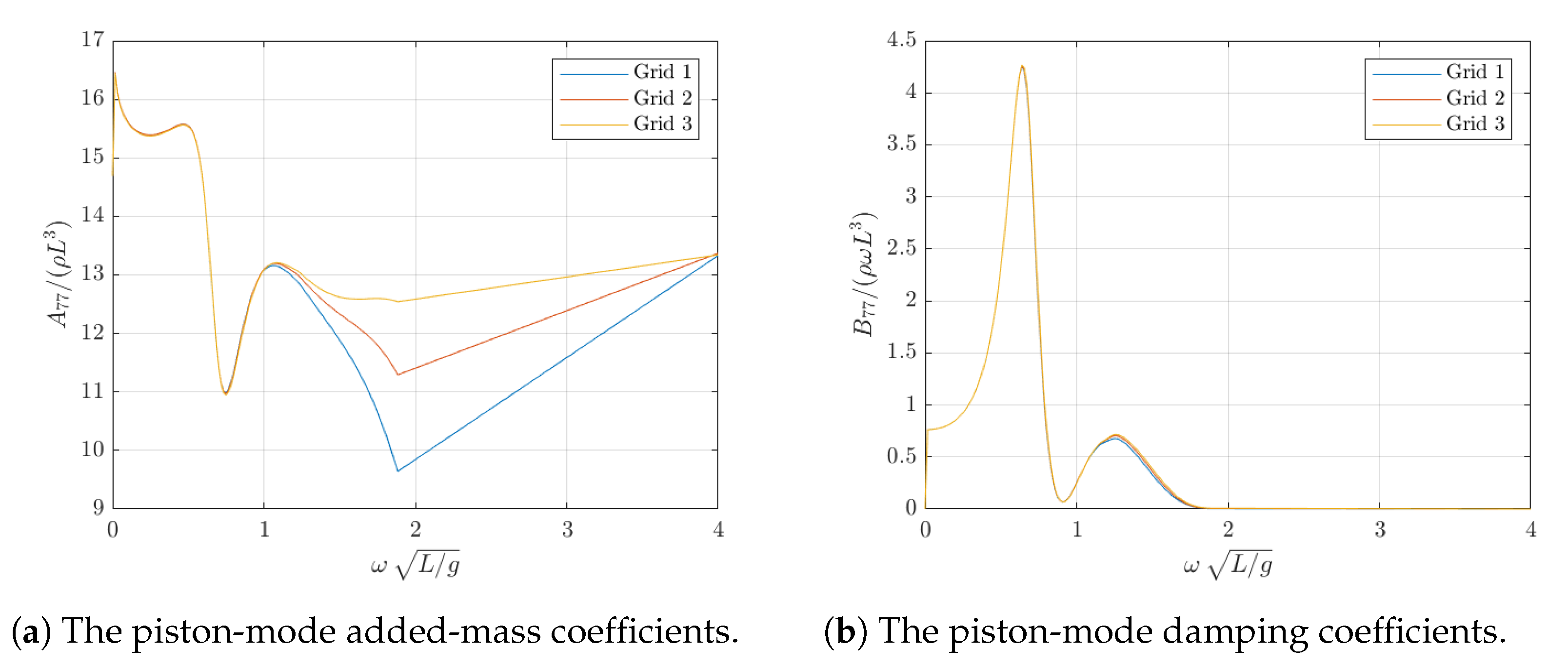
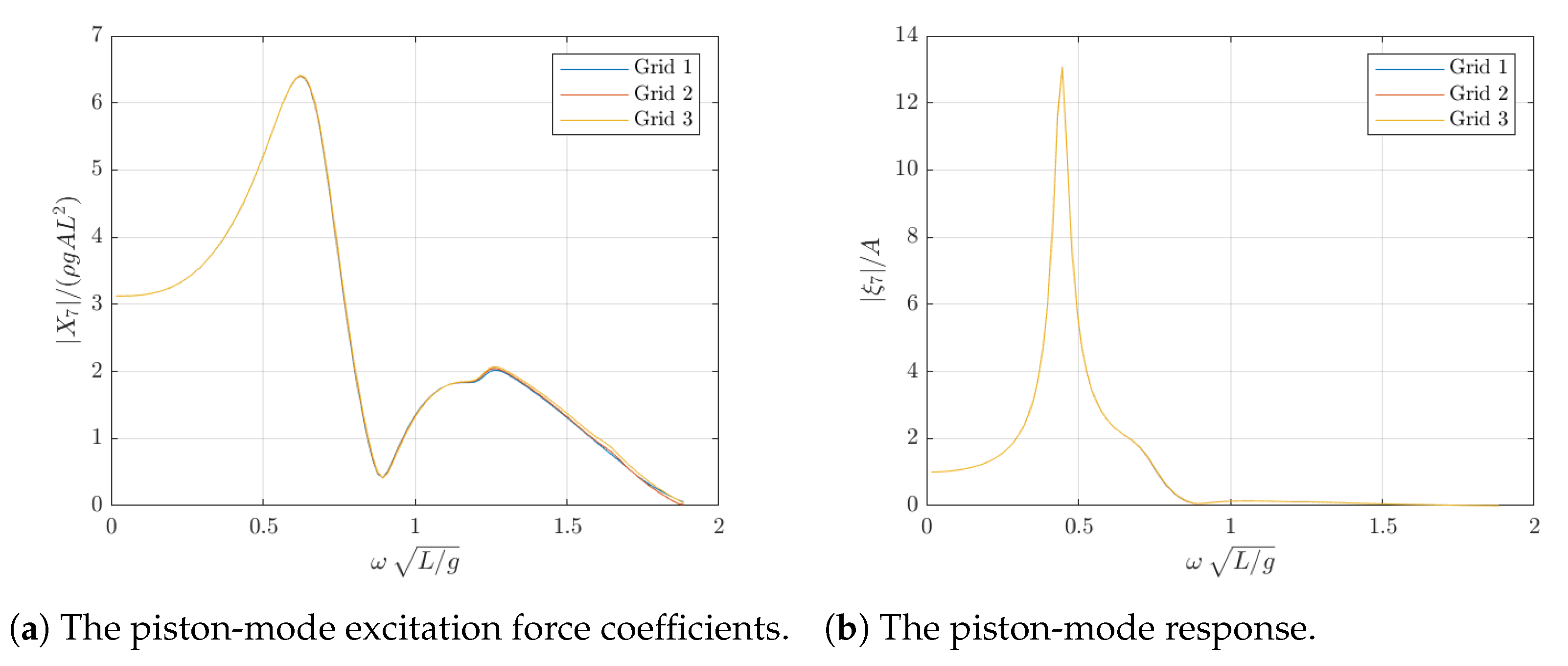
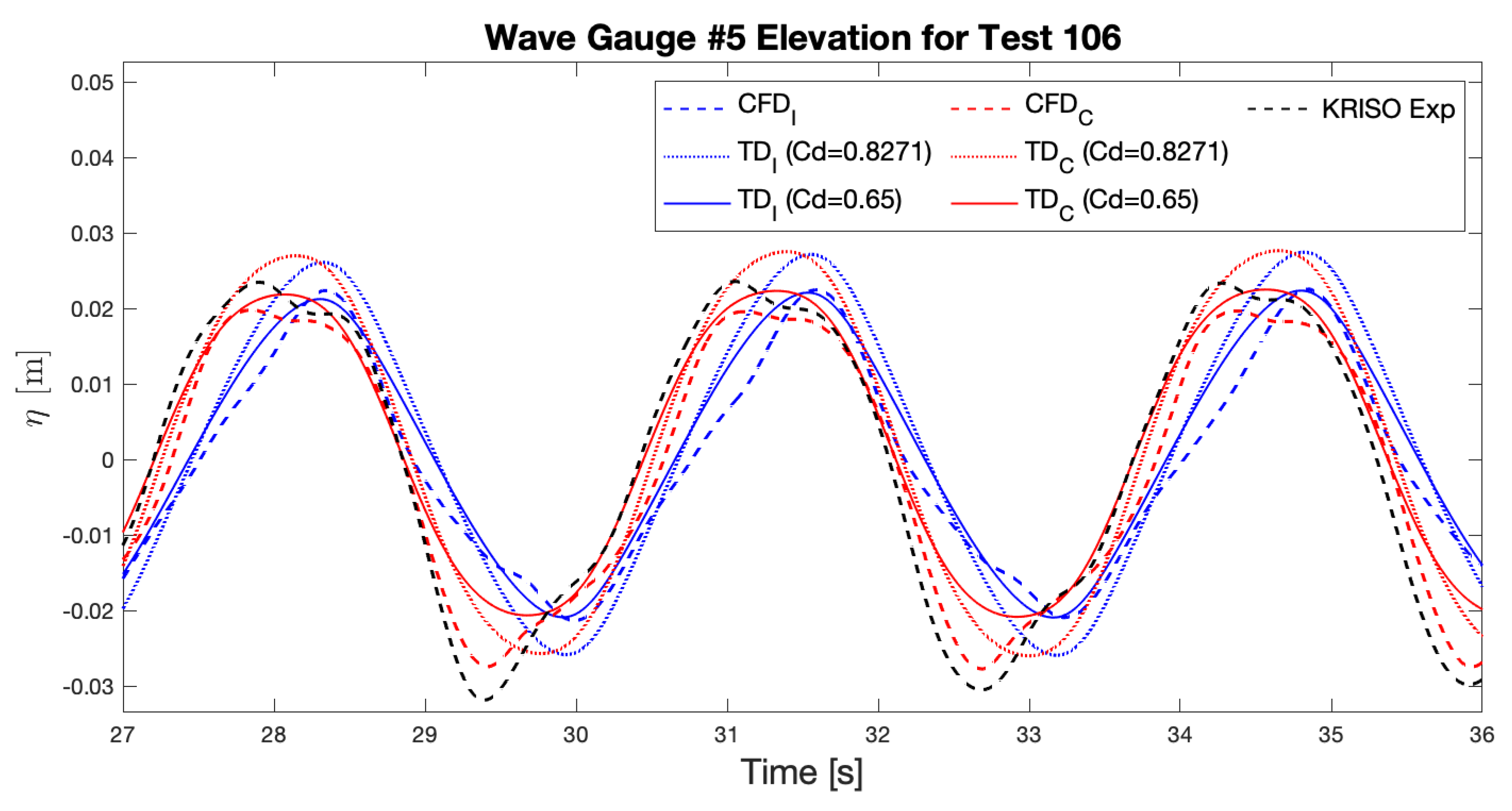
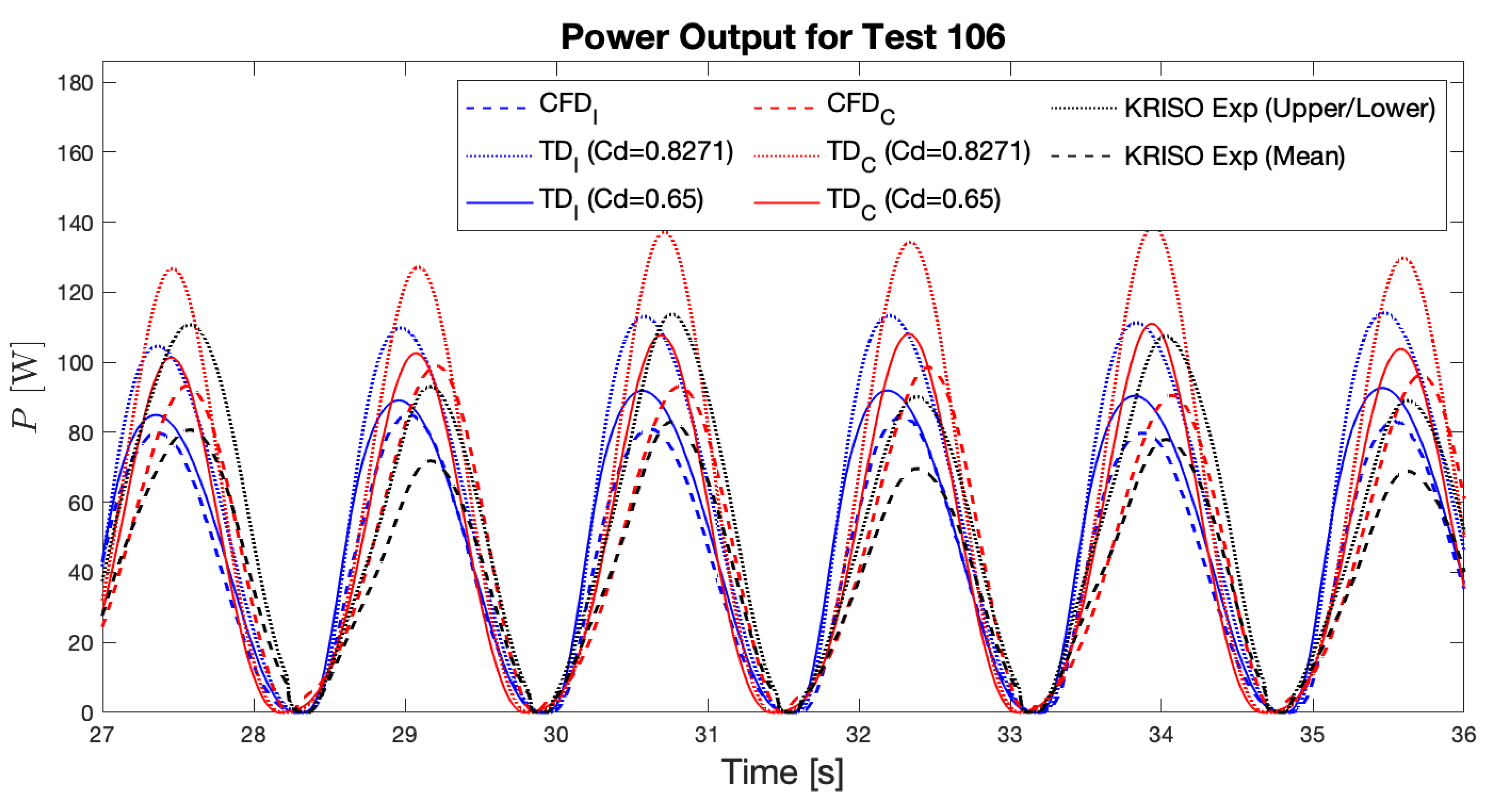
5.1. Potential Flow Solutions
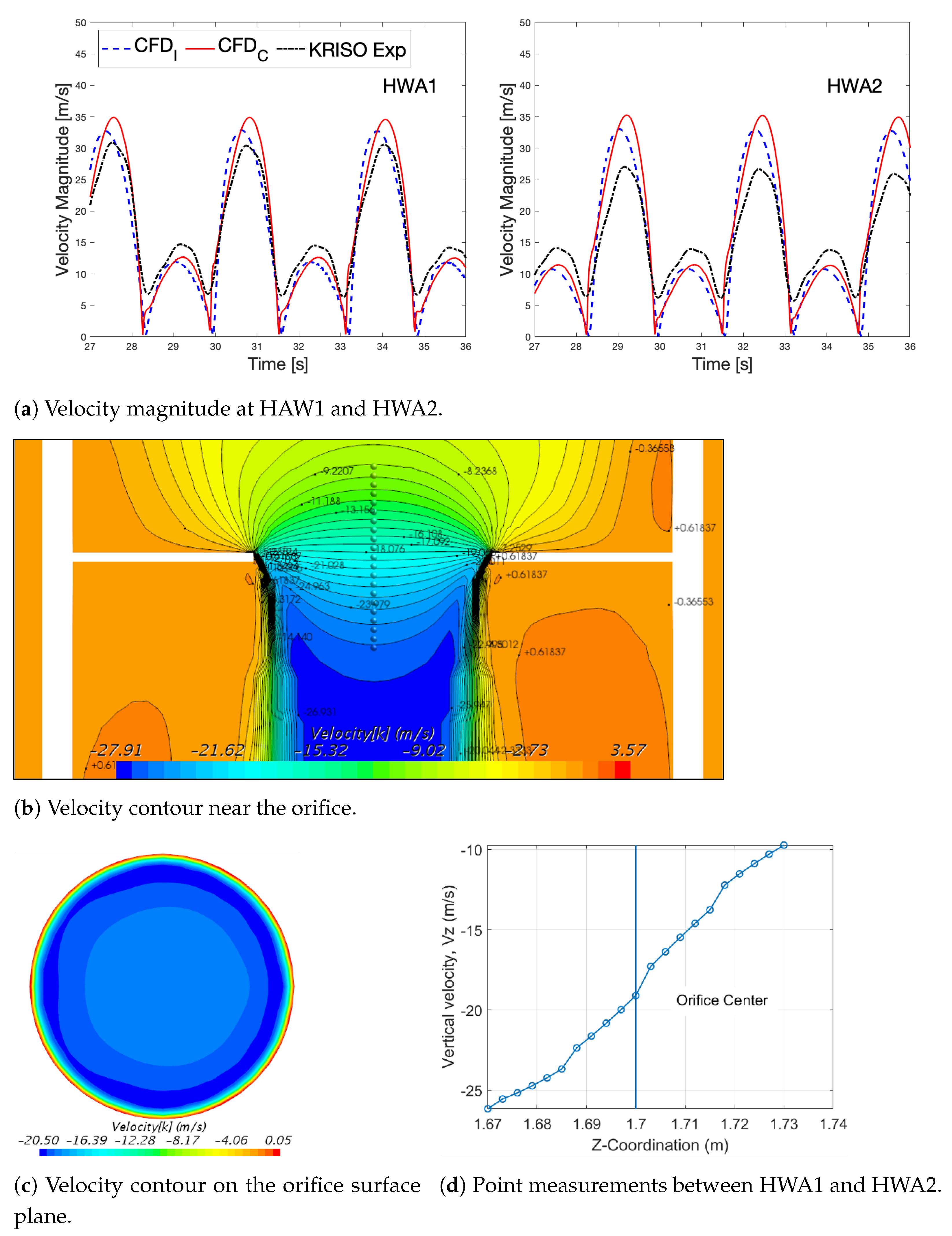
5.2. CFD Simulations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BEM | Boundary element method |
| CFD | Computational fluid dynamics |
| DkIT | Dundalk IT |
| DOF | Degrees of freedom |
| DTU | Technical University of Denmark |
| FFT | Fast Fourier transform |
| FSP | Free-surface pressure modes |
| HWA | Hot wire anemometer |
| KRISO | Korean Research Institute of Ships and Ocean Engineering |
| MU | Maynooth University |
| NREL | National Renewable Energy Laboratory |
| OES | Ocean Energy Systems |
| OWC | Oscillating water column |
| RANS | Reynolds-averaged Navier–Stokes |
| URANS | Unsteady Reynolds-averaged Navier–Stokes |
| WEC | Wave energy converter |
References
- Dallman, A.; Jenne, D.S.; Neary, V.; Driscoll, F.; Thresher, R.; Gunawan, G. Evaluation of performance metrics for the Wave Energy Prize converters tested at 1/20th scale. Renew. Sustain. Energy Rev. 2018, 98, 79–91. [Google Scholar] [CrossRef]
- Wendt, F.; Nielsen, K.; Yu, Y.H.; Bingham, H.B.; Eskilsson, C.; Kramer, M.; Babarit, A.; Bunnik, T. Ocean energy systems wave energy modelling task: Modelling, verification and validation of wave energy converters. J. Mar. Sci. Eng. 2019, 7, 379. [Google Scholar] [CrossRef]
- Heath, T. A review of oscillating water columns. Philos. Trans. Roy. Soc. Lond. A 2012, 370, 235–245. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Henriques, J.C.C. Model-prototype similarity of oscillating-water-column wave energy converters. Int. J. Mar. Energy 2014, 6, 18–34. [Google Scholar] [CrossRef]
- Vicinanza, D.; Di Lauro, E.; Contestabile, P.; Gisonni, C.; Lara, J.L.; Losada, I.J. Review of innovative harbor breakwaters for wave-energy conversion. J. Waterway Port Coastal Ocean Eng. 2019, 145, 1–18. [Google Scholar] [CrossRef]
- Babarit, A. Wave Energy Conversion. Resource, Technology and Performance; ISTE Press Ltd.: London, UK, 2018. [Google Scholar] [CrossRef]
- Cruz, J. Ocean Wave Energy. Current Status and Future Perspectives; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Yu, Y.H.; Lawson, M.; Ruehl, K.; Michelen, C. Development and demonstration of the WEC-Sim wave energy converter simulation tool. In Proceedings of the 2nd Marine Energy Technology Symposium, U.S. Department of Energy, Seattle, WA, USA, 15–18 April 2014. [Google Scholar]
- Papillon, L.; Costello, R.; Ringwood, J.V. Boundary element and integral methods in potential flow theory: A review with a focus on wave energy applications. J. Ocean. Eng. Mar. Energy 2020, 6, 303–337. [Google Scholar] [CrossRef]
- Windt, C.; Davidson, J.; Ringwood, J.V. High-fidelity numerical modelling of ocean wave energy systems: A review of computational fluid dynamics-based numerical wave tanks. Renew. Sustain. Energy Rev. 2018, 93, 610–630. [Google Scholar] [CrossRef]
- Bingham, H.B.; Ducasse, D.; Nielsen, K.; Read, R. Hydrodynamic Analysis of Oscillating Water Column, Wave Energy Devices. J. Ocean Eng. Mar. Energy 2015, 1, 405–419. [Google Scholar] [CrossRef]
- WAMIT. WAMIT; User Manual, Version 7.0; WAMIT, Inc.: Chestnut Hill, MA, USA, 2008–2012; Available online: http://www.wamit.com (accessed on 17 March 2021).
- Sheng, W.; Alcom, R.; Lewis, A. Assessment of primary energy conversions of oscillating water columns. I. Hydrodynamic analysis. J. Renew. Sustain. Energy 2014, 6, 053113. [Google Scholar] [CrossRef]
- Luczko, E.; Robertson, B.; Bailey, H.; Hiles, C.; Buckham, B. Representing non-linear wave energy converters in coastal wave models. Renew. Energy 2018, 118, 376–385. [Google Scholar] [CrossRef]
- Henriques, J.C.C.; Sheng, W.; Falcão, A.F.O.; Gato, L.M.C. A comparison of biradial and Wells air turbines on the Mutriku breakwater OWC wave power plant. In Proceedings of the 36th International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Henriques, J.C.C.; Gomes, R.P.F.; Gato, L.M.C.; Robles, E.; Ceballos, S. Testing and control of a power take-off system for an oscillating-water-column wave energy converter. Renew. Energy 2016, 85, 714–724. [Google Scholar] [CrossRef]
- Park, S.; Kim, K.H.; Nam, B.W.; Kim, J.S.; Hong, K. Experimental and numerical analysis of performance of oscillating water column wave energy converter applicable to breakwaters. In Proceedings of the 38th International Conference on Ocean, Offshore and Arctic Engineering, Glasgow, Scotland, 9–14 June 2019. [Google Scholar]
- Fenton, J.D. Nonlinear wave theories. In The Sea; Le Mehaute, B., Hanes, D.M., Eds.; John Wiley & Sons.: Hoboken, NJ, USA, 1990; pp. 3–25. [Google Scholar]
- Bullen, P.R.; Cheeseman, D.J.; Hussain, L.A.; Ruffell, A.E. The determination of pipe contraction pressure loss coeffients for incompressible turbulent flow. Heat Fluid Flow 1987, 8, 111–118. [Google Scholar] [CrossRef]
- Newman, J.N. Marine Hydrodynamics; The MIT Press: Cambridge, MA, USA, 1977. [Google Scholar]
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Evans, D.V. Wave-power absoption by systems of oscillating surface pressure distributions. J. Fluid Mech. 1982, 114, 481–499. [Google Scholar] [CrossRef]
- Lee, C.H.; Nielsen, F.G. Analysis of Oscillating Water Column Device Using a Panel Method. 1996. Available online: http://www.iwwwfb.org (accessed on 17 March 2021).
- Lee, C.H.; Newman, J.N.; Nielsen, F.G. Wave Interactions with an Oscillating Water Column. In Proceedings of the 6th International Offshore and Polar Engineering Conference, Los Angeles, CA, USA, 26–31 May 1996. [Google Scholar]
- Newman, J.N.; Lee, C.H. WAMIT: A Radiation-Diffraction Panel Program for Wave-Body Interactions. 2020. Available online: http://www.wamit.com (accessed on 17 March 2021).
- Newman, J.N. Wave effects on deformable bodies. Appl. Ocean. Res. 1994, 16, 47–59. [Google Scholar] [CrossRef]
- Cummins, W.E. The impulse response function and ship motions. Schiffstecknik 1962, 9, 101–109. [Google Scholar]
- Kelly, T.; Campbell, J.; Dooley, T.; Ringwood, J. Modelling and results for an array of 32 oscillating water columns. In Proceedings of the EWTEC 2013, Aalborg, DK, 2–5 September 2013. [Google Scholar]
- Sheng, W.; Alcorn, R.; Lewis, A. On thermodynamics in the primary power conversion of oscillating water column wave energy converters. J. Renew. Sustain. Energy 2013, 5, 023105. [Google Scholar] [CrossRef]
- Kelly, T. Experimental and Numerical Modelling of a Multiple Oscillating Water Column Structure. Ph.D. Thesis, Maynooth University, Maynooth, Ireland, 2018. [Google Scholar]
- Cunningham, R. Orifice Meters with Supercritical Compressible Flow. Trans. ASME 1951, 73, 625–638. [Google Scholar]
- Newman, J.N. (Woods Hole, MA, USA). Personal communication. 2018.
- Davidson, J.; Costello, R. Efficient Nonlinear Hydrodynamic Models for Wave Energy Converter Design—A Scoping Study. J. Mar. Sci. Eng. 2020, 8, 35. [Google Scholar] [CrossRef]
- Roenby, J.; Bredmose, H.; Jasak, H. A computational method for sharp interface advection. R. Soc. Open Sci. 2016, 3, 160405. [Google Scholar] [CrossRef]
- Bingham, H.B.; Read, R. DTUMotionSimulator: A Matlab Package for Simulating Linear or Weakly Nonlinear Response of a Floating Structure to Ocean Waves. 2020. Available online: https://gitlab.gbar.dtu.dk/oceanwave3d/DTUMotionSimulator (accessed on 17 March 2021).
- Bingham, H.B. A hybrid Boussinesq-panel method for predicting the motions of a moored ship. Coast. Eng. 2000, 40, 21–38. [Google Scholar] [CrossRef]
- WEC-Sim (Wave Energy Converter SIMulator). Available online: https://wec-sim.github.io/WEC-Sim/ (accessed on 17 March 2021).
- Guo, Y.; Yu, Y.H.; van Rij, J.; Tom, N. Inclusion of Structural Flexibility in Design Load Analysis for Wave Energy Converters. In Proceedings of the 12th European Wave and Tidal Energy Conference, EWTEC, Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Faedo, N.; Pena-Sanchez, Y.; Ringwood, J.V. Finite-Order Hydrodynamic Model Determination Using Moment-Matching. Ocean. Eng. 2018, 163, 251–263. [Google Scholar] [CrossRef]
- Guo, B.; Patton, R.J.; Jin, S.; Lan, J. Numerical and experimental studies of excitation force approximation for wave energy conversion. Renew. Energy 2018, 125, 877–889. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College of Science, Technology & Medicine, London, UK, 2002. [Google Scholar]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFOAM®. Int. J. Numer. Methods Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]

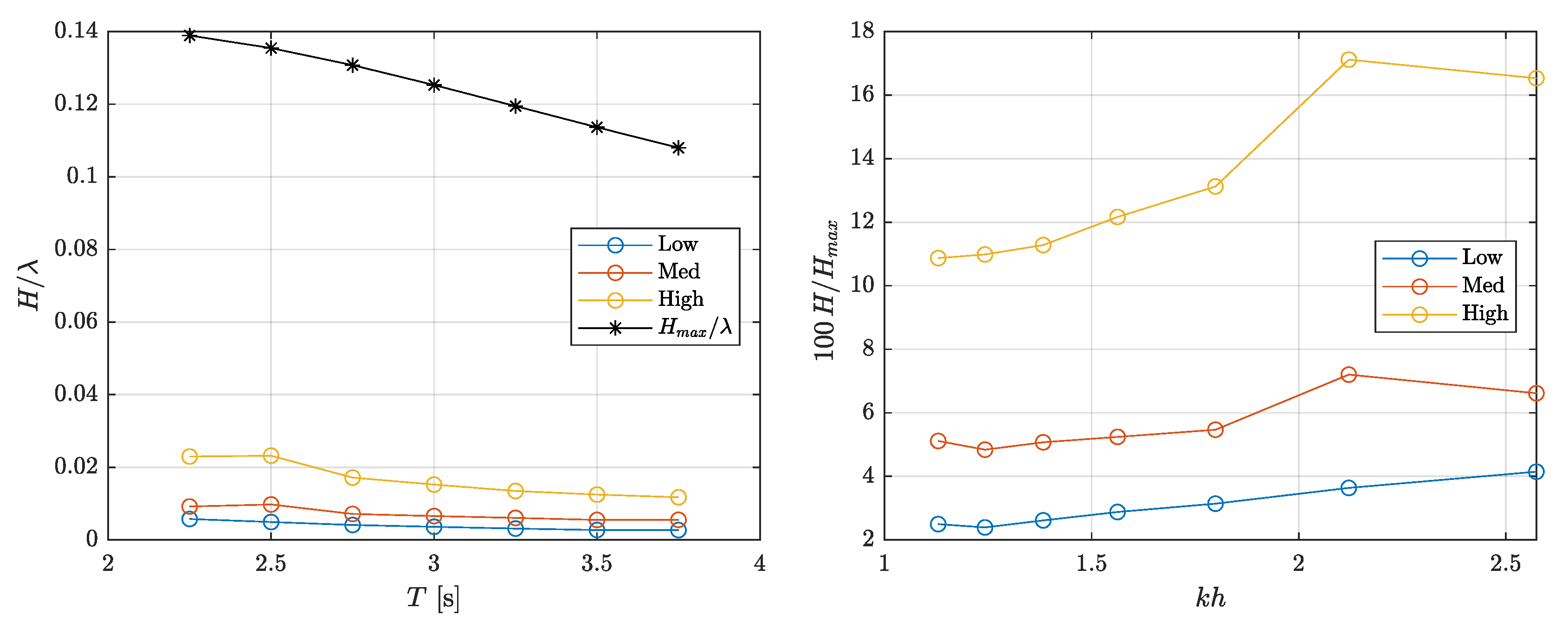



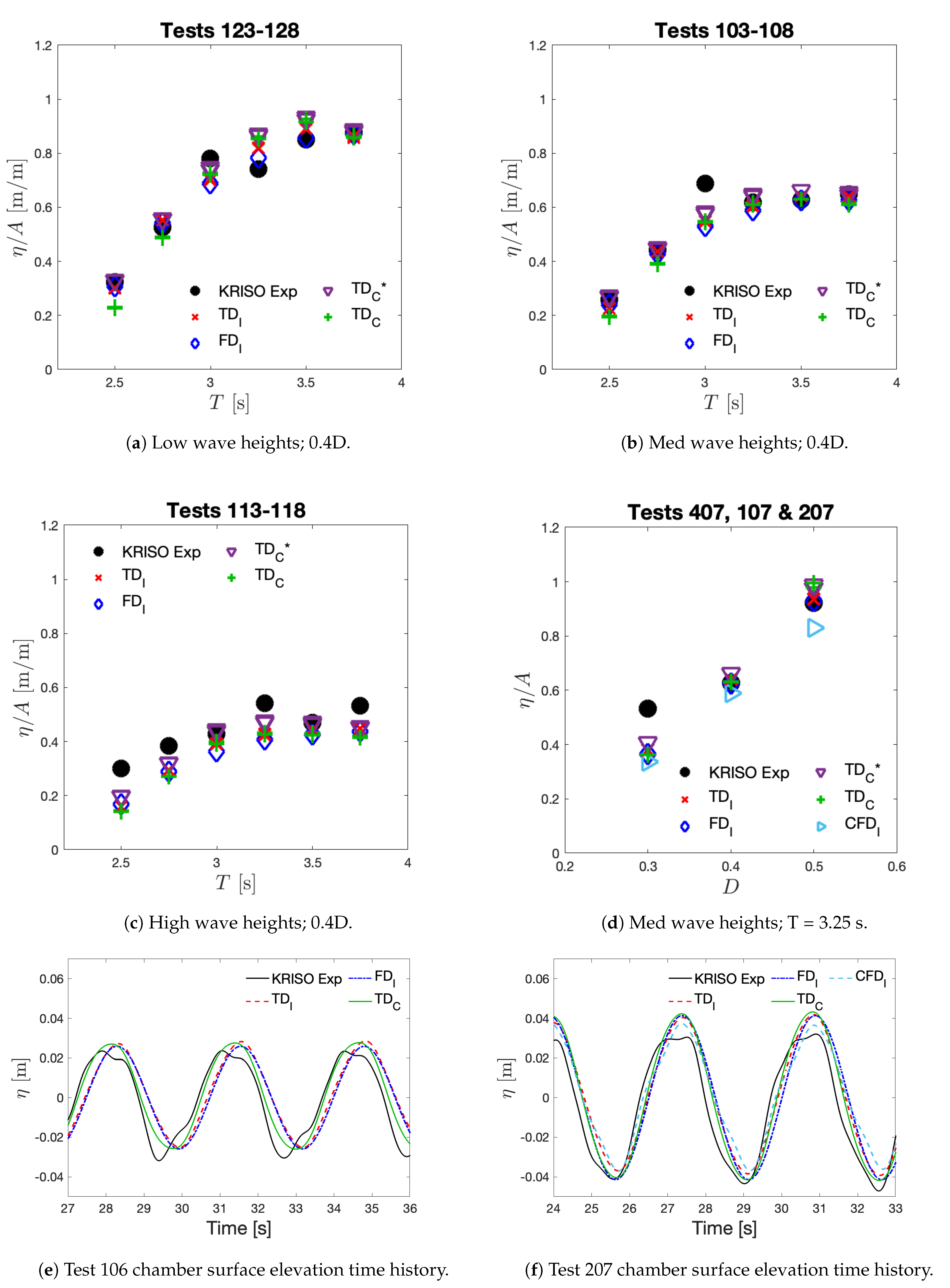

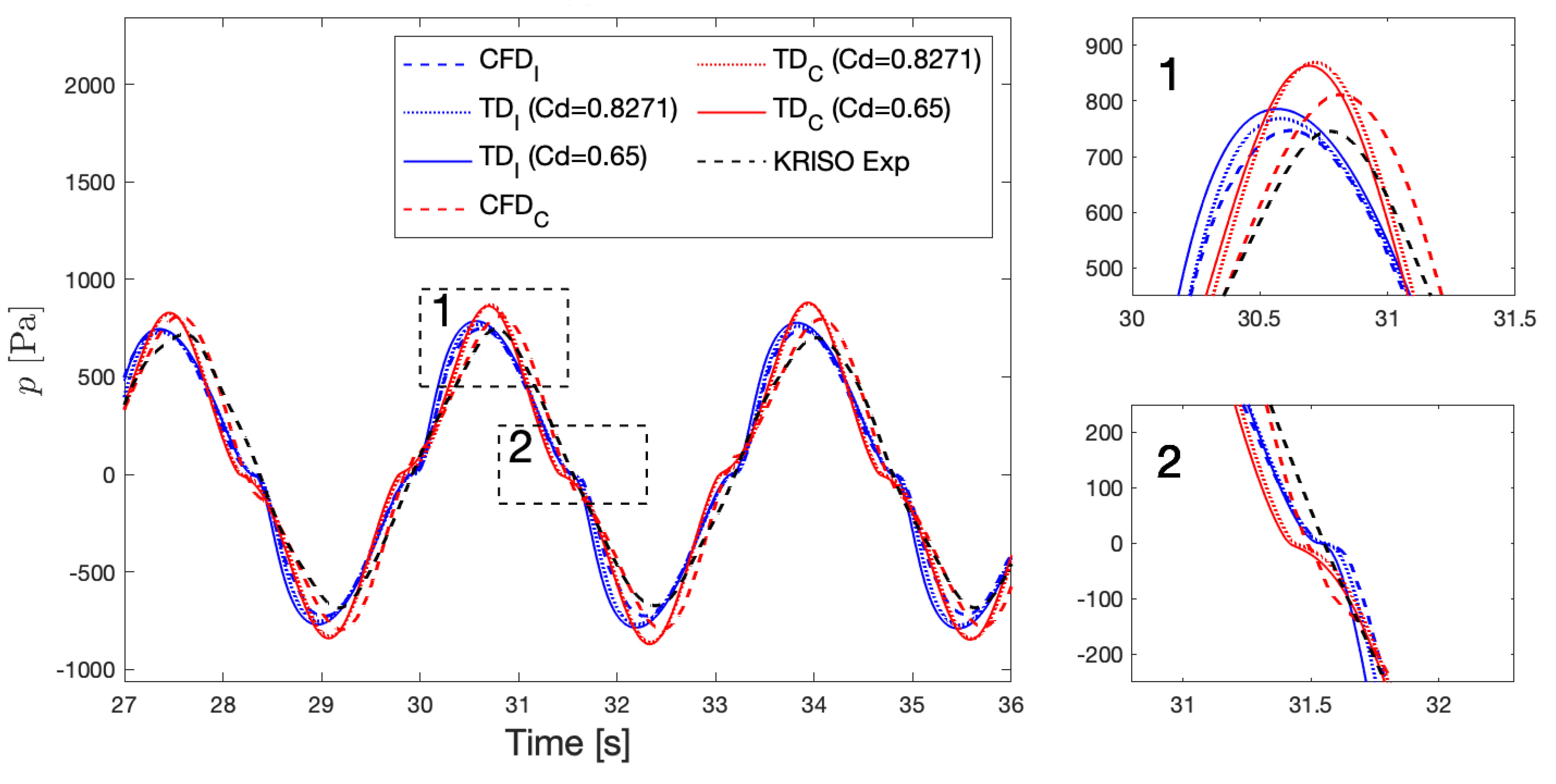
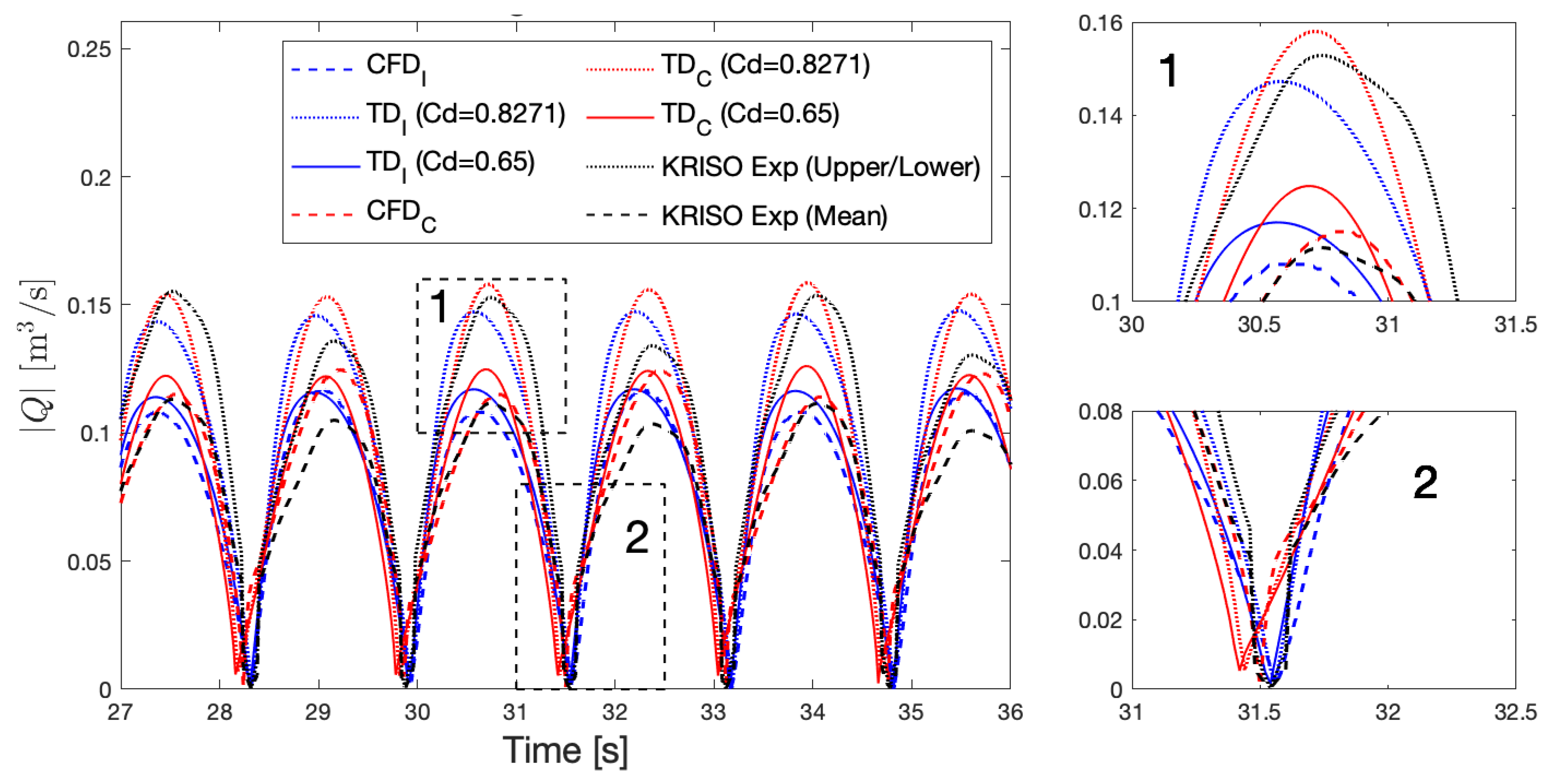
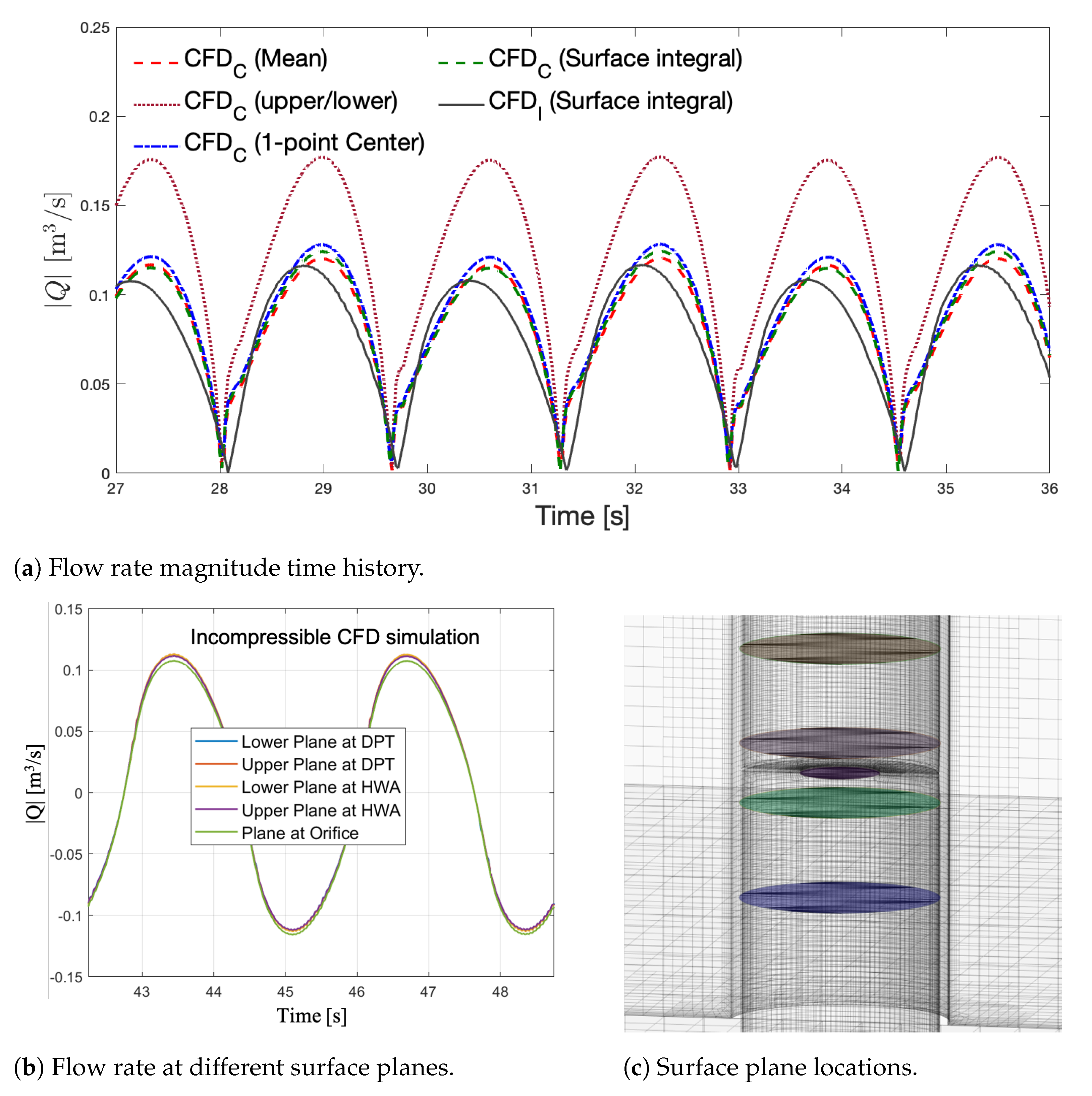
| WaveID | T [s] | H [m] | WaveID | T [s] | H [m] | WaveID | T [s] | H [m] |
|---|---|---|---|---|---|---|---|---|
| Low02 | 2.25 | 0.0450 | Med02 | 2.25 | 0.0718 | High02 | 2.25 | 0.1794 |
| Low03 | 2.50 | 0.0467 | Med03 | 2.50 | 0.0925 | High03 | 2.50 | 0.2198 |
| Low04 | 2.75 | 0.0459 | Med04 | 2.75 | 0.0799 | High04 | 2.75 | 0.1918 |
| Low05 | 3.00 | 0.0464 | Med05 | 3.00 | 0.0845 | High05 | 3.00 | 0.1961 |
| Low06 | 3.25 | 0.0454 | Med06 | 3.25 | 0.0881 | High06 | 3.25 | 0.1959 |
| Low07 | 3.50 | 0.0440 | Med07 | 3.50 | 0.0890 | High07 | 3.50 | 0.2020 |
| Low08 | 3.75 | 0.0480 | Med08 | 3.75 | 0.0983 | High08 | 3.75 | 0.2090 |
| TestID | Orifice | WaveID | TestID | Orifice | WaveID | TestID | Orifice | WaveID |
|---|---|---|---|---|---|---|---|---|
| 402 * | Med02 | 202 * | Med02 | 302 * | Med02 | |||
| 403 | Med03 | 203 | Med03 | 303 | Med03 | |||
| 404 | Med04 | 204 | Med04 | 304 | Med04 | |||
| 405 | Med05 | 205 | Med05 | 305 | Med05 | |||
| 406 | Med06 | 206 | Med06 | 306 | Med06 | |||
| 407 | Med07 | 207 | Med07 | 307 | Med07 | |||
| 408 | Med08 | 208 | Med08 | 308 | Med08 | |||
| TestID | Orifice | WaveID | TestID | Orifice | WaveID | TestID | Orifice | WaveID |
| 122 * | Low02 | 102 * | Med02 | 112 | High02 | |||
| 123 | Low03 | 103 | Med03 | 113 | High03 | |||
| 124 | Low04 | 104 | Med04 | 114 | High04 | |||
| 125 | Low05 | 105 | Med05 | 115 | High05 | |||
| 126 | Low06 | 106 | Med06 | 116 | High06 | |||
| 127 | Low07 | 107 | Med07 | 117 | High07 | |||
| 128 | Low08 | 108 | Med08 | 118 | High08 |
| Maximum Percentage Difference from the KRISO Exp | ||||
|---|---|---|---|---|
| Model | Pressure Difference | Chamber Surface Elevation | Flow Rate | Power |
| TD | 14% | 16% | 5% | 15% |
| FD | 13% | 18% | 6% | 10% |
| TD | 21% | 18% | 15% | 17% |
| TD | 37% | 14% | 11% | 17% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bingham, H.B.; Yu, Y.-H.; Nielsen, K.; Tran, T.T.; Kim, K.-H.; Park, S.; Hong, K.; Said, H.A.; Kelly, T.; Ringwood, J.V.; et al. Ocean Energy Systems Wave Energy Modeling Task 10.4: Numerical Modeling of a Fixed Oscillating Water Column. Energies 2021, 14, 1718. https://doi.org/10.3390/en14061718
Bingham HB, Yu Y-H, Nielsen K, Tran TT, Kim K-H, Park S, Hong K, Said HA, Kelly T, Ringwood JV, et al. Ocean Energy Systems Wave Energy Modeling Task 10.4: Numerical Modeling of a Fixed Oscillating Water Column. Energies. 2021; 14(6):1718. https://doi.org/10.3390/en14061718
Chicago/Turabian StyleBingham, Harry B., Yi-Hsiang Yu, Kim Nielsen, Thanh Toan Tran, Kyong-Hwan Kim, Sewan Park, Keyyong Hong, Hafiz Ahsan Said, Thomas Kelly, John V. Ringwood, and et al. 2021. "Ocean Energy Systems Wave Energy Modeling Task 10.4: Numerical Modeling of a Fixed Oscillating Water Column" Energies 14, no. 6: 1718. https://doi.org/10.3390/en14061718
APA StyleBingham, H. B., Yu, Y.-H., Nielsen, K., Tran, T. T., Kim, K.-H., Park, S., Hong, K., Said, H. A., Kelly, T., Ringwood, J. V., Read, R. W., Ransley, E., Brown, S., & Greaves, D. (2021). Ocean Energy Systems Wave Energy Modeling Task 10.4: Numerical Modeling of a Fixed Oscillating Water Column. Energies, 14(6), 1718. https://doi.org/10.3390/en14061718













