Nonlinear Modelling, Flatness-Based Current Control, and Torque Ripple Compensation for Interior Permanent Magnet Synchronous Machines
Abstract
1. Introduction
2. Mathematical Modelling
2.1. Voltage Equations
2.2. Torque Characteristics
- Torque ripple due to the interaction of the stator field distribution with the electromagnetic rotor properties, which is excited by
- (a)
- a non-sinusoidal rotor field distribution and
- (b)
- a varying reluctance distribution over the circumference of the rotor.
- Cogging torque due to the interaction of the rotor field distribution with the circumferential variation of the stator reluctance.
- Pulsating torque: sum of the torque ripple and the cogging torque.
2.3. Simplified Model for Embedded Control
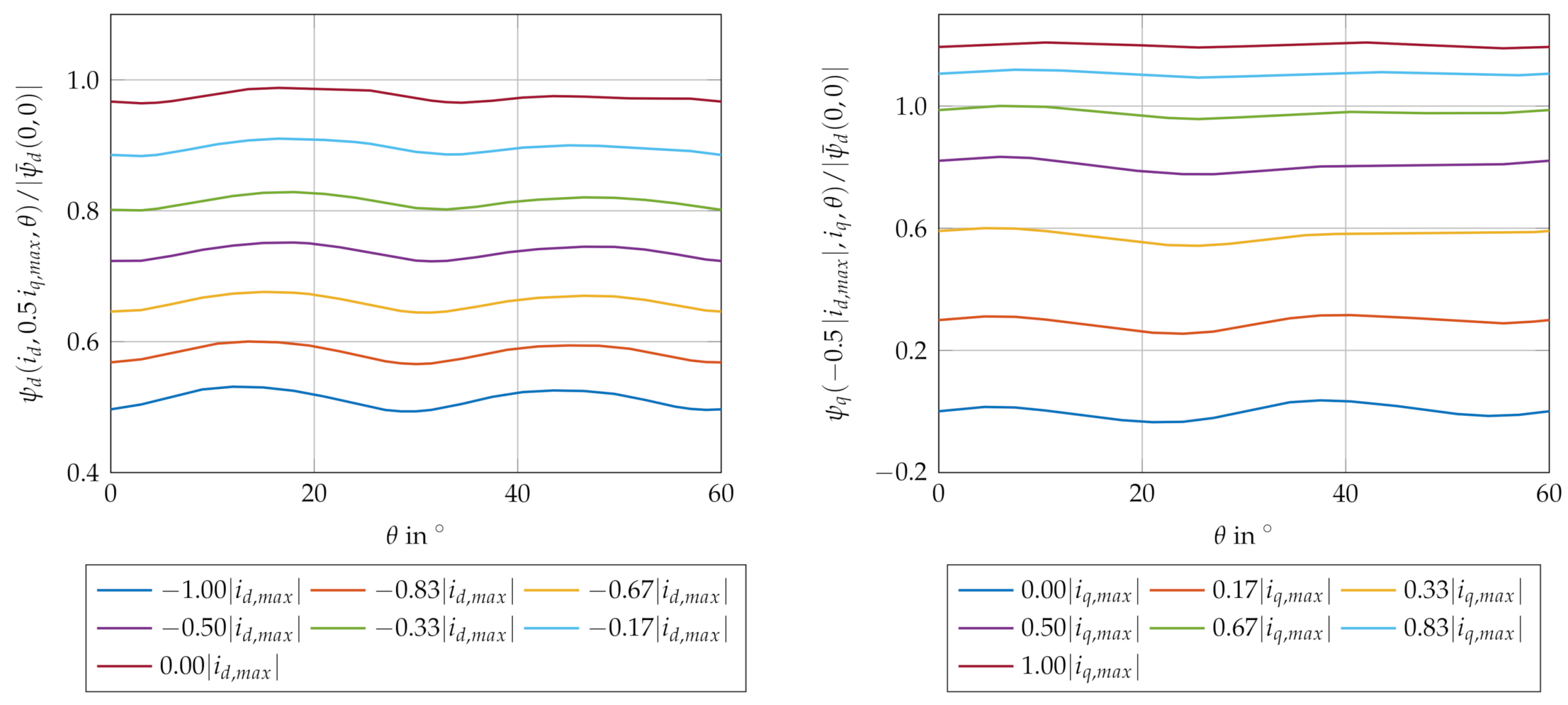
- Due to the interaction of the nonsinusoidal stator field distribution with both that of the rotor as well as that of the reluctance, only integer multiples of the 6th fundamental stator frequency are present in and . This is due to the interaction of the three phases, see e.g., [11,12,27,31]. For the motor studied in this research, it has turned out that the 18th harmonic and frequencies greater than the 24th harmonic almost vanish. Additionally, linear regression models for the phase shifts are sufficiently accurate for the particular type of motor.
- The fundamental frequency of the cogging torque can be derived from the number of pole pairs of the rotor and the stator slots, as presented e.g., in [32]. For the present machine, is achieved. It has turned out that subharmonics also need to be considered. Here, constant approximations of the phase shifts are sufficient.
2.4. Model Calibration
3. Control Algorithm
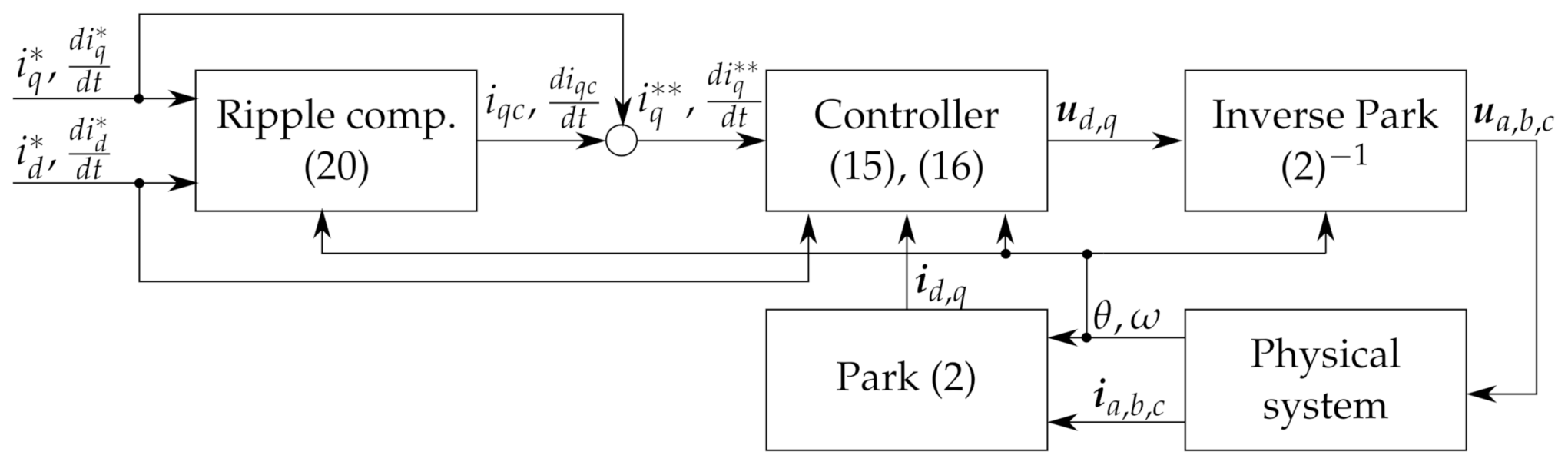
3.1. Flatness-Based Current Control
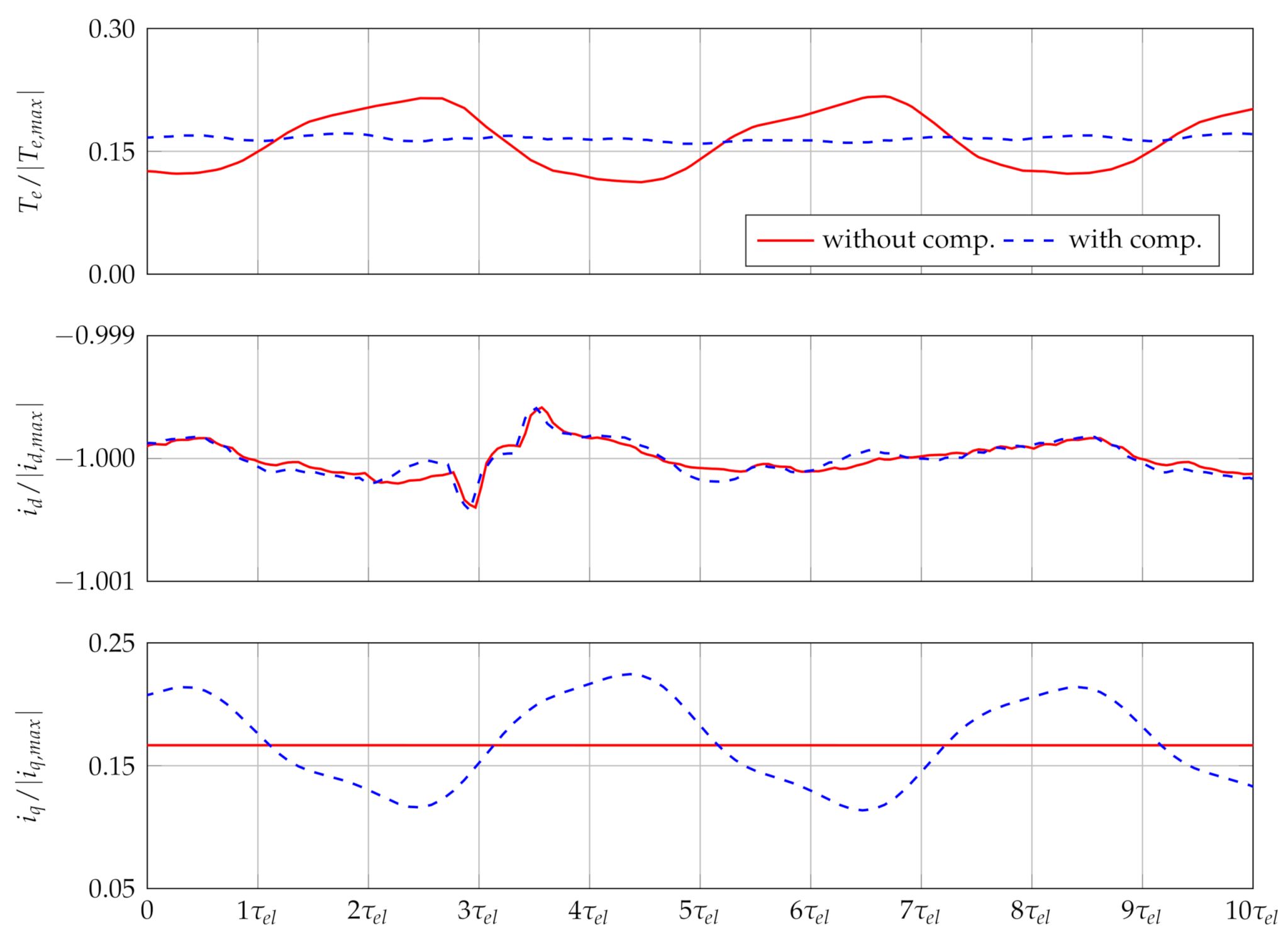
3.2. Torque Control and Compensation of Torque Ripples
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kampker, A.; Vallée, D.; Schnettler, A. (Eds.) Elektromobilität: Grundlagen einer Zukunftstechnologie; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ackermann, C. Optimale Regelung der Permanentmagneterregten Synchronmaschine unter Nutzung des Reluktanzmoments. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2012. [Google Scholar]
- Hwang, M.-H.; Han, J.-H.; Kim, D.-H.; Cha, H.-R. Design and analysis of rotor shapes for IPM motors in EV power traction platforms. Energies 2018, 11, 2601. [Google Scholar] [CrossRef]
- Hu, Y.; Xiao, Y.; Chen, B.; Li, Q. Topology optimization of a consequent-pole rotor with V-shaped magnet placement. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Korea, 7–10 October 2018; pp. 234–239. [Google Scholar]
- Kim, H.; Lee, T.; Kwon, S.; Hong, J. Vibration analysis according to stator shape design in a PMSM. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Korea, 10–13 October 2010; pp. 1235–1238. [Google Scholar]
- Lavrinovicha, L.; Dirba, J. Comparison of permanent magnet synchronous motor and synchronous reluctance motor based on their torque per unit volume. In Proceedings of the 2014 Electric Power Quality and Supply Reliability Conference (PQ), Rakvere, Estonia, 11–13 June 2014; pp. 233–236. [Google Scholar]
- Binder, A. Untersuchung zur magnetischen Kopplung von Längs- und Querachse durch Sättigung am Beispiel der Reluktanzmaschine. Arch. Elektrotech. 1989, 72, 277–282. [Google Scholar] [CrossRef]
- Mink, F. Modellierung und Hochdynamische Stromregelung von PM-Synchronmaschinen unter Berücksichtigung von Sättigungseffekten. Ph.D. Thesis, Technical University of Darmstadt, Darmstadt, Germany, 2013. [Google Scholar]
- Faustner, D.; Kemmetmüller, W.; Kugi, A. Optimal torque control of permanent magnet synchronous machines using magnetic equivalent circuits. Mechatronics 2015, 32, 22–33. [Google Scholar]
- Faustner, D.; Kemmetmüller, W.; Kugi, A. Flatness-based torque control of saturated surface-mounted permanent magnet synchronous machines. IEEE Trans. Control Syst. Technol. 2016, 24, 1201–1213. [Google Scholar] [CrossRef]
- Wallmark, O. On Control of Permanent-Magnet Synchronous Motors in Hybrid-Electric Vehicle Applications. Ph.D. Thesis, Chalmers University of Technology, Göteborg, Germany, 2004. [Google Scholar]
- Yi, P.; Sun, Z.; Wang, X. Research on PMSM harmonic coupling models based on magnetic co-energy. IET Electr. Power Appl. 2019, 13, 571–579. [Google Scholar] [CrossRef]
- Zhong, Z.; Jiang, S.; Zhou, Y.; Zhou, S. Magnetic coenergy based modelling of PMSM for HEV/EV application. Prog. Electromagn. Res. 2016, 50, 11–22. [Google Scholar] [CrossRef]
- Kemmetmüller, W.; Faustner, D.; Kugi, A. Modeling of a permanent magnet synchronous machine with internal magnets using magnetic equivalent circuits. IEEE Trans. Magn. 2014, 50, 1–14. [Google Scholar]
- Sriprang, S.; Nahid-Mobarakeh, B.; Pierfederici, S.; Takorabet, N.; Bizon, N.; Kumam, P.; Mungporn, P.; Thounthong, P. Robust flatness control with extended Luenberger observer for PMSM drive. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo, Asia-Pacific, Bangkok, Thailand, 6–9 June 2018; pp. 1–8. [Google Scholar]
- Thounthong, P.; Sikkabut, S.; Poonnoy, N.; Mungporn, P.; Yodwong, B.; Kumam, P.; Bizon, N.; Nahid-Mobarakeh, B.; Pierfederici, S. Differential flatness based speed/torque control with state-observers of permanent magnet synchronous motor drives. IEEE Trans. Ind. Appl. 2018, 54, 2874–2884. [Google Scholar] [CrossRef]
- Obeid, N.H.; Battiston, A.; Dufresnes, C. Very high speed flatness based current control for a permanent magnet synchronous motor: Application on internal combustion engines electrification. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018; pp. 1–6. [Google Scholar]
- Cuenot, J.; Zaim, S.; Pierfederici, S.; Monmasson, E.; Nahid-Mobarakeh, B.; Meuret, R.; Meibody-Tabar, F. Flatness based control of a high-speed saturable permanent magnet synchronous machine. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 27–29 June 2016; pp. 1–6. [Google Scholar]
- Sira-Ramírez, H.; Linares-Flores, J.; García-Rodríguez, C.; Contreras-Ordaz, M.A. On the control of the permanent magnet synchronous motor: An active disturbance rejection control approach. IEEE Trans. Control Syst. Technol. 2014, 22, 2056–2063. [Google Scholar] [CrossRef]
- Aschemann, H.; Rauh, A.; Prabel, R. Nonlinear control of a pressurised water supply driven by a permanent magnet synchronous motor. In Proceedings of the 2010 15th International Conference on Methods and Models in Automation and Robotics, Miedzyzdroje, Poland, 23–26 August 2010; pp. 423–428. [Google Scholar]
- Delaleau, E.; Stanković, A.M. Flatness.based hierarchical control of the PM synchronous motor. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; pp. 65–70. [Google Scholar]
- Nalepa, R.; Mink, F.; Beineke, S.; Bahr, A. Influence of magnetic saturation of non-salient pole permanent magnets synchronous motors on performance of a servo drive. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Larsen, N.; Gensior, A.; Hein, P. Torque ripple reduction based on current control for a flux switching permanent magnet machine. In Proceedings of the International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20–22 June 2012; pp. 712–717. [Google Scholar]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Control of imperfect dynamical systems. Nonlinear Dyn. 2019, 98, 2989–2999. [Google Scholar] [CrossRef]
- Kim, S.H. Electric Motor Control: DC, AC, and BLDC Motors; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Binder, A. Elektrische Maschinen und Antriebe: Grundlagen, Betriebsverhalten, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Jahns, T.M.; Soong, W.L. Pulsating torque minimization techniques for permanent magnet AC motor drives—A review. IEEE Trans. Ind. Electron. 1996, 43, 321–330. [Google Scholar] [CrossRef]
- Štumberger, G.; Štumberger, B.; Marčič, T. Magnetically nonlinear dynamic models of synchronous machines and experimental methods for determining their parameters. Energies 2019, 12, 3519. [Google Scholar] [CrossRef]
- Hadžiselimović, M.; Štumberger, G.; Štumberger, B.; Zagradišnik, I. Modeling of permanent magnet synchronous motor in d-q coordinates. Przeglad Elektrotechniczny 2005, 81, 38–42. [Google Scholar]
- Rojas, S.; Pérez, M.A.; Rodríguez, J.; Zelaya, H. Torque ripple modeling of a permanent magnet synchronous motor. In Proceedings of the 2010 IEEE International Conference on Industrial Technology, Via del Mar, Chile, 14–17 March 2010; pp. 433–438. [Google Scholar]
- Favre, E.; Cardoletti, L.; Jufer, M. Permanent-magnet synchronous motors: A comprehensive approach to cogging torque suppression. IEEE Trans. Ind. Appl. 1993, 29, 1141–1149. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S. Design techniques for reducing the cogging torque in surface-mounted PM motors. IEEE Trans. Ind. Appl. 2002, 38, 1259–1265. [Google Scholar] [CrossRef]
- Clerc, M. Standard Particle Swarm Optimisation. 2012. Available online: https://hal.archives-ouvertes.fr/hal-00764996/document (accessed on 11 March 2021).
- Rothfuß, R.; Rudolph, J.; Zeitz, M. Flachheit: Ein neuer Zugang zur Steuerung und Regelung nichtlinearer Systeme. at-Automatisierungstechnik 1997, 45, 517–525. [Google Scholar] [CrossRef]
- Bonifacio, J.; Kennel, R. Online maximum torque per ampere control of interior permanent magnet synchronous machines (IPMSM) for automotive applications. In Proceedings of the 8th IET International Conference on Power Electronics, Machines and Drives (PEMD), Glasgow, UK, 19–21 April 2016; pp. 1–5. [Google Scholar]
- Xiao, X.; Chen, C. Reduction of torque ripple due to demagnetization in PMSM using current compensation. IEEE Trans. Appl. Superconduct. 2010, 20, 1068–1071. [Google Scholar] [CrossRef]
- Momeni, M.; Rahimi, M. Simple expressions for suppression of torque and speed vibrations in PMSM drives. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Pisa, Italy, 14–16 June 2010; pp. 953–958. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veeser, F.; Braun, T.; Kiltz, L.; Reuter, J. Nonlinear Modelling, Flatness-Based Current Control, and Torque Ripple Compensation for Interior Permanent Magnet Synchronous Machines. Energies 2021, 14, 1590. https://doi.org/10.3390/en14061590
Veeser F, Braun T, Kiltz L, Reuter J. Nonlinear Modelling, Flatness-Based Current Control, and Torque Ripple Compensation for Interior Permanent Magnet Synchronous Machines. Energies. 2021; 14(6):1590. https://doi.org/10.3390/en14061590
Chicago/Turabian StyleVeeser, Felix, Tristan Braun, Lothar Kiltz, and Johannes Reuter. 2021. "Nonlinear Modelling, Flatness-Based Current Control, and Torque Ripple Compensation for Interior Permanent Magnet Synchronous Machines" Energies 14, no. 6: 1590. https://doi.org/10.3390/en14061590
APA StyleVeeser, F., Braun, T., Kiltz, L., & Reuter, J. (2021). Nonlinear Modelling, Flatness-Based Current Control, and Torque Ripple Compensation for Interior Permanent Magnet Synchronous Machines. Energies, 14(6), 1590. https://doi.org/10.3390/en14061590






