Analysis of Aeroacoustic Properties of the Local Radial Point Interpolation Cumulant Lattice Boltzmann Method
Abstract
1. Introduction
2. The Lattice Boltzmann Method
2.1. Collision Step
2.2. Streaming Step
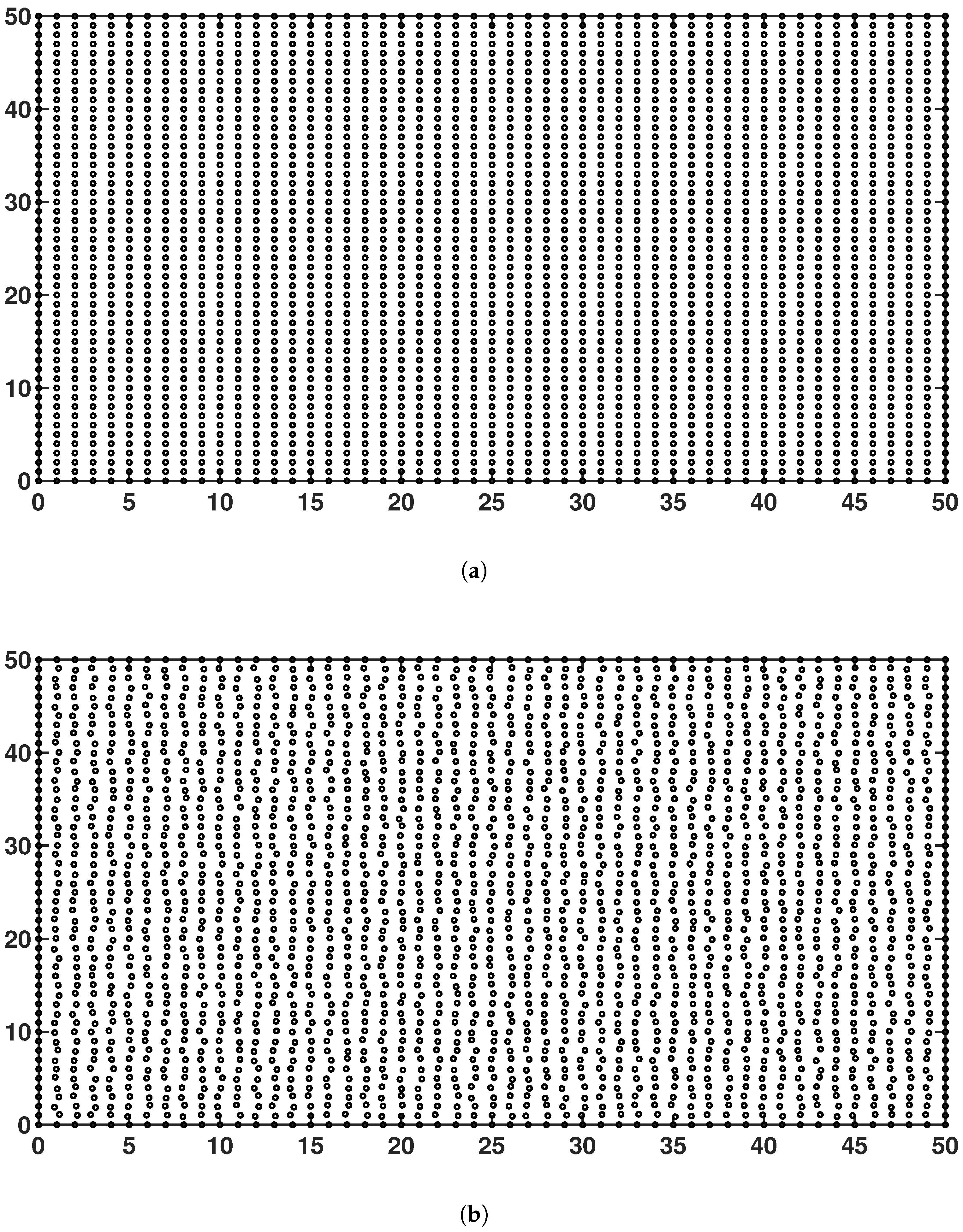
2.2.1. MFree Shape Function Construction—Radial Point Interpolation Shape Functions
2.2.2. Semi-Discrete Formulation—Time Discretization
2.2.3. Semi-Discrete Formulation—Space Discretization
3. Results and Discussion
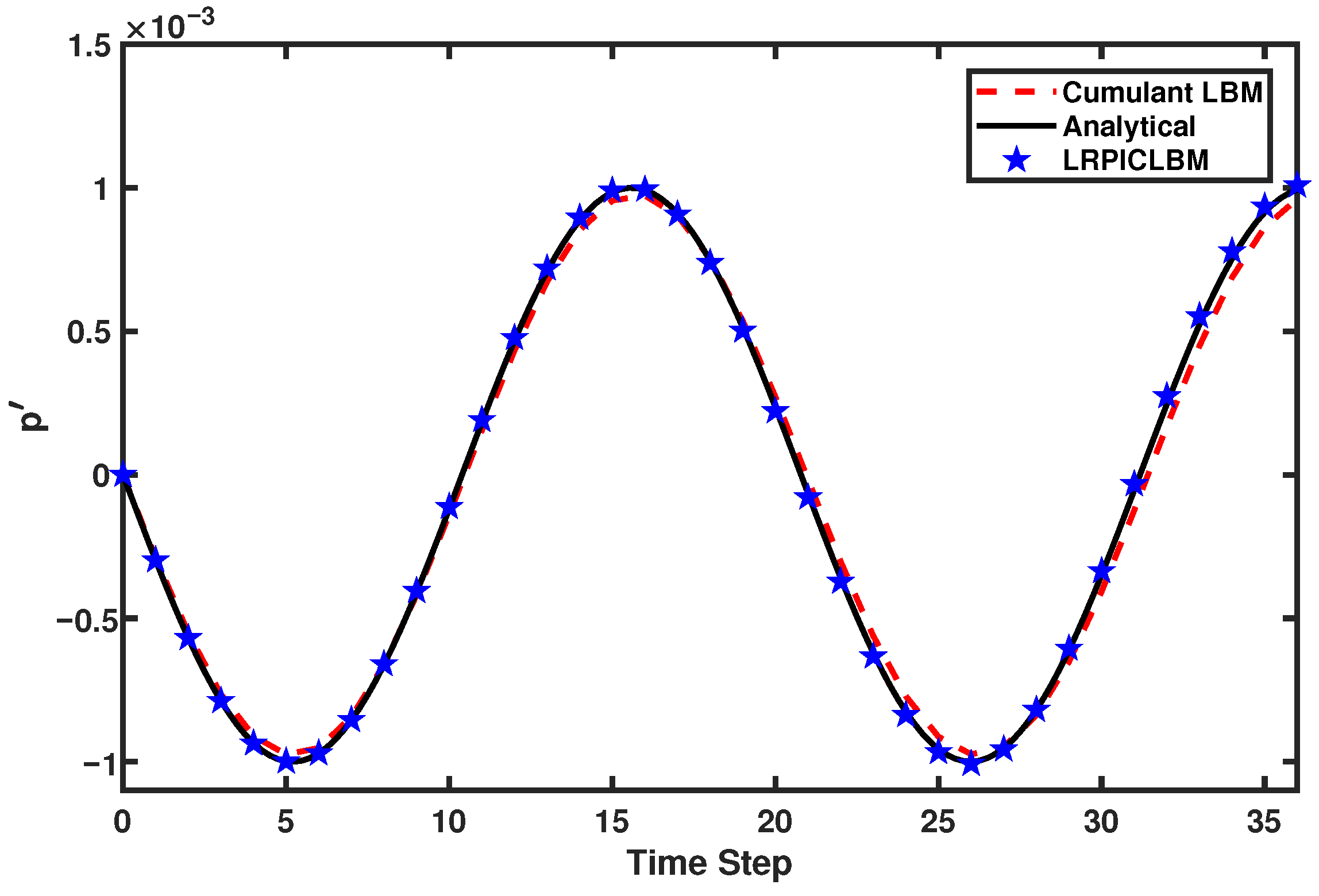
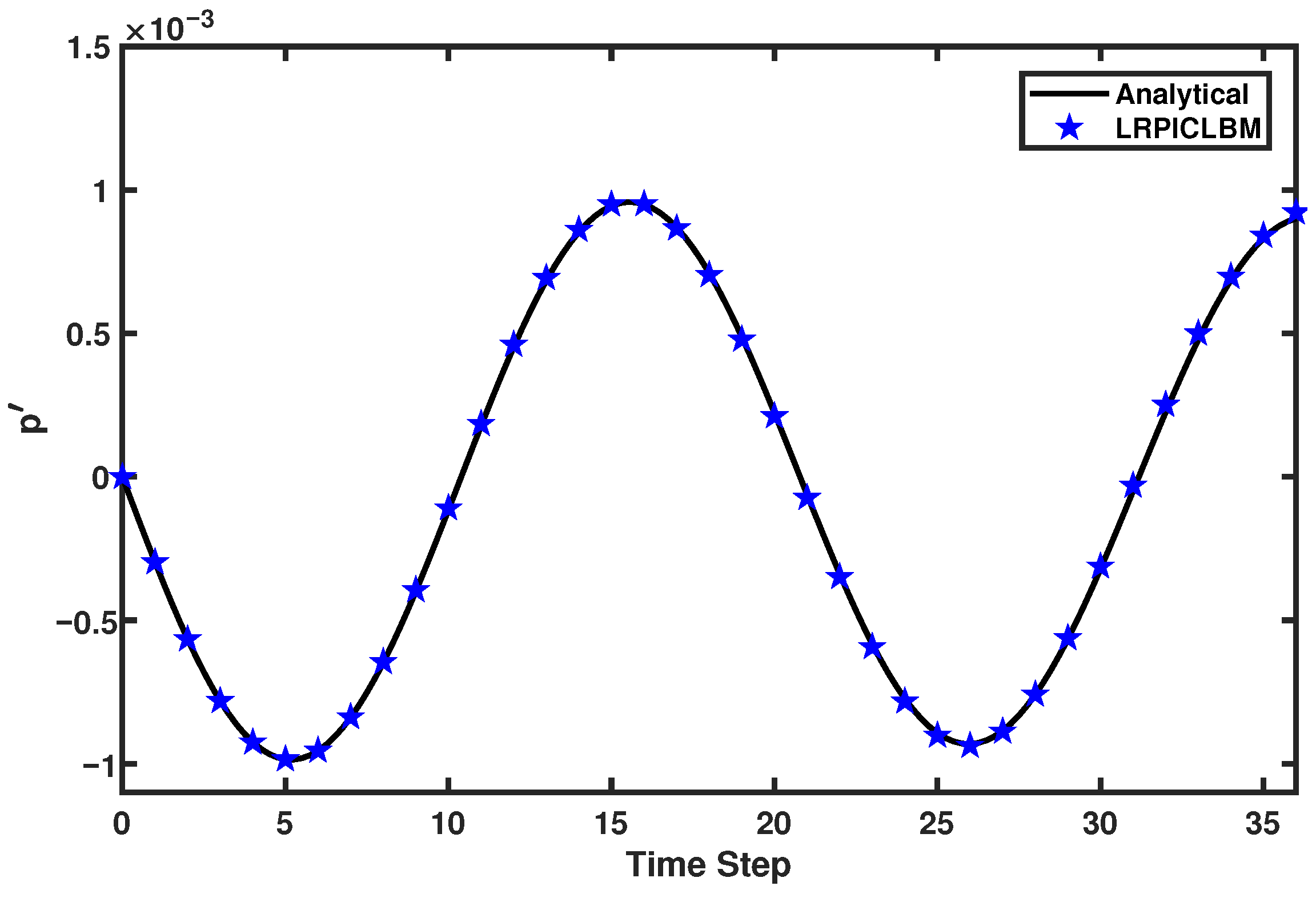
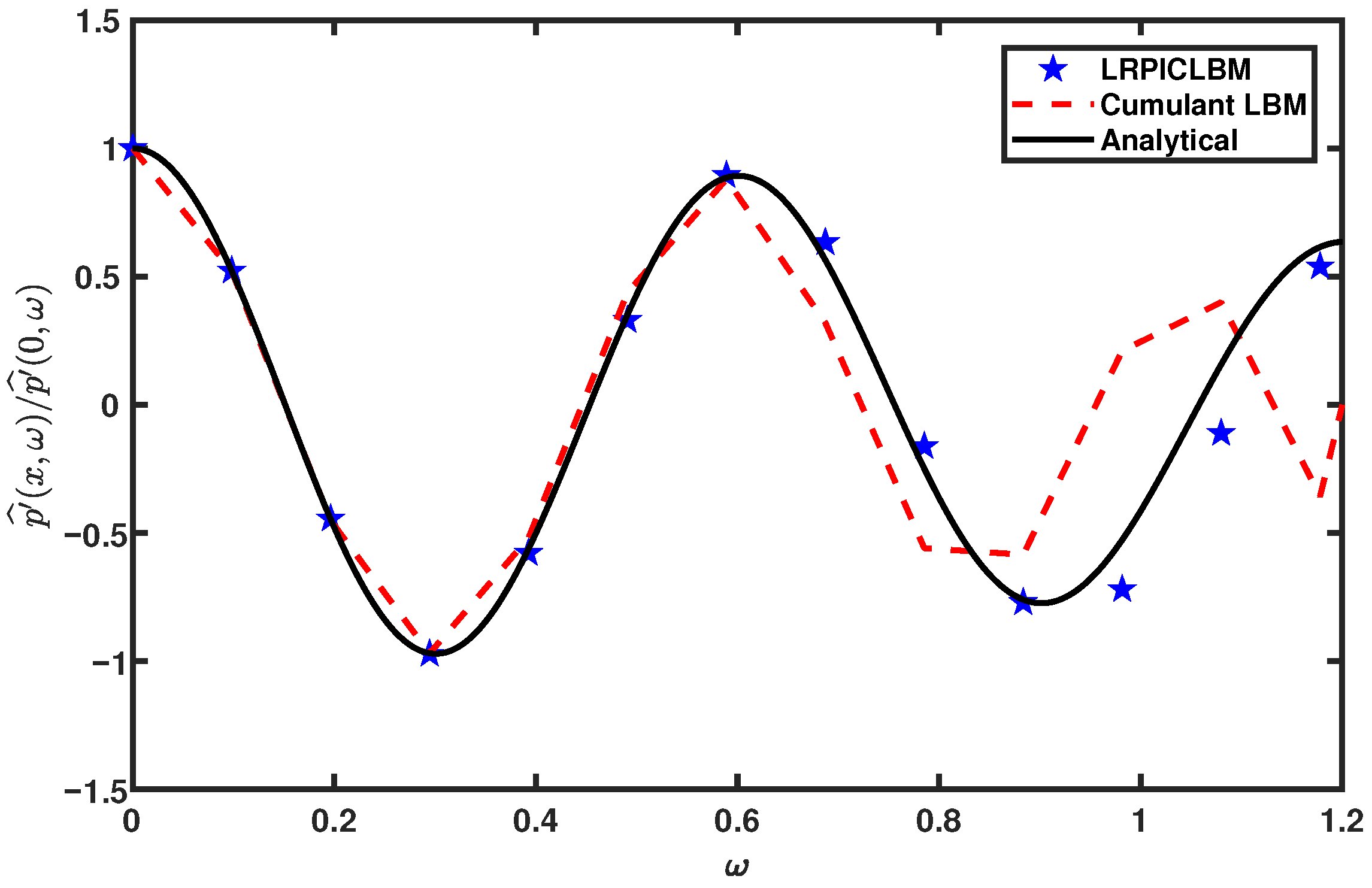
3.1. Planar Standing Wave
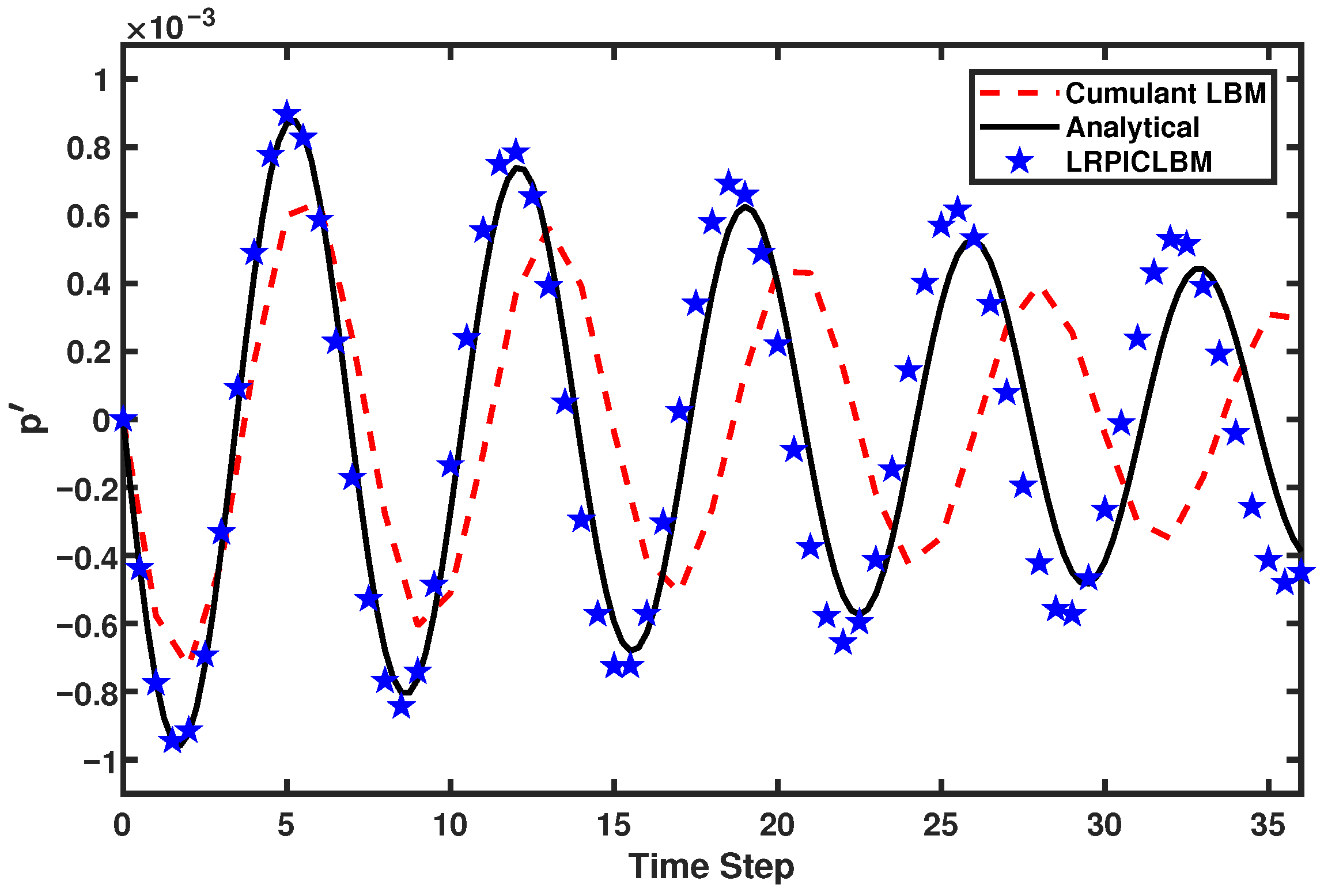
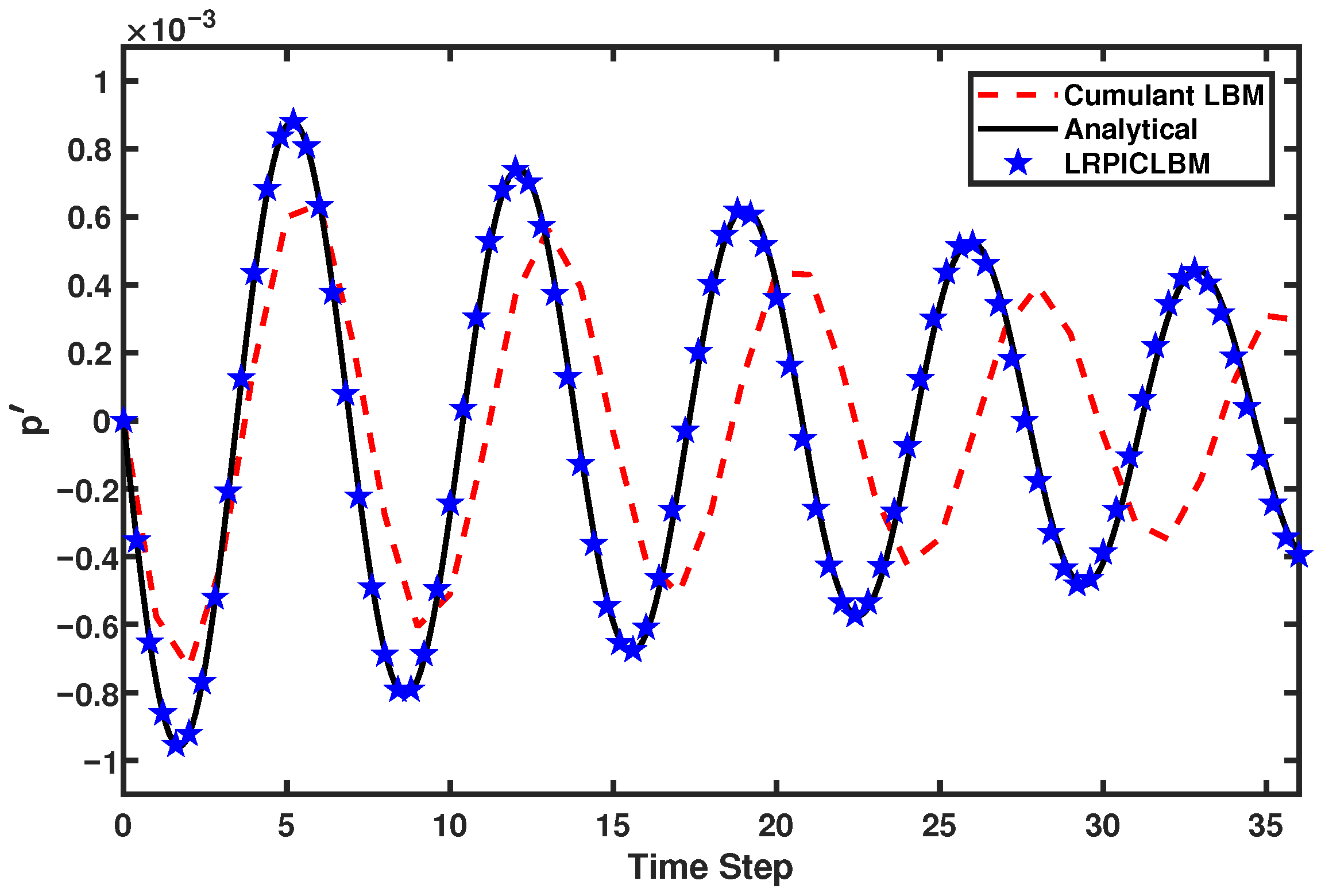
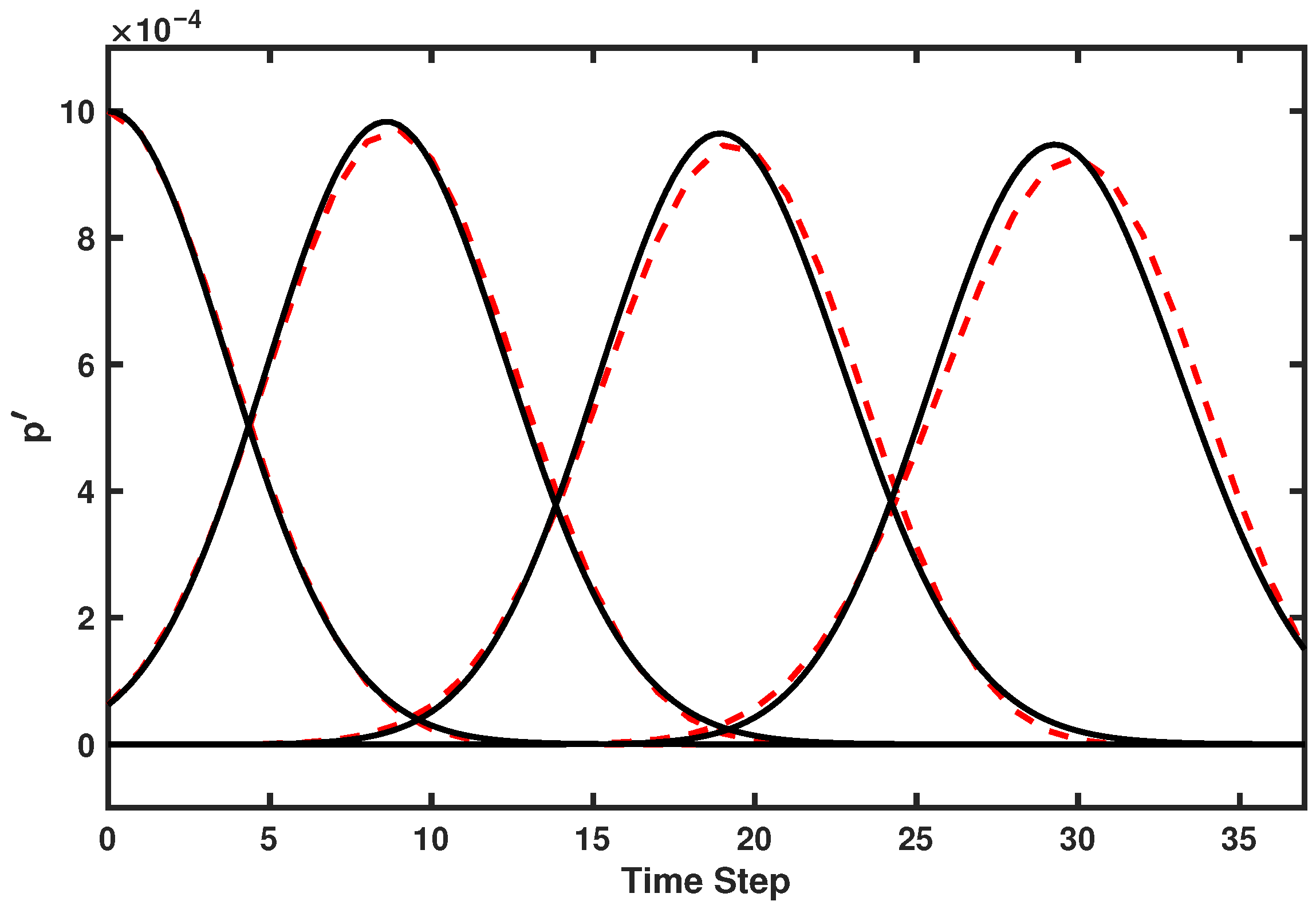
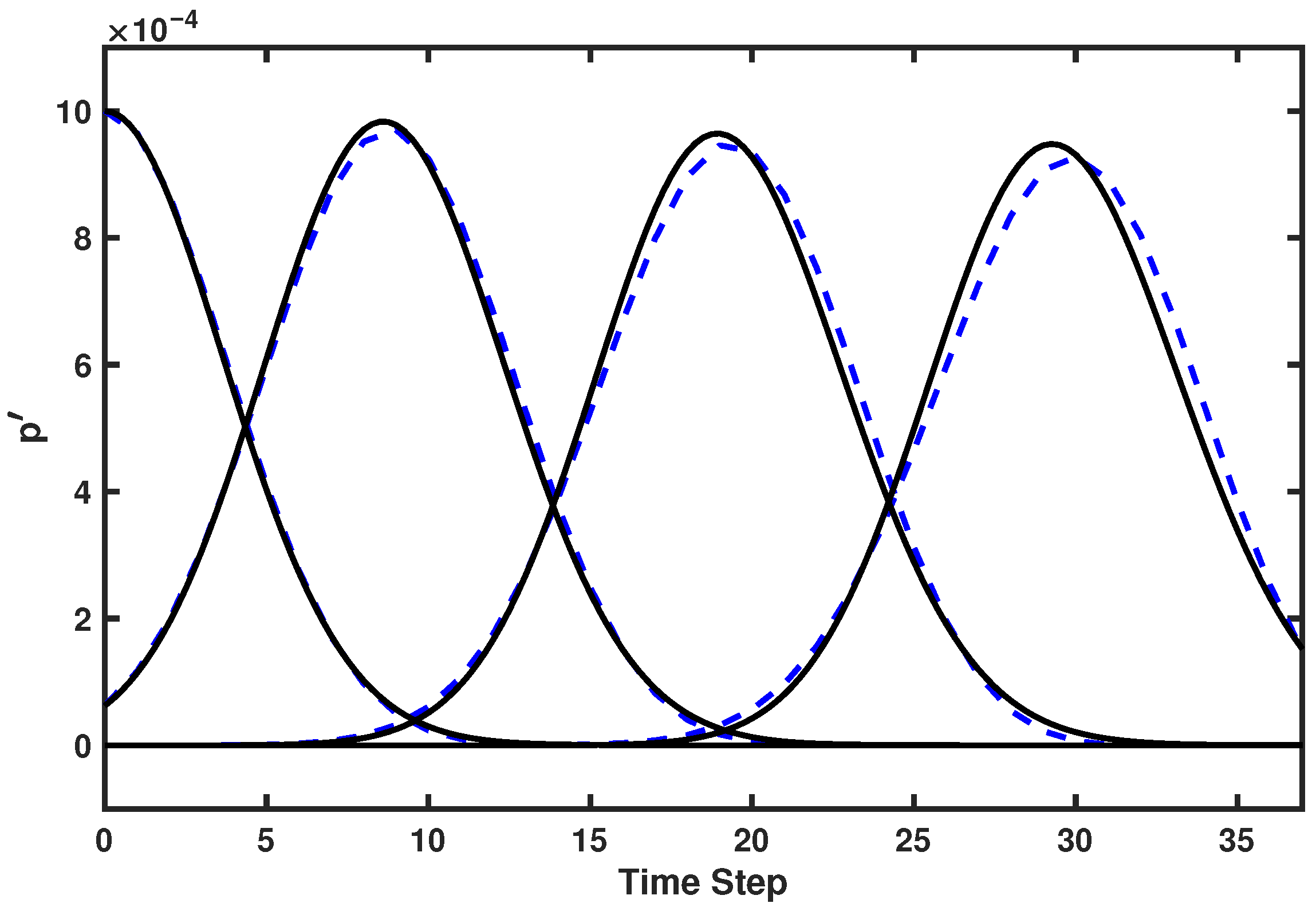
3.2. Planar Pulse Wave
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LRPIC-LBM | Local radial point interpolation cumulant lattice Boltzmann method |
| LBM | Lattice Boltzmann method |
| RPIM | Radial point interpolation method |
| NREL | National Renewable Energy Laboratory |
| NWTC | National Wind Technology Center |
| CAA | Computational aeroacoustic |
| DRP | Dispersion relation preserving scheme |
| GODRP | Grid optimized dispersion relation preserving schemes |
| BGK-LBM | Bhatnagar Gross Krook lattice Boltzmann method |
| LBM-rrBGK | Lattice Boltzmann method recursive regularized Bhatnagar Gross Krook |
| IS-LBM | Interpolation supplemented lattice Boltzmann method |
| FDLBE | Finite difference lattice Boltzmann equation |
| FVLBE | Finite volume lattice Boltzmann Equation |
| FELBE | Finite element lattice Boltzmann equation |
| TLLBM | Taylor-series expansion and least-squares-based lattice Boltzmann method |
| FSI | Fluid structure interaction |
| FDM | Finite difference method |
| SPH | Smoothed particle hydrodynamics |
| LPIM | Local point interpolation method |
| LRPIM | Local radial point interpolation method |
| MLPG | Meshless local Petrov–Galerkin method |
| MRT | Multi-relaxation times |
| Probability density function | |
| PIM | Point interpolation method |
| RBF | Radial basis functions |
| MQ | Multi-quadrics |
| WR | Weighted residuals |
| PDE | Partial differential equation |
References
- Burton-Jones, A. Knowledge Capitalism: Business, Work, and Learning in the New Economy; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Letcher, T.M. Wind Energy Engineering: A Handbook for Onshore and Offshore Wind Turbines; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Bowdler, D.; Leventhall, H. Wind Turbine Noise; Multi-Science Pub.: Brentwood, CA, USA, 2011. [Google Scholar]
- Wagner, S.; Bareiss, R.; Guidati, G. Wind Turbine Noise; Springer Science & Business Media: Berli/Heidelberg, Germany, 2012. [Google Scholar]
- Singer, B.A.; Lockard, D.P.; Brentner, K.S. Computational aeroacoustic analysis of slat trailing-edge flow. AIAA J. 2000, 38, 1558–1564. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Geier, M.; Kian Far, E. A Sliding Grid Method For The Lattice Boltzmann Method Using Compact Interpolation. In Proceedings of the The First International Workshop on Lattice Boltzmann for Wind Energy, Online Conference, 25–26 February 2021. [Google Scholar]
- Morris, P.; Long, L.; Brentner, K. An aeroacoustic analysis of wind turbines. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004; p. 1184. [Google Scholar]
- Robinson, M.C.; Hand, M.; Simms, D.; Schreck, S. Horizontal Axis Wind Turbine Aerodynamics: Three-Dimensional, Unsteady, and Separated Flow Influences; Technical Report; National Renewable Energy Lab.: Golden, CO, USA, 1999.
- Tummala, A.; Velamati, R.K.; Sinha, D.K.; Indraja, V.; Krishna, V.H. A review on small scale wind turbines. Renew. Sustain. Energy Rev. 2016, 56, 1351–1371. [Google Scholar] [CrossRef]
- Spera, D.A. Wind Turbine Technology; Wind Energy Technologies Office: Washington, DC, USA, 1994.
- Tam, C.K. Computational aeroacoustics-Issues and methods. AIAA J. 1995, 33, 1788–1796. [Google Scholar] [CrossRef]
- Wells, V.L.; Renaut, R.A. Computing aerodynamically generated noise. Annu. Rev. Fluid Mech. 1997, 29, 161–199. [Google Scholar] [CrossRef]
- Kim, J.W.; Lee, D.J. Optimized compact finite difference schemes with maximum resolution. AIAA J. 1996, 34, 887–893. [Google Scholar] [CrossRef]
- Tam, C.K.; Webb, J.C. Dispersion-Relation-Preserving Schemes for Computational Aeroacoustics; NASA: Washington, DC, USA, 1992.
- Cheong, C.; Lee, S. Grid-optimized dispersion-relation-preserving schemes on general geometries for computational aeroacoustics. J. Comput. Phys. 2001, 174, 248–276. [Google Scholar] [CrossRef]
- Gröschel, E.; Schröder, W.; Renze, P.; Meinke, M.; Comte, P. Noise prediction for a turbulent jet using different hybrid methods. Comput. Fluids 2008, 37, 414–426. [Google Scholar] [CrossRef]
- Delfs, J.; Bertsch, L.; Zellmann, C.; Rossian, L.; Kian Far, E.; Ring, T.; Langer, S.C. Aircraft Noise Assessment—From Single Components to Large Scenarios. Energies 2018, 11, 429. [Google Scholar] [CrossRef]
- Colonius, T.; Lele, S.K.; Moin, P. The scattering of sound waves by a vortex: Numerical simulations and analytical solutions. J. Fluid Mech. 1994, 260, 271–298. [Google Scholar] [CrossRef]
- Mitchell, B.; Lele, S.; Moin, P. Direct computation of the sound from a compressible co-rotating vortex pair. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; p. 374. [Google Scholar]
- Kian Far, E.; Geier, M.; Kutscher, K.; Krafczyk, M. Implicit Large Eddy Simulation of Flow in a Micro-Orifice with the Cumulant Lattice Boltzmann Method. Computation 2017, 5, 23. [Google Scholar] [CrossRef]
- Kian Far, E. A Cumulant LBM approach for Large Eddy Simulation of Dispersion Microsystems. Ph.D. Thesis, Universität Braunschweig, Braunschweig, Germany, 2015. [Google Scholar]
- Buick, J.; Greated, C.; Campbell, D. Lattice BGK simulation of sound waves. EPL (Europhysics Lett.) 1998, 43, 235. [Google Scholar] [CrossRef]
- Dellar, P.J. Bulk and shear viscosities in lattice Boltzmann equations. Phys. Rev. E 2001, 64, 031203. [Google Scholar] [CrossRef]
- Bres, G.; Pérot, F.; Freed, D. Properties of the lattice Boltzmann method for acoustics. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference (30th AIAA Aeroacoustics Conference), Miami, FL, USA, 11–13 May 2009; p. 3395. [Google Scholar]
- Gorakifard, M.; Cuesta, I.; Salueña, C.; Kian Far, E. Acoustic Wave Propagation and its Application to Fluid Structure Interaction using the Cumulant Lattice Boltzmann Method. Comput. Math. Appl. 2021, 87, 91–106. [Google Scholar] [CrossRef]
- Latt, J.; Chopard, B. Lattice Boltzmann method with regularized pre-collision distribution functions. Math. Comput. Simul. 2006, 72, 165–168. [Google Scholar] [CrossRef]
- Malaspinas, O. Increasing stability and accuracy of the lattice Boltzmann scheme: Recursivity and regularization. arXiv 2015, arXiv:1505.06900. [Google Scholar]
- Brogi, F.; Malaspinas, O.; Chopard, B.; Bonadonna, C. Hermite regularization of the lattice Boltzmann method for open source computational aeroacoustics. J. Acoust. Soc. Am. 2017, 142, 2332–2345. [Google Scholar] [CrossRef]
- Chávez-Modena, M.; Martínez, J.; Cabello, J.; Ferrer, E. Simulations of aerodynamic separated flows using the lattice Boltzmann solver XFlow. Energies 2020, 13, 5146. [Google Scholar] [CrossRef]
- Filippova, O.; Hänel, D. Grid Refinement for Lattice-BGK Models. J. Comput. Phys. 1998, 147, 219–228. [Google Scholar] [CrossRef]
- Wood, S.L. Lattice Boltzmann Methods for Wind Energy Analysis. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2016. [Google Scholar]
- Deiterding, R.; Wood, S.L. Predictive Wind Turbine Simulation with an Adaptive Lattice Boltzmann Method for Moving Boundaries; Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2016; Volume 753, p. 082005. [Google Scholar]
- Gorakifard, M.; Salueña, C.; Cuesta, I.; Kian Far, E. Acoustical analysis of fluid structure interaction using the Cumulant lattice Boltzmann method. In Proceedings of the 16th International Conference for Mesoscopic Methods in Engineering and Science, Heriot-Watt University, Edinburgh, UK, 22–26 July 2019. [Google Scholar]
- Chen, Z.; Shu, C.; Tan, D.S. The simplified lattice Boltzmann method on non-uniform meshes. Commun. Comput. Phys 2018, 23, 1131. [Google Scholar] [CrossRef]
- He, X.; Luo, L.S.; Dembo, M. Some Progress in Lattice Boltzmann Method. Part I. Nonuniform Mesh Grids. J. Comput. Phys. 1996, 129, 357–363. [Google Scholar] [CrossRef]
- He, X.; Doolen, G. Lattice Boltzmann Method on Curvilinear Coordinates System: Flow around a Circular Cylinder. J. Comput. Phys. 1997, 134, 306–315. [Google Scholar] [CrossRef]
- Chen, H. Volumetric formulation of the lattice Boltzmann method for fluid dynamics: Basic concept. Phys. Rev. E 1998, 58, 3955–3963. [Google Scholar] [CrossRef]
- Mei, R.; Shyy, W. On the finite difference-based lattice Boltzmann method in curvilinear coordinates. J. Comput. Phys. 1998, 143, 426–448. [Google Scholar] [CrossRef]
- Xi, H.; Peng, G.; Chou, S.H. Finite-volume lattice Boltzmann method. Phys. Rev. E 1999, 59, 6202. [Google Scholar] [CrossRef] [PubMed]
- Nannelli, F.; Succi, S. The lattice Boltzmann equation on irregular lattices. J. Stat. Phys. 1992, 68, 401–407. [Google Scholar] [CrossRef]
- Peng, G.; Xi, H.; Duncan, C.; Chou, S.H. Finite volume scheme for the lattice Boltzmann method on unstructured meshes. Phys. Rev. E 1999, 59, 4675. [Google Scholar] [CrossRef]
- Lee, T.; Lin, C.L. A Characteristic Galerkin Method for Discrete Boltzmann Equation. J. Comput. Phys. 2001, 171, 336–356. [Google Scholar] [CrossRef]
- Li, Y.; LeBoeuf, E.J.; Basu, P.K. Least-squares finite-element scheme for the lattice Boltzmann method on an unstructured mesh. Phys. Rev. E 2005, 72, 046711. [Google Scholar] [CrossRef] [PubMed]
- Min, M.; Lee, T. A spectral-element discontinuous Galerkin lattice Boltzmann method for nearly incompressible flows. J. Comput. Phys. 2011, 230, 245–259. [Google Scholar] [CrossRef]
- Shu, C.; Niu, X.; Chew, Y. Taylor-series expansion and least-squares-based lattice Boltzmann method: Two-dimensional formulation and its applications. Phys. Rev. E 2002, 65, 036708. [Google Scholar] [CrossRef] [PubMed]
- Shu, C.; Chew, Y.; Niu, X. Least-squares-based lattice Boltzmann method: A meshless approach for simulation of flows with complex geometry. Phys. Rev. E 2001, 64, 045701. [Google Scholar] [CrossRef]
- Fard, E.G.; Shirani, E.; Geller, S. The Fluid Structure Interaction Using the Lattice Boltzmann Method. In Proceedings of the 13th Annual International Conference fluid dynamic conference, Shiraz, Iran, 26–28 October 2010. [Google Scholar]
- Liu, G.R.; Gu, Y.T. An Introduction to Meshfree Methods and Their Programming; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Liu, G. Meshfree Methods: Moving Beyond the Finite Element Method, Second Edition, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009; pp. 1–692. [Google Scholar]
- Liu, G.; Gu, Y. A local point interpolation method for stress analysis of two-dimensional solids. Struct. Eng. Mech. 2001, 11, 221–236. [Google Scholar] [CrossRef]
- Liu, G.; Gu, Y. A local radial point interpolation method (LRPIM) for free vibration analyses of 2-D solids. J. Sound Vib. 2001, 246, 29–46. [Google Scholar] [CrossRef]
- Atluri, S.N.; Zhu, T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics. Comput. Mech. 1998, 22, 117–127. [Google Scholar] [CrossRef]
- Li, Q.; Yang, H.; Yang, F.; Yao, D.; Zhang, G.; Ran, J.; Gao, B. Calculation of Hybrid Ionized Field of AC/DC Transmission Lines by the Meshless Local Petorv–Galerkin Method. Energies 2018, 11, 1521. [Google Scholar] [CrossRef]
- Musavi, S.H.; Ashrafizaadeh, M. Meshless lattice Boltzmann method for the simulation of fluid flows. Phys. Rev. E 2015, 91, 023310. [Google Scholar] [CrossRef] [PubMed]
- Musavi, S.H.; Ashrafizaadeh, M. Development of a three dimensional meshless numerical method for the solution of the Boltzmann equation on complex geometries. Comput. Fluids 2019, 181, 236–247. [Google Scholar] [CrossRef]
- Bawazeer, S. Lattice Boltzmann Method with Improved Radial Basis Function Method. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2019. [Google Scholar]
- Tanwar, S. A meshfree-based lattice Boltzmann approach for simulation of fluid flows within complex geometries: Application of meshfree methods for LBM simulations. In Analysis and Applications of Lattice Boltzmann Simulations; IGI Global: Hershey, PA, USA, 2018; pp. 188–222. [Google Scholar]
- Kian Far, E.; Geier, M.; Krafczyk, M. Simulation of rotating objects in fluids with the cumulant lattice Boltzmann model on sliding meshes. Comput. Math. Appl. 2018. [Google Scholar] [CrossRef]
- Kian Far, E.; Geier, M.; Kutscher, K.; Konstantin, M. Simulation of micro aggregate breakage in turbulent flows by the cumulant lattice Boltzmann method. Comput. Fluids 2016, 140, 222–231. [Google Scholar] [CrossRef]
- Kian Far, E.; Langer, S. Analysis of the cumulant lattice Boltzmann method for acoustics problems. In Proceedings of the 13th International Conference on Theoretical and Computational Acoustics, Vienna, Austria, 31 July–3 August 2017. [Google Scholar]
- Geier, M. Ab Initio Derivation of the Cascaded Lattice Boltzmann Automaton. Ph.D. Thesis, University of Freiburg–IMTEK, Freiburg, Germany, 2006. [Google Scholar]
- Geier, M.; Greiner, A.; Korvink, J.G. Reference Frame Independent Partitioning of the Momentum Distribution Function in Lattice Boltzmann Methods with Multiple Relaxation Rates; University of Freiburg: Freiburg, Germany, 2008. [Google Scholar]
- Seeger, S.; Hoffmann, H. The cumulant method for computational kinetic theory. Contin. Mech. Thermodyn. 2000, 12, 403–421. [Google Scholar] [CrossRef]
- Seeger, S.; Hoffmann, K. The cumulant method for the space-homogeneous Boltzmann equation. Contin. Mech. Thermodyn. 2005, 17, 51–60. [Google Scholar] [CrossRef]
- Kian Far, E.; Geier, M.; Kutscher, K.; Krafczyk, M. Distributed cumulant lattice Boltzmann simulation of the dispersion process of ceramic agglomerates. J. Comput. Methods Sci. Eng. 2016, 16, 231–252. [Google Scholar] [CrossRef]
- Kian Far, E. A sliding mesh LBM approach for the simulation of the rotating objects. In Proceedings of the 13th International Conference for Mesoscopic Methods in Engineering and Science, Hamburg, Germany, 18–22 July 2016. [Google Scholar]
- Geier, M.; Schönherr, M.; Pasquali, A.; Krafczyk, M. The cumulant lattice Boltzmann equation in three dimensions: Theory and validation. Comput. Math. Appl. 2015, 70, 507–547. [Google Scholar] [CrossRef]
- Kian Far, E. Turbulent Flow Simulation of Dispersion Microsystem with Cumulant Lattice Boltzmann Method, FORMULA X. 24 June 2019. Available online: https://www.formulation.org.uk/images/stories/FormulaX/Posters/P-27.pdf (accessed on 2 March 2021).
- Schäfer, R.; Böhle, M. Validation of the Lattice Boltzmann Method for Simulation of Aerodynamics and Aeroacoustics in a Centrifugal Fan. In Acoustics; Multidisciplinary Digital Publishing Institute: Basel, Switzerland, 2020; Volume 2, pp. 735–752. [Google Scholar]
- Ye, Q.; Avallone, F.; Van Der Velden, W.; Casalino, D. Effect of Vortex Generators on NREL Wind Turbine: Aerodynamic Performance and Far-Field Noise; Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; Volume 1618, p. 052077. [Google Scholar]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]



| Variables | A | ||||
| Description | 0 |
| Variables | A | |||||
| Description | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorakifard, M.; Salueña, C.; Cuesta, I.; Far, E.K. Analysis of Aeroacoustic Properties of the Local Radial Point Interpolation Cumulant Lattice Boltzmann Method. Energies 2021, 14, 1443. https://doi.org/10.3390/en14051443
Gorakifard M, Salueña C, Cuesta I, Far EK. Analysis of Aeroacoustic Properties of the Local Radial Point Interpolation Cumulant Lattice Boltzmann Method. Energies. 2021; 14(5):1443. https://doi.org/10.3390/en14051443
Chicago/Turabian StyleGorakifard, Mohsen, Clara Salueña, Ildefonso Cuesta, and Ehsan Kian Far. 2021. "Analysis of Aeroacoustic Properties of the Local Radial Point Interpolation Cumulant Lattice Boltzmann Method" Energies 14, no. 5: 1443. https://doi.org/10.3390/en14051443
APA StyleGorakifard, M., Salueña, C., Cuesta, I., & Far, E. K. (2021). Analysis of Aeroacoustic Properties of the Local Radial Point Interpolation Cumulant Lattice Boltzmann Method. Energies, 14(5), 1443. https://doi.org/10.3390/en14051443






