Influence of the Fin Shape on Heat Transport in Phase Change Material Heat Sink with Constant Heat Loads
Abstract
1. Introduction
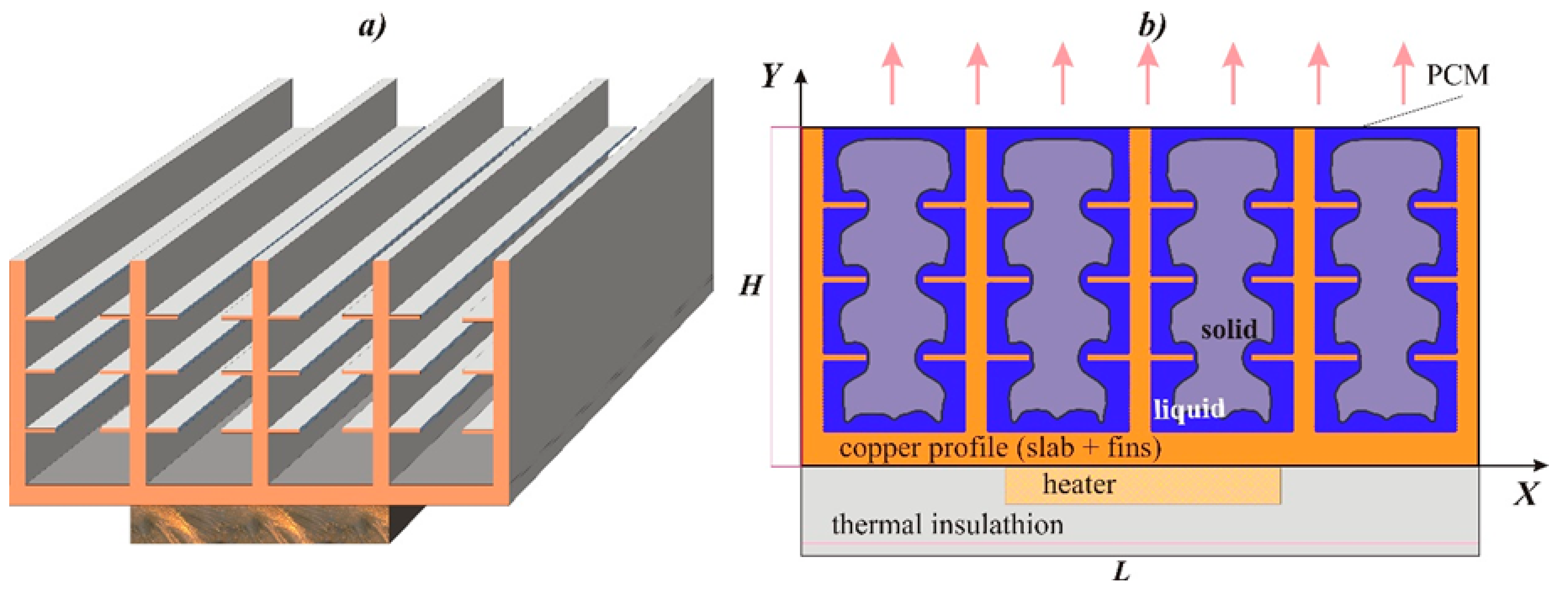
2. Basic Equations
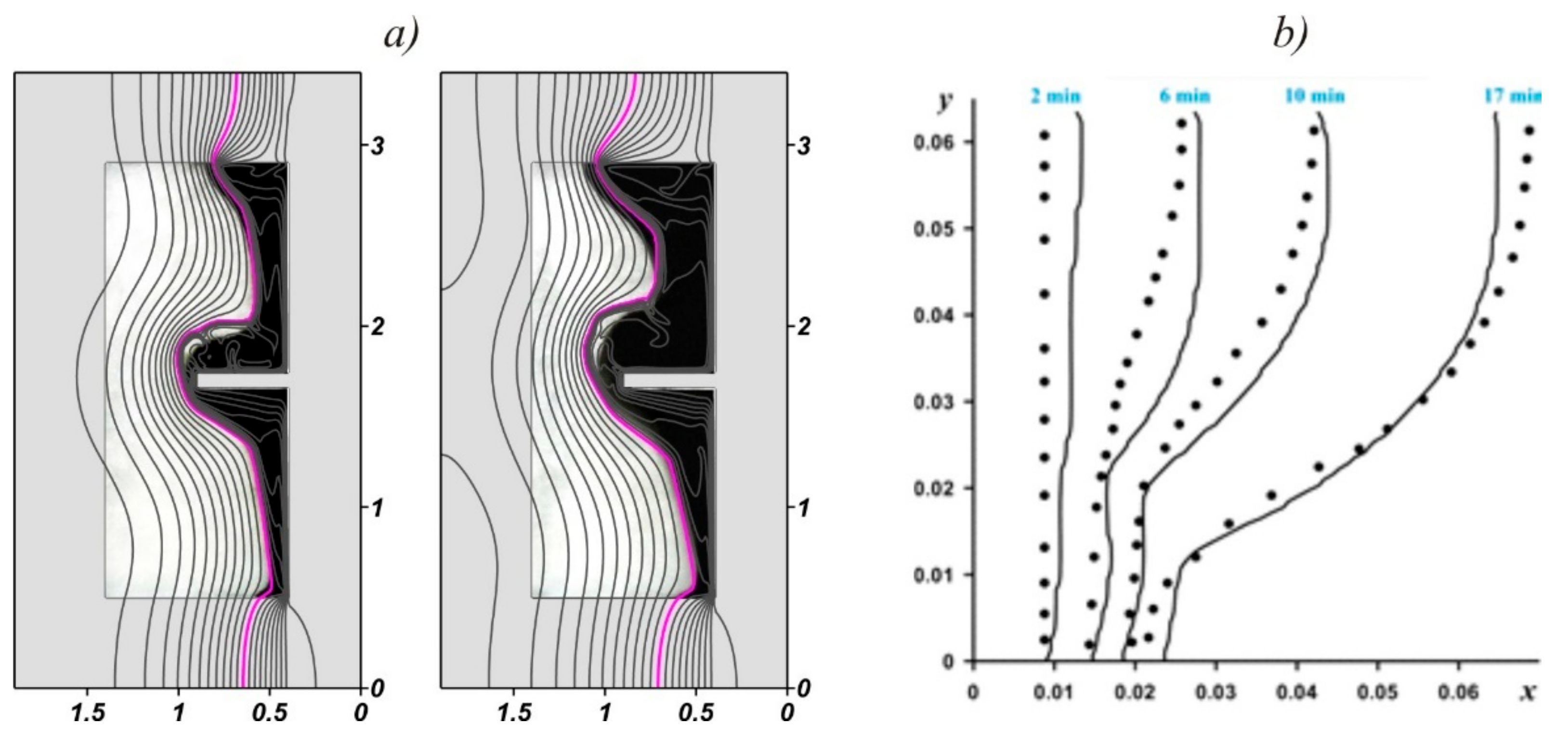
3. Numerical Technique
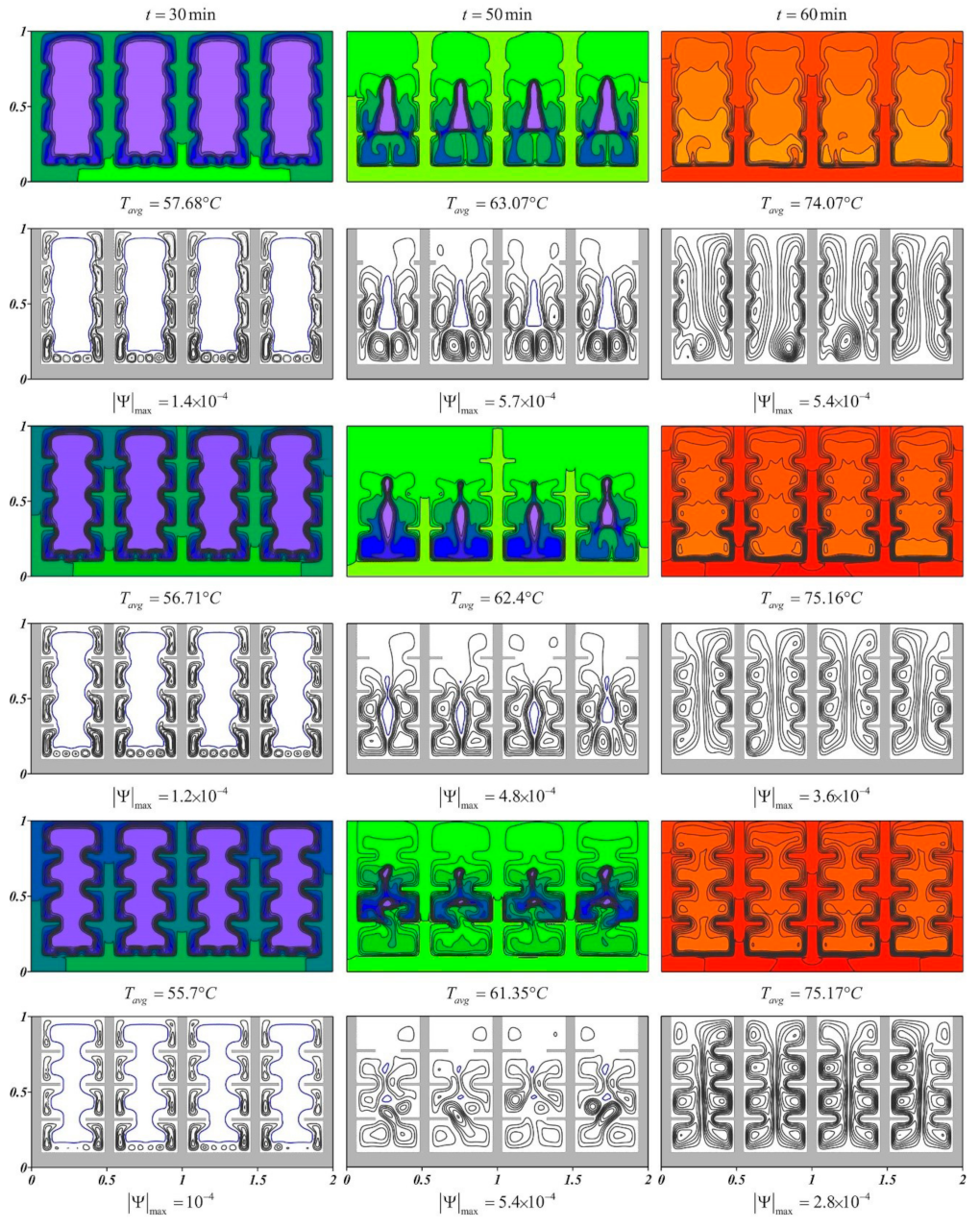
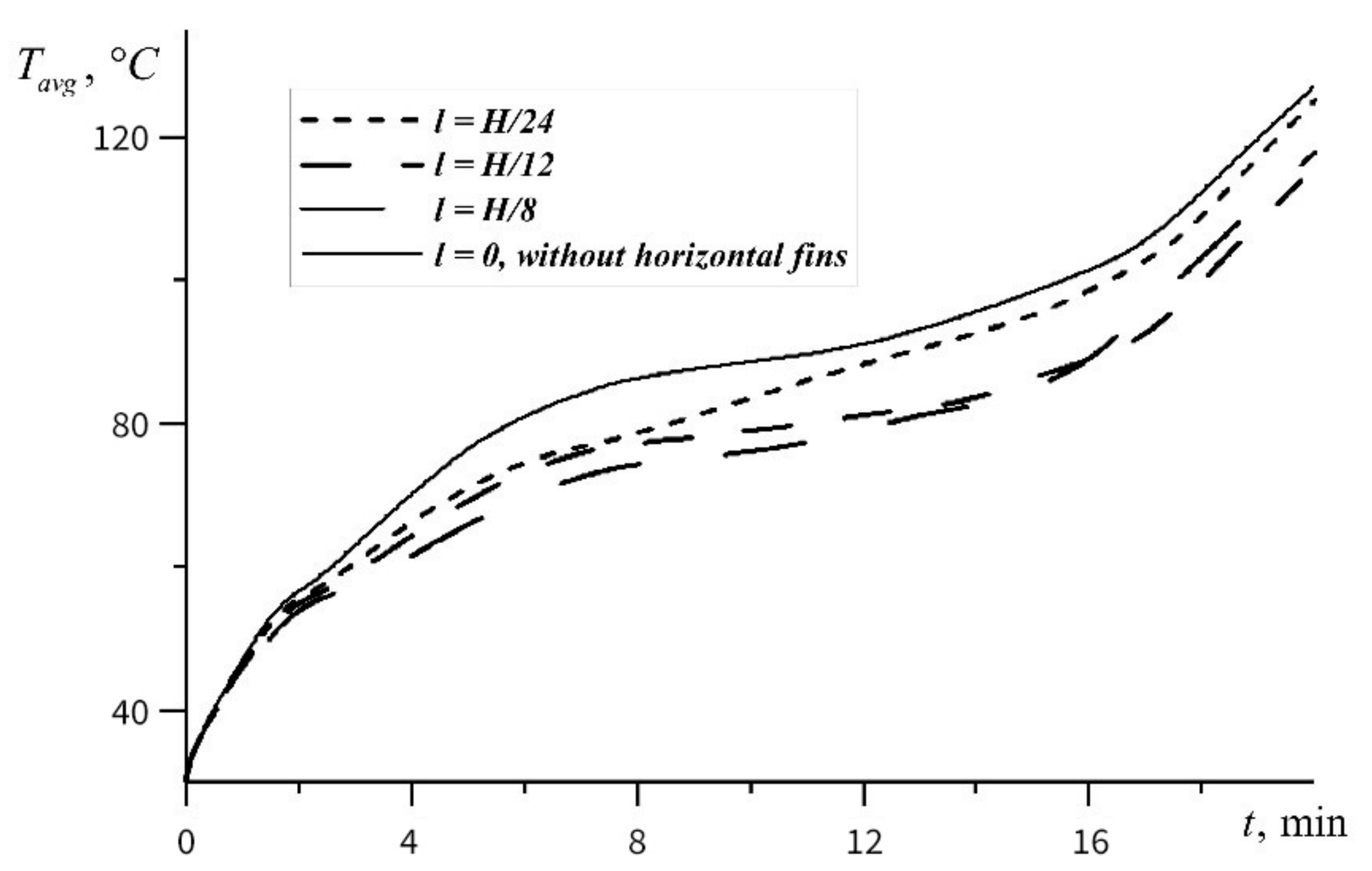
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Bi | Biot number |
| c | specific heat, JK−1 kg−1 |
| g | gravity acceleration, ms−2 |
| H | chamber size, m |
| h | specific enthalpy, Jkg−1 |
| k | heat conductivity, WK−1m−1 |
| L | cavity length, m |
| Lf | fusion energy or latent heat of melting, Jkg−1 |
| Os | Ostrogradsky number |
| p | pressure, Pa |
| Pr | Prandtl number |
| Q | energy production strength per unit of volume, W m−3 |
| Ra | Rayleigh number |
| Ste | Stefan number |
| t | time, s |
| T | temperature, K |
| Tm | melting temperature, K |
| u, v | velocity projections in Cartesian coordinate along x and y, ms−1 |
| U, V | non-dimensional velocity projections |
| x, y | Cartesian coordinates, m |
| X, Y | non-dimensional Cartesian coordinates |
| Greek symbols | |
| α | heat diffusivity, m2 s−1 |
| β | coefficient of thermal expansion, K−1 |
| γ | energy transference coefficient, WK−1m−2 |
| η | smoothing characteristic (or melting temperature range), K |
| Θ | non-dimensional temperature |
| μ | dynamic viscosity, Pa s |
| ν | kinematic viscosity, m2 s−1 |
| ρ | density, kgm−3 |
| τ | non-dimensional time |
| φ | volume fraction of the melt |
| ψ | stream function, m2 s−1 |
| Ψ | non-dimensional stream function |
| ω | vorticity, s−1 |
| Ω | non-dimensional vorticity |
| Subscripts | |
| 0 | initial condition or ambient |
| 1 | cooler |
| 2 | heated unit |
| l | liquid |
| m | melting |
| s | solid |
References
- Alam, M.W.; Bhattacharyya, S.; Souayeh, B.; Dey, K.; Hammami, F.; Rahimi-Gorji, M.; Biswas, R. CPU heat sink cooling by triangular shape micro-pin-fin: Numerical study. Int. Commun. Heat Mass Transf. 2020, 112, 104455. [Google Scholar] [CrossRef]
- Hosseinirad, E.; Khoshvaght-Aliabadi, M.; Hormozi, F. Effects of splitter shape on thermal-hydraulic characteristics of plate-pin-fin heat sink (PPFHS). Int. J. Heat Mass Transf. 2019, 143, 118586. [Google Scholar] [CrossRef]
- Mandal, P.K.; Sengupta, S.; Rana, S.C.; Bhanja, D. Effect of orientation angle in thermal performance analysis of a horizontal heat sink of perforated pin fins. Aip Conf. Proc. 2019, 2148, 030003. [Google Scholar]
- Kim, S.J.; Kim, D.-K.; Oh, H.H. Comparison of fluid flow and thermal characteristics of plate-fin and pin-fin heat sinks subject to a parallel flow. Heat Transf. Eng. 2008, 29, 169–177. [Google Scholar] [CrossRef]
- Iasiello, M.; Bianco, N.; Chiu, W.K.S.; Naso, V. The effects of variable porosity and cell size on the thermal performance of functionally-graded foams. Int. J. Therm. Sci. 2021, 160, 106696. [Google Scholar] [CrossRef]
- Andreozzi, A.; Bianco, N.; Iasiello, M.; Naso, V. Numerical study of metal foam heat sinks under uniform impinging flow. Iop Conf. Ser. J. Phys. 2017, 796, 012002. [Google Scholar] [CrossRef]
- Bianco, N.; Iasiello, M.; Mauro, G.M.; Pagano, L. Multi-objective optimization of finned metal foam heat sinks: Tradeoff between heat transfer and pressure drop. Appl. Therm. Eng. 2021, 182, 116058. [Google Scholar] [CrossRef]
- Feng, S.S.; Kuang, J.J.; Lu, T.J.; Ichimiya, K. Heat transfer and pressure drop characteristics of finned metal foam heat sinks under uniform impinging flow. J. Electron. Packag. 2015, 137, 021014. [Google Scholar] [CrossRef]
- Setoh, G.; Tan, F.L.; Fok, S.C. Experimental studies on the use of a phase change material for cooling mobile phones. Int. Commun. Heat Mass Transf. 2010, 37, 1403–1410. [Google Scholar] [CrossRef]
- Sharifi, N.; Bergman, T.L.; Faghri, A. Enhancement of PCM melting in enclosures with horizontally-finned internal surfaces. Int. J. Heat Mass Transf. 2011, 54, 4182–4192. [Google Scholar] [CrossRef]
- Xie, J.; Choo, K.F.; Xiang, J.; Lee, H.M. Characterization of natural convection in a PCM-based heat sink with novel conductive structures. Int. Commun. Heat Mass Transf. 2019, 108, 104306. [Google Scholar] [CrossRef]
- Lv, Y.; Yang, X.; Li, X.; Zhang, G.; Wang, Z.; Yang, C. Experimental study on a novel battery thermal management technology based on low density polyethylene-enhanced composite phase change materials coupled with low fins. Appl. Energy 2016, 178, 376–382. [Google Scholar] [CrossRef]
- Kenisarin, M.; Mahkamov, K. Solar energy storage using phase change materials. Renew. Sustain. Energy Rev. 2007, 11, 1913–1965. [Google Scholar] [CrossRef]
- Abhat, A. Low temperature latent heat thermal energy storage: Heat storage materials. Sol. Energy 1983, 10, 313–332. [Google Scholar] [CrossRef]
- Yousef, M.S.; Hassan, H.; Kodama, S.; Sekiguchi, H. An experimental study on the performance of single slope solar still integrated with a PCM-based pin-finned heat sink. Energy Procedia 2019, 56, 100–104. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, Z.; Zuo, J.; Huang, K.; Zhang, L. Phase change materials for solar thermal energy storage in residential buildings in cold climate. Renew. Sustain. Energy Rev. 2015, 48, 692–703. [Google Scholar] [CrossRef]
- Iasiello, M.; Mameli, M.; Filippeschi, S.; Bianco, N. Simulations of paraffine melting inside metal foams at different gravity levels with preliminary experimental validation. J. Phys. Conf. Ser. 2020, 1599, 012008. [Google Scholar] [CrossRef]
- Hasan, A.; McCormack, S.J.; Huang, M.J.; Sarwar, J.; Norton, B. Increased photovoltaic performance through temperature regulation by phase change materials: Materials comparison in different climates. Sol. Energy 2015, 115, 264–276. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Das, M.K.; Rath, P. Application of TCE-PCM based heat sinks for cooling of electronic components: A review. Renew. Sustain. Energy Rev. 2016, 59, 550–582. [Google Scholar] [CrossRef]
- Avci, M.; Yazici, M.Y. An experimental study on effect of inclination angle on the performance of a PCM-based flat-type heat sink. Appl. Therm. Eng. 2018, 131, 806–814. [Google Scholar] [CrossRef]
- Kalbasi, R.; Afrand, M.; Alsarraf, J.; Tran, M.-D. Studies on optimum fins number in PCM-based heat sinks. Energy 2019, 171, 1088–1099. [Google Scholar] [CrossRef]
- Ali, H.M.; Ashraf, M.J.; Giovannelli, A.; Irfan, M.; Irshad, T.B.; Hamid, H.M.; Hassan, F.; Arshad, A. Thermal management of electronics: An experimental analysis of triangular, rectangular and circular pin-fin heat sinks for various PCMs. Int. J. Heat Mass Transf. 2018, 123, 272–284. [Google Scholar] [CrossRef]
- Fan, L.-W.; Xiao, Y.-Q.; Zeng, Y.; Fang, X.; Wang, X.; Xu, X.; Yu, Z.-T.; Hong, R.-H.; Hu, Y.-C.; Cen, K.-F. Effects of melting temperature and the presence of internal fins on the performance of a phase change material (PCM)-based heat sink. Int. J. Therm. Sci. 2013, 70, 114–126. [Google Scholar] [CrossRef]
- Ghanbarpour, A.; Hosseini, M.J.; Ranjbar, A.A.; Rahimi, M.; Bahrampoury, R.; Ghanbarpour, M. Evaluation of heat sink performance using PCM and vapor chamber/heat pipe. Renew. Energy 2021, 163, 698–719. [Google Scholar] [CrossRef]
- Pakrouh, R.; Hosseini, M.J.; Ranjbar, A.A.; Bahrampoury, R. A numerical method for PCM-based pin fin heat sinks optimization. Energy Convers. Manag. 2015, 103, 542–552. [Google Scholar] [CrossRef]
- Ali, H.M.; Arshad, A.; Janjua, M.M.; Baig, W.; Sajjad, U. Thermal performance of LHSU for electronics under steady and transient operations modes. Int. J. Heat Mass Transf. 2018, 127, 1223–1232. [Google Scholar] [CrossRef]
- Pakrouh, R.; Hosseini, M.J.; Ranjbar, A.A. A parametric investigation of a PCM-based pin fin heat sink. Mech. Sci. 2015, 6, 65–73. [Google Scholar] [CrossRef]
- Arshad, A.; Ali, H.M.; Ali, M.; Manzur, S. Thermal performance of phase change material (PCM) based pin–finned heat sinks for electronics devices: Effect of pin thickness and PCM volume fraction. Appl. Therm. Eng. 2017, 112, 143–155. [Google Scholar] [CrossRef]
- Dammak, K.; El Hami, A. Thermal reliability-based design optimization using Kriging model of PCM based pin fin heat sink. Int. J. Heat Mass Transf. 2021, 166, 120745. [Google Scholar] [CrossRef]
- Srikanth, R.; Balaji, C. Experimental investigation on the heat transfer performance of a PCM based pin fin heat sink with discrete heating. Int. J. Therm. Sci. 2017, 111, 188–203. [Google Scholar] [CrossRef]
- Saha, S.K.; Dutta, P. Heat transfer correlations for PCM-based heat sinks with plate fins. Appl. Therm. Eng. 2010, 30, 2485–2491. [Google Scholar] [CrossRef]
- Wang, G.; Wei, G.; Xu, C.; Ju, X.; Yang, Y.; Du, X. Numerical simulation of effective thermal conductivity and pore-scale melting process of PCMs in foam metals. Appl. Therm. Eng. 2019, 147, 464–472. [Google Scholar] [CrossRef]
- El Idi, M.M.; Karkri, M. Heating and cooling conditions effects on the kinetic of phase change of PCM embedded in metal foam. Case Stud. Therm. Eng. 2020, 21, 100716. [Google Scholar] [CrossRef]
- Dinesh, B.V.S.; Bhattacharya, A. Comparison of energy absorption characteristics of PCM-metal foam systems with different pore size distributions. J. Energy Storage 2020, 28, 101190. [Google Scholar] [CrossRef]
- Rehman, T.; Ali, H.M.; Saieed, A.; Pao, W.; Ali, M. Copper foam/PCMs based heat sinks: An experimental study for electronic cooling systems. Int. J. Heat Mass Transf. 2018, 127, 381–393. [Google Scholar] [CrossRef]
- Sardari, P.T.; Babaei-Mahani, R.; Giddings, D.; Yasseri, S.; Moghimi, M.A.; Bahai, H. Energy recovery from domestic radiators using a compact composite metal Foam/PCM latent heat storage. J. Clean. Prod. 2020, 257, 120504. [Google Scholar] [CrossRef]
- Buonomo, B.; Ercole, D.; Manca, O.; Nardini, S. Thermal behaviors of latent thermal energy storage system with PCM and aluminum foam. Int. J. Heat Technol. 2016, 34, 359–364. [Google Scholar] [CrossRef]
- Qu, Z.G.; Li, W.Q.; Wang, J.L.; Tao, W.Q. Passive thermal management using metal foam saturated with phase change material in a heat sink. Int. Commun. Heat Mass Transf. 2012, 39, 1546–1549. [Google Scholar] [CrossRef]
- Zhu, F.; Zhang, C.; Gong, X. Numerical analysis on the energy storage efficiency of phase change material embedded in finned metal foam with graded porosity. Appl. Therm. Eng. 2017, 123, 256–265. [Google Scholar] [CrossRef]
- Hu, C.; Li, H.; Tang, D.; Zhu, J.; Wang, K.; Hu, X.; Bai, M. Pore-scale investigation on the heat-storage characteristics of phase change material in graded copper foam. Appl. Therm. Eng. 2020, 178, 115609. [Google Scholar] [CrossRef]
- Baby, R.; Balaji, C. Thermal optimization of PCM based pin fin heat sinks: An experimental study. Appl. Therm. Eng. 2013, 54, 65–77. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A. Conjugate heat transfer in the PCM-based heat storage system with finned copper profile: Application in electronics cooling. Int. J. Heat Mass Transf. 2018, 124, 1275–1284. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A. Effect of inclined magnetic field on natural convection melting in a square cavity with a local heat source. J. Magn. Magn. Mater. 2016, 419, 476–484. [Google Scholar] [CrossRef]
- Kamkari, B.; Groulx, D. Experimental investigation of melting behavior of phase change material in finned rectangular enclosures under different inclination angles. Exp. Therm. Fluid Sci. 2018, 97, 94–108. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Gibanov, N.S.; Sheremet, M.A. Computational study of heat transfer inside different PCMs enhanced by Al2O3 nanoparticles in a copper heat sink at high heat loads. Nanomaterials 2020, 10, 284. [Google Scholar] [CrossRef] [PubMed]
- Gau, C.; Viskanta, R. Melting and solidification of a pure metal on a vertical wall. J. Heat Transf. 1986, 108, 174–181. [Google Scholar] [CrossRef]




| Phase Change Material | Lauric Acid [44] | Copper (Radiator) | Silicon (Heat Source) |
|---|---|---|---|
| Tm, °C | 46 | – | – |
| Lf, kJ/Kg | 187.2 | – | – |
| ks/kl, W/(m∙K) | 0.16/0.14 | 401 | 148 |
| ρs/ρl, kg/m3 | 940/885 | 8900 | 2330 |
| cs/cl, J/(kg∙K) | 2180/2390 | 385 | 714 |
| μ, Pa∙s | 8 × 10–3 | – | – |
| β, 1/K | 8 × 10–4 | – | – |
| Ostrogradsky Number | Length of Horizontal Fins | ||
|---|---|---|---|
| l = H/24 | l = H/12 | l = H/8 | |
| 0.169 | 55 min | 53 min 9 s | 51 min 30 s |
| 0.338 | 30 min 9 s | 29 min 20 s | 27 min 45 s |
| 0.676 | 17 min 23 s | 17 min 7 s | 16 min 4 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bondareva, N.S.; Ghalambaz, M.; Sheremet, M.A. Influence of the Fin Shape on Heat Transport in Phase Change Material Heat Sink with Constant Heat Loads. Energies 2021, 14, 1389. https://doi.org/10.3390/en14051389
Bondareva NS, Ghalambaz M, Sheremet MA. Influence of the Fin Shape on Heat Transport in Phase Change Material Heat Sink with Constant Heat Loads. Energies. 2021; 14(5):1389. https://doi.org/10.3390/en14051389
Chicago/Turabian StyleBondareva, Nadezhda S., Mohammad Ghalambaz, and Mikhail A. Sheremet. 2021. "Influence of the Fin Shape on Heat Transport in Phase Change Material Heat Sink with Constant Heat Loads" Energies 14, no. 5: 1389. https://doi.org/10.3390/en14051389
APA StyleBondareva, N. S., Ghalambaz, M., & Sheremet, M. A. (2021). Influence of the Fin Shape on Heat Transport in Phase Change Material Heat Sink with Constant Heat Loads. Energies, 14(5), 1389. https://doi.org/10.3390/en14051389







