Optimal Selection of Metering Points for Power Quality Measurements in Distribution System †
Abstract
:1. Introduction
1.1. Motivation
- The proposition of an equivalent model and formulation of the optimization problem. The model should allow for expressing measurement goals in an analytical form. Usually, it requires a simplified model of the grid. In order to define the optimization problem, a criterion should be selected and formulated in an analytical form.
- Solving the optimization problem—which requires selecting the solving method. In most cases, the problem does not have an analytical solution, so numerical methods are utilized. Due to the problem complexity, heuristic methods are preferred. It is also assumed that a sequential approach can be utilized to find a near-optimal solution.
1.2. Literature Review
- State estimation (SE) problem, also referred to as power flow (PF) or load flow analysis,
- Fault detection (FD) based on voltage event recording and analysis,
- Harmonics flow analysis, also referred to as harmonic state estimation (HSE).
1.3. Contribution and Paper Organization
2. Materials and Methods
2.1. Selected Methods
- Kirchhoff current law criterion states that current in a line can be computed by the summation of currents in other lines. It means that in a node comprising n lines, only n−1 can be monitored without losing the system’s observability.
- Customer connection point—when a PQ parameter exceeds limits, it may affect customers. Therefore, branch customers connected to it should be selected to monitor with a high priority.
- The number of branches fed form a node. Elements near the supply source are more important for monitoring due to the total number of elements connected.
- Connection point (the beginning) of a branch—allows for monitoring all branches elements when a meter is installed in the node. It increases the observability of the system.
- Observability analysis using an iterative procedure referred to as index method. Nodes are selected based on mutual connection analysis in a way that the total observability is maximized. This stage decreases the number of nodes to analyze in the next stage. It comes from the assumption that the optimal solution can be found from a reduced set of nodes.
- Optimization procedure finds a minimal set of nodes to monitor, having preselected those chosen in Stage 1. The procedure minimizes a fitness function which depends on the number of used meters (in this stage) and the metering redundancy, i.e., the number of meters that can monitor a single node. The fitness function is nonlinear, and the optimization procedure also has to keep constraints related to observability. Therefore, there is no analytical solution, and heuristic algorithms should be used for the performance reason. In [38], binary particle swarm optimization (BPSO) procedure is used for this task, but any other solver for binary problems can also be used.
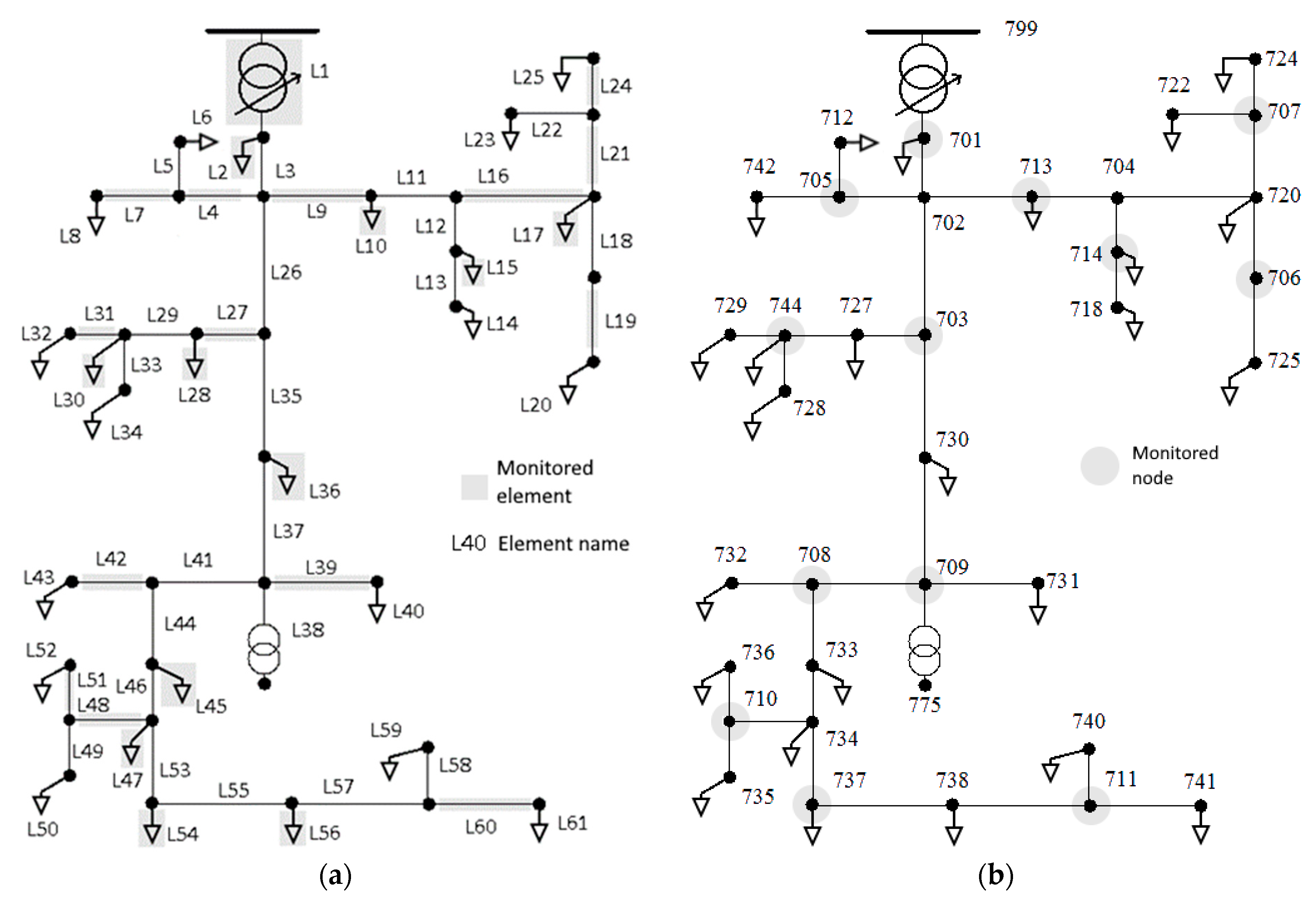
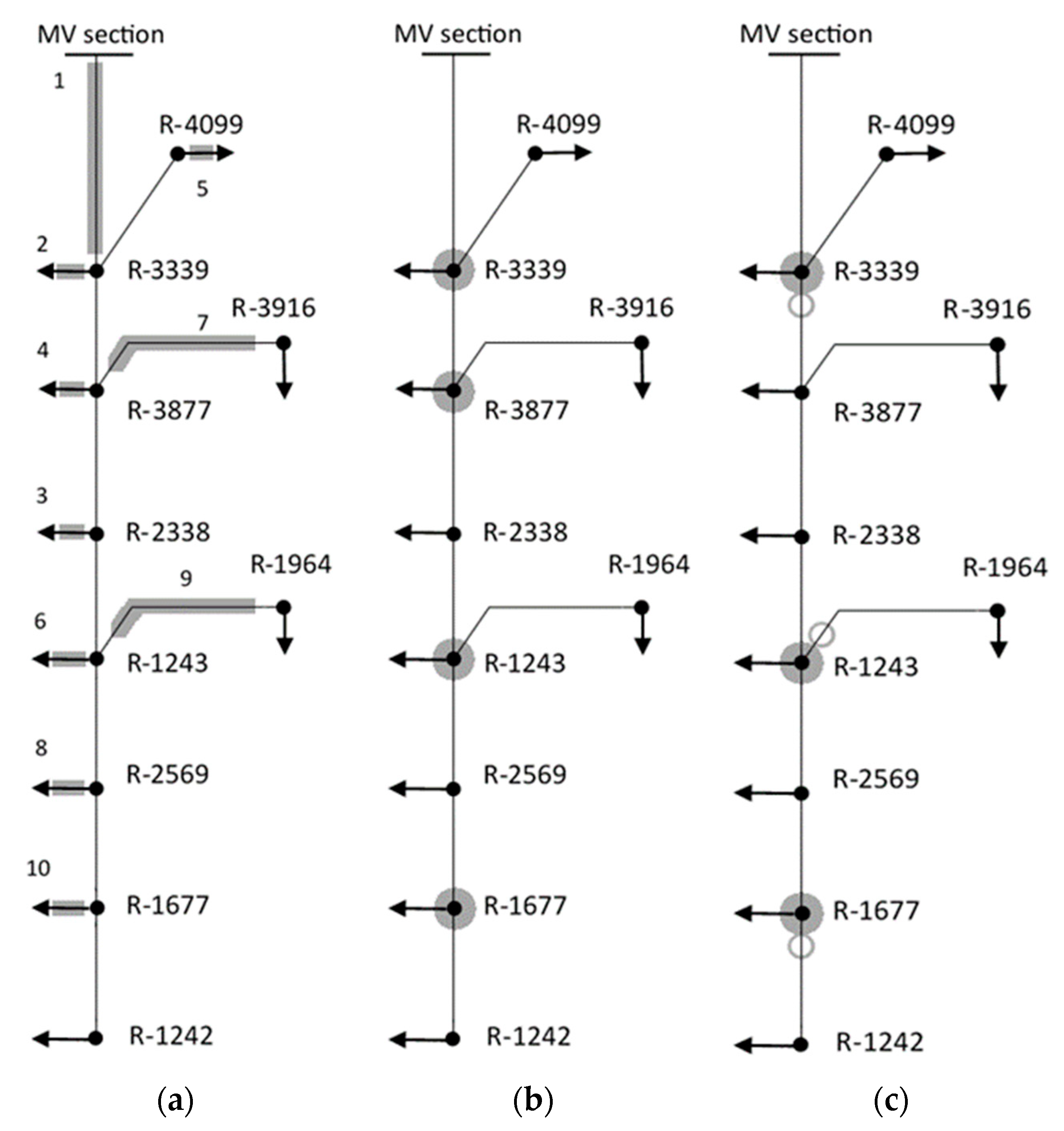
2.2. Test Grids
- IEEE test feeders: 13-node, 34-node, and 37-node test feeder [48],
- A typical MV feeder in an urban area.
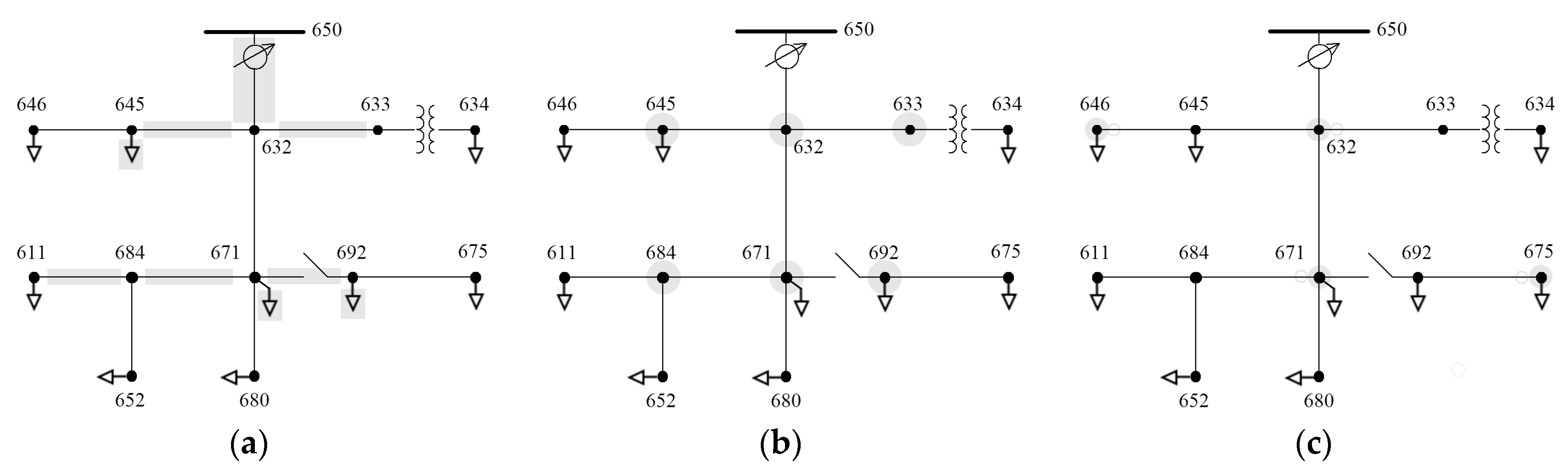
- for IEEE 13-node: 650, 632, 617, and 680,
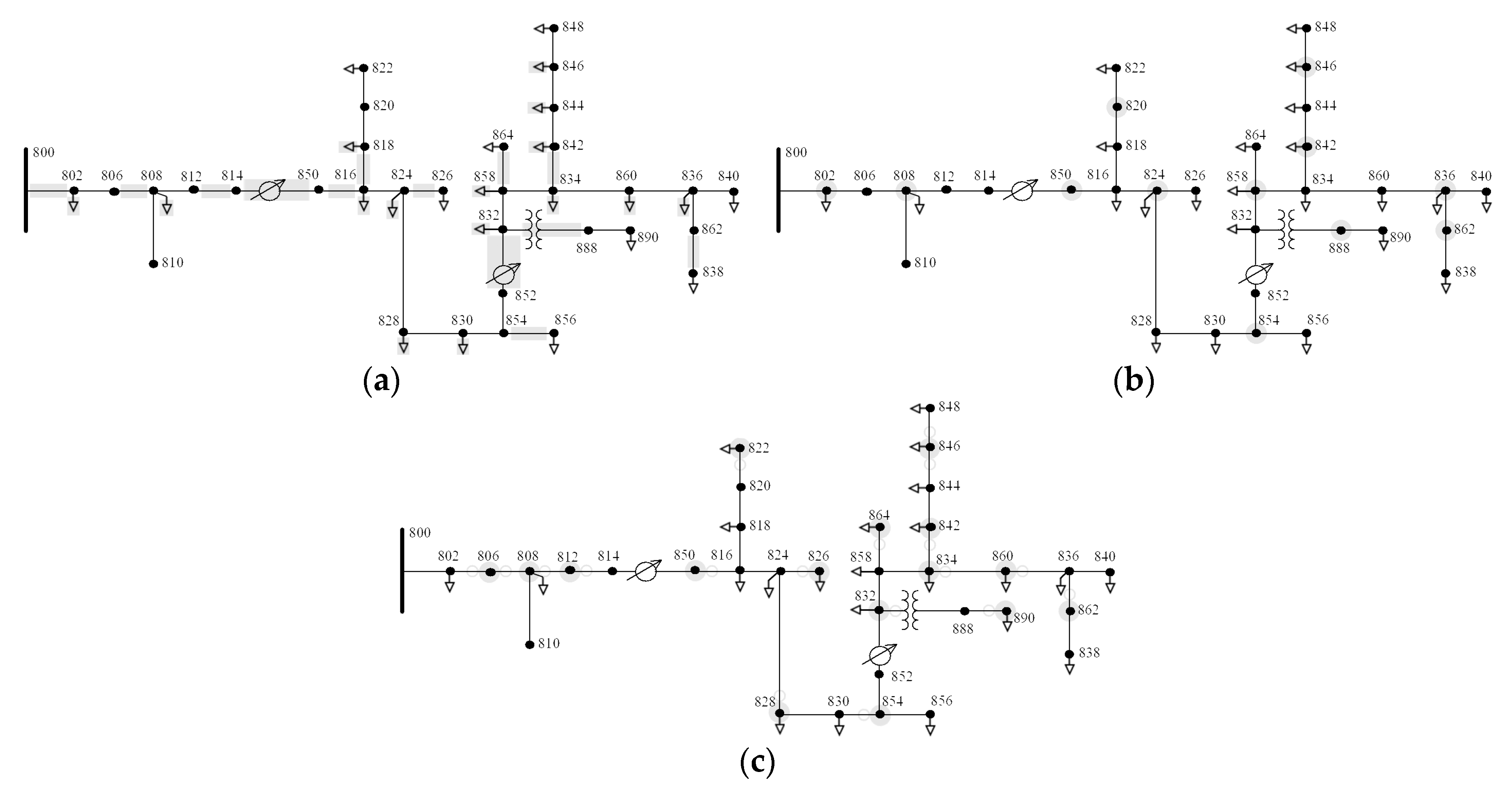
- for IEEE 34-node: 800, 802, 806, 808, 812, 814, 850, 816, 824, 828, 830, 854, 852, 832, 858, 834, 860, and 836.
2.3. Implementation
3. Results
3.1. Application to the IEEE 37-Node Test Feeder
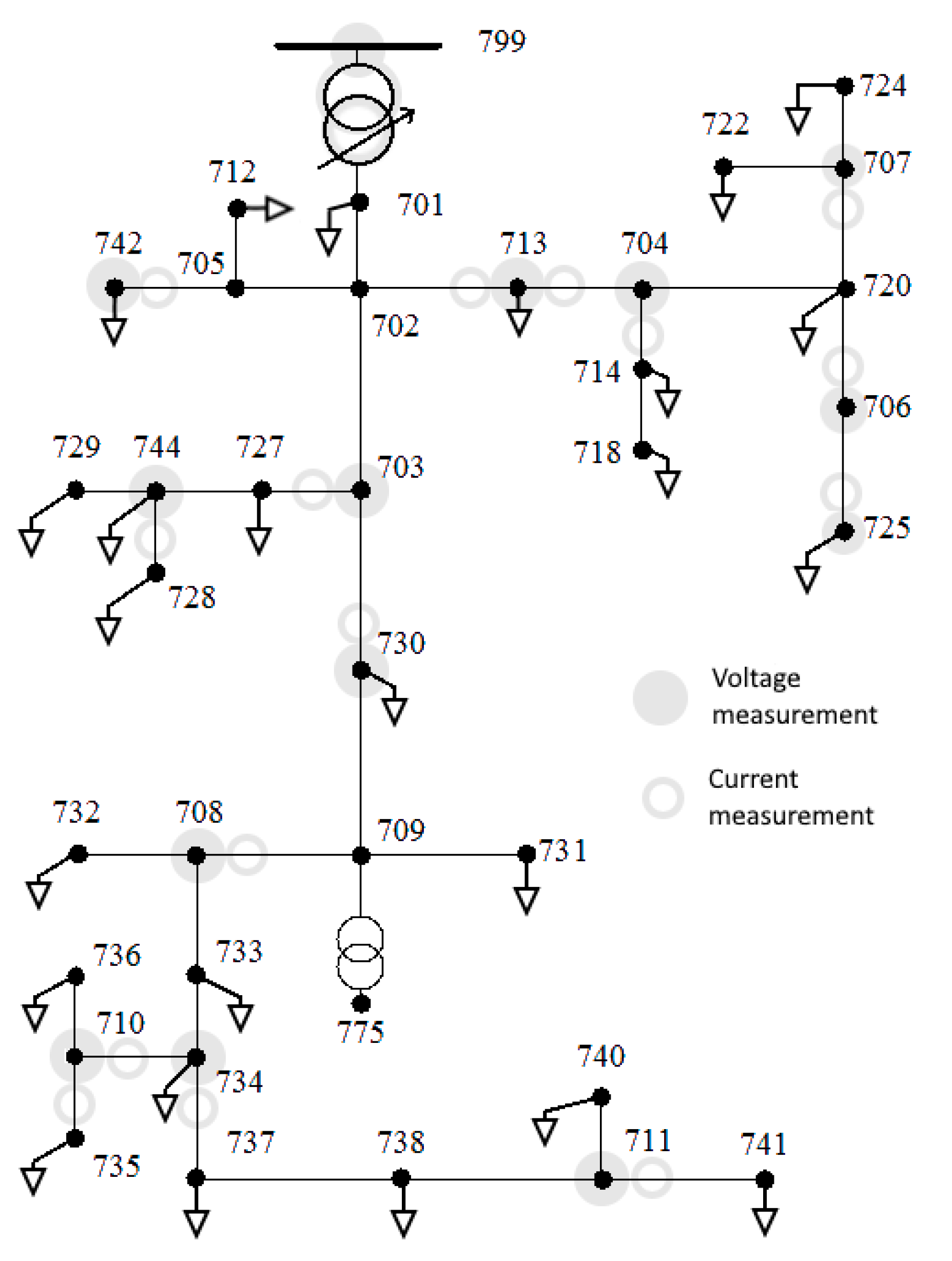
3.2. Application to Others IEEE Test Feeders
3.3. Application to a Typical MV Distribution Feeder
4. Discussion
5. Conclusions
- the definition of the state and the state vector,
- observability analysis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AHP | Analytic Hierarchy Process |
| ASE | Adaptive State Optimization |
| BILP | Binary Integer Linear Programming |
| BPSO | Binary Particle Swarm Optimization |
| CE | Complete Enumeration |
| CEER | Council of European Energy Regulators |
| CIGRE | International Council on Large Electric Systems |
| DSO | Distribution System Operator |
| FD | Fault Detection |
| GA | Genetic Algorithm |
| HSE | Harmonic State Estimation |
| HV | High Voltage |
| LV | Low Voltage |
| MRA | Meter Reach Area |
| MV | Medium Voltage |
| PF | Power Flow |
| PMU | Phasor Measurement Unit |
| PSO | Particle Swarm Optimization |
| PQ | Power Quality |
| RMSE | Root Mean Squared Error |
| SE | State Estimation |
| SVD | Singular Value Decomposition |
| TMRA | Topological Meter Reach Area |
References
- Chen, Y.; Zhang, Y.; Wang, J.; Lu, Z. Optimal operation for integrated electricity–heat system with improved heat pump and storage model to enhance local energy utilization. Energies 2020, 13, 6729. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, Q.; Wen, J.; Lin, Z.; Fang, F.; Chen, Q. Optimal operation of integrated electricity and heat system: A review of modeling and solution methods. Renew. Sustain. Energy Rev. 2021, 135, 110098. [Google Scholar] [CrossRef]
- Piatek, K.; Firlit, A.; Chmielowiec, K.; Dutka, M.; Barczentewicz, S.; Hanzelka, Z. Optimal Selection of Metering Points for Power Quality Measurements in Distribution System. In Proceedings of the 12th International Conference and Exhibition on Electrical Power Quality and Utilisation (EPQU), Kraków, Poland, 14–15 September 2020. [Google Scholar]
- Gomez-Gonzalez, M.; Hernandez, J.; Vera, D.; Jurado, F. Optimal sizing and power schedule in PV household-prosumers for improving PV self-consumption and providing frequency containment reserve. Energy 2020, 191, 116554. [Google Scholar] [CrossRef]
- Hernandez, J.C.; Sanchez-Sutil, F.; Munoz-Rodriguez, F.J.; Baier, C.R. Optimal sizing and management strategy for PV household-prosumers with self-consumption/sufficiency enhancement and provision of frequency containment reserve. Appl. Energy 2020, 277, 115529. [Google Scholar] [CrossRef]
- Hernandez, J.C.; Sanchez-Sutil, F.; Munoz-Rodriguez, F.J. Design criteria for the optimal sizing of a hybrid energy storage system in PV household-prosumers to maximize self-consumption and self-sufficiency. Energy 2019, 186, 115827. [Google Scholar] [CrossRef]
- Kilter, J. Guidelines for Power Quality Monitoring—Results from CIGRE/CIRED JWG C4.112. In Proceedings of the 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014. [Google Scholar]
- Bollen, M.H.J. CIGRE/CIRED JWG C4.112—Power Quality Monitoring. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ), Cordoba, Spain, 8–10 April 2014. [Google Scholar]
- Guidelines of Good Practice on the Implementation and Use of Voltage Quality Monitoring Systems for Regulatory Purposes. Council of European Energy Regulators (CEER), Energy Community Regulatory Board. Available online: https://www.ceer.eu/documents/104400/-/-/bdd2c6cb-5ccf-b342-2728-3e6c38536daf (accessed on 22 January 2021).
- Ahmad, M. Power System State Estimation; Artech House: Boston, MA, USA, 2013. [Google Scholar]
- Muscas, C.; Pilo, F.; Pisano, G.; Sulis, S. Optimal Allocation of Multichannel Measurement Devices for Distribution State Estimation. IEEE Trans. Instrum. Meas. 2009, 58, 1929–1937. [Google Scholar] [CrossRef]
- Muscas, C.; Pilo, F.; Pisano, G.; Sulis, S. Optimal Placement of Measurement Devices in Electric Distribution Systems. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference (IMTC), Sorrento, Italy, 24–27 April 2006. [Google Scholar]
- Liu, J.; Ponci, F.; Monti, A.; Muscas, C.; Pegoraro, P.A.; Sulis, S. Optimal Placement for Robust Distributed Measurement Systems in Active Distribution Grids. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013. [Google Scholar]
- Abur, A.; Magnago, F.H. Optimal Meter Placement against Contingencies. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Vancouver, BC, Canada, 24–27 April 2001. [Google Scholar]
- Baran, M.E.; Zhu, J.; Zhu, H.; Garren, K.E. A meter placement method for state estimation. IEEE Trans. Power Syst. 1995, 10, 1704–1710. [Google Scholar] [CrossRef]
- Chen, X.; Lin, J.; Wan, C.; Song, Y.; You, S.; Zong, Y.; Guo, W.; Li, Y. Optimal Meter Placement for Distribution Network State Estimation: A Circuit Representation Based MILP Approach. IEEE Trans. Power Syst. 2016, 31, 4357–4370. [Google Scholar] [CrossRef]
- Prasad, S.; Kumar, D.M.V. Optimal Allocation of Measurement Devices for Distribution State Estimation Using Multiobjective Hybrid PSO—Krill Herd Algorithm. IEEE Trans. Instrum. Meas. 2017, 66, 2022–2035. [Google Scholar] [CrossRef]
- Singh, R.; Pal, B.C.; Jabr, R.A.; Vinter, R.B. Meter Placement for Distribution System State Estimation: An Ordinal Optimization Approach. IEEE Trans. Power Syst. 2011, 26, 2328–2335. [Google Scholar] [CrossRef]
- Milbradt, R.G.; Canha, L.N.; Zorrilla, P.B.; Abaide, A.R.; Pereira, P.R.; Schmaedecke, S.M. A Multicriteria Approach for Meter Placement in Distribution Systems. In Proceedings of the 10th Int. Conf. the European Energy Market (EEM), Stockholm, Sweden, 27–31 May 2013. [Google Scholar]
- Buscher, M.; Lehnhoff, S.; Rohjans, S. Optimized Allocation of Measurement Points in Under-Determined Power Syst. In Proceedings of the IEEE Int. Energy Conf. (ENERGYCON), Leuven, Belgium, 4–8 April 2016. [Google Scholar]
- Yu, D.C.; Liu, H.; Chiang, H.D. A Heuristic Meter Placement Method for Load Estimation. IEEE Power Eng. Rev. 2002, 22, 913–917. [Google Scholar] [CrossRef]
- Divsheli, P.H.; Ghadiri, H.; Hesaminia, A.H.; Amini, B. A Novel Approach for Meter Placement for Load Estimation in Radial Distribution Networks. In Proceedings of the Third International Conference Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Nanjing, China, 6–9 April 2008. [Google Scholar]
- Won, D.-J.; Moon, S.-I. Optimal number and locations of power quality monitors considering system topology. IEEE Tran. Power Deliv. 2008, 23, 288–295. [Google Scholar] [CrossRef]
- Xie, Z.; Yu, Z.; Weng, G.; Wang, Q. Research on Allocation Optimization for Power Quality Monitors in Smart Distribution Grid. In Proceedings of the International Conference Power System Technology, Chengdu, China, 20–22 October 2014. [Google Scholar]
- Li, H. Optimal Number and Location of Power Quality Monitors for Power System. In Proceedings of the Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015. [Google Scholar]
- Eldery, M.A.; El-Saadany, E.F.; Salama, M.M.A.; Vannelli, A. A novel power quality monitoring allocation algorithm. IEEE Trans. Power Deliv. 2006, 21, 768–777. [Google Scholar] [CrossRef]
- Freitas, A.F.; Amaral, F.V.; Silva, J.A.L.; Saldanha, R.R.; Silva, S.M. Optimum allocation of power quality monitors in electric Power Systems—A case study. In Proceedings of the 17th International Conference Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016. [Google Scholar]
- Gou, B. Generalized Integer Linear Programming Formulation for Optimal PMU Placement. IEEE Trans. Power Syst. 2008, 23, 1099–1104. [Google Scholar] [CrossRef]
- Gou, B. Optimal Placement of PMUs by Integer Linear Programming. IEEE Trans. Power Syst. 2008, 23, 1525–1526. [Google Scholar] [CrossRef]
- Abbasy, N.H.; Ismail, H.M. A Unified Approach for the Optimal PMU Location for Power System State Estimation. IEEE Trans. Power Syst. 2009, 24, 806–813. [Google Scholar] [CrossRef]
- Aminifar, F.; Fotuhi-Firuzabad, M.; Shahidehpour, M.; Khodaei, A. Probabilistic Multistage PMU Placement in Electric Power Syst. IEEE Trans. Power Deliv. 2011, 26, 841–849. [Google Scholar] [CrossRef]
- Madtharad, C.; Premrudeepreechacharn, S.; Watson, N.R.; Saeng-Udom, R. An optimal measurement placement method for power system harmonic state estimation. IEEE Trans. Power Deliv. 2005, 20, 1514–1521. [Google Scholar] [CrossRef]
- Farach, J.E.; Grady, W.M.; Arapostathis, A. An optimal procedure for placing sensors and estimating the locations of harmonic sources in Power Syst. IEEE Trans. Power Deliv. 1993, 8, 1303–1310. [Google Scholar] [CrossRef]
- Rad, M.S.; Mokhtari, H.; Karimi, H. An Optimal Measurement Placement Method for Power System Harmonic State Estimation. In Proceedings of the International Conference and Exposition on Electrical and Power Engineering, Iasi, Romania, 25–27 October 2012. [Google Scholar]
- Kumar, A.; Das, B.; Sharma, J. Genetic algorithm-based meter placement for static estimation of harmonic sources. IEEE Trans. Power Deliv. 2005, 20, 1088–1096. [Google Scholar] [CrossRef]
- Almeida, C.F.M.; Kagan, N. Harmonic state estimation through optimal monitoring systems. IEEE Trans. Smart Grid 2013, 4, 467–478. [Google Scholar] [CrossRef]
- Almeida, C.F.M.; Kagan, N.; Souza, T.P.; Matsuo, N.M.; Duarte, S.X.; Neto, A.B.; Suematsu, A.K. Locating Power Quality Meters in Order to Perform Harmonic State Estimation. In Proceedings of the IEEE 15th International Conference Harmonics and Quality of Power (ICHQP), Hong Kong, China, 17–20 June 2012. [Google Scholar]
- Saxena, D.; Bhaumik, S.; Singh, S.N. Identification of Multiple Harmonic Sources in Power System Using Optimally Placed Voltage Measurement Devices. IEEE Trans. Ind. Electr. 2014, 61, 2483–2492. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, A.K.; Singh, N. Fuzzy Expert System Based Power Quality Meter Placement. In Proceedings of the IEEE 15th International Conference Harmonics and Quality of Power (ICHQP), Hong Kong, China, 17–20 June 2012. [Google Scholar]
- Olguin, G.; Vuinovich, F.; Bollen, M.H.J. An optimal monitoring program for obtaining voltage sag system indexes. IEEE Trans. Power Syst. 2006, 21, 378–384. [Google Scholar] [CrossRef]
- Kempner, T.R.; Oleskovicz, M.; Santos, A.Q. Optimal Allocation of Monitors by Analyzing the Vulnerability Area against Voltage Sags. In Proceedings of the 16th International Conference on Harmonics and Quality of Power (ICHQP), Bucharest, Romania, 25–28 May 2014. [Google Scholar]
- Haghbin, M.; Farjah, E. Optimal Placement of Monitors in Transmission Systems Using Fuzzy Boundaries for Voltage Sag Assessment. In Proceedings of the IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009. [Google Scholar]
- Ibrahim, A.A.; Mohamed, A.; Shareef, H.; Ghoshal, S.P. Optimal Placement of Voltage Sag Monitors Based on Monitor Reach area and Sag Severity Index. In Proceedings of the IEEE Student Conference on Research and Development (SCOReD), Putrajaya, Malaysia, 13–14 December 2010. [Google Scholar]
- Ibrahim, A.A.; Mohamed, A.; Shareef, H.; Ghoshal, S.P. A new approach for optimal power quality monitor placement in power system considering system topology. Przeglad Elektrotechniczny 2012, 88, 272–276. [Google Scholar]
- Cebrian, J.C.; Almeida, C.F.M.; Kagan, N. Genetic Algorithms Applied for the Optimal Allocation of Power Quality Monitors in Distribution Networks. In Proceedings of the 14th International Conference on Harmonics and Quality of Power (ICHQP), Bergamo, Italy, 26–29 September 2010. [Google Scholar]
- Farzanehrafat, A.; Watson, N.R. Review of Power Quality State Estimation. In Proceedings of the 20th Australasian Universities Power Engineering Conference, Christchurch, New Zealand, 5–8 December 2010. [Google Scholar]
- Farzanehrafat, A.; Watson, N.R. Power Quality State Estimator for Smart Distribution Grids. IEEE Trans. Power Syst. 2013, 28, 2183–2191. [Google Scholar] [CrossRef]
- Kersting, W.H. Radial distribution test feeders. IEEE Trans. Power Syst. 1991, 6, 975–985. [Google Scholar] [CrossRef]
- Mwakabuta, N.; Sekar, A. Comparative Study of the IEEE 34 Node Test Feeder under Practical Simplifications. In Proceedings of the 9th North American Power Symposium, Las Cruces, 30 September–2 October 2007. [Google Scholar]

| Method 1 | Method 2 | Method 3 | |
|---|---|---|---|
| MV feeder (Simple grid) | 8 m (10 m 1) | 9 m (14 m 1) | 8 m (13 m 1) |
| IEEE 13-node | 9 m | 15 m (6 m 2) | 13 m (4 m 2) |
| IEEE 34-node | 28 m | 35 m (12 m 2) | 41 m (18 m 2) |
| IEEE 37-node (Complex grid) | 26 m | 38 m (13 m 2) | 41 m (16 m 2) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piatek, K.; Firlit, A.; Chmielowiec, K.; Dutka, M.; Barczentewicz, S.; Hanzelka, Z. Optimal Selection of Metering Points for Power Quality Measurements in Distribution System. Energies 2021, 14, 1202. https://doi.org/10.3390/en14041202
Piatek K, Firlit A, Chmielowiec K, Dutka M, Barczentewicz S, Hanzelka Z. Optimal Selection of Metering Points for Power Quality Measurements in Distribution System. Energies. 2021; 14(4):1202. https://doi.org/10.3390/en14041202
Chicago/Turabian StylePiatek, Krzysztof, Andrzej Firlit, Krzysztof Chmielowiec, Mateusz Dutka, Szymon Barczentewicz, and Zbigniew Hanzelka. 2021. "Optimal Selection of Metering Points for Power Quality Measurements in Distribution System" Energies 14, no. 4: 1202. https://doi.org/10.3390/en14041202
APA StylePiatek, K., Firlit, A., Chmielowiec, K., Dutka, M., Barczentewicz, S., & Hanzelka, Z. (2021). Optimal Selection of Metering Points for Power Quality Measurements in Distribution System. Energies, 14(4), 1202. https://doi.org/10.3390/en14041202








