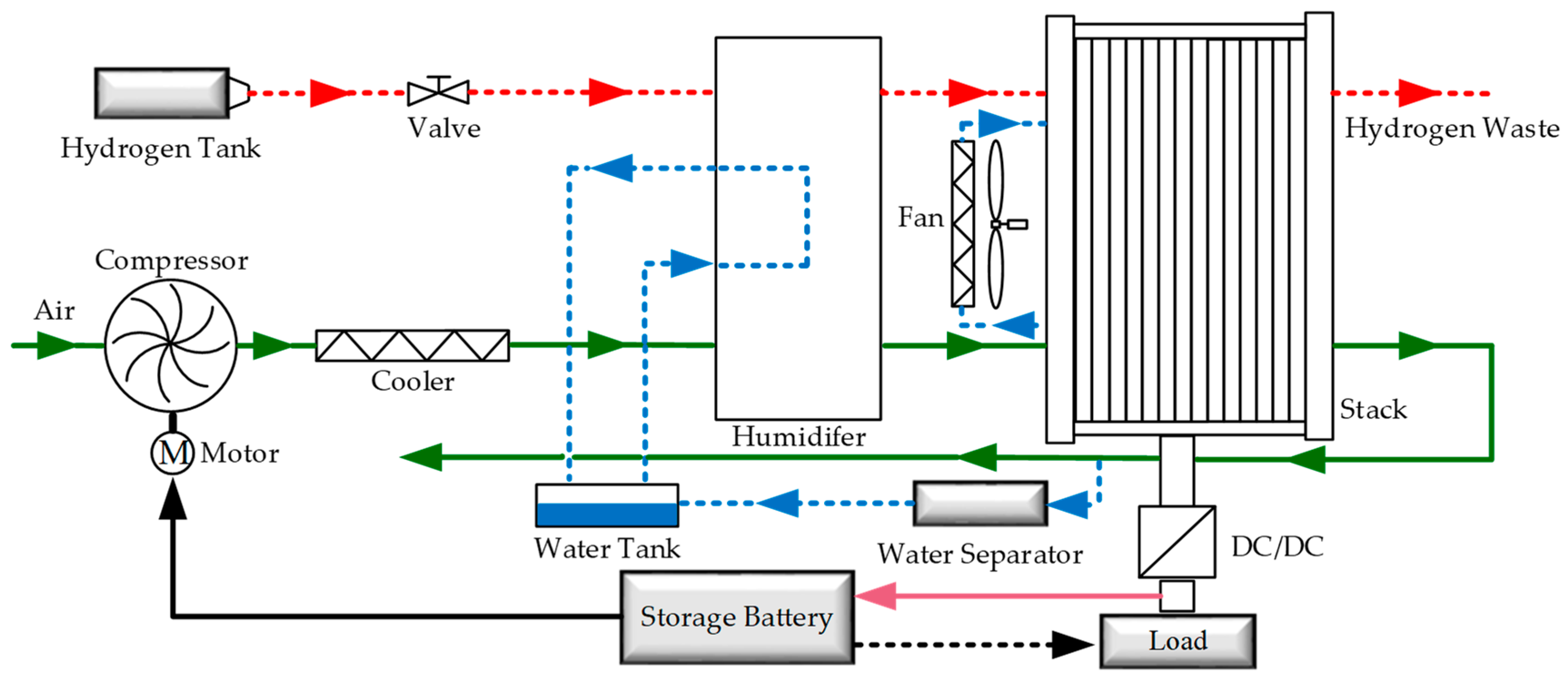
There are two main gas supply control strategies for PEMFC in the existing research. The flow of hydrogen into the anode is controlled by adjusting the opening and closing degree of the solenoid valve and the flow of air into the cathode by adjusting the voltage and speed of the air compressor. The research method of this paper is to control the air flow into the cathode side of the stack by controlling the working voltage of the air compressor. The oxygen supply state of PEMFC system is measured by the oxygen excess ratio (OER). The oxygen excess ratio reflects the excess degree of oxygen flow provided by the air compressor, which is expressed as:
where
is the oxygen excess ratio,
inlet flow rate of oxygen,
is reaction consumed rate of oxygen.
In the actual operation of PEMFC systems, the load occasionally needs a transient current to satisfy the stable operation of the system, while the air compressor usually fails to provide sufficient air supply to respond to this transient demand. If this phenomenon is serious, the value of oxygen excess ratio is less than 1 where , and it is called oxygen starvation. When the PEMEC system remain in this state for a long time it can cause permanent damage to the membrane, which causes serious damage to the fuel cell performance. A high-speed air compressor can effectively alleviate this phenomenon, but it will create the problem that the parasitic power loss of an auxiliary system increases and negatively influences the net power.
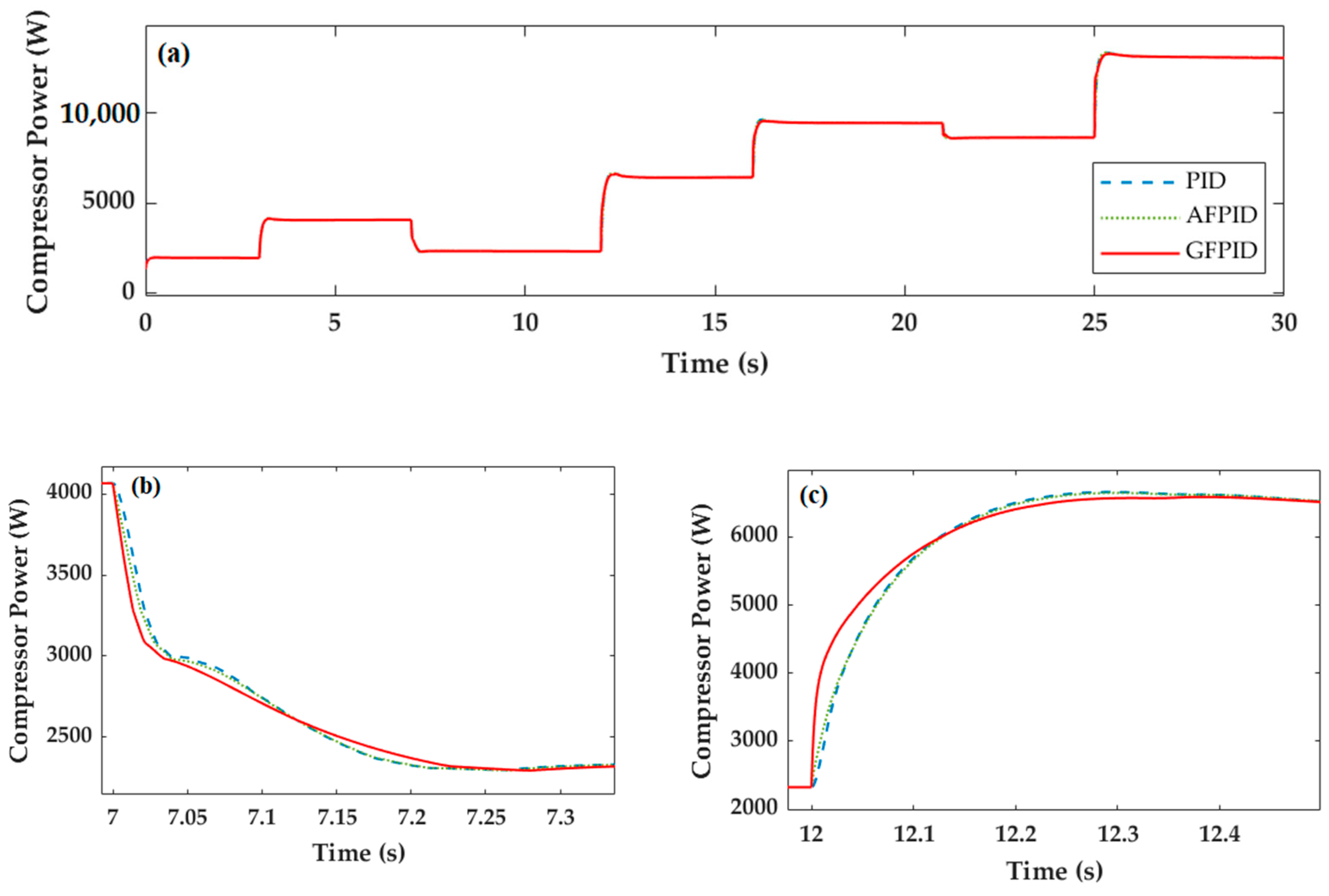
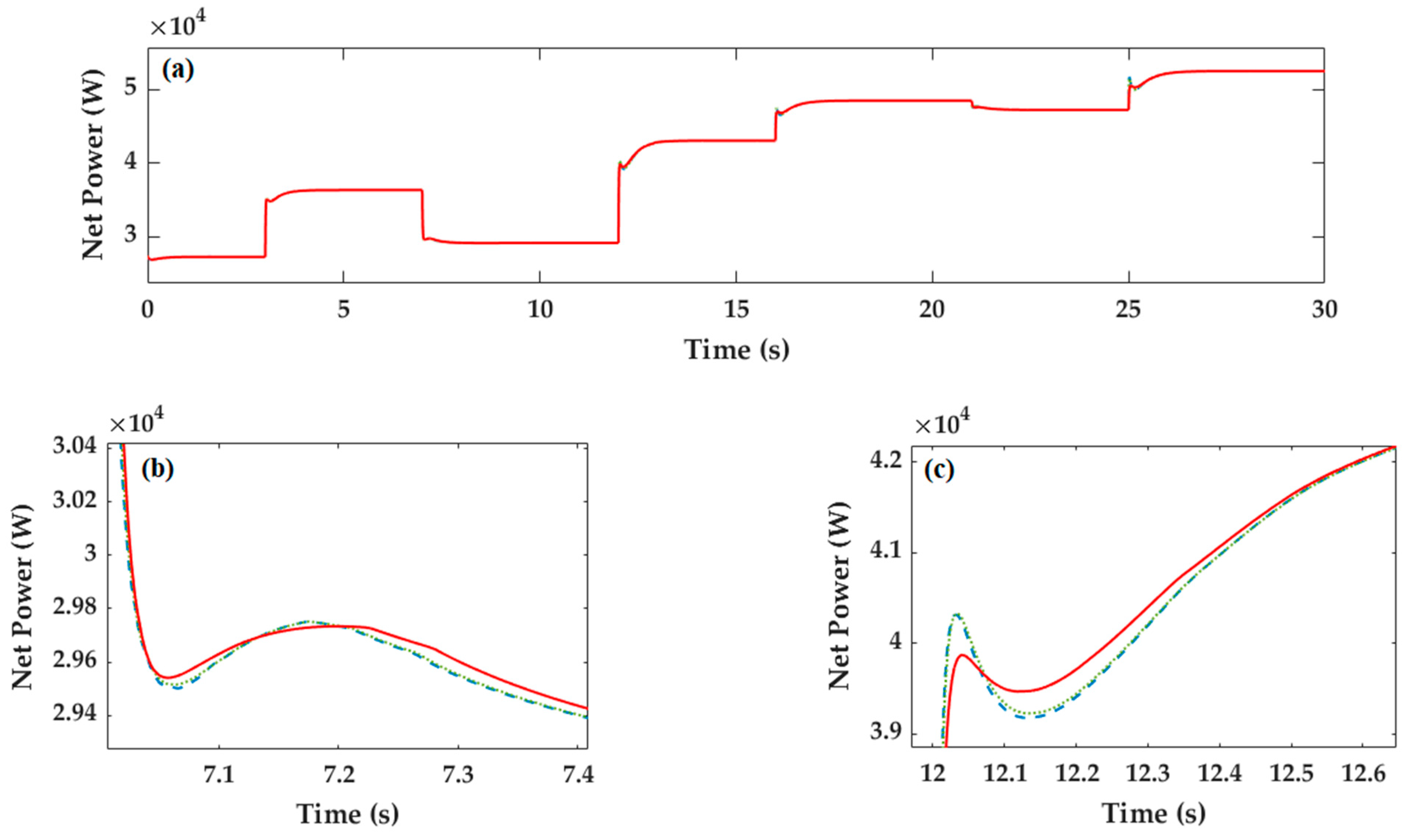
The optimal oxygen excess ratio operating point will determine the performance of the system, and the optimal oxygen excess ratio operating point of the system can be obtained by a step test. According to the step test, the system established in this paper can obtain a higher net power when the operating point of the peroxide ratio is set to 2. Therefore, was selected as the optimal oxygen excess ratio of the system.
An effective control method was adopted to avoid an oxygen starvation phenomenon and adjust the oxygen excess ratio in time. In this paper, three oxygen excess ratio control strategies were investigated respectively to obtain better control performance and effectively reduce the extra power loss caused by parasitic power.
3.2. Adaptive Fuzzy PID
Non-linear systems exist widely in practical industrial control systems and have complex characteristics such as strong coupling, great inertia and large time delay. As a non-linear system, the internal parameters of proton exchange membrane fuel cell (PEMFC) system change with the operation condition. When the internal parameters fluctuate sharply, the PID control for the oxygen excess ratio (OER) has some problems, such as slow reaction time, large fluctuation of air compressor pressure and net output power. PID control is difficult to solve.
Fuzzy control has the advantages of not relying on the accurate mathematical model of the controlled object, easy to be understood, strong robustness, and strong adaptability. Fuzzy control is based upon the control decision table to decide the size of the control amount. It can effectively control proton exchange membrane fuel cells. The adaptive fuzzy PID control strategy was adopted in this paper. Combining the conventional PID controller with fuzzy controller realizes fuzzy self-tuning of PID parameters through adjustment of the variables
and
.
and
are gain adjustments for
,
and
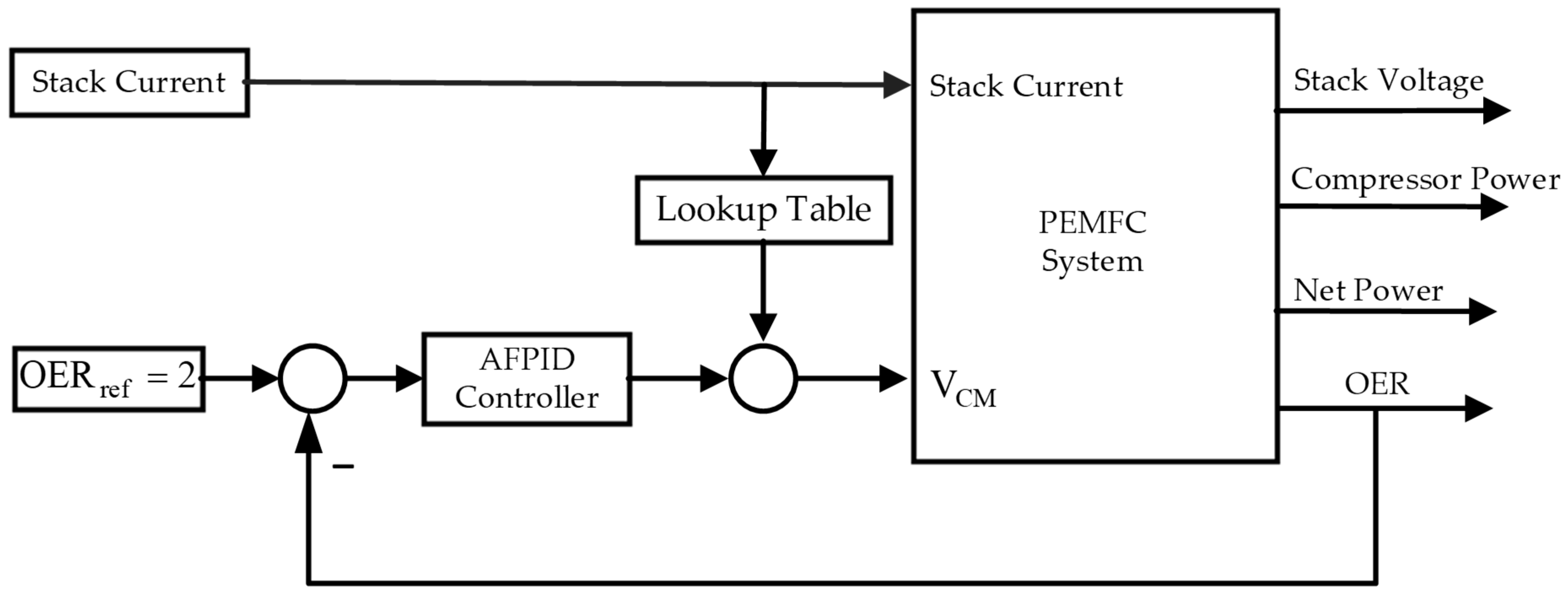
, respectively. The adaptive Fuzzy PID control framework of PEMFC is shown in
Figure 2.
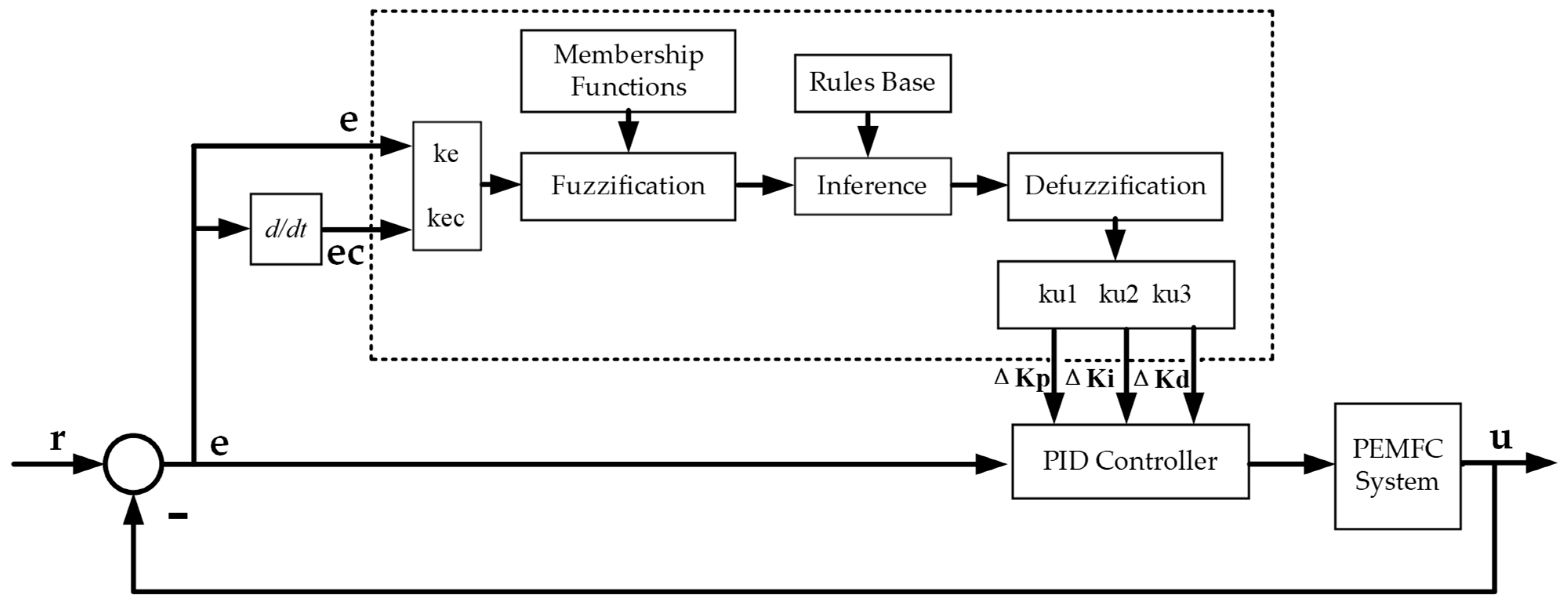
The adaptive fuzzy PID controller architecture is shown in
Figure 3. The controller has two input variables
and three output variables
and
. In two input variables,
is the error between the actual oxygen excess ratio and the reference oxygen excess ratio and
is the change of error. The output variables
and
express real-time adjustment of the gain, respectively. Three gain variations were adjusted online by using three fuzzy controllers
and
, respectively.
is the oxygen excess ratio of PEM fuel cell.
Fuzzification is to assign the input variables of a system to an appropriate fuzzy set according to their corresponding membership functions. Two input variables of the fuzzy controller (
and
) are the initial inputs, which are crisp set. The quantization factor (
and
) is a quantization factor, which can convert the initial input to the fuzzy domain (
and
).
and
are converted into fuzzy domain
and
respectively. The fuzzy domain for
is [−5, 5],
is [−5, 5]. In
Table 2, since the change of proportional gain
has the greatest influence on the system, when the input deviation
is PZ (Positive Zero) and NZ (Negative Zero), the influence on the output is different, so the linguistic value of the
controller is set as 8.
fuzzy variable
is different from
. This paper took
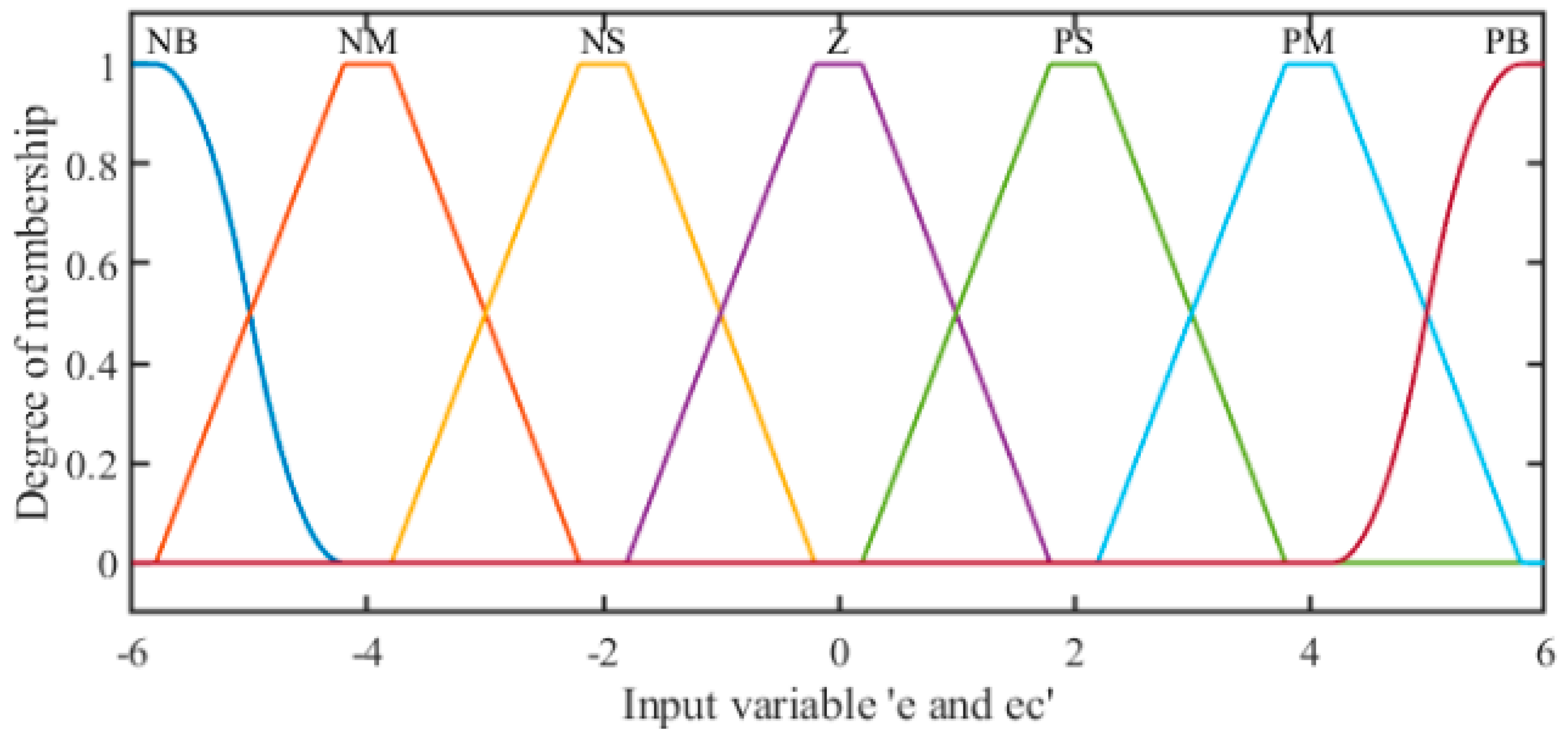
as an example, the two input and output fuzzy variables based on linguistic are expressed as NB (Negative Big), NM (Negative Medium), NS (Negative Small), Z (Zero), PS (Positive Small), PM (Positive Middle) and PB (Positive Big).
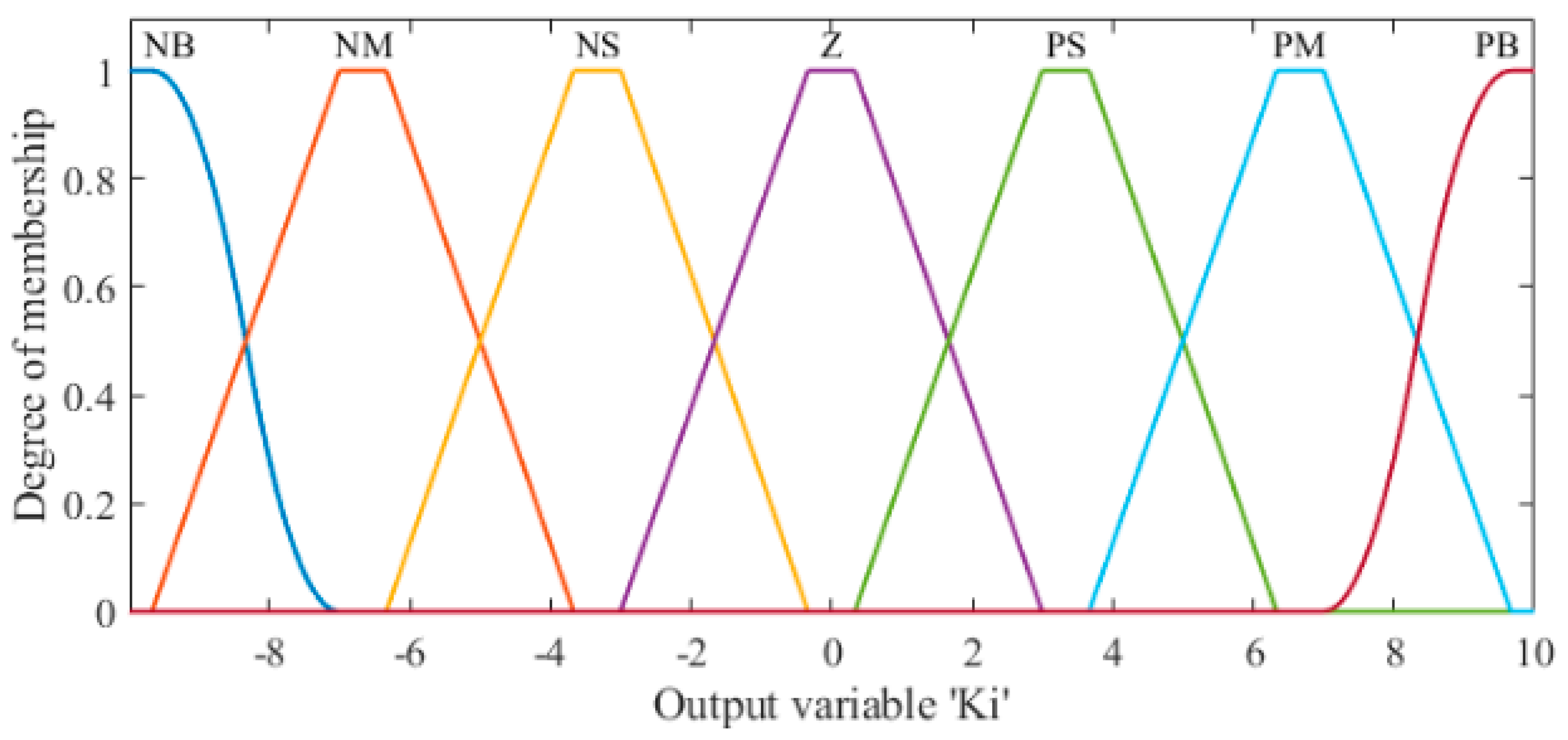
The membership functions employed in this paper include trimf type (triangle-shape grade of membership function), trapmf type (trapezoid shaped membership function) and smf type (sigmoid membership function). The membership function curves for
and
are shown in
Figure 4 and
Figure 5. The membership degree is calculated by the membership function curve. Fuzzy rules for the form of ‘‘If... Then” stated had a total of
rule base, which was available for each output. For example: part of the rules in
Table 3 is as follows:
The fuzzy rule base is the core part of the fuzzy system. General fuzzy rules can be obtained in the following two ways: empirical generalizations or adopting the learning algorithm based on the measured data. The fuzzy rule is obtained based on the behavior and experience of PEMFC in this paper. The fuzzy logic rule bases in this paper were designed as expressed in
Table 2,
Table 3 and
Table 4.
Based on the fuzzy rule base, the fuzzy inference machine maps the fuzzy set on the input space to the fuzzy set on the output space. The output fuzzy set are identified using the fuzzy implication method. The inference rule of min-max fuzzy implication is selected in this paper.
After the fuzzy logic inference engine, the output is a fuzzy set, and the fuzzy value is equivalent to a crisp value by means of defuzzification. Defuzzification completes the transformation of mapping a fuzzy set of output space to a definite point to achieve the aim of practical application. , and are the scale factor of three fuzzy controllers and , which can calculate the final values and through the transformation of the domain.
There are five common defuzzification strategies, namely centroid (centroid of area), bisector (bisector of area), mom (mean value of maximum), som (smallest value of maximum), and lom (largest value of maximum). In this paper, bisector is selected for defuzzification for its advantages of intuitive, reasonable and simple calculation. The fuzzy controller surface is shown in
Figure 6.
3.3. Granular Function Fuzzy PID
In recent study, Granular computing is a research hotspot in artificial intelligence field. Granular computation is mainly used in uncertain, fuzzy, imprecise and mass information objects. The process of granulating information is more consistent with human cognition so that it is easier to be understood. In the process of realizing the accurate control of the controlled object, the conventional fuzzy control inevitably needs to formulate the corresponding fuzzy rule base, but in order to achieve higher control accuracy, the fuzzy explosion phenomenon will occur when the number of fuzzy rules is set to a certain extent. This problem has also become a technical bottleneck that makes fuzzy control difficult to solve at the present stage. Based on this phenomenon, a PEMFC oxygen excess ratio fuzzy control algorithm based on granular function is proposed. The process of fuzzification and defuzzification is eliminated. After the fuzzy information is granulated, the granular function is obtained by fitting the data to replace the fuzzy controller in AFPID, which can avoid fuzzy explosion.
In an adaptive fuzzy control system based on granular function, the whole system is controlled by the granular response function. The granular function fuzzy PID control structure is shown in
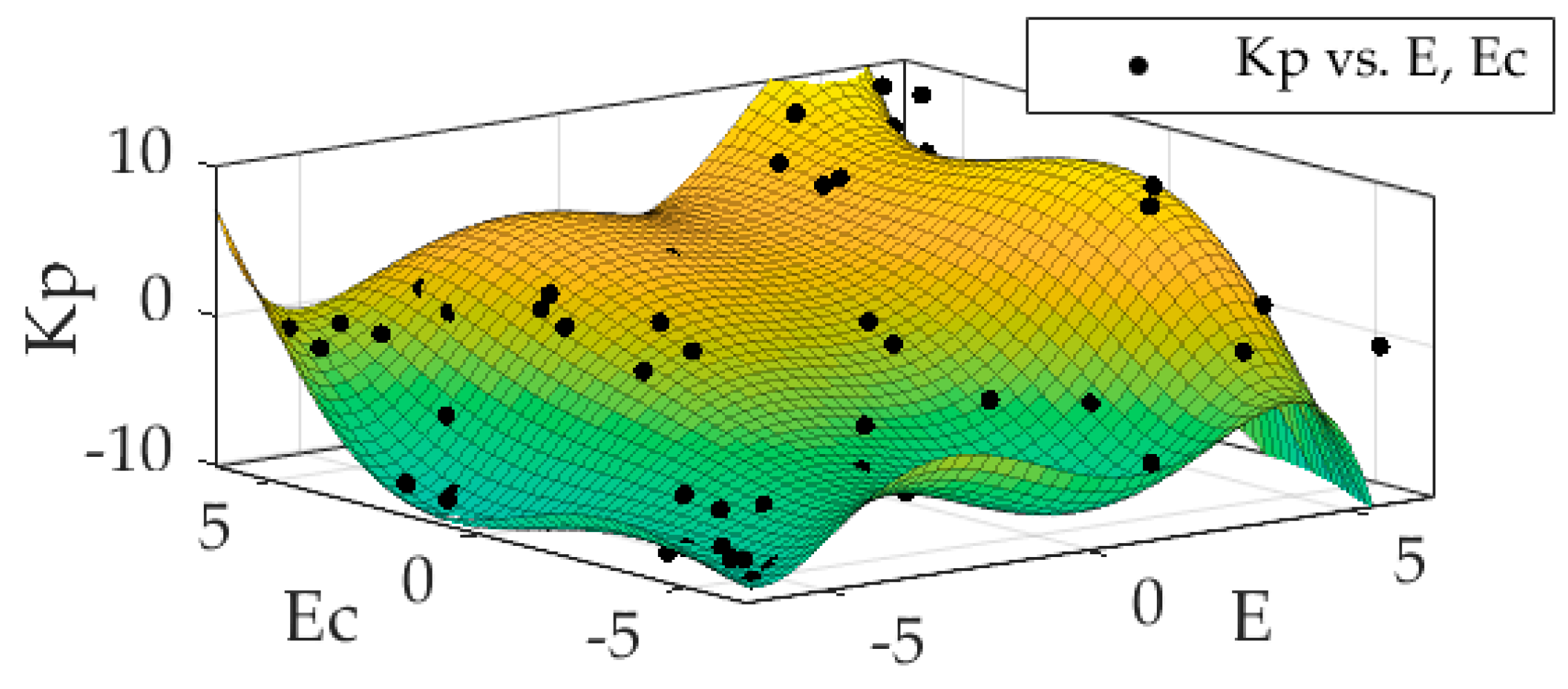
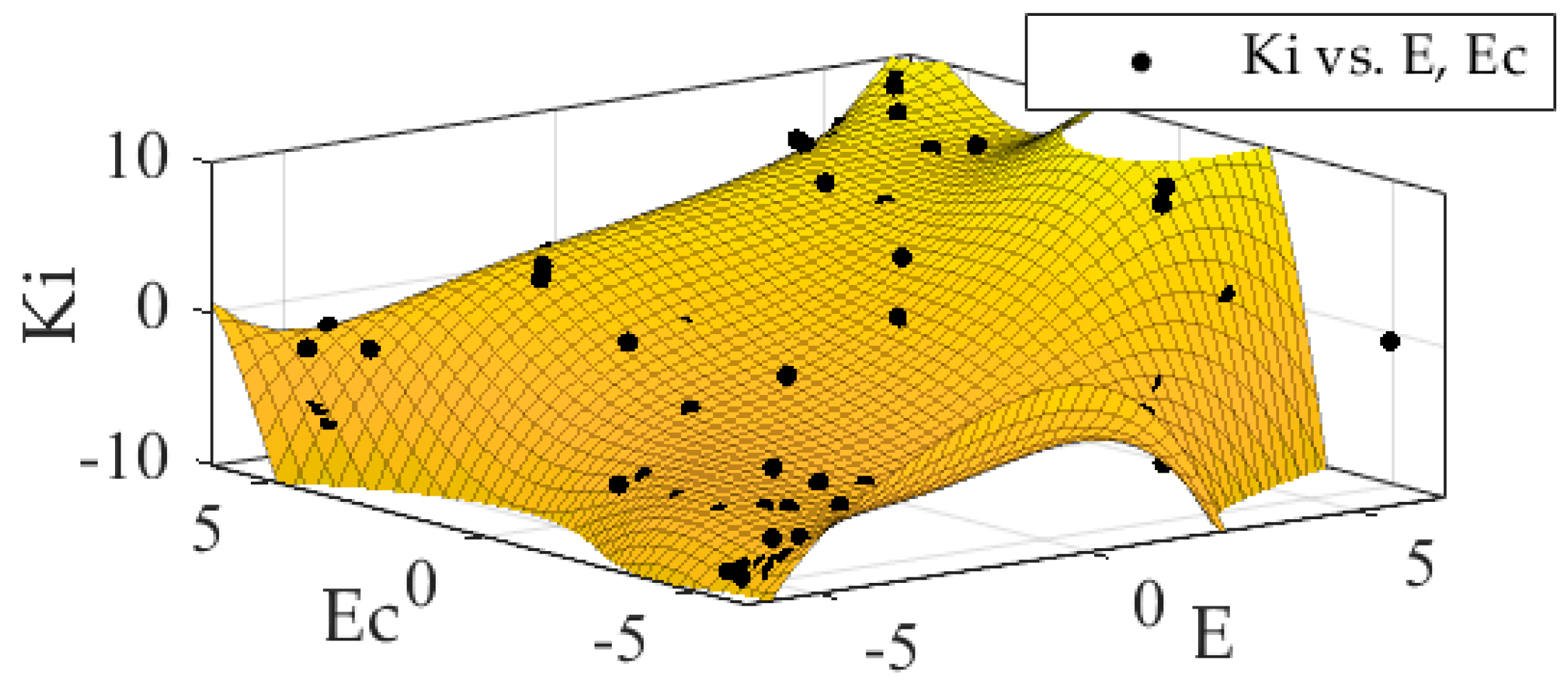
Figure 7. The number of rules would not affect the operation of the system, but are only related to the fuzzy points of the granule response function after being fitted. The design scheme is as follows. Firstly, according to the fuzzy rule base established by AFPID, the fuzzy rule granule points of
and
are uniformly selected to accomplish the granulation of fuzzy information. Secondly, the cftool tool of MATLAB/Simulink is used to complete the 5-order fitting of fuzzy regular grain points. Finally, as shown in
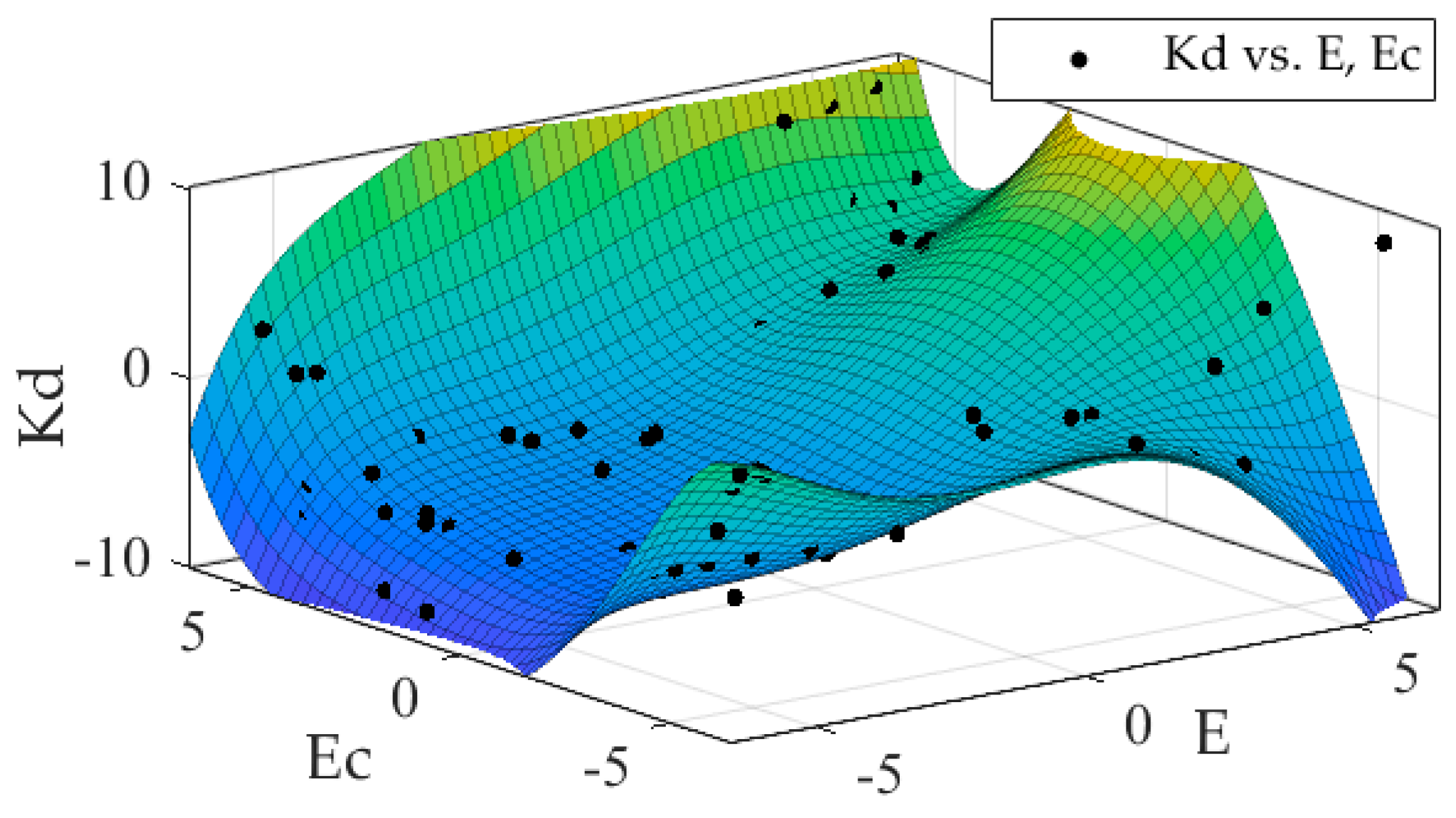
Figure 8,
Figure 9 and
Figure 10,
and
obtained a fitting surface and a fitting polynomial equation which is the granular function defined beforehand, respectively.
For example: the coefficients of the fifth-order fitting granular function for
are shown in
Table 5.
Accordingly, the fitting polynomial equation for
is as follows:
where
and
are independent variables of functional equation,
and
are dependent variables of corresponding granular functional equation. Finally, the granular functions were introduced into the system instead of the original fuzzy controller.