Combined Aggregated Sampling Stochastic Dynamic Programming and Simulation-Optimization to Derive Operation Rules for Large-Scale Hydropower System
Abstract
1. Introduction
2. Materials and Methods
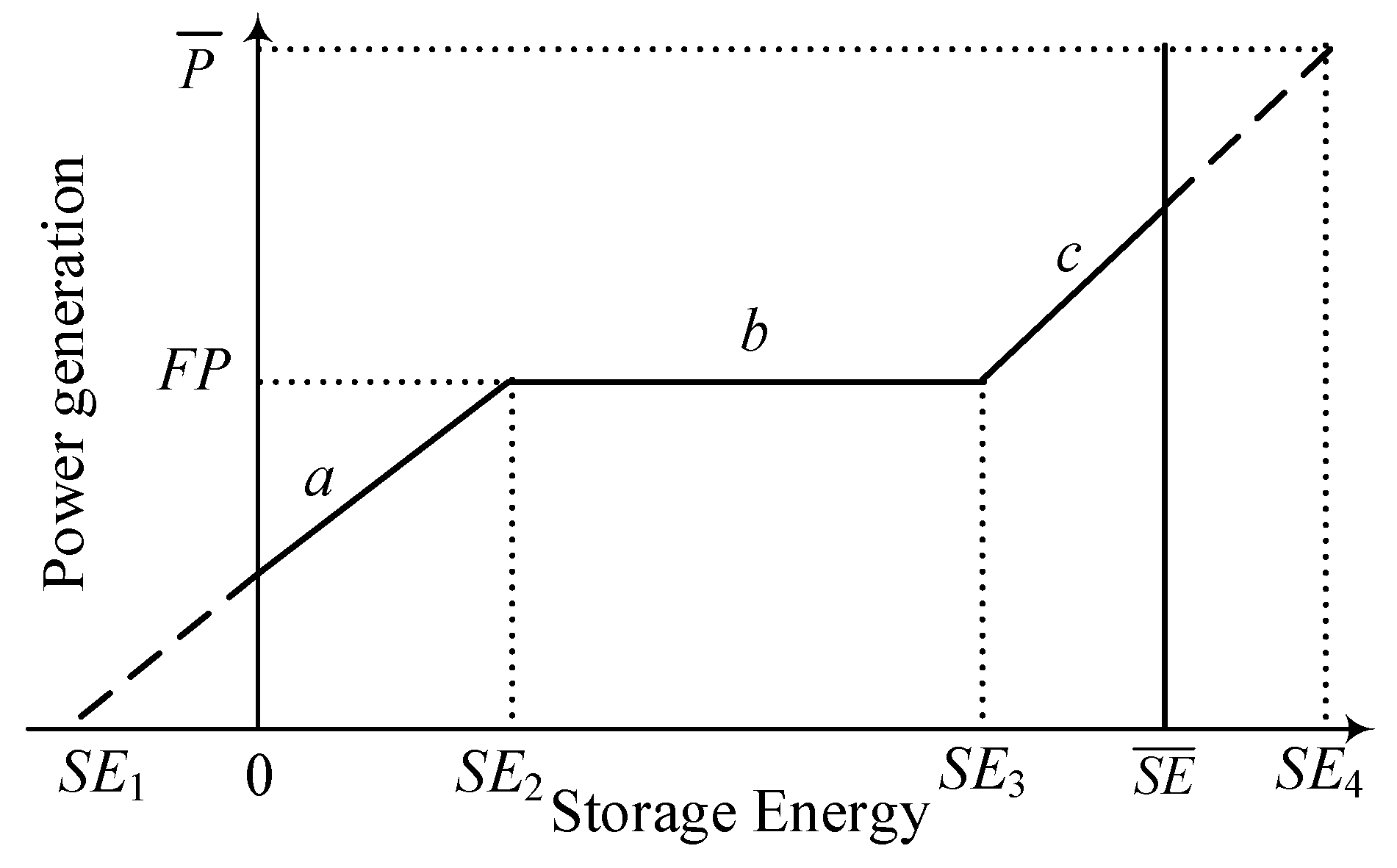
2.1. Operation Rule for Large-Scale Hydropower System
2.2. Optimization Model for Operation Rule
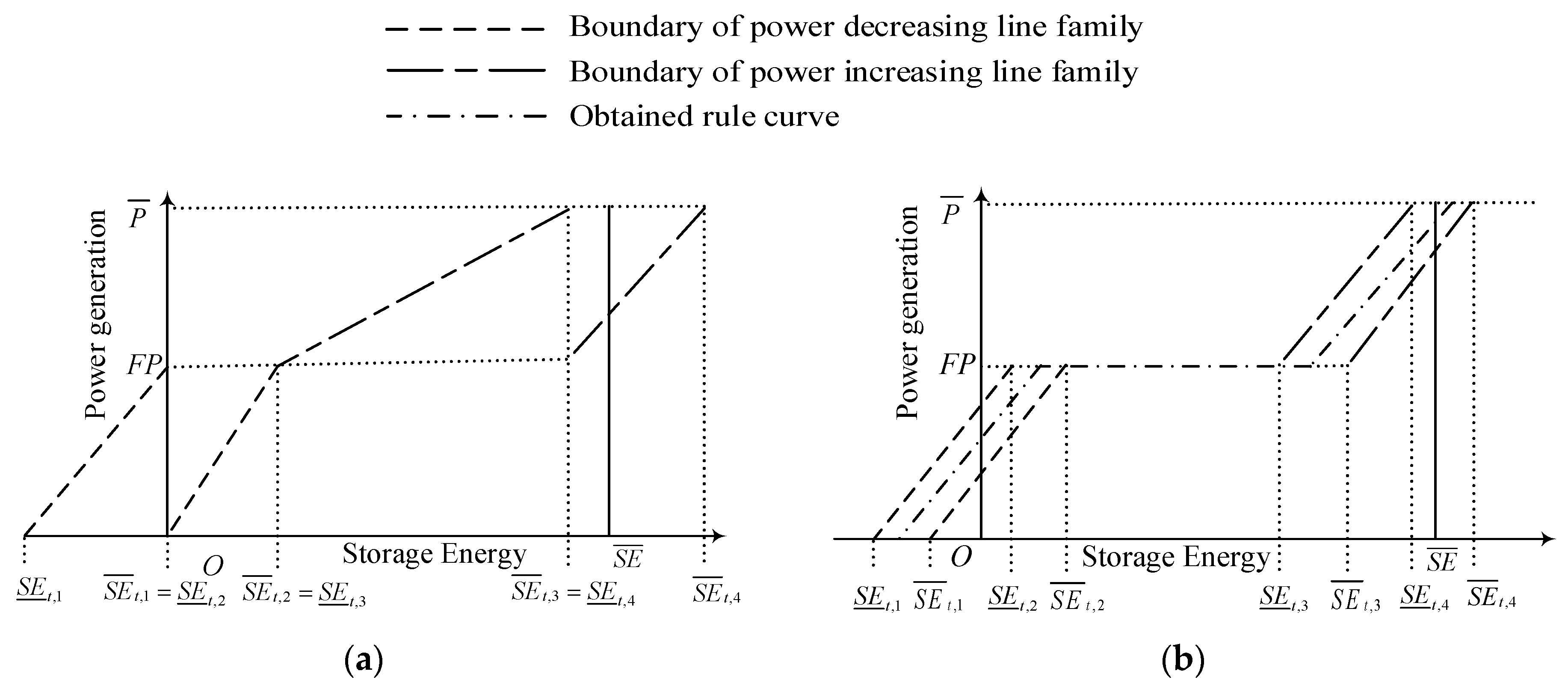
2.3. GA-Based Simulation-Optimization Method for Operation Rule
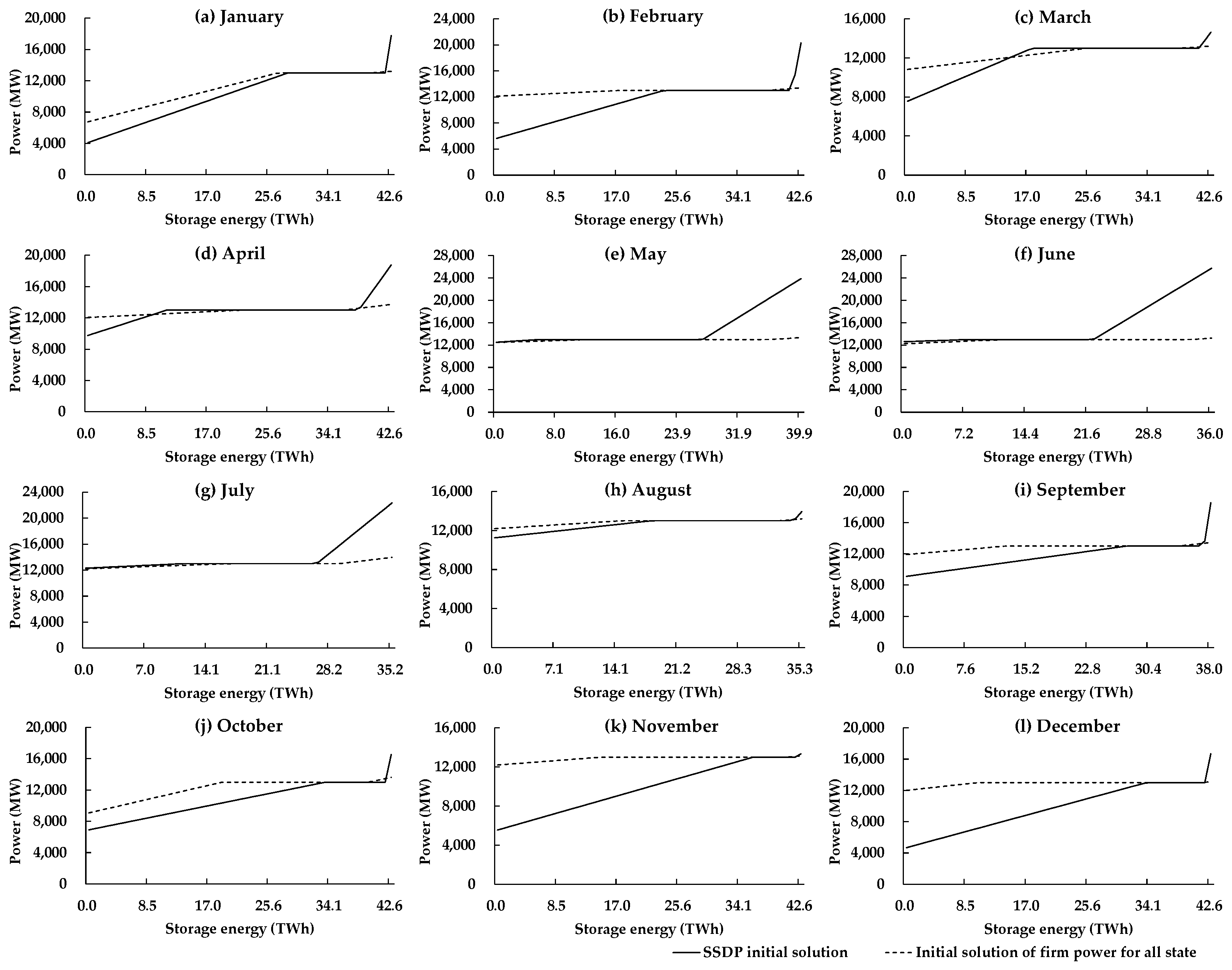
2.4. Derive Initial Operation Rule Using an Aggregated SSDP
3. Case Study
3.1. Introduction to the Engineering Background
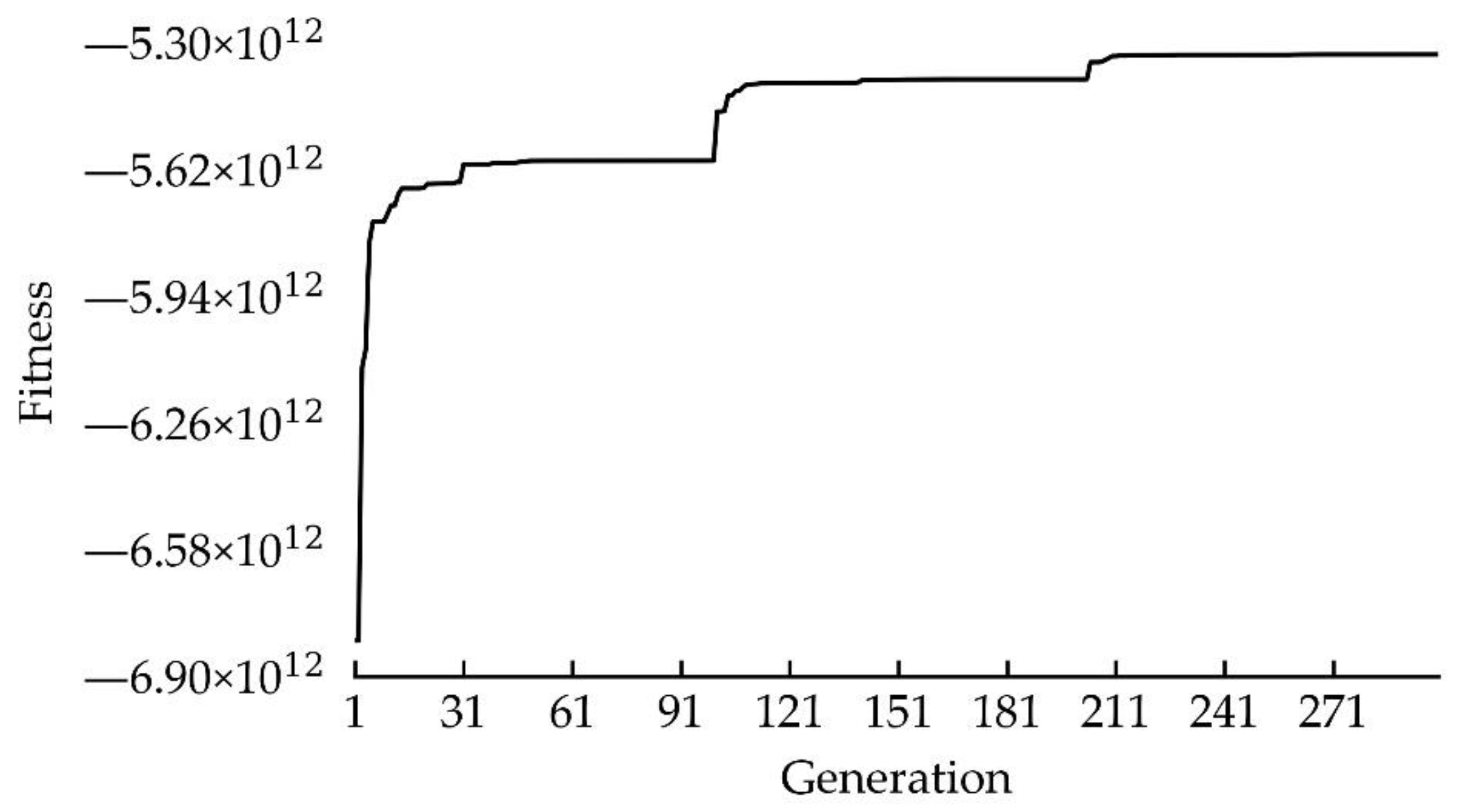
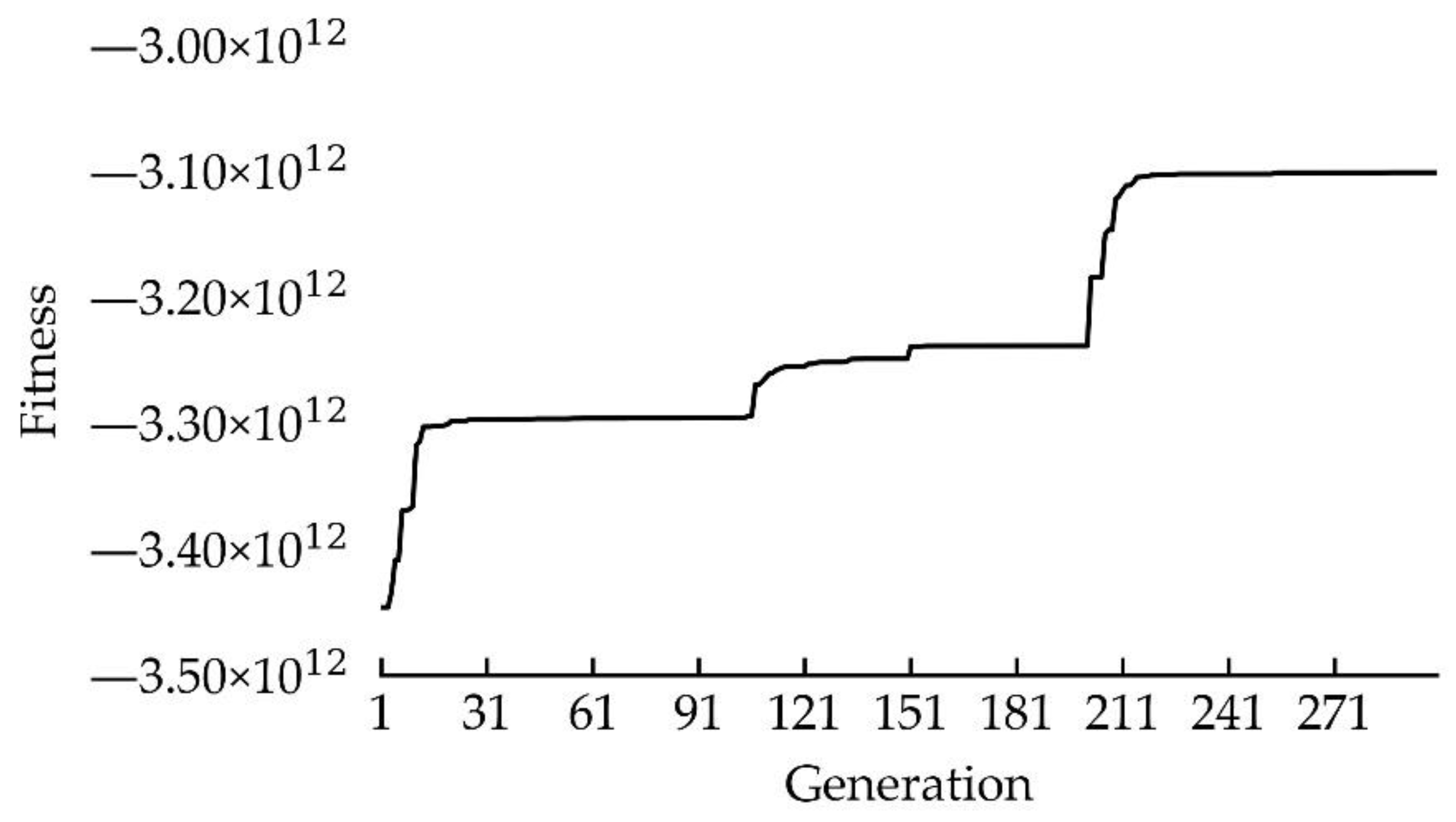
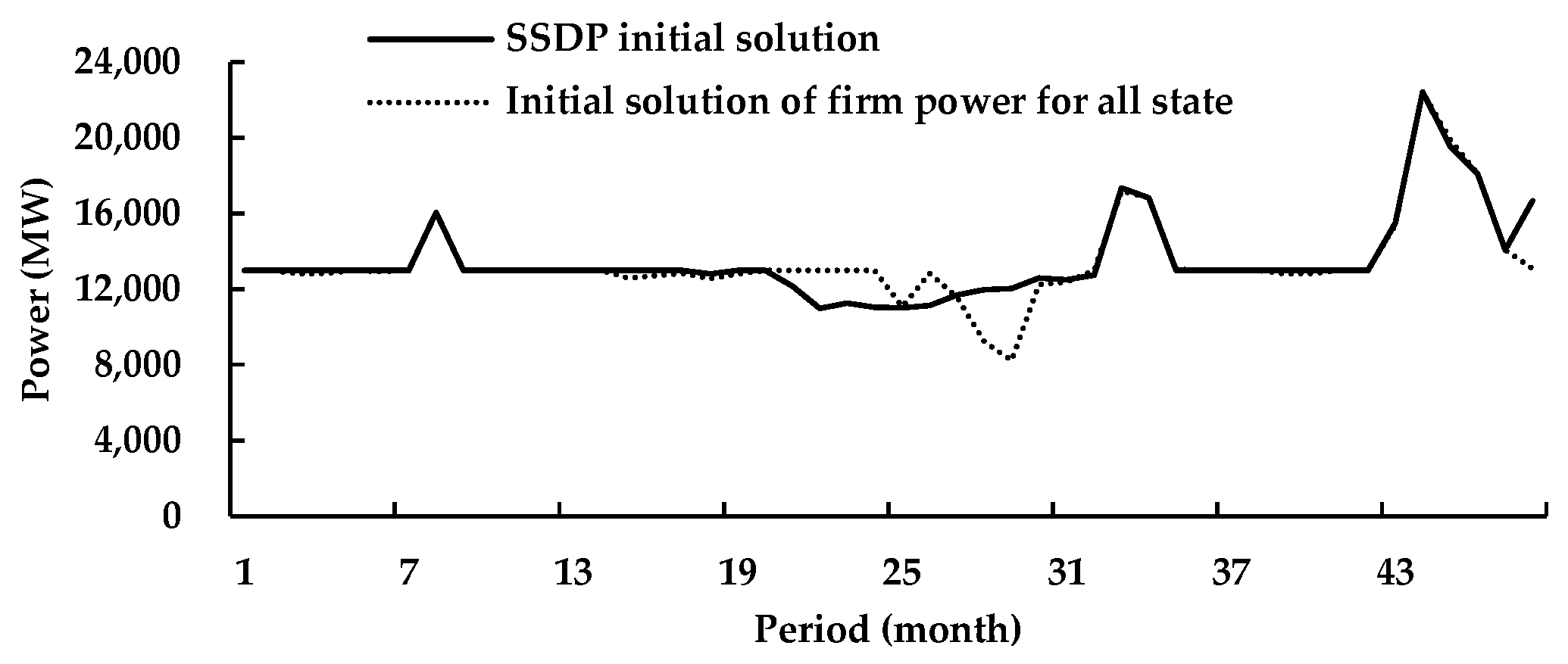
3.2. Numerical Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Initial storage energy at period t () | |
| Efficiency of power generation | |
| Initial active storage at period t ( | |
| Function to calculate power generating head under a given reservoir level | |
| Function to calculate the center of gravity of the water volume above | |
| Function to calculate the initial reservoir level | |
| Initial reservoir storage ( | |
| Ending storage at period ( | |
| Expected release-weighted hydropower head from the end of the current time step t until reservoir refill or emptying | |
| Expected turbine release volume from the end of the current period t until reservoir refill or emptying () | |
| Release captured by downstream reservoir j from upstream reservoir m () | |
| Total energy () | |
| Objective function of energy generation in simulation horizon | |
| T | Number of periods in simulation horizon |
| Energy generation ( | |
| Turbine release volume () | |
| Initial reservoir level () | |
| Initial reservoir storage () | |
| Average tailwater level () | |
| Water inflow volume () | |
| Water spillage () | |
| Reservoir release volume () | |
| Minimum water release volume () | |
| Lower bound for reservoir storage () | |
| Upper bound for reservoir storage () | |
| Power generation () | |
| Installed capacity () | |
| Number of the period hour | |
| Firm power for the hydropower system () | |
| a | Penalty coefficient for firm power |
| b | Penalty coefficient for minimum release |
| Rate of release flow () | |
| Minimum constraint for rate of release flow () | |
| Objective function at state | |
| Objective function for inflow scenario n | |
| Benefit function at period t for inflow scenario n | |
| Future value function for inflow scenario n | |
| T0 | Period number in a year |
References
- Feng, Z.K.; Niu, W.J.; Cheng, X.; Wang, J.Y.; Wang, S.; Song, Z.G. An effective three-stage hybrid optimization method for source-network-load power generation of cascade hydropower reservoirs serving multiple interconnected power grids. J. Clean. Prod. 2020, 246, 119035. [Google Scholar] [CrossRef]
- Lei, X.-H.; Tan, Q.-F.; Wang, X.; Wang, H.; Wen, X.; Wang, C.; Zhang, J.-W. Stochastic optimal operation of reservoirs based on copula functions. J. Hydrol. 2018, 557, 265–275. [Google Scholar] [CrossRef]
- Côté, P.; Arsenault, R. Efficient Implementation of Sampling Stochastic Dynamic Programming Algorithm for Multireservoir Management in the Hydropower Sector. J. Water Resour. Plan. Manag. 2019, 145. [Google Scholar] [CrossRef]
- Turgeon, A. Optimal operation of multireservoir power systems with stochastic inflows. Water Resour. Res. 1980, 16, 275–283. [Google Scholar] [CrossRef]
- Turgeon, A.C. Raymond An aggregation-disaggregation approach to long-term reservoir management. Water Resour. Res. 1998, 34, 3585–3594. [Google Scholar] [CrossRef]
- Tan, Q.-F.; Wang, X.; Wang, H.; Wang, C.; Lei, X.-H.; Xiong, Y.-S.; Zhang, W. Derivation of optimal joint operating rules for multi-purpose multi-reservoir water-supply system. J. Hydrol. 2017, 551, 253–264. [Google Scholar] [CrossRef]
- Pan, Z.; Chen, L.; Teng, X. Research on joint flood control operation rule of parallel reservoir group based on aggregation–decomposition method. J. Hydrol. 2020, 590. [Google Scholar] [CrossRef]
- Helseth, A.; Braaten, H. Efficient Parallelization of the Stochastic Dual Dynamic Programming Algorithm Applied to Hydropower Scheduling. Energies 2015, 8, 14287–14297. [Google Scholar] [CrossRef]
- Raso, L.; Chiavico, M.; Dorchies, D. Optimal and Centralized Reservoir Management for Drought and Flood Protection on the Upper Seine–Aube River System Using Stochastic Dual Dynamic Programming. J. Water Resour. Plan. Manag. 2019, 145. [Google Scholar] [CrossRef]
- Yeh, W.W.G. Reservoir management and operations models: A state-of-the-art review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multireservoir systems: State-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Powell, W.B. Approximate Dynamic Programming: Solving the Curses of Dimensionality; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 703. [Google Scholar]
- Giuliani, M.; Castelletti, A.; Pianosi, F.; Mason, E.; Reed, P.M. Curses, Tradeoffs, and Scalable Management: Advancing Evolutionary Multiobjective Direct Policy Search to Improve Water Reservoir Operations. J. Water Resour. Plan. Manag. 2016, 142, 04015050. [Google Scholar] [CrossRef]
- Lund, J.R.; Ferreira, I. Operating rule optimization for Missouri River reservoir system. J. Water Resour. Plan. Manag. Asce 1996, 122, 287–295. [Google Scholar] [CrossRef]
- Ji, C.M.; Zhou, T.; Huang, H.T. Operating Rules Derivation of Jinsha Reservoirs System with Parameter Calibrated Support Vector Regression. Water Resour. Manag. 2014, 28, 2435–2451. [Google Scholar] [CrossRef]
- Jiang, Z.; Song, P.; Liao, X. Optimization of Year-End Water Level of Multi-Year Regulating Reservoir in Cascade Hydropower System Considering the Inflow Frequency Difference. Energies 2020, 13, 5345. [Google Scholar] [CrossRef]
- Liu, P.; Guo, S.L.; Xu, X.W.; Chen, J.H. Derivation of Aggregation-Based Joint Operating Rule Curves for Cascade Hydropower Reservoirs. Water Resour. Manag. 2011, 25, 3177–3200. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.E. Athanasia Evaluation of the parameterization-simulation-optimization approach for the control of reservoir systems. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Rani, D.; Moreira, M.M. Simulation–Optimization Modeling: A Survey and Potential Application in Reservoir Systems Operation. Water Resour. Manag. 2009, 24, 1107–1138. [Google Scholar] [CrossRef]
- Oliveira, R.; Loucks, D.P. Operating rules for multireservoir systems. Water Resour. Res. 1997, 33, 839–852. [Google Scholar] [CrossRef]
- Chang, L.C.; Chang, F.J.; Wang, K.W.; Dai, S.Y. Constrained genetic algorithms for optimizing multi-use reservoir operation. J. Hydrol. 2010, 390, 66–74. [Google Scholar] [CrossRef]
- Liu, X.; Guo, S.; Liu, P.; Chen, L.; Li, X. Deriving Optimal Refill Rules for Multi-Purpose Reservoir Operation. Water Resour. Manag. 2010, 25, 431–448. [Google Scholar] [CrossRef]
- Taghian, M.; Rosbjerg, D.; Haghighi, A.; Madsen, H. Optimization of Conventional Rule Curves Coupled with Hedging Rules for Reservoir Operation. J. Water Resour. Plan. Manag. 2014, 140, 693–698. [Google Scholar] [CrossRef]
- Latorre, J.M.; Cerisola, S.; Ramos, A.; Perea, A.; Bellido, R. Coordinated Hydropower Plant Simulation for Multireservoir Systems. J. Water Resour. Plan. Manag. 2014, 140, 216–227. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Qin, H.; Ji, C.M.; Hu, D.C.; Zhou, J.Z. Effect Analysis of Operation Stage Difference on Energy Storage Operation Chart of Cascade Reservoirs. Water Resour. Manag. 2019, 33, 1349–1365. [Google Scholar] [CrossRef]
- Lund, J.R. Derived power production and energy drawdown rules for reservoir. J. Water Resour. Plan. Manag. Asce 2000, 126, 108–111. [Google Scholar] [CrossRef]
- Wu, X.Y.; Cheng, C.T.; Zeng, Y.; Lund, J.R. Centralized versus Distributed Cooperative Operating Rules for Multiple Cascaded Hydropower Reservoirs. J. Water Resour. Plan. Manag. 2016, 142, 05016008. [Google Scholar] [CrossRef]
- Cheng, C.-T.; Wang, W.-C.; Xu, D.-M.; Chau, K.W. Optimizing Hydropower Reservoir Operation Using Hybrid Genetic Algorithm and Chaos. Water Resour. Manag. 2007, 22, 895–909. [Google Scholar] [CrossRef]
- Chang, J.X.; Bai, T.; Huang, Q.; Yang, D.W. Optimization of Water Resources Utilization by PSO-GA. Water Resour. Manag. 2013, 27, 3525–3540. [Google Scholar] [CrossRef]
- Tayebiyan, A.; Ali, T.A.M.; Ghazali, A.H.; Malek, M.A. Optimization of Exclusive Release Policies for Hydropower Reservoir Operation by Using Genetic Algorithm. Water Resour. Manag. 2016, 30, 1203–1216. [Google Scholar] [CrossRef]
- Yun, R.A.; Singh, V.P.; Dong, Z.C. Long-Term Stochastic Reservoir Operation Using a Noisy Genetic Algorithm. Water Resour. Manag. 2010, 24, 3159–3172. [Google Scholar] [CrossRef]
- Akbari-Alashti, H.; Bozorg-Haddad, O.; Marino, M.A. Application of Fixed Length Gene Genetic Programming (FLGGP) in Hydropower Reservoir Operation. Water Resour. Manag. 2015, 29, 3357–3370. [Google Scholar] [CrossRef]
- Chang, F.J.; Chen, L.; Chang, L.C. Optimizing the reservoir operating rule curves by genetic algorithms. Hydrol. Process. 2005, 19, 2277–2289. [Google Scholar] [CrossRef]
- Askew, A.J. Chance-constrained dynamic programing and the optimization of water resource systems. Water Resour. Res. 1974, 10, 1099–1106. [Google Scholar] [CrossRef]
- Rossman, L.A. Reliability-constrained dynamic programing and randomized release rules in reservoir management. Water Resour. Res. 1977, 13, 247–255. [Google Scholar] [CrossRef]
- Jian-Xia, C.; Qiang, H.; Yi-min, W. Genetic Algorithms for Optimal Reservoir Dispatching. Water Resour. Manag. 2005, 19, 321–331. [Google Scholar] [CrossRef]
- Cheng, C.-T.; Ou, C.P.; Chau, K.W. Combining a fuzzy optimal model with a genetic algorithm to solve multi-objective rainfall–runoff model calibration. J. Hydrol. 2002, 268, 72–86. [Google Scholar] [CrossRef]
- Wu, X.Y.; Cheng, C.T.; Lund, J.R.; Niu, W.J.; Miao, S.M. Stochastic dynamic programming for hydropower reservoir operations with multiple local optima. J. Hydrol. 2018, 564, 712–722. [Google Scholar] [CrossRef]
- Cheng, C.; Shen, J.; Wu, X.; Chau, K. Operation challenges for fast-growing China’s hydropower systems and respondence to energy saving and emission reduction. Renew. Sustain. Energy Rev. 2012, 16, 2386–2393. [Google Scholar] [CrossRef]

| Hongshui River | Lancang River | Wu River | ||||||
|---|---|---|---|---|---|---|---|---|
| Reservoir | Installed Capacity (MW) | Beneficial Storage (108 m3) | Reservoir | Installed Capacity (MW) | Beneficial Storage (108 m3) | Reservoir | Installed Capacity (MW) | Beneficial Storage (108 m3) |
| Tianshengqiao-1 | 1200 | 57.95 | Xiaowan | 4200 | 98.77 | Hongjiadu | 600 | 33.60 |
| Tianshengqiao-2 | 1320 | 0.08 | Manwan | 1670 | 2.57 | Dongfeng | 695 | 4.90 |
| Pingban | 405 | 0.27 | Dachaoshan | 1350 | 3.70 | Suofengying | 600 | 0.67 |
| Longtan | 4900 | 111.49 | Nuozhadu | 5850 | 113.35 | Wujiangdu | 1250 | 13.60 |
| Yantan | 1210 | 10.50 | Jinghong | 1750 | 3.09 | Goupitan | 3000 | 29.02 |
| Silin | 1050 | 3.18 | ||||||
| Total | 9035 | Total | 14,820 | Total | 7195 | |||
| Solution | Energy Generation (TWh) | Total Firm Power Shortage (MW) | Maximum Firm Power Shortage (MW) | Objective Function |
|---|---|---|---|---|
| All firm power rules | 7339.4 | 18,652 | 7993 | −1.01 × 1013 |
| SSDP rule | 7343.0 | 27,318 | 2449 | −3.59 × 1012 |
| Rule 1 | 7344.5 | 41,293 | 4761 | −5.33 × 1012 |
| Rule 2 | 7344.5 | 26,442 | 2016 | −3.10 × 1012 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Guo, R.; Cheng, X.; Cheng, C. Combined Aggregated Sampling Stochastic Dynamic Programming and Simulation-Optimization to Derive Operation Rules for Large-Scale Hydropower System. Energies 2021, 14, 625. https://doi.org/10.3390/en14030625
Wu X, Guo R, Cheng X, Cheng C. Combined Aggregated Sampling Stochastic Dynamic Programming and Simulation-Optimization to Derive Operation Rules for Large-Scale Hydropower System. Energies. 2021; 14(3):625. https://doi.org/10.3390/en14030625
Chicago/Turabian StyleWu, Xinyu, Rui Guo, Xilong Cheng, and Chuntian Cheng. 2021. "Combined Aggregated Sampling Stochastic Dynamic Programming and Simulation-Optimization to Derive Operation Rules for Large-Scale Hydropower System" Energies 14, no. 3: 625. https://doi.org/10.3390/en14030625
APA StyleWu, X., Guo, R., Cheng, X., & Cheng, C. (2021). Combined Aggregated Sampling Stochastic Dynamic Programming and Simulation-Optimization to Derive Operation Rules for Large-Scale Hydropower System. Energies, 14(3), 625. https://doi.org/10.3390/en14030625





