Application of Computer Graphics Flow Visualization Methods in Vortex Rope Investigations
Abstract
1. Introduction
2. Vortex Rope Visualizations
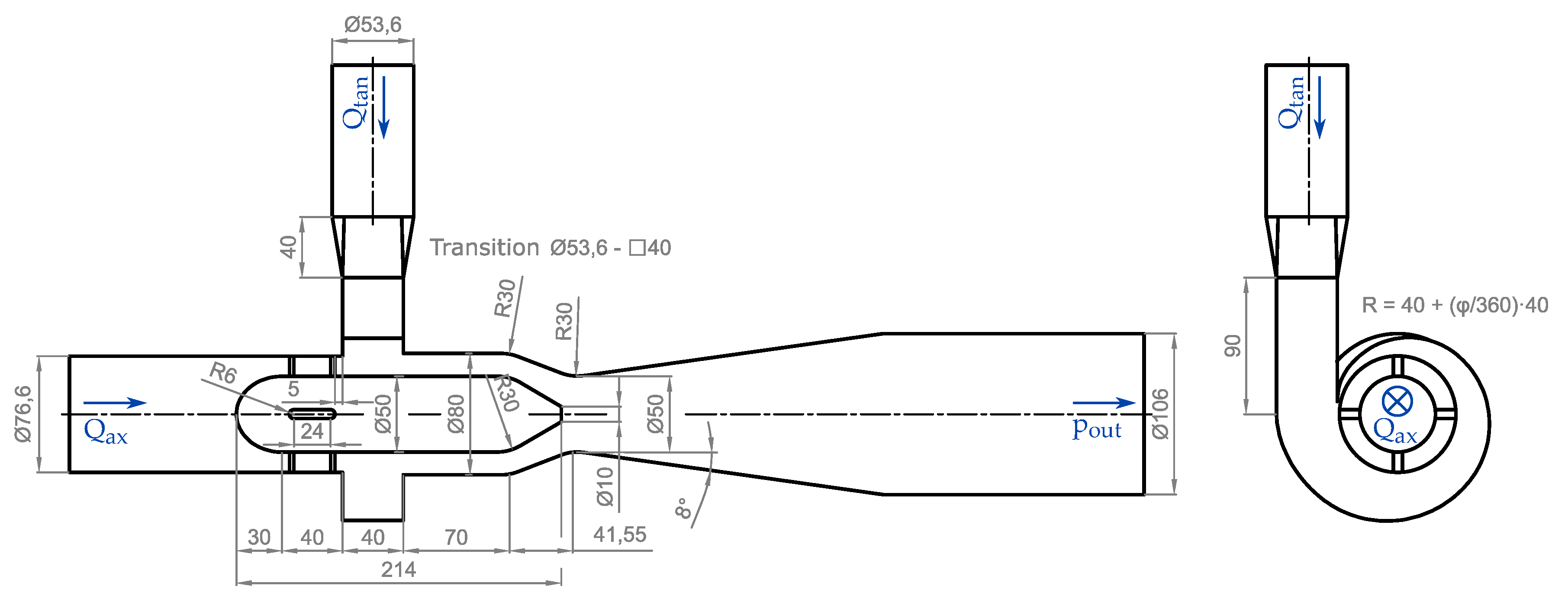
2.1. Test Case
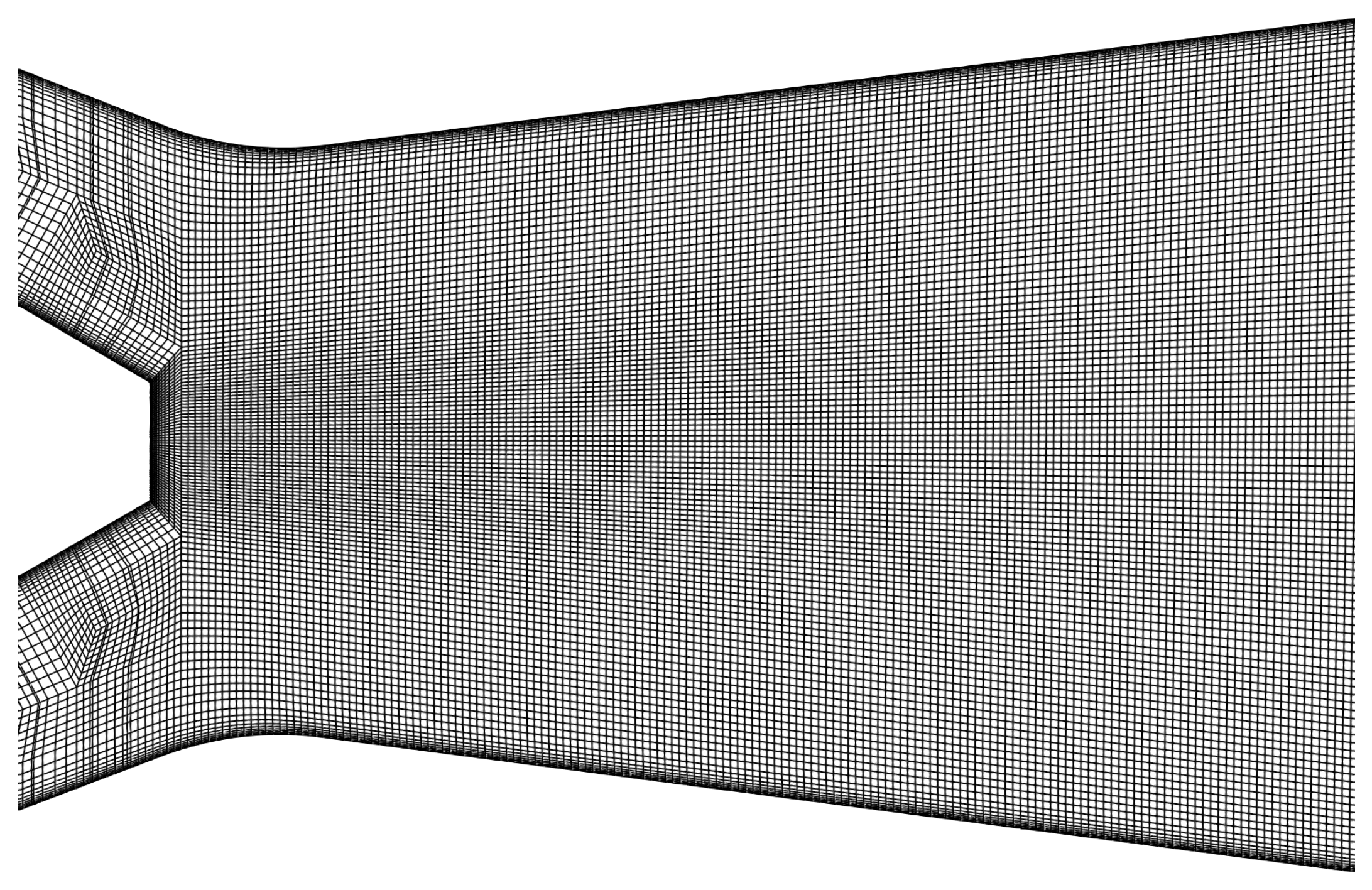
2.2. CFD Simulation
2.3. Software and Methodology
2.4. Vortex Identification Methods
2.5. Hybrid Methods for Investigations of the Vortex Rope
2.5.1. The -Criterion Combined with the Residual Vorticity
2.5.2. Combination of the Static Pressure and the Residual Vorticity
2.5.3. Combination of the Axial Vorticity and Vortex Identification Methods
2.6. Finite-Time Lyapunov Exponent
2.7. Visualization of the Features of the Vortex Rope
- the vortex rope itself,
- backflow zone,
- swirling flow at the outer wall, and
- unsteadiness and regularity of the flow.
- Extract the cells with the pressure value below certain threshold. The threshold should be selected so that the vortex rope is present, while any other structures are excluded. This limits this approach to states with a distinct vortex rope only. In other words, we wish to extract the vortex rope from the whole domain.
- Perform a plane slice passing through the top part of the vortex rope. The plane normal and the vortex rope axis should optimally be collinear.
- Compute a suitable average (e.g., pressure-weighted) of the cell centers. This will be the first point of the resultant center line.
- Compute the center of the second plane slice. It lies in the direction of the first plane normal at a given distance from the first point of the center line. The second plane normal is the same as the first plane normal. Perform the slice.
- Compute the average of the cell centers. This will be the second point of the resultant center line.
- From now on, the algorithm runs automatically. The normal of the next plane slice is given by the direction vector joining the last two points of the center line. Its center lies at a given distance from the last point in the direction of the plane normal. The next point of the center line is again defined as an average of the cell centers.
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CT | Computed Tomography |
| DFT | Discrete Fourier Transform |
| FLINDT | FLow INvestigation in a Francis Draft Tube |
| FTLE | Finite-Time Lyapunov Exponent |
| LES | Large Eddy Simulation |
| MRI | Magnetic Resonance Imaging |
| PISO | Pressure-Implicit with Splitting of Operators |
| PRESTO! | PREssure STaggering Option |
| RANS | Reynolds-Averaged Navier-Stokes equations |
| SBES | Stress-Blended Eddy Simulation |
| SST | Shear Stress Transport |
| TIFF | Tagged Image File Format |
| URANS | Unsteady Reynolds-Averaged Navier-Stokes equations |
| VTK | The Visualization ToolKit |
| WALE | Wall-Adapting Local Eddy-viscosity model |
| X3D | eXtensible 3D |
Appendix A. Volume Rendering of Data from Paraview in Blender



References
- Post, F.H.; van Walsum, T. Fluid Flow Visualization. In Focus on Scientific Visualization; Hagen, H., Müller, H., Nielson, G.M., Eds.; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Fuchs, R. The Visible Vortex—Interactive Analysis and Extraction of Vortices in Large Time-Dependent Flow Data Sets. Ph.D. Thesis, TU Wien, Vienna, Austria, 2008. [Google Scholar]
- Sadlo, F.; Peikert, R.; Sick, M. Visualization Tools for Vorticity Transport Analysis in Incompressible Flow. IEEE Trans. Vis. Comput. Graph. 2006, 12, 949–956. [Google Scholar] [CrossRef]
- Kaufman, A.; Hohne, K.; Kruger, W.; Rosenblum, L.; Schroder, P. Research issues in volume visualization. IEEE Comput. Graph. Appl. 1994, 14, 63–67. [Google Scholar] [CrossRef]
- Rosenblum, L.J. Research issues in scientific visualization. IEEE Comput. Graph. Appl. 1994, 14, 61–63. [Google Scholar] [CrossRef]
- Leibovich, S. The Structure of Vortex Breakdown. Annu. Rev. Fluid Mech. 2007, 10, 221–246. [Google Scholar] [CrossRef]
- Lugt, H. Vortex Flow in Nature and Technology; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1983. [Google Scholar]
- Peckham, D.H.; Atkinson, S.A. Preliminary Results of Low Speed Wind Tunnel Test on a Ghotic Wing of Aspect Ratio 1.0; Aeronautical Research Council Current Papers; The Stationery Office: London, UK, 1960; Available online: http://naca.central.cranfield.ac.uk/reports/arc/cp/0508.pdf (accessed on 25 January 2021).
- Escudier, M. Vortex breakdown: Observations and explanations. Prog. Aerosp. Sci. 1988, 25, 189–229. [Google Scholar] [CrossRef]
- Althaus, W.; Brücker, C.; Weimar, M. Breakdown of Slender Vortices. In Fluid Vortices; Green, S.H., Ed.; Kluwer Academic: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Lucca-Negro, O.; O’Doherty, T. Vortex breakdown: A review. Prog. Energy Combust. Sci. 2001, 27, 431–481. [Google Scholar] [CrossRef]
- Dörfler, P.K.; Sick, M.; Coutu, A. Flow-Induced Pulsation and Vibration in Hydroelectric Machinery: Engineer’s Guidebook for Planning, Design and Troubleshooting; Springer: London, UK, 2013. [Google Scholar]
- Nishi, M.; Wang, X.M.; Yoshida, K.; Takahashi, T.; Tsukamoto, T. An Experimental Study on Fins, Their Role in Control of the Draft Tube Surging; Hydraulic Machinery and Cavitation; Springer: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Dörfler, P.K. Design criteria for air admission systems in Francis turbines. In Proceedings of the 13th Symposium of IAHR Section for Hydraulic Machinery, Equipment and Cavitation, Montreal, QC, Canada, 2–5 September 1986. [Google Scholar]
- Gogstad, P.J.; Dahlhaug, O.G. Evaluation of runner cone extension to dampen pressure pulsations in a Francis model turbine. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 082019. [Google Scholar] [CrossRef]
- Susan-Resiga, R.; Vu, T.C.; Muntean, S.; Ciocan, G.D.; Nennemann, B. Jet Control of the Draft Tube Vortex Rope in Francis Turbines at Partial Discharge. In Proceedings of the 23rd IAHR Symposium on Hydraulic Machinery and Systems, Yokohama, Japan, 17–21 October 2006. [Google Scholar]
- Ruprecht, A. Numerical prediction of vortex instabilities in turbomachinery. In Advances in High Performance Computing and Computational Sciences; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Ciocan, G.D.; Iliescu, M.S.; Vu, T.C.; Nennemann, B.; Avellan, F. Experimental Study and Numerical Investigation of the FLINDT Draft Tube Rotating Vortex. J. Fluids Eng. 2007, 129, 146–158. [Google Scholar] [CrossRef]
- Minakov, A.; Sentyabov, A.; Platonov, D. Numerical investigation of flow structure and pressure pulsation in the Francis-99 turbine during startup. J. Phys. Conf. Ser. 2017, 782, 012004. [Google Scholar] [CrossRef]
- Pasche, S.; Avellan, F.; Gallaire, F. Part Load Vortex Rope as a Global Unstable Mode. J. Fluids Eng. 2017, 139, 051102. [Google Scholar] [CrossRef]
- Hunt, J.C.R.; Wray, A.A.; Moin, P. Eddies, Streams, and Convergence Zones in Turbulent Flows. In Proceedings of the Summer Program 1988. pp. 193–208. Available online: https://ntrs.nasa.gov/citations/19890015184 (accessed on 25 January 2021).
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Zhou, J.; Adrian, R.J.; Balachandar, S.; Kendall, T.M. Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 1999, 387, 353–396. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, K.; Xian, H.; Du, X. A review of methods for vortex identification in hydroturbines. Renew. Sustain. Energy Rev. 2018, 81, 1269–1285. [Google Scholar] [CrossRef]
- Rajan, G.K.; Cimbala, M. Computational and Theoretical Analyses of the Precessing Vortex Rope in a Simplified Draft Tube of a Scaled Model of a Francis Turbine. J. Fluid Eng. 2017, 139, 021102. [Google Scholar] [CrossRef]
- Avellan, F. Flow Investigation in a Francis Draft Tube: The Flindt Project. In Proceedings of the 20th IAHR Symposium on Hydraulic Machinery and Systems, Charlotte, NC, USA, 6–9 August 2000. [Google Scholar]
- Haller, G. An objective definition of a vortex. J. Fluid Mech. 2005, 525, 1–26. [Google Scholar] [CrossRef]
- Kolář, V. Vortex identification: New requirements and limitations. Int. J. Heat Fluid Flow 2007, 28, 638–652. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian Coherent Structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Menter, F. Stress-Blended Eddy Simulation (SBES)—A New Paradigm in Hybrid RANS-LES Modeling. In Progress in Hybrid RANS-LES Modelling; Springer: Cham, Switzerland, 2016; pp. 27–37. [Google Scholar]
- Sheen, H.J.; Chen, W.J.; Jeng, S.Y.; Huang, T.L. Correlation of swirl number for a radial-type swirl generator. Exp. Therm. Fluid Sci. 1996, 12, 444–451. [Google Scholar] [CrossRef]
- Štefan, D.; Rudolf, P.; Hudec, M.; Uruba, V.; Procházka, P.; Urban, O. Experimental investigation of vortex ring formation as a consequence of spiral vortex re-connection. IOP Conf. Ser. Earth Environ. Sci. 2019, 405, 012033. [Google Scholar] [CrossRef]
- Urban, O.; Rudolf, P. POD analysis of a vortex rope with transient boundary conditions. IOP Conf. Ser. Earth Environ. Sci. 2019, 405, 012034. [Google Scholar] [CrossRef]
- Ayachit, U. The ParaView Guide; Kitware: New York, NY, USA, 2017. [Google Scholar]
- Kurosaka, M.; Cain, C.B.; Srigrarom, S.; Wimer, J.D.; Dabiri, D.; Johnson, W.F.; Hatcher, J.C.; Thompson, B.R.; Kikuchi, M.; Hirano, K.; et al. Azimuthal vorticity gradient in the formative stages of vortex breakdown. J. Fluid Mech. 2006, 569. [Google Scholar] [CrossRef]
- Haller, G. Defining coherent vortices objectively from the vorticity. J. Fluid Mech. 2016, 795, 136–173. [Google Scholar] [CrossRef]
- Green, M.A.; Rowley, C.W.; Haller, G. Detection of Lagrangian coherent structures in three-dimensional turbulence. J. Fluid Mech. 2007, 572, 111–120. [Google Scholar] [CrossRef]
- Lipinski, D.; Cardwell, B.; Mohseni, K. A Lagrangian analysis of a two-dimensional airfoil with vortex shedding. J. Phys. A Math. Theor. 2008, 41, 344011. [Google Scholar] [CrossRef]
- Peng, J.; Dabiri, J.O. The ’upstream wake’ of swimming and flying animals and its correlation with propulsive efficiency. J. Exp. Biol. 2008, 211, 2669–2677. [Google Scholar] [CrossRef][Green Version]
- Wilson, M.M.; Peng, J.; Dabiri, J.O.; Eldredge, J.D. Lagrangian coherent structures in low Reynolds number swimming. J. Phys. Condens. Matter 2009, 21, 204105. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Olascoaga, M.J.; Goni, G.J. Oceanic mesoscale eddies as revealed by Lagrangian coherent structures. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Shadden, S.C.; Lekien, F.; Mardsen, J.E. Definition and properties of Lagrangian coherent structures from finite-time Lyapunov exponents in two-dimensional aperiodic flows. Phys. D Nonlinear Phenom. 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian coherent structures from approximate velocity data. Phys. Fluids 2002, 14, 1851–1861. [Google Scholar] [CrossRef]
- Brunton, S.; Rowley, C.W. Fast computation of finite-time Lyapunov exponent fields for unsteady flows. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 017503. [Google Scholar] [CrossRef]
- Levi, Y.; Degani, D.; Seginer, A. Graphical visualization of vortical flows by means of helicity. AIAA J. 1990, 28, 1347–1352. [Google Scholar] [CrossRef]
- Sujudi, D.; Haimes, R. Identification of swirling flow in 3-D vector fields. In Proceedings of the 12th Computational Fluid Dynamics Conference, San Diego, CA, USA, 19–22 June 1995. [Google Scholar]
- ParaView Plugins. Available online: https://vcg.iwr.uni-heidelberg.de/plugins/ (accessed on 20 December 2020).
- Skripkin, S.G.; Tsoy, M.A.; Kuibin, P.A.; Shtork, S.I. Study of Pressure Shock Caused by a Vortex Ring Separated From a Vortex Rope in a Draft Tube Model. J. Fluids Eng. 2017, 139, 081103. [Google Scholar] [CrossRef]
- Kida, S.; Miura, H. Identification and analysis of vortical structures. Eur. J. Mech. B/Fluids 1998, 17, 471–488. [Google Scholar] [CrossRef]
- Using Image Sequence of Medical Scans as Volume Data in Cycles. Available online: https://blender.stackexchange.com/questions/62110/using-image-sequence-of-medical-scans-as-volume-data-in-cycles/ (accessed on 9 January 2021).






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urban, O.; Kurková, M.; Rudolf, P. Application of Computer Graphics Flow Visualization Methods in Vortex Rope Investigations. Energies 2021, 14, 623. https://doi.org/10.3390/en14030623
Urban O, Kurková M, Rudolf P. Application of Computer Graphics Flow Visualization Methods in Vortex Rope Investigations. Energies. 2021; 14(3):623. https://doi.org/10.3390/en14030623
Chicago/Turabian StyleUrban, Ondřej, Michaela Kurková, and Pavel Rudolf. 2021. "Application of Computer Graphics Flow Visualization Methods in Vortex Rope Investigations" Energies 14, no. 3: 623. https://doi.org/10.3390/en14030623
APA StyleUrban, O., Kurková, M., & Rudolf, P. (2021). Application of Computer Graphics Flow Visualization Methods in Vortex Rope Investigations. Energies, 14(3), 623. https://doi.org/10.3390/en14030623




