Techno-Economic Assessment of a Standalone Hybrid System Using Various Solar Tracking Systems for Kalpeni Island, India
Abstract
1. Introduction
2. Literature Review
2.1. Survey of the Hybrid Renewable Energy System
2.2. Survey of Various PV Tracking Systems
3. Methodology
3.1. Site Description
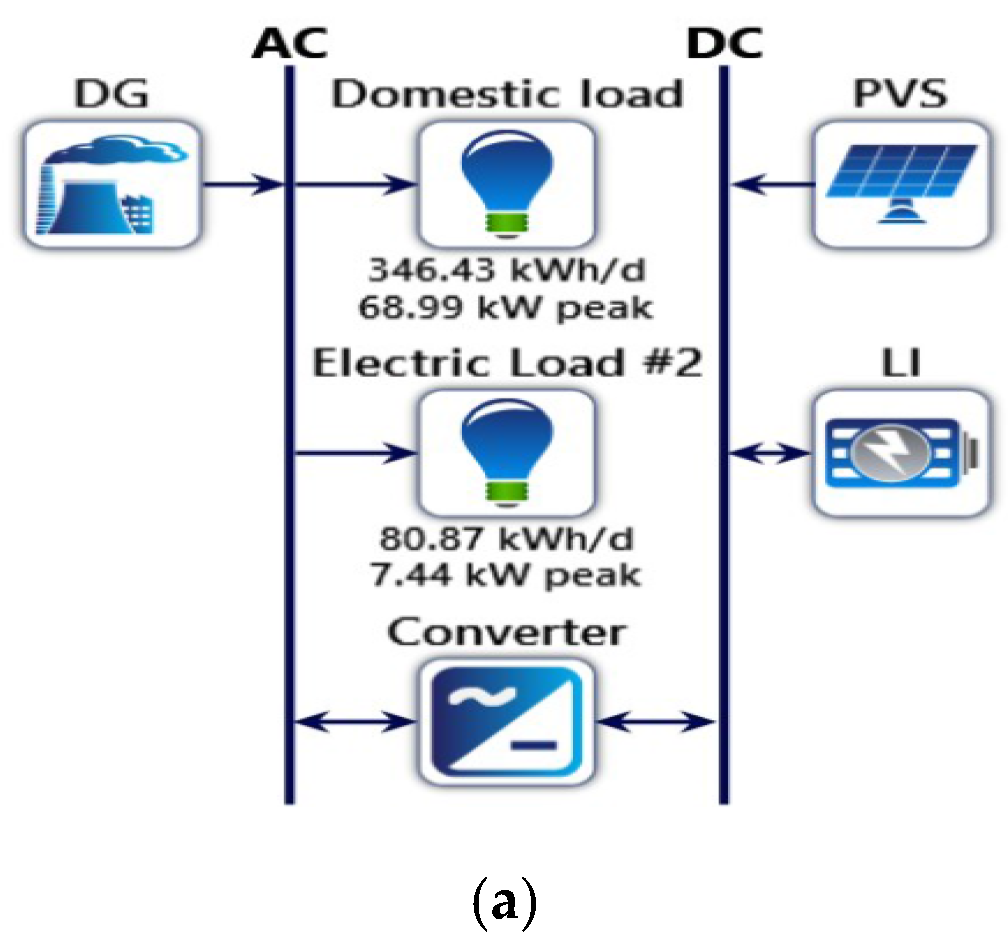
3.2. Load Profile
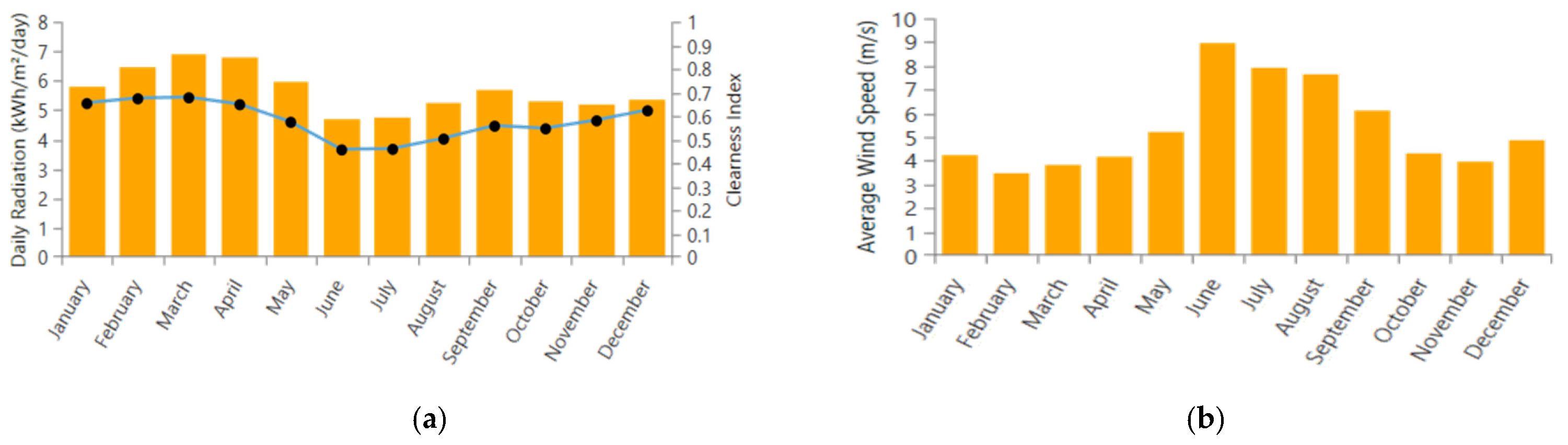
3.3. Solar Radiation and Speed of Wind
3.4. Hybrid System Block Diagram for Different Configurations
3.5. Mathematical Model of Each Component
3.5.1. Modelling of Solar PVS
3.5.2. Modelling of Wind Turbine System
3.5.3. Modelling of Battery
3.5.4. Modelling of Converter
3.5.5. Modelling of Generator
3.6. Economic and Reliability Features
3.7. Electrical Features
4. Optimization Results and Discussion
4.1. Analysis of Various Tracking Systems Used in Different Hybrid Configurations Based on Various Aspects
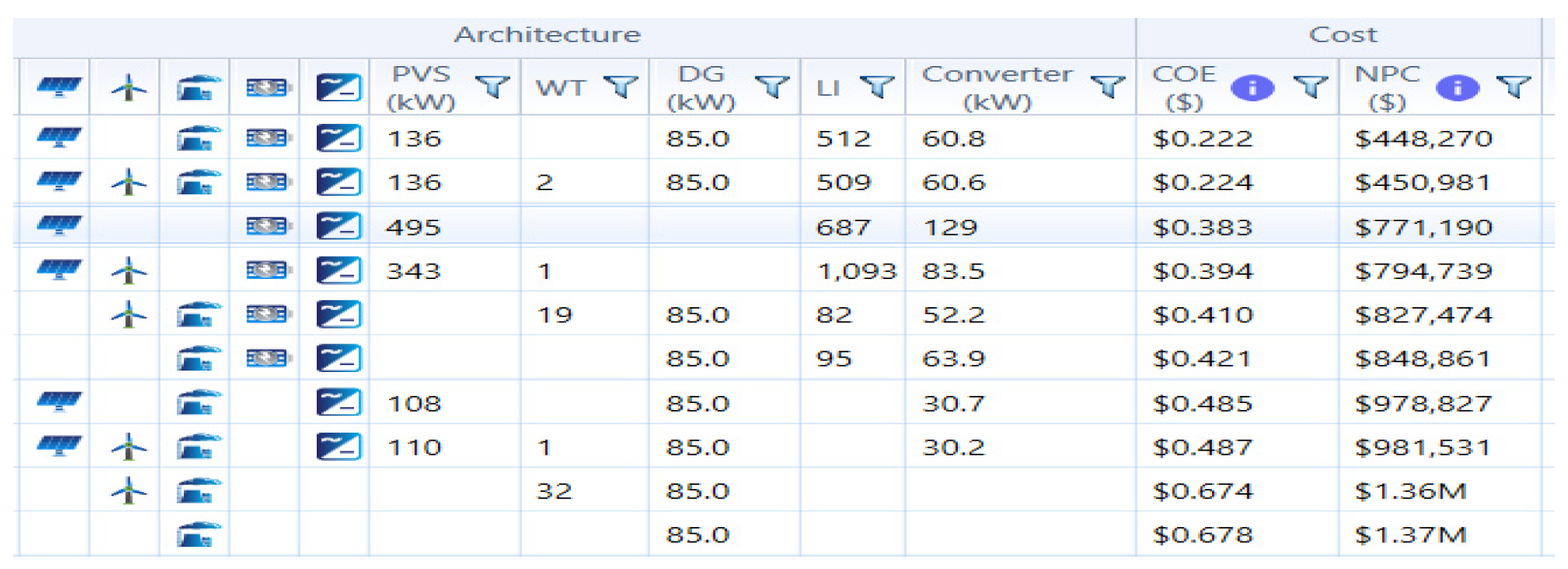
4.2. Analysis of Best System Based on Solar Tracking Technique–Optimization Results
4.3. Benefits of Solar DG Source with TSVA on Kalpeni Island
4.4. Reliability Assessment for Solar DG Source Configuration with TSVA
4.5. Cost Assessment for Solar DG Source Configuration with TSVA
4.6. Energy Balance of Solar DG with TSVA
4.7. Multi-Year Analysis for Solar DG with TSVA
Effect of Load Growth
4.8. Sensitivity Analysis for Solar DG with TSVA
4.8.1. Effect of Rising Diesel Price
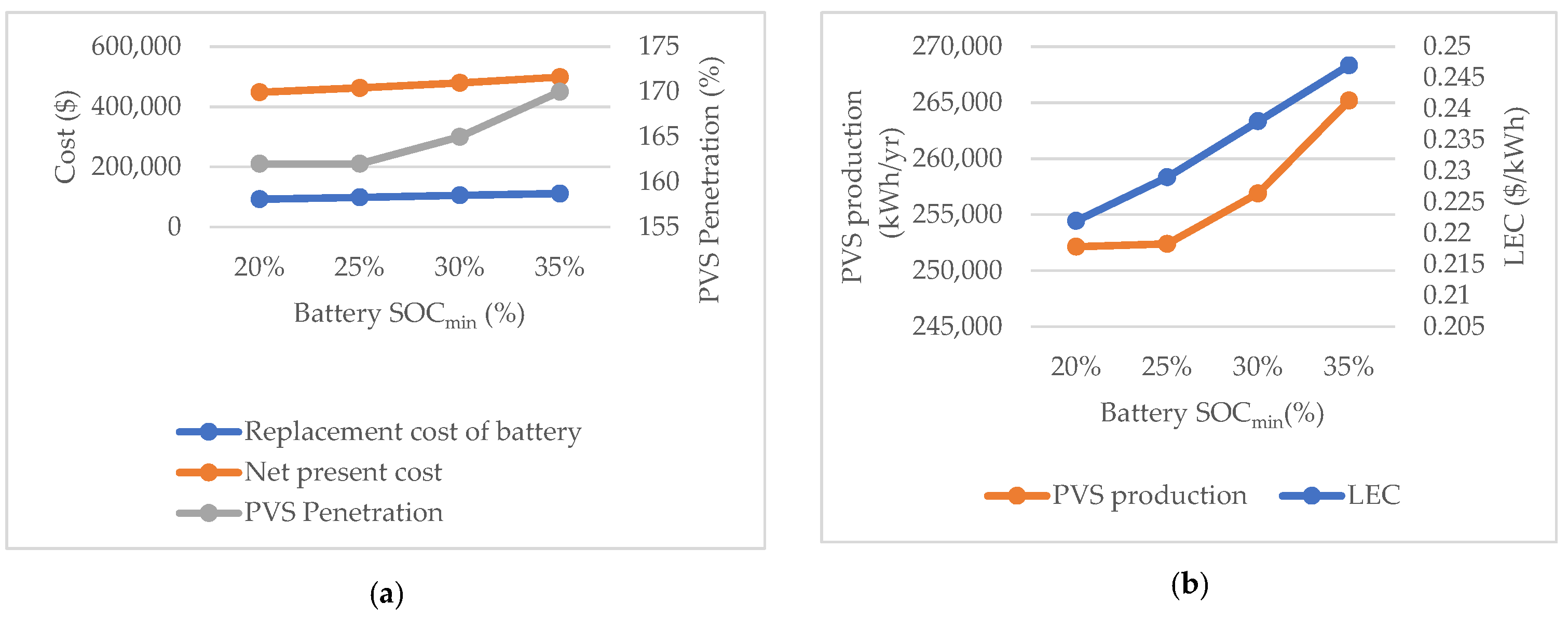
4.8.2. Effect of Rising Battery Minimum SOC
4.8.3. Effect of Rising PVS Derating
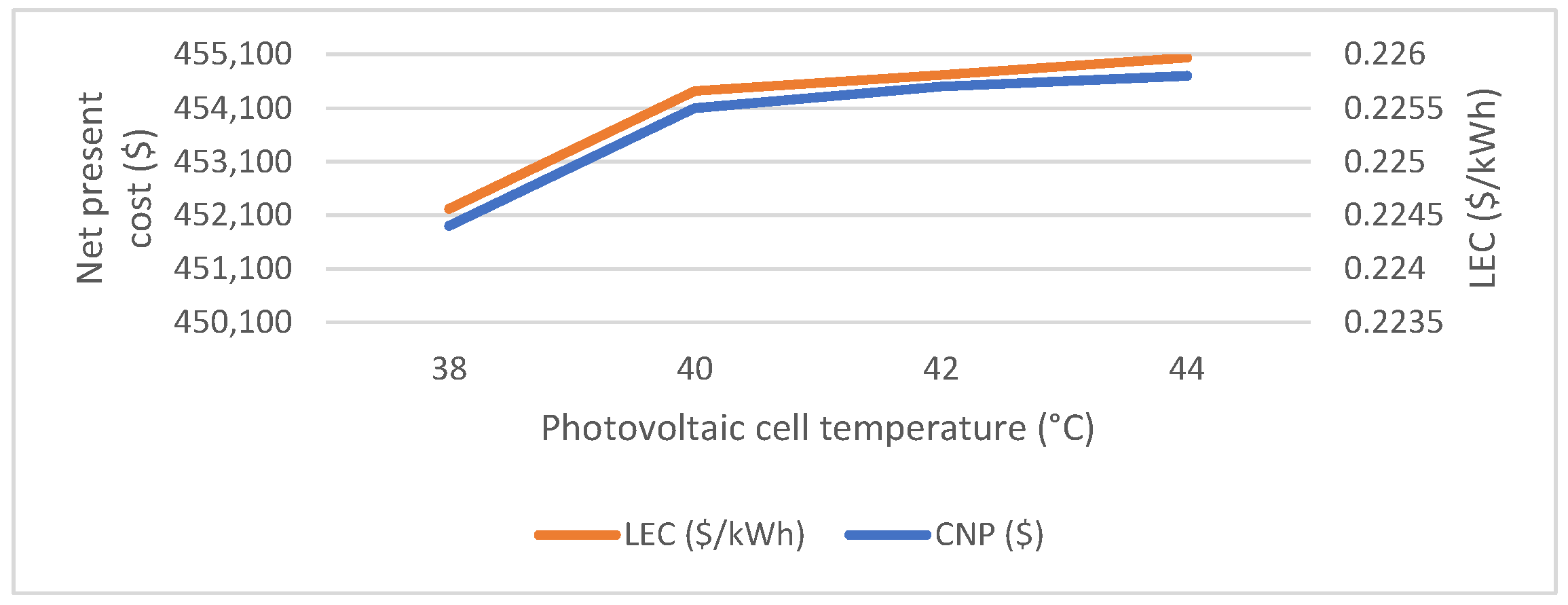
4.8.4. Effect of Rising Photovoltaic Cell Temperature
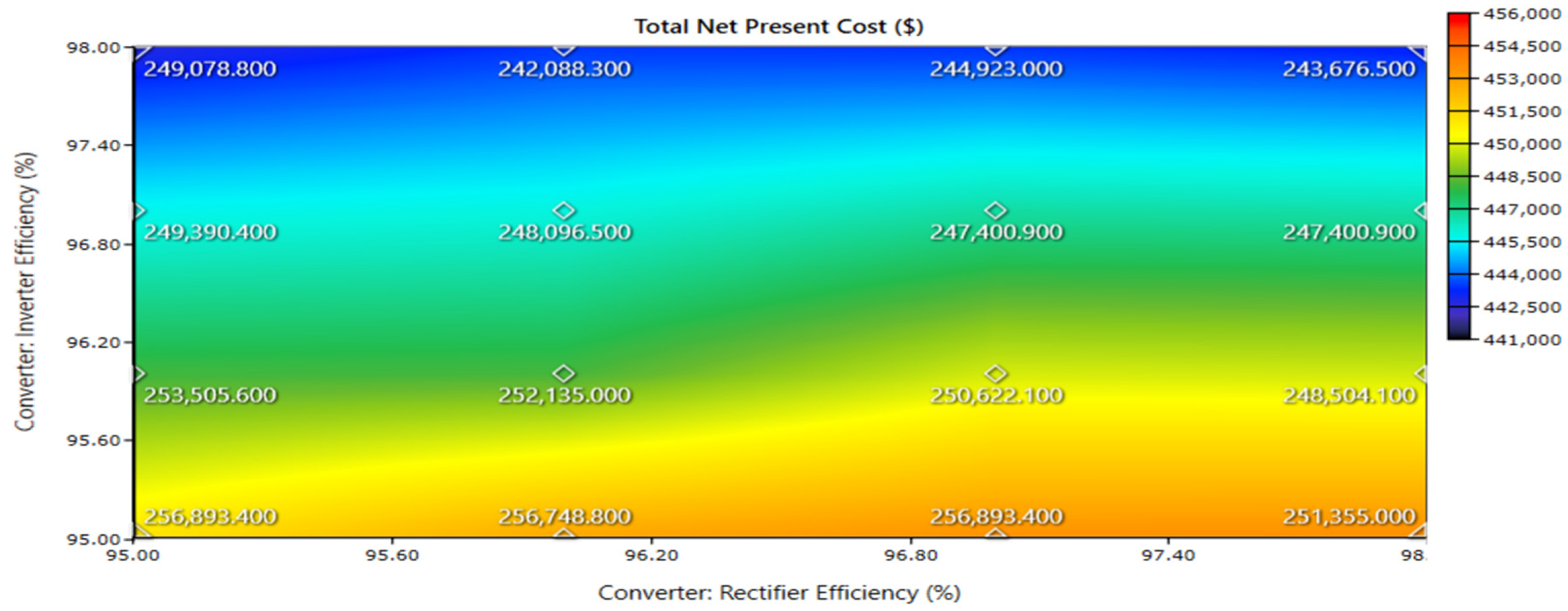
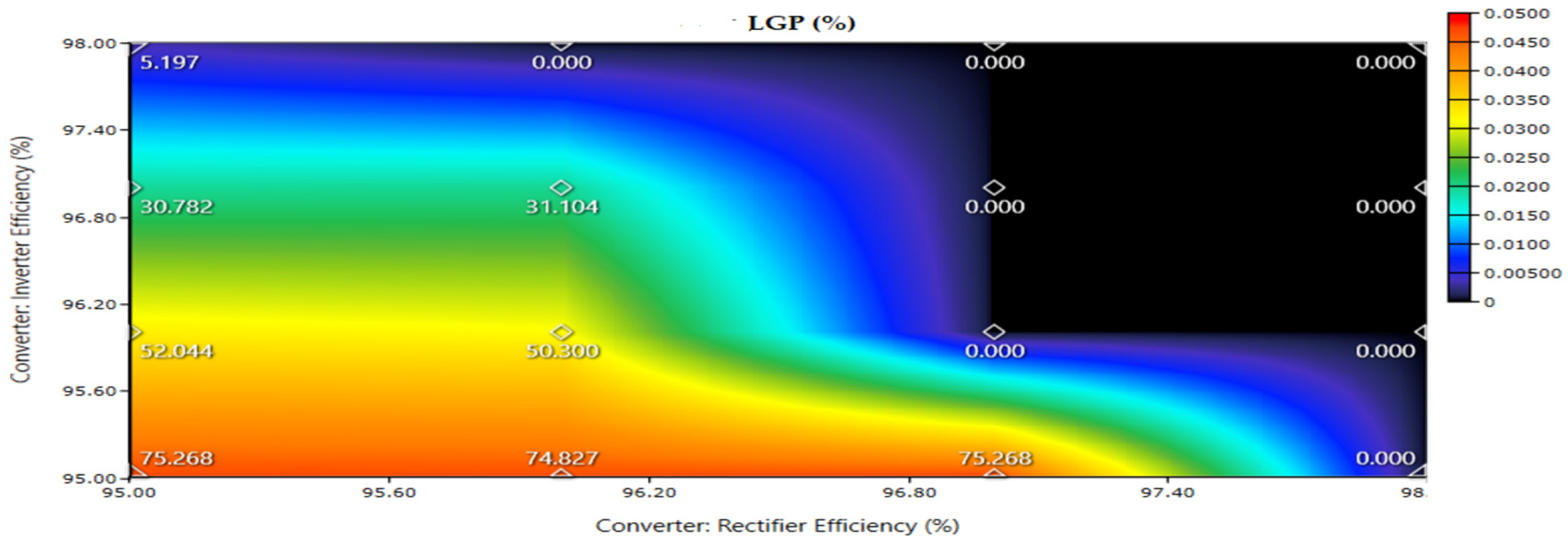
4.8.5. Effect of Changing Inverter and Rectifier Efficiency
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- India-Cumulative Installed Power Capacity Mix (%). Available online: https://mercomindia.com/wp-content/uploads/2020/04/India-Cumulative-Installed-Power-Capacity-Mix.png (accessed on 27 September 2021).
- Xie, J.; Zheng, Y.; Pan, X.; Zheng, Y.; Zhang, L.; Zhan, Y. A Short-Term Optimal Scheduling Model for Wind-Solar-Hydro Hybrid Generation System with Cascade Hydropower Considering Regulation Reserve and Spinning Reserve Requirements. IEEE Access 2021, 9, 10765–10777. [Google Scholar] [CrossRef]
- Bandoc, G.; Florescu, A.-M.S.; Degeratu, M.; Pravalie, R. Use of hybrid renewable energy systems for small communities. Renew. Energy Environ. Sustain. 2016, 1, 29. [Google Scholar] [CrossRef][Green Version]
- Kharrich, M.; Kamel, S.; Abdeen, M.; Mohammed, O.H.; Akherraz, M.; Khurshaid, T.; Rhee, S.-B. Developed Approach Based on Equilibrium Optimizer for Optimal Design of Hybrid PV/Wind/Diesel/Battery Microgrid in Dakhla, Morocco. IEEE Access 2021, 9, 13655–13670. [Google Scholar] [CrossRef]
- Ahmed, M.; Meegahapola, L.; Vahidnia, A.; Datta, M. Stability and Control Aspects of Microgrid Architectures—A Comprehensive Review. IEEE Access 2020, 8, 144730–144766. [Google Scholar] [CrossRef]
- Al-Ismail, F.S. DC Microgrid Planning, Operation, and Control: A Comprehensive Review. IEEE Access 2021, 9, 36154–36172. [Google Scholar] [CrossRef]
- Wild, J.; Boutin, V.; Barton, P.; Haines, L. Microgrid Benefits and Example Projects; Schneider Electric: Paris, France, 2016. [Google Scholar]
- Arkhangelski, J.; Abdou-Tankari, M.; Lefebvre, G. Day-Ahead Optimal Power Flow for Efficient Energy Management of Urban Microgrid. IEEE Trans. Ind. Appl. 2021, 57, 1285–1293. [Google Scholar] [CrossRef]
- Pacheco, F.E.; Foreman, J.C. Microgrid Reference Methodology for Understanding Utility and Customer Interactions in Mi-crogrid Projects. Electr. J. 2017, 30, 44–50. [Google Scholar]
- Vaahedi, E.; Nodehi, K.; Heim, D.; Rahimi, F.; Ipakchi, A. The Emerging Transactive Microgrid Controller: Illustrating Its Concept, Functionality, and Business Case. IEEE Power Energy Mag. 2017, 15, 80–87. [Google Scholar] [CrossRef]
- Carpintero-Rentería, M.; Santos-Martín, D.; Guerrero, J.M. Microgrids Literature Review through a Layers Structure. Energies 2019, 12, 4381. [Google Scholar] [CrossRef]
- Al-Ghussain, L.; Ahmad, A.D.; Abubaker, A.M.; Mohamed, M.A. An integrated photovoltaic/wind/biomass and hybrid energy storage systems towards 100% renewable energy microgrids in university campuses. Sustain. Energy Technol. Assess. 2021, 46, 101273. [Google Scholar] [CrossRef]
- Mostafaeipour, A.; Rezayat, H.; Rezaei, M. A thorough investigation of solar-powered hydrogen potential and accurate location planning for big cities: A case study. Int. J. Hydrogen Energy 2020, 45, 31599–31611. [Google Scholar] [CrossRef]
- Rezaei, M.; Mostafaeipour, A.; Jafari, N.; Naghdi-Khozani, N.; Moftakharzadeh, A. Wind and solar energy utilization for seawater desalination and hydrogen production in the coastal areas of southern Iran. J. Eng. Des. Technol. 2020, 18, 1951–1969. [Google Scholar] [CrossRef]
- Kong, X.; Liu, X.; Ma, L.; Lee, K.Y. Hierarchical Distributed Model Predictive Control of Standalone Wind/Solar/Battery Power System. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 1570–1581. [Google Scholar] [CrossRef]
- Adetunji, K.E.; Akinlabi, O.; Joseph, M.K. Developing a Microgrid for Tafelkop Using HOMER. In Proceedings of the 2018 International Conference on Advances in Big Data, Computing and Data Communication Systems (icABCD), Durban, South Africa, 6–7 August 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Nurunnabi, M.; Roy, N.K.; Hossain, E.; Pota, H.R. Size Optimization and Sensitivity Analysis of Hybrid Wind/PV Micro-Grids—A Case Study for Bangladesh. IEEE Access 2019, 7, 150120–150140. [Google Scholar] [CrossRef]
- Menicou, M.; Exizidou, P.; Vassiliou, V.; Christou, P. An economic analysis of Cyprus ‘residential buildings’ energy ret-rofits potential. Int. J. Sustain. Energy 2015, 34, 166–187. [Google Scholar] [CrossRef]
- Vuyyuru, U.; Maiti, S.; Chakraborty, C. Active Power Flow Control between DC Microgrids. IEEE Trans. Smart Grid 2019, 10, 5712–5723. [Google Scholar] [CrossRef]
- Kumar, P.; Pukale, R.; Kumabhar, N.; Patil, U. Optimal Design Configuration Using HOMER. Procedia Technol. 2016, 24, 499–504. [Google Scholar] [CrossRef]
- Pookoya, C.G. Kalpeni Island: History, People and Culture, 1st ed.; Notion Press: Kalpeni Island, India, 2018; pp. 2–10. [Google Scholar]
- Sinha, S.; Chandel, S. Review of software tools for hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2014, 32, 192–205. [Google Scholar] [CrossRef]
- Tribioli, L.; Cozzolino, R. Techno-economic analysis of a stand-alone microgrid for a commercial building in eight different climate zones. Energy Convers. Manag. 2018, 179, 58–71. [Google Scholar] [CrossRef]
- Çetinbaş, I.; Tamyürek, B.; Demirtaş, M. Design, Analysis and Optimization of a Hybrid Microgrid System Using HOMER Software: Eskişehir Osmangazi University Example. Int. J. Renew. Energy Dev. 2019, 8, 65–79. [Google Scholar] [CrossRef]
- Kumar Garg, V.; Sharma, S. Optimum Sizing and Economic Assessment of Hybrid Microgrid for Domestic Load Under Various Scenario. Int. J. Renew. Energy Res. 2021, 11, 235–246. [Google Scholar]
- Akinyele, D. Analysis of photovoltaic mini-grid systems for remote locations: A techno-economic approach. Int. J. Energy Res. 2017, 42, 1363–1380. [Google Scholar] [CrossRef]
- Al-Ammar, E.A.; Habib, H.U.R.; Kotb, K.M.; Wang, S.; Ko, W.; Elmorshedy, M.F.; Waqar, A. Residential Community Load Management Based on Optimal Design of Standalone HRES With Model Predictive Control. IEEE Access 2020, 8, 12542–12572. [Google Scholar] [CrossRef]
- Vera, Y.E.G.; Dufo-López, R.; Bernal-Agustín, J.L. Energy Management in Microgrids with Renewable Energy Sources: A Literature Review. Appl. Sci. 2019, 9, 3854. [Google Scholar] [CrossRef]
- Chambon, C.L.; Karia, T.; Sandwell, P.; Hallett, J.P. Techno-economic assessment of biomass gasification-based mini-grids for productive energy applications: The case of rural India. Renew. Energy 2020, 154, 432–444. [Google Scholar] [CrossRef]
- Guo, Y.; Li, S.; Li, C.; Peng, H. Short-Term Reliability Assessment for Islanded Microgrid Based on Time-Varying Probability Ordered Tree Screening Algorithm. IEEE Access 2019, 7, 37324–37333. [Google Scholar] [CrossRef]
- Peyghami, S.; Palensky, P.; Blaabjerg, F. An Overview on the Reliability of Modern Power Electronic Based Power Systems. IEEE Open J. Power Electron. 2020, 1, 34–50. [Google Scholar] [CrossRef]
- Patowary, M.; Panda, G.; Deka, B.C. Reliability Modeling of Microgrid System Using Hybrid Methods in Hot Standby Mode. IEEE Syst. J. 2019, 13, 3111–3119. [Google Scholar] [CrossRef]
- Baghaee, H.; Mirsalim, M.; Gharehpetian, G.; Talebi, H. Reliability/cost-based multi-objective Pareto optimal design of stand-alone wind/PV/FC generation microgrid system. Energy 2016, 115, 1022–1041. [Google Scholar] [CrossRef]
- Priyadharshini, B.; Ganapathy, V.; Sudhakara, P. An Optimal Model to Meet the Hourly Peak Demands of a Specific Region with Solar, Wind, and Grid Supplies. IEEE Access 2020, 8, 13179–13194. [Google Scholar] [CrossRef]
- Ali, T.; Ma, H.; Nahian, A.J. Techno-Economic Analysis of a Hybrid Mini-grid in Rural Areas: A Case Study of Bangladesh. J. Energy Res. Rev. 2020, 4, 10–29. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, I.; Jamil, F.; Kim, D. Toward the Optimal Operation of Hybrid Renewable Energy Resources in Microgrids. Energies 2020, 13, 5482. [Google Scholar] [CrossRef]
- Lee, H.-J.; Vu, B.H.; Zafar, R.; Hwang, S.-W.; Chung, I.-Y. Design Framework of a Stand-Alone Microgrid Considering Power System Performance and Economic Efficiency. Energies 2021, 14, 457. [Google Scholar] [CrossRef]
- Alturki, F.A.; Awwad, E.M. Sizing and Cost Minimization of Standalone Hybrid WT/PV/Biomass/Pump-Hydro Storage-Based Energy Systems. Energies 2021, 14, 489. [Google Scholar] [CrossRef]
- Hinokuma, T.; Farzaneh, H.; Shaqour, A. Techno-Economic Analysis of a Fuzzy Logic Control Based Hybrid Renewable Energy System to Power a University Campus in Japan. Energies 2021, 14, 1960. [Google Scholar] [CrossRef]
- Riou, M.; Dupriez-Robin, F.; Grondin, D.; Le Loup, C.; Benne, M.; Tran, Q. Multi-Objective Optimization of Autonomous Microgrids with Reliability Consideration. Energies 2021, 14, 4466. [Google Scholar] [CrossRef]
- Fathy, A.; Kaaniche, K.; Alanazi, T.M. Recent Approach Based Social Spider Optimizer for Optimal Sizing of Hybrid PV/Wind/Battery/Diesel Integrated Microgrid in Aljouf Region. IEEE Access 2020, 8, 57630–57645. [Google Scholar] [CrossRef]
- Yu, Z.-X.; Li, M.-S.; Xu, Y.-P.; Aslam, S.; Li, Y.-K. Techno-Economic Planning and Operation of the Microgrid Considering Real-Time Pricing Demand Response Program. Energies 2021, 14, 4597. [Google Scholar] [CrossRef]
- Odou, O.D.T.; Bhandari, R.; Adamou, R. Hybrid off-grid renewable power system for sustainable rural electrification in Benin. Renew. Energy 2020, 145, 1266–1279. [Google Scholar] [CrossRef]
- Yahyaoui, I.; Atieh, A.; Serna, A.; Tadeo, F. Sensitivity analysis for photovoltaic water pumping systems: Energetic and eco-nomic studies. Energy Convers. Manag. 2017, 135, 402–415. [Google Scholar] [CrossRef]
- Halabi, L.M.; Mekhilef, S.; Olatomiwa, L.; Hazelton, J. Performance analysis of hybrid PV/diesel/battery system using HOMER: A case study Sabah, Malaysia. Energy Convers. Manag. 2017, 144, 322–339. [Google Scholar] [CrossRef]
- Veilleux, G.; Potisat, T.; Pezim, D.; Ribback, C.; Ling, J.; Krysztofiński, A.; Ahmed, A.; Papenheim, J.; Pineda, A.M.; Sembian, S.; et al. Techno-economic analysis of microgrid projects for rural electrification: A systematic approach to the redesign of Koh Jik off-grid case study. Energy Sustain. Dev. 2020, 54, 1–13. [Google Scholar] [CrossRef]
- Dhundhara, S.; Verma, Y.P.; Williams, A. Techno-economic analysis of the lithium-ion and lead-acid battery in microgrid systems. Energy Convers. Manag. 2018, 177, 122–142. [Google Scholar] [CrossRef]
- Rashid, F.; Hoque, E.; Aziz, M.; Sakib, T.N.; Islam, T.; Robin, R.M. Investigation of Optimal Hybrid Energy Systems Using Available Energy Sources in a Rural Area of Bangladesh. Energies 2021, 14, 5794. [Google Scholar] [CrossRef]
- Phan, B.C.; Lai, Y.-C. Control Strategy of a Hybrid Renewable Energy System Based on Reinforcement Learning Approach for an Isolated Microgrid. Appl. Sci. 2019, 9, 4001. [Google Scholar] [CrossRef]
- Beza, T.; Wu, C.-H.; Kuo, C.-C. Optimal Sizing and Techno-Economic Analysis of Minigrid Hybrid Renewable Energy System for Tourist Destination Islands of Lake Tana, Ethiopia. Appl. Sci. 2021, 11, 7085. [Google Scholar] [CrossRef]
- Cai, G.; Kong, L. Techno-economic analysis of wind curtailment/hydrogen production/fuel cell vehicle system with high wind penetration in China. CSEE J. Power Energy Syst. 2017, 3, 44–52. [Google Scholar] [CrossRef]
- Lu, J.; Wang, W.; Zhang, Y.; Cheng, S. Multi-Objective Optimal Design of Stand-Alone Hybrid Energy System Using Entropy Weight Method Based on HOMER. Energies 2017, 10, 1664. [Google Scholar] [CrossRef]
- Singh, S.; Chauhan, P.; Aftab, M.A.; Ali, I.; Hussain, S.M.S.; Ustun, T.S. Cost Optimization of a Stand-Alone Hybrid Energy System with Fuel Cell and PV. Energies 2020, 13, 1295. [Google Scholar] [CrossRef]
- Katsivelakis, M.; Bargiotas, D.; Daskalopulu, A.; Panapakidis, I.; Tsoukalas, L. Techno-Economic Analysis of a Stand-Alone Hybrid System: Application in Donoussa Island, Greece. Energies 2021, 14, 1868. [Google Scholar] [CrossRef]
- Mun, H.; Moon, B.; Park, S.; Yoon, Y. A Study on the Economic Feasibility of Stand-Alone Microgrid for Carbon-Free Island in Korea. Energies 2021, 14, 1913. [Google Scholar] [CrossRef]
- Nasab, N.M.; Kilby, J.; Bakhtiaryfard, L. Case Study of a Hybrid Wind and Tidal Turbines System with a Microgrid for Power Supply to a Remote Off-Grid Community in New Zealand. Energies 2021, 14, 3636. [Google Scholar] [CrossRef]
- Nazir, R.; Laksono, H.; Waldi, E.; Ekaputra, E.; Coveria, P. Renewable Energy Sources Optimization: A Micro-Grid Model Design. Energy Procedia 2014, 52, 316–327. [Google Scholar] [CrossRef]
- Murty, V.V.V.S.N.; Kumar, A. Optimal Energy Management and Techno-economic Analysis in Microgrid with Hybrid Renewable Energy Sources. J. Mod. Power Syst. Clean Energy 2020, 8, 929–940. [Google Scholar] [CrossRef]
- Mas’Ud, A.; Al-Garni, H. Optimum Configuration of a Renewable Energy System Using Multi-Year Parameters and Advanced Battery Storage Modules: A Case Study in Northern Saudi Arabia. Sustainability 2021, 13, 5123. [Google Scholar] [CrossRef]
- Iqbal, F.; Siddiqui, A.S. Optimal configuration analysis for a campus microgrid—A case study. Prot. Control Mod. Power Syst. 2017, 2, 23. [Google Scholar] [CrossRef]
- Sadat, S.A.; Faraji, J.; Babaei, M.; Ketabi, A. Techno-economic comparative study of hybrid microgrids in eight climate zones of Iran. Energy Sci. Eng. 2020, 8, 3004–3026. [Google Scholar] [CrossRef]
- Rousis, A.O.; Tzelepis, D.; Konstantelos, I.; Booth, C.; Strbac, G. Design of a Hybrid AC/DC Microgrid Using HOMER Pro: Case Study on an Islanded Residential Application. Inventions 2018, 3, 55. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Huda, A.S.N.; Sanusi, K. Techno-economic analysis of hybrid PV–diesel–battery and PV–wind–diesel–battery power systems for mobile BTS: The way forward for rural development. Energy Sci. Eng. 2015, 3, 271–285. [Google Scholar] [CrossRef]
- Hossain, S.; Jahid, A.; Islam, K.Z.; Rahman, F. Solar PV and Biomass Resources-Based Sustainable Energy Supply for Off-Grid Cellular Base Stations. IEEE Access 2020, 8, 53817–53840. [Google Scholar] [CrossRef]
- Xia, T.; Rezaei, M.; Dampage, U.; Alharbi, S.; Nasif, O.; Borowski, P.; Mohamed, M. Techno-Economic Assessment of a Grid-Independent Hybrid Power Plant for Co-Supplying a Remote Micro-Community with Electricity and Hydrogen. Processes 2021, 9, 1375. [Google Scholar] [CrossRef]
- Rezaei, M.; Dampage, U.; Das, B.K.; Nasif, O.; Borowski, P.F.; Mohamed, M.A. Investigating the Impact of Economic Uncertainty on Optimal Sizing of Grid-Independent Hybrid Renewable Energy Systems. Processes 2021, 9, 1468. [Google Scholar] [CrossRef]
- Sanjay, K.C.; Karthikeyan, M.; Prasannakumaran, K.M.; Kirubakaran, V. Techno Commercial Study of Hybrid Systems for the Agriculture Farm Using Homer Software. In Hybrid Renewable Energy Systems; Wiley: Beverly, MA, USA, 2021; pp. 115–133. [Google Scholar] [CrossRef]
- Shahzad, M.K.; Zahid, A.; Rashid, T.U.; Rehan, M.A.; Ali, M.; Ahmad, M. Techno-economic feasibility analysis of a solar-biomass off grid system for the electrification of remote rural areas in Pakistan using HOMER software. Renew. Energy 2017, 106, 264–273. [Google Scholar] [CrossRef]
- Aziz, A.; Tajuddin, M.; Adzman, M.; Ramli, M.; Mekhilef, S. Energy Management and Optimization of a PV/Diesel/Battery Hybrid Energy System Using a Combined Dispatch Strategy. Sustainability 2019, 11, 683. [Google Scholar] [CrossRef]
- Beitelmal, W.; Okonkwo, P.; Al Housni, F.; Alruqi, W.; Alruwaythi, O. Accessibility and Sustainability of Hybrid Energy Systems for a Cement Factory in Oman. Sustainability 2020, 13, 93. [Google Scholar] [CrossRef]
- Chauhan, A.; Upadhyay, S.; Khan, M.; Hussain, S.; Ustun, T. Performance Investigation of a Solar Photovoltaic/Diesel Generator Based Hybrid System with Cycle Charging Strategy Using BBO Algorithm. Sustainability 2021, 13, 8048. [Google Scholar] [CrossRef]
- Yadav, A.; Pal, N.; Bhukya, J. Design and development of PV-wind based hybrid renewable energy system. In Proceedings of the International Conference on Electronics and Sustainable Communication Systems, Coimbatore, India, 2–4 July 2020; pp. 1045–1051. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Sawle, Y. Design, analysis and optimal sizing of standalone PV/diesel/battery hybrid energy system using HOMER. IOP Conf. Ser. Mater. Sci. Eng. 2020, 937, 12034. [Google Scholar] [CrossRef]
- Ruelas, J.; Muñoz, F.; Lucero, B.; Palomares, J. PV Tracking Design Methodology Based on an Orientation Efficiency Chart. Appl. Sci. 2019, 9, 894. [Google Scholar] [CrossRef]
- González-Peña, D.; García-Ruiz, I.; Díez-Mediavilla, M.; Dieste-Velasco, M.; Alonso-Tristán, C. Photovoltaic Prediction Software: Evaluation with Real Data from Northern Spain. Appl. Sci. 2021, 11, 5025. [Google Scholar] [CrossRef]
- Seme, S.; Štumberger, B.; Hadžiselimović, M.; Sredenšek, K. Solar Photovoltaic Tracking Systems for Electricity Generation: A Review. Energies 2020, 13, 4224. [Google Scholar] [CrossRef]
- Kuttybay, N.; Saymbetov, A.; Mekhilef, S.; Nurgaliyev, M.; Tukymbekov, D.; Dosymbetova, G.; Meiirkhanov, A.; Svanbayev, Y. Optimized Single-Axis Schedule Solar Tracker in Different Weather Conditions. Energies 2020, 13, 5226. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Zhao, Y.; Yue, H.; Gao, D.; Zhang, H.; Chen, H. Performance Comparison of Solar Single-Axis Tracking Low-Concentrating Photovoltaic/Thermal System with Different Axes. IEEE Access 2021, 9, 28632–28645. [Google Scholar] [CrossRef]
- Fahad, H.M.; Islam, A.; Islam, M.; Hasan, F.; Brishty, W.F.; Rahman, M. Comparative Analysis of Dual and Single Axis Solar Tracking System Considering Cloud Cover. In Proceedings of the International Conference on Energy and Power Engineering (ICEPE), Dhaka, Bangladesh, 14–16 March 2019. [Google Scholar]
- Al-Rousan, N.; Isa, N.A.M.; Desa, M.K.M. Advances in solar photovoltaic tracking systems: A review. Renew. Sustain. Energy Rev. 2018, 82, 2548–2569. [Google Scholar] [CrossRef]
- Safieh, A.; Elnosh, A.; Kaiss, E.-C.A.K.; John, J.J.; Alnuaimi, A. Field Comparison Study of Fixed-Tilted and Single-Axis Tracking PV Structures in the Desert Environment of Dubai, UAE. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PVSC), Calgary, AB, Canada, 15 June–21 August 2020; pp. 2136–2139. [Google Scholar] [CrossRef]
- Babatunde, O.M.; Munda, J.L.; Hamam, Y. Photovoltaic system sizing for household use: Effects of temperature, orientation and sun tracking. In Proceedings of the 2019 Open Innovations (OI), Cape town, South Africa, 2–4 October 2019; pp. 190–195. [Google Scholar] [CrossRef]
- Campos, M.D.S.; Tiba, C. npTrack: A n-Position Single Axis Solar Tracker Model for Optimized Energy Collection. Energies 2021, 14, 925. [Google Scholar] [CrossRef]
- Frydrychowicz-Jastrzębska, G.; Bugała, A. Solar Tracking System with New Hybrid Control in Energy Production Optimization from Photovoltaic Conversion for Polish Climatic Conditions. Energies 2021, 14, 2938. [Google Scholar] [CrossRef]
- Hammoumi, A.E.; Motahhir, S.; Ghzizal, A.E.; Chalh, A.; Derouich, A. A simple and low-cost active dual-axis solar tracker. Energy Sci. Eng. 2018, 6, 607–620. [Google Scholar] [CrossRef]
- Mpodi, E.K.; Tjiparuro, Z.; Matsebe, O. Review of dual axis solar tracking and development of its functional model. Procedia Manuf. 2019, 35, 580–588. [Google Scholar] [CrossRef]
- Berrian, D.; Libal, J.; Klenk, M.; Nussbaumer, H.; Kopecek, R. Performance of Bifacial PV Arrays with Fixed Tilt and Horizontal Single-Axis Tracking: Comparison of Simulated and Measured Data. IEEE J. Photovolt. 2019, 9, 1583–1589. [Google Scholar] [CrossRef]
- Mubaarak, S.; Zhang, D.; Chen, Y.; Liu, J.; Wang, L.; Yuan, R.; Wu, J.; Zhang, Y.; Li, M. Techno-Economic Analysis of Grid-Connected PV and Fuel Cell Hybrid System Using Different PV Tracking Techniques. Appl. Sci. 2020, 10, 8515. [Google Scholar] [CrossRef]
- Alvarado-M, J.F.; Betancur, E.; Velasquez-Lopez, A. Optimization of Single-Axis Discrete Solar Tracking. In Proceedings of the 2020 9th International Conference on Renewable Energy Research and Application (ICRERA), Glasgow, UK, 27–30 September 2020; pp. 271–275. [Google Scholar] [CrossRef]
- Fuke, P.; Yadav, A.K.; Anil, I. Techno-Economic Analysis of Fixed, Single and Dual-Axis Tracking Solar PV System. In Proceedings of the 2020 IEEE 9th Power India International Conference (PIICON), Sonepat, India, 28 February–1 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Alexandru, C. Optimization of the Bi-Axial Tracking System for a Photovoltaic Platform. Energies 2021, 14, 535. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel Online Sensorless Dual-Axis Sun Tracker. IEEE/ASME Trans. Mechatronics 2016, 22, 321–328. [Google Scholar] [CrossRef]
- Konneh, K.V.; Masrur, H.; Othman, M.L.; Wahab, N.I.A.; Hizam, H.; Islam, S.Z.; Crossley, P.; Senjyu, T. Optimal Design and Performance Analysis of a Hybrid Off-Grid Renewable Power System Considering Different Component Scheduling, PV Modules, and Solar Tracking Systems. IEEE Access 2021, 9, 64393–64413. [Google Scholar] [CrossRef]
- Smirnov, A.A.; Malugin, S.A.; Bakanov, A.V. Designing Integrated PV Facility with Dual-Axis Solar Tracking System Mounted on the South Building Face. In Proceedings of the 2017 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), St. Petersburg, Russia, 16–19 May 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Pelaez, S.A.; Deline, C.; Greenberg, P.; Stein, J.S.; Kostuk, R.K. Model and Validation of Single-Axis Tracking with Bifacial PV. IEEE J. Photovolt. 2019, 9, 715–721. [Google Scholar] [CrossRef]
- Rodriguez-Gallegos, C.D.; Gandhi, O.; Panda, S.K.; Reindl, T. On the PV Tracker Performance: Tracking the Sun Versus Tracking the Best Orientation. IEEE J. Photovolt. 2020, 10, 1474–1480. [Google Scholar] [CrossRef]
- Saeedi, M.; Effatnejad, R. A New Design of Dual-Axis Solar Tracking System with LDR Sensors by Using the Wheatstone Bridge Circuit. IEEE Sens. J. 2021, 21, 14915–14922. [Google Scholar] [CrossRef]
- Zaghba, L.; Khennane, M.; Borni, A.; Fezzani, A.; Bouchakour, A.; Mahammed, I.H.; Oudjana, S.H. An Enhancement of Grid Connected PV System Performance Based on ANFIS MPPT Control and Dual Axis Solar Tracking. In Proceedings of the 2019 1st International Conference on Sustainable Renewable Energy Systems and Applications (ICSRESA), Tebessa, Algeria, 4–5 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Lithium Battery Cost Have Fallen by 98% in Three Decades. Available online: https://www.economist.com/graphic-detail/2021/03/31/lithium-battery-costs-have-fallen-by-98-in-three-decades (accessed on 16 June 2021).





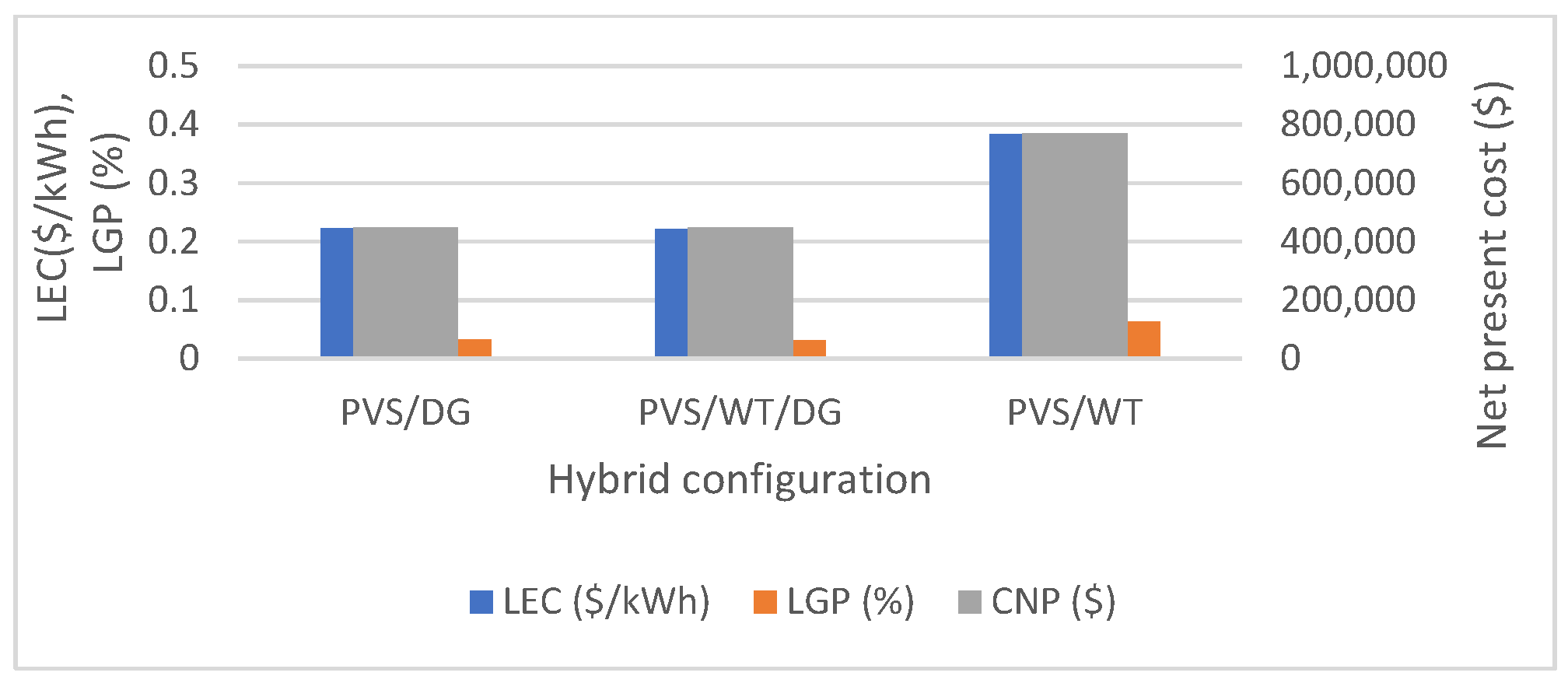


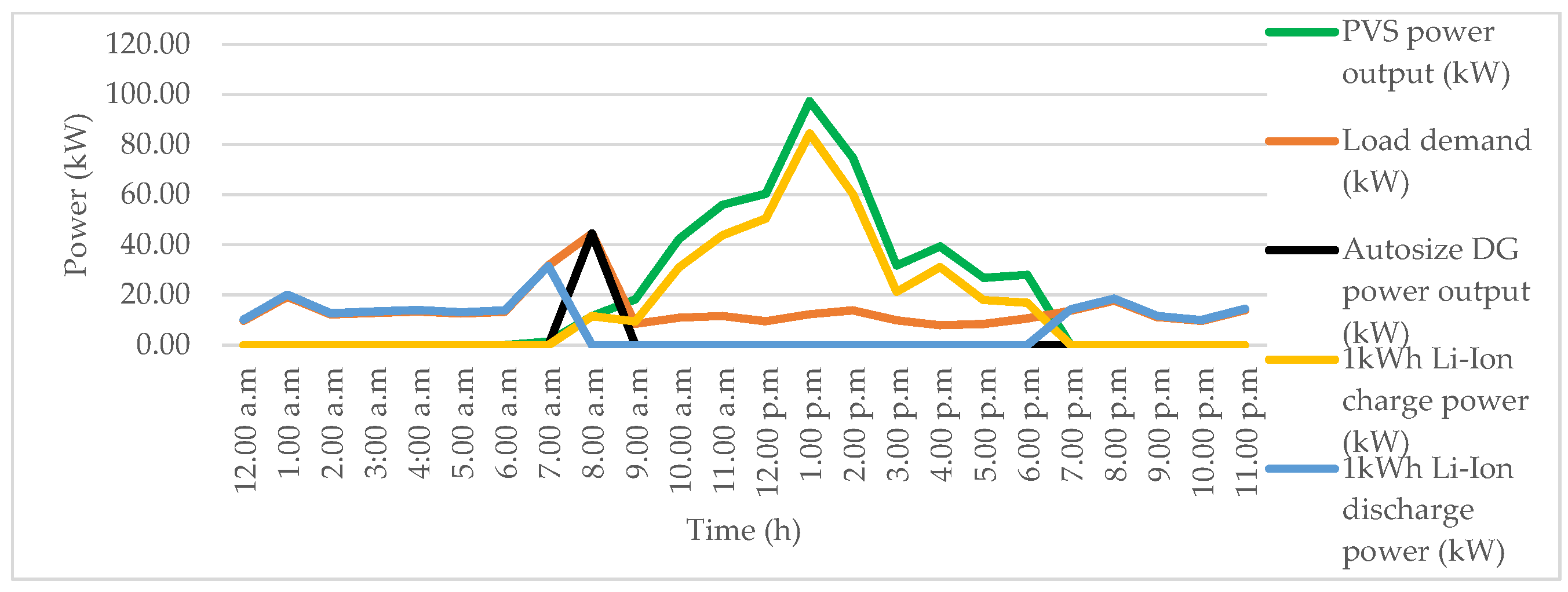

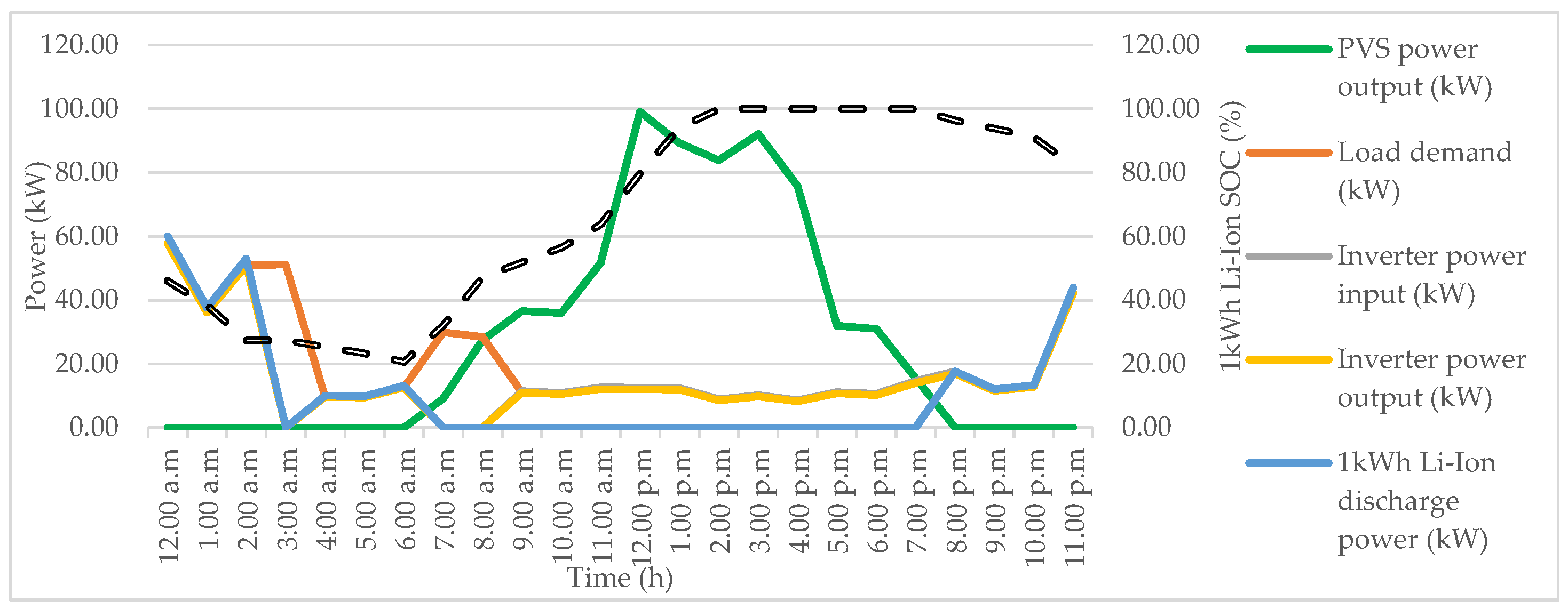
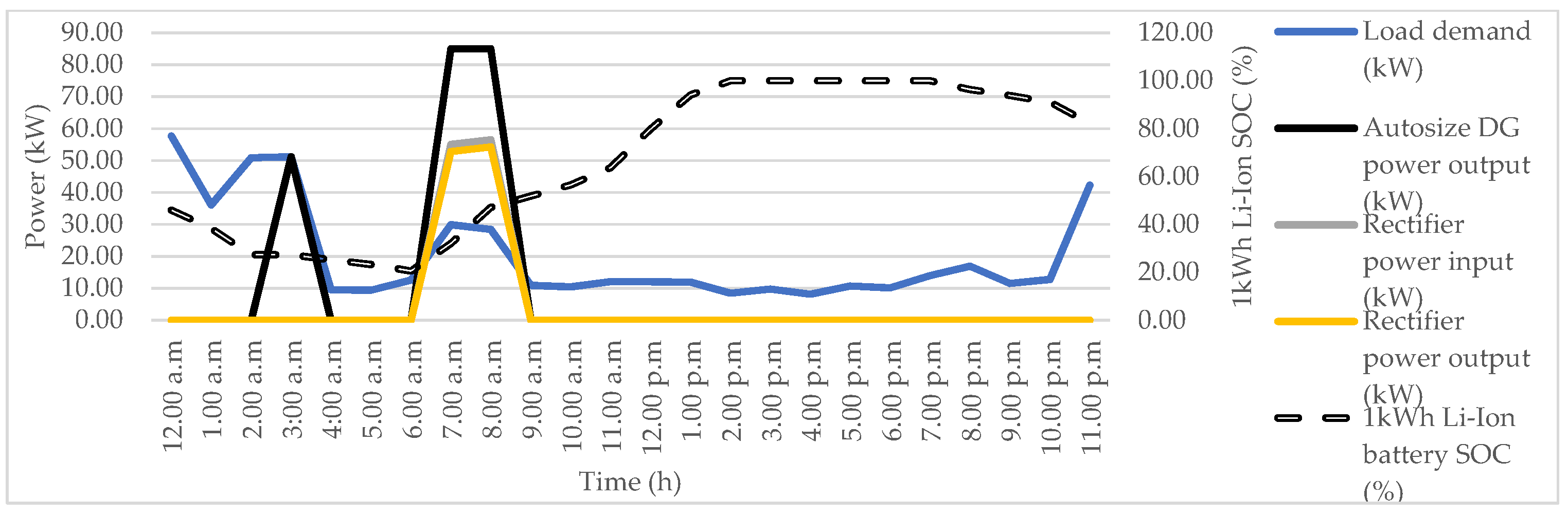
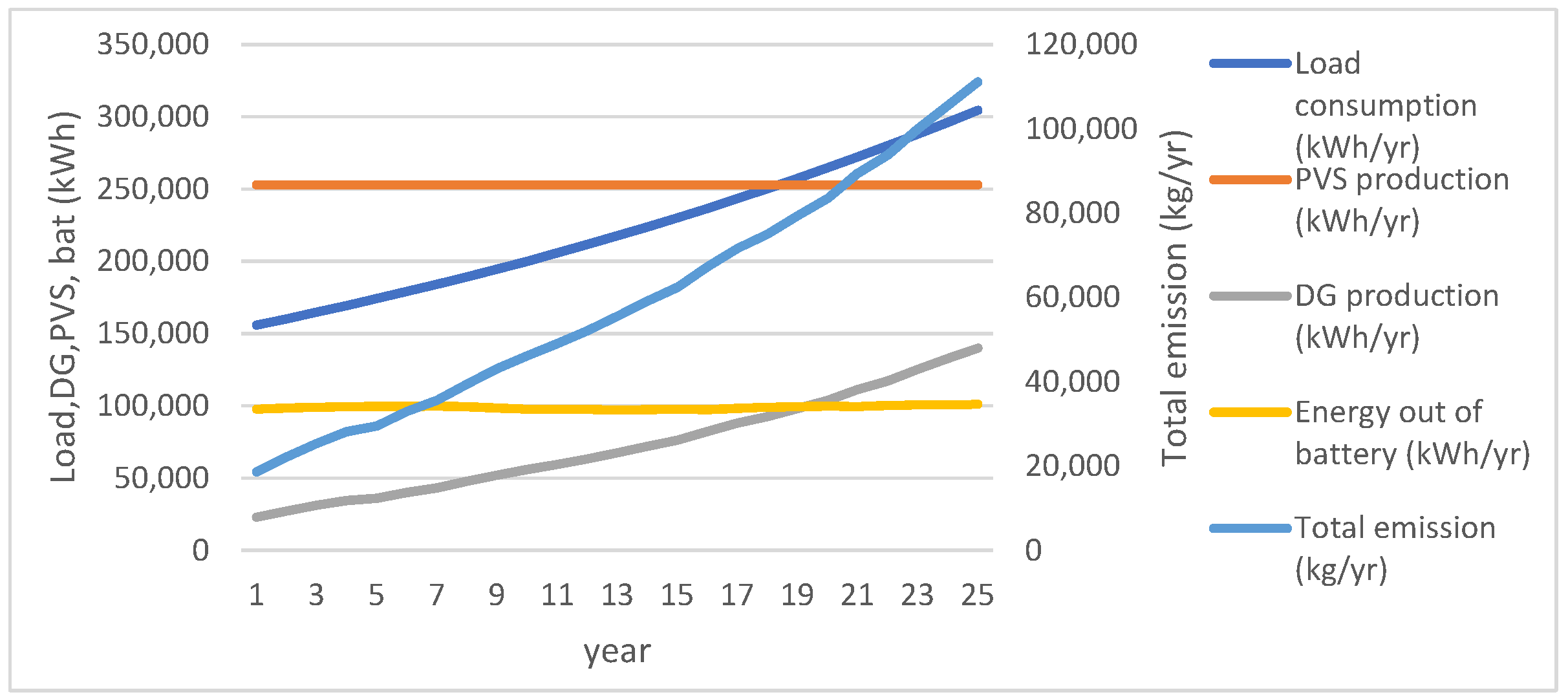



| Operating Mode | System Considered | Parmeter | Details | Ref. |
|---|---|---|---|---|
| Stand-alone | PVS/WT/FC/DG | LEC | The objective of this study is to create a stand-alone microgrid with implementation in rural island and rural electricity. | [49] |
| Stand-alone | PVS/DG, PVS alone, PVS/WT, DG alone | LEC | The survey shows that the PVS/diesel/battery can provide adequate energy to the island of Ethiopia throughout the duration of the work. | [50] |
| Grid connected | WT/FC | Emission, CNP | The system’s total income and return are calculated and examined for saving energy, decarbonization, and green infrastructure. | [51] |
| Stand-alone | PVS/WT/DG | LPSP, LEC | The result determined based on reliability, cost, technical feasibility, and ecological responsibility are all important factors to consider | [52] |
| Stand-alone | PVS/FC | LEC, CNP | The result shows that the system operate without emission and the reliability index like loss of generation probability (LGP) is 0.05% and levelized energy cost (LEC) is 0.22 $/kWh | [53] |
| Stand-alone | WT/DG/SPV, WT/PVS/DG, WT/PVS | LEC, CNP | The system operated with 0% excess power flow and the levelized energy cost as 0.24 euro in the island | [54] |
| Stand-alone | DG, PVS/WT, PVS/WT/FC | LEC, LPSP | The cost and reliability factor for the different system configuration are analysed and compared | [55] |
| Grid-connected | WT/tidal, WT/tidal/DG | LEC, CNP, emission | The wind turbine is operated 90% annual for the site considered | [56] |
| Grid-connected | PVS/Hydro | LEC, emission | The system operated with low cost and emission and higher degree of renewables | [57] |
| Stand-alone | PVS/WT/DG, PVS/DG, WT/DG, PVS/WT, PVS alone, WT alone | LEC, emission, CNP | The levelized energy cost analysed according to the different level of renewable %. The system with PVS/wind/DG has less emission compared to the system only operated with diesel generator | [58] |
| Stand-alone | PVS/WT/DG | LEC, emission, CNP | The sensitivity analysis is performed for variation in temperature to know about the effect of levelized energy cost (LEC) and net present cost (CNP) | [59] |
| TS | Details | Ref. |
|---|---|---|
| TSDA | Investigated the planning of solar tracker cost of investment and compared the TSDA with FSWT. The result shows that the tracking system on dual axis (TSDA) collected 35.6% and 44.7% more energy during the 1st and 2nd year compared to a fixed system without tracking (FSWT). | [84] |
| TSDA | Implemented a simple model of multi axis tracking PVS. The proposed model of two axis PVS collected 36.2% more energy than the traditional fixed tracking model of PVS. | [85] |
| TSDA | Reviewed the tracking system on dual axis and determine the efficiency which is ranging from 35% to 43%. | [86] |
| Single axis TS | Presented the results of power generation evaluations of bifacial PVS with fixed angle and tracking system on a horizontal axis (TSHA) in contrast to their mono facial equivalents. Furthermore, the projected information is compared to the existing results. | [87] |
| TSVA, TSHA, TSDA | The result shows that tracking system on a vertical axis (TSVA) produces less emission while compared with a two axis tracking system | [88] |
| Single axis TS | Various orientations of a single axis tracking system are studied for each day | [89] |
| Single axis and TSDA | The result shows that 27 to 30% and 30 to 34% more power produced using single and dual axis tracking systems respectively when compared to FSWT | [90] |
| Single axis and TSDA | The result shows that in a single and tracking system on dual axis (TSDA), the efficiency of tracking are 99.1 and 89.2% | [91] |
| TSDA | In the proposed method of tracking sun position, the result shows that 28% to 43% energy from solar captured | [92] |
| TSVA, TSHA, TSDA | The result shows that 28.8% extra power is generated from the photovoltaic system compared to an ideal tracking system | [93] |
| Single axis and TSDA | The efficiency analysis comparison of single and two axis tracking system are obtained in the result | [94] |
| Domestic Load (1 Household) | Electric Load-2 (12 Street Light and 1 Grocery Shop) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Type of Load | PLD (W) | Summer | Winter | Type of Load | PLD (W) | Summer | Winter | ||||
| Hrs | Wh | Hrs | Wh | Hrs | Wh | Hrs | Wh | ||||
| Ceiling fan (3 Nos) | 60 W (each) | 12, 4, 4 | 1200 | 12, 4, 4 | 1200 | LED street light (12 Nos) | 100W (each) | 12 ∗ 13 | 15,600 | 12 ∗ 13.5 | 16,200 |
| Air conditioner | 1510 | 5 | 7550 | 0.1 | 151 | ||||||
| Laptop | 60 | 1 | 60 | 1 | 60 | Refrigerator-1 | 550 | 24 | 13,200 | 24 | 13,200 |
| LED TV | 40 | 7 | 280 | 7 | 280 | Refrigerator-2 | 290 | 24 | 6960 | 24 | 6960 |
| Water geyser | 2000 | 0.3 | 600 | 0.6 | 1200 | ||||||
| Grinder | 150 | 0.5 | 75 | 0.5 | 75 | Ceiling fan (2 Nos) | 60W (each) | 15, 15 | 1800 | 15, 15 | 1800 |
| Washing machine | 500 | 0.5 | 250 | 0.5 | 250 | ||||||
| Electric motor | 1511 | 0.5 | 755.5 | 0.5 | 755.5 | LED tube light (5 Nos) | 20W (each) | 4, 4, 0, 0 | 160 | 5, 5, 1, 1 | 240 |
| Mobile charging (3 Nos) | 5 W (each) | 1, 1, 1 | 15 | 1,1,1 | 15 | ||||||
| LED tube light (5 Nos) | 20 W (each) | 5, 2, 1, 0.1, 0.1 | 164 | 6, 2.5, 2, 0.1, 0.1 | 214 | Domestic load (1 household) | |||||
| Iron box | 1000 | 0.1 | 100 | 0.1 | 100 | ||||||
| LED bulb (3 Nos) | 9 W (each) | 0.1, 4, 0.1 | 37.8 | 0.1, 5, 0.1 | 46.8 | Refrigerator | 250 | 24 | 6000 | 24 | 6000 |
| Components | Description | Specification | Components | Description | Specification |
|---|---|---|---|---|---|
| Solar PVS [69] | Capacity | 1 kW | Converter [23] | Capacity | 1 kW |
| Capital cost | 640 $/kW | ||||
| Replacement cost | 640 $/kW | Efficiency | 96% | ||
| O&M cost | 10 $/year | ||||
| Lifetime | 25 years | Capital cost | 300 $/kW | ||
| Wind turbine [65] | Capacity | 1 kW | Converter [23] | Replacement cost | 300 $/kW |
| Hub height | 16 m | ||||
| Capital cost | 2000 $/kW | O&M cost | 0 $/year | ||
| Replacement cost | 1200 $/kW | ||||
| O&M cost | 100 $/year | Lifetime | 15 years | ||
| Lifetime | 20 years | ||||
| Li-Ion battery [99] | Nominal voltage | 6V | Diesel generator (Autosize) [69] | Minimum load ratio | 25% |
| Nominal capacity | 1 kWh/ 167 Ah | Fuel price | 1 $/liter | ||
| Roundtrip efficiency | 90% | Capital cost | 220 $/kW | ||
| SOCmin | 20% | Replacement cost | 200 $/kW | ||
| SOCmax | 100% | O&M cost | 0.020 $/operating hrs | ||
| Capital cost | 140 $ | Lifetime | 15,000 h | ||
| Replacement cost | 140 $ | Other inputs [23] | Lifetime of project | 25 | |
| O&M cost | 10 $/year | Inflation rate | 2% | ||
| Lifetime | 8 years | Nominal discount rate (%) | 8% |
| TS | Parameters | PVS/DG | WT/DG | PVS/WT/DG | PVS/WT | TS | PVS/DG | PVS/WT/DG | PVS/WT |
|---|---|---|---|---|---|---|---|---|---|
| FSWT | LEC ($/kWh) | 0.223 | 0.410 | 0.223 | 0.361 | TSVA | 0.223 | 0.222 | 0.383 |
| CNP ($) | 449,574 | 827,473 | 449,573 | 727,327 | 448,532 | 448,269 | 771,189 | ||
| LGP (%) | 0 | 0 | 0 | 0.0673 | 0.0330 | 0.0323 | 0.0628 | ||
| ENS (kWh/yr) | 0 | 0 | 0 | 105 | 51.5 | 50.3 | 97.9 | ||
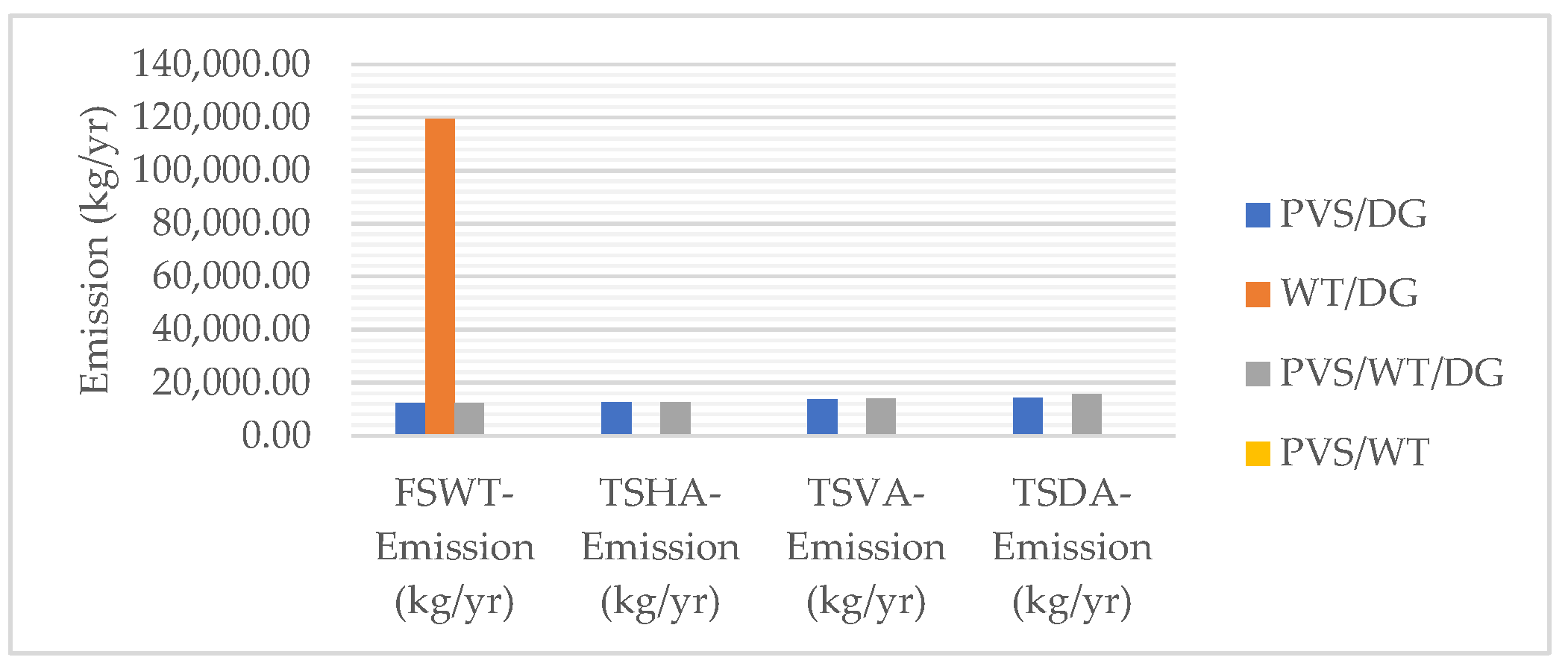
| CO2 emission (kg/yr) | 12,048 | 117,775 | 12,148 | 0 | 13,552 | 13,836 | 0 | ||
| Other emission (kg/yr) | 180.47 | 1763.9 | 182 | 0 | 203 | 207 | 0 | ||
| Total emission (kg/yr) | 12,228.4 | 119,538 | 12,330 | 0 | 13,755 | 14,043 | 0 | ||
| TSHA | LEC ($/kWh) | 0.224 | - | 0.224 | 0.336 | TSDA | 0.226 | 0.226 | 0.400 |
| CNP ($) | 452,516 | - | 452,516 | 676,153 | 455,751 | 455,327 | 806,655 | ||
| LGP (%) | 0 | - | 0 | 0.0722 | 0 | 0.0168 | 0.0635 | ||
| ENS (kWh/yr) | 0 | - | 0 | 113 | 0 | 26.1 | 99 | ||
| CO2 emission (kg/yr) | 12,449 | - | 12,449 | 0 | 14,055 | 15,590 | 0 | ||
| Other emission(kg/yr) | 186.5 | - | 186.5 | 0 | 210.6 | 233.6 | 0 | ||
| Total emission (kg/yr) | 12,635.5 | - | 12,635.5 | 0 | 14,265.6 | 15,823.6 | 0 |
| TS | Components | Parameters | PVS/DG | WT/DG | PVS/WT/DG | PVS/WT | TS | PVS/DG | PVS/WT/DG | PVS/WT |
|---|---|---|---|---|---|---|---|---|---|---|
| FSWT | PVS | Capacity (kW) | 146 | - | 146 | 519 | TSVA | 135 | 136 | 495 |
| Production (kWh/yr) | 245,487 | - | 246,575 | 874,855 | 251,356 | 252,135 | 920,740 | |||
| Capacity factor (%) | 19.3 | - | 19.3 | 19.3 | 21.2 | 21.2 | 21.2 | |||
| PVS penetration (%) | 157 | - | 158 | 561 | 161 | 162 | 590 | |||
| WT | Capacity (kW) | - | 19 | - | - | - | - | - | ||
| Production (kWh/yr) | - | 17,939 | - | - | - | - | - | |||
| Capacity factor (%) | - | 10.8 | - | - | - | - | - | |||
| LI battery | Nominal Capacity (kWh) | 527 | 82 | 526 | 703 | 517 | 512 | 687 | ||
| Energy out (kWh/yr) | 99,278 | 79,458 | 99,080 | 100,714 | 97,468 | 97,690 | 98,182 | |||
| FSWT | DG | Capacity (kW) | 85 | 85 | 85 | - | TSVA | 85 | 85 | - |
| Production (kWh/yr) | 13,039 | 154,310 | 13,103 | - | 17,636 | 18,058 | - | |||
| Fuel consumption (L/yr) | 4603 | 44993 | 4641 | - | 5177 | 5286 | - | |||
| Converter | Capacity (kW) | 70.3 | 52.2 | 68.3 | 81.9 | 60.7 | 60.8 | 129 | ||
| Energy output (kWh/yr) | 143,978 | 76,280 | 143,884 | 155,861 | 146,110 | 146,206 | 155,868 | |||
| Capacity factor (%) | 23.4 | 16.7 | 24.1 | 21.7 | 27.5 | 27.5 | 13.8 | |||
| Renewable fraction (%) | 91.6 | 1.06 | 91.6 | 100 | 88.7 | 88.4 | 100 | |||
| TSHA | PVS | Capacity (kW) | 135 | - | 135 | 243 | TSDA | 115 | 121 | 419 |
| Production (kWh/yr) | 244,647 | - | 244,647 | 439,843 | 257,949 | 271,603 | 937,777 | |||
| Capacity factor (%) | 20.7 | - | 20.7 | 20.7 | 25.5 | 25.5 | ||||
| PVS penetration (%) | 157 | - | 157 | 282 | 165 | 174 | 601 | |||
| WT capacity | Capacity (kW) | - | - | - | 38 | - | - | - | ||
| Production (kWh/yr) | - | - | - | 35,877 | - | - | - | |||
| Capacity factor (%) | - | - | - | 10.8 | - | - | - | |||
| LI battery | Nominal Capacity (kWh) | 519 | - | 519 | 716 | 519 | 510 | 894 | ||
| Energy out (kWh/yr) | 96,054 | - | 96,054 | 91,090 | 93,231 | 95,881 | 99,047 | |||
| DG | Capacity (kW) | 85 | - | 85 | - | 85 | 85 | - | ||
| Production (kWh/yr) | 13,472 | - | 13,472 | - | 15,317 | 20,328 | - | |||
| Fuel consumption (L/yr) | 4756 | - | 4756 | - | 5369 | 5956 | - | |||
| Converter | Capacity (kW) | 69.7 | - | 69.7 | 87.4 | 70.6 | 63 | 82.3 | ||
| Energy output (kWh/yr) | 143,633 | - | 143,633 | 130,279 | 142,119 | 145,778 | 155,867 | |||
| Capacity factor | 23.5 | - | 23.5 | 17.0 | 23 | 26.4 | 21.6 | |||
| Renewable fraction (%) | 91.4 | - | 91.4 | 100 | 90.2 | 87 | 100 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prakash, V.J.; Dhal, P.K. Techno-Economic Assessment of a Standalone Hybrid System Using Various Solar Tracking Systems for Kalpeni Island, India. Energies 2021, 14, 8533. https://doi.org/10.3390/en14248533
Prakash VJ, Dhal PK. Techno-Economic Assessment of a Standalone Hybrid System Using Various Solar Tracking Systems for Kalpeni Island, India. Energies. 2021; 14(24):8533. https://doi.org/10.3390/en14248533
Chicago/Turabian StylePrakash, Vinoth John, and Pradyumna Kumar Dhal. 2021. "Techno-Economic Assessment of a Standalone Hybrid System Using Various Solar Tracking Systems for Kalpeni Island, India" Energies 14, no. 24: 8533. https://doi.org/10.3390/en14248533
APA StylePrakash, V. J., & Dhal, P. K. (2021). Techno-Economic Assessment of a Standalone Hybrid System Using Various Solar Tracking Systems for Kalpeni Island, India. Energies, 14(24), 8533. https://doi.org/10.3390/en14248533







