Linearized Frequency-Dependent Reflection Coefficient and Attenuated Anisotropic Characteristics of Q-VTI Model
Abstract
:1. Introduction
2. Theories and Methods
2.1. Approximation of Frequency-Dependent Complex Stiffness Tensors for Q-VTI Model
2.2. Approximation of Frequency-Dependent Reflection Coefficient for Q-VTI Model
3. Test and Analysis
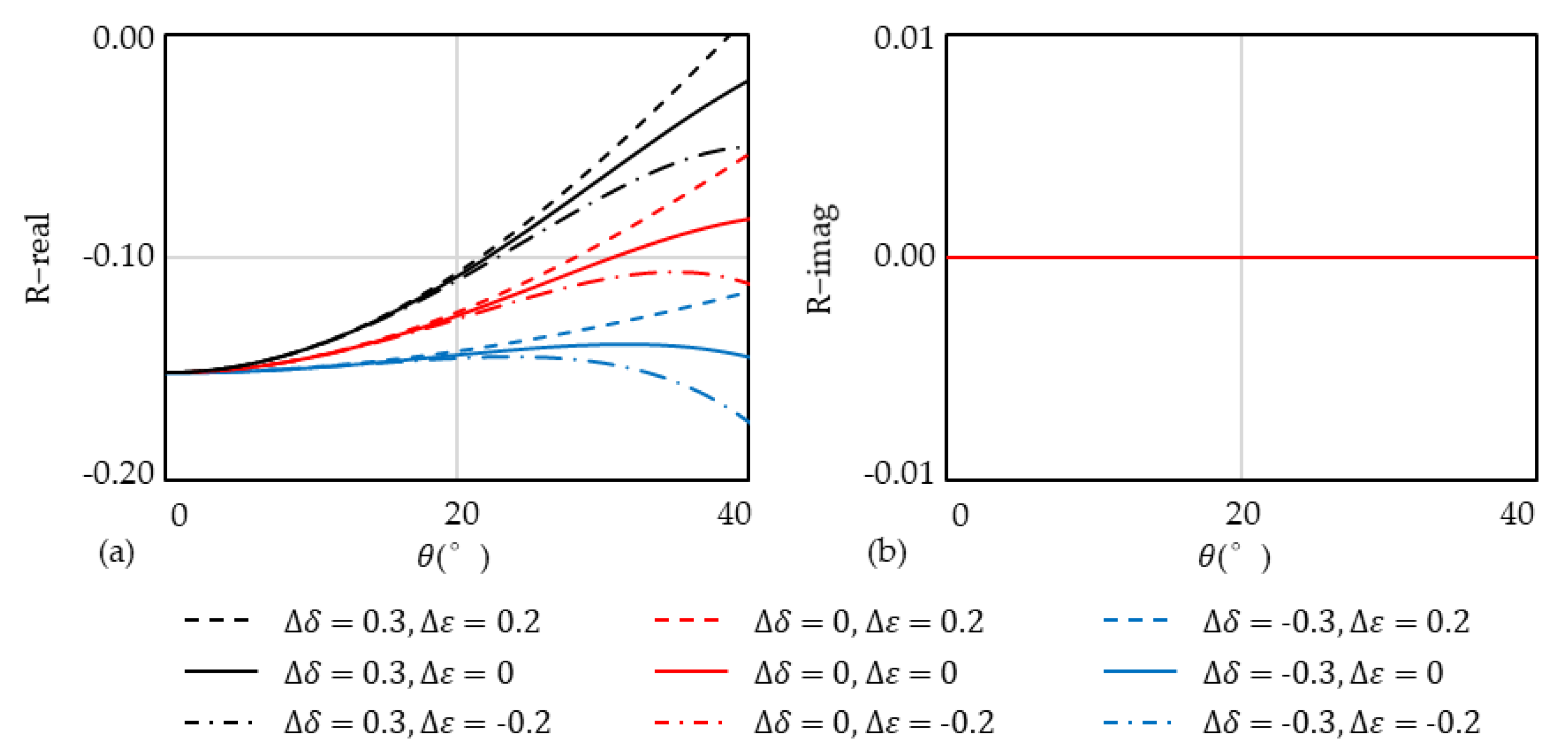
3.1. Characteristics of Reflection Coefficients for Q-VTI Model
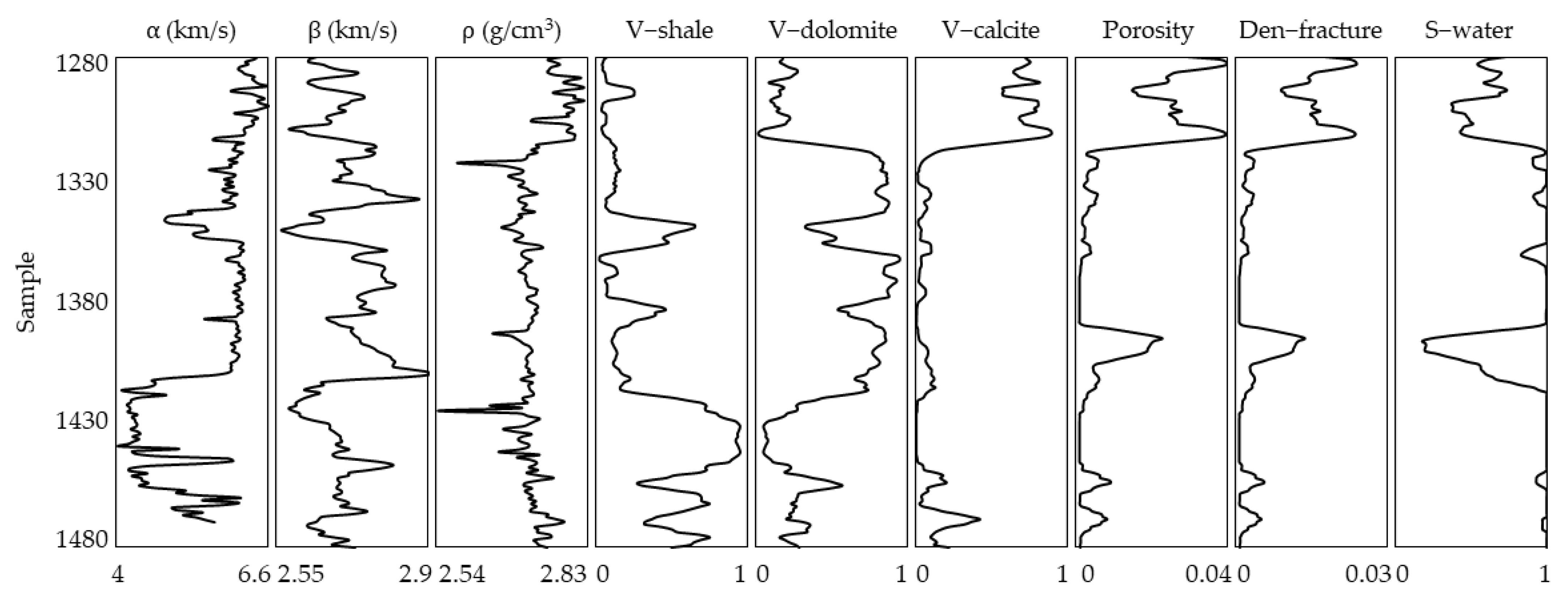
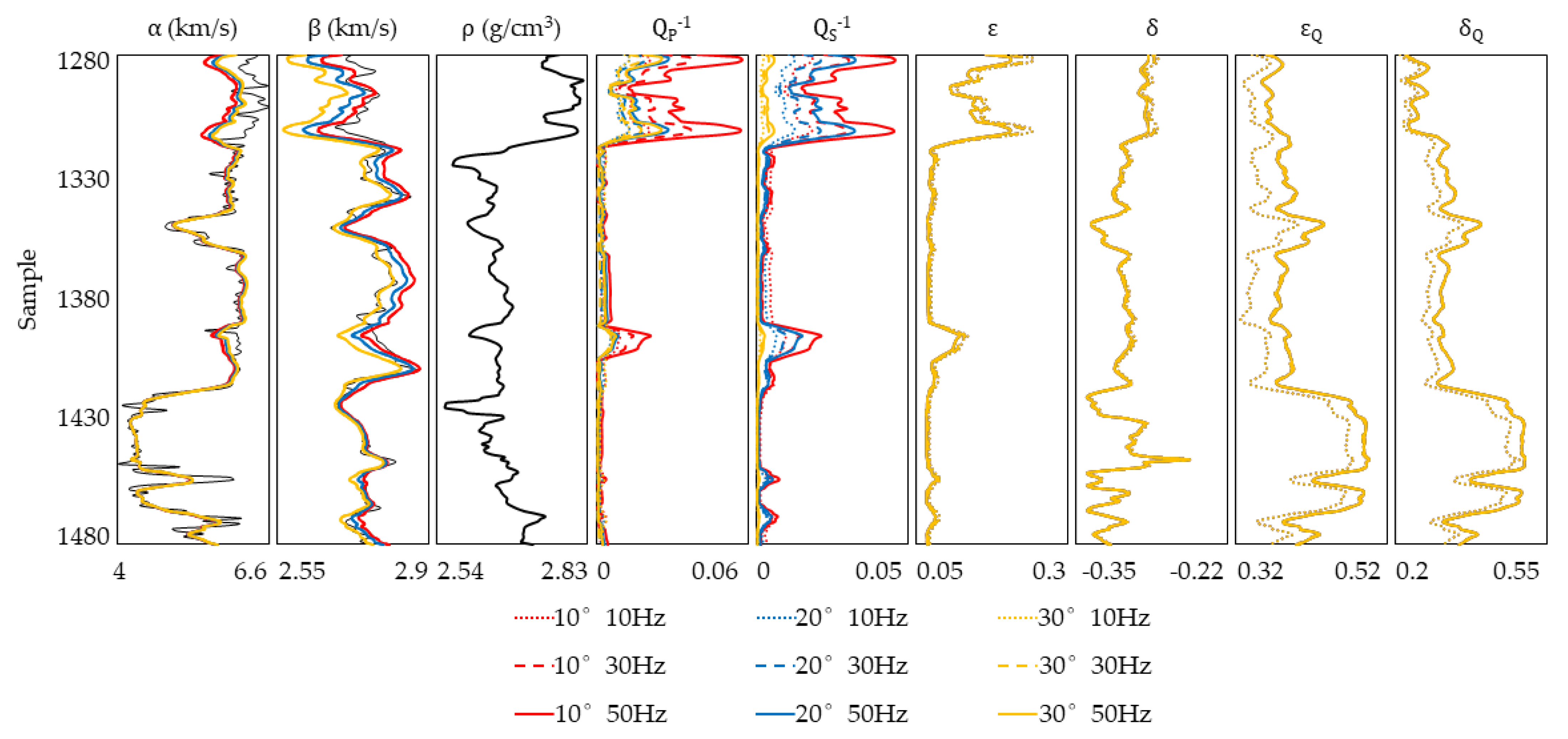
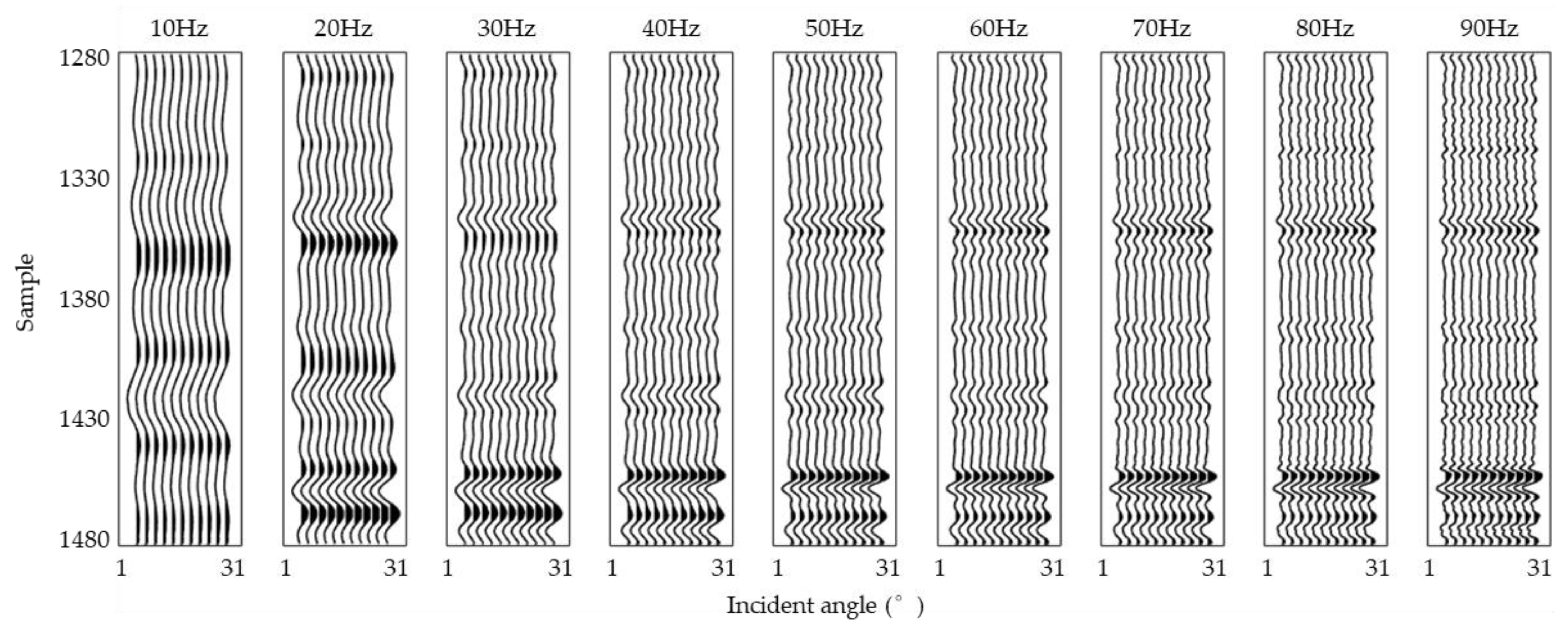
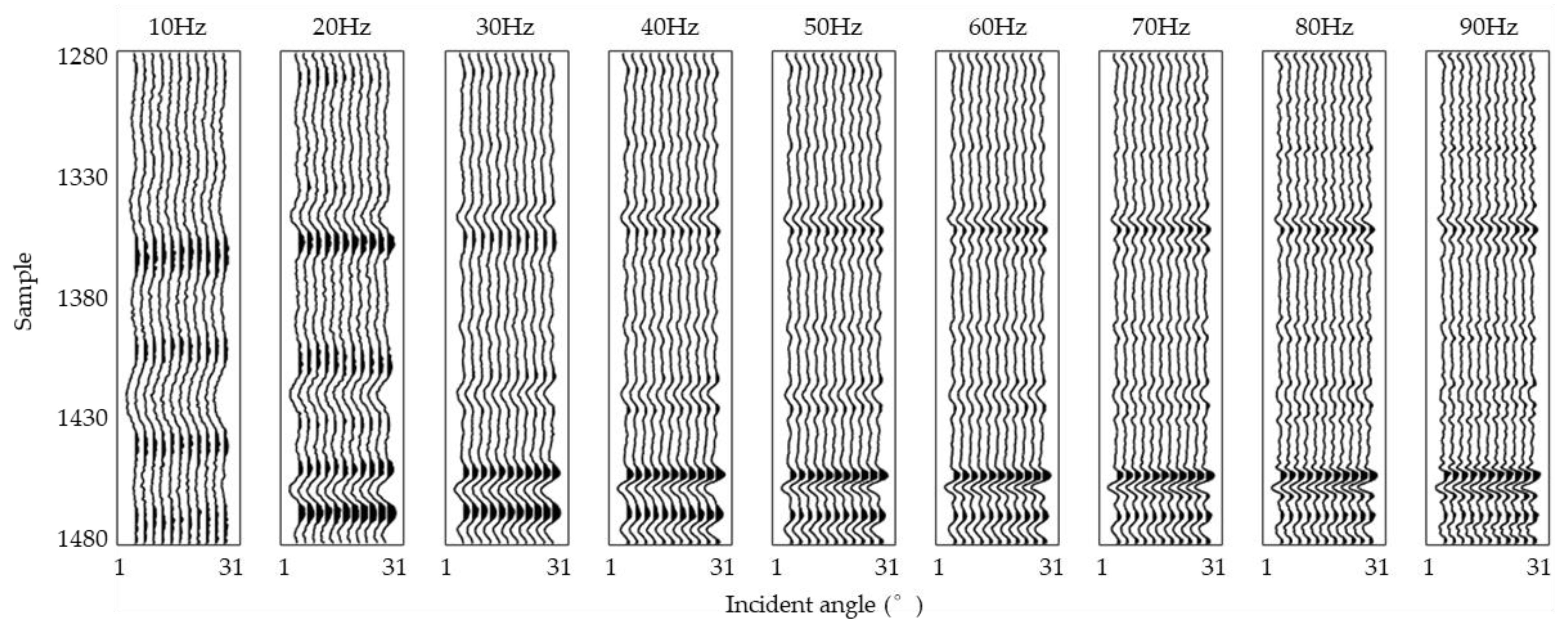
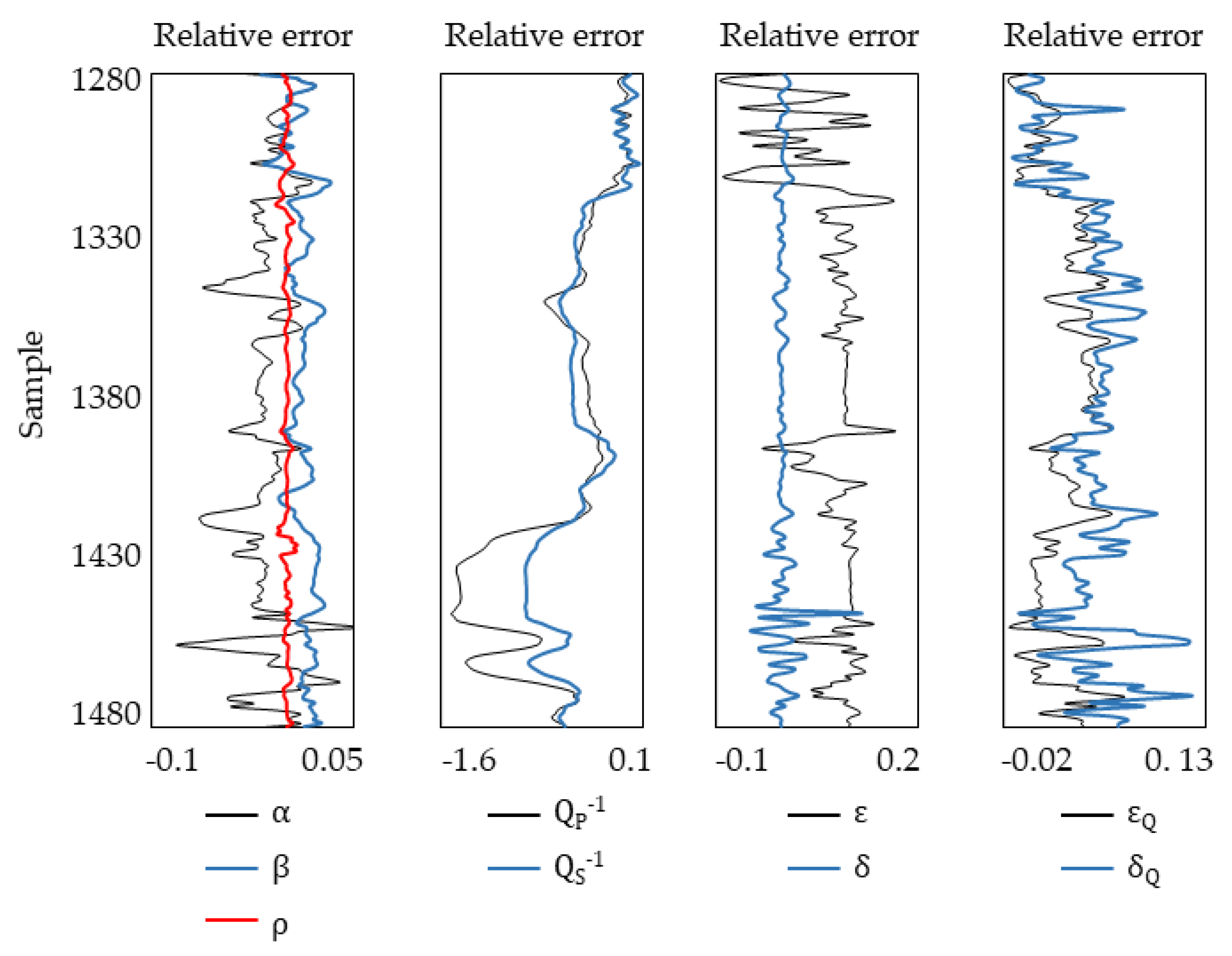
3.2. Inversion Test for Q-VTI Model
4. Result and Discussion
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Thomsen, L. Elastic anisotropy due to aligned cracks in porous rock. Geophys. Prospect. 1995, 43, 805–829. [Google Scholar] [CrossRef]
- Carcione, J.M. Constitutive model and wave equations for linear, viscoelastic, anisotropic media. Geophysics 1995, 60, 537–548. [Google Scholar] [CrossRef]
- Carcione, J.M. Wave Fields in Real Media: Wave Propagation in Anisotropic, Anelastic, Porous and Electromagnetic Media, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Chapman, M. Frequency-dependent anisotropy due to meso-scale fractures in the presence of equate porosity. Geophys. Prospect. 2003, 51, 369–379. [Google Scholar] [CrossRef] [Green Version]
- Chapman, M.; Liu, E.; Li, X. The influence of fluid-sensitive dispersion and attenuation on AVO analysis. Geophys. J. Int. 2006, 167, 89–105. [Google Scholar] [CrossRef] [Green Version]
- Chapman, M. Modeling the effect of multiple sets of mesoscale fractures in porous rock on frequency-dependent anisotropy. Geophysics 2009, 74, D97–D103. [Google Scholar] [CrossRef] [Green Version]
- Ba, J.; Cao, H.; Yao, F.; Nie, J.; Yang, H. Double-porosity rock model and squirt flow in the laboratory frequency band. Appl. Geophys. 2008, 5, 261–276. [Google Scholar] [CrossRef]
- Guo, J.; Shuai, D.; Wei, J.; Ding, P.; Gurevich, B. P-wave dispersion and attenuation due to scattering by aligned fluid saturated fractures with finite thickness: Theory and experiment. Geophys. J. Int. 2018, 215, 2114–2133. [Google Scholar] [CrossRef]
- Guo, J.; Gurevich, B.; Shuai, D. Frequency-dependent P-wave anisotropy due to scattering in rocks with aligned fractures. Geophysics 2020, 85, MR97–MR105. [Google Scholar] [CrossRef]
- Thanh, H.V.; Sugai, Y.; Nguele, R.; Sasaki, K. A New Petrophysical Modeling Workflow for Fractured Granite Basement Reservoir in Cuu Long Basin, Offshore Vietnam. In Proceedings of the 81st EAGE conference and exhibition, London, UK, 3–6 June 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Thanh, H.V.; Sugai, Y.; Nguele, R.; Sasaki, K. Integrated workflow in 3D geological model construction for evaluation of CO2 storage capacity of a fractured basement reservoir in Cuu Long Basin, Vietnam- Sciencedirect. Int. J. Greenh. Gas Control 2019, 90, 102826. [Google Scholar] [CrossRef]
- Schoenberg, M. Elastic wave behavior across linear slip interfaces. J. Acoust. Soc. Am. 1980, 68, 1516–1521. [Google Scholar] [CrossRef] [Green Version]
- Hudson, J.A. Wave speeds and attenuation of elastic waves in material containing cracks. Geophys. J. Int. 1981, 64, 133–150. [Google Scholar] [CrossRef]
- Gurevich, B. Elastic properties of saturated porous rocks with aligned fractures. J. Appl. Geophys. 2003, 54, 203–218. [Google Scholar] [CrossRef]
- Chapman, M.; Maultzsch, M.; Liu, E.; Li, X. The effect of fluid saturation in an anisotropic multi-scale equant porosity model. J. Appl. Geophys. 2003, 54, 191–202. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P.G. Quantitative Seismology: Theory and Methods; W.H. Freeman: San Francisco, CA, USA, 1980; p. 932. [Google Scholar]
- Shaw, R.K.; Sen, M.K. Use of AVOA data to estimate fluid indicator in a vertically fractured medium. Geophysics 2006, 71, C15–C24. [Google Scholar] [CrossRef]
- Zong, Z.; Yin, X.; Wu, G. Complex seismic amplitude inversion for P-wave and S-wave quality factors. Geophys. J. Int. 2015, 202, 564–577. [Google Scholar] [CrossRef]
- Moradi, S.; Innanen, K.A. Born scattering and inversion sensitivities in viscoelastic transversely isotropic media. Geophys. J. Int. 2017, 211, 1177–1188. [Google Scholar] [CrossRef]
- Moradi, S. Scattering of Seismic Waves from Arbitrary Viscoelastic-Isotropic and Anisotropic Structures with Applications to Data Modelling, FWI Sensitivities and Linearized AVO-AVAz Analysis. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2017. [Google Scholar]
- Chen, H.; Innanen, K.A.; Chen, T. Estimating P- and S-wave inverse quality factors from observed seismic data using an attenuative elastic impedance. Geophysics 2018, 83, R173–R187. [Google Scholar] [CrossRef]
- Chen, H.; Li, J.; Innanen, K.A. Inversion of differences in frequency components of azimuthal seismic data for indicators of oil-bearing fractured reservoirs based on an attenuative cracked model. Geophysics 2020, 85, 1MJ-Z13. [Google Scholar] [CrossRef]
- Pan, X.; Zhang, G.; Cui, Y. Matrix-fluid-fracture decoupled-based elastic impedance variation with angle and azimuth inversion for fluid modulus and fracture weaknesses. J. Pet. Sci. Eng. 2020, 189, 106974. [Google Scholar] [CrossRef]
- Kjartansson, E. Constant Q-wave propagation and attenuation. J. Geophys. Res. Atmos. 1979, 84, 4737–4748. [Google Scholar] [CrossRef] [Green Version]
- Thomsen, L. Weak elastic anisotropy. Geophysics 1986, 51, 1954–1966. [Google Scholar] [CrossRef]
- Thomsen, L. Reflection seismology over azimuthally anisotropic media. Geophysics 1988, 53, 304–313. [Google Scholar] [CrossRef]
- Zhu, Y.; Tsvankin, I. Plane-wave propagation in attenuative transversely isotropic media. Geophysics 2006, 71, T17–T30. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Tsvankin, I.; Dewangan, P.; Wijk, K.V. Physical modeling and analysis of P-wave attenuation anisotropy in transversely isotropic media. Geophysics 2007, 72, D1–D7. [Google Scholar] [CrossRef]
- Shaw, R.K.; Sen, M.K. Born integral, stationary phase and linearized reflection coefficients in weak anisotropic media. Geophys. J. Int. 2004, 158, 225–238. [Google Scholar] [CrossRef] [Green Version]
- Rüger, A. Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media. Ph.D. Thesis, Colorado School of Mines, Denver, CO, USA, 1996. [Google Scholar]
- Rüger, A. Variation of P-wave reflectivity with offset and azimuth in anisotropic media. Geophysics 1998, 63, 935–947. [Google Scholar] [CrossRef]
- Shuey, R.T. A simplification of the Zoeppritz equations. Geophysics 1985, 50, 609–614. [Google Scholar] [CrossRef]

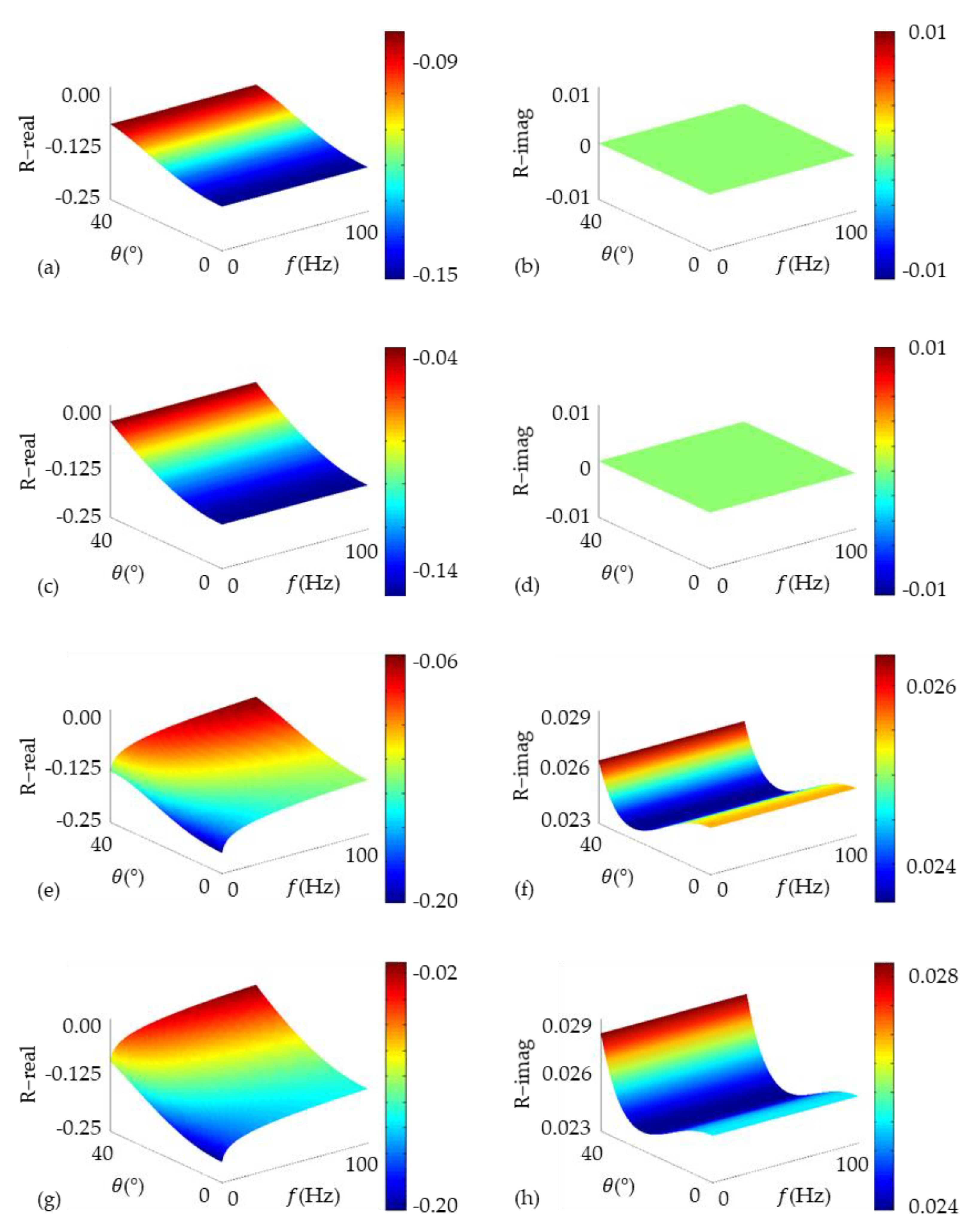
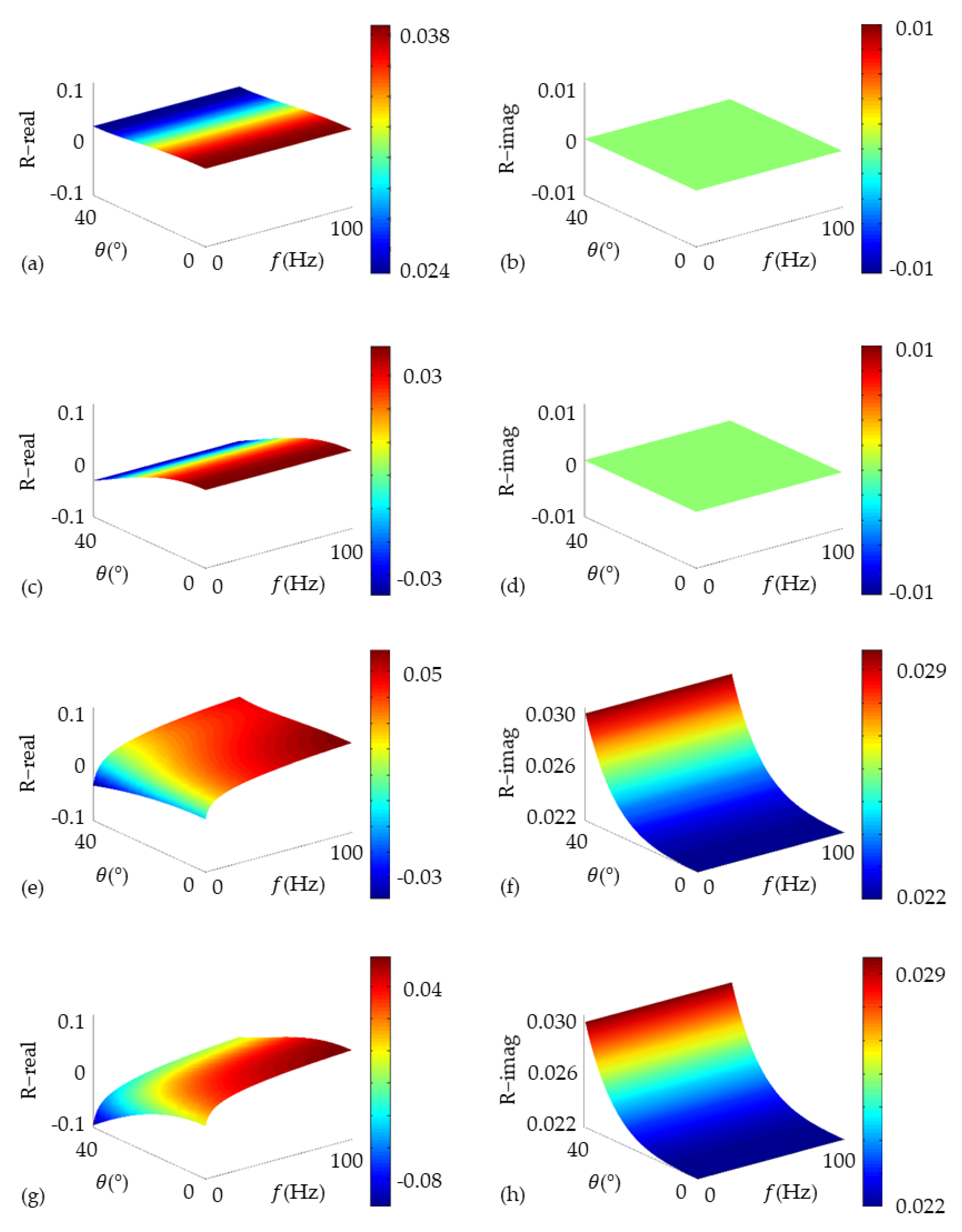


| Layer | (km/s) | (km/s) | (g/cm3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mud-shale | 5.073 | 2.998 | 2.68 | 0.010 | 0.012 | 0.001 | 0.001 | 0.001 | 0.001 |
| Oil-shale | 4.231 | 2.539 | 2.37 | 0.200 | 0.100 | 0.205 | 0.118 | 0.046 | 0.025 |
| Layer | (km/s) | (km/s) | (g/cm3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Mud-shale | 5.073 | 2.998 | 2.68 | 0.010 | 0.012 | 0.001 | 0.001 | 0.001 | 0.001 |
| Calcareous Sandstone | 5.460 | 3.219 | 2.69 | 0.000 | −0.264 | 0.177 | 0.056 | −0.025 | 0.050 |
| Anisotropic Perturbation | 1 | 2 | 3 |
|---|---|---|---|
| 0.3 | 0 | −0.3 | |
| 0.2, 0, −0.2 | 0.2, 0, −0.2 | 0.2, 0, −0.2 |
| Attenuated Perturbation | 1 | 2 | 3 |
|---|---|---|---|
| 0 | 0.02 | 0.2 | |
| 0 | 0, 0.012 | 0, 0.012, 0.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Yin, X.; Zhang, B.; Cao, D.; Gao, G. Linearized Frequency-Dependent Reflection Coefficient and Attenuated Anisotropic Characteristics of Q-VTI Model. Energies 2021, 14, 8506. https://doi.org/10.3390/en14248506
Yang Y, Yin X, Zhang B, Cao D, Gao G. Linearized Frequency-Dependent Reflection Coefficient and Attenuated Anisotropic Characteristics of Q-VTI Model. Energies. 2021; 14(24):8506. https://doi.org/10.3390/en14248506
Chicago/Turabian StyleYang, Yahua, Xingyao Yin, Bo Zhang, Danping Cao, and Gang Gao. 2021. "Linearized Frequency-Dependent Reflection Coefficient and Attenuated Anisotropic Characteristics of Q-VTI Model" Energies 14, no. 24: 8506. https://doi.org/10.3390/en14248506
APA StyleYang, Y., Yin, X., Zhang, B., Cao, D., & Gao, G. (2021). Linearized Frequency-Dependent Reflection Coefficient and Attenuated Anisotropic Characteristics of Q-VTI Model. Energies, 14(24), 8506. https://doi.org/10.3390/en14248506





