Abstract
The energy return on energy invested, EROI or EROEI, is the ratio of the energy produced by a system to the energy expended to build, maintain, and finally dismantle the system. It is an important parameter for evaluating the efficiency of energy-producing technologies. In this paper, we examine the concept of EROEI from the general viewpoint of dynamic dissipative systems, providing insights on a wider range of applications. In general, natural resources can be assimilated to energy stocks characterized by a potential that can be exploited by creating intermediate stocks. This transformation is typical of dissipative systems and for the first time, we report that the Lotka–Volterra model, usually confined to the study of the biology of populations, can represent a powerful tool to estimate the EROEI of dissipative systems and, in particular, those systems subjected to depletion. This assessment is important to evaluate the ongoing energy transition since it provides us with a model for the decline of the EROEI in the exploitation of fossil fuels.
1. Introduction
The energy return on energy invested (EROEI or EROI) [1] is defined as the ratio of the energy produced over the lifetime of an energy production system divided by the energy necessary to build, maintain, and finally dismantle and recycle the system. It is a fundamental parameter for the evaluation of energy-producing technologies. An EROEI > 1 is necessary for a technology to be a net producer of energy rather than a sink and, in general, the larger the EROEI, the more efficient the technology will be.
Being based on the ratio of two physical parameters, the EROEI is independent of the vagaries of markets and of consumer preferences and it can provide, at least in principle, an objective comparison of the performance of energy-producing technologies [2]. It is normally calculated by the direct evaluation of the energy flows in real systems, typically making use of life cycle analysis (LCA) techniques [3]. Unfortunately, the uncertainties inherent in the calculation or the improper applications of the correct procedures [4] may lead to different results for the same systems [5,6,7,8].
In the present study, we use system dynamics to examine the concept of EROEI from the general viewpoint of the behavior of non-equilibrium systems and in particular that of the “complex dissipative systems” (CASs) [9]. This analysis is not supposed to replace conventional LCA methods, but to provide a conceptual model of the role of EROEI in the exploitation of natural resources, in particular of fossil fuels.
For this purpose, we used the well-known Lotka–Volterra (LV) model [10,11]. Even though LV model applications in population biology turned out to be problematic [12], we show here how a version of the model that we call the “Single-Cycle Lotka–Volterra” (SCLV) can provide a conceptual model for the decline of the EROEI of the systems called “dissipative” that is those dynamic systems that form as the result of the dissipation of thermodynamic potentials [13,14]. Such models are a fundamental factor in the planning of the transition toward renewable energy. We need to know, at least conceptually, how fast the energy produced by a non-renewable system will decline as a function of declining EROEI. On this basis, it is possible to plan for the phasing out of fossils during the transition phase, a concept termed the “Sower’s strategy” [15,16].
Our analysis also sheds light on the relationship between EROEI and the phenomenon called “overexploitation”, also referred to as “overshoot” [17,18], which is responsible for the decline or the collapse of the economic systems that exploit natural resources. Finally, the concept of EROEI as determined by the SCLV model can be used to gain insight into the behavior of a remarkable variety of real word systems, including fields, such as engineering [19,20], social sciences [21,22], business management [23], decision-making [24], environmental sciences [25], and more.
2. Methods
The Lotka–Volterra (LV) model was the first mathematical model describing a complex adaptive system (CAS) [9]. It was independently developed in the 1920s by Alfred Lotka [10] and Vito Volterra [11]. It was conceived to model the interplay between two biological populations at two different trophic levels: one of the two species being the predator and the other the prey. Often, these two levels are referred to as “foxes” and “rabbits”. In a wider sense, this model can describe the energy transfer between two energy levels, or stocks, linked by feedback relationships. Because of these feedbacks, this system can also be defined as “autocatalytic”.
The LV model is not necessarily limited to a biological population. It was first applied to a non-biological predation dynamics, the fisheries of the Mediterranean sea, in an early work by Volterra himself in collaboration with Roberto D’Ancona [26]. These results were replicated later on in other fisheries [27,28]. In general, when the model is applied to economic systems, the first stock (assimilable to the prey in biological systems) may be termed “resource” (e.g., an oil field), whereas the second stock (assimilable to the predator in biological systems) is the ensemble of “capital” (equipment, materials, building, workers, etc.) needed to exploit the resource.
The LV model dynamics can be described in a graphical form using the system dynamics (SD) conventions [29]. Stocks are represented as rectangles, flows between stocks are represented by double-edged arrows, and the regulation of flows is based on “valves”, which may be affected by stocks or by other variables. Single line arrows describe the relations of stocks with flows, highlighting feedback loops.
The LV model can be represented as shown in Figure 1, drawn using the Vensim™ software package.
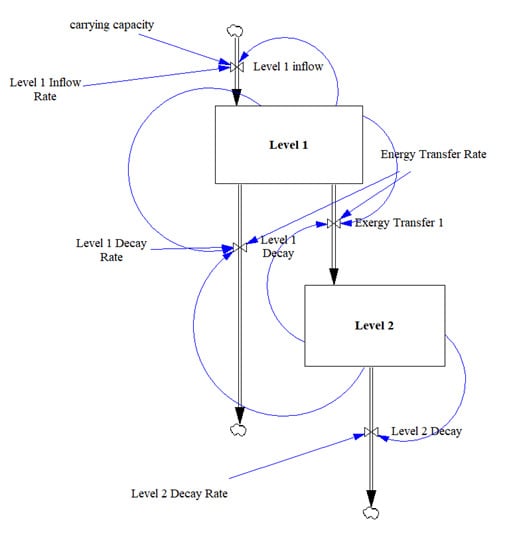
Figure 1.
An interpretation of the 2-stock trophic chain model according to the conventions of system dynamics.
In this model, we label the two stocks as L1 and L2. We assume that level 1 is at higher potential energy than level 2, so that energy flows from L1 to L2 but not the reverse (rabbits do not eat foxes, not normally at least). These stocks are normally measured in terms of population; that is, the number of individuals. However, what moves from one stock to the other is not individual rabbits (prey), but the metabolic energy they provide to foxes (predator). Therefore, a more general version of the model sees the L1 (prey) and L2 (predator) stocks as energy stocks. Energy comes into the system from a non-quantified stock (grass) represented as a small cloud in the SD graphical representation. This energy accumulates into the L1 stock (rabbits), and it gradually moves to the L2 stock (foxes), but some of it is lost to the environment in the form of waste heat. We will see that it is this view that allows us to use the LV model to define the EROEI of the energy transfer between the stocks.
This graphical representation is useful for an intuitive understanding of the conventional differential equations describing the LV model (see Equations (1) and (2)). The model is drawn in such a way to emphasize how the flow of energy goes “down” as the potentials are dissipated. It is just a graphical convention, and it does not affect the equations of the model. The equations are written below, with k1, k2, k3, and η as fixed parameters:
dL1/dt = k1L1 − k2L1L2
dL2/dt = ηk2L1L2 − k3L2
Dimensionally, L1 and L2 can be measured in energy units. The k1 and k3 parameters are measured in units of [time]−1; that is, as frequencies. Their values are proportional to how fast the system replenishes or empties its stocks. k2 has the dimension of [time]−1 ∗ [energy]−1 and it is proportional to the rate of interaction of the two stocks. Note that k2 is the dimension of the inverse of an “action” (energy ∗ time). It is an attribute of the dynamics of a physical system from which the equations of motion of the system can be derived through the principle of the least action. As recently discussed by Sharma and Annila, the second law of thermodynamics can be understood in terms of an equation of motion [30]. According to Annila, the natural process (energy dissipation in trophic levels) moves following the steepest descents of the potential energy landscape by equalizing differences in energy via various transport, transformation, and dissipative processes, e.g., diffusion, heat flows, electric currents, and chemical reactions [31].
In the equations, η (eta) is a dimensionless efficiency parameter that can go from zero to one. In many cases, it can be seen as describing the fraction of energy lost as low-temperature heat in the transformation, according to the second law of thermodynamics. Nevertheless, in the case of human-managed systems, a fraction of the flow of the energy produced may not be (and usually is not) reinvested into the capital stock used to produce more energy. Humans tend to use a large fraction of this energy flow in activities that may be defined as “ludic”: tourism, politics, football, pyramids, and many more. In the present section, we assume that these factors are incorporated in the η factor. The role of the distribution of the energy production in different societal sectors will be discussed later, in the section dedicated to world models.
Although the LV equations are not solvable analytically, the time evolution of the L1 and L2 stocks can be easily determined by numerical methods. In the form written above, the two stocks undergo an unending series of oscillations as a function of time (Figure 2). This behavior makes the LV system an example of a biological clock. It can be shown that it has a frequency equal to (1/2π) (k1ηk2)1/2 [32].
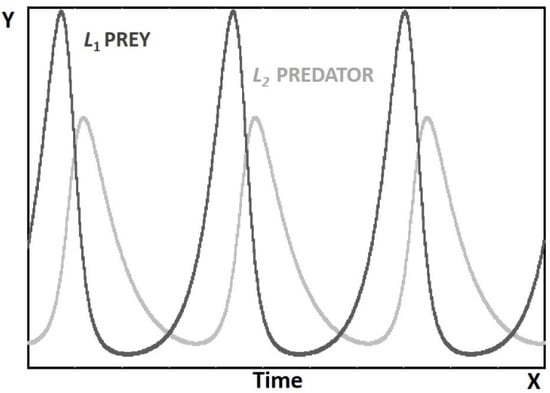
Figure 2.
The result of the simplest version of the Lotka–Volterra 2-stock model.
The periodic behavior of the system becomes clearer by looking at a plot of L1 and L2 in phase space, where the oscillations are represented by a closed trajectory (Figure 3). In this version of the model, all the cycles are identical and superimposable.
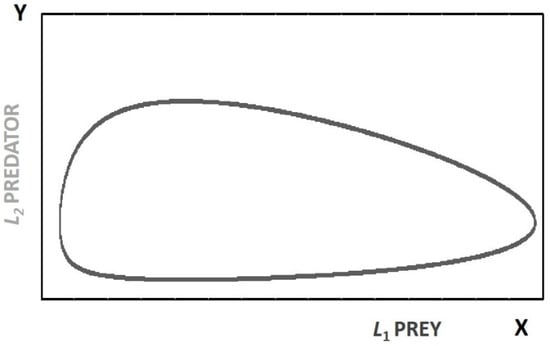
Figure 3.
Prey–predator periodic behaviors represented in the space of the two stocks.
The equations of the basic LV model can be modified in various ways [33]. Perhaps the most common variant is the “competition” or “competitive” model, where the growth of one or both stocks is limited by a parameter called the “carrying capacity” of the system, which is the maximum number of individuals (or their total metabolic energy) that the system can sustain in one or both stocks considered. Other variants add more parameters and relations, e.g., predator satiation, visual range, speed, and more [34,35]. Most of the alternative models maintain the two-species trophic chain, although it is possible to generalize the model considering “n” trophic levels [36].
In the present paper, we use the simplest form of the Lotka–Volterra model to derive a variant, where the k1 parameter is set to 0. It means that the higher potential stock is not replenished. We call this version the “Single Cycle Lotka–Volterra” model (SCLV). These are the equations for the model:
dL1/dt = −k2L1L2
dL2/dt = ηk2L1L2 − k3L2.
The SCLV model is not formally different from the standard LV model, since the only constraint for it is that it is supposed to describe a physical system and then the constants must not be <0. Nevertheless, we use the term SCLV (Equations (3) and (4)) to clearly identify this variant in the present paper. We already used this variant to describe such systems as the whaling industry, which exploits a resource (whales) that reproduces very slowly [27,37]. The resulting behavior for the production as a function of time is a single “bell-shaped curve” for both L2 stock and for the flow from L1 and L2 (with the dL1/dt labeled as “Production”). Instead, L1 decreases monotonically.
Typical results for the SCLV model are shown in Figure 4. Since this model can be used to describe the production cycle of non-renewable economic resources (e.g., crude oil) [27], as discussed before, the “predator” (L2) can be defined as the ensemble of resources used to exploit the resource (L1) and therefore it can be labeled as “capital” in order to align the terminology of the model with the commonly used nomenclature in economics.
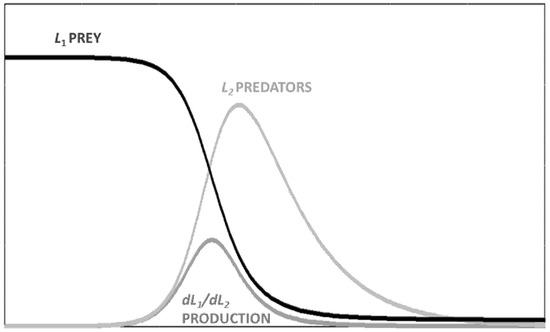
Figure 4.
Single-cycle two-stock model (SCLV): Resources = L1; Capital = L2; Production = dL1/dt.
The SCLV model has a stable attractor for L2 = 0 (extinction of the predators) but not necessarily for L1 = 0. In the case of an economic system, it means that the resource will not be completely exploited before the capital stock goes to zero.
In the following, we will maintain the “foxes and rabbits” intuitive image for the stocks even though, of course, rabbits do reproduce. However, even when rabbits reproduce “like rabbits”, every single cycle of the standard LV model can be qualitatively seen as a case of the SCLV model.
3. Results: Modeling the EROEI Parameter
The LV and SCLV models describe the transfer of energy from a stock to another in a dissipative system. How fast this energy is transferred determines the growth or decline of the whole system. The ratio (Eout)/(Ein) was defined by Charles Hall in 1979 as EROI or EROEI (energy return on energy invested) [1,2,3,38]. More explicitly, it is the energy gained by a stock divided by the energy lost by the stock.
The EROEI parameter does not appear in the standard version of the LV equations, but it is the same thing as the “net reproduction rate”, a well-known parameter in population biology. This parameter is defined as the ratio of the new individuals being born divided by the number of individuals that are dead or removed from the population by other factors (e.g., emigration). If we define a population as a stock of metabolic energy, this definition is equivalent to the (Eout)/(Ein) ratio.
Since the LV equations describe the evolution of biological populations, the net reproduction rate must be contained in the interplay of the variables and the coefficients. It can be made explicit by rearranging the terms in the equations. For this purpose, note that the “production” of energy can be identified as the flow of energy from the L1 (resource) stock into the L2 (capital) stock (dL1/dt or −k2L1L2). In the same way, the “expended” energy is the energy that the L2 stock loses; that is, the flow out of the L2 stock (k3L2).
Note that the flow out of the L1 stock is not the same thing as the flow into the L2 stock. Because of the second law of thermodynamics, one unit of energy resource creates much less than one unit of capital energy. The loss for the predator/prey trophic level in vertebrate biological chains is called the “Lindemann efficiency” and it is often estimated as ca. 10%, with a high degree of uncertainty. Recent data [39] indicate that it can be as low as 1%. This feature is considered in the LV/SCLV model by means of the η parameter, which is always <1.
Accordingly, in the simple case of a two-level biological trophic chain, the EROEI can be written as the flow of exergy (useful energy) that goes into L2 (ηk2L1L2) divided by the flow of energy out of L2, (k3L2). Specifically:
EROEI2stocks = ηk2L1/k3
This term (Equation (5)) represents the flow of energy turned into capital (gain) divided by the capital dissipated (loss) in the process. The formula is valid in the same way for the SCLV model and for the multicycle standard LV model. However, while in the SCLV model, the EROEI declines irreversibly with L1, in the multicycle LV model, it oscillates periodically in proportion to L1. Note also that EROEI is directly proportional to three factors: the efficiency of the transformation, η; the transformation rate factor, k2; and the amount of the resource, L1. The EROEI is also inversely proportional to k3, the factor that describes how fast capital disappears because of depreciation (definable also as maintenance, the term dL2/dt). Note that the L2 stock does not appear in the formula. In the LV model, foxes are assumed to chase rabbits at a rate independent from their number. Of course, in the real world, economies of scale occur, and some predators do band together to hunt their prey. The formula could be modified making it explicitly proportional to L2. However, in the present study, we will remain with the basic model assumptions.
In this form, the model is highly aggregated with all the capital stock measured using energy as a proxy. We can say that foxes are described at the same time as energy producers (rabbit hunters) and equipment producers (foxling generators). So, a single stock, L2, describes both activities. However, in many cases, the two activities can be separated, especially in the case of the human economy. For instance, the oil industry is an energy producer, but oil wells do not directly spawn other oil wells. Society dedicates a stock of resources and energy to generate a complete industrial sector that provides the oil industry with materials, equipment, and human power. This differentiation can be accounted for in the model by adding another stock. This version of the model is the result of a common procedure in system dynamics, where systems can be complexified by adding more stocks and more interactions among them. For instance, the “World3” model used in one of the first dynamic studies of the world system, the Limits to Growth [40], consisted of five main stocks of capital and resources. Other more recent models include renewable energies [41] and use larger numbers of parameters (see, e.g., the MEDEAS world model [42]). In the present case, we aim at keeping the model simple to be able to use it to determine the EROEI in an explicit form. This determination is more difficult to do univocally in a more complex model. Nevertheless, we use this three-stock model as an example to outline how the procedure can be expanded.
In the three-stock model, the second stock (L2) stock is “society”, the entity that grows on the exploitation of the resources (Equation (7)). It grows proportionally to the flow of resources it obtains from the resource stock (Equation (6)). η12 represents the efficiency of transformation of resources into an increase of societal capital. At the same time, the societal capital does not directly exploit resources, but it must allocate some capital to the third stock, L3, that aggregates the “producers”—that fraction of the stocks that directly exploits natural resources (Equation (8)). The resulting three equations are (still in the single cycle assumption):
dL1/dt = −k2L1L2
dL2/dt = η12k2L1L2L3 − k3L2L3
dL3/dt = η23k3L2L3 − k4L3
It may be thought, for instance, of as the “oil industry”. Note how production, intended as the flow of energy into the L2 stock, is proportional to the producer stock, L3, to the amounts of resources available and to the whole society that provides a market pull for the production: the efficiency of this transformation is represented by η23. The flow of resources into the producer stock is proportional to the societal stock and to the producer stock itself in terms of compensating capital depreciation.
In this model, the numerator of the EROEI ratio is given by the energy that goes into the L2 stock (societal stock), which is equal to η12k2L1L2L3. The denominator is given by the outflow from L2 (k3L2L3). The resulting EROEI is the same as it was defined for the simpler two-stock system:
EROEI3stocks = η12k2L1L2/k3
There are, of course, many possible ways to rearrange the model that could be further itemized by separately considering the various industrial sectors engaged in the task. This would generate different forms for the Eout/Ein ratio. Nevertheless, we believe that this version is the least arbitrary choice.
Now, returning to the two-stock model, EROEI2stocks = ηk2L1/k3.
Therefore, L1 = k3 EROEI2stocks/ηk2. Substituting these values in the LV equations, we have that:
dL1/dt = (1/η) EROEI2stocks (k1k3/k2 − k3L2)
dL2/dt = L2k3 (EROEI2stocks − 1)
Just as for the standard LV system, Equations (10) and (11) produce oscillations for both stocks. The EROEI2stocks parameter oscillates, too, since it is proportional to the L1 stock.
In the case of the SCLV model, k1 is set to zero and the equations become:
dL1/dt = −(1/η) k3L2EROEISCLV
dL2/dt = L2k3 (EROEISCLV − 1)
In this version of the model, the L1 stock declines monotonically with time since all terms in the first equation are positive. Since the EROEISCLV and L1 are directly proportional to each other, the EROEISCLV will also decline monotonically along the production cycle. Neither needs to go to zero but will stabilize in the long run at values > 0. The second equation shows that the growth of the L2 stock is exponential when we have EROEISCLV >> 1, which may happen during the initial phases of growth. The L2 stock reaches a maximum for EROEISCLV = 1, then it declines when EROEISCLV < 1. The exergy that flows into L2, ηk2L1L2 is conventionally termed “production”, especially in the case of the oil industry. This quantity can be expressed in terms of the EROEISCLV parameter as k2L2EROEI for the SCLV system.
In Figure 5, we show the behavior of the EROEISCLV according to the SCLV model. We also show the related parameter known as “Net Energy”, which is equal to Eout-Ein and is related to EROEISCLV by the formula: Net Energy = (EROEISCLV − 1)∙Ein. Note that the Net Energy is negative when EROEISCLV < 1.
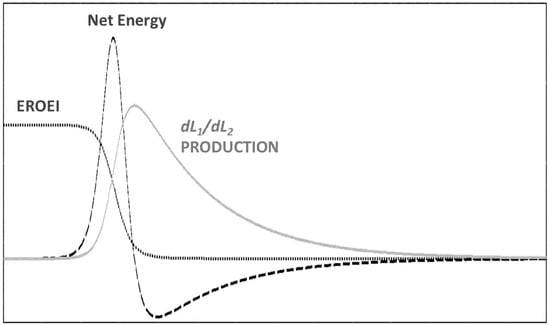
Figure 5.
Behavior of the EROEISCLV and Net Energy according to the SCLV model.
In previous papers [37,43,44], we showed that the production curve of a system described by the SCLV model (e.g., oil production) typically follows a “bell-shaped” curve, known as the “Hubbert Curve” in the field of crude oil production [45]. The production curve generated by the SCLV model is shown in Figure 4 and Figure 5. The maximum value of the Hubbert curve is often defined as the “Hubbert Peak” or “peak oil”, a concept that has generated much interest in the debate about oil depletion [46,47,48]. It is normally believed that the production curve will be bell-shaped and symmetric, but this is not always the case [48,49].
The Hubbert curve is often simulated by means of the derivative of a logistic function, but this approach is based on parameters that cannot be directly related to the energy flows—and hence to the EROEI—of the system. Instead, the SCLV model provides the tools needed to determine the relation of the peak with the EROEI of the system. Taking the second derivative of dL2/dt and setting it to zero for the SCLV case, considering the expression EROEISCLV = ηk2L1/k3, we find that the maximum production occurs when EROEISCLV = k2L2/k3 + 1. All the terms in this expression are positive, so the production curve will peak and start declining before the EROEI of extraction has become lower than one. In other words, production will peak for an EROEISCLV > 1.
This is a relevant result relative to the discussion about peak oil, often centered on discussing how dwindling EROEI affects production [50]. Since, as we saw, “peak capital” occurs for EROEI = 1, the production curve will peak before the capital curve. This has been observed in studies based on the iterative solution of the LV equations [37,43,44].
The determination of the numerical value of the EROEI of a dissipative system could be obtained by fitting the available time-dependent data to the SCLV model, obtaining the model parameters, and calculating the EROEISCLV from the formula EROEISCLV = ηk2L1/k3. The practical feasibility of this method depends on the availability of data expressed in suitable energy units, which is rare. In the present study, we are not going into this subject, limiting ourselves to general considerations on the effect of the EROEI parameter on systems that can be described using the LV model.
4. Discussion
The concept of EROEI has been used so far only as a parameter to compare different energy production technologies, for instance, renewable energy and fossil energy. However, the EROEI parameter is much more general, and it is a characteristic of several real-world systems: biological, economic, and social ones. In most cases, the discussion must remain qualitative since we lack the data that could allow a quantitative determination of the EROEI. Nevertheless, we believe that the EROEI in these systems plays a key role that needs to be understood if we are to face the effects of changes involving such phenomena as the exploitation of natural resources or the growth and decline of civilizations.
4.1. Biological Systems
The Lotka–Volterra model is normally described as pertaining to the behavior of biological populations. In practice, in its simplest form, the oscillations that the model produces can be seen in the laboratory for unicellular creatures [51,52] but almost never in nature [12]. It seems that the ecosystem is normally able to maintain homeostatic stability if it is not perturbed by humans or other kinds of external perturbations [53]. In these conditions, the flow of energy in and out the stocks of the trophic chains must balance: a biological system in homeostasis must have EROEI = 1. An especially interesting case is that of the Earth’s climate, where the feedbacks among the various stocks generate homeostatic stability [54], a characteristic that has been termed “Gaia” by Margulis and Lovelock [55]. Gaia, apparently, operates at EROEI ≈ 1.
However, cycles of rapid growth and collapse can be observed when the system is strongly perturbed by human activity. We may mention here the case of the reindeer of St. Matthew island [56], whose population went through a single cycle of growth and collapse, ending in the death of the whole population. Reindeer were introduced by humans, they were not part of the island population, their collapse was due to the overexploitation of the local resources (grass), and the system never reached a stable state with EROEI = 1,
4.2. Epidemics
Epidemics are a special case of biological systems, where the predator is a pathogen and the prey is a multicellular organism, often human beings. Dynamic epidemiological models were developed in parallel with that of the Lotka–Volterra model, but a few years later, with the “SIR” model (Susceptible, Infectious, Removed) published in 1927 [57]. The simplest version of the SIR model is equivalent to the SCLV (single cycle) model because the stock of the susceptible people is not replenished (k1 = 0). In the SIR approach, the efficiency parameter is taken as unity; that is, η = 1. This does not mean that viruses and bacteria do not obey the laws of thermodynamics, just that in this system, the entropy factor can be neglected.
A parameter called Rt is often utilized in epidemiology. It is equal to the number of new infections divided by the fraction of infected people. Specifically, it is the same as the “net reproduction rate” parameter in population biology. The SIR equations show that Rt is given by the number of new infections divided by the number of recoveries (or deaths) (k3I). Determining Rt for ongoing epidemics requires complex procedures [58,59] and this necessity often clouds the issue of what Rt really is. However, on the basis of the definitions given in this paper, Rt is conceptually and mathematically the same thing as the energy return for energy invested (EROEI), expressed by the same formula, except for the different notation and the lack of the η efficiency parameter. An infection spreads for Rt > 1 and declines for Rt < 1. For Rt = 1, the curve of the number of infected cases reaches a maximum, which is sometimes defined as the “herd immunity” point.
A variant of the epidemiologic model deals with the transmission of “memes” in virtual space. The concept of meme was proposed for the first time by Richard Dawkins [60] as a unit of information that can replicate in the virtual space of human communication (the “memesphere”). Memes tend to “infect” human minds and replicate by a positive feedback (autocatalytic) mechanism. In this case, the meme is described as the predator, whereas the prey is a stock that describes the number of infected human minds. It can be assumed that the infection period is limited in time and that, after a while, people lose interest in the meme, thus becoming immune—nobody dies because of a memetic infection (or, at least, not directly). The result is that memes generate the same curves as for real viruses in real populations. The SCLV model has been successfully used to describe the propagation of memes in virtual space [61]. According to these considerations, it is possible to define an EROEI for meme propagation with the condition that the meme “goes viral” when EROEI > 1. Unfortunately, we have no data on the actual number of people actually “infected” by a particular meme, only proxy data relative to the number of searches. Nevertheless, the concept of “memetic EROEI” may be a useful mental tool to understand the meme propagation mechanisms.
4.3. Economic Systems
In thermodynamic terms, economic systems are not different from biological and physical dissipative systems: in both cases, we have trophic chains that irreversibly dissipate thermodynamic potentials. For example, energy production in modern society is mostly based on the dissipation of the chemical potential associated with burning buried hydrocarbons (“fossil fuels”). In this case, the fuel stock is the prey while the extracting industry is the predator. In previous papers [37,43,44], we showed how the LV model in the SCLV form can be used to describe this kind of system, both qualitatively and quantitatively. For the case of oil extraction, the result is a “bell-shaped” curve that agrees with the early model for oil extraction proposed in 1956 by Marion King Hubbert [45], a model that was found to account for 38 of 46 oil-producing nations [62]. The SCLV model shows how the “bell-shaped” curve is the unavoidable result of the gradually declining EROEI of extraction, related to the progressive depletion of the less expensive resources.
In this field, much attention has been paid to the concept of “peak oil”, the moment when the world’s oil production reaches a historical maximum and starts an irreversible decline [63]. From the previous discussion, the SCLV model shows that in an ideal system, the peak is reached at an EROEI > 1. It is the capital curve that peaks at EROEI = 1. In other words, oil production starts declining when the system is still generating useful energy. Most analysis of oil production indicates that, at present, the average current EROEI is still larger than one but that is not incompatible with the possibility of having reached the production peak in recent times.
The SCLV model could also be successfully applied to the fishing industry, the original subject of Vito Volterra’s studies [11]. We were able to show that the model provides a good description of the historical data for the overexploitation of fishing stocks by the fishing industry [28]. Some other examples of the use of the SCLV for the extractive industry are reported in a previous article by Bardi and Lavacchi [37].
4.4. Socioeconomic Systems
The largest existing social systems are called “civilizations” and it has been known for a long time that they follow cycles of growth and decline. A classic example is that of the Roman Empire [64]. Today, the reasons for these cycles are still the object of an extensive debate [65,66]. Recently, Bardi et al. proposed a variant of the LV model based on the concept of the trophic chain to describe the fall of empires [67], assuming that civilizations act as predators with respect to natural resources (Figure 6). Even if the resource is potentially renewable, e.g., fertile soil, when it is overexploited, its yield is rapidly reduced, and the result is a decline of the flow of resource into the L2 stock. This eventually leads to decline.
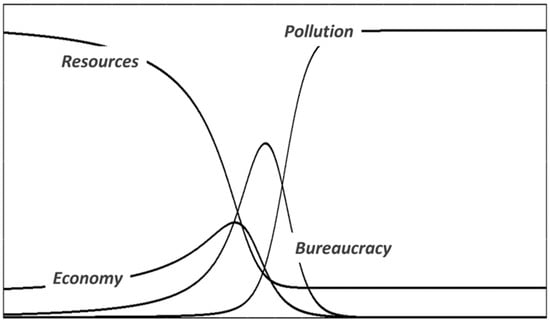
Figure 6.
Example of the dissipative 3-stock system: the collapse of a complex society (from Bardi et al. [67]).
This simple model provides results that are qualitatively comparable to those of more sophisticated “world models”, starting with the pioneering work by Jay Forrester [68] and of the group of authors who produced the study titled “The Limits to Growth” [40], a milestone in this area of study.
In this area, Hall et al. [69,70] argued that there exists a minimum value of the EROEI that makes the existence of a complex society possible and estimated that such a value was about 5:1 for society or perhaps 12:1 for a sophisticated modern economy. A large value of the EROEI for the specific kind of resource being exploited generates an excess of energy that may be utilized either for the growth of energy production or for other consumptive purposes. A society that reinvests all the energy it produces into energy production facilities would attain a steady state with EROEI = 1:1. This would leave no space for activities that are not directly related to energy production but that we consider important (health care, tourism, art, leisure, sport), although not necessarily worthwhile (war).
We can use the equations developed in the present study to examine this kind of system. We may consider the fraction of energy diverted to non-productive purposes by multiplying the η parameter by a factor written as (1 − fs), where fs stands for the “societal factor” and it indicates the fraction of resources that are not re-invested into more resource production. We can call “fs“ the “societal disposable income fraction”. In this case, we can modify the equations of the single cycle (SCLV) model as:
dL1/dt = −k2L1L2
dL2/dt = η(1 − fs) k2L1L2 − k3L2.
Remembering that EROEI = ηk2L1/k3:
dL1/dt = −(1/η) k3L2EROEI
dL2/dt = L2k3 ((1 − fs) EROEI − 1)
The 1 − fs factor does not affect the EROEI of the exploitation of whatever resource a civilization is relying on, but it affects the growth rate of the L2 stock (dL2/dt). If, for instance, fs is equal to 1, even if the EROEI is much larger than one, all the production is used for building societal capital. In this case, dL2/dt = 0 and society does not grow. There are historical cases in which a society is believed to have declined as the result of excessive military expenses; that is, having dedicated too much of the produced resources to non-producing assets. This may have been the case, for instance, for the Soviet Union in the 1980s [71,72] even though this is unlikely to be the only factor involved.
Provided that EROEI > 1, then it is always possible to reduce fs to a value small enough that growth can be maintained or, at least, decline is slowed. In the modern Western society, we may be seeing this effect as the result of depletion of the high EROEI fossil resources [70]. The consequence is that economic growth is maintained at the expense of downsizing or the elimination of services, such as universal health care, state pensions, public schools, and more. Fossil fuels allowed the production of many more goods and services by requiring only 20 percent (1850, coal) or even 10 percent or less of all economic activity to be required to run the rest of the economy [67,69]. Alternatively, for example, in England in 1500, about half of all economic activity was dedicated to obtaining the energy (food, fodder, wood) necessary to run society, with much less left over for amenities [73]. A similar phenomenon may have taken place for the decline of the Roman Empire, generated by the progressive depletion of the mineral resources it was dependent upon [74].
These considerations provide guidelines for understanding the deep reasons of the decline of many societies in history. Unfortunately, the definition of an “fs” factor is frayed with uncertainties. For instance, we might say that the large budget allocated to military expenses in the US is an example of an unnecessary burden on society. On the other hand, it might be argued that, according to the so-called “Carter Doctrine” [75], without such expenses, the US could not access the production of fossil resources in regions such as the Middle East. In such an interpretation, a large fraction of the US military budget should be factored in the calculation of the EROEI of fossil fuels, which would be consequently reduced, perhaps well below unity. This does not detract from the general observation that a declining EROEI may be the main factor involved in civilization decline or collapse.
5. Conclusions
The EROEI [3] parameter is historically defined as a yield and it is evaluated with several models, which are mainly energy models [76,77]. The aim of this work was to show that the concept of EROEI goes beyond the assessment of the efficiency in the exploitation of energy resources embodying a key parameter to describe all those complex systems where the dissipation of energy potentials occurs.
Many of these systems can be described by a simple model, the well-known Lotka–Volterra (LV) one [10,11]. In the form we call here single-cycle Lotka–Volterra (SCLV), the model turned out to be a powerful tool to evaluate the efficiency in resource use in several different fields.
We highlighted how the diminishing EROEI typical of non-renewable (or slowly renewable) resources provides a qualitative understanding of the decline and collapse of economic and social systems, here modelled by LV. Of course, everyone understands that fossil fuels are a finite resource and that their exploitation cannot last forever. However, our approach shows the problems with the depletion of finite resources (or slowly renewable resources) start way earlier as we “run out” of them. The whole productive process must be seen as a cycle dominated by the diminishing value of the EROEI, and it is necessary to plan for exiting it much before it becomes a drain of resources rather than a source.
EROEI also provides an understanding of how a society that feels the crunch of reduced available energy tends to react by cutting back on societal segments viewed as dispensable, such as universal health care or other state-managed public services.
The SCLV model coupled with the concept of EROEI provides a window of understanding on the “overexploitation” trap in the way many natural and human-made systems work. Moreover, the SCLV model allowed some mathematical and conceptual equivalence of the Rt parameter to be unveiled in epidemiologic studies to the energy return on energy invested (EROI or EROEI) parameter in the biophysical approach to energy economics [78], which, to our knowledge, had not been pointed out in the scientific literature before.
Author Contributions
Conceptualization, U.B., A.L. and I.P.; methodology, A.L. and U.B.; software, I.P.; validation, U.B., A.L. and I.P.; formal analysis, I.P.; writing—original draft preparation, U.B. and I.P.; writing—review and editing, U.B. and I.P.; supervision, U.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to Charles Hall for his comments and criticism of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hall, C.A.S.; Lavine, M.; Sloane, J. Efficiency of energy delivery systems: Part I. An economic and energy analysis. Environ. Manag. 1979, 3, 493–504. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Lambert, J.G.; Balogh, S.B. EROI of different fuels and the implications for society. Energy Policy 2014, 64, 141–152. [Google Scholar] [CrossRef] [Green Version]
- Gupta, A.K.; Hall, C.A.S.C.; Gupta, A.K.; Hall, C.A.S.C. A Review of the Past and Current State of EROI Data. Sustainability 2011, 3, 1796–1809. [Google Scholar] [CrossRef] [Green Version]
- Hall, C.A.S. The History, Future, and Implications of EROI for Society. In Energy Return on Investment: A Unifying Principle for Biology, Economics, and Sustainability; Hall, C.A.S., Ed.; Springer: Cham, Switzerland, 2017; pp. 145–169. [Google Scholar] [CrossRef]
- Ferroni, F.; Hopkirk, R.J. Energy Return on Energy Invested (ERoEI) for photovoltaic solar systems in regions of moderate insolation. Energy Policy 2016, 94, 336–344. [Google Scholar] [CrossRef] [Green Version]
- Raugei, M.; Sgouridis, S.; Murphy, D.; Fthenakis, V.; Frischknecht, R.; Breyer, C.; Bardi, U.; Barnhart, C.; Buckley, A.; Carbajales-Dale, M.; et al. Energy Return on Energy Invested (ERoEI) for photovoltaic solar systems in regions of moderate insolation: A comprehensive response. Energy Policy 2017, 102, 377–384. [Google Scholar] [CrossRef]
- Carbajales-Dale, M.; Raugei, M.; Fthenakis, V.; Barnhart, C. Energy Return on Investment (EROI) of Solar PV: An Attempt at Reconciliation [Point of View]. Proc. IEEE 2015, 103, 995–999. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Dale, B.E.; Pimentel, D. Seeking to Understand the Reasons for Different Energy Return on Investment (EROI) Estimates for Biofuels. Sustainability 2011, 3, 12. [Google Scholar] [CrossRef] [Green Version]
- Mobus, G.E.; Kalton, M.C. Principles of System Science; Springer: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Lotka, A.J. Elements of Physical Biology; Baltimore, M.D., Ed.; Williams and Wilkins Company: Baltimore, MD, USA, 1925. [Google Scholar] [CrossRef]
- Volterra, V. Fluctuations in the abundance of a species considered mathematically. Nature 1926, 118, 558–560. [Google Scholar] [CrossRef]
- Hall, C.A.S. An assessment of several of the historically most influential theoretical models used in ecology and of the data provided in their support. Ecol. Model. 1988, 43, 5–31. [Google Scholar] [CrossRef] [Green Version]
- Prigogine, I. On Symmetry-Breaking Instabilities in Dissipative Systems. J. Chem. Phys. 1967, 46, 3542. [Google Scholar] [CrossRef]
- Prigogine, I. Symmetry Breaking Instabilities in Dissipative Systems, II. J. Chem. Phys. 1968, 48, 1695. [Google Scholar] [CrossRef]
- Bardi, U. The Sower’s Strategy: A Way to Speed Up the Energy Transition. In Disrupting the Future: Great Ideas for Creating a Much Better World; Visser, W., Ed.; Kaleidoscope Futures: London, UK, 2014; pp. 15–19. [Google Scholar]
- Sgouridis, S.; Csala, D.; Bardi, U. The sower’s way: Quantifying the narrowing net-energy pathways to a global energy transition. Environ. Res. Lett. 2016, 11, 094009. [Google Scholar] [CrossRef] [Green Version]
- Catton, W. Overshoot, the Ecological Basis of Revolutionary Change; Illinin Books Edition: Chicago, IL, USA, 1982. [Google Scholar]
- Perissi, I.; Bardi, U. The Sixth Law of Stupidity: A Biophysical Interpretation of Carlo Cipolla’s Stupidity Laws. Systems 2021, 9, 3. [Google Scholar] [CrossRef]
- Wiener, N. Cybernetics: Or, Control and Communication in the Animal and the Machine, 2nd ed.; The Mit Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Åström, K.J.; Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2021. [Google Scholar]
- Bowen, M.G. Feedback thought in social science and systems theory. In System Dynamics Review; Richardson, G.P., Ed.; University of Pennsylvania Press: Philadelphia, PA, USA, 1991; Volume 8, pp. 105–107. [Google Scholar] [CrossRef]
- Wolstenholme, E.; McKelvie, D. Feedback Dynamics. In The Dynamics of Care; Springer: Cham, Switzerland, 2019; pp. 89–105. [Google Scholar] [CrossRef]
- Simon, H.A. On the Application of Servomechanism Theory in the Study of Production Control–A Study in the Theory of Organization; RAND Corporation: Santa Monica, CA, USA, 1951. [Google Scholar]
- Forrester, J.W. Industrial Dynamics: A Major Breakthrough for Decision Makers. Harv. Bus. Rev. 1958, 36, 37–66. [Google Scholar] [CrossRef]
- Wang, X.; Fu, F. Eco-evolutionary dynamics with environmental feedback: Cooperation in a changing world. EPL 2020, 132, 10001. [Google Scholar] [CrossRef]
- D’Ancona, U. La Lotta Per l’Esistenza; Giulio Einaudi Editore: Torino, Italy, 1942. [Google Scholar]
- Perissi, I.; Bardi, U.; Bardi, U.; el Asmar, T. Dynamic patterns of overexploitation in fisheries. Ecol. Model. 2017, 359, 285–292. [Google Scholar] [CrossRef]
- Bardi, U.; Perissi, I. The Empty Sea. What Future for the Blue Economy? Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Bruckmann, G. Elements of the system dynamics method. Technol. Forecast. Soc. Chang. 1982, 21, 85–87. [Google Scholar] [CrossRef]
- Sharma, V.; Annila, A. Natural process--natural selection. Biophys. Chem. 2007, 127, 123–128. [Google Scholar] [CrossRef] [Green Version]
- Dilip, K.; Ilya, P. Modern Thermodynamics; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Demirel, Y. Chapter 13—Nonequilibrium thermodynamics approaches. In Nonequilibrium Thermodynamics; Demirel, Y., Ed.; Elsevier Science: Amsterdam, The Netherlands, 2002; pp. 356–372. [Google Scholar] [CrossRef]
- Tyutyunov, Y.; Titova, L. From Lotka-Volterra to Arditi-Ginzburg: 90 Years of Evolving Trophic Functions. Biol. Bull. Rev. 2020, 10, 167–185. [Google Scholar] [CrossRef]
- Arditi, R.; Ginzburg, L.R. Coupling in predator-prey dynamics: Ratio-Dependence. J. Theor. Biol. 1989, 139, 311–326. [Google Scholar] [CrossRef]
- Clark, W.C.; Jones, D.D.; Holling, C.S. Lessons for ecological policy design: A case study of ecosystem management. Ecol. Model. 1979, 7, 1–53. [Google Scholar] [CrossRef] [Green Version]
- Michaelian, K. Thermodynamic stability of ecosystems. J. Theor. Biol. 2006, 237, 323–335. [Google Scholar] [CrossRef]
- Bardi, U.; Lavacchi, A. A Simple Interpretation of Hubbert’s Model of Resource Exploitation. Energies 2009, 2, 646–661. [Google Scholar] [CrossRef]
- Hall, C.A.; Cleveland, C.J.; Kaufmann, R. Energy and Resource Quality: The Ecology of the Economic Process; Wiley Interscience: New York, NY, USA, 1986; Available online: http://www.amazon.com/Energy-Resource-Quality-Environmental-Wiley-Interscience/dp/0471087904 (accessed on 7 August 2015).
- McIntosh, A.R.; McHugh, P.A.; Plank, M.J.; Jellyman, P.G.; Warburton, H.J.; Greig, H.S. Capacity to support predators scales with habitat size. Sci. Adv. 2018, 4, eaap7523. [Google Scholar] [CrossRef] [Green Version]
- Meadows, D.H.; Meadows, D.L.; Randers, J.; Bherens, W., III. The Limits to Growth; Universe Books: New York, NY, USA, 1972. [Google Scholar]
- Perissi, I. Highlighting the archetypes of sustainability management by means of simple dynamics models. J. Simul. 2019, 15, 51–64. [Google Scholar] [CrossRef]
- The MEDEAS Project. 2016. Available online: www.medeas.com (accessed on 19 November 2016).
- Bardi, U.; Lavacchi, A.; Yaxley, L. Modelling EROEI and net energy in the exploitation of non renewable resources. Ecol. Model. 2011, 223, 54–58. [Google Scholar] [CrossRef]
- Bardi, U. Mind Sized World Models. Sustainability 2013, 5, 896–911. [Google Scholar] [CrossRef] [Green Version]
- Hubbert, M.K. Nuclear Energy and the Fossil Fuels; Princeton University Press: San Antonio, TX, USA, 1956. [Google Scholar]
- Murphy, D.D.J.; Hall, C.A.S.C. Energy return on investment, peak oil, and the end of economic growth. Ann. N. Y. Acad. Sci. 2011, 1219, 52–72. [Google Scholar] [CrossRef]
- Bardi, U. No Peak Oil Yet? The limits of the Hubbert Model. The Oil Drum, 2011. Available online: http://www.theoildrum.com/node/7241 (accessed on 12 June 2013).
- Bardi, U. Peak Oil. In International Encyclopedia of Social and Behavioral Sciences, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Brandt, A.R. Testing Hubbert. Energy Policy 2007, 35, 3074–3088. [Google Scholar] [CrossRef]
- Heun, M.; de Wit, M. Energy Return on (Energy) Invested (Eroi), Oil Prices, and Energy Transitions, Energy Policy. 2012. Available online: http://www.sciencedirect.com/science/article/pii/S0301421511006975 (accessed on 11 January 2015).
- Gause, G.F. Experimental Studies on the Struggle for Existence: I. Mixed Population of Two Species of Yeast. J. Exp. Biol. 1932, 9, 389–402. [Google Scholar] [CrossRef]
- Gause, G.F. Experimental demonstration of Volterra’s periodic oscillations in the numbers of animals. J. Exp. Biol. 1935, 12, 44–48. [Google Scholar] [CrossRef]
- Gorshkov, V.G.; Mikhaĭlovna, A.M.; Gorshkov, V.V. Biotic Regulation of the Environment: Key Issue of Global Change; Springer: Berlin/Heidelberg, Germany, 2000; Available online: http://www.springer.com/it/book/9781852331818 (accessed on 24 September 2017).
- Berner, R.A. The long-term carbon cycle, fossil fuels and atmospheric composition. Nature 2003, 426, 323–326. [Google Scholar] [CrossRef] [PubMed]
- Lovelock, J.E.; Margulis, L. Atmospheric homeostasis by and for the biosphere: The gaia hypothesis. Tellus 1974, 26, 2–10. [Google Scholar] [CrossRef] [Green Version]
- Klein, D.R. The Introduction, Increase, and Crash of Reindeer on St. Matthew Island. J. Wildl. Manag. 1968, 32, 350–367. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G.; Walker, G.T. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef] [Green Version]
- Brauer, F.; Castillo-Chavez, C. Continuous Population Models. In Mathematical Models in Population Biology and Epidemiology; Brauer, F., Castillo-Chavez, C., Eds.; Springer: New York, NY, USA, 2012; pp. 3–47. [Google Scholar] [CrossRef]
- Saltelli, A.; Bammer, G.; Bruno, I.; Charters, E.; Di Fiore, M.; Didier, E.; Espeland, W.N.; Kay, J.; Piano, S.L.; Mayo, D.; et al. Five ways to ensure that models serve society: A manifesto. Nature 2020, 582, 7813. [Google Scholar] [CrossRef]
- Dawkins, R. The Selfish Gene; Oxford University Press: New York, NY, USA, 1976. [Google Scholar]
- Perissi, I.; Falsini, S.; Bardi, U. Mechanisms of meme propagation in the mediasphere: A system dynamics model. Kybernetes 2018, in press. [Google Scholar] [CrossRef]
- Hallock, J.L.; Wu, W.; Hall, C.A.S.; Jefferson, M. Forecasting the limits to the availability and diversity of global conventional oil supply: Validation. Energy 2014, 64, 130–153. [Google Scholar] [CrossRef] [Green Version]
- Campbell, C.J.; Laherrere, J.F. The End of Cheap Oil. Sci. Am. 1998, 278, 78–83. [Google Scholar] [CrossRef]
- Gibbon, E. History of the Decline and Fall of the Roman Empire; Strahan & Cadell: London, UK, 1776. [Google Scholar]
- Tainter, J. The Collapse of Complex Societies; Cambridge University Press: New York, NY, USA, 1988; Available online: http://books.google.it/books?hl=en&lr=&id=YdW5wSPJXIoC&oi=fnd&pg=PA1&dq=joseph+tainter&ots=OHNQiiLjo3&sig=uKdDdi07GVQuqwILJkOr_9M1eBA (accessed on 13 November 2013).
- Tainter, J. Complexity, Problem Solving, and Sustainable Societies. In Getting Down to Earth-Practical Applications of Ecological Economics; Human Sciences Press, Inc.: Basel Switzerland, 1996; Available online: https://www.goldonomic.com/tainter.htm (accessed on 24 September 2017).
- Bardi, U.; Falsini, S.; Perissi, I. Toward a General Theory of Societal Collapse: A Biophysical Examination of Tainter’s Model of the Diminishing Returns of Complexity. Biophys. Econ. Resour. Qual. 2019, 4, 3. [Google Scholar] [CrossRef] [Green Version]
- Forrester, J. World Dynamics; Wright-Allen Press: Cambridge, MA, USA, 1971; Available online: http://documents.irevues.inist.fr/handle/2042/29441 (accessed on 3 June 2017).
- Hall, C.; Balogh, S.; Murphy, D. What is the minimum EROI that a sustainable society must have? Energies 2009, 2, 25–47. [Google Scholar] [CrossRef]
- Lambert, J.G.; Hall, C.A.S.; Balogh, S.; Gupta, A.; Arnold, M. Energy, EROI and quality of life. Energy Policy 2014, 64, 153–167. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, D.B. Cold War Energy: The Rise and Fall of the Soviet Union; Alaska Chena LLC: Fairbanks, AK, USA, 2016. [Google Scholar]
- Reynolds, D.; Kolodziej, M. Former Soviet Union oil production and GDP Decline: Granger Causality and the Multi-Cycle Hubbert Curve. Energy Economics, 2008. Available online: http://www.sciencedirect.com/science/article/pii/S0140988306000727 (accessed on 13 November 2017).
- King, C.W.; Maxwell, J.P.; Donovan, A. Comparing World Economic and Net Energy Metrics, Part 1: Single Technology and Commodity Perspective. Energies 2015, 8, 11. [Google Scholar] [CrossRef] [Green Version]
- Bardi, U. The Seneca Effect. Why Growth Is Slow but Collapse Is Rapid; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Klare, M. Protecting Overseas Oil Supplies: The Globalization of the ‘Carter Doctrine’. In Transforming Power; Routledge: New York, NY, USA, 2006; Available online: https://www.taylorfrancis.com/chapters/edit/10.4324/9781351301329-4/protecting-overseas-oil-supplies-globalization-carter-doctrine-michael-klare (accessed on 12 June 2017).
- Rye, C.D.; Jackson, T. A review of EROEI-dynamics energy-transition models. Energy Policy 2018, 122, 260–272. [Google Scholar] [CrossRef]
- Hall, C.A.S. Synthesis to Special Issue on New Studies in EROI (Energy Return on Investment). Sustainability 2011, 3, 2496–2499. [Google Scholar] [CrossRef] [Green Version]
- Hall, C.; Lindenberger, D.; Kümmel, R. The Need to Reintegrate the Natural Sciences with Economics: Neoclassical Economics, the Dominant form of Economics Today, has at Least Three Fundamental Flaws. BioScience, 2001. Available online: http://www.bioone.org/doi/abs/10.1641/0006-3568(2001)051%5B0663:TNTRTN%5D2.0.CO%3B2 (accessed on 24 August 2017).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).