Big Data Analysis and Research on Fracturing Construction Parameters of Shale Gas Horizontal Wells—A Case Study of Horizontal Wells in Fuling Demonstration Area, China
Abstract
:1. Introduction
2. Basic Overview of Study Area
3. Methodology
3.1. Data Collection
3.2. Data Preprocessing
3.3. Classification of High-Production Wells
3.4. Correlation and Clustering Analysis Methods
4. Analysis process
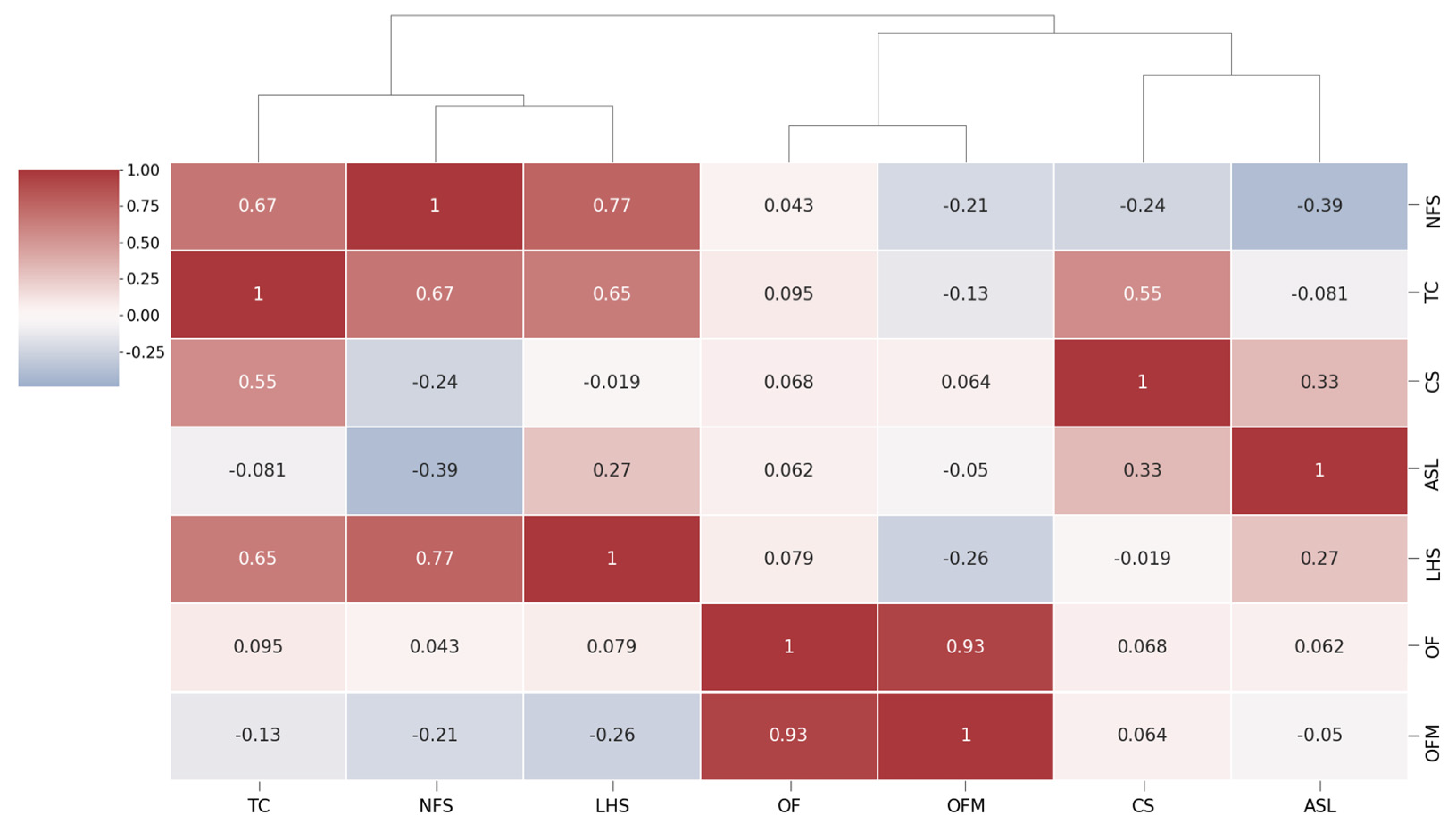
4.1. Process Design Correlation and Clustering Analysis Results
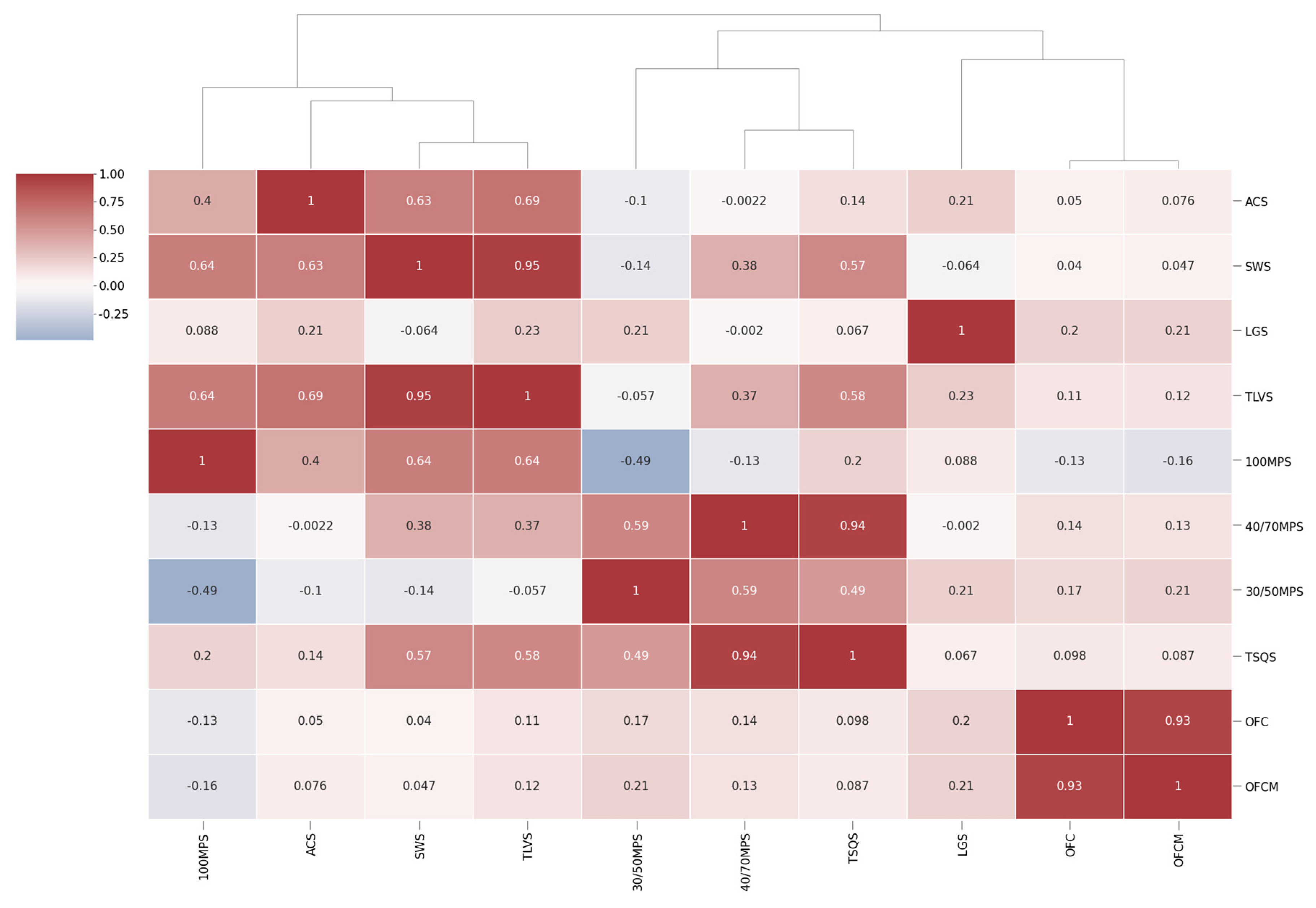
4.2. Correlation and Clustering Analysis Results of Fracturing Construction Parameters
4.3. Analysis of Fracturing Construction Parameters
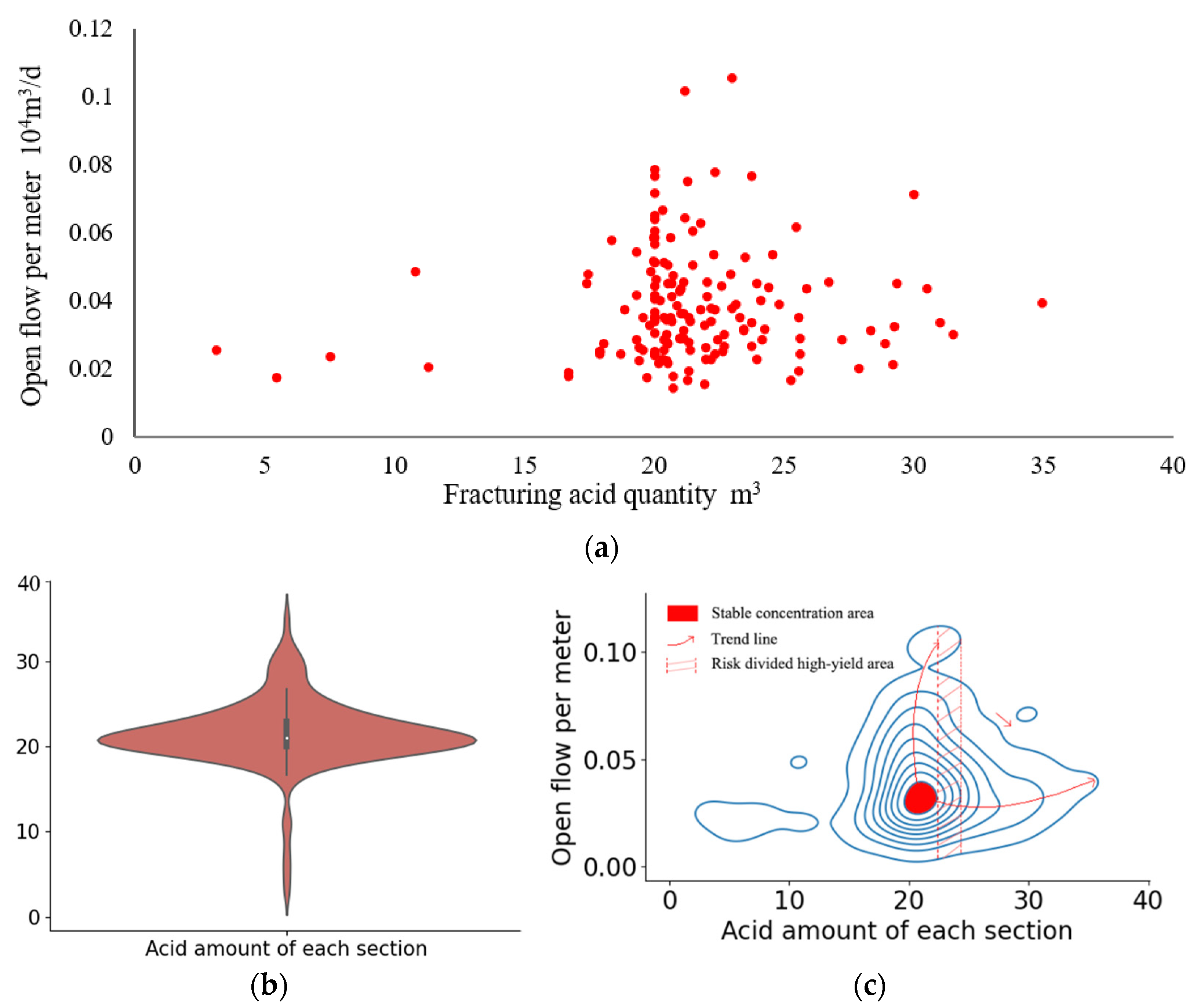
4.3.1. Optimization of Acid Amount in Each Section
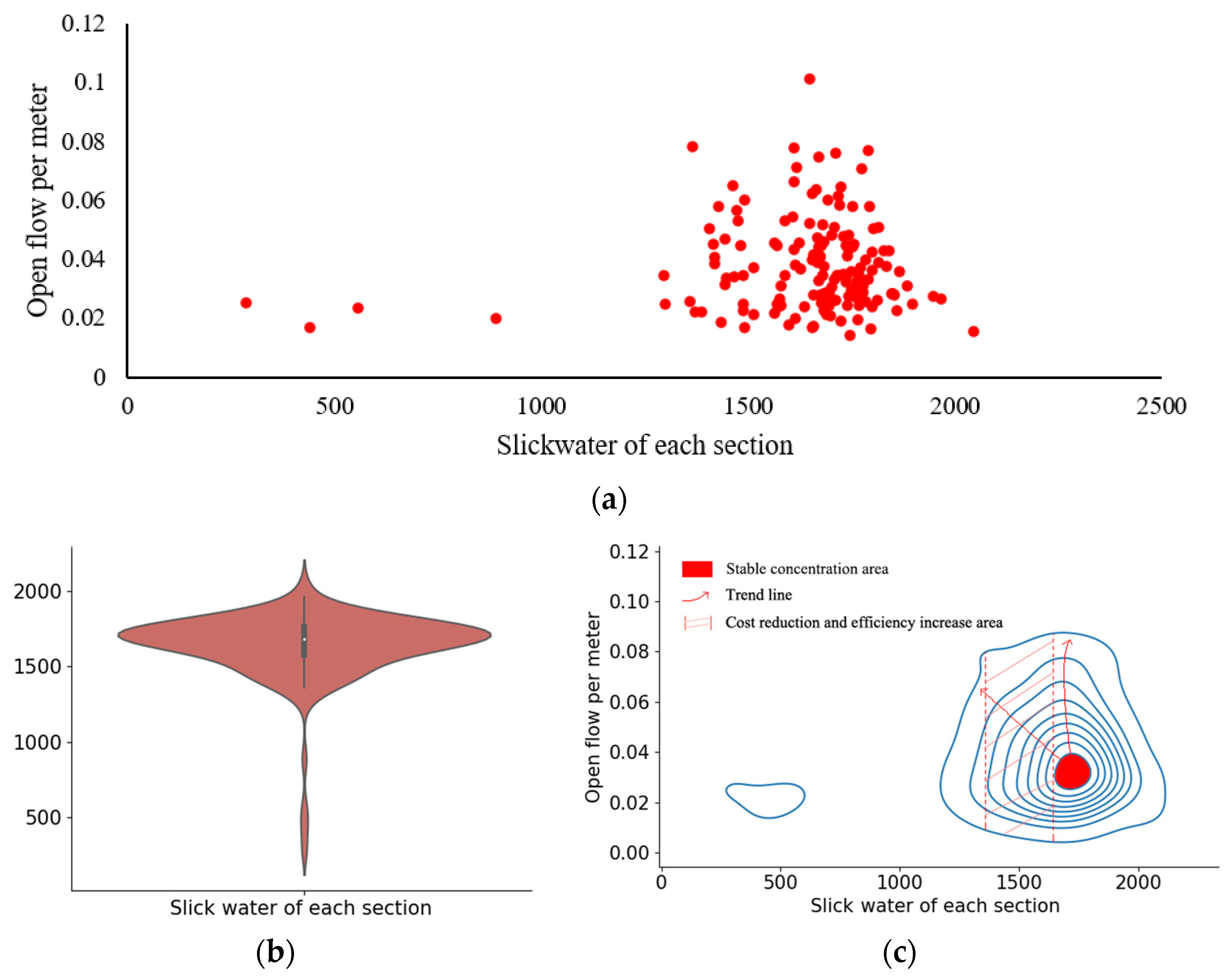
4.3.2. Optimization of Each Section of Slickwater
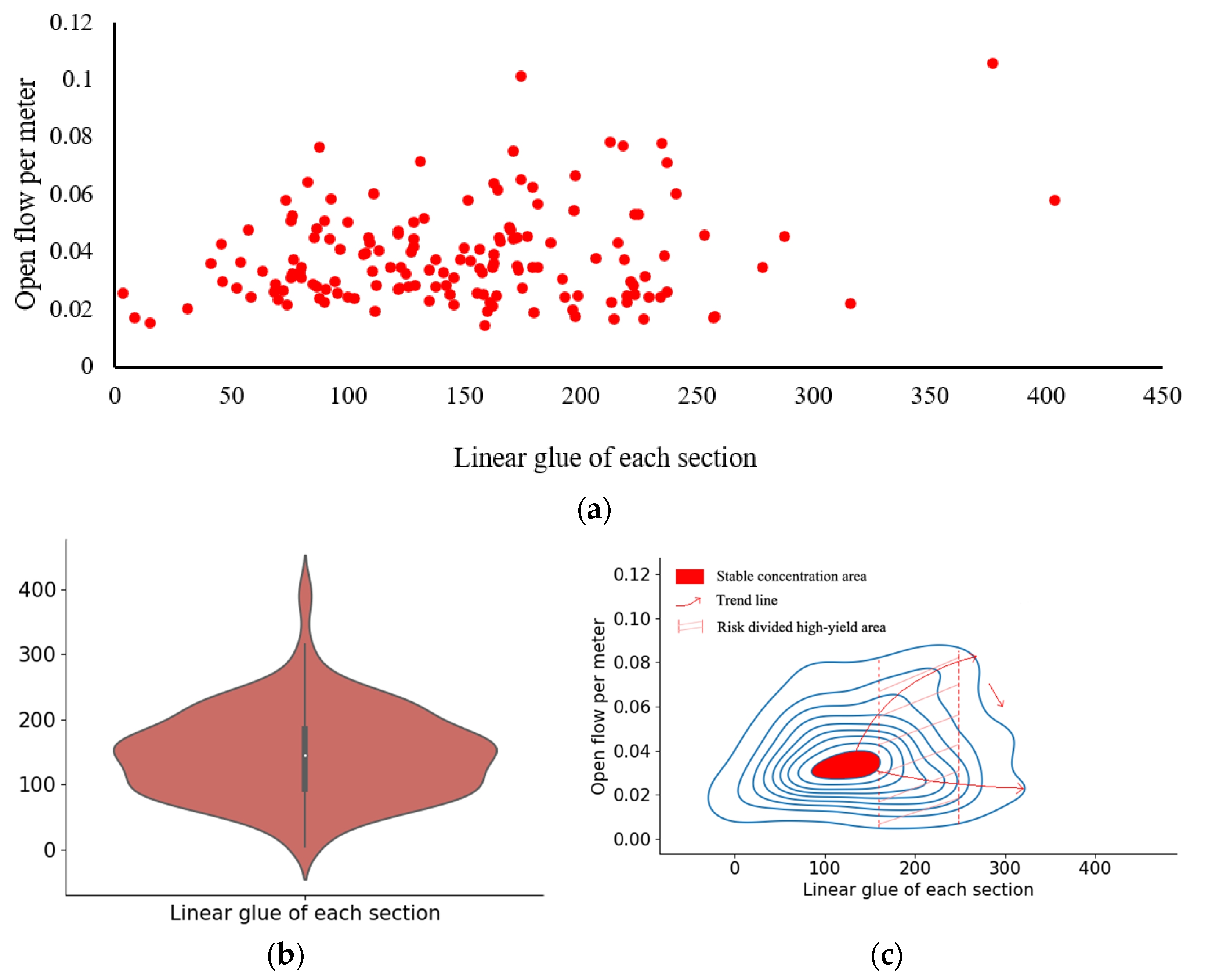
4.3.3. Linear Glue of Each Section
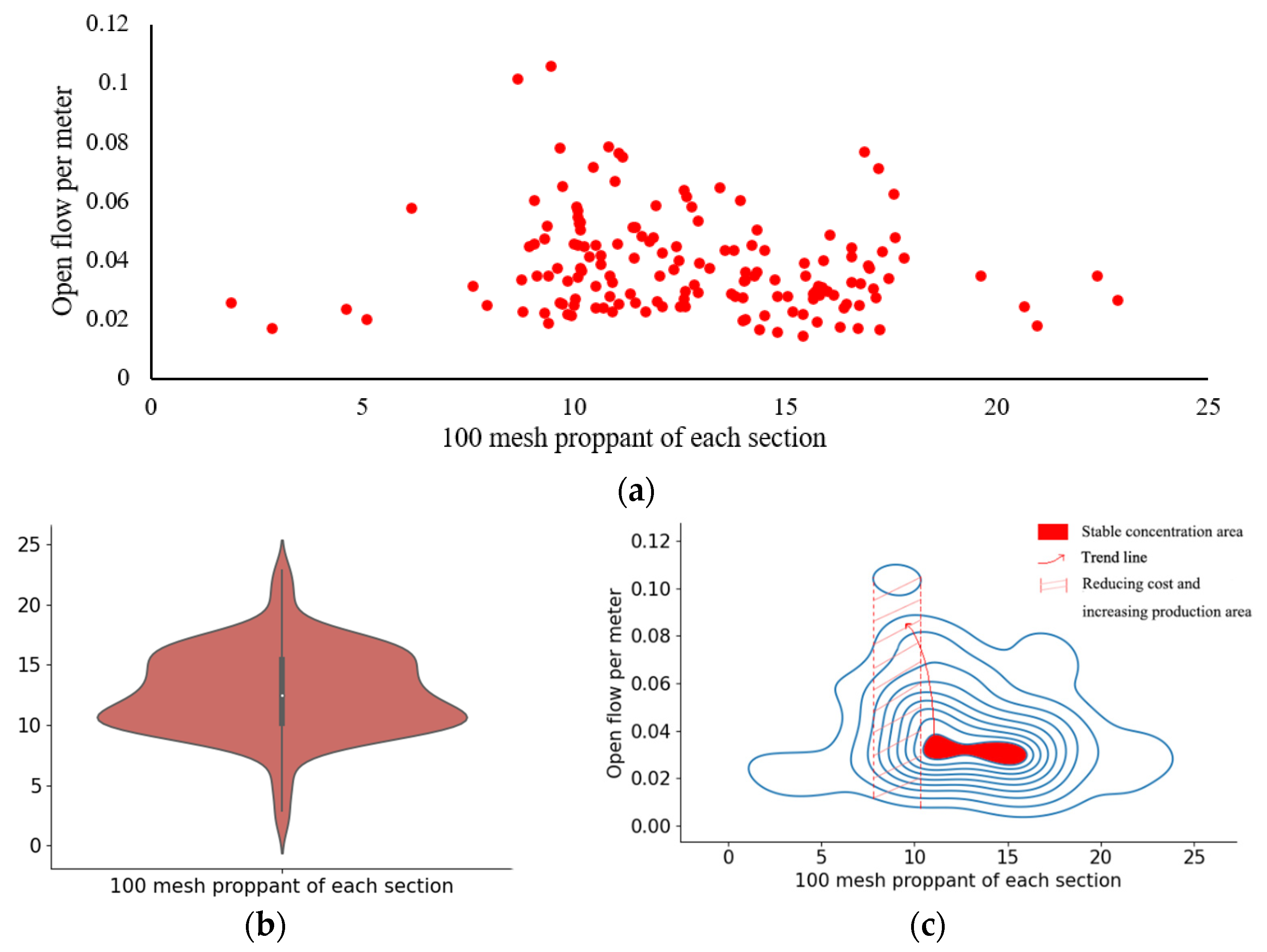
4.3.4. 100 Mesh Proppant Per Section
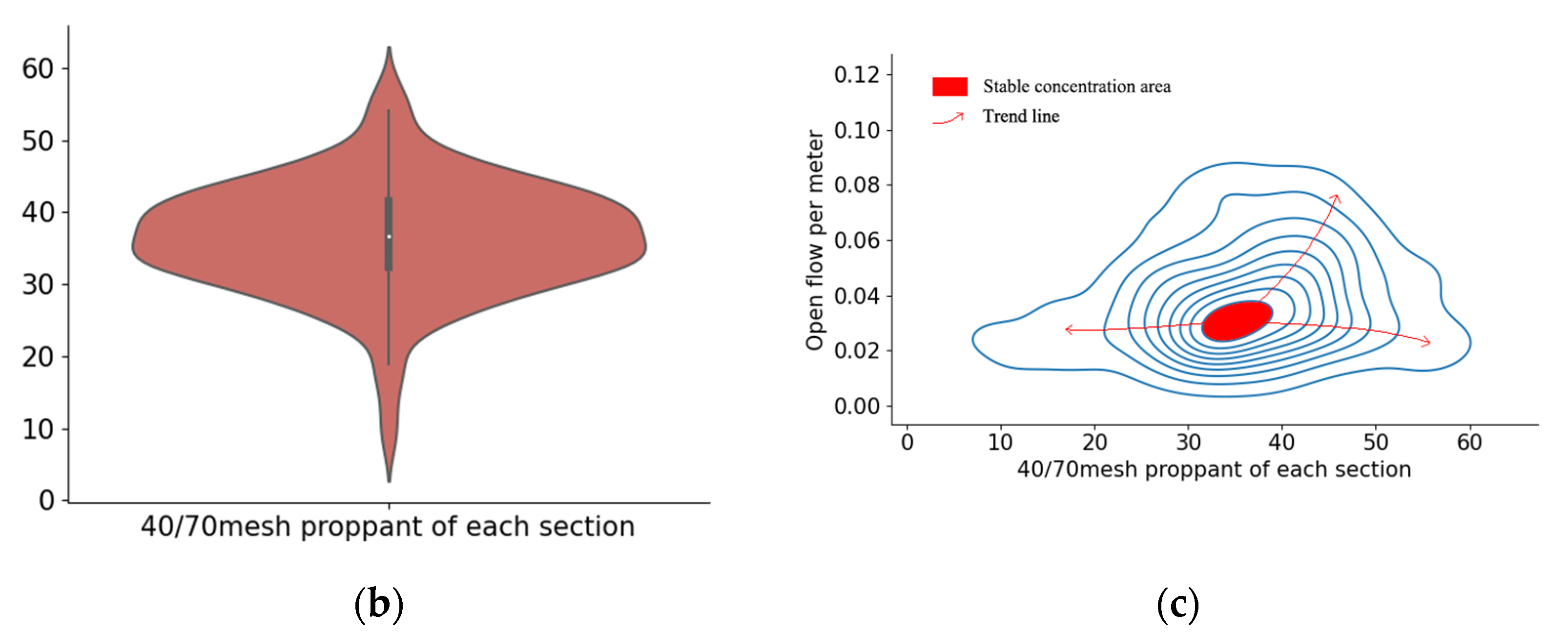
4.3.5. Proppant of 40/70 Mesh in Each Section
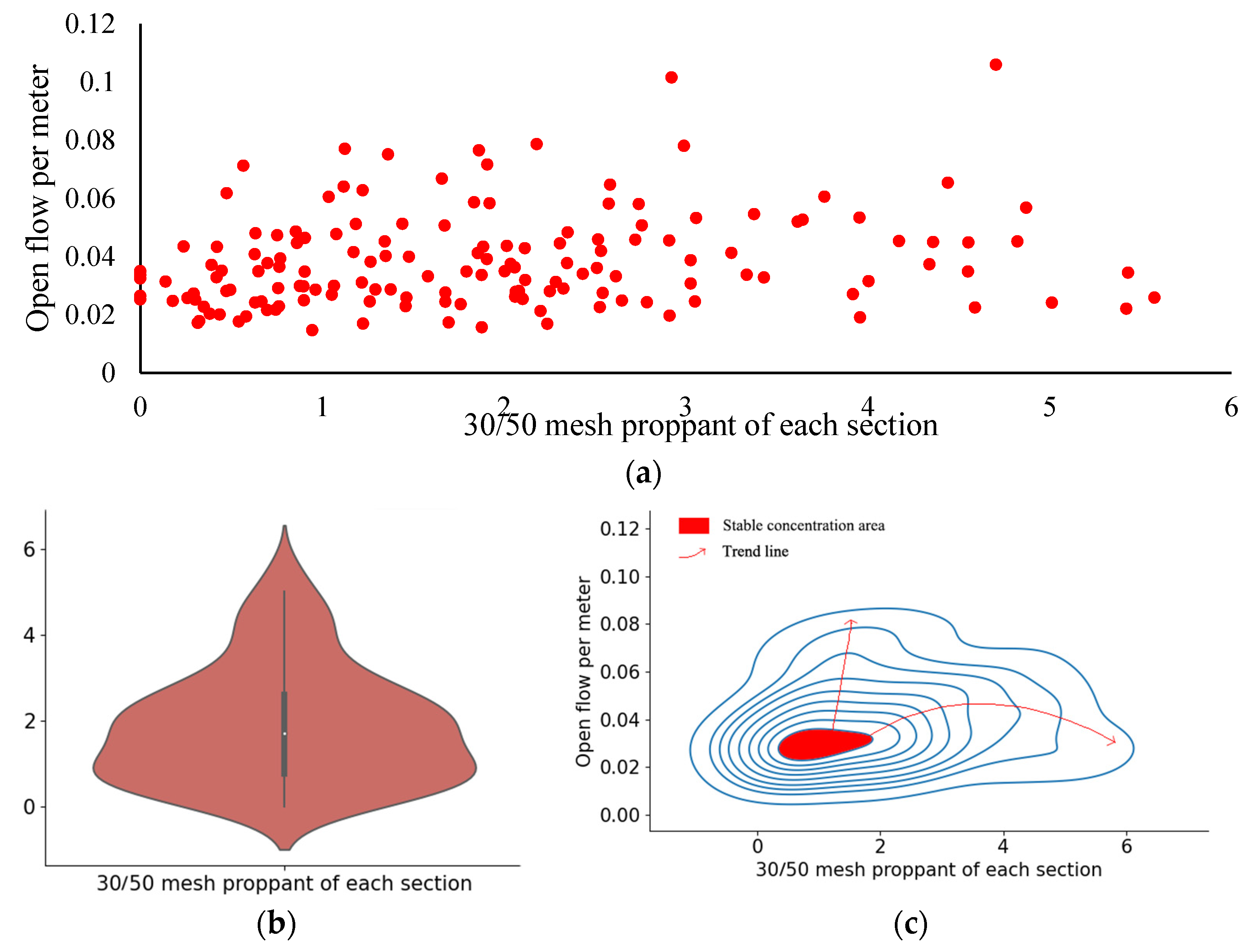
4.3.6. Proppant of 30/50 Mesh in Each Section
5. Validation of Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ping, Y.Q.; Sheng, F.L.; Zhou, N.; Li, P.; Lv, J. Analysis of the Application of Big Data Technology in Oil and Gas Geological Exploration. Sci. Technol. Inf. 2019, 17, 59–60. [Google Scholar]
- Yang, C.S.; Zhang, H.L. An Introduction to the Application and Challenges of Big Data in the Domestic Oil Exploration and Development Industry. Sci. Inform. 2019, 20, 19–20. [Google Scholar]
- Tian, J.H.; Zhang, B. The Practice and Prospect of Big Data Technology in Petrochemical Industry; Sinopec Publishing House: Beijing, China, 2016. [Google Scholar]
- Hailin, S.; Peng, Z.; Xiaotao, Y.; Kebin, X.; Qing, C.; Qi, Z. Parameter Design Method for Re-Fracturing Scheme of Water Injection Block in Oil and Gas Field. Well Test 2020, 29, 6–13. [Google Scholar]
- Dou, X.; Liao, X.; Hou, T.; Zhao, T.; Zhiming, C.; Ren, W.; Zhang, R. Fracture Optimization for Multi-Stage Fractured Horizontal Well with Time & Stress-Sensitive Parameters. In Proceedings of the Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 2 August 2015. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, J.; Huang, Z.; Tian, M. Study on the Optimization of Fracturing Parameters and Interpretation of CBM Fractured Wells. J. Nat. Gas Geosci. 2018, 3, 109–117. [Google Scholar] [CrossRef]
- Yao, J.; Li, Z.; Liu, L.; Fan, W.; Zhang, M.; Zhang, K. Optimization of Fracturing Parameters by Modified Variable-Length Particle-Swarm Optimization in Shale-Gas Reservoir. SPE J. 2021, 26, 1032–1049. [Google Scholar] [CrossRef]
- Fan, Y.L. Optimization of Hydraulic Fracturing Treatment Parameters for Tight Gas Reservoirs Using Machine Learning. Ph.D. Thesis, Xi’an Shiyou University, Xi’an, China, 2021. [Google Scholar]
- Tang, C.; Chen, X.; Du, Z.; Yue, P.; Wei, J. Numerical Simulation Study on Seepage Theory of a Multi-Section Fractured Horizontal Well in Shale Gas Reservoirs Based on Multi-Scale Flow Mechanisms. Energies 2018, 11, 2329. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Liu, Y.; Wang, Y.; Yang, G.; Yu, Q.; Wang, F. A New Method and Application of Full 3D Numerical Simulation for Hydraulic Fracturing Horizontal Fracture. Energies 2019, 12, 48. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.Z.; Lei, J.J.; Ren, J. Optimization of Volumetric Fracturing Parameters for Tight Oil Reservoirs in Southern Exploration Area. Unconv. Oil Gas 2020, 7, 113–120. [Google Scholar]
- Wang, J.; Sun, J.; Liu, D.; Zhu, X. Production Capacity Evaluation of Horizontal Shale Gas Wells in Fuling District. FDMP Fluid Dyn. Mater. Process. 2019, 15, 613–625. [Google Scholar] [CrossRef]
- Liu, M.J.; Wang, X.F.; Huang, Y. Data Preprocessing in Data Mining. Comput. Sci. 2000, 27, 56–59. [Google Scholar]
- Kan, Z.G.; Jin, X. Research and Implementation of Data Preprocessing in Data Mining. Comput. Appl. Res. 2004, 07, 118–119. [Google Scholar]
- Pearson, K. Notes on Regression and Inheritance in the Case of Two Parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- Myers, J.L.; Well, A.D. Research Design and Statistical Analysis, 2nd ed.; Lawrence Erlbaum: Mahwah, NJ, USA, 2003. [Google Scholar]
- Wang, X. Nonparametric Statistics; Renmin University of China Press: Beijing, China, 2005. [Google Scholar]
- Gronau, I.; Moran, S. Optimal Implementations of UPGMA and Other Common Clustering Algorithms. Inf. Process. Lett. 2007, 104, 205–210. [Google Scholar] [CrossRef]



| NFS − | TC − | ASL (m) | LHS (m) | CS − | |
|---|---|---|---|---|---|
| Maximum | 29 | 75 | 97 | 2136 | 3 |
| Minimum | 11 | 9 | 53 | 660 | 1 |
| Average | 19 | 50 | 50 | 1467 | 2 |
| Number of wells | 303 | ||||
| AC (m3) | SW (m3) | LG (m3) | TLV (m3) | 100 MP (m3) | 40/70 MP (m3) | 30/50 MP (m3) | TSQ (m3) | ASR (m3) | |
|---|---|---|---|---|---|---|---|---|---|
| Maximum | 820 | 57,188 | 7916 | 65,924 | 502 | 1104 | 103 | 1709 | 11 |
| Minimum | 60 | 5427 | 66 | 5553 | 36 | 158 | 0 | 158 | 0 |
| Average | 424 | 32,299 | 2892 | 35,615 | 254 | 715 | 35 | 750 | 7 |
| Number of wells | 303 | ||||||||
| ACS (m3) | SWS (m3) | LGS (m3) | TLVS (m3) | 100 MPS (m3) | 40/70MPS (m3) | 30/50MPS (m3) | TSQS (m3) | |
|---|---|---|---|---|---|---|---|---|
| Conversion | ||||||||
| Maximum | 34 | 2042 | 403 | 2479 | 23 | 57 | 6 | 86 |
| Minimum | 3 | 285 | 3 | 291 | 2 | 8 | 0 | 10 |
| Average | 21 | 1637 | 147 | 1805 | 13 | 37 | 2 | 52 |
| Number of wells | 303 | |||||||
| CS − | LHS (m3) | NFS − | ACS (m3) | SWS (m3) | LGS (m3) | TLVS (m3) | TSQS (m3) | ASR (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Reasonable scope | >2 | 500–2500 | <30 | <35 | <2100 | <500 | <2635 | <100 | <11 |
| Type I (m3) | Type Ⅱ (m3) | Type Ⅲ (m3) | Type Ⅳ (m3) | |
|---|---|---|---|---|
| Acid amount of each section | 20–22 | 22–24 | 20–22 | 22–24 |
| Slickwater of each section | 1660–1720 | 1660–1720 | 1420–1660 | 1660–1720 |
| Linear glue of each section | 85–160 | 160–250 | 85–160 | 160–250 |
| 100 mesh proppant of each section | 10.5–16 | 10.5–16 | 7.5–10.5 | 7.5–10.5 |
| 40–70 mesh proppant of each section | 32–38 | 32–38 | 32–38 | 32–38 |
| 30–50 mesh proppant of each section | 0.4–1.8 | 0.4–1.8 | 0.4–1.8 | 0.4–1.8 |
| Open Flow Capacity (m3) | Fracturing Construction Materials Costs (¥) | Cost Benefit (m3/¥) | Average Open Flow Capacity (m3) | Average Cost Benefit (m3/¥) | Category | |
|---|---|---|---|---|---|---|
| A1 | 453,000 | 3,013,520 | 0.1503 | 462,700 | 0.1480 | I |
| A2 | 441,900 | 3,242,040 | 0.1363 | |||
| A3 | 493,200 | 3,134,270 | 0.1573 | |||
| A4 | 461,100 | 3,217,520 | 0.1433 | 471,200 | 0.1411 | Ⅱ |
| A5 | 493,400 | 3,425,089 | 0.1441 | |||
| A6 | 459,100 | 3,376,986 | 0.1359 | |||
| A7 | 522,300 | 2,686,160 | 0.1944 | 481,767 | 0.1691 | Ⅲ |
| A8 | 421,800 | 2,867,590 | 0.1470 | |||
| A9 | 501,200 | 3,024,794 | 0.1656 | |||
| A10 | 568,300 | 3,246,729 | 0.1750 | 526,733 | 0.1536 | Ⅳ |
| A11 | 453,000 | 3,494,560 | 0.1296 | |||
| A12 | 558,900 | 3,578,237 | 0.1562 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Cheng, L.; Liu, D.; Hu, J.; Zhang, W.; Li, K.; Xiao, J.; Wang, X.; Zhang, F. Big Data Analysis and Research on Fracturing Construction Parameters of Shale Gas Horizontal Wells—A Case Study of Horizontal Wells in Fuling Demonstration Area, China. Energies 2021, 14, 8357. https://doi.org/10.3390/en14248357
Li M, Cheng L, Liu D, Hu J, Zhang W, Li K, Xiao J, Wang X, Zhang F. Big Data Analysis and Research on Fracturing Construction Parameters of Shale Gas Horizontal Wells—A Case Study of Horizontal Wells in Fuling Demonstration Area, China. Energies. 2021; 14(24):8357. https://doi.org/10.3390/en14248357
Chicago/Turabian StyleLi, Minxuan, Liang Cheng, Dehua Liu, Jiani Hu, Wei Zhang, Kuidong Li, Jialin Xiao, Xiaojun Wang, and Feng Zhang. 2021. "Big Data Analysis and Research on Fracturing Construction Parameters of Shale Gas Horizontal Wells—A Case Study of Horizontal Wells in Fuling Demonstration Area, China" Energies 14, no. 24: 8357. https://doi.org/10.3390/en14248357
APA StyleLi, M., Cheng, L., Liu, D., Hu, J., Zhang, W., Li, K., Xiao, J., Wang, X., & Zhang, F. (2021). Big Data Analysis and Research on Fracturing Construction Parameters of Shale Gas Horizontal Wells—A Case Study of Horizontal Wells in Fuling Demonstration Area, China. Energies, 14(24), 8357. https://doi.org/10.3390/en14248357





