Assessment of Machine-Learned Turbulence Models Trained for Improved Wake-Mixing in Low-Pressure Turbine Flows
Abstract
:1. Introduction
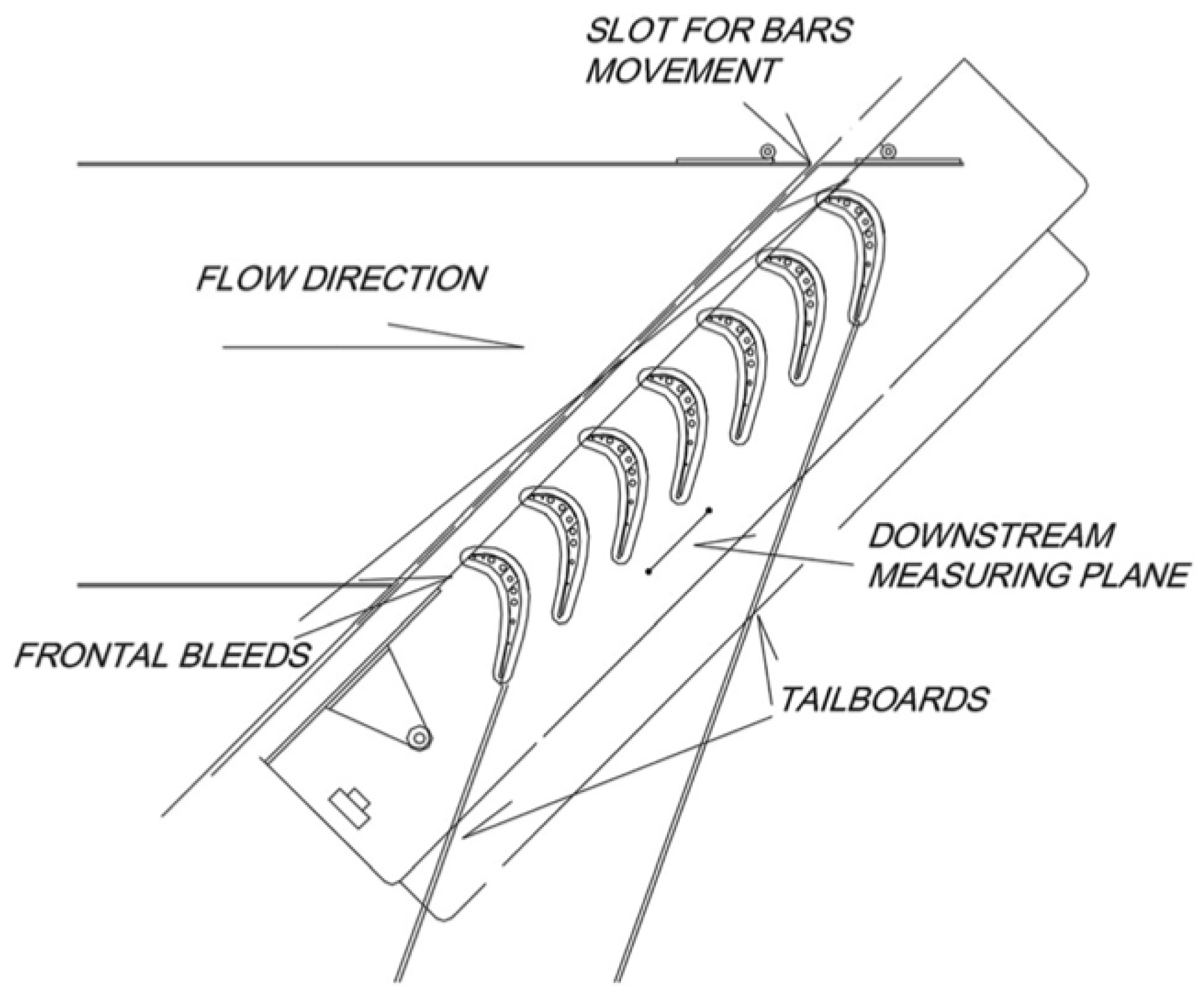
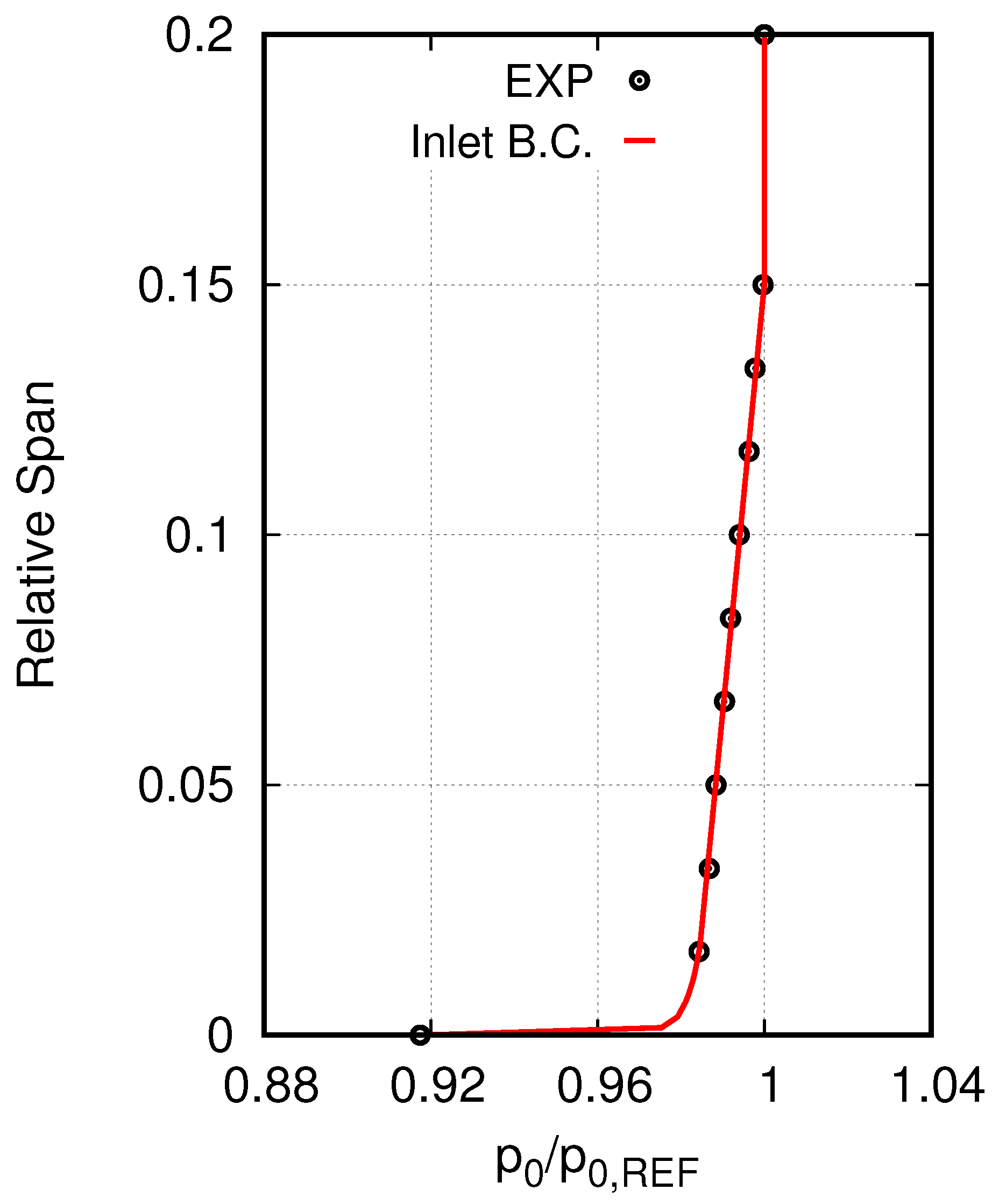
2. Test Case and Boundary Conditions
3. Domain Discretization
4. Computational Framework
5. Discussion of Results
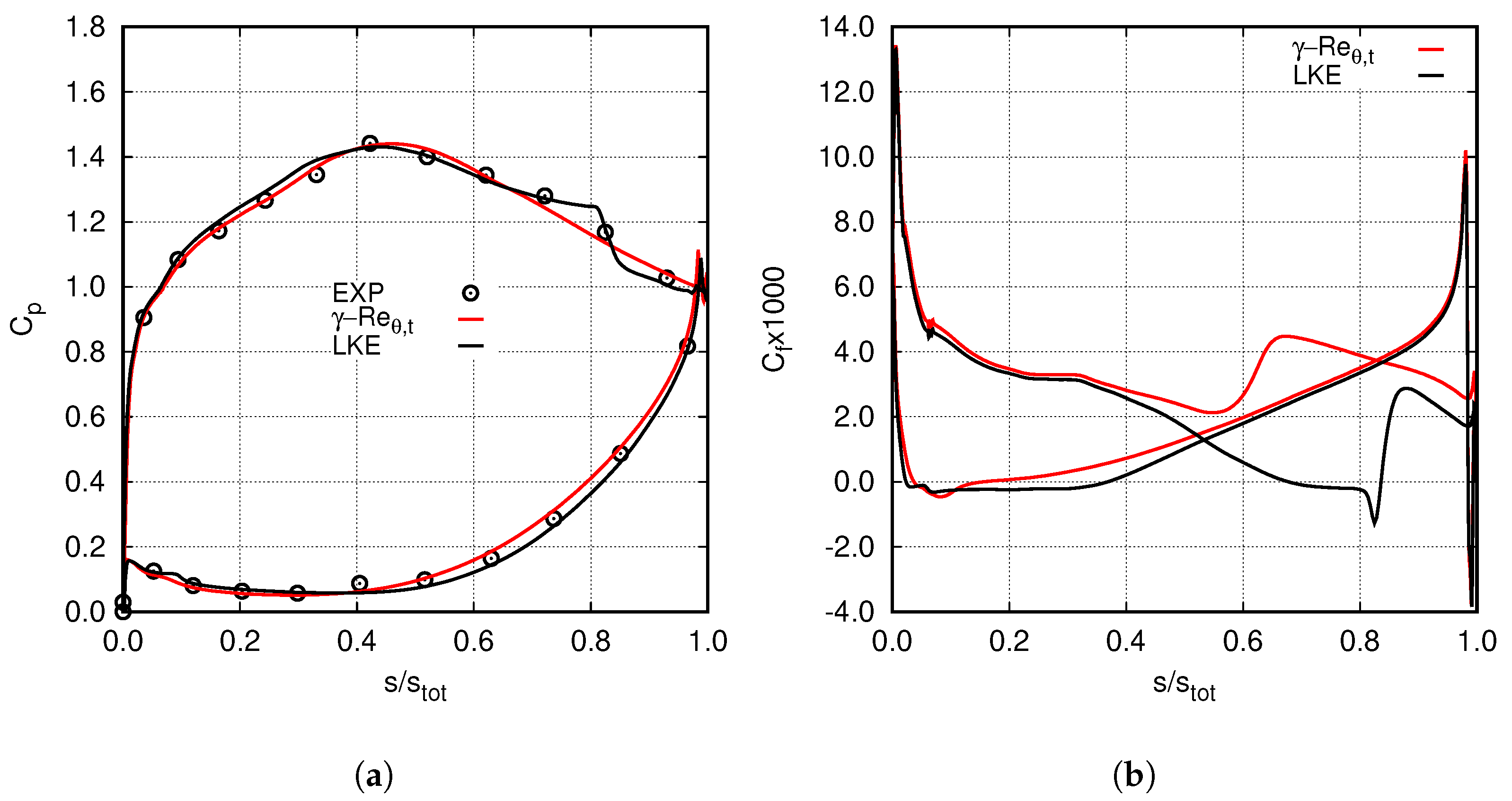
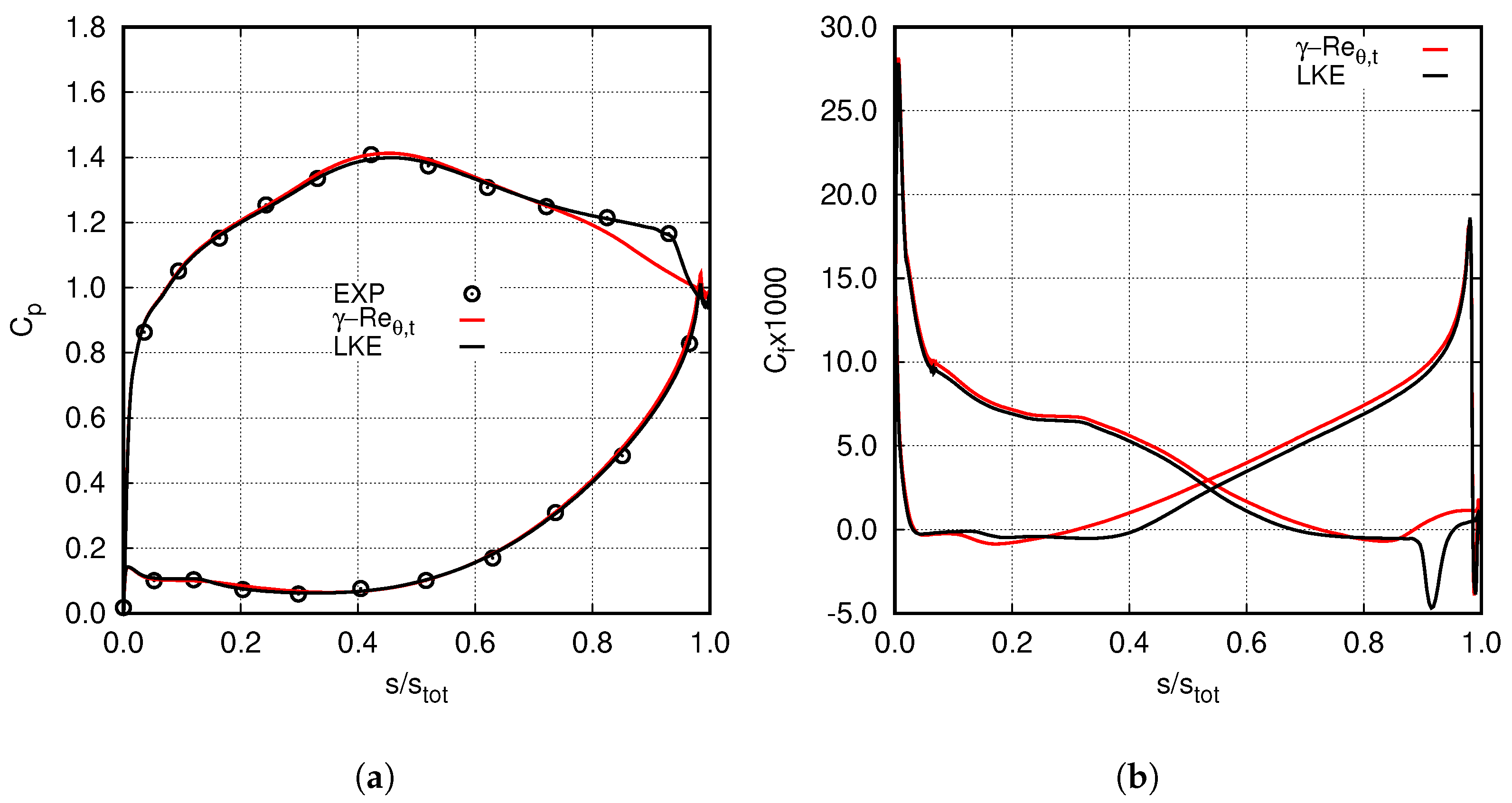
5.1. Blade Boundary-Layers and Effect of Transition Modelling
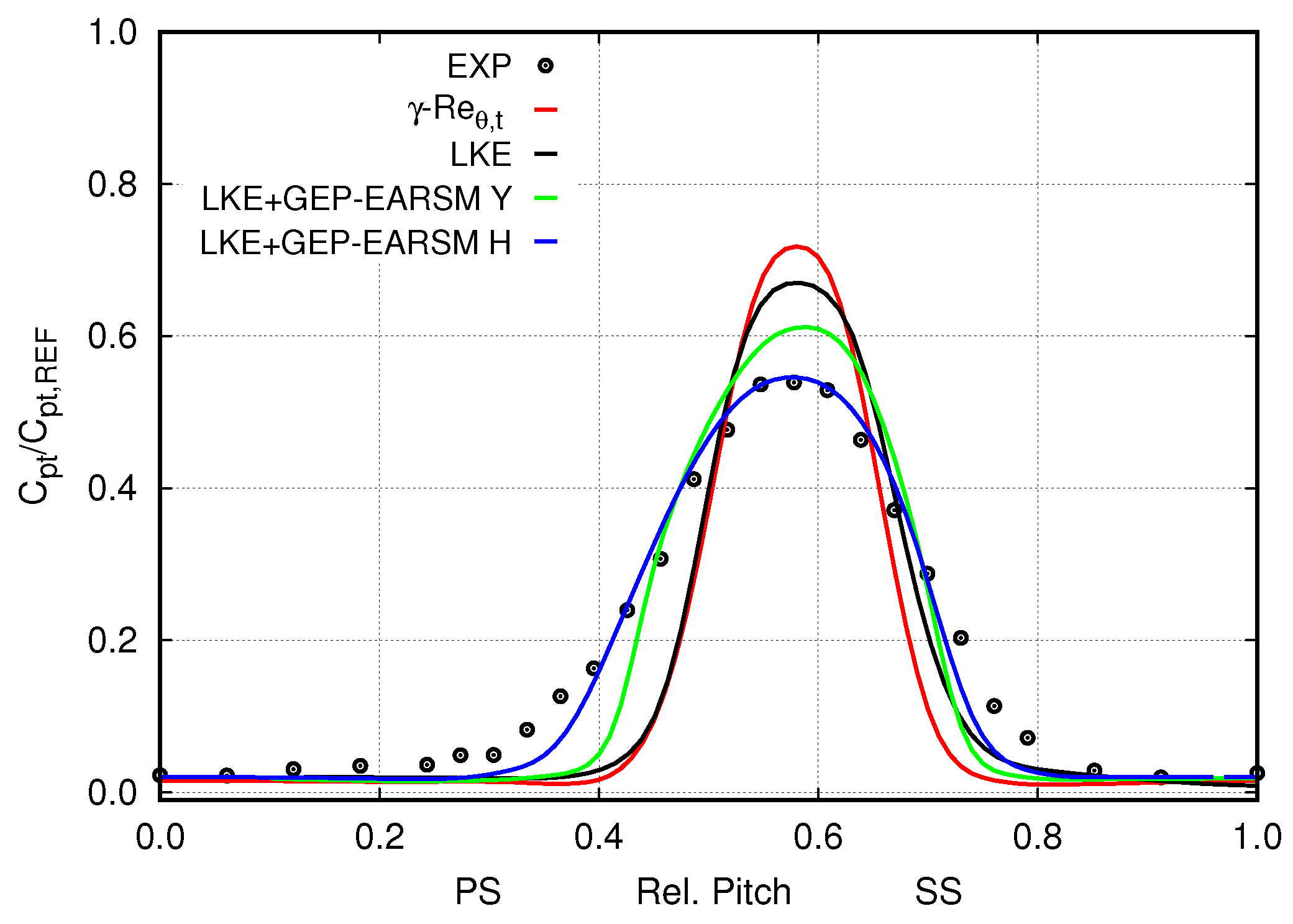
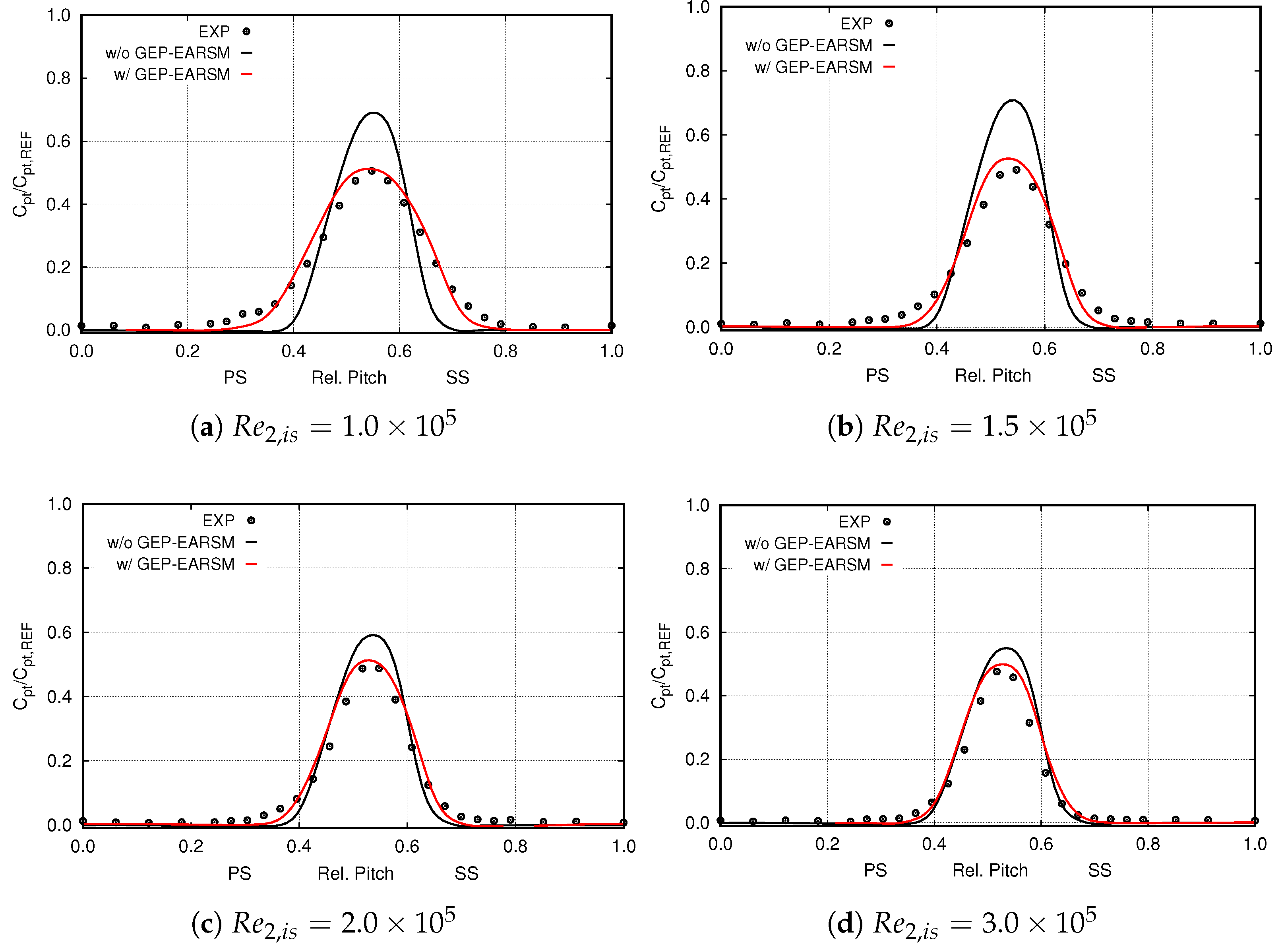
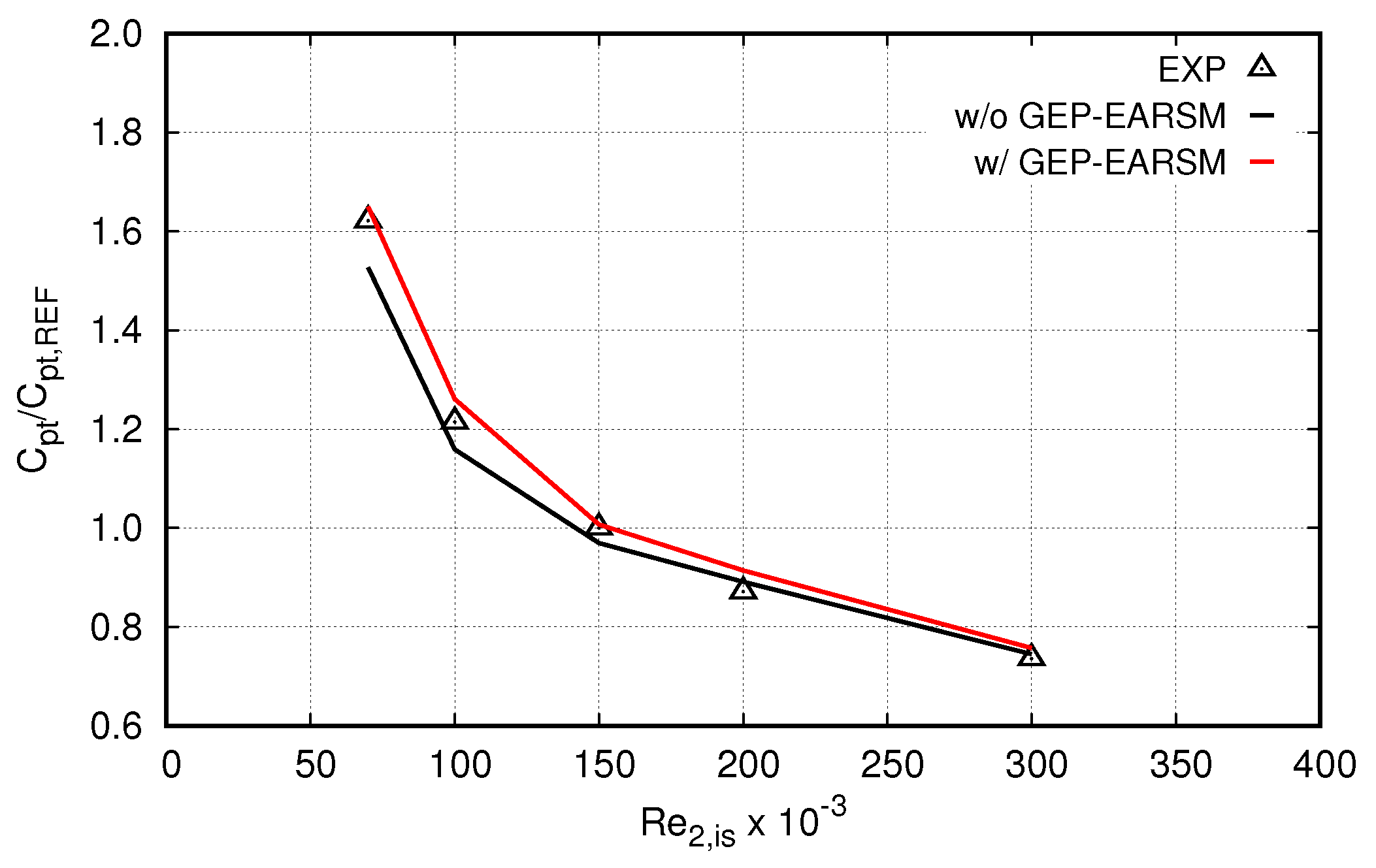
5.2. Wake Diffusion and Effect of the EARSMs
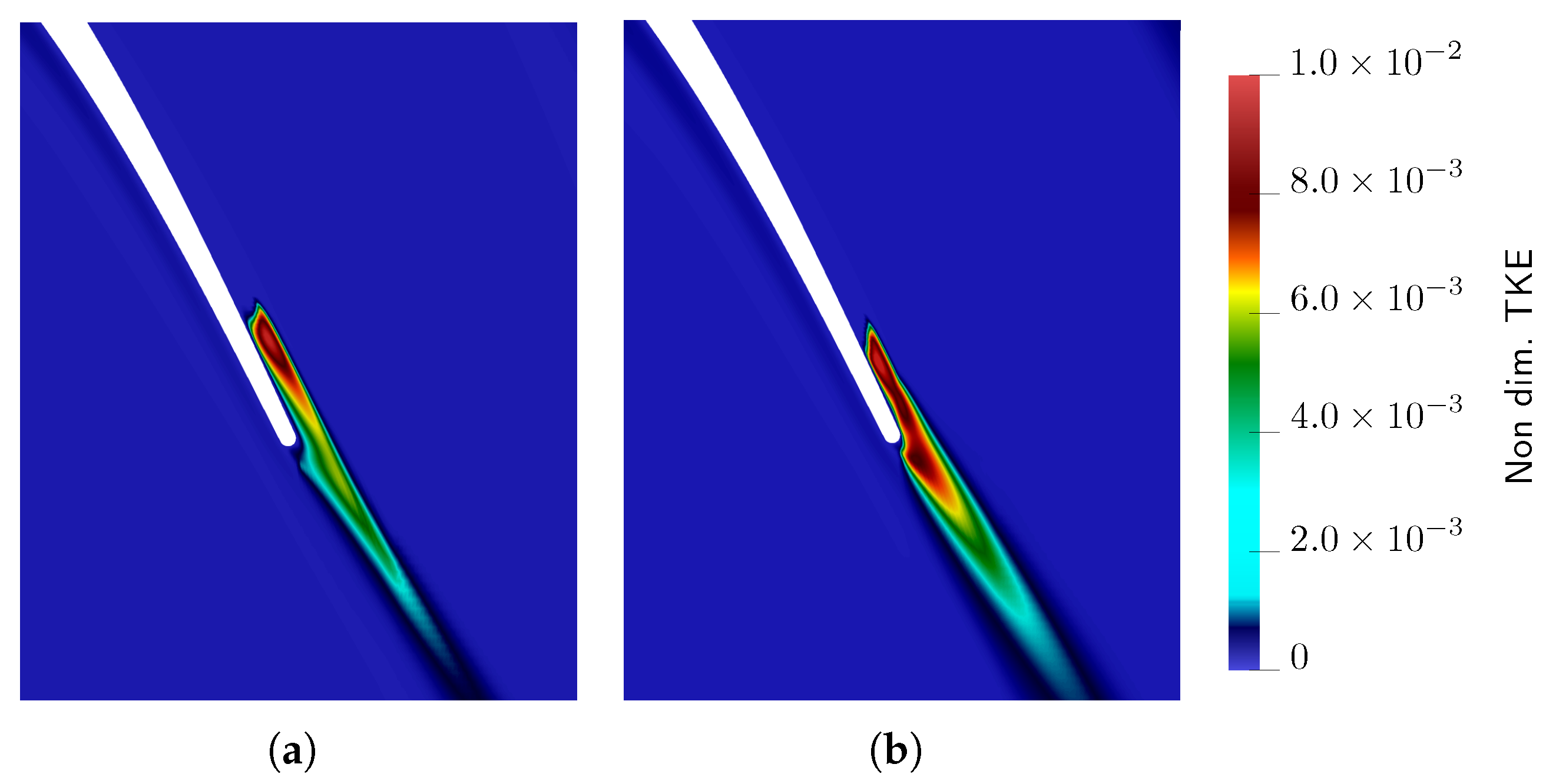
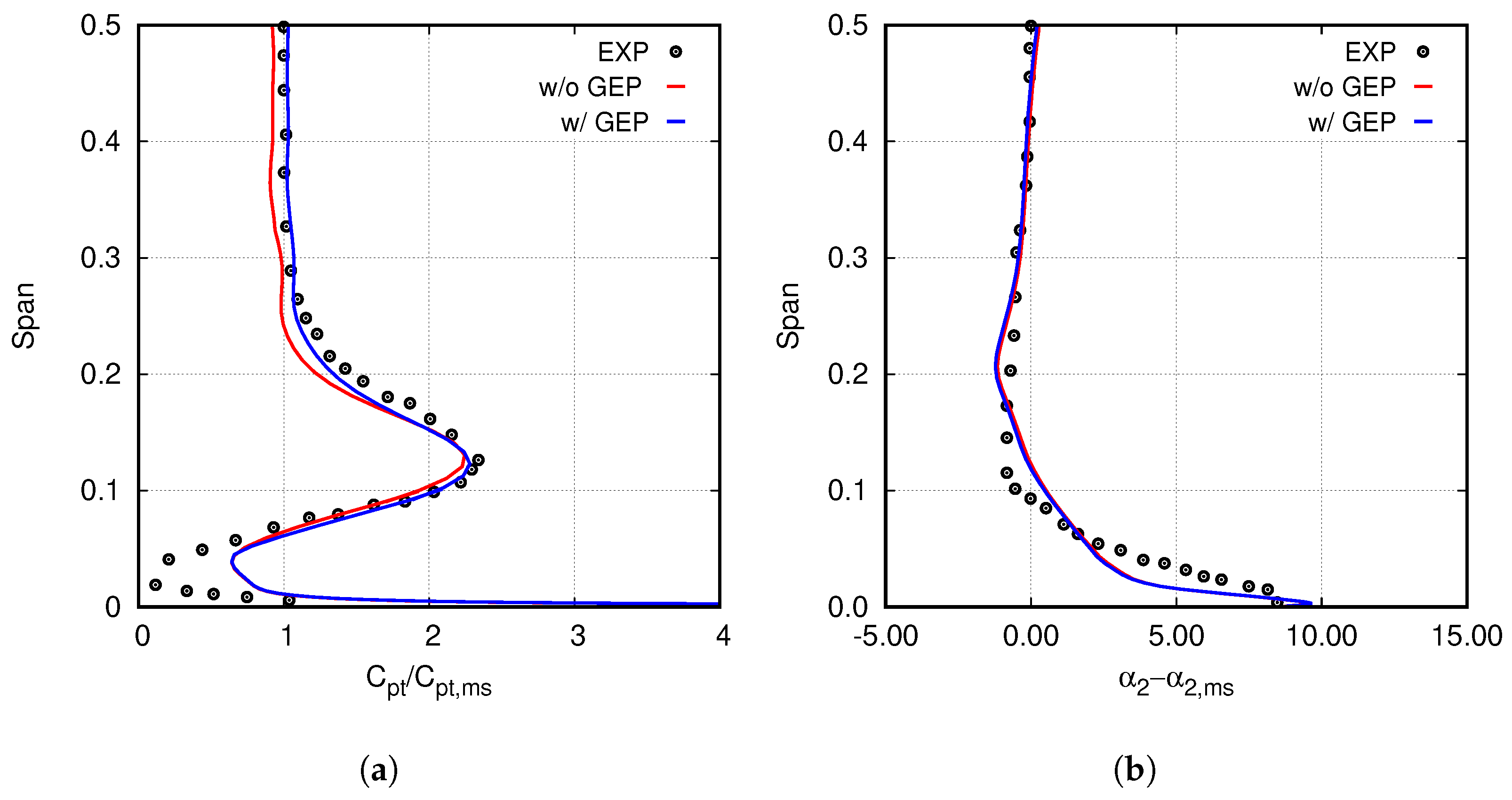
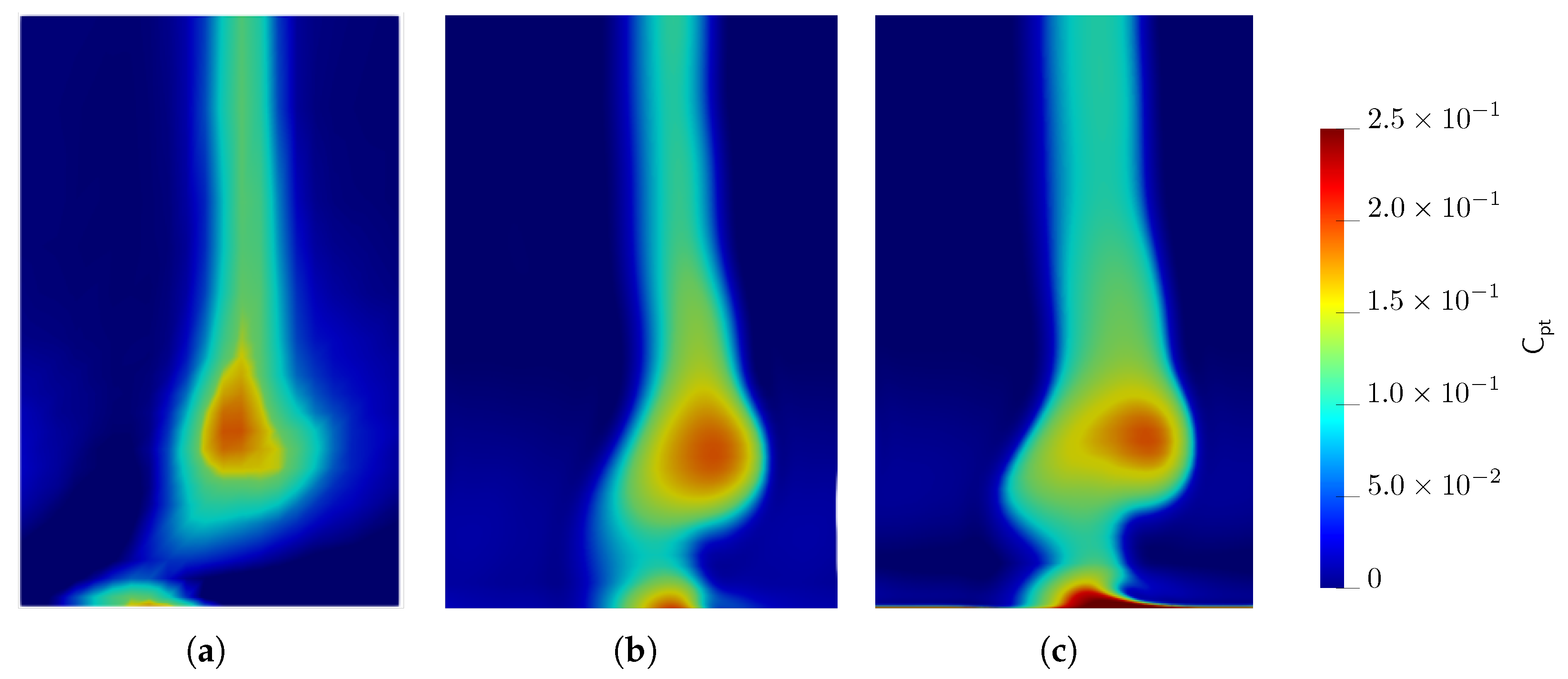
5.3. Secondary Flows
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DNS | Direct Numerical Simulation |
| EARSM | Explicit Algebraic Reynolds Stress Model |
| FSTI | Free Stream Turbulence Intensity |
| GEP | Gene Expression Programming |
| LES | Large Eddy Simulation |
| LKE | Laminar Kinetic Energy |
| LPT | Low Pressure Turbine |
| TVD | Total Variation Diminishing |
Nomenclature
| Anisotropy tensor | |
| Blade aspect ratio, | |
| C | blade chord |
| Pressure coefficient | |
| Total Pressure Loss Coefficient | |
| Skin Friction Coefficient | |
| Diffusion rate, | |
| g | Tangential gap |
| h | Blade height |
| I | Invariant |
| k | Turbulent Kinetic Energy |
| p | Pressure |
| Isentropic exit Reynolds number, | |
| s | Curvilinear abscissa along airfoil surface |
| Strain rate tensor | |
| v | Flow velocity |
| Tensor basis element | |
| x | Axial, axial coordinate |
| y | Pitchwise coordinate |
| z | Spanwise coordinate |
| Zweifel coefficient, | |
| Kronecker tensor | |
| Dinamic viscosity | |
| Fluid density | |
| Turbulence time scale | |
| Reynolds stress tensor | |
| Specific dissipation rate | |
| Rotation tensor |
Subscripts
| 0 | Total quantity |
| 1 | Inlet |
| 2 | Outlet |
| Isentropic | |
| Midspan | |
| Relative to the suction peak velocity | |
| Reference | |
| Total | |
| w | Wall |
References
- Intergovernmental Panel on Climate Change (IPCC). Global Warming of 1.5 °C, Summary for Policymakers. In Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Michelassi, V.; Chen, L.W.; Pichler, R.; Sandberg, R.D. Compressible Direct Numerical Simulation of Low-Pressure Turbines: Part II - Effect of Inflow Disturbances. J. Turbomach. 2015, 137, 071005. [Google Scholar] [CrossRef]
- Praisner, T.J.; Clark, J.P.; Nash, T.C.; Rice, M.J.; Grover, E.A. Performance Impacts Due to Wake Mixing in Axial-Flow Turbomachinery. In Proceedings of the ASME Turbo Expo, Barcelona, Spain, 8–11 May 2006. ASME paper GT2006-90666. [Google Scholar]
- Marconcini, M.; Pacciani, R.; Arnone, A.; Michelassi, V.; Pichler, R.; Zhao, Y.; Sandberg, R. Large Eddy Simulation and RANS Analysis of the End-Wall Flow in a Linear Low-Pressure-Turbine Cascade—Part II: Loss Generation. J. Turbomach. 2019, 141, 051004. [Google Scholar] [CrossRef]
- Hodson, H.P.; Howell, R.J. The Role of Transition in High-Lift Low-Pressure Turbines for Aeroengines. Prog. Aerosp. Sci. 2005, 41, 419–454. [Google Scholar] [CrossRef]
- Uzol, O.; Zhang, X.F.; Cranstone, A.; Hodson, H.P. Investigation of Unsteady Wake-Separated Boundary Layer Interaction Using Particle-Image-Velocimetry. In Proceedings of the ASME Turbo Expo, Montreal, QC, Canada, 14–17 May 2007. ASME paper No. GT2007-28099. [Google Scholar]
- Moreau, S. Turbomachinery Noise Predictions: Present and Future. Acoustics 2019, 1, 92–116. [Google Scholar] [CrossRef] [Green Version]
- Burberi, C.; Ghignoni, E.; Pinelli, L.; Marconcini, M. Validation of an URANS approach for direct and indirect noise assessment in a high pressure turbine stage. Energy Procedia 2018, 148, 130–137. [Google Scholar] [CrossRef]
- Pinelli, L.; Poli, F.; Marconcini, M.; Arnone, A.; Spano, E.; Torzo, D. Validation of a 3D Linearized Method for Turbomachinery Tone Noise Analysis. In Proceedings of the ASME Turbo Expo, Vancouver, BC, Canada, 6–10 June 2011. ASME paper GT2011-45886. [Google Scholar]
- Pacciani, R.; Marconcini, M.; Arnone, A.; Bertini, F. A CFD Study of Low Reynolds Number Flow in High Lift Cascades. In Proceedings of the ASME Turbo Expo, Glasgow, UK, 14–18 June 2010. ASME paper GT2010-23300. [Google Scholar]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence Modeling in the Age of Data. Annu. Rev. Fluid Mech. 2019, 53, 357–377. [Google Scholar] [CrossRef] [Green Version]
- Weatheritt, J.; Sandberg, R.D. The development of algebraic stress models using a novel evolutionary algorithm. Int. J. Heat Fluid Flow 2017, 68, 298–318. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: A New Adaptive Algorithm for Solving Problems. Complex Syst. 2001, 13, 87–129. [Google Scholar]
- Akolekar, H.D.; Weatheritt, J.; Hutchins, N.; Sandberg, R.D.; Laskowski, G.; Michelassi, V. Development and Use of Machine-Learnt Algebraic Reynolds Stress Models for Enhanced Prediction of Wake Mixing in Low Pressure Turbines. J. Turbomach. 2019, 141, 041010. [Google Scholar] [CrossRef]
- Akolekar, H.D.; Sandberg, R.D.; Hutchins, N.; Michelassi, V.; Laskowski, G. Machine-Learnt Turbulence Closures for Low Pressure Turbines with Unsteady Inflow Conditions. J. Turbomach. 2019, 141, 101009. [Google Scholar] [CrossRef]
- Zhao, Y.; Akolekar, H.D.; Weatheritt, J.; Michelassi, V.; Sandberg, R.D. RANS Turbulence Model Development using CFD-Driven Machine Learning. J. Comput. Phisycs 2020, 411, 109413. [Google Scholar] [CrossRef] [Green Version]
- Akolekar, H.; Zhao, Y.; Sandberg, R.D.; Pacciani, R. Integration of Machine Learning and Computational Fluid Dynamics to Develop Turbulence Models for Improved Low-Pressure Turbine Wake Mixing. J. Turbomach. 2021, 143, 121001. [Google Scholar] [CrossRef]
- Lav, C.; Sandberg, R.D.; Philip, J. A Framework to Develop Data-Driven Turbulence Models for Flows with Organised Unsteadiness. J. Comput. Phisycs 2019, 383, 148–165. [Google Scholar] [CrossRef]
- Langtry, R.B.; Menter, F.R. Correlation-Based Transition Modeling for Unstructured Parallelized Computational Fluid Dynamics Codes. AIAA J. 2009, 47, 2894–2906. [Google Scholar] [CrossRef]
- Pacciani, R.; Marconcini, M.; Fadai-Ghotbi, A.; Lardeau, S.; Leschziner, M.A. Calculation of High-Lift Cascades in Low Pressure Turbine Conditions Using a Three-Equation Model. J. Turbomach. 2011, 133, 031016. [Google Scholar] [CrossRef]
- Wilcox, D.C. Multiscale Model for Turbulent Flows. AIAA J. 1988, 26, 1311–1320. [Google Scholar] [CrossRef]
- Simoni, D.; Berrino, M.; Ubaldi, M.; Zunino, P.; Bertini, F. Off-Design Performance of a Highly Loaded LP Turbine Cascade Under Steady and Unsteady Incoming Flow Conditions. J. Turbomach. 2015, 137, 071009. [Google Scholar] [CrossRef]
- Marconcini, M.; Pacciani, R.; Arnone, A.; Bertini, F. Low-Pressure Turbine Cascade Performance Calculations with Incidence Variation and Periodic Unsteady Inflow Conditions. In Proceedings of the ASME Turbo Expo, Montreal, QC, Canada, 15–19 June 2015. ASME paper GT2015-42276. [Google Scholar]
- Giovannini, M.; Rubechini, F.; Marconcini, M.; Simoni, D.; Yepmo, V.; Bertini, F. Secondary Flows in Low- Pressure Turbines Cascades: Numerical and Experimental Investigation of the Impact of the Inner Part of the Boundary Layer. J. Turbomach. 2018, 140, 111002. [Google Scholar] [CrossRef]
- Pichler, R.; Zhao, Y.; Sandberg, R.; Michelassi, V.; Pacciani, R.; Marconcini, M.; Arnone, A. Large-Eddy Simulation and RANS Analysis of the End-Wall Flow in a Linear Low-Pressure Turbine Cascade, Part I: Flow and Secondary Vorticity Fields Under Varying Inlet Condition. J. Turbomach. 2019, 141, 121005. [Google Scholar] [CrossRef]
- Ricci, M.; Pacciani, R.; Marconcini, M.; Arnone, A. Prediction of Tip Leakage Vortex Dynamics in an Axial Compressor Cascade Using RANS Analyses. In Proceedings of the ASME Turbo Expo, London, UK, 22–26 June 2020. ASME paper GT2020-14797. [Google Scholar]
- Arnone, A. Viscous Analysis of Three–Dimensional Rotor Flow Using a Multigrid Method. J. Turbomach. 1994, 116, 435–445. [Google Scholar] [CrossRef]
- Chorin, A.J. A Numerical Method for Solving Incompressible Viscous Flow Problems. J. Comput. Phys. 1967, 2, 12–26. [Google Scholar] [CrossRef]
- Pacciani, R.; Marconcini, M.; Arnone, A. Comparison of the AUSM+-up and Other Advection Schemes for Turbomachinery Applications. Shock Waves 2019, 29, 705–716. [Google Scholar] [CrossRef]
- Pacciani, R.; Marconcini, M.; Arnone, A.; Bertini, F. An Assessment of the Laminar Kinetic Energy Concept for the Prediction of High-Lift, Low-Reynolds Number Cascade Flows. Proc. Inst. Mech. E Part A J. Power Energy 2011, 225, 995–1003. [Google Scholar] [CrossRef]
- Pacciani, R.; Marconcini, M.; Arnone, A.; Bertini, F. Predicting High-Lift LP Turbine Cascades Flows Using Transition-Sensitive Turbulence Closures. J. Turbomach. 2014, 136, 051007. [Google Scholar] [CrossRef]
- Pope, S.B. A More General Effective-Viscosity Hypothesis. J. Fluid Mech. 1975, 72, 331–340. [Google Scholar] [CrossRef] [Green Version]

| Zw | DR | AR |
|---|---|---|
| 1.1 | 0.5 | 3.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pacciani, R.; Marconcini, M.; Bertini, F.; Rosa Taddei, S.; Spano, E.; Zhao, Y.; Akolekar, H.D.; Sandberg, R.D.; Arnone, A. Assessment of Machine-Learned Turbulence Models Trained for Improved Wake-Mixing in Low-Pressure Turbine Flows. Energies 2021, 14, 8327. https://doi.org/10.3390/en14248327
Pacciani R, Marconcini M, Bertini F, Rosa Taddei S, Spano E, Zhao Y, Akolekar HD, Sandberg RD, Arnone A. Assessment of Machine-Learned Turbulence Models Trained for Improved Wake-Mixing in Low-Pressure Turbine Flows. Energies. 2021; 14(24):8327. https://doi.org/10.3390/en14248327
Chicago/Turabian StylePacciani, Roberto, Michele Marconcini, Francesco Bertini, Simone Rosa Taddei, Ennio Spano, Yaomin Zhao, Harshal D. Akolekar, Richard D. Sandberg, and Andrea Arnone. 2021. "Assessment of Machine-Learned Turbulence Models Trained for Improved Wake-Mixing in Low-Pressure Turbine Flows" Energies 14, no. 24: 8327. https://doi.org/10.3390/en14248327
APA StylePacciani, R., Marconcini, M., Bertini, F., Rosa Taddei, S., Spano, E., Zhao, Y., Akolekar, H. D., Sandberg, R. D., & Arnone, A. (2021). Assessment of Machine-Learned Turbulence Models Trained for Improved Wake-Mixing in Low-Pressure Turbine Flows. Energies, 14(24), 8327. https://doi.org/10.3390/en14248327








