Impact of Cryogenics on Cavitation through an Orifice: A Review
Abstract
1. Introduction
1.1. Statement of the Problem
1.2. Cavitation Regimes
1.3. Thermodynamic Effect
2. Cavitation Modeling
2.1. Bubbly Flow Models
2.2. Homogeneous Models
2.3. Multiphase Models
3. Cavitation Instabilities
Cryogenic Cavitation Dynamics
4. The Issue of Determining the Speed of Sound (SoS) and Void Fraction in a Cavitating Flow
SoS and Void Fraction Measurements with Cryogenics
5. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| 3PT | three pressure transducers |
| mPOD | multiscale proper orthogonal decomposition |
| POD | proper orthogonal decomposition |
| Symbols | |
| A | area |
| c | speed of sound |
| discharge coefficient | |
| specific heat at constant pressure | |
| specific heat at constant volume | |
| D | pipe diameter |
| d | orifice diameter |
| internal energy | |
| f | frequency |
| mass volume fraction | |
| latent heat of vaporization | |
| H | enthalpy |
| heat transfer coefficient | |
| n | polytropic coefficient |
| pressure | |
| pressure pulsation amplitude | |
| Prandtl number | |
| Q | mass flow rate |
| heat exchange between phases | |
| volumetric flow rate | |
| R | bubble radius |
| characteristic radius | |
| superheat ratio | |
| s | orifice thickness |
| surface tension | |
| Strouhal number | |
| T | temperature |
| t | time |
| orifice dimensionless thickness | |
| U | velocity |
| V | volume |
| void fraction | |
| thermal diffusivity | |
| variation | |
| thermal boundary layer thickness | |
| characteristic temperature difference | |
| subcooling degree | |
| liquid fraction | |
| viscosity | |
| density | |
| thermodynamic parameter | |
| cavitation number | |
| downstream pressure ratio | |
| Poisson ratio | |
| Subscripts | |
| channel | |
| downstream | |
| L | laminar |
| l | liquid |
| m | mixture |
| o | orifice |
| generic phases | |
| saturation | |
| T | turbulent |
| t | throat |
| upstream | |
| v | vapor |
References
- Yan, Y.; Thorpe, R. Flow regime transitions due to cavitation in the flow through an orifice. Int. J. Multiph. Flow 1990, 16, 1023–1045. [Google Scholar] [CrossRef]
- Avellan, F.; Dupont, P.; Farhat, M. Cavitation erosion power. In Proceedings of the Cavitation’91 Symposium, 1st ASME-JSME Fluid Engineering Conference, Portland, OR, USA, 23–27 June; 1991; FED-Vol. 116, pp. 135–140. [Google Scholar]
- Burzio, E.; Bersani, F.; Caridi, G.; Vesipa, R.; Ridolfi, L.; Manes, C. Water disinfection by orifice-induced hydrodynamic cavitation. Ultrason. Sonochem. 2020, 60, 104740. [Google Scholar] [CrossRef]
- Jahangir, S.; Hogendoorn, W.; Poelma, C. Dynamics of partial cavitation in an axisymmetric converging-diverging nozzle. Int. J. Multiph. Flow 2018, 106, 34–45. [Google Scholar] [CrossRef]
- Capocelli, M.; Prisciandaro, M.; Lancia, A.; Musmarra, D. Hydrodynamic cavitation of p-nitrophenol: A theoretical and experimental insight. Chem. Eng. J. 2014, 254, 1–8. [Google Scholar] [CrossRef]
- Šarc, A.; Stepišnik-Perdih, T.; Petkovšek, M.; Dular, M. The issue of cavitation number value in studies of water treatment by hydrodynamic cavitation. Ultrason. Sonochem. 2017, 34, 51–59. [Google Scholar] [CrossRef]
- Esposito, C.; Mendez, M.; Steelant, J.; Vetrano, M. Spectral and modal analysis of a cavitating flow through an orifice. Exp. Therm. Fluid Sci. 2021, 121, 110251. [Google Scholar] [CrossRef]
- Esposito, C.; Peveroni, L.; Gouriet, J.; Steelant, J.; Vetrano, M. On the influence of thermal phenomena during cavitation through an orifice. Int. J. Heat Mass Transf. 2021, 164, 120481. [Google Scholar] [CrossRef]
- Mishra, C.; Peles, Y. Cavitation in flow through a micro-orifice inside a silicon microchannel. Phys. Fluids 2005, 17, 013601. [Google Scholar] [CrossRef]
- Brennen, C.E. Cavitation and Bubble Dynamics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Gustavsson, J.; Denning, K.; Segal, C. Experimental study of Cryogenic Cavitation Using Fluoroketone. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 576. [Google Scholar]
- Arndt, R.E.; Keller, A.P. Water quality effects on cavitation inception in a trailing vortex. J. Fluids Eng. 1992, 114, 430–438. [Google Scholar] [CrossRef]
- Palau-Salvador, G.; Altozano, P.G.; Arviza-Valverde, J. Numerical modeling of cavitating flows for simple geometries using FLUENT V6.1. Span. J. Agric. Res. 2007, 5, 460. [Google Scholar] [CrossRef]
- Tullis, J.P. Cavitation Guide for Control Valves; Technical Report; Nuclear Regulatory Commission: Washington, DC, USA; Div. of Engineering, Tullis Engineering Consultants: Logan, UT, USA, 1993.
- Chaves, H.; Knapp, M.; Kubitzek, A.; Obermeier, F.; Schneider, T. Experimental study of cavitation in the nozzle hole of diesel injectors using transparent nozzles. SAE Trans. 1995, 104, 645–657. [Google Scholar]
- Holl, J.W.; Billet, M.L.; Weir, D.S. Thermodynamic Effects on Developed Cavitation. J. Fluids Eng. 1975, 97, 507–513. [Google Scholar] [CrossRef]
- Franc, J.P.; Michel, J.M. Fundamentals of Cavitation; Springer Science & Business Media: Dordrecht, The Netherlands, 2006; Volume 76. [Google Scholar]
- Franc, J.P.; Rebattet, C.; Coulon, A. An Experimental Investigation of Thermal Effects in a Cavitating Inducer. J. Fluids Eng. 2004, 126, 716–723. [Google Scholar] [CrossRef]
- Linstrom, P.; Mallard, W. NIST Chemistry WebBook, NIST Standard Reference Database Number 69. Available online: https://webbook.nist.gov/chemistry/fluid/ (accessed on 11 February 2017).
- Tani, N.; Nagashima, T. Cryogenic cavitating flow in 2D laval nozzle. J. Therm. Sci. 2003, 12, 157–161. [Google Scholar] [CrossRef]
- Hosangadi, A.; Ahuja, V. Numerical Study of Cavitation in Cryogenic Fluids. J. Fluids Eng. 2005, 127, 267–281. [Google Scholar] [CrossRef]
- Tseng, C.C.; Shyy, W. Modeling for isothermal and cryogenic cavitation. Int. J. Heat Mass Transf. 2010, 53, 513–525. [Google Scholar] [CrossRef]
- Niiyama, K.; Hasegawa, S.; Tsuda, S.; Yoshida, Y.; Tamura, T.; Oike, M. Thermodynamic Effects on Cryogenic Cavitating Flow in an Orifice. In Proceedings of the CAV2009—7th International Symposium on Cavitation, Ann Arbor, MI, USA, 16–20 August 2009. [Google Scholar]
- Wallis, G.B. Critical two-phase flow. Int. J. Multiph. Flow 1980, 6, 97–112. [Google Scholar] [CrossRef]
- Franc, J.P.; Pellone, C. Analysis of Thermal Effects in a Cavitating Inducer Using Rayleigh Equation. J. Fluids Eng. 2007, 129, 974. [Google Scholar] [CrossRef]
- Goncalves, E.; Patella, R.F. Numerical simulation of cavitating flows with homogeneous models. Comput. Fluids 2009, 38, 1682–1696. [Google Scholar] [CrossRef]
- Decaix, J.; Goncalvès, E. Time-dependent simulation of cavitating flow with k-ℓ turbulence models. Int. J. Numer. Methods Fluids 2011, 68, 1053–1072. [Google Scholar] [CrossRef]
- Hickel, S.; Mihatsch, M.; Schmidt, S.J. Implicit Large Eddy Simulation of Cavitation in Micro Channel Flows. arXiv 2014, arXiv:1401.6548. [Google Scholar]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T. A preconditioned Navier–Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical Basis and Validation of the Full Cavitation Model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Chen, T.; Wang, G.; Huang, B.; Wang, K. Numerical study of thermodynamic effects on liquid nitrogen cavitating flows. Cryogenics 2015, 70, 21–27. [Google Scholar] [CrossRef]
- Senocak, I.; Shyy, W. Interfacial dynamics-based modelling of turbulent cavitating flows, Part-1: Model development and steady-state computations. Int. J. Numer. Methods Fluids 2004, 44, 975–995. [Google Scholar] [CrossRef]
- Jin, W.; Xu, X.; Tang, Y.; Zhou, H.; Ren, X.; Zhou, H. Coefficient Adaptation Method for the Zwart Model. J. Appl. Fluid Mech. (JAFM) 2018, 11, 1665–1678. [Google Scholar] [CrossRef]
- Zhou, H.; Xiang, M.; Okolo, P.N.; Wu, Z.; Bennett, G.J.; Zhang, W. An efficient calibration approach for cavitation model constants based on OpenFOAM platform. J. Mar. Sci. Technol. 2019, 24, 1043–1056. [Google Scholar] [CrossRef]
- Sikirica, A.; Čarija, Z.; Lučin, I.; Grbčić, L.; Kranjčević, L. Cavitation Model Calibration Using Machine Learning Assisted Workflow. Mathematics 2020, 8, 2107. [Google Scholar] [CrossRef]
- Xing, T.; Frankel, S.H. Effect of Cavitation on Vortex Dynamics in a Submerged Laminar Jet. AIAA J. 2002, 40, 2266–2276. [Google Scholar] [CrossRef]
- Abuaf, N.; Wu, B.J.; Zimmer, G.; Saha, P. Study of Nonequilibrium Flashing of Water in a Converging-Diverging Nozzle. Volume 1: Experimental; Technical Report; Brookhaven National Lab.: Upton, NY, USA, 1981.
- Örley, F.; Trummler, T.; Hickel, S.; Mihatsch, M.; Schmidt, S.; Adams, N. Large-eddy simulation of cavitating nozzle flow and primary jet break-up. Phys. Fluids 2015, 27, 086101. [Google Scholar] [CrossRef]
- Hord, J. Cavitation in Liquid Cryogens. 2: Hydrofoil; NASA-CR-2156; National Bureau of Standards: Boulder, CO, USA, 1973.
- Rodio, M.; Giorgi, M.D.; Ficarella, A. Influence of convective heat transfer modeling on the estimation of thermal effects in cryogenic cavitating flows. Int. J. Heat Mass Transf. 2012, 55, 6538–6554. [Google Scholar] [CrossRef]
- Travis, J.; Koch, D.P.; Breitung, W. A homogeneous non-equilibrium two-phase critical flow model. Int. J. Hydrogen Energy 2012, 37, 17373–17379. [Google Scholar] [CrossRef]
- Hendricks, R.C.; Simoneau, R.J.; Barrows, R.F. Two-Phase Choked Flow of Subcooled Oxygen and Nitrogen; NASA Technical Note: Cleveland, OH, USA, 1976.
- Dumond, J.; Magagnato, F.; Class, A. Stochastic-field cavitation model. Phys. Fluids 2013, 25, 073302. [Google Scholar] [CrossRef]
- Valiño, L. A field Monte Carlo formulation for calculating the probability density function of a single scalar in a turbulent flow Flow Turbul. Combust. 1998, 60, 157–172. [Google Scholar] [CrossRef]
- Yuan, W.; Sauer, J.; Schnerr, G.H. Modeling and computation of unsteady cavitation flows in injection nozzles. Mécanique Ind. 2001, 2, 383–394. [Google Scholar] [CrossRef]
- Xue, R.; Ruan, Y.; Liu, X.; Cao, F.; Hou, Y. The influence of cavitation on the flow characteristics of liquid nitrogen through spray nozzles: A CFD study. Cryogenics 2017, 86, 42–56. [Google Scholar] [CrossRef]
- Saurel, R.; Petitpas, F.; Abgrall, R. Modelling phase transition in metastable liquids: Application to cavitating and flashing flows. J. Fluid Mech. 2008, 607, 313–350. [Google Scholar] [CrossRef]
- Janet, J.P.; Liao, Y.; Lucas, D. Heterogeneous nucleation in CFD simulation of flashing flows in converging–diverging nozzles. Int. J. Multiph. Flow 2015, 74, 106–117. [Google Scholar] [CrossRef]
- Lauer, E.; Hu, X.; Hickel, S.; Adams, N. Numerical modelling and investigation of symmetric and asymmetric cavitation bubble dynamics. Comput. Fluids 2012, 69, 1–19. [Google Scholar] [CrossRef]
- Hu, X.; Khoo, B.; Adams, N.; Huang, F. A conservative interface method for compressible flows. J. Comput. Phys. 2006, 219, 553–578. [Google Scholar] [CrossRef]
- Christopher, D.M.; Wang, H.; Peng, X. Numerical analysis of the dynamics of moving vapor bubbles. Int. J. Heat Mass Transf. 2006, 49, 3626–3633. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Ficarella, A. Simulation of Cryogenic Cavitation by Using Both Inertial and Heat Transfer Control Bubble Growth. In Proceedings of the 39th AIAA Fluid Dynamics Conference, San Antonio, TX, USA, 22–25 June 2019. [Google Scholar] [CrossRef]
- Hutli, E.A.F.; Nedeljkovic, M.S. Frequency in Shedding/Discharging Cavitation Clouds Determined by Visualization of a Submerged Cavitating Jet. J. Fluids Eng. 2008, 130, 021304. [Google Scholar] [CrossRef]
- Ganesh, H.; Mäkiharju, S.A.; Ceccio, S.L. Bubbly shock propagation as a mechanism for sheet-to-cloud transition of partial cavities. J. Fluid Mech. 2016, 802, 37–78. [Google Scholar] [CrossRef]
- Arakeri, V.H.; Shanmuganathan, V. On the evidence for the effect of bubble interference on cavitation noise. J. Fluid Mech. 1985, 159, 131. [Google Scholar] [CrossRef]
- Furness, R.A.; Hutton, S.P. Experimental and Theoretical Studies of Two-Dimensional Fixed-Type Cavities. J. Fluids Eng. 1975, 97, 515. [Google Scholar] [CrossRef]
- Knapp, R.T. Recent investigations of the mechanics of cavitation and cavitation damage. Trans. ASME 1955, 77, 1045–1054. [Google Scholar]
- Wade, R.B.; Acosta, A.J. Experimental Observations on the Flow Past a Plano-Convex Hydrofoil. J. Basic Eng. 1966, 88, 273. [Google Scholar] [CrossRef]
- Le, Q.; Franc, J.P.; Michel, J.M. Partial Cavities: Global Behavior and Mean Pressure Distribution. J. Fluids Eng. 1993, 115, 243. [Google Scholar] [CrossRef]
- Reisman, G.; Wang, Y.C.; Brennen, C.E. Observations of shock waves in cloud cavitation. J. Fluid Mech. 1998, 355, 255–283. [Google Scholar] [CrossRef]
- Leroux, J.B.; Astolfi, J.A.; Billard, J.Y. An Experimental Study of Unsteady Partial Cavitation. J. Fluids Eng. 2004, 126, 94. [Google Scholar] [CrossRef]
- Brennen, C.E.; Brennen, C.E. Fundamentals of Multiphase Flow; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Sato, K.; Wada, Y.; Noto, Y.; Sugimoto, Y. Reentrant Motion in Cloud Cavitation due to Cloud Collapse and Pressure Wave Propagation. In Proceedings of the ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting, Montreal, QC, Canada, 1–5 August 2010; Volume 2. [Google Scholar] [CrossRef]
- Stanley, C.; Barber, T.; Rosengarten, G. Re-entrant jet mechanism for periodic cavitation shedding in a cylindrical orifice. Int. J. Heat Fluid Flow 2014, 50, 169–176. [Google Scholar] [CrossRef]
- Callenaere, M.; Franc, J.P.; Michel, J.M.; Riondet, M. The cavitation instability induced by the development of a re-entrant jet. J. Fluid Mech. 2001, 444. [Google Scholar] [CrossRef]
- Soyama, H.; Sekine, Y. Sustainable surface modification using cavitation impact for enhancing fatigue strength demonstrated by a power circulating-type gear tester. Int. J. Sustain. Eng. 2010, 3, 25–32. [Google Scholar] [CrossRef]
- Soyama, H. Enhancing the Aggressive Intensity of a Cavitating Jet by Means of the Nozzle Outlet Geometry. J. Fluids Eng. 2011, 133, 101301. [Google Scholar] [CrossRef]
- Stanley, C.; Barber, T.; Milton, B.; Rosengarten, G. Periodic cavitation shedding in a cylindrical orifice. Exp. Fluids 2011, 51, 1189–1200. [Google Scholar] [CrossRef]
- Nishimura, S.; Takakuwa, O.; Soyama, H. Similarity Law on Shedding Frequency of Cavitation Cloud Induced by a Cavitating Jet. J. Fluid Sci. Technol. 2012, 7, 405–420. [Google Scholar] [CrossRef][Green Version]
- Danlos, A.; Ravelet, F.; Coutier-Delgosha, O.; Bakir, F. Cavitation regime detection through Proper Orthogonal Decomposition: Dynamics analysis of the sheet cavity on a grooved convergent–divergent nozzle. Int. J. Heat Fluid Flow 2014, 47, 9–20. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Fontanarosa, D.; Ficarella, A. Characterization of cavitating flow regimes in an internal sharp-edged orifice by means of Proper Orthogonal Decomposition. Exp. Therm. Fluid Sci. 2018, 93, 242–256. [Google Scholar] [CrossRef]
- Zhu, J.; Zhao, D.; Xu, L.; Zhang, X. Interactions of vortices, thermal effects and cavitation in liquid hydrogen cavitating flows. Int. J. Hydrogen Energy 2016, 41, 614–631. [Google Scholar] [CrossRef]
- Hord, J. Cavitation in Liquid Cryogens. 3: Ogives; Technical Report; NASA CR-2242; National Bureau of Standards: Boulder, CO, USA, 1973.
- Long, X.; Liu, Q.; Ji, B.; Lu, Y. Numerical investigation of two typical cavitation shedding dynamics flow in liquid hydrogen with thermodynamic effects. Int. J. Heat Mass Transf. 2017, 109, 879–893. [Google Scholar] [CrossRef]
- Lee, C.; Roh, T.S. Flow instability due to cryogenic cavitation in the downstream of orifice. J. Mech. Sci. Technol. 2009, 23, 643–649. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Bello, D.; Ficarella, A. Analysis of Thermal Effects in a Cavitating Orifice Using Rayleigh Equation and Experiments. J. Eng. Gas Turbines Power 2010, 132, 092901. [Google Scholar] [CrossRef]
- Hitt, M.; Lineberry, D.; Ahuja, V.; Frederick, R. Experimental Investigation of Cavitation Induced Feedline Instability from an Orifice. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, GA, USA, 30 July–1 August 2012. [Google Scholar] [CrossRef]
- Ohira, K.; Nakayama, T.; Nagai, T. Cavitation flow instability of subcooled liquid nitrogen in converging–diverging nozzles. Cryogenics 2012, 52, 35–44. [Google Scholar] [CrossRef]
- Chen, T.; Chen, H.; Liu, W.; Huang, B.; Wang, G. Unsteady characteristics of liquid nitrogen cavitating flows in different thermal cavitation mode. Appl. Therm. Eng. 2019, 156, 63–76. [Google Scholar] [CrossRef]
- Chen, T.; Chen, H.; Liang, W.; Huang, B.; Xiang, L. Experimental investigation of liquid nitrogen cavitating flows in converging-diverging nozzle with special emphasis on thermal transition. Int. J. Heat Mass Transf. 2019, 132, 618–630. [Google Scholar] [CrossRef]
- Leppinen, D.; Dalziel, S. A light attenuation technique for void fraction measurement of microbubbles. Exp. Fluids 2001, 30, 214–220. [Google Scholar] [CrossRef]
- Ceccio, S.L.; Brennen, C.E. Observations of the dynamics and acoustics of travelling bubble cavitation. J. Fluid Mech. 1991, 233, 633–660. [Google Scholar] [CrossRef]
- George, D.L.; Iyer, C.O.; Ceccio, S.L. Measurement of the bubbly flow beneath partial attached cavities using electrical impedance probes. J. Fluids Eng. 2000, 122, 151–155. [Google Scholar] [CrossRef]
- Wu, Q.; Ishii, M. Sensitivity study on double-sensor conductivity probe for the measurement of interfacial area concentration in bubbly flow. Int. J. Multiph. Flow 1999, 25, 155–173. [Google Scholar] [CrossRef]
- Elbing, B.R.; Mäkiharju, S.; Wiggins, A.; Perlin, M.; Dowling, D.R.; Ceccio, S.L. On the scaling of air layer drag reduction. J. Fluid Mech. 2013, 717, 484–513. [Google Scholar] [CrossRef]
- Lucas, G.; Mishra, R. Measurement of bubble velocity components in a swirling gas–liquid pipe flow using a local four-sensor conductance probe. Meas. Sci. Technol. 2005, 16, 749. [Google Scholar] [CrossRef]
- Coutier-Delgosha, O.; Devillers, J.F.; Pichon, T.; Vabre, A.; Woo, R.; Legoupil, S. Internal structure and dynamics of sheet cavitation. Phys. Fluids 2006, 18, 017103. [Google Scholar] [CrossRef]
- Stutz, B.; Reboud, J.L. Measurements within unsteady cavitation. Exp. Fluids 2000, 29, 545–552. [Google Scholar] [CrossRef]
- Heindel, T.J. A review of X-ray flow visualization with applications to multiphase flows. J. Fluids Eng. 2011, 133, 074001. [Google Scholar] [CrossRef]
- Bauer, D.; Chaves, H.; Arcoumanis, C. Measurements of void fraction distribution in cavitating pipe flow using X-ray CT. Meas. Sci. Technol. 2012, 23, 055302. [Google Scholar] [CrossRef][Green Version]
- Jahangir, S.; Wagner, E.G.; Mudden, R.F.; Poelma, C. X-ray computed tomography of cavitating flow in a converging-diverging nozzle. In Proceedings of the CAV2018: 10th International Symposium on Cavitation, Baltimore, MD, USA, 14–16 May 2018. [Google Scholar]
- Hassis, H. Noise caused by cavitating butterfly and monovar valves. J. Sound Vib. 1999, 225, 515–526. [Google Scholar] [CrossRef]
- Henry, R.; Grolmes, M.; Fauske, H.K. Pressure-Pulse Propagation in Two-Phase One-and Two-Component Mixtures; Technical Report; Argonne National Lab.: Argonne, IL, USA, 1971.
- Gysling, D.L.; Myers, M.R. Distributed Sound Speed Measurements for Multiphase Flow Measurement. U.S. Patent 6,813,962, 9 November 2004. [Google Scholar]
- Margolis, D.; Brown, F. Measurement of the propagation of long-wavelength disturbances through turbulent flow in tubes. J. Fluids Eng. 1976, 98, 70–78. [Google Scholar] [CrossRef]
- Testud, P.; Moussou, P.; Hirschberg, A.; Aurégan, Y. Noise generated by cavitating single-hole and multi-hole orifices in a water pipe. J. Fluids Struct. 2007, 23, 163–189. [Google Scholar] [CrossRef]
- Shamsborhan, H.; Coutier-Delgosha, O.; Caignaert, G.; Nour, F.A. Experimental determination of the speed of sound in cavitating flows. Exp. Fluids 2010, 49, 1359–1373. [Google Scholar] [CrossRef]
- Kashima, A.; Lee, P.J.; Nokes, R. Numerical errors in discharge measurements using the KDP method. J. Hydraul. Res. 2012, 50, 98–104. [Google Scholar] [CrossRef]
- Blommaert, G. Étude du Comportement Dynamique Des Turbines Francis: Contrôle Actif de Leur Stabilité de Fonctionnement. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2000. [Google Scholar]
- Simon, A.; Martinez-Molina, J.J.; Fortes-Patella, R. A new process to estimate the speed of sound using three-sensor method. Exp. Fluids 2016, 57, 10. [Google Scholar] [CrossRef]
- Coutier-Delgosha, O.; Reboud, J.; Delannoy, Y. Numerical simulation of the unsteady behaviour of cavitating flows. Int. J. Numer. Methods Fluids 2003, 42, 527–548. [Google Scholar]
- Harada, K.; Murakami, M.; Ishii, T. PIV measurements for flow pattern and void fraction in cavitating flows of He II and He I. Cryogenics 2006, 46, 648–657. [Google Scholar] [CrossRef]
- Zhu, J.; Xie, H.; Feng, K.; Zhang, X.; Si, M. Unsteady cavitation characteristics of liquid nitrogen flows through venturi tube. Int. J. Heat Mass Transf. 2017, 112, 544–552. [Google Scholar] [CrossRef]
- Wallis, G.B. One-Dimensional Two-Phase Flow; McGraw-Hill, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Rapposelli, E.; d’Agostino, L. A barotropic cavitation model with thermodynamic effects. In Proceedings of the Fifth International. Symposium on Cavitation (CAV2003), Osaka, Japan, 1–4 November 2003; pp. 1–4. [Google Scholar]
- Mendez, M.; Scelzo, M.; Buchlin, J.M. Multiscale modal analysis of an oscillating impinging gas jet. Exp. Therm. Fluid Sci. 2018, 91, 256–276. [Google Scholar] [CrossRef]
- Mendez, M.A.; Balabane, M.; Buchlin, J.M. Multi-Scale Proper Orthogonal Decomposition of Complex Fluid Flows. arXiv 2018, arXiv:1804.09646v5. [Google Scholar] [CrossRef]
- Mendez, M.; Gosset, A.; Buchlin, J.M. Experimental analysis of the stability of the jet wiping process, part II: Multiscale modal analysis of the gas jet-liquid film interaction. Exp. Therm. Fluid Sci. 2019, 106, 48–67. [Google Scholar] [CrossRef]
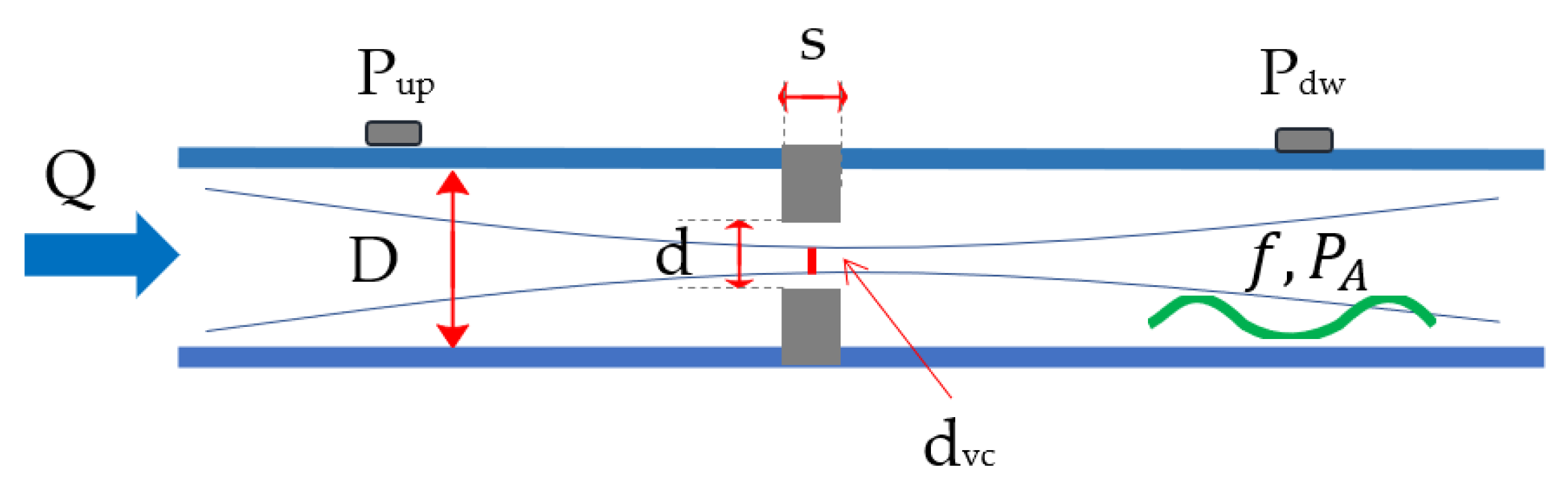

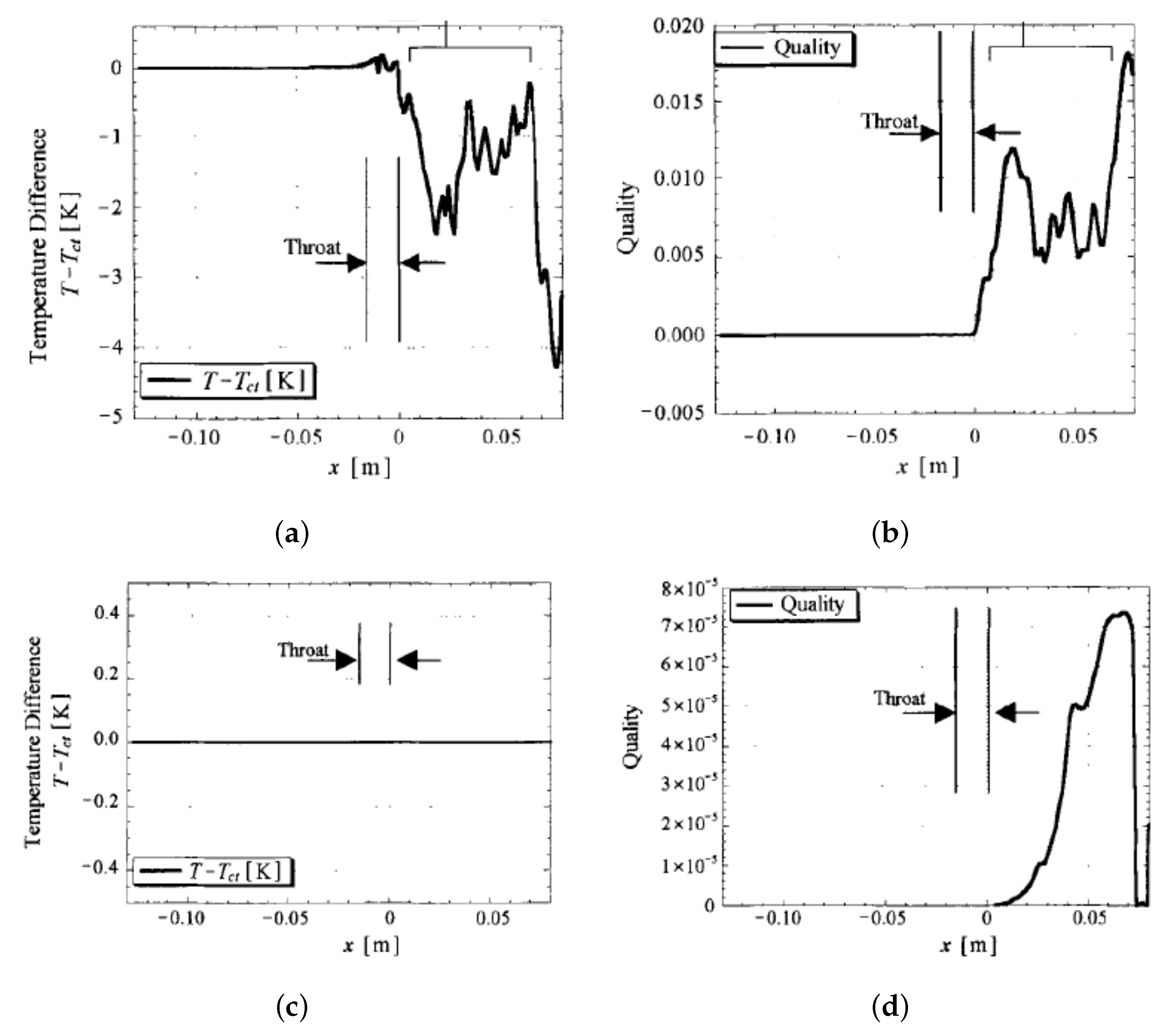


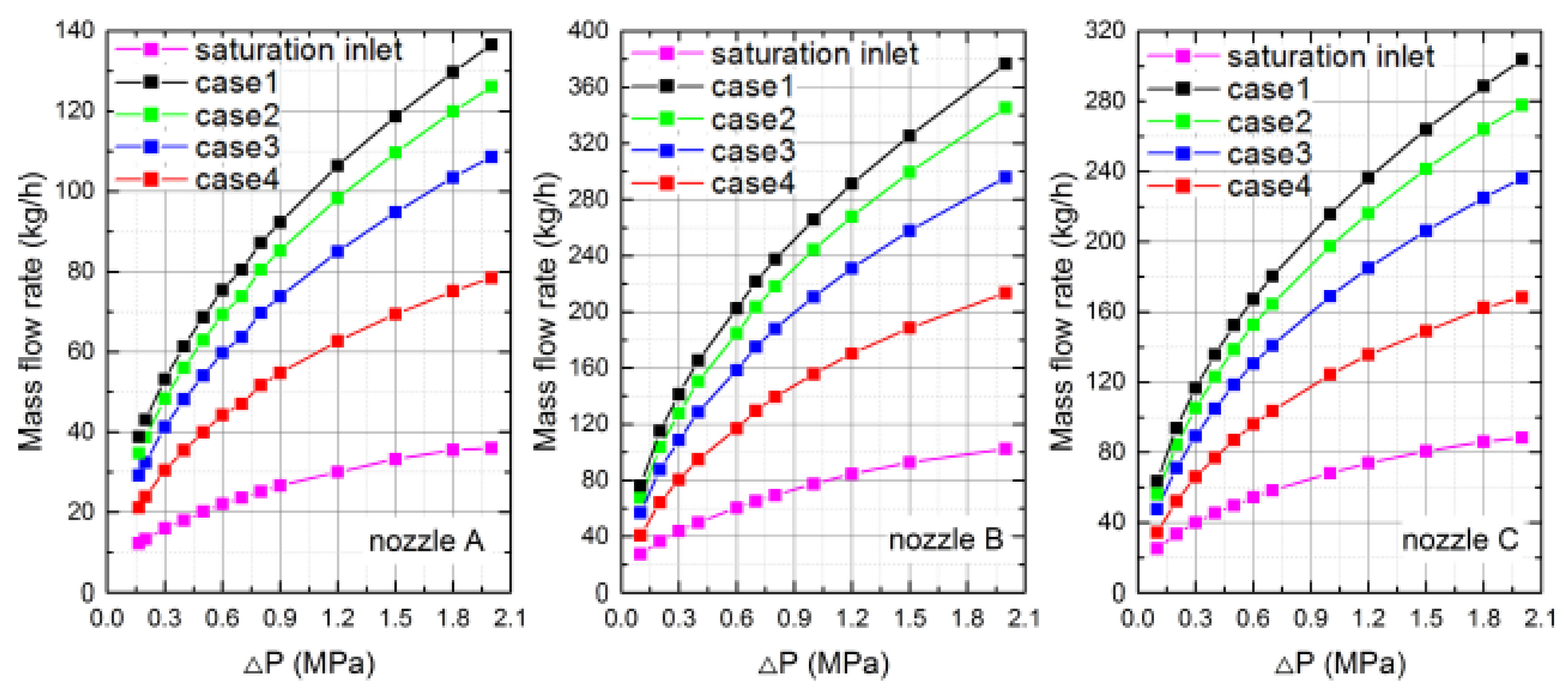
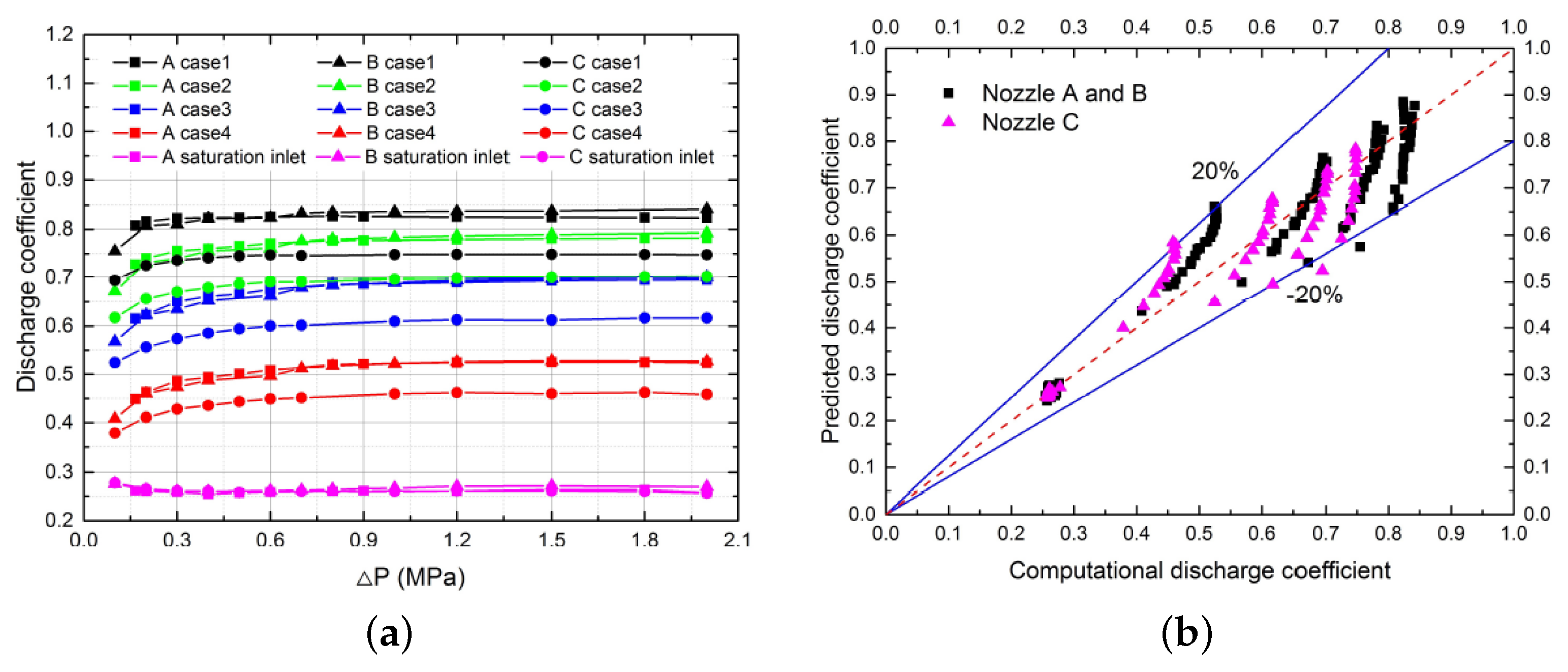

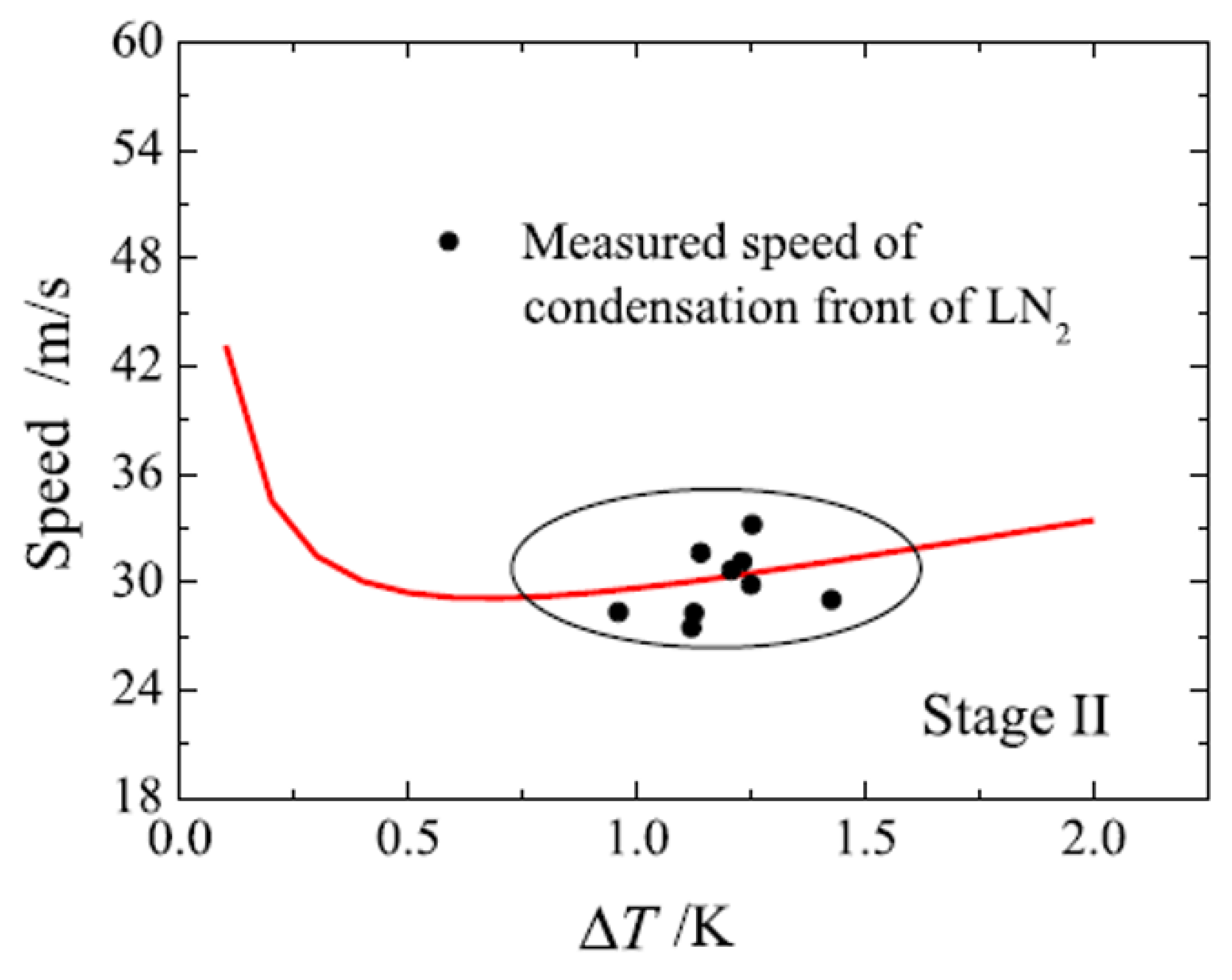
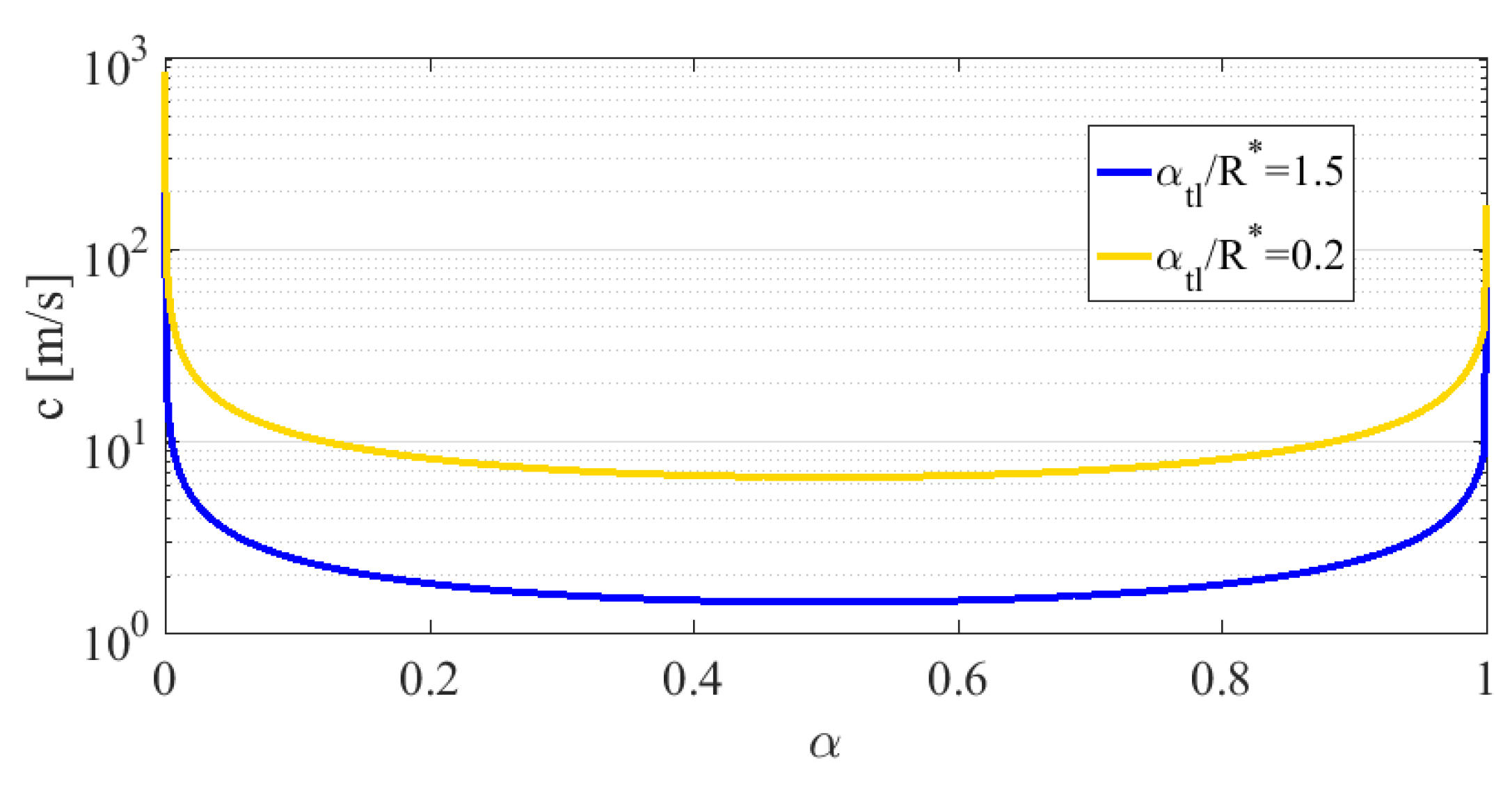
| HO | LO | LN | LCH | LH | |
|---|---|---|---|---|---|
| T | |||||
| Nozzle | Case 0 | Case 1 | Case 2 | Case 3 | Case 4 | |||
|---|---|---|---|---|---|---|---|---|
| sat | sub | sub | sub | sub | ||||
| [kPa] | [kPa] | [MPa] | [K] | [K] | [K] | [K] | [K] | |
| A | 270 | 101 | ||||||
| 2100 | 101 | 2 | ||||||
| B | 200 | 101 | ||||||
| 2100 | 101 | 2 | ||||||
| C | 200 | 101 | ||||||
| 2100 | 101 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esposito, C.; Steelant, J.; Vetrano, M.R. Impact of Cryogenics on Cavitation through an Orifice: A Review. Energies 2021, 14, 8319. https://doi.org/10.3390/en14248319
Esposito C, Steelant J, Vetrano MR. Impact of Cryogenics on Cavitation through an Orifice: A Review. Energies. 2021; 14(24):8319. https://doi.org/10.3390/en14248319
Chicago/Turabian StyleEsposito, Claudia, Johan Steelant, and Maria Rosaria Vetrano. 2021. "Impact of Cryogenics on Cavitation through an Orifice: A Review" Energies 14, no. 24: 8319. https://doi.org/10.3390/en14248319
APA StyleEsposito, C., Steelant, J., & Vetrano, M. R. (2021). Impact of Cryogenics on Cavitation through an Orifice: A Review. Energies, 14(24), 8319. https://doi.org/10.3390/en14248319






