Dynamics of Electromechanical Systems Containing Long Elastic Couplings and Safety of Their Operation
Abstract
1. Introduction
2. Mathematical Model of an Electromechanical System Containing a Long Elastic Coupling
2.1. Mathematical Model of a Transmission Shaft
2.2. Mathematical Model of an Induction Motor
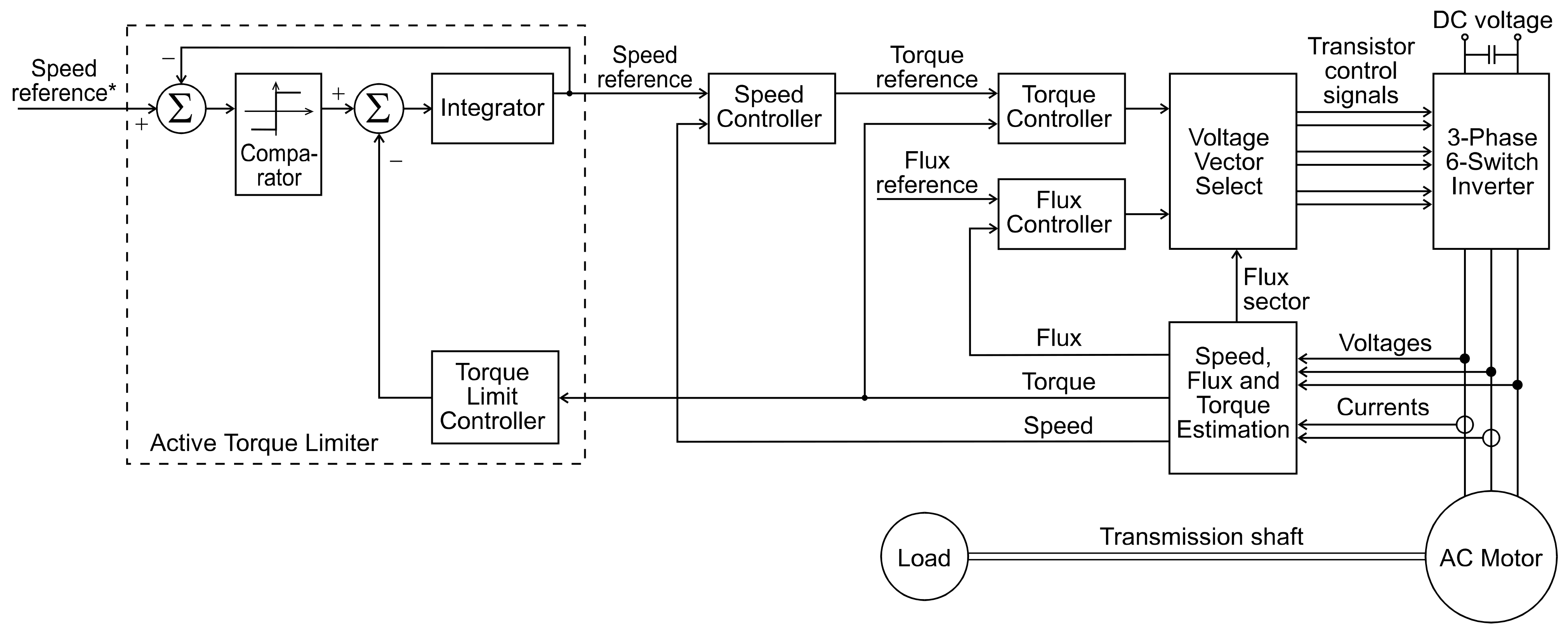
3. The Control Structure of an Induction Motor
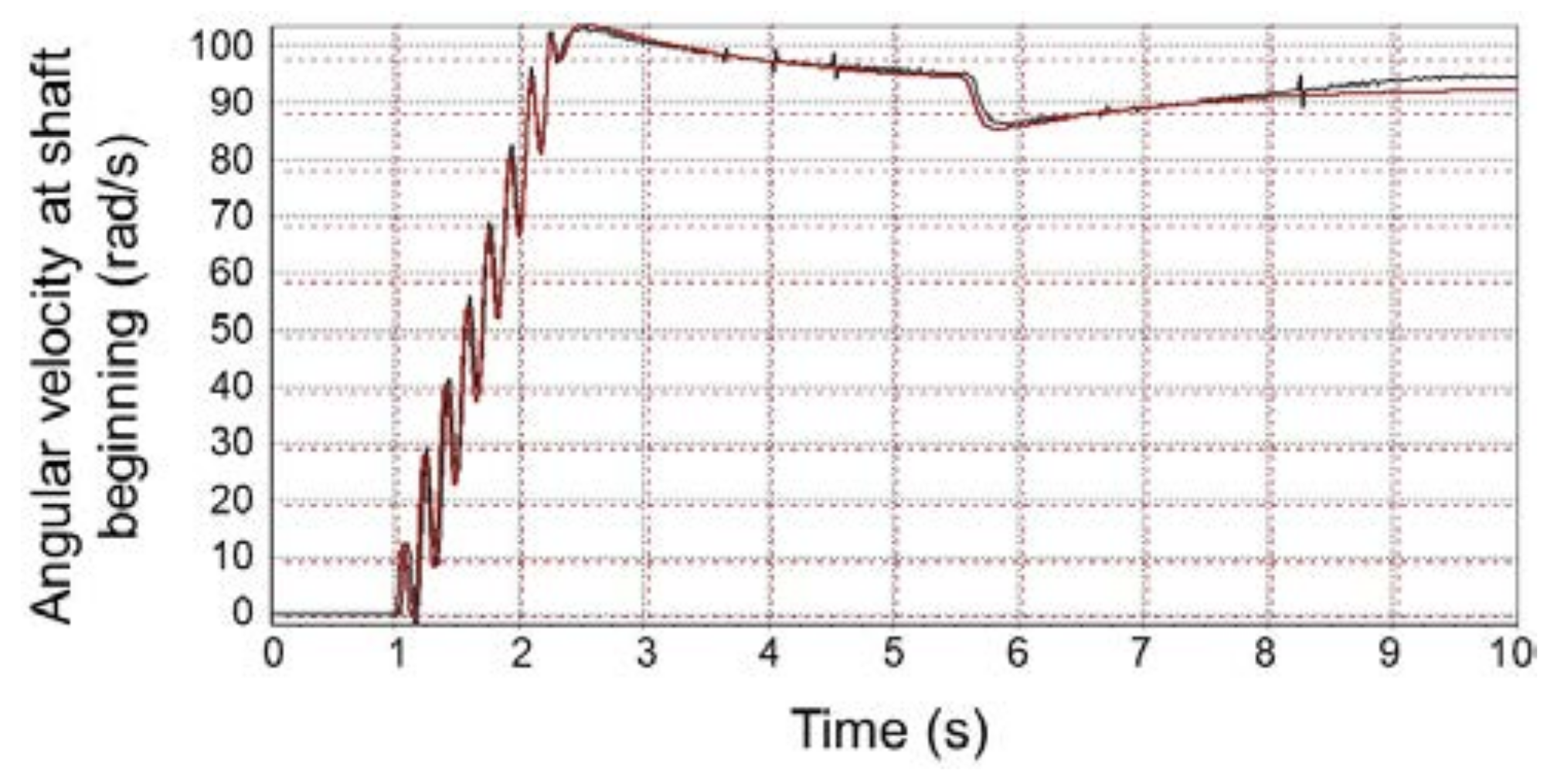
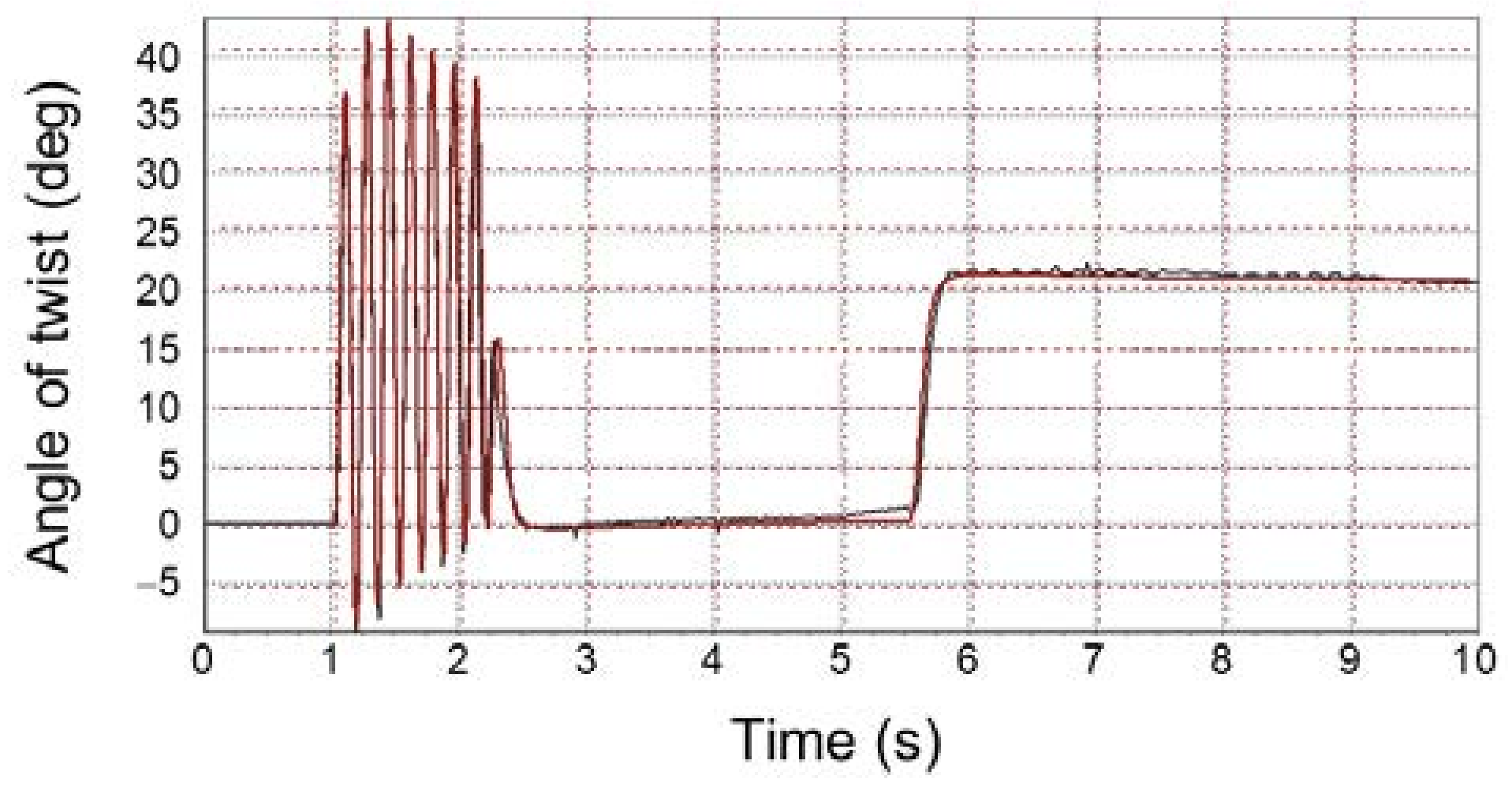
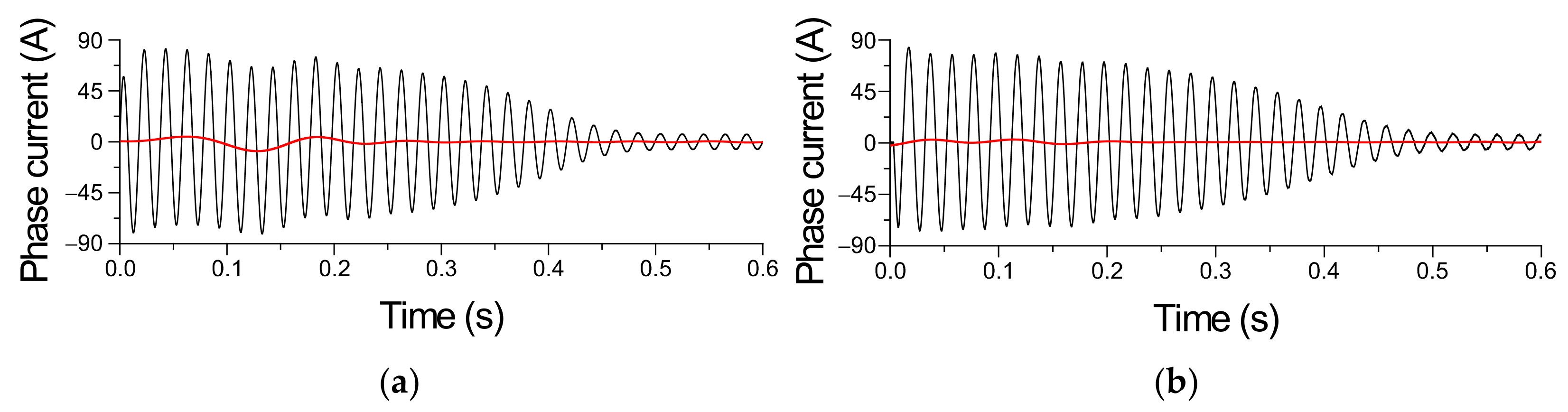
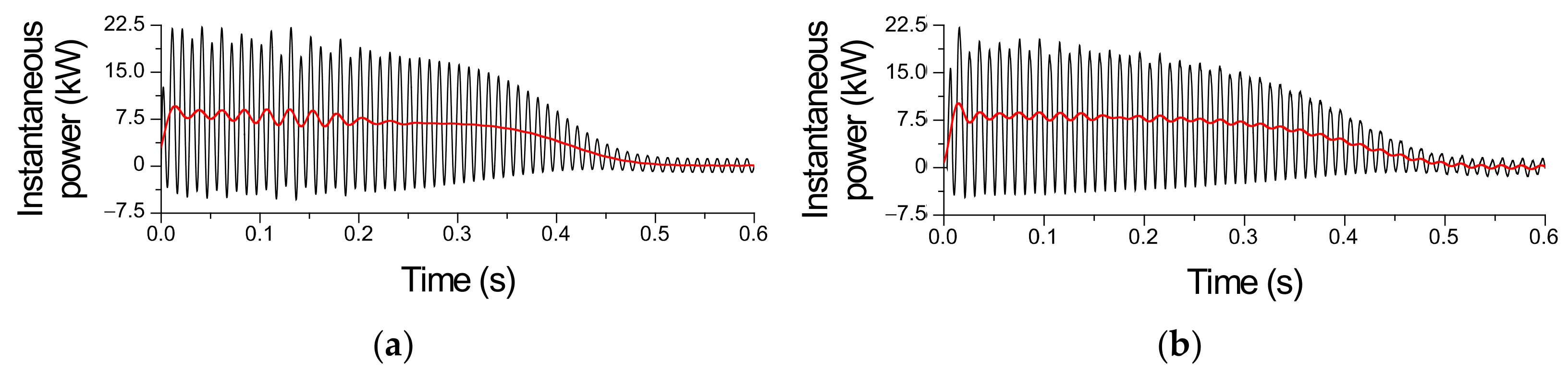
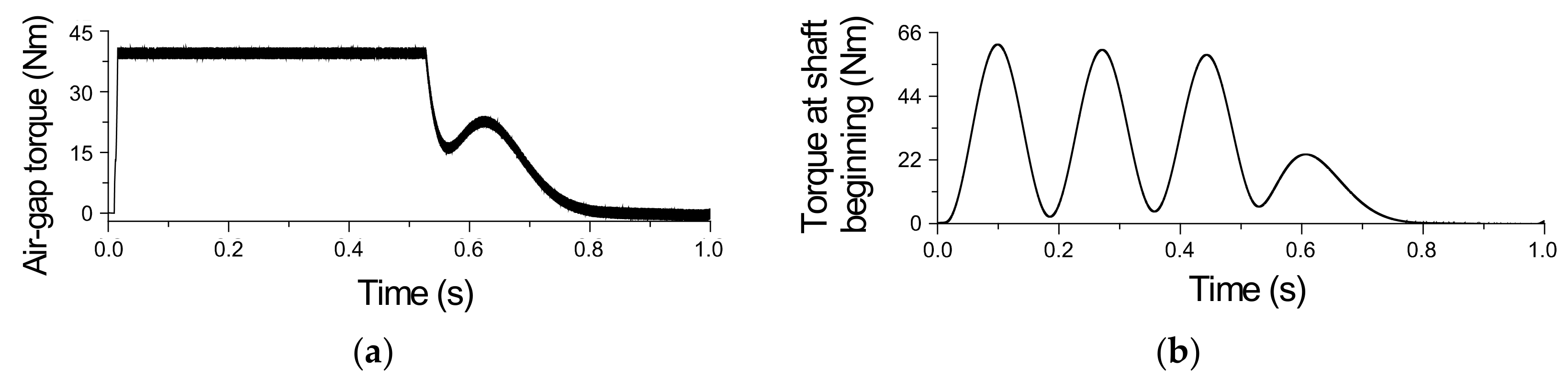
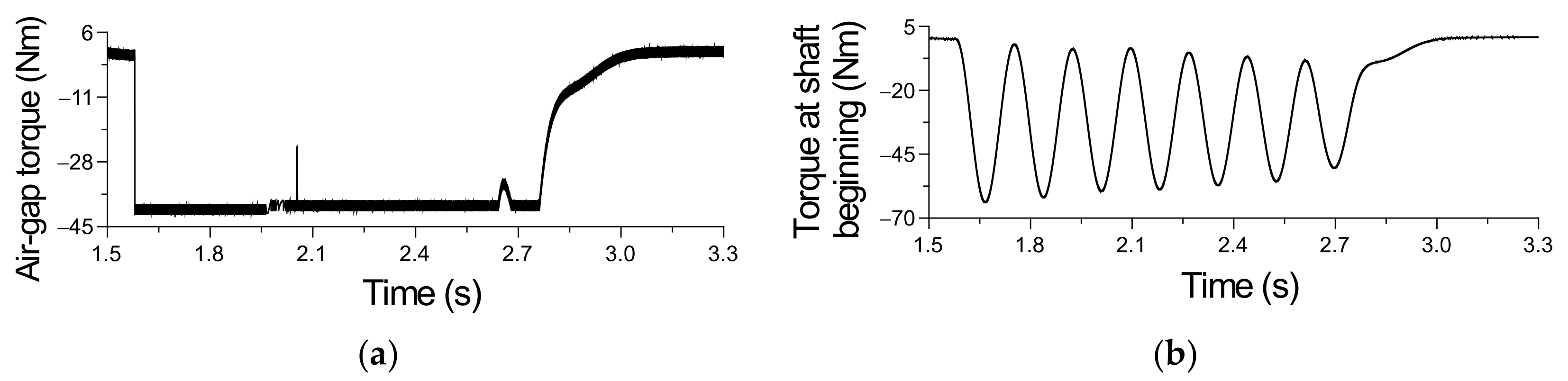
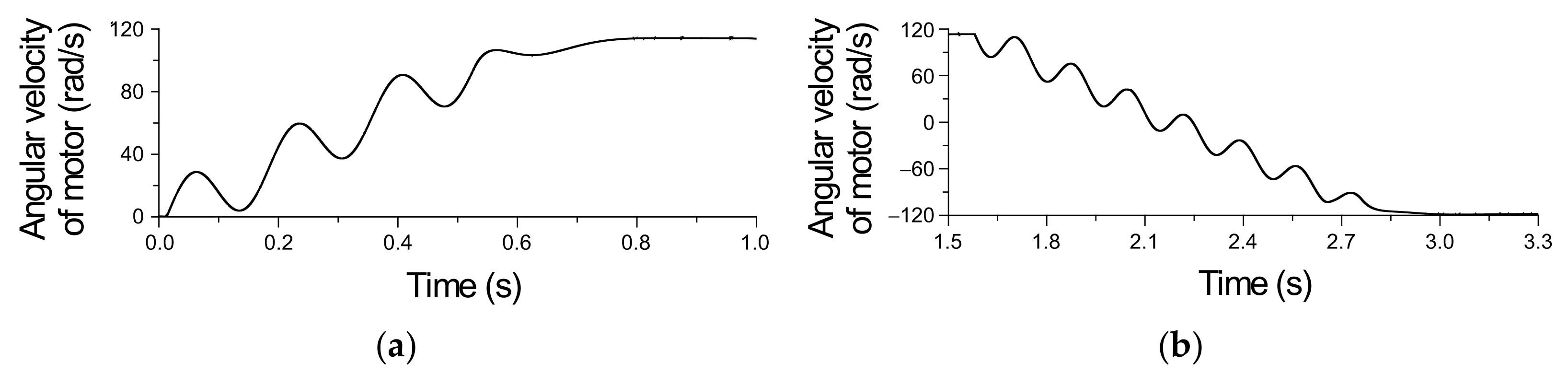
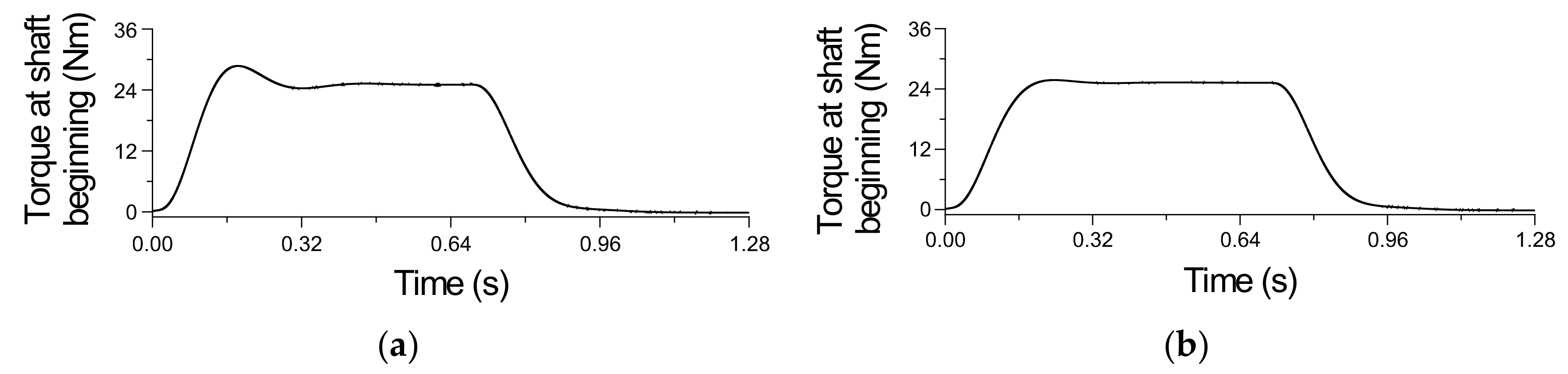
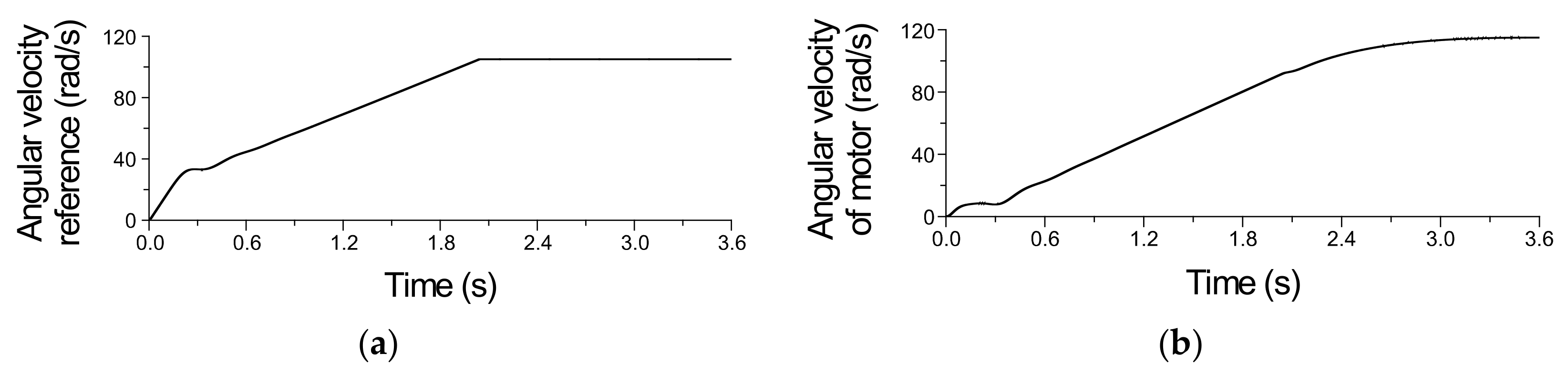
4. The Results of Investigations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rabb, S.F.; Kahnamouei, J.T.; Liang, X.; Yang, J. Shaft Failure Analysis in Soft-Starter Fed Electrical Submersible Pump Systems. IEEE Open J. Ind. Appl. 2020, 1, 1–10. [Google Scholar] [CrossRef]
- Ekemb, G.; Slaoui-Hasnaoui, F.; Song-Manguelle, J.; Lingom, P.M.; Fofana, I. Instantaneous electromagnetic torque components in synchronous motors fed by load-commutated inverters. Energies 2021, 14, 3223. [Google Scholar] [CrossRef]
- Dong, X.; Wang, C.; Yang, Q.; Si, W. System identification of distributed parameter system with recurrent trajectory via deterministic learning and interpolation. Nonlinear Dyn. 2019, 95, 73–86. [Google Scholar] [CrossRef]
- Lozynskyy, A.; Chaban, A.; Perzyński, T.; Szafraniec, A.; Kasha, L. Application of fractional-order calculus to improve the mathematical model of a two-mass system with a long shaft. Energies 2021, 14, 1854. [Google Scholar] [CrossRef]
- Łukasik, Z.; Czaban, A.; Szafraniec, A.; Żuk, V. The mathematical model of the drive system with asynchronous motor and vertical pump. Przegląd Elektrotechniczny 2018, 1, 133–138. [Google Scholar] [CrossRef]
- Popenda, A. Mathematical modelling of transmission shafts based on electrical and mechanical similarities. Przegląd Elektrotechniczny 2019, 12, 196–199. [Google Scholar] [CrossRef]
- Peng, R.; Zhang, X.; Shi, P. Vertical–horizontal coupling vibration of hot rolling mill rolls under multi-piecewise nonlinear constraints. Metals 2021, 11, 170. [Google Scholar] [CrossRef]
- Fan, X.B.; Zang, Y.; Jin, K. Rolling process and its influence analysis on hot continuous rolling mill vibration. Appl. Phys. A 2016, 122, 1008. [Google Scholar] [CrossRef]
- Ramírez, G.A.; Valenzuela, M.A.; Pittman, S.; Lorenz, R.D. Modeling and Evaluation of Paper Machine Coater Sections Part 1: 1-Coater Section and Tension Setpoints. IEEE Trans. Ind. Appl. 2019, 55, 2144–2154. [Google Scholar] [CrossRef]
- Song, M.-H.; Pham, X.D.; Vuong, Q.D. Torsional vibration stress and fatigue strength analysis of marine propulsion shafting system based on engine operation patterns. J. Mar. Sci. Eng. 2020, 8, 613. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, G.H.; Liu, Z.S. Research on large ship propulsion shafting alignment multi-nonlinear-elastic support model. J. Ship Mech. 2016, 1, 176–183. [Google Scholar]
- Jee, J.; Kim, C.; Kim, Y. Design improvement of a viscous-spring damper for controlling torsional vibration in a propulsion shafting system with an engine acceleration problem. J. Mar. Sci. Eng. 2020, 8, 428. [Google Scholar] [CrossRef]
- Chaban, A.; Lis, M.; Szafraniec, A.; Jedynak, R. Application of genetic algorithm elements to modelling of rotation processes in motion transmission including a long shaft. Energies 2021, 14, 115. [Google Scholar] [CrossRef]
- Czaban, A.; Lis, M. Mathematical model of an electromechanical system with a long elastic element (in Polish). Prz. Elektrotech. 2012, 12, 167–170. [Google Scholar]
- Szabat, K.; Orłowska-Kowalska, T. Application of the Kalman filters to the high-performance drive system with elastic coupling. IEEE Trans. Ind. Electron. 2012, 11, 4226–4235. [Google Scholar] [CrossRef]
- Serkies, P.; Szabat, K. Application of the MPC controller to the Position Control of the Two-Mass Drive System. IEEE Trans. Ind. Electron. 2013, 9, 3679–3688. [Google Scholar] [CrossRef]
- Chaban, A.; Łukasik, Z.; Popenda, A.; Szafraniec, A. Mathematical Modelling of Transient Processes in an Asynchronous Drive with a Long Shaft Including Cardan Joints. Energies 2021, 14, 5692. [Google Scholar] [CrossRef]
- O’Sullivan, T.; Bingham, C.C.; Schofield, N. High-performance control of dual-inertia servo-drive systems using low-cost integrated SAW torque transducers. IEEE Trans. Ind. Electron. 2006, 4, 1226–1237. [Google Scholar] [CrossRef]
- Li, W.; Hori, Y. Vibration suppression using single neuron-based PI fuzzy controller and fractional-order disturbance observer. IEEE Trans. Ind. Electron. 2007, 1, 117–126. [Google Scholar] [CrossRef]
- Valenzuela, M.A.; Bentley, J.M.; Lorenz, R.D. Evaluation of torsional oscillations in paper machine sections. IEEE Trans. Ind. Electron. 2005, 2, 493–501. [Google Scholar] [CrossRef]
- Popenda, A.; Lis, M.; Nowak, M.; Blecharz, K. Mathematical Modelling of Drive System with an Elastic Coupling Based on Formal Analogy between the Transmission Shaft and the Electric Transmission Line. Energies 2020, 13, 1181. [Google Scholar] [CrossRef]
- Pielorz, A. Dynamic analysis of torsional discrete-continuous systems with position-dependent variable inertia. J. Theor. Appl. Mech. 2014, 1, 107–115. [Google Scholar]
- Grządziela, A. Modelling of propeller shaft dynamics at pulse load. Pol. Marit. Res. 2008, 4, 52–58. [Google Scholar] [CrossRef][Green Version]
- Jinli, X.; Xingyi, S.; Bo, P. Numerical Analysis and Demonstration: Transmission Shaft Influence on Meshing Vibration in Driving and Driven Gears. Hindawi Publ. Corp. Shock Vib. Vol. 2015, 10, 1–10. [Google Scholar] [CrossRef][Green Version]
- Swanson, D.C. Signal Processing for Intelligent Sensor Systems with MATLAB®, 2nd ed.; CRC Press: Abingdon, UK, 2017; pp. 7–23. [Google Scholar]
- Łuczak, D. Mathematical model of multi-mass electric drive system with flexible connection. In Proceedings of the 19th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 2–5 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 290–295. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Mohd, H.A.; Takahashi, R.; Murata, T.; Tamura, J.; Tomaki, Y.; Sakahara, A.; Sasano, E. Transient Stability Analysis of Wind Generator System with the Consideration of Multi-Mass Shaft Model. In Proceedings of the International Conference on Power Electronics and Drive Systems, Kuala Lumpur, Malaysia, 28 November–1 December 2005; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Saarakkala, S.; Hinkkanen, M. Identification of Two-Mass Mechanical Systems Using Torque Excitation: Design and Experimental Evaluation. IEEE Trans. Ind. Appl. 2015, 51, 4180–4189. [Google Scholar] [CrossRef]
- Kabziński, J.; Mosiołek, P. Adaptive, nonlinear state transformation-based control of motion in presence of hard constraints. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 963–971. [Google Scholar]
- Lee, D.; Lee, J.H.; Ahn, J. Mechanical vibration reduction control of two-mass permanent magnet synchronous motor using adaptive notch filter with fast Fourier transform analysis. IET Electr. Power Appl. 2012, 6, 455–461. [Google Scholar] [CrossRef]
- Kabziński, J.; Mosiołek, P.; Jastrzębski, M. Adaptive position tracking with hard constraints—barrier lyapunov functions approach. Stud. Syst. Decis. Control 2017, 75, 27–52. [Google Scholar]
- Szabat, K.; Orlowska-Kowalska, T. Vibration suppression in a two-mass drive system using PI speed controller and additional feedbacks—Comparative study. IEEE Trans. Ind. Electron. 2007, 54, 1193–1206. [Google Scholar] [CrossRef]
- Kabziński, J.; Mosiołek, P. Integrated, Multi-Approach, Adaptive Control of Two-Mass Drive with Nonlinear Damping and Stiffness. Energies 2021, 14, 5475. [Google Scholar] [CrossRef]
- Xu, S.; Sun, G.; Cheng, Z. Fractional order modeling and residual vibration suppression for flexible two-mass system. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 3658–3664. [Google Scholar]
- Popenda, A. Model-simulation investigations of induction motor with the consideration of skin effect in rotor bars. Przegląd Elektrotechniczny 2012, 12, 29–31. [Google Scholar]
- Takahashi, I.; Noguchi, T. A New Quick-Response and High-Efficiency Control Strategy of an Induction Motor. IEEE Trans. Ind. Appl. 1986, 5, 820–827. [Google Scholar] [CrossRef]








| Component of the Stand | Parameters |
|---|---|
| Brushless DC motor PMSg 132 S4 from Komel | rated power: 4.0 kW |
| rated voltage: 400 V | |
| rated current: 11.5 A | |
| rated speed: 1500 rpm | |
| DC generator PKMa44a/117 from Elmor | rated power: 4.6 kW |
| rated voltage: 230 V | |
| rated current: 20 A | |
| rated speed: 1450 rpm | |
| Incremental encoder Sendix 5000 from Kuebler | supply voltage: 5–24 V DC |
| resolution: 3600 ppr | |
| interfaces: RS 422 | |
| switching frequency: 300 kHz | |
| Steel shaft | length: 66 mm |
| diameter: 8 mm | |
| mass density: 7900 kg/m3 | |
| shear module: 77.5 GPa | |
| wave impedance: 0.01 Nms | |
| phase velocity: 3132 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popenda, A.; Szafraniec, A.; Chaban, A. Dynamics of Electromechanical Systems Containing Long Elastic Couplings and Safety of Their Operation. Energies 2021, 14, 7882. https://doi.org/10.3390/en14237882
Popenda A, Szafraniec A, Chaban A. Dynamics of Electromechanical Systems Containing Long Elastic Couplings and Safety of Their Operation. Energies. 2021; 14(23):7882. https://doi.org/10.3390/en14237882
Chicago/Turabian StylePopenda, Andrzej, Andrzej Szafraniec, and Andriy Chaban. 2021. "Dynamics of Electromechanical Systems Containing Long Elastic Couplings and Safety of Their Operation" Energies 14, no. 23: 7882. https://doi.org/10.3390/en14237882
APA StylePopenda, A., Szafraniec, A., & Chaban, A. (2021). Dynamics of Electromechanical Systems Containing Long Elastic Couplings and Safety of Their Operation. Energies, 14(23), 7882. https://doi.org/10.3390/en14237882






