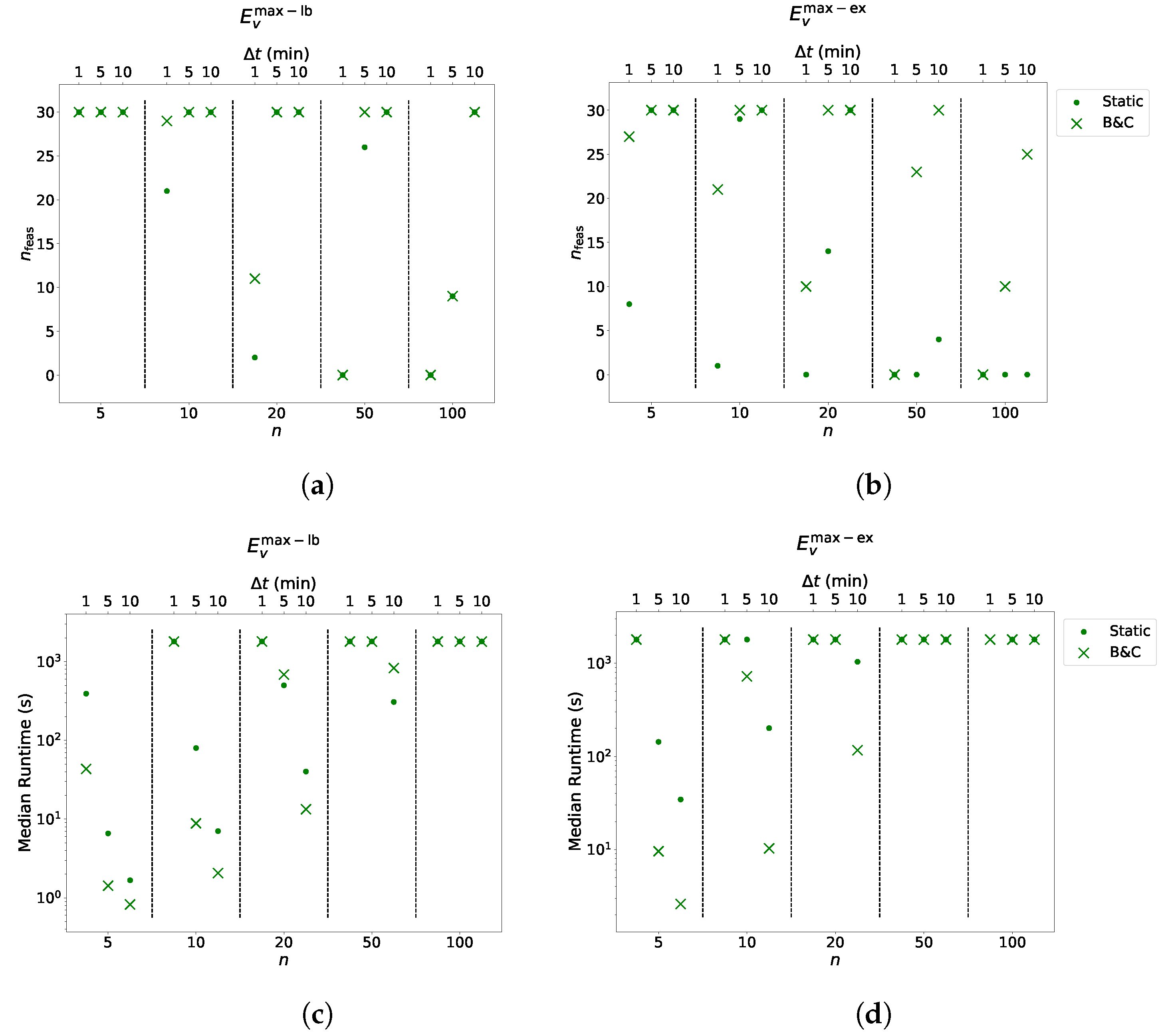Smart Charging of Electric Vehicles Considering SOC-Dependent Maximum Charging Powers

Abstract

The aim of this work is to schedule the charging of electric vehicles (EVs) at a single charging station such that the temporal availability of each EV as well as the maximum available power at the station are considered. The total costs for charging the vehicles should be minimized w.r.t. time-dependent electricity costs. A particular challenge investigated in this work is that the maximum power at which a vehicle can be charged is dependent on the current state of charge (SOC) of the vehicle. Such a consideration is particularly relevant in the case of fast charging. Considering this aspect for a discretized time horizon is not trivial, as the maximum charging power of an EV may also change in between time steps. To deal with this issue, we instead consider the energy by which an EV can be charged within a time step. For this purpose, we show how to derive the maximum charging energy in an exact as well as an approximate way. Moreover, we propose two methods for solving the scheduling problem. The first is a cutting plane method utilizing a convex hull of the, in general, nonconcave SOC–power curves. The second method is based on a piecewise linearization of the SOC–energy curve and is effectively solved by branch-and-cut. The proposed approaches are evaluated on benchmark instances, which are partly based on real-world data. To deal with EVs arriving at different times as well as charging costs changing over time, a model-based predictive control strategy is usually applied in such cases. Hence, we also experimentally evaluate the performance of our approaches for such a strategy. The results show that optimally solving problems with general piecewise linear maximum power functions requires high computation times. However, problems with concave, piecewise linear maximum charging power functions can efficiently be dealt with by means of linear programming. Approximating an EV’s maximum charging power with a concave function may result in practically infeasible solutions, due to vehicles potentially not reaching their specified target SOC. However, our results show that this error is negligible in practice.

1. Introduction

The number of electric vehicles (EVs) is rapidly increasing. At the end of 2020, there were around 10 million EVs on the world’s roads, and the number of EV registrations increased by 41% in 2020 [1]. The uncontrolled charging of this rising number of EVs, together with an increasing share of renewable energy, imposes significant challenges for the stable operation of the power grid in terms of the power quality, voltage stability, peak demand, and reliability [2]. In addition to further measures, like time-of-use prices [3] and dynamic pricing schemes [4], smart charging [5,6] is considered a promising strategy to mitigate these issues. Smart charging refers to the coordination of the charging of a number of EVs in an intelligent way. Numerous approaches for smart charging, considering different objectives and different constraints have been proposed in the literature [7,8,9,10,11,12,13,14].

These approaches typically assume that the maximum charging power of an EV remains constant over the planning horizon. However, in practice, the maximum charging power depends on the state of charge (SOC) of the EV’s battery. Typically, with an increasing SOC, the maximum charging power is regulated down by the battery controller. For slow AC charging, the decrease of the maximum power is usually only marginal and can be neglected for most applications. For modern, fast DC charging, however, the effect of the decreasing maximum power can be substantial as can be seen from the exemplary SOC–power curve shown in Figure 1.

The exact form of the curve not only depends on the type of battery and its charging controller but also on other factors, including the ambient temperature or the state of health of the battery [16]. In most cases, the curve is highly nonlinear, making it difficult to consider it in mixed integer linear programming (MILP) approaches, which are frequently used for charging planning. However, not considering the SOC-dependent maximum charging power in the charging planning is likely to result in suboptimal or even infeasible charging schedules, particularly in the case of fast charging.

For example, Frendo et al. [17] concludde from numerical experiments that, under the constraint of a limited total charging power, up to 21% more energy can be charged if the SOC-dependent maximum charging power is considered in the planning, compared to not considering it. Frendo et al. also indicated that, in the literature on smart charging, the integration of nonlinear SOC–power curves is frequently mentioned as future work. However, to date, the number of works that actually address this issue are still limited.

In the present paper, we assume a basic use case of smart charging with the objective of minimizing the energy cost under time-varying electricity prices and with the constraint of a limited total charging power per time step. In order to allow a better integration of nonlinear SOC–power curves, we formulate the scheduling problem in terms of planning the charging energy instead of the charging power. Therefore, we consider two approaches for converting the SOC–power curves to SOC–energy curves. The first approach is an exact approach; however, it can only guarantee that the average total charging power does not exceed the limit in a time step. The second approach is an approximate approach, which guarantees that the total charging power never exceeds the limit, but it might lead to suboptimal costs.

We propose two methods for solving the resulting problems. The first one is an extension of a cutting plane method proposed by Korolko and Sahinoglu [18] and utilizes a convex hull of the, in general, nonconcave SOC–power curves. The second method makes use of a piecewise linearization of the SOC–energy curve and is accelerated by branch-and-cut. In extensive numerical experiments, we evaluate and compare the proposed approaches. The key contributions of the present paper are

• a reformulation of the scheduling problem in terms of the control of charging energy, which facilitates the integration of SOC-dependent maximum charging power,
• a proposal of two transformations of SOC–power curves into SOC–energy curves, and
• a proposal and evaluation of two mixed integer linear programming based solution methods that consider SOC-dependent maximum charging powers.

The current work is based on parts of Schaden’s master thesis [19], where more details and further results can be found. The rest of the paper is organized as follows. The next section discusses related work. In Section 3, our EV charging scheduling problem is formalized. Additionally, we show how to derive the exact as well as an approximate maximum charging energy function from the maximum charging power function. Next, Section 4 presents the different problem solving approaches. Section 5 explains how we generated problem instances for the empirical evaluation, and respective experimental results are presented in Section 6. Finally, Section 7 concludes this work and outlines promising future research directions.

2. Related Work

Some works consider an SOC-dependent maximum charging power by integrating nonlinear physical battery models in the charging schedule optimization. Sundström and Binding [20] compare the use of a linear and a quadratic approximation of such a model in the optimization of EV schedules with the goal of minimizing charging costs. They concluded that, although the linear approximation results in small violations in the SOCs requested by the EV drivers, the benefit of the quadratic approximation does not justify the increase in computation time.

Morstyn et al. [21] proposed a nonlinear battery circuit model and integrated it in an optimization model in the form of a second-order cone program. They considered the maximization of charged energy taking into account network constraints and the constraints of a limited total charging power. They demonstrated that problem instances with up to 500 vehicles can be solved within less than 100 s. In practice, the behavior of the battery (controller) can significantly differ from an idealized battery model. Thus, other works—including the present work—abstract from a specific battery model.

Different battery model-free heuristic approaches for smart charging with SOC-dependent maximum power can be found in the literature. Cao et al. [22] proposed a rule-based approach for EV charging control with the objectives of energy cost reduction and load flattening, respecting the SOC-dependent maximum charging powers of EVs. Frendo et al. [17] described the use of a data-driven approach for the prediction of power curves of EVs. The authors proposed a rule-based control, which schedules the charging of the EVs with the objective of a fair distribution of the available energy taking into account the predicted power curves.

El-Bayeh et al. [23] proposed a model-free exact approach. They approximated a nonlinear power curve with a piecewise linear function. Subsequently, they drew a comparison between the charging costs resulting from charging with a constant maximum charging power and the charging costs resulting from charging with a vehicle specific SOC-dependent piecewise linear function. For solving the optimization problem, they use mixed integer nonlinear programming, which distinguishes their approach from our problem solving techniques.

Han, Park, and Lee [24] considered a problem setting similar to that considered in the present paper. The authors assumed that the charging station has limited grid capacity, which may be exceeded at the price of paying penalty costs. They presented a MILP formulation of the problem, which integrates nonlinear power curves with help of a discretization of SOC levels. In contrast to the present work, it was assumed that EVs can only charge with maximum or zero power, which is quite restrictive and hardly the case in practice. Two network flow approaches in Schaden’s Master thesis [19] extend the MILP formulation from [24] with the possibility to charge with power levels from a discrete set of values. However, we refrain from considering these approaches here as they were found to be uncompetitive—primarily due to the much larger memory requirements even when the number of EVs is low.

A further model-free exact approach was proposed by Korolko and Sahinoglu [18]. They assumed a problem setting similar to that considered in [24] but with continuous charging power values. A nonlinear problem formulation was presented and solved as a series of linear problems with the help of a cutting plane approach. The described approach, however, requires the power curve to be concave. Our approaches partly build upon this work.

The approaches proposed in the present paper are model-free linear exact approaches for a continuous power modulation, which are applicable to concave and nonconcave power curves. None of the previous works considered the issue that the variable maximum charging power varies within a time step of the planning horizon. To the best of our knowledge, we are the first to consider this aspect in detail.

3. Problem Description

The EV charging scheduling problem with SOC-dependent maximum charging power (EVS-SOC) we consider formalizes the task of scheduling the charging of a number of EVs such that the total charging costs are minimized. The charging schedule is preemptive, which means that the charging process of an EV may be interrupted an arbitrary number of times. It is assumed that electricity costs change over time and that they are known in advance. Discrete finite time steps $T=\{0,\dots ,t_{max}\}$ are used to model the considered time horizon. Each of these represents a time interval of constant duration $\Delta t$.

The charging is controlled by a single central entity, the so-called aggregator. The total power that can be used from the grid at any time is limited by $P^{\mathrm{gridmax}}>0$. Electricity costs per unit of consumed energy are given by $c_t$ individually for each time step $t\in T$. Note that these costs may also be negative in practice.

The set of EVs to be considered is $V=\{1,\dots ,n\}$, and they are all assumed to be currently connected to the charging station, i.e., immediately available for charging. Each vehicle is associated with an initial state of charge $s_{v,0}\in [0,1]$, i.e., the SOC at the beginning of time step zero, and a minimum required state $s_v^{\mathrm{dep}}\in [s_{v,0},1]$ that must be reached at the vehicle’s known departure time $t_v^{\mathrm{dep}}\in T$.

Additionally, for each vehicle $v\in V$, the energy capacity $C_v>0$ of its battery is known as well as a function $P_v^{max}:[0,1]\mapsto {\mathbb{R}}^{+}$ for the battery’s maximum charging power given its SOC. Note that $P_v^{max}$ must be strictly positive for any SOC less than one and is zero for SOC one. Otherwise, we do not restrict this function in any way, in particular it does not necessarily have to be concave or continuous. Note that we neglect the effect of minor further factors, like the battery temperature and its state of health, on the maximum charging power. Furthermore, we assume a charging efficiency of 100%.

We remark that, in practice, the domain of $P_v^{max}$ is often not defined on the entire SOC interval $[0,1]$ but only for some restricted $[s_v^{\min },s_v^{\max }]$, $0\le s_v^{\min }<s_v^{\max }\le 1$. In the following, we regard this issue as an implementation detail and assume the domain of $P_v^{max}$ to be $[0,1]$.

The goal of EVS-SOC is to find a feasible charging schedule that minimizes the total charging costs while charging each vehicle v from SOC $s_{v,0}$ to (at least) SOC $s_v^{\mathrm{dep}}$ by time step $t_v^{\mathrm{dep}}$ such that the total power used from the grid at any time does not exceed $P^{\mathrm{gridmax}}>0$.

Since the maximum charging power function $P_v^{max}$ depends on the SOC, it is, in general, not constant within a single time step of duration $\Delta t$. This may lead to the problem that a charging power value set for a time step is not allowed throughout the whole charging interval. The vehicle’s charging controller will then dynamically adjust (reduce) the actually used power to never exceed the SOC-dependent maximum power. One may argue that the resulting error may be reduced by increasing the resolution of the time discretization until it becomes negligible. A larger number of time steps, however, directly affects the problem size and practical solvability. Therefore, we refrain here from increasing $t_{max}$ only because of this reason.

Instead, we turn from considering the charging power to considering the energy by which an EV may actually be charged in a time step, taking care of the above aspects. We propose alternative approaches for deducing an (approximate) maximum energy function $E_v^{max}\left(s\right):[0,1]\mapsto {\mathbb{R}}^{+}$ from $P_v^{max}$ that states the maximum energy by which EV v with SOC s can be charged within duration $\Delta t$.

In Section 3.1, we give an exact way for deducing $E_v^{max}$, referred to as $E_v^{\max -\mathrm{ex}}$. However, using $E_v^{\max -\mathrm{ex}}$, we are, in general, only able to express that the maximum grid power is not exceeded on average within a time step, since we consider the time horizon in a discretized fashion. While this might be sufficient for some applications, like limiting peak load charges, it may be a too weak condition for other applications, like limiting transformer loads. Therefore, in Section 3.2, we also show how to deduce a lower bound $E_v^{\max -\mathrm{lb}}$ to $E_v^{max}$ that never overestimates the real maximum energy at which charging can take place.

3.1. Exact Maximum Energy

We determine the maximum charging energy $E_v^{\max -\mathrm{ex}}$ that is achieved when applying the dynamic charging power $P_v^{max}$ throughout a whole time step. Considering an EV $v\in V$ with initial SOC $s_{v,t}\in [0,1]$ at some time step $t\in \{0,\dots ,t_v^{\mathrm{dep}}-1\}$, the time needed to charge the EV to some SOC $s^{\prime }\in [s_{v,t},1]$ using the dynamic maximum charging power is

$$T_v^{\min -\mathrm{ex}}(s_{v,t},s^{\prime })=C_v·{\int }_{s_{v,t}}^{s^{\prime }}\frac{1}{P_v^{max}\left(s\right)}ds.$$

(1)

The maximum energy by which the EV can be charged during a time step of duration $\Delta t$ is then

$$E_v^{\max -\mathrm{ex}}\left(s_{v,t}\right)=C_v·(s^{\prime }-s_{v,t})s.t.\left\{\begin{array}{cc}{T}_v^{\min -\mathrm{ex}}(s_{v,t},s^{\prime })=\Delta t\hfill & \mathrm{for}{T}_v^{\min -\mathrm{ex}}(s_{v,t},1)>\Delta t\hfill \\ s^{\prime }=1\hfill & \mathrm{else}.\hfill \end{array}\right.$$

(2)

Hereby, we consider in the else case that charging always stops when SOC value one is reached. While calculating the integral for $\frac{1}{P_v^{max}\left(s\right)}$ might be nontrivial from a theoretical point-of-view for some power functions, it is, in practice, not difficult to efficiently determine approximate values for $E_v^{\max -\mathrm{ex}}\left(s_{v,t}\right)$ computationally by conventional numerical integration methods. As previously mentioned, the problem with the usage of $E_v^{\max -\mathrm{ex}}\left(s_{v,t}\right)$ is primarily that it is hard to express the maximum grid power constraint since, within a time step, the actually used power may vary for each EV substantially, i.e., we will only be able to express that the maximum grid power is not exceeded on average within a time step.

3.2. Lower Bound for Maximum Energy

To address the aforementioned problem, we consider the largest power that can be constantly applied throughout a whole time step of duration $\Delta t$ without requiring the charging controller to reduce the power. The time needed to charge the EV to some SOC $s^{\prime }\in [s_{v,t},1]$ using the maximum power that can be constantly applied is

$$\begin{array}{c}\hfill T_v^{\min -\mathrm{lb}}(s_{v,t},s^{\prime })=\frac{C_v·(s^{\prime }-s_{v,t})}{{min}_{s\in [s_{v,t},s^{\prime }]}{P}_v^{max}\left(s\right)}.\end{array}$$

(3)

The maximum energy by which the EV can be charged during a time step of duration $\Delta t$ is then again obtained by Equation (2) but in conjunction with the above $T_v^{\min -\mathrm{lb}}$ (3) instead of $T_v^{\min -\mathrm{ex}}$ (1). We refer to this variant by $E_v^{\max -\mathrm{lb}}$.

By avoiding to set, for a time step, a power that will have to be reduced by the charging controller at some point of time, the maximum energy $E_v^{\max -\mathrm{lb}}$ is a lower bound for the actually obtainable energy $E_v^{\max -\mathrm{ex}}$. Using $E_v^{\max -\mathrm{lb}}$ in our whole problem setting means that an obtained solution will guarantee that, indeed, all EVs are charged to the desired departure SOCs. As we may occasionally use a more restricted charging power than could actually be applied, the schedule might not be optimal in the original sense, and a solution’s objective value will be an upper bound for the real optimum.

We want to highlight the following relationships between $P_v^{max}$ and its corresponding maximum energy functions.

• If $P_v^{max}$ is a piecewise linear function, then $E_v^{\max -\mathrm{lb}}$ is piecewise linear as well. On the contrary, $E_v^{\max -\mathrm{ex}}$ might not be a piecewise linear function, even if $P_v^{max}$ is piecewise linear.
• If $P_v^{max}$ is a concave function, so are $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$.

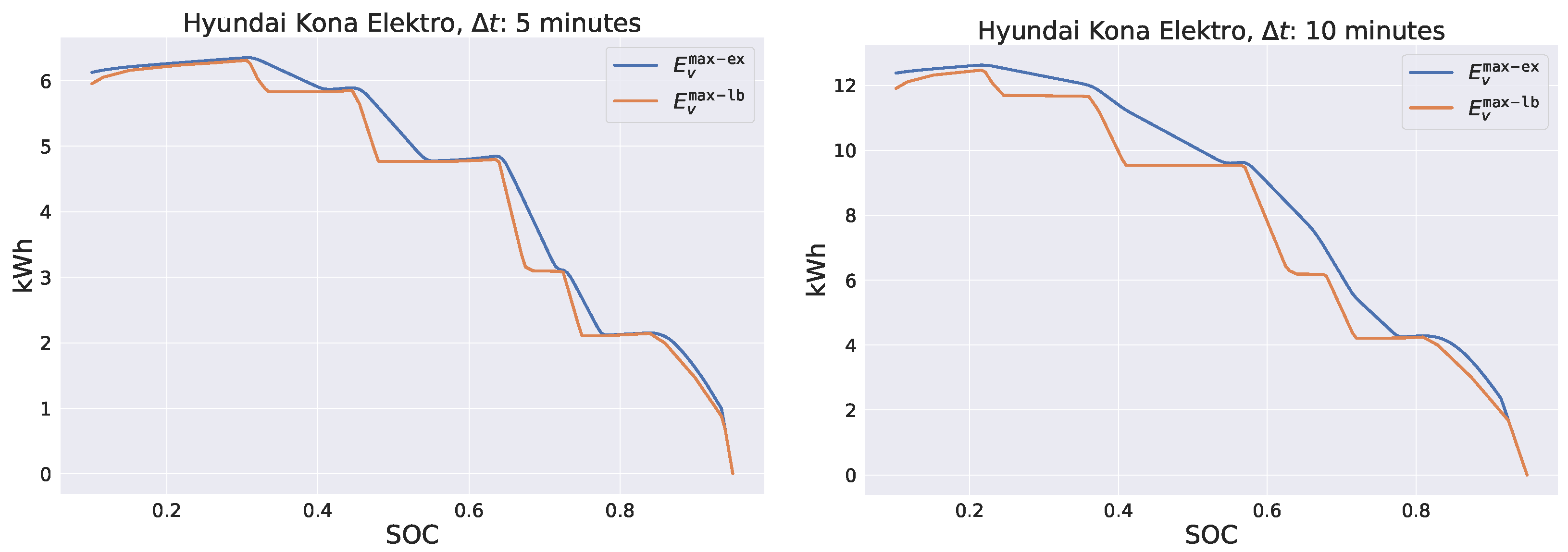
To give the reader an impression of how $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$ relate to each other, Figure 2 shows these functions for different $\Delta t$ values for a Hyundai Kona Elektro. Note that the area between $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$ decreases with smaller $\Delta t$ values. Hence, as we will also see in Section 6, the smaller $\Delta t$ is chosen to be, the smaller the size of the error introduced by $E_v^{\max -\mathrm{lb}}$ will be in general.

In the following sections, we pursue $E_v^{\max -\mathrm{ex}}$ and $E_v^{\max -\mathrm{lb}}$ and investigate the pros and cons of each in comparison. We use the notation $E_v^{max}$ as a placeholder for any specific energy function from $\{E_v^{\max -\mathrm{ex}},E_v^{\max -\mathrm{lb}}\}$.

3.3. Converting Energy Back to Power

In practice, the charging aggregator usually regulates the maximum charging power instead of the maximum charging energy. Consequently, when scheduling with energy values, we have to convert energy values back to power values. For schedules created with $E_v^{\max -\mathrm{lb}}$, the computed energy values of a schedule can be simply divided by $\Delta t$ to obtain charging power values that can be constantly applied throughout a single time step.

For schedules created with the exact $E_v^{\max -\mathrm{ex}}$, due to the possible interference of the EV’s charging controller, it is, in general, not obvious which power value $P_{v,t}$ should be provided to the charging aggregator in order to actually charge a certain amount of energy $x_{v,t}$ in a next time step t. Considering $P_v^{max}\left(s\right)$, this value $P_{v,t}$ can be determined computationally by numerically solving the equation

$$C_v·{\int }_{s_{v,t}}^{s_{v,t}+x_{v,t}/C_v}\frac{1}{min(P_v^{max}\left(s\right),P_{v,t})}ds=\Delta t,$$

(4)

where the left side corresponds to the time needed for charging $x_{v,t}$ when applying as power always the minimum of $P_v^{max}\left(s\right)$ and $P_{v,t}$. Still, there remains the issue that, a solution to our scheduling problem ${\sum }_{v\in V}{P}_{v,t}\le P^{\mathrm{gridmax}}$ is not guaranteed anymore, and either $P^{\mathrm{gridmax}}$ may be exceeded or some $P_{v,t}$ needs to be reduced to avoid this problem. Note that Equation (4) is well defined for all $x_{v,t}\in [0,C_v(s^{\prime }-s_{v,t})]$ where $s^{\prime }$ is determined according to Equation (2).

Therefore, schedules created with $E_v^{\max -\mathrm{ex}}$ mainly serve here as a comparison for schedules created with $E_v^{\max -\mathrm{lb}}$ to provide an idea of the size of the error introduced by time discretization.

3.4. Nonlinear Model

We now formally define EVS-SOC by the following nonlinear program, where variables $x_{v,t}$ represent the energy by which EV $v\in V$ is charged in time step $t=0,\dots ,t_v^{\mathrm{dep}}-1$. Variables $s_{v,t}$ indicate the SOC of each EV $v\in V$ at the beginning of each time step $t=0,\dots ,t_v^{\mathrm{dep}}$.

$$\begin{array}{}\mathrm{(5)}& min& \sum _{v\in V}\sum _{t=0}^{t_v^{\mathrm{dep}}-1}{c}_t·x_{v,t}\hfill \mathrm{(6)}& & x_{v,t}\le E_v^{max}\left(s_{v,t}\right)\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}}-1\mathrm{(7)}& & \sum _{v\in V\mid 0\le t<t_v^{\mathrm{dep}}}{x}_{v,t}\le \Delta t·P^{\mathrm{gridmax}}\hfill & \hfill t\in T\mathrm{(8)}& & s_v^{\mathrm{dep}}\le s_{v,t_v^{\mathrm{dep}}}\hfill & \hfill v\in V\mathrm{(9)}& & s_{v,t}=s_{v,t-1}+x_{v,t-1}/C_v\hfill & \hfill v\in V,t=1,\dots ,t_v^{\mathrm{dep}}\mathrm{(10)}& & x_{v,t}\ge 0\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}}-1\mathrm{(11)}& & 0\le s_{v,t}\le 1\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}}\end{array}$$

The objective function (5) minimizes the sum of the costs for the total consumed energy over all time steps. Inequalities (6) ensure that the energy by which each EV is charged during each time step does not exceed the SOC-dependent maximum energy. Note that this inequality is, in general, nonlinear.

Constraints (7) limit the total energy consumed from the grid during each time step to $\Delta t·P^{\mathrm{gridmax}}$. The departure SOCs are enforced by Inequalities (8). Equalities (9) determine the SOC at the beginning of each time step $t=1,\dots ,t_v^{\mathrm{dep}}$ for each EV v. Thereunto, the previous state of charge $s_{v,t-1}$ is considered together with the charging rate of the previous time slot $x_{v,t-1}$ and the total battery capacity $C_v$. Variable domains are defined in (10) and (11). Due to the domain of variable $x_{v,t}$, an EV may not discharge.

4. Problem Solving Approaches

In the following, we study different ways to deal with the nonlinear maximum charging energy constraints (6). We first consider the simpler case that the maximum power function is concave where we can essentially solve the problem with a linear programming (LP) formulation or a cutting plane approach. Afterward, we consider a more general approach that does not make any assumptions regarding the concavity of the maximum power function. The approach is based on a piecewise linearization of the SOC–energy curve and is accelerated by branch-and-cut.

4.1. Concave Maximum Energy Functions

As already mentioned before, if $P_v^{max}$ is concave, it follows that also $E_v^{max}\in \{E_v^{\max -\mathrm{ex}},$$E_v^{\max -\mathrm{lb}}\}$ is concave as well. For nonconcave $P_v^{max}$, we now determine the convex hull to obtain a concave approximation of the original $P_v^{max}$ for deriving the respective maximum energy function.

In the following, we further assume that $E_v^{max}$ is differentiable. We are aware that, depending on $P_v^{max}$, this assumption might not be completely valid in practice. Instead, $E_v^{max}$ might have breakpoints, in which the left-sided and right-sided limits of the differential do not coincide. Nevertheless, we treat $E_v^{max}$ as if it were differentiable at any SOC of its domain, since differing left-sided and right-sided limits will not affect the results of the following modeling approach.

Due to the assumed properties of $E_v^{max}$, we can replace the nonlinear Inequality (6) from EVS-SOC with the combination of the infinite set of linear inequalities

$$x_{v,t}\le {E_v^{max}}^{\prime }\left(\widehat{s}\right)·(s_{v,t}-\widehat{s})+E_v^{max}\left(\widehat{s}\right)v\in V,t=0,\dots ,t_v^{\mathrm{dep}}-1,\widehat{s}\in [s_{v,0},s_v^{\mathrm{dep}}]$$

(12)

where ${E_v^{max}}^{\prime }$ is the first derivative of $E_v^{max}$. We call the resulting linear programming model EVS-SOC-LIN.

Note that if $P_v^{max}$ is a piecewise linear function, then so is $E_v^{\max -\mathrm{lb}}$. The set of inequalities reduces then to a finite one where we have one inequality corresponding to each linear function segment.

In the spirit of [18], who essentially consider a similar kind of inequalities, we can solve EVS-SOC-LIN by a cutting plane approach. Thereby, the relaxation of EVS-SOC-LIN without Inequalities (12) is first solved. Then, Inequalities (12) that are violated by the current LP solution are iteratively determined and added, and the LP problem is re-solved. The process is repeated until no more Inequalities (12) are violated.

The separation of a violated inequality for a current solution $(x^{\mathrm{LP}},s^{\mathrm{LP}})$ to the relaxed EVS-SOC-LIN works as follows. For all $v\in V,t=0,\dots ,t_v^{\mathrm{dep}}-1$, we check if $x_{v,t}^{\mathrm{LP}}>E_v^{max}\left(s_{v,t}^{\mathrm{LP}}\right)$. In this case, we add the violated Inequality (12) for vehicle v, time step t, and $\widehat{s}=s_{v,t}^{\mathrm{LP}}$. Note that, for one vehicle, multiple inequalities for different time steps can be added within a single cutting plane iteration. This separation procedure is performed for all vehicles $v\in V$ and as long as any violated inequalities are found, the augmented LP problem is then re-solved.

An alternative to the above is the following. Whenever $x_{v,t}^{\mathrm{LP}}>E_v^{max}\left(s_{v,t}^{\mathrm{LP}}\right)$ for some EV v and time step t, one can add the violated Inequality (12) not only for time step t but for all time steps $t^{\prime }=0,\dots ,t_v^{\mathrm{dep}}-1$. The intention here is to possibly reduce the number of needed resolving iterations; however, clearly the size of the LP formulation increases more quickly. Preliminary experiments indicated that, indeed, this variant performed better in practice in most cases. Therefore, we apply it in all our experiments documented in the remainder of this work.

We also compared this variant with the approach presented in [18], where, in one iteration, cuts are only added for the smallest time steps that violate Inequality (12). We found that our variant usually performed slightly better at least in our problem instances.

4.2. General Piecewise Linear Maximum Energy Functions

In the following model, we assume for each EV $v\in V$ that the maximum charging energy function $E_v^{max}$ is a piecewise linear function or is approximated by such. In contrast to EVS-SOC-LIN, we do not make assumptions on the concavity of $E_v^{max}$. We assume that we are given a finite set of SOC values $\{S_{v,k}\mid k=1,\dots ,k_v^{\max }\}$ in increasingly sorted order, with $S_{v,1}=0$ and $S_{v,k_v^{\max }}=1$ and the values in between representing the breakpoints of the piecewise linear function. These values are pairwise distinct and can be unevenly distributed among the SOC interval $[0,1]$. For each $S_{v,k}$ we know the value of the maximum charging energy $E_v^{max}\left(S_{v,k}\right)$.

We model the piecewise linear function as suggested in Chapter 10.1 of [25]. Thereunto, we use continuous variables ${\alpha }_{v,t,k}$ to express the SOC $s_{v,t}$ as a convex combination of $S_{v,k}$ and ${\alpha }_{v,t,k}$. The variables ${\alpha }_{v,t,k}$ are also used to represent the maximum charging energy function as a convex combination of $E_v^{max}\left(S_{v,k}\right)$ and ${\alpha }_{v,t,k}$.

Furthermore, we introduce additional binary variables ${\beta }_{v,t,k}$, which are used to ensure that at most two consecutive ${\alpha }_{v,t,k}$ and ${\alpha }_{v,t,k+1}$ variables are nonzero. By replacing Constraints (6) in Formulation (5)–(11) with the following Constraints (13)–(21), we obtain a MILP model, which we refer to as EVS-SOC-GLIN.

$$\begin{array}{}\mathrm{(13)}& s_{v,t}=\sum _{k=1}^{k_v^{\max }}{S}_{v,k}·{\alpha }_{v,t,k}\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}}\mathrm{(14)}& x_{v,t}\le \sum _{k=1}^{k_v^{\max }}{E}_v^{max}\left(S_{v,k}\right)·{\alpha }_{v,t,k}\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}}-1\mathrm{(15)}& \sum _{k=1}^{k_v^{\max }}{\alpha }_{v,t,k}=1\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}}\end{array}$$

$$\begin{array}{}\mathrm{(16)}& \sum _{k=1}^{k_v^{\max }-1}{\beta }_{v,t,k}=1\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}}\mathrm{(17)}& {\alpha }_{v,t,0}\le {\beta }_{v,t,0}\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}}\mathrm{(18)}& {\alpha }_{v,t,k}\le {\beta }_{v,t,k-1}+{\beta }_{v,t,k}\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}},k=2,\dots ,k_v^{\max }-1\mathrm{(19)}& {\alpha }_{v,t,k_v^{\max }}\le {\beta }_{v,t,k_v^{\max }-1}\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}}\mathrm{(20)}& 0\le {\alpha }_{v,t,k}\le 1\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}},k=1,\dots ,k_v^{\max }\mathrm{(21)}& {\beta }_{v,t,k}\in \{0,1\}\hfill & \hfill v\in V,t=0,\dots ,t_v^{\mathrm{dep}},k=1,\dots ,k_v^{\max }-1\end{array}$$

Equations (13) link the SOC values $s_{v,t}$ with the continuous weight variables ${\alpha }_{v,t,k}$. The charging energy $x_{v,t}$ of EV v at time slot t is limited by Inequalities (14) to the maximum charging energy. Constraints (15) set the sum of the continuous weights ${\alpha }_{v,t,k}$ over all discrete SOC levels $k=1,\dots ,k_v^{\max }$ to one. Equations (16) ensure that exactly one ${\beta }_{v,t,k}$ variable is active for each EV v and time slot t. The ${\alpha }_{v,t,k}$ variables are linked with the ${\beta }_{v,t,k}$ variables by Inequalities (17)–(19). Altogether, (16)–(19) are the so-called adjacency constraints, which ensure that at most two consecutive variables ${\alpha }_{v,t,k}$ and ${\alpha }_{v,t,k+1}$ are nonzero. Constraints (20)–(21) define the domains of ${\alpha }_{v,t,k}$ and ${\beta }_{v,t,k}$, respectively.

As we will see in Section 6, the previously introduced EVS-SOC-LIN formulation, which requires $E_v^{max}$ to be concave, performs remarkably well. Therefore, we propose a branch-and-cut approach for solving EVS-SOC-GLIN, in which we initially work on the convex hull of $\{(S_{v,k},E_v^{max}\left(S_{v,k}\right))\mid k=1,\dots ,k_v^{\max }\}\cup \{(S_{v,1},0),(S_{v,k_v^{\max }},0)\}$. To obtain this relaxation, we consider the original EVS-SOC-GLIN formulation with all its variables and constraints except the linking constraints (17)–(19).

Then, whenever a solution candidate is found, we check for all $v\in V,t=0,\dots ,t_v^{\mathrm{dep}}-1$ whether $x_{v,t}$ exceeds the actual $E_v^{max}$ value at SOC $s_{v,t}$, i.e., if $x_{v,t}>E_v^{max}\left(s_{v,t}\right)$. If this is the case, a cut is added that links all nonzero ${\alpha }_{v,t,k}$ variables with their respective ${\beta }_{v,t,k}$ variables, as we did in Constraints (17)–(19). Such cuts are separated and added until for all $v\in V,t=0,\dots ,t_v^{\mathrm{dep}}-1$, it holds that $x_{v,t}\le E_v^{max}\left(s_{v,t}\right)$.

5. Benchmark Instances

Due to the lack of pure real-world problem instances, we randomly generate benchmark instances and use real-world data as far as possible. Specifically, battery capacities and maximum power functions are adopted from real-world data. We first consider individual EVS-SOC instances that represent snapshot scenarios at certain times with a specific number of vehicles that are assumed to have arrived at the charging station following a homogenous Poisson process. Afterward, in Section 5.2, we consider whole-model-based predictive control scenarios with a rolling horizon in which vehicles arrive at different times of a day.

All of the benchmark instances are available at https://www.ac.tuwien.ac.at/research/problem-instances/ (accessed on 11 November 2021).

5.1. Individual EVS-SOC Instances

We distinguish between three types of problem parameters depending on whether the parameter is set by the user, randomly generated, or based on real-world data. To the input provided by the user, we count the number n of EVs, the length $\Delta t$ of a time step, and the grid’s power capacity $P^{\mathrm{gridmax}}$. We generate 30 instances for each combination of $n\in \{10,20,50,100\}$, $\Delta t\in \{1,5,10\}$ min, and $P^{\mathrm{gridmax}}\in \{10n,25n,40n\}$.

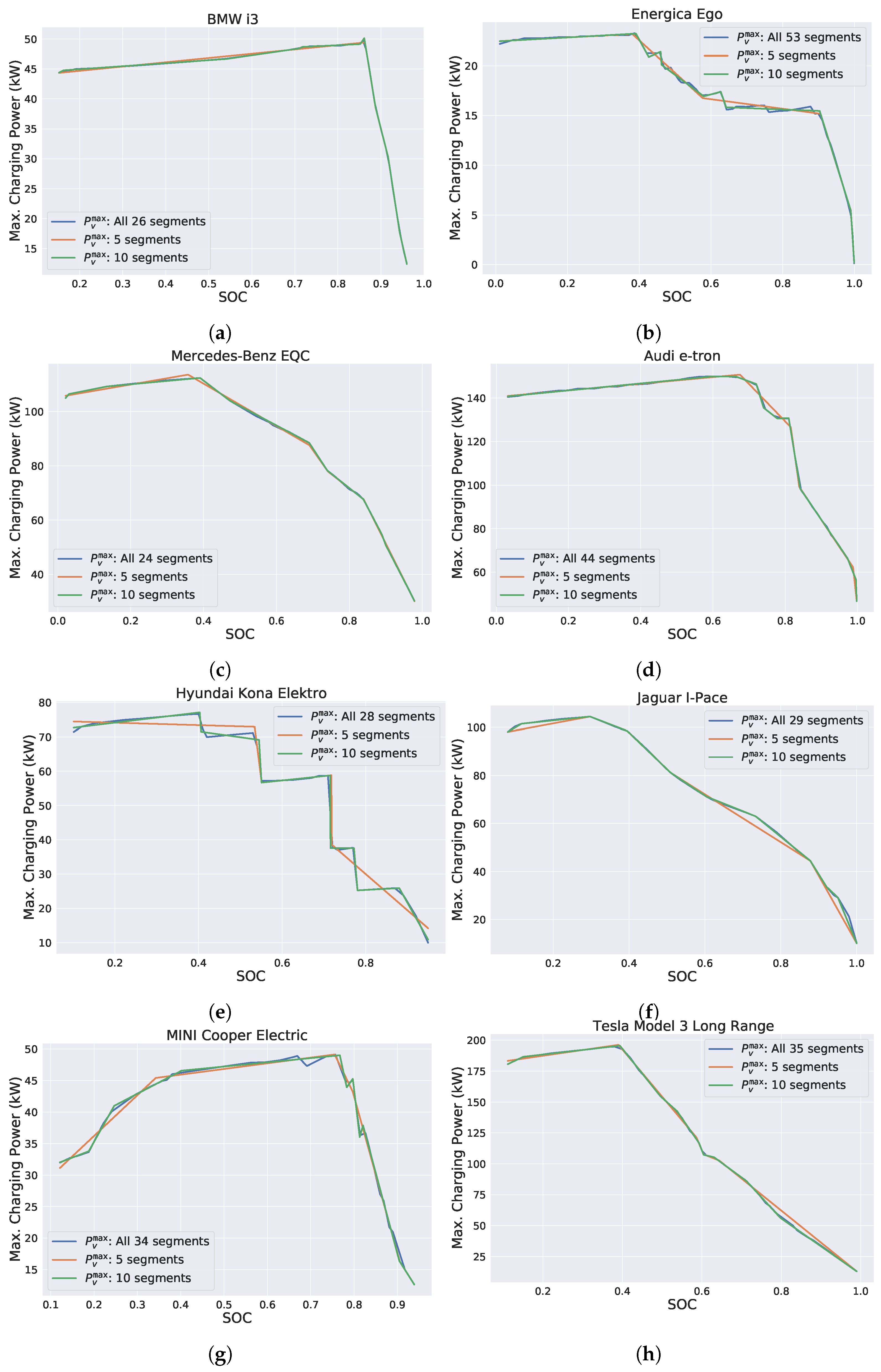
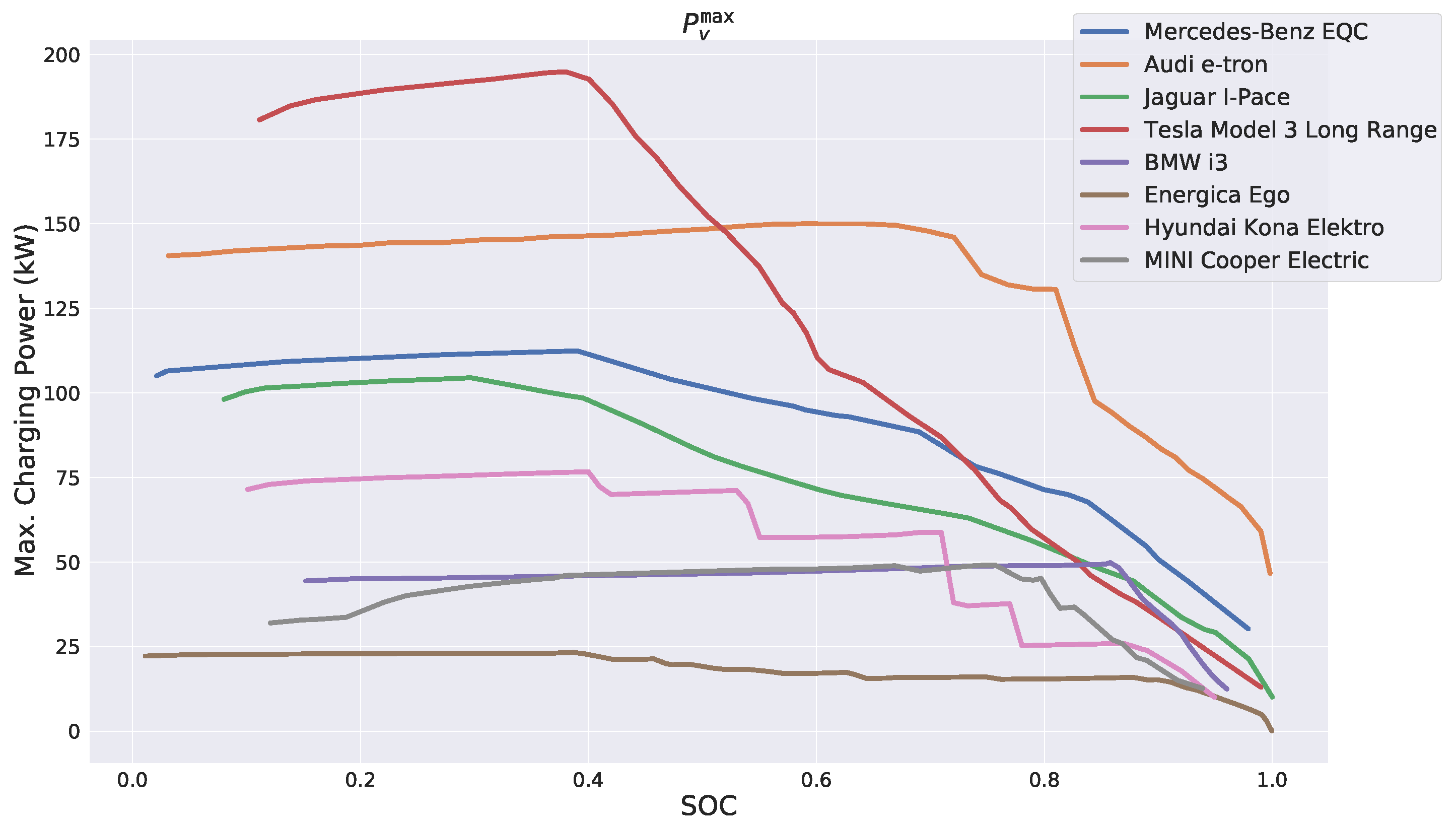
We consider eight different types of real EVs shown in

Table 1. Used EV types with battery capacity $C_v$, $P_v^{max}$ domain $[s_v^{\min },s_v^{\max }]$ and the number of linear pieces of $P_v^{max}$.

EV Name	${\mathit{C}}_{\mathit{v}}$ (kWh)	${\mathit{s}}_{\mathit{v}}^{\mathbf{min}}$	${\mathit{s}}_{\mathit{v}}^{\mathbf{max}}$	#${\mathit{P}}_{\mathit{v}}^{max}$-lin. Pieces
Energica Ego	21.5	1.1	99.9	53
MINI Cooper Electric	32.6	12.1	93.8	34
BMW i3	42.2	15.1	96.0	26
Hyundai Kona Elektro	67.5	10.1	94.9	28
Tesla Model 3 Long Range	82.0	11.1	99.0	35
Mercedes-Benz EQC	85.0	2.1	97.8	24
Jaguar I-Pace	90.0	8.0	100.0	29
Audi e-tron	95.0	3.1	99.8	44

. The EV’s battery capacities were taken from the EV Database https://www.ev-database.de (accessed on 11 November 2021). The respective maximum power functions $P_v^{max}$ were manually extracted from plots found on the website of the Dutch EV charging station operator FASTNED https://fastnedcharging.com (accessed on 11 November 2021). More specifically, 25 up to 70 points of a plot were manually determined in dependence of notable changes of the gradient, and linear interpolation was applied in between. All these $P_v^{max}$ functions are shown in Figure 3. 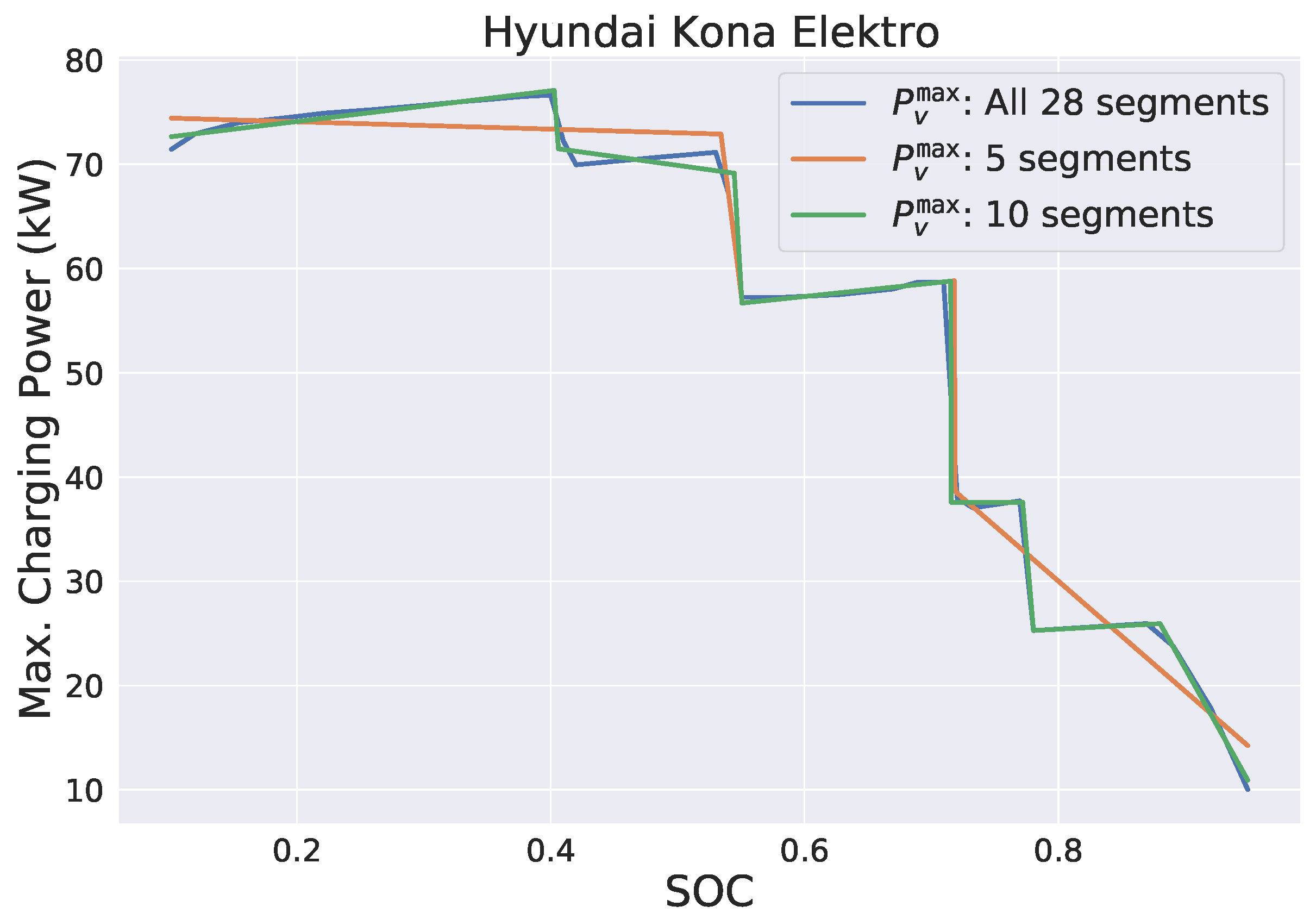Observe that the maximum power function’s available domain of definition $[s_v^{\min },s_v^{\max }]$ varies among the EVs. If a vehicle type supports speed charging, the respective most powerful charging curve is used.

Since the $P_v^{max}$ data extracted from the original plots is quite fine-grained, we additionally derive simplified piecewise linear approximations with only five and ten linear pieces, respectively. For this task, we utilized the Python package pwlf https://github.com/cjekel/piecewise_linear_fit_py (accessed on 11 November 2021) to determine the approximately optimal breakpoints automatically.

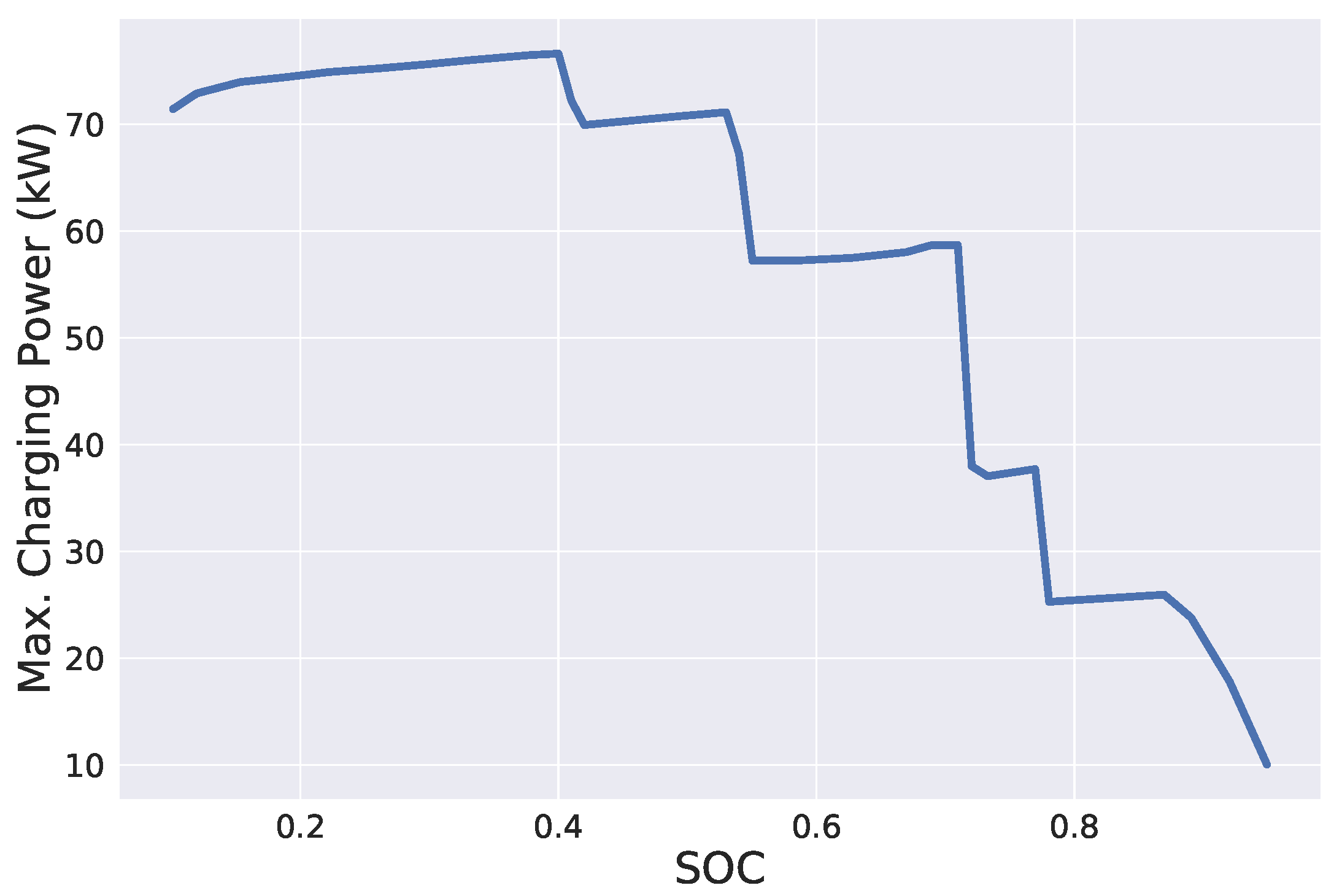
A comparison between the original $P_v^{max}$ and these simpler piecewise approximations is shown in Figure 4 exemplarily for the Hyundai Kona Elektro. Observe that the approximation of the original $P_v^{max}$ function with 10 segments is already quite good for this rather challenging vehicle type. For $P_v^{max}$ of the other vehicle types, see Appendix A.

For each EV $v\in V$ in a benchmark instance, one of the above EV types is chosen uniformly at random. Moreover, we choose an availability duration at the charging station $d_v^{\mathrm{avail}}$ randomly according to a normal distribution with a mean value of six hours and a standard deviation of 1.5 h.

Next, from the interval $(-d_v^{\mathrm{avail}}/\Delta t,0)$ we select an arrival time $t_v^{\mathrm{arr}}$ uniformly at random and obtain a respective departure time $t_v^{\mathrm{dep}}=\lceil t_v^{\mathrm{arr}}+d_v^{\mathrm{avail}}/\Delta t\rceil$. Considering the available domains of definition of the maximum power functions, we generally assume that each vehicle shall be charged from a SOC of 20% at arrival to a SOC of 90% at departure. In our benchmark instances, we therefore choose the initial SOC proportional to the already bygone availability time, i.e., for all $v\in V$,

$$s_{v,0}=\frac{-t_v^{\mathrm{arr}}}{d_v^{\mathrm{avail}}/\Delta t}·0.7+0.2.$$

(22)

The departure SOC $s_v^{\mathrm{dep}}$ is set to $90\%$ for all EVs.

The end of the time horizon is obtained from the last EV’s departure time, i.e., $t_{max}={max}_{v\in V}{t}_v^{\mathrm{dep}}$. Electricity costs per unit of consumed energy $c_t$ are independently chosen for each time step $t\in T$ uniformly at random from $[1.9,3.5)$ cent/kWh.

5.2. Rolling Horizon Benchmark Scenarios

In addition to the individual benchmark instances, we consider rolling horizon simulations over whole days starting at time 0:00 and ending at 24:00. To deal with such a scenario in which vehicles arrive at different times at the charging station, the schedule is (re-)optimized at time 0:00 and then every $\tau =10$ min, always considering only EVs that are currently available at the charging station. The found charging schedule is then assumed to be applied for the next $\tau$ minutes until a new schedule is determined.

The time is again discretized into equally long time steps of $\Delta t\in \{5,10\}$ min. Electricity costs per unit of consumed energy are chosen as explained in Section 5.1, and it is assumed that they are known in advance for the whole charging period. For the number of vehicles, we use $n\in \{10,20,50,100\}$. Again, we pick each vehicle type uniformly at random from the set of available vehicle types.

We assumed that most vehicles arrive around two peak times: at 6:00 and 14:00. For picking the arrival time $t_v^{\mathrm{arr}}$ for a vehicle $v\in V$, we therefore first randomly select with equal probability one of these two peak times and then sample $t_v^{\mathrm{arr}}$ from a normal distribution with the chosen peak time as mean value and a standard deviation of two hours. Times outside of the considered horizon of 24 h are re-sampled.

The charging duration $d_v^{\mathrm{avail}}$ is chosen as described in Section 5.1 and $t_v^{\mathrm{dep}}$ is derived correspondingly. $s_v^{\mathrm{dep}}$ and $P^{\mathrm{gridmax}}$ are set as before. At time 0:00, we set $s_{v,0}=0.2$ and with each rescheduling, we determine $s_{v,0}$ based on the charging schedule of the previous iteration. Thirty independent whole-day scenarios were constructed and are considered in the experimental evaluation.

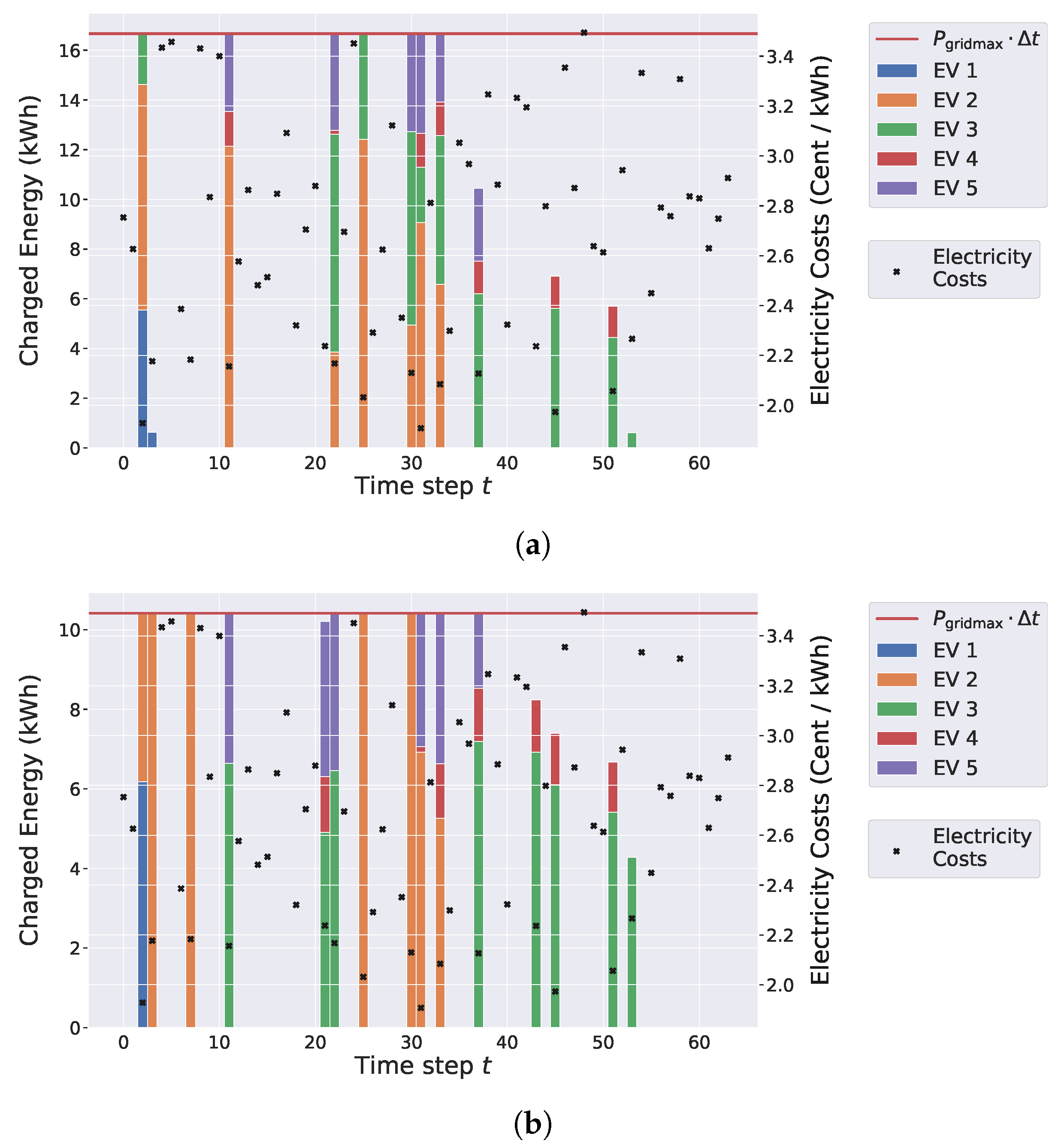
Exemplary Solutions

Figure exemplarily visualizes optimal solutions for a single individual instance with $n=5$ EVs and $\Delta t=5$ min obtained from EVS-SOC-GLIN with decreasing grid power capacity $P^{\mathrm{gridmax}}\in \{50,125,200\}$ kW. As the maximum energy function, we chose $E_v^{\max -\mathrm{lb}}$ based on $P_v^{max}$ with five piecewise linear segments. Each sub-figure represents an optimal charging schedule of a vehicle fleet. Bars specify the energy a vehicle is charged with at each time step. The corresponding scale is located on the left y-axis. The grid’s maximum energy supply $P^{\mathrm{gridmax}}·\Delta t$ is indicated as horizontal line in the plots. Crosses reveal the electricity costs for each time step and the corresponding scale is located on the right-sided y-axis.

For $P^{\mathrm{gridmax}}=200$ kW it can be observed in Figure 5a that vehicles are charged usually in parallel within a single time step, and cheap electricity costs can be exploited more effectively. Moreover, at some time steps, the charged energy is well below the grid’s power capacity. Figure 5b shows how the charging schedule changes when lowering $P^{\mathrm{gridmax}}$ to 125 kW. By reducing the grid’s power capacity, more time steps are required for charging the vehicles to their target SOC, resulting in higher total charging costs. In contrast to the solution shown in Figure 5a, the charging costs only slightly increase even though the grid’s power capacity has been almost halved.

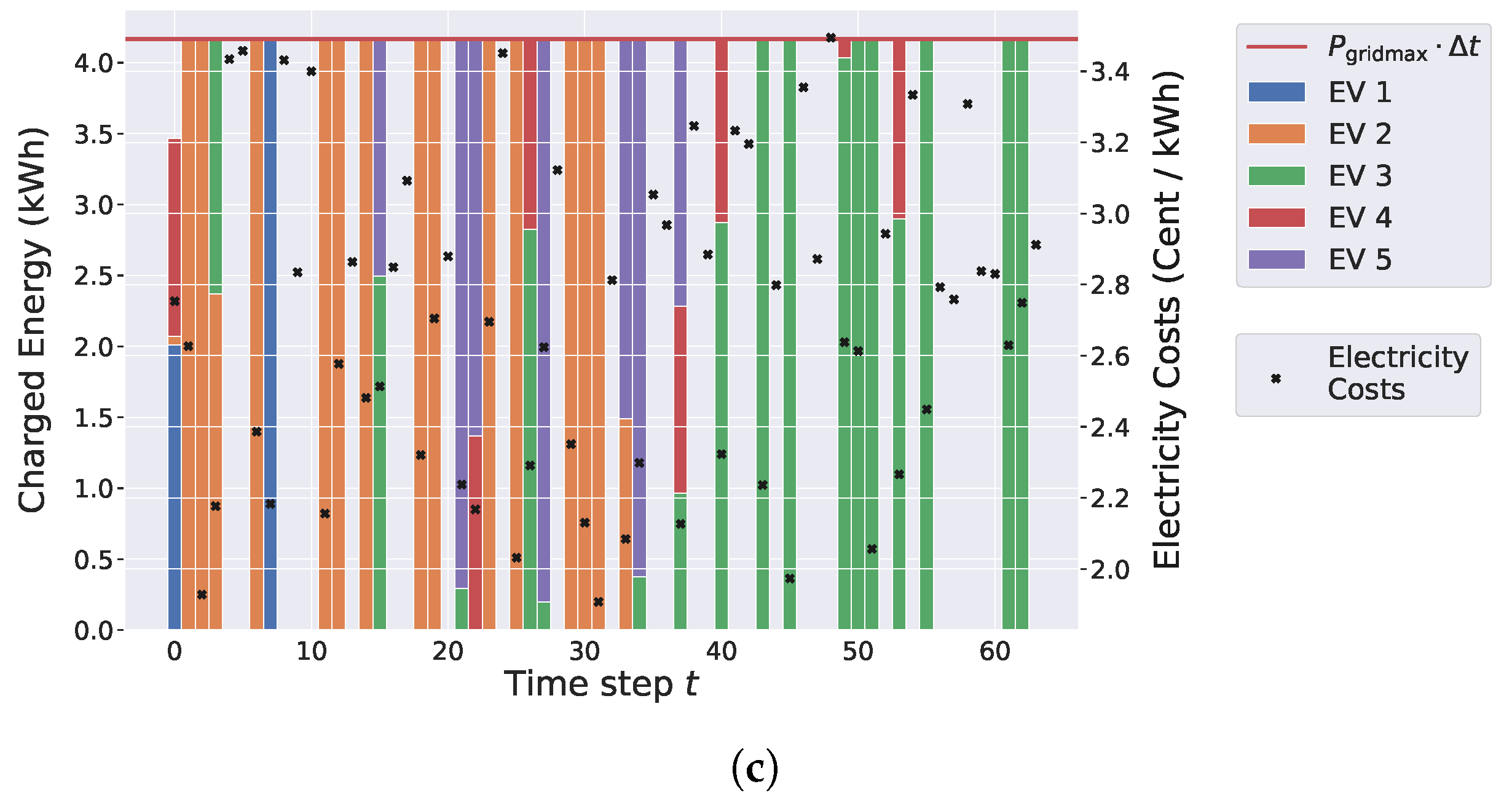
When reducing $P^{\mathrm{gridmax}}$ even further to 50 kW, as shown in Figure 5c, the number of time steps required for charging the vehicles drastically increases. Moreover, in contrast to Figure 5a, at most time steps, only a single vehicle is charged with usually the maximal possible energy. Finally, note that, independent of the choice of $P^{\mathrm{gridmax}},$ the generated solutions always utilize the time steps at which charging is the cheapest.

In summary, Figure 5 shows how the choice of $P^{\mathrm{gridmax}}$ affects a respective optimal charging schedule: The smaller the power capacity of the grid, the more time steps are required for charging the vehicles and, therefore, the higher the total resulting charging costs are.

6. Experimental Results

All solution approaches were implemented in Julia 1.6.0 https://julialang.org (accessed on 11 November 2021) using the the optimization modeling package JuMP v0.21.5 and Gurobi 9.1.0 https://www.gurobi.com (accessed on 11 November 2021) as LP/MILP solver. Gurobi was configured to run in single-threaded mode with a time limit of 30 min per instance. All remaining Gurobi parameters were kept at their default values. The experiments were conducted on an Intel Xeon E5-2640 v4 with 2.40 GHz and 16 GB memory limit. If not stated otherwise, we report in the following mean or median results on the 30 problem instances per instance parameter combination $(n,\Delta t,P^{\mathrm{gridmax}},E_v^{max})$.

We first show individual results for EVS-SOC-LIN and EVS-SOC-GLIN, respectively. Afterward, solutions generated by both approaches for the same instances w.r.t. the same configurations are compared to each other in Section 6.3. Finally, we present results for the rolling horizon scenarios.

6.1. EVS-SOC-LIN

We compare two variants of EVS-SOC-LIN. Recall that, for piecewise linear $E_v^{max}$ only a finite set of inequalities as described by (12) exists. Hence, next to the variant in which these constraints are dynamically separated as cuts via the cutting plane approach as described in Section 4.1, we also consider the variant in which all maximum charging energy constraints (12) are statically added to the LP upfront.

The results of this comparison are reported in

Table 2. EVS-SOC-LIN runtime comparison for concave maximum power functions and $P^{\mathrm{gridmax}}=25n$: solving the static MILP versus the cutting plane method.

n	$\mathbf{\Delta }\mathit{t}$ (min)	${\mathit{n}}_{\mathbf{seg}}$	Runtime (s)				${\mathit{n}}_{\mathbf{cuts}}$
			Static		Cutting Plane		Cutting Plane
		Mean	Median	StdDev	Median	StdDev	Mean	StdDev
$E_v^{\max -\mathrm{lb}}$
5	1	49	0.07	0.04	1.34	0.26	10,423	5209
5	5	46	0.01	0.00	1.04	0.23	574	269
5	10	43	0.01	0.00	1.03	0.24	190	85
10	1	99	0.18	0.15	1.52	0.38	15,949	5580
10	5	93	0.02	0.01	1.05	0.28	1243	520
10	10	86	0.01	0.00	1.03	0.26	416	159
20	1	199	0.60	0.30	2.09	0.49	25,549	6715
20	5	187	0.05	0.02	1.10	0.25	2593	747
20	10	172	0.02	0.01	1.05	0.25	862	245
50	1	495	2.78	1.02	6.72	2.07	87,375	19,749
50	5	464	0.16	0.06	1.28	0.31	6499	1167
50	10	427	0.06	0.02	1.10	0.23	2157	335
100	1	994	9.34	2.60	12.84	3.99	193,069	27,979
100	5	931	0.56	0.22	1.68	0.32	13,502	1664
100	10	858	0.13	0.05	1.25	0.27	4367	475
$E_v^{\max -\mathrm{ex}}$
5	1	901	1.19	1.02	1.31	0.38	12,800	5986
5	5	901	0.23	0.11	0.90	0.25	1102	542
5	10	901	0.08	0.07	0.97	0.26	322	205
10	1	1802	4.98	3.27	1.65	0.52	25,271	9541
10	5	1802	0.59	0.22	1.06	0.24	2341	950
10	10	1802	0.22	0.10	1.01	0.20	757	387
20	1	3605	14.33	8.48	3.29	0.83	60,778	18,725
20	5	3605	1.21	0.45	1.16	0.27	5117	1547
20	10	3605	0.68	0.20	1.07	0.21	1585	516
50	1	9041	70.69	31.89	9.11	2.66	175,979	28,195
50	5	9041	4.17	1.58	1.57	0.33	13,737	2329
50	10	9041	1.57	0.54	1.15	0.21	3989	858
100	1	18,086	280.22	100.87	25.45	9.66	390,873	44,162
100	5	18,086	13.11	4.73	2.11	0.51	27,920	3515
100	10	18,086	3.80	1.35	1.32	0.34	8126	1419

. As a maximum energy function $E_v^{\max -\mathrm{lb}}$ as well as $E_v^{\max -\mathrm{ex}}$ are considered. The energy functions are derived from the convex hull of $P_v^{max}$ as described in Section 4.1. Moreover, $P^{\mathrm{gridmax}}$ is set to $25n$ for all shown instances. The table lists for each instance group, identified by n and $\Delta t$, the average total number of piecewise linear segments $n_{\mathrm{seg}}$ of the $E_v^{max}$ functions over all vehicles, a comparison of the runtimes between the cutting plane and the static approach, as well as the average total number of added cuts, denoted by $n_{\mathrm{cuts}}$, for the cutting plane approach.

Note that all reported instances were solved to optimality w.r.t. both maximum energy functions. Using $E_v^{\max -\mathrm{lb}}$ as the maximum energy function, the static approach as well as the cutting plane approach were both able to solve all instances within few seconds. However, the static approach was significantly faster than the cutting plane method for all considered instance groups.

Using $E_v^{\max -\mathrm{ex}}$ as a maximum energy function, the cutting plane method demonstrated its performance advantages with growing n. Due to how $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$ are derived, the number of piecewise linear segments for $E_v^{\max -\mathrm{ex}}$ is, in general, much higher than for $E_v^{\max -\mathrm{lb}}$. As the number of segments increases, we can observe that the cutting plane approach scales significantly better than the static approach. This improvement is particularly noticeable if we fix n and consider decreasing $\Delta t$ values. Observe that, for a fixed $\Delta t$, the number of cuts increases with larger n values, whereas, for a fixed n, the number of cuts increases with smaller $\Delta t$ values.

Therefore, the results indicate that the cutting plane technique shows performance benefits when a larger number of cuts has to be separated, i.e., the maximum charging power condition was not easily fulfilled. Overall, it can be said that the cutting plane variant outperforms the static model on larger instances and when $n_{\mathrm{seg}}$ is large. We additionally conducted the experiments for $P^{\mathrm{gridmax}}=10n$ and $40n$ and observed the same trends.

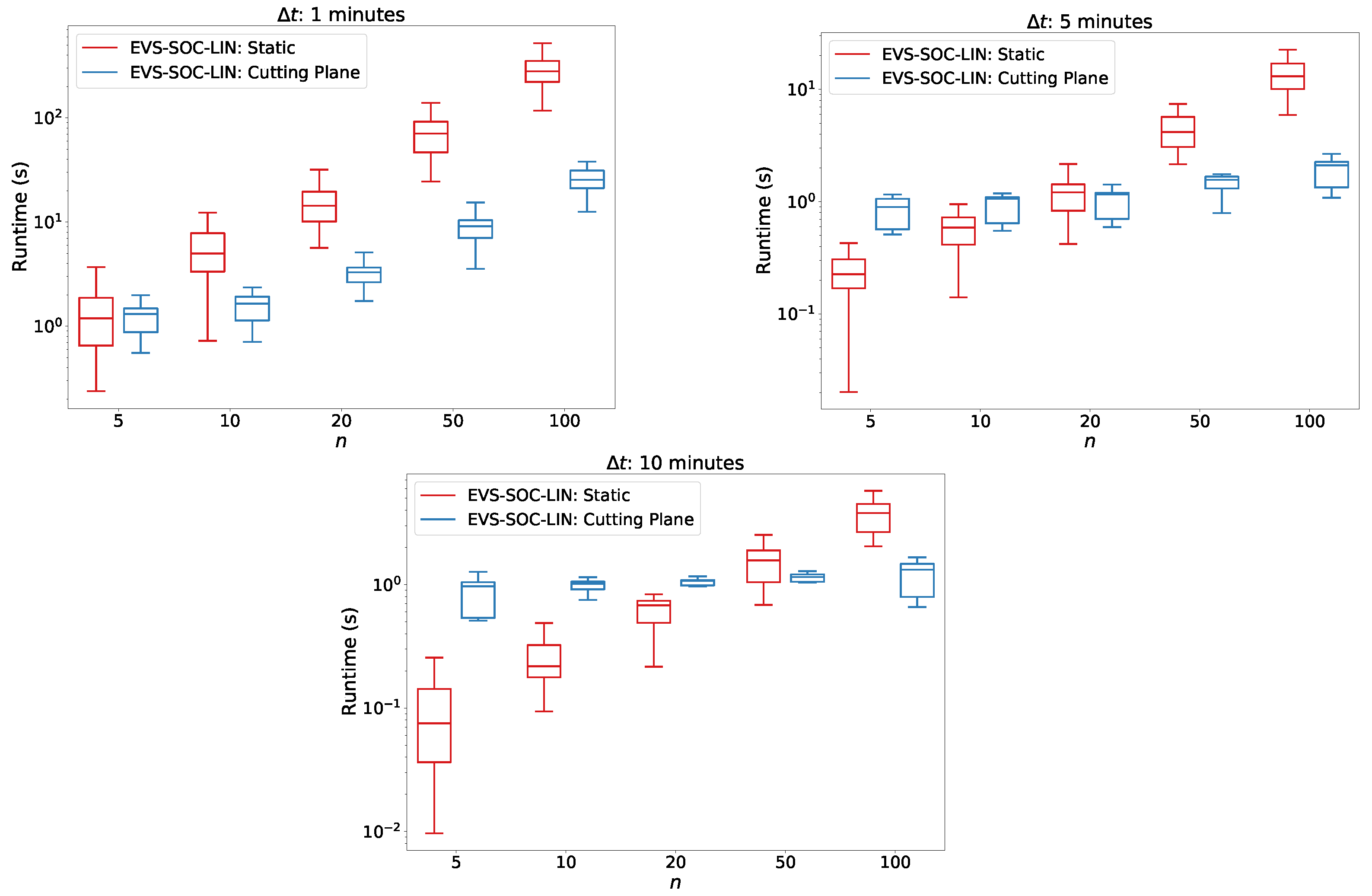
In Figure 6, we give a more detailed comparison of the runtimes between the static approach and the cutting plane approach with $E_v^{\max -\mathrm{ex}}$ as the maximum energy function.

The figure shows that, when fixing $\Delta t$, the static approach does not scale as well as the cutting plane approach in terms of the computation time with an increasing number of vehicles. For $\Delta t\in \{5,10\}$, the runtimes of the cutting plane approach barely increase as n grows. Only for $\Delta t=1$ min, the runtimes of the cutting plane approach increase slightly with a growing number of vehicles. In contrast, for the static approach, the computation times increase more strongly than their cutting plane counterparts. As $\Delta t$ decreases, the difference in performance becomes increasingly obvious.

6.2. EVS-SOC-GLIN

Similar to before, we compare two variants of EVS-SOC-GLIN for the general nonconcave maximum charging power functions. In the first variant, we directly solve the static MILP in which all linking constraints (17)–(19) are included from the beginning, whereas the second approach is the branch-and-cut variant (B & C) in which these linking constraints are dynamically separated as needed, cf. Section 4.2. As maximum energy function we use $E_v^{\max -\mathrm{ex}}$ and $E_v^{\max -\mathrm{lb}}$, both based on the original full resolution $P_v^{max}$ functions. For $P^{\mathrm{gridmax}}\in \{10n,25n,40n\}$, we report the results in

Table 3. EVS-SOC-GLIN results for solving the static model versus B & C with $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$ based on the original $P_v^{max}$ functions and $P^{\mathrm{gridmax}}=10n$.

n	$\mathbf{\Delta }\mathit{t}$ (min)	${\mathit{n}}_{\mathbf{seg}}$	${\mathit{n}}_{\mathbf{feas}}$		Runtime (s)		${\mathit{n}}_{\mathbf{cuts}}$	%-gap
		Mean			Median		Median	Median
			Static	B & C	Static	B & C	B & C	Static	B & C
$E_v^{\max -\mathrm{lb}}$
5	1	155	30	30	391.75	43.39	1038	0.01	0.01
5	5	139	30	30	6.58	1.43	144	0.00	0.01
5	10	119	30	30	1.67	0.83	56	0.00	0.00
10	1	311	21	29	1800.00	1800.00	4068	0.03	0.03
10	5	279	30	30	79.94	8.84	498	0.01	0.01
10	10	242	30	30	7.04	2.06	194	0.00	0.01
20	1	612	2	11	1800.00	1800.00	8974	0.08	0.19
20	5	553	30	30	500.49	684.63	1846	0.01	0.01
20	10	475	30	30	40.18	13.35	505	0.01	0.01
50	1	1544	0	0	1800.00	1800.00	15,910	-	-
50	5	1393	26	30	1800.00	1800.00	6106	0.05	0.05
50	10	1192	30	30	307.62	827.59	1930	0.01	0.01
100	1	3095	0	0	1800.00	1800.00	11,886	-	-
100	5	2796	9	9	1800.00	1800.00	9961	0.08	0.12
100	10	2399	30	30	1800.00	1800.00	4434	0.01	0.03
$E_v^{\max -\mathrm{ex}}$
5	1	901	8	27	1800.00	1800.00	5304	0.03	0.01
5	5	901	30	30	143.42	9.59	820	0.00	0.00
5	10	901	30	30	34.53	2.60	319	0.00	0.00
10	1	1802	1	21	1800.00	1800.00	13,982	0.04	0.08
10	5	1802	29	30	1800.00	725.37	2858	0.01	0.01
10	10	1802	30	30	201.32	10.29	680	0.00	0.01
20	1	3605	0	10	1800.00	1800.00	23,449	-	0.14
20	5	3605	14	30	1800.00	1800.00	6479	0.07	0.05
20	10	3605	30	30	1038.91	116.59	1507	0.01	0.01
50	1	9041	0	0	1800.00	1800.00	6856	-	-
50	5	9041	0	23	1800.00	1800.00	15,048	-	0.11
50	10	9041	4	30	1800.00	1800.00	6160	0.18	0.03
100	1	18,078	0	0	-	1800.00	0	-	-
100	5	18,086	0	10	1800.00	1800.00	18,944	-	0.08
100	10	18,086	0	25	1800.00	1800.00	10,750	-	0.06

,

Table 4. EVS-SOC-GLIN results for solving the static model versus B & C with $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$ based on the original $P_v^{max}$ functions and $P^{\mathrm{gridmax}}=25n$.

n	$\mathbf{\Delta }\mathit{t}$ (min)	${\mathit{n}}_{\mathbf{seg}}$	${\mathit{n}}_{\mathbf{feas}}$		Runtime (s)		${\mathit{n}}_{\mathbf{cuts}}$	%-gap
		Mean			Median		Median	Median
			Static	B & C	Static	B & C	B & C	Static	B & C
$E_v^{\max -\mathrm{lb}}$
5	1	155	29	30	1800.00	1800.00	3184	0.02	0.06
5	5	139	30	30	25.52	6.68	422	0.01	0.01
5	10	119	30	30	1.27	1.62	153	0.01	0.01
10	1	312	20	23	1800.00	1800.00	7298	0.10	0.12
10	5	279	30	30	183.39	770.59	1132	0.01	0.01
10	10	242	30	30	17.87	11.88	452	0.01	0.01
20	1	612	4	3	1800.00	1800.00	11,938	0.26	0.28
20	5	553	30	30	1800.00	1800.00	2702	0.01	0.05
20	10	475	30	30	60.59	201.06	967	0.01	0.01
50	1	1544	0	0	1800.00	1800.00	22,034	-	-
50	5	1393	29	30	1800.00	1800.00	6997	0.08	0.11
50	10	1192	30	30	902.21	1800.00	2575	0.01	0.03
100	1	3095	0	0	1800.00	1800.00	29,193	-	-
100	5	2796	14	7	1800.00	1800.00	11,737	0.12	0.18
100	10	2399	30	30	1800.00	1800.00	5340	0.03	0.06
$E_v^{\max -\mathrm{ex}}$
5	1	901	9	25	1800.00	1800.00	15,258	0.21	0.20
5	5	901	30	30	448.47	761.59	2153	0.01	0.01
5	10	901	30	30	56.12	16.43	866	0.00	0.01
10	1	1802	1	18	1800.00	1800.00	23,328	0.23	0.33
10	5	1802	26	30	1800.00	1800.00	5220	0.04	0.06
10	10	1802	30	30	204.26	233.60	2063	0.01	0.01
20	1	3605	0	2	1800.00	1800.00	17,970	-	0.32
20	5	3605	15	29	1800.00	1800.00	10,784	0.08	0.12
20	10	3605	29	30	1097.26	1800.00	4647	0.01	0.03
50	1	9041	0	0	1800.00	1800.00	23,986	-	-
50	5	9041	0	17	1800.00	1800.00	23,708	-	0.18
50	10	9041	16	28	1800.00	1800.00	12,160	0.04	0.08
100	1	18,086	0	0	1800.00	1800.00	0	-	-
100	5	18,086	0	0	1800.00	1800.00	25,754	-	-
100	10	18,086	0	19	1800.00	1800.00	19,752	-	0.09

and

Table 5. EVS-SOC-GLIN results for solving the static model versus B & C with $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$ based on the original $P_v^{max}$ functions and $P^{\mathrm{gridmax}}=40n$.

n	$\mathbf{\Delta }\mathit{t}$ (min)	${\mathit{n}}_{\mathbf{seg}}$	${\mathit{n}}_{\mathbf{feas}}$		Runtime (s)		${\mathit{n}}_{\mathbf{cuts}}$	%-gap
		Mean			Median		Median	Median
			Static	B & C	Static	B & C	B & C	Static	B & C
$E_v^{\max -\mathrm{lb}}$
5	1	155	29	29	1800.00	1800.00	4476	0.04	0.15
5	5	139	30	30	31.04	55.93	619	0.01	0.01
5	10	119	30	30	2.49	4.05	247	0.01	0.01
10	1	311	20	20	1800.00	1800.00	8161	0.21	0.17
10	5	279	30	30	301.14	1800.00	1410	0.01	0.03
10	10	242	30	30	27.80	36.06	456	0.01	0.01
20	1	612	2	1	1800.00	1800.00	13,361	0.27	0.48
20	5	553	30	30	1800.00	1800.00	2863	0.04	0.10
20	10	475	30	30	69.51	571.16	1078	0.01	0.01
50	1	1544	0	0	1800.00	1800.00	25,908	-	-
50	5	1393	28	28	1800.00	1800.00	7110	0.12	0.21
50	10	1192	30	30	1097.80	1800.00	2748	0.01	0.05
100	1	3095	0	0	1800.00	1800.00	29,066	-	-
100	5	2796	7	2	1800.00	1800.00	11,782	0.22	0.21
100	10	2399	29	30	1800.00	1800.00	5650	0.06	0.10
$E_v^{\max -\mathrm{ex}}$
5	1	901	9	24	1800.00	1800.00	20,190	0.23	0.44
5	5	901	30	30	582.18	1800.00	3180	0.01	0.07
5	10	901	30	30	80.12	34.07	1228	0.00	0.01
10	1	1802	1	13	1800.00	1800.00	24,450	0.49	0.77
10	5	1802	26	30	1800.00	1800.00	6026	0.02	0.17
10	10	1802	30	30	245.17	1147.26	2161	0.01	0.01
20	1	3605	0	0	1800.00	1800.00	17,460	-	-
20	5	3605	15	29	1800.00	1800.00	13,276	0.14	0.22
20	10	3605	29	30	1437.18	1800.00	5692	0.01	0.08
50	1	9041	0	0	1800.00	1800.00	12,253	-	-
50	5	9041	0	11	1800.00	1800.00	27,617	-	0.21
50	10	9041	14	27	1800.00	1800.00	13,538	0.10	0.12
100	1	18,083	0	0	-	1800.00	0	-	-
100	5	18,086	0	0	1800.00	1800.00	31,692	-	-
100	10	18,086	0	11	1800.00	1800.00	23,081	-	0.14

, respectively.

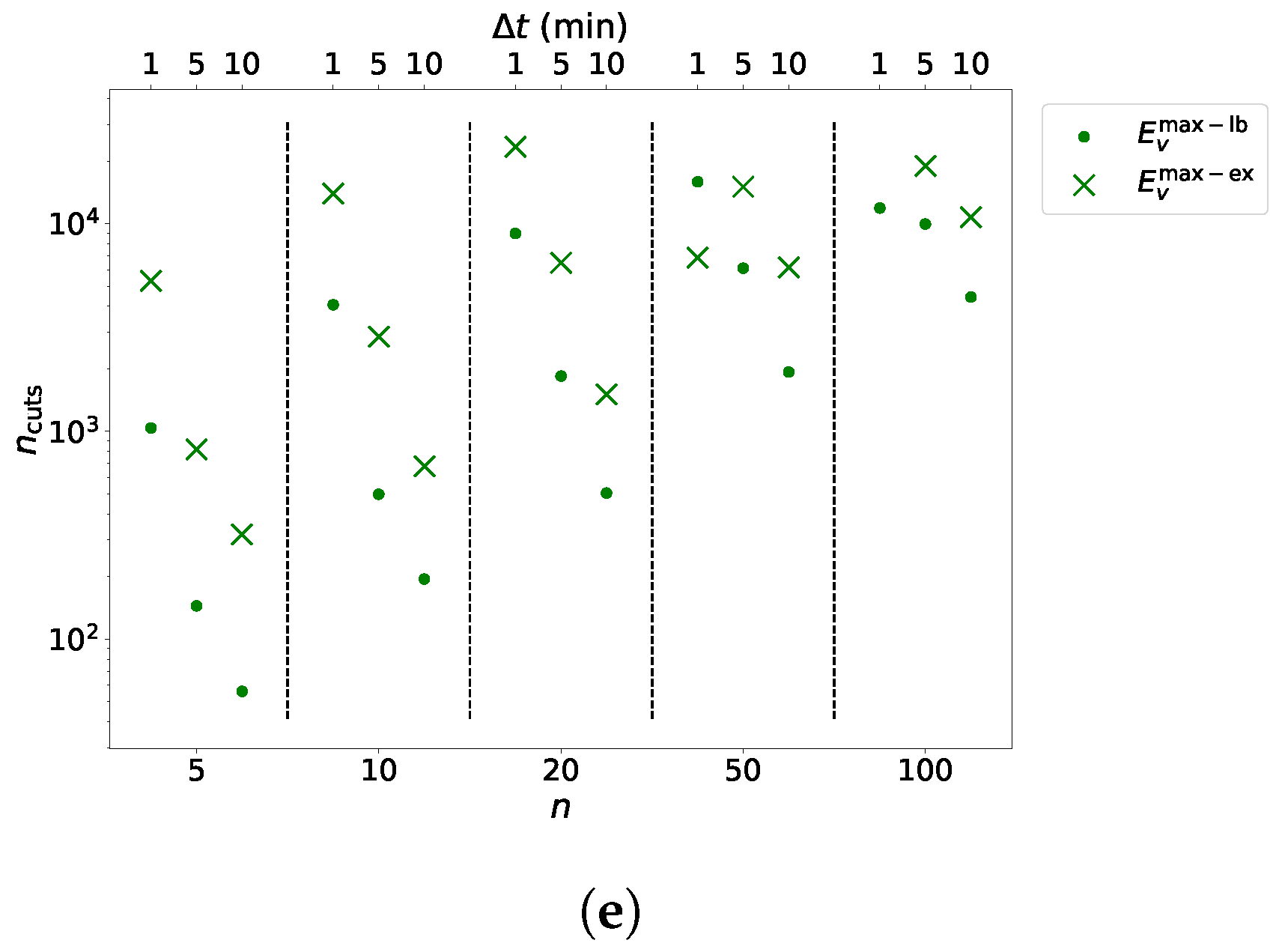
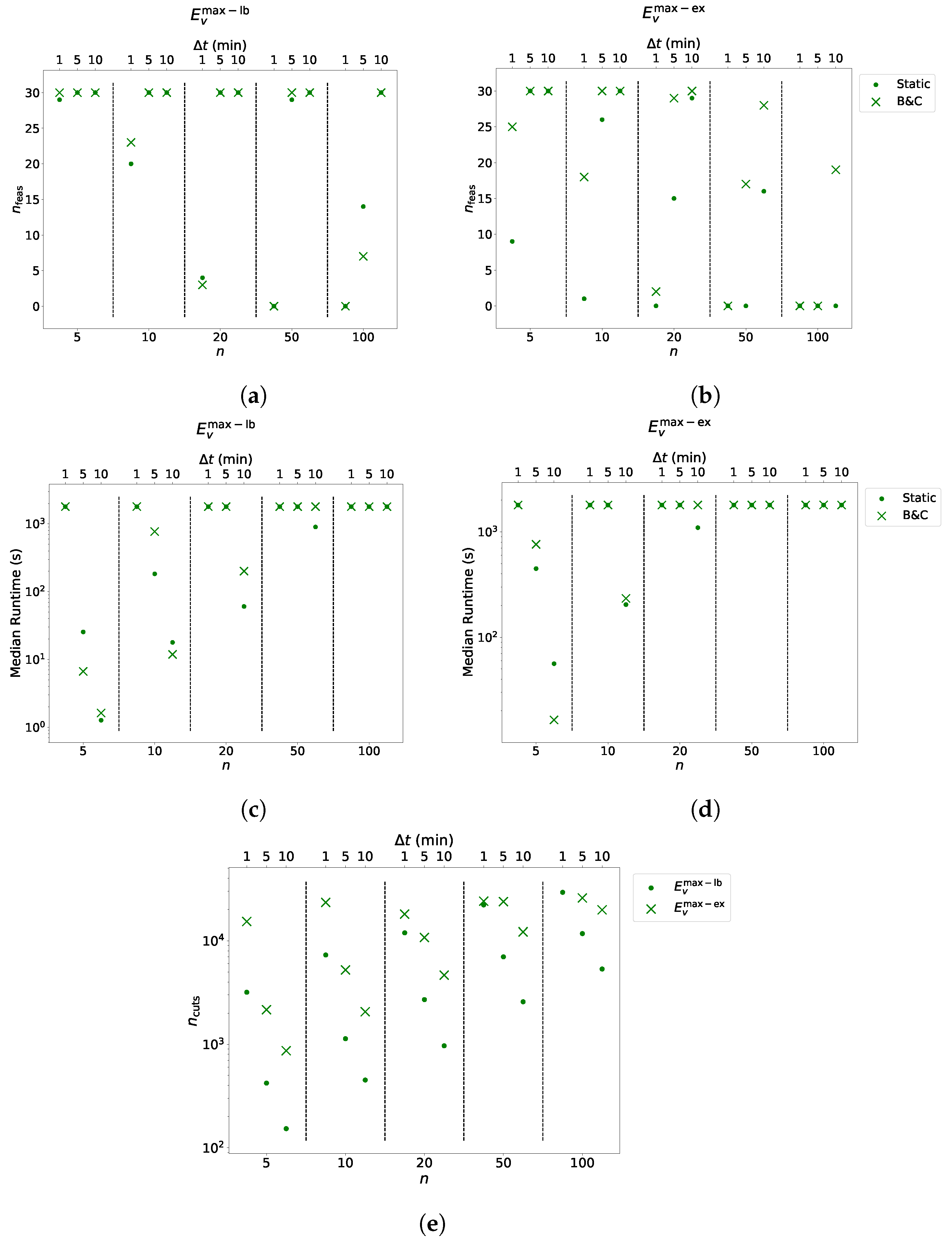
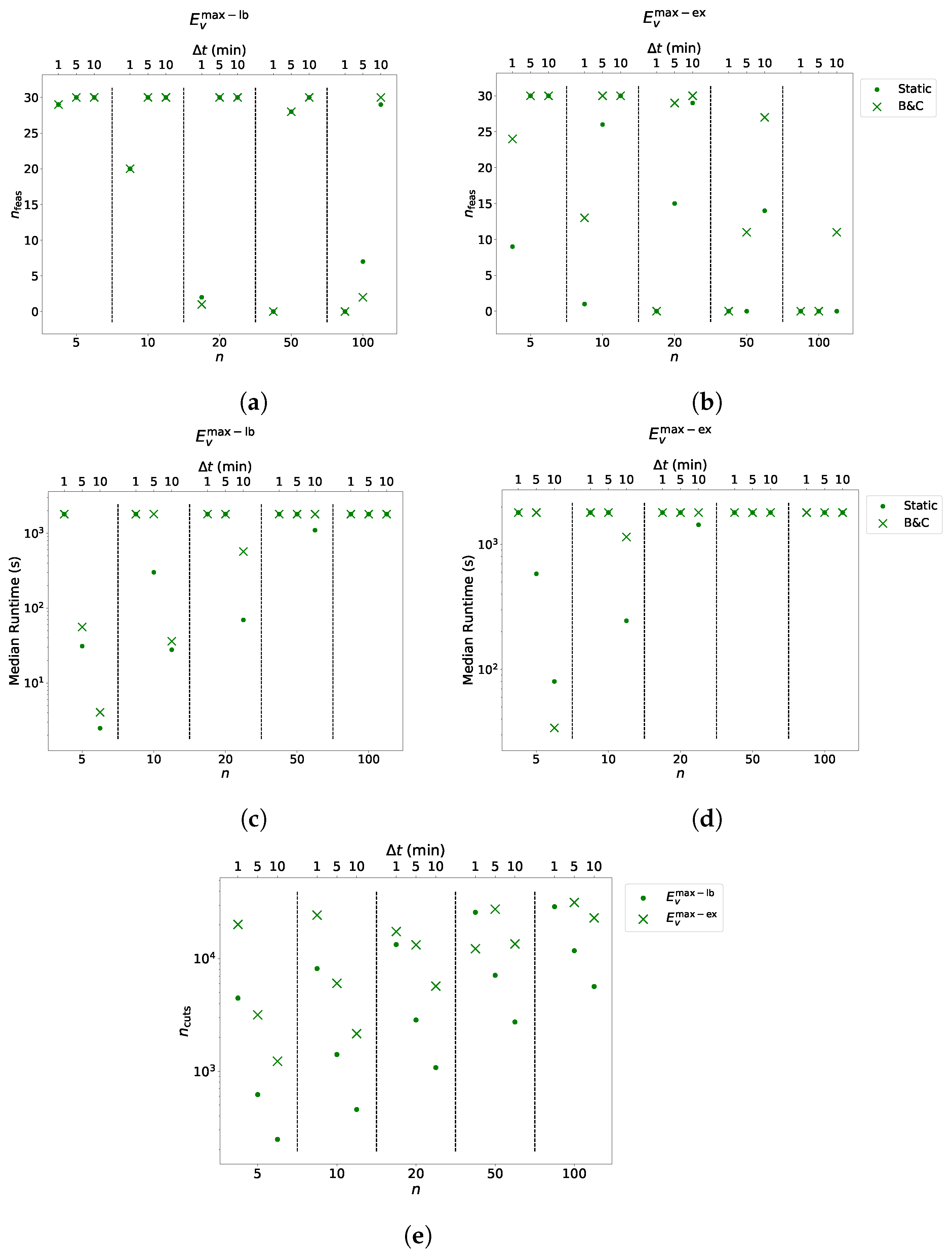
Columns, $n_{\mathrm{seg}}$ denote the total number of piecewise linear segments functions $E_v^{max}$ consist of, summed over all n vehicles of an instance. Columns $n_{\mathrm{feas}}$ indicate the numbers of instances per group to which feasible solutions have been found, and columns “Runtime” list the median computation times per group. Again, $n_{\mathrm{cuts}}$ refers to the total number of cuts added within B & C. The last columns indicate the finally remaining optimality gaps between lower and upper bounds as reported by Gurobi.

These gaps are calculated as the absolute difference between the respective upper and lower bounds divided by the upper bound. Moreover, for visual representation of the number of feasibly solved instances, the median runtimes, and the number of added cuts within B & C see Figure 7, Figure 8 and Figure 9.

Only gaps of instances with a feasible solution are considered. For parameter combinations without gaps (marked with “-”), no feasible solution has been found for any instance within the time limit. For parameter combinations where no runtime is reported, all corresponding runs terminated due to an out-of-memory error. More detailed results can be found in Appendix A where also the number of instances solved to optimality as well as standard deviations for runtimes, and the numbers of cuts are reported.

Opposed to EVS-SOC-LIN, not all instances could be solved by the EVS-SOC-GLIN variants within the time limit. Considering the results with $P^{\mathrm{gridmax}}=10n$, one can notice that the B & C approach shows performance benefits, as the approach was able to always find feasible solutions to as many or more instances than the static approach. It is difficult to compare the quality of the solutions obtained by each approach as the static approach sometimes found fewer feasible solutions. For groups for which both approaches could obtain feasible solutions to all instances, the quality of the generated solutions was almost identical. Moreover, except for two instance groups, the B & C approach was either as fast or faster than the static approach.

For the results with $P^{\mathrm{gridmax}}=25n$, the runtime performance benefit of B & C is still noticeable for small n; however, it is not as strong as for $P^{\mathrm{gridmax}}=10n$. Moreover, for $E_v^{\max -\mathrm{lb}}$ the number of feasible solutions found by the static approach is, except for one group, never worse than for B & C. Though, for $E_v^{\max -\mathrm{ex}}$ B & C still yielded significantly more feasible solutions.

A similar observation can be made for $P^{\mathrm{gridmax}}=40n$. For $P^{\mathrm{gridmax}}=40n$, the static approach has a better runtime with almost all parameter configurations.

A possible explanation for this observation seems to be that, for $P^{\mathrm{gridmax}}=10n$, the charging energy of a vehicle v is more limited by $P^{\mathrm{gridmax}}$ than by $E_v^{max}$. Initial solutions of B & C will then violate Constraints (14) less often, which implies spending less time for the separation of cuts. This presumption is supported by considering the number of added cuts. Fixing n and $\Delta t$, one can observe that, with growing $P^{\mathrm{gridmax}}$, clearly more cuts are added.

When comparing $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$ for any fixed $P^{\mathrm{gridmax}}$, n, and $\Delta t$, $E_v^{\max -\mathrm{ex}}$ has more segments than $E_v^{\max -\mathrm{lb}}$ due to the nature of its computation. For $E_v^{\max -\mathrm{lb}}$, smaller $\Delta t$ values imply a higher number of $E_v^{\max -\mathrm{lb}}$ segments. For a fixed n and $\Delta t$, the larger number of $E_v^{\max -\mathrm{ex}}$ segments comes with fewer feasible solutions and higher runtimes for the static approach and the B & C.

In general, regardless of $P^{\mathrm{gridmax}}$, all reported median gaps for both approaches are below $0.2\%$. Moreover, while the B & C approach usually finds a higher number of feasible solutions, the static approach finds generally more optimal solutions, as can be seen in Appendix A.

In order to see how both solution approaches to EVS-SOC-GLIN perform on instances with fewer piecewise linear segments in $E_v^{max}$, we conduct similar experiments using the approximations of $P_v^{max}$ with five segments. For this, we only consider $E_v^{\max -\mathrm{lb}}$, since the number of $E_v^{\max -\mathrm{ex}}$ segments does not depend on the number of $P_v^{max}$ segments. Experimental results for $P^{\mathrm{gridmax}}=25n$ are given in

Table 6. EVS-SOC-GLIN results for solving the static model versus B & C with $E_v^{\max -\mathrm{lb}}$ based on five-segment piecewise linear approximations of the original $P_v^{max}$ functions, $P^{\mathrm{gridmax}}=25n$.

n	$\mathbf{\Delta }\mathit{t}$ (min)	${\mathit{n}}_{\mathbf{seg}}$	${\mathit{n}}_{\mathbf{feas}}$		Runtime (s)		${\mathit{n}}_{\mathbf{cuts}}$	%-gap
		Mean			Median		Median	Median
			Static	B & C	Static	B & C	B & C	Static	B & C
$E_v^{\max -\mathrm{lb}}$
5	1	40	30	30	60.14	19.63	387	0.01	0.01
5	5	46	30	30	2.40	1.98	88	0.01	0.01
5	10	43	30	30	0.64	1.13	42	0.00	0.01
10	1	80	30	30	509.28	1800.00	1162	0.01	0.02
10	5	92	30	30	11.01	8.34	232	0.01	0.01
10	10	87	30	30	1.49	2.68	118	0.01	0.01
20	1	160	12	30	1800.00	1800.00	2488	0.03	0.06
20	5	185	30	30	54.58	61.09	516	0.01	0.01
20	10	174	30	30	5.03	7.45	217	0.01	0.01
50	1	398	0	12	1800.00	1800.00	5598	-	0.24
50	5	459	30	30	640.74	1800.00	1556	0.01	0.02
50	10	433	30	30	37.23	36.95	624	0.01	0.01
100	1	798	0	0	1800.00	1800.00	9312	-	-
100	5	921	30	30	1800.00	1800.00	3237	0.01	0.06
100	10	871	30	30	112.16	84.83	1360	0.01	0.01

. The table shows, again, the total number of piecewise linear segments of $E_v^{\max -\mathrm{lb}}$ ($n_{\mathrm{seg}}$), the number of instances for which a feasible solutions was found within the time limit ($n_{\mathrm{feas}}$ ), the median computation time (“Runtime”), the total number of cuts added within B & C $\left(n_{\mathrm{cuts}}\right)$, and optimality gaps (%-gap) of the generated solutions.

For each parameter group, B & C always finds at least as many feasible solutions as the static approach. When the static and the B & C approaches find the same number of feasible solutions, the resulting gaps are almost identical; however, the solutions of the static variant are typically slightly better than the ones of B & C. In terms of computation times, no approach was significantly faster than the other.

Due to the smaller number of segments in the $P_v^{max}$ functions and consequently also simpler $E_v^{\max -\mathrm{lb}}$ functions, a higher number of feasible as well as optimal solutions could generally be found, when comparing Table 4 and Table 6. Moreover, the impact of fewer $P_v^{max}$ segments is also observable when we consider the median runtimes and the number of added cuts. For almost all parameter combinations of n and $\Delta t$, fewer $P_v^{max}$ segments lead to lower median runtimes and fewer cuts.

Charging Cost Differences & Charging Errors

While the simpler approximations of the original $P_v^{max}$ functions lead to shorter runtimes, there is clearly a tradeoff concerning the precision of the model, introduced errors, and final solution qualities. We take a closer look on these aspects in the following. Specifically, we are interested in the error made when using $E_v^{\max -\mathrm{lb}}$ instead of $E_v^{\max -\mathrm{ex}}$ and the error between the five-segment $P_v^{max}$ approximation compared to the original $P_v^{max}$. For this purpose, we evaluate EVS-SOC-GLIN on four different $E_v^{max}$ functions: $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$, each based on the five-segment $P_v^{max}$ approximation and the original $P_v^{max}$.

As we want to measure the impact of the different charging curves on the charging costs, we select a high $P^{\mathrm{gridmax}}$ value of $40n$ as, in this case, the variable maximum charging power constraints have higher impacts. Only results on instances solved to optimality are reported. We only consider instances where an optimal solution for all four $E_v^{max}$ functions was found. Parameter combinations where no such instances exist are omitted. The mean charging costs can be found in

Table 7. Objective value comparison using EVS-SOC-GLIN and different $E_v^{max}$ functions based on the five-segment $P_v^{max}$ approximation and the original $P_v^{max}$; $P^{\mathrm{gridmax}}=40n$.

n	$\mathbf{\Delta }\mathit{t}$ (min)	${\mathit{n}}_{\mathbf{opt}}$	Charging Costs
			${\mathit{E}}_{\mathit{v}}^{\mathbf{max}-\mathbf{lb}}$	${\mathit{E}}_{\mathit{v}}^{\mathbf{max}-\mathbf{ex}}$	%-gap
			Mean	Mean	Mean	StdDev
Original $P_v^{max}$
5	1	2	109.08	108.97	0.10	0.01
5	5	25	209.40	208.83	0.29	0.18
5	10	30	227.10	225.78	0.64	0.40
10	5	11	374.24	372.98	0.34	0.13
10	10	28	447.51	445.05	0.59	0.35
20	10	19	882.53	877.33	0.60	0.30
5-segment approx. $P_v^{max}$
5	1	2	109.10	108.98	0.10	0.01
5	5	25	209.38	208.82	0.29	0.17
5	10	30	227.11	225.77	0.64	0.41
10	5	11	374.14	372.92	0.33	0.13
10	10	28	447.44	445.04	0.57	0.32
20	10	19	882.39	877.26	0.60	0.30

. The charging cost %-gaps are calculated by $100\%·\left(\right|E_v^{\max -\mathrm{ex}}-E_v^{\max -\mathrm{lb}}\left|\right)/E_v^{\max -\mathrm{ex}}$.

Observe that, for fixed $\Delta t$ and varying n, the charging cost gap between $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$ does not change significantly. It seems that the difference in charging costs mainly depends on $\Delta t$. Specifically, one might notice that the charging cost gaps become smaller as $\Delta t$ decreases. Overall, the largest mean charging cost gap is 0.64%; the differences, therefore, seem to be negligible for practical purposes for the considered parameter groups. Not all instances could be solved to optimality (even when increasing the time limit), and hence the number of reported instances in some instance groups varies for each instance group. Therefore, to give a better idea about the distribution of the charging cost gaps, we additionally provide standard deviations to the charging cost gaps in Table 7. For groups with the same $\Delta t$, we can observe that the standard deviations are quite similar.

When comparing the five-segment $P_v^{max}$ approximation to the original $P_v^{max}$, the difference in charging costs is marginal, even for large instances. For example, consider $n=20,\Delta t=10$ min and $E_v^{\max -\mathrm{ex}}$ and observe that the objective value differs on average by about $0.07$ cents only between the original $P_v^{max}$ and the five-segment approximation. This insight appears to be particularly relevant, since it shows that approximating $P_v^{max}$ with a lower number of linear pieces is reasonable for practice.

When realizing a charging plan in practice with a different $E_v^{max}$ function than used for scheduling, the specified target SOCs $s_v^{\mathrm{dep}}$ might not be reached for some vehicles. We measure this error by generating an optimal charging schedule with $E_v^{\max -\mathrm{ex}}$ and simulating the actual maximum energy function with $E_v^{\max -\mathrm{lb}}$. In the simulation, the actually charged energy is set to the minimum from the corresponding planned charged energy and the actual maximum energy function.

The resulting mean deviation from the target SOC in percent, the mean charging error, can be seen in

Table 8. Charging error comparison when scheduling with $E_v^{\max -\mathrm{ex}}$ using EVS-SOC-GLIN and realizing the schedule with $E_v^{\max -\mathrm{lb}}$; $P^{\mathrm{gridmax}}=40n$.

n	$\mathbf{\Delta }\mathit{t}$ (min)	${\mathit{n}}_{\mathbf{opt}}$	Mean Charging Error (% SOC)
			Original ${\mathit{P}}_{\mathit{v}}^{max}$		5-seg. Approx. ${\mathit{P}}_{\mathit{v}}^{max}$
			Mean	StdDev	Mean	StdDev
5	1	3	0.23	0.08	0.21	0.08
5	5	25	1.14	0.26	1.06	0.28
5	10	30	2.01	0.58	1.94	0.60
10	5	12	1.14	0.16	1.18	0.18
10	10	29	2.03	0.45	2.03	0.46
20	10	20	2.01	0.29	1.97	0.34

. For a single instance, we determined the mean charging error over all vehicles, whereas, for an instance group, we again report the mean and the standard deviation of these mean charging errors from the individual instances.

Similarly to before, it seems that the size of the charging error mainly depends on $\Delta t$: Fixing the number of vehicles n, the mean charging error decreases with smaller $\Delta t$, the number of vehicles does not seem to influence the mean charging error for fixed $\Delta t$.

6.3. Comparison of EVS-SOC-LIN and EVS-SOC-GLIN

Charging cost gaps between solutions of formulation EVS-SOC-LIN and EVS-SOC-GLIN can be found in Figure 10. As before, we only consider instances that were solved to optimality. For EVS-SOC-LIN, we use $E_v^{\max -\mathrm{lb}}$ based on the concave $P_v^{max}$, whereas, for EVS-SOC-GLIN, we use $E_v^{\max -\mathrm{lb}}$ based on $P_v^{max}$ with five segments. The grid capacity $P^{\mathrm{gridmax}}$ is again set to $40n$. Charging cost gaps are calculated by dividing the difference of the EVS-SOC-GLIN objective values from the EVS-SOC-LIN objectives by the EVS-SOC-GLIN objective values. For $n\in \{50,100\}$ and $\Delta t=1$ min, all mean charging cost gaps are zero; therefore, the respective bars are not shown in the figure.

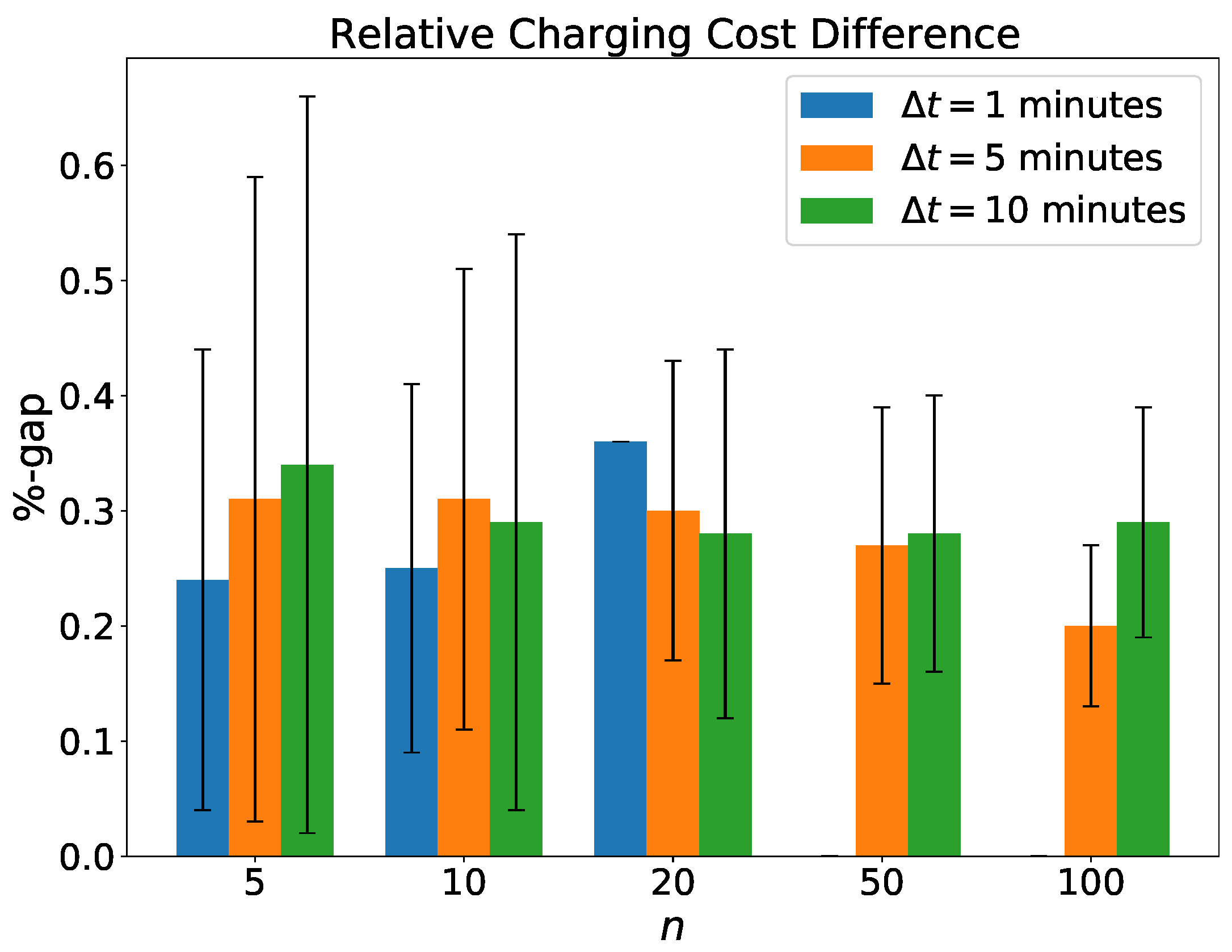
Comparing the gaps of both formulations, one can notice that the charging costs of solutions generated by EVS-SOC-LIN are slightly too optimistic, underestimating the actual costs. In comparison to the more exact EVS-SOC-GLIN, the costs of the solutions generated by EVS-SOC-LIN are lower by at most by 0.35%. Moreover, there are no significant differences between the charging cost gaps when varying n or $\Delta t$ values. When it comes to computation times, both variants of EVS-SOC-LIN are significantly faster than any EVS-SOC-GLIN variant, as we have seen before in Table 2 and Table 4.

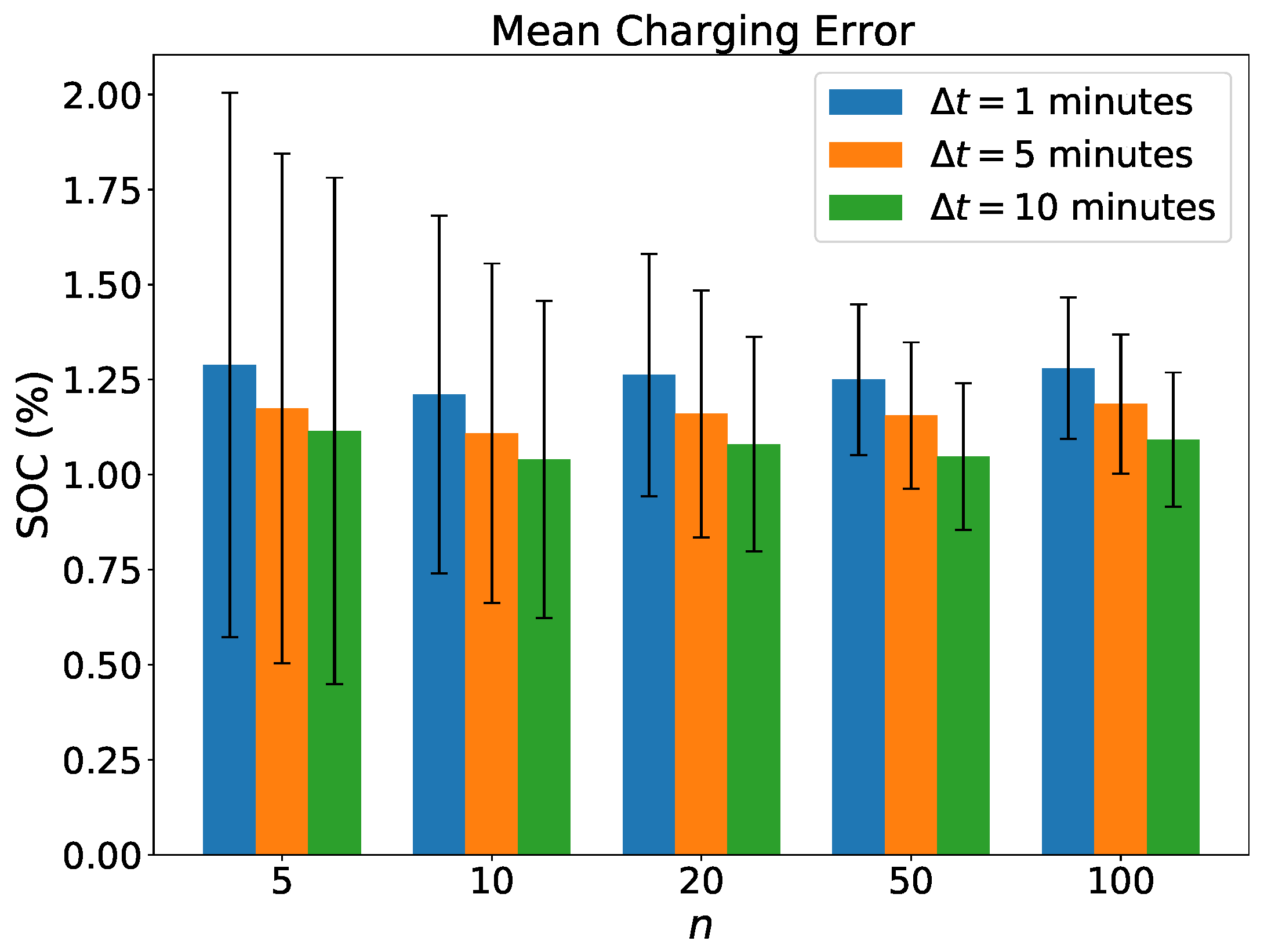
For the exact same setting as above, we also measure the charging error when scheduling with the convex $E_v^{\max -\mathrm{lb}}$ used in EVS-SOC-LIN and realizing the plan with the, in general, nonconvex $E_v^{\max -\mathrm{lb}}$ used in EVS-SOC-GLIN. The mean charging error is shown in Figure 11. For a fixed $\Delta t$, the mean charging error does not significantly change for a varying number of vehicles n. However, for a fixed number n, the mean charging error grows with decreasing $\Delta t$.

An explanation for this behavior seems to be that on instances with smaller $\Delta t$, solutions tend to be more precise in terms of the error induced by the time discretization. Therefore, the difference between a convex and nonconvex $E_v^{max}$ function could have more impact on solutions of instances with small $\Delta t$ values. Overall, the mean charging cost difference does not exceed 1.5% SOC for any n and any $\Delta t$ and, thus, may be negligible in practice.

6.4. Model Based Predictive Control Simulations

For the rolling horizon scenarios, we conduct experiments using formulations EVS-SOC-LIN and EVS-SOC-GLIN. We use $E_v^{\max -\mathrm{lb}}$ for both formulations, but, for EVS-SOC-LIN, the corresponding concave approximation of $P_v^{max}$, whereas, for EVS-SOC-GLIN, the five-segment approximation of $P_v^{max}$. $P^{\mathrm{gridmax}}$ is set to $40n$. The results of the experiments are shown in

Table 9. Rolling horizon charging cost difference for EVS-SOC-LIN vs. EVS-SOC-GLIN using $E_v^{\max -\mathrm{lb}}$; $P^{\mathrm{gridmax}}=40n$.

n	$\mathbf{\Delta }\mathit{t}$ (min)	Charging Cost Difference
		Absolute (Cent)		Relative (%)
		Mean	StdDev	Mean	StdDev
5	5	0.97	0.73	0.22	0.16
5	10	0.91	0.60	0.20	0.12
10	5	1.75	0.99	0.20	0.11
10	10	1.78	0.77	0.20	0.08
20	5	3.78	1.34	0.21	0.08
20	10	3.80	1.03	0.21	0.06
50	5	9.14	2.42	0.20	0.05
50	10	9.39	2.64	0.21	0.06
100	5	24.42	2.40	0.27	0.03
100	10	19.96	4.82	0.22	0.05

. Absolute charging cost differences are determined by subtracting the EVS-SOC-GLIN objective values from the EVS-SOC-LIN objective values. The relative charging costs are based on the absolute charging costs divided by the objective values of EVS-SOC-GLIN.

Similarly to before, for fixed n and $\Delta t$, the charging costs of EVS-SOC-LIN and EVS-SOC-GLIN only differ marginally. The maximum gap is 0.27% for $n=100$ and $\Delta t=5$ min. As expected, the absolute charging cost difference increases with a higher number of vehicles. The gaps, however, seem to stay in the same order of magnitude for growing n.

7. Conclusions

We formally introduced the EVS-SOC problem in which we put particular focus on dealing with vehicle-specific SOC-dependent maximum charging power limitations. We addressed the issue that the maximum charging power $P_v^{max}$ may be regulated within a single time step in a time discretized solution approach by turning toward considering the maximum amount of energy that can be charged in a time step. To this end, we proposed an exact derivation $E_v^{\max -\mathrm{ex}}$ as well as a simpler lower bound $E_v^{\max -\mathrm{lb}}$. One should keep in mind that the gap between $E_v^{\max -\mathrm{lb}}$ and $E_v^{\max -\mathrm{ex}}$ decreases with smaller time step duration $\Delta t$. We recall that charging schedules generated with $E_v^{\max -\mathrm{lb}}$ are guaranteed to be realizable in practice, whereas schedules generated with $E_v^{\max -\mathrm{ex}}$ help us with the estimation of the charging cost differences and charging errors induced by the time discretization.

Let us recapitulate the most important experimental results. Two different MILP formulations, EVS-SOC-LIN and EVS-SOC-GLIN, were proposed, where EVS-SOC-LIN relies on the assumption that $E_v^{max}$ is concave. When taking a closer look at EVS-SOC-LIN, both the static as well as the cutting plane variant are quite fast. Compared to EVS-SOC-GLIN, EVS-SOC-LIN performs an order of magnitude faster in our experiments. Considering the runtime difference between the static and the cutting plane approach, a substantial performance benefit of the latter can be observed. Moreover, we have seen that the runtime of the cutting plane approach scales better with larger numbers of vehicles or decreasing $\Delta t$ values. Its advantages become even more visible when the maximum charging energy of a vehicle has to be exploited, i.e., a large number of cuts has to be separated.

Concerning the static solution approach and the B & C for solving EVS-SOC-GLIN, we found that B & C performs better for instances with a small number of vehicles. For larger instances, however, the static variant is usually superior in terms of runtime. It also shows performance advantages for larger grid capacities. The results of the experiments indicate that the B & C is slower than the static variant when a large number of cuts has to be separated. Nevertheless, there are cases where B & C is faster—for example, when $E_v^{max}$ consists of many linear segments. Additionally, we realized that B & C finds more feasible solutions in the majority of the experiments when solving to optimality is not possible anymore within the runtime limit. Overall, for both EVS-SOC-GLIN solution approaches, fewer $P_v^{max}$ segments usually clearly reduce the runtime.

Different approximations of the maximum charging power (e.g., piecewise linear approximation or convex hull approximation), as well as the maximum charging energy ($E_v^{\max -\mathrm{lb}}$, $E_v^{\max -\mathrm{ex}}$) have been proposed. We studied the charging cost differences and the charging errors induced by these approximations. Regarding the charging cost differences, it turned out that there were only marginal charging cost differences between schedules generated with $E_v^{\max -\mathrm{lb}}$ and schedules generated with $E_v^{\max -\mathrm{ex}}$.

The number of vehicles did not show any noticeable impact on the cost differences for this comparison. Naturally, a smaller step duration $\Delta t$ reduces the charging cost differences. Moreover, in the case of our benchmark instances, the approximation of $P_v^{max}$ with five piecewise linear segments does not have any noticeable impact on the charging costs, despite the rather complex original functions. We also inspected the charging cost differences when generating schedules based on the original $P_v^{max}$ function and its concave approximation. We found that the charging cost differences were quite small; the mean differences did not exceed 0.35% for any shown parameter group.

As already mentioned, approximating the maximum charging energy might lead to the issue that vehicles do not reach their desired target SOCs. To measure this effect, we generated charging schedules with $E_v^{\max -\mathrm{ex}}$ and simulated the actual charging with $E_v^{\max -\mathrm{lb}}$. Experimental results demonstrated that the mean charging error did not exceed 2.1% SOC even for $\Delta t=10$ min.

For these experiments, we also detected a correlation between the size of $\Delta t$ and the charging error, more specifically, the mean charging error decreases with smaller $\Delta t$. In another simulation, we considered the mean charging error when generating a charging schedule based on a concave $P_v^{max}$ approximation and realizing it with the original $P_v^{max}$. The mean charging error was rather small again, the mean deviation from the vehicles’ target SOCs were, at most, 1.5%.

To see whether the concave approximation of $P_v^{max}$ accumulates large charging cost differences in a whole day scenario, we conducted model-based predictive control simulations with the original $P_v^{max}$ and its concave approximation. The relative charging cost gaps were even smaller with a maximum value 0.27% for 100 vehicles and $\Delta t=5$ min.

Overall, where we utilize one of the formulations within a model based predictive control strategy, we recommend the usage of EVS-SOC-LIN or EVS-SOC-GLIN together with a reasonably small $\Delta t$ value of few minutes, in order to reduce errors introduced by time discretization. Depending on whether EVS-SOC-GLIN is performant enough for a given application setting (i.e., it finds a charging schedule within the re-optimization interval), its usage is advised to reduce the danger of significant charging cost differences and charging errors. It seems promising to approximate $P_v^{max}$ with five to ten piecewise linear segments to improve the runtime in this scenario.

In case EVS-SOC-GLIN does not find charging schedules in a reasonable time, one might fall back to EVS-SOC-LIN and its cutting plane approach to rapidly generate charging schedules for a concave approximation of $P_v^{max}$. The introduced errors are usually negligible as we have seen.

In future work, it would be interesting to investigate whether the runtime of solving EVS-SOC-GLIN can be further improved. As we have seen, B & C is frequently slower than the static variant. A more detailed polyhedral study of the model may reveal additional strengthening inequalities. Concerning the computational complexity of EVS-SOC, it is an open question of whether or not the problem is NP-hard if $P_v^{max}$ is a general nonconcave function. Another aspect worth pursuing is the question of whether known vehicle arrival times have a significant impact on the charging costs of a rolling horizon schedule. In the presented scenario, successively arriving vehicles are simulated; however, they are not incorporated into the schedule before arrival at the charging station. One may expect that arrival times known in advance lead to better exploitation of cheap charging time slots and, therefore, come along with cheaper total charging costs.

A further direction of future work should be the consideration of uncertainties, e.g., in the future power limits or in the future occupation of charging stations. Furthermore it would be interesting to study the effect of the rescheduling interval on charging costs and charging errors in the rolling horizon context. Last, but not least, it would be interesting to consider a problem variant in which the discharging of vehicles is allowed in order to enable the mutual charging of EVs. This idea has already been mentioned in [26]; however, its impact on the total charging costs has not yet been studied. One could further extend the model by allowing the charging station to supply energy to the electricity grid in exchange for a monetary reward.