Statistical Feature Extraction Combined with Generalized Discriminant Component Analysis Driven SVM for Fault Diagnosis of HVDC GIS
Abstract
:1. Introduction
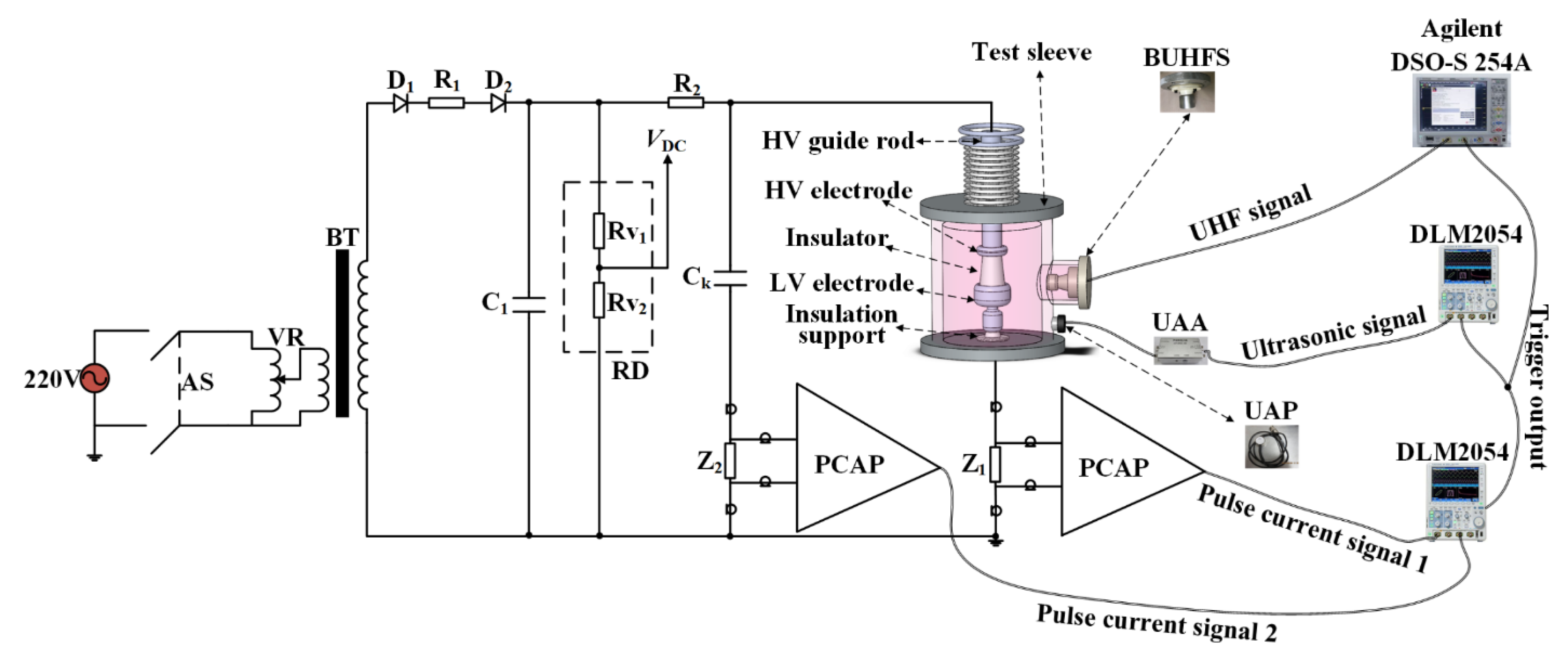
2. Experimental Platform and Insulation Defects
2.1. Experimental Platform
2.2. Insulation Defects
3. Statistical Features Extraction from the Inherent Physical Quantities
- A.
- Hn(q)
- B.
- Hn(WP)
- C.
- Hn(Δq)
- D.
- Hn(ln(Δt))
- E.
- Hq(CP)
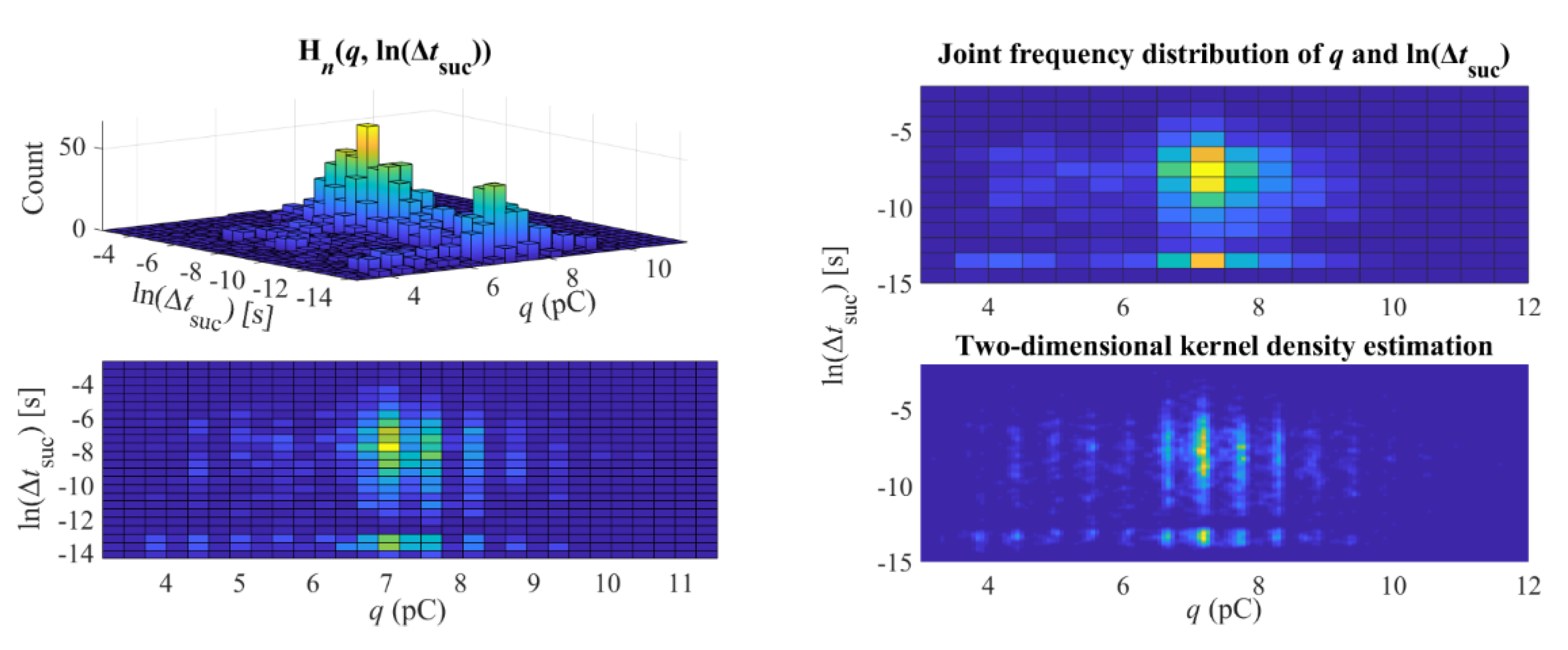
- F.
- Hqn(ln(Δtsuc))
- G.
- Hqmax(Δtsuc)
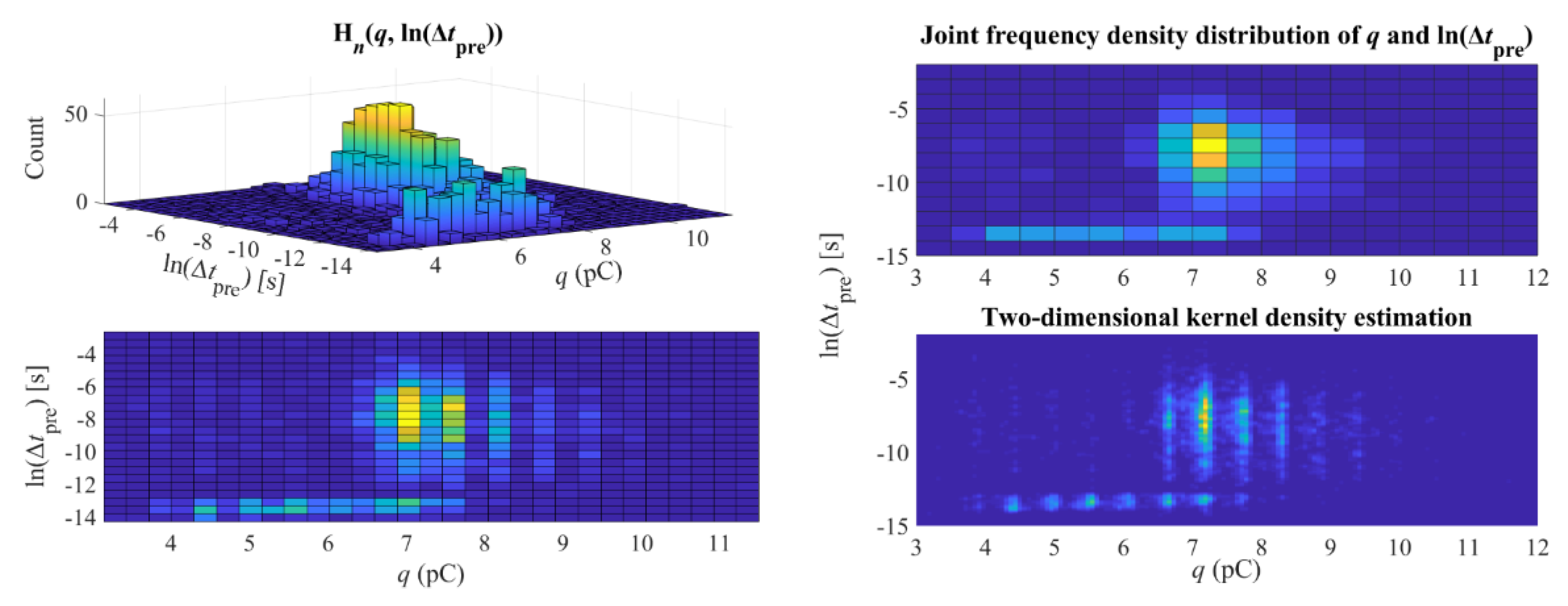
- H.
- Hqn(ln(Δtpre))
- I.
- Hqmax(ln(Δtpre))
- J.
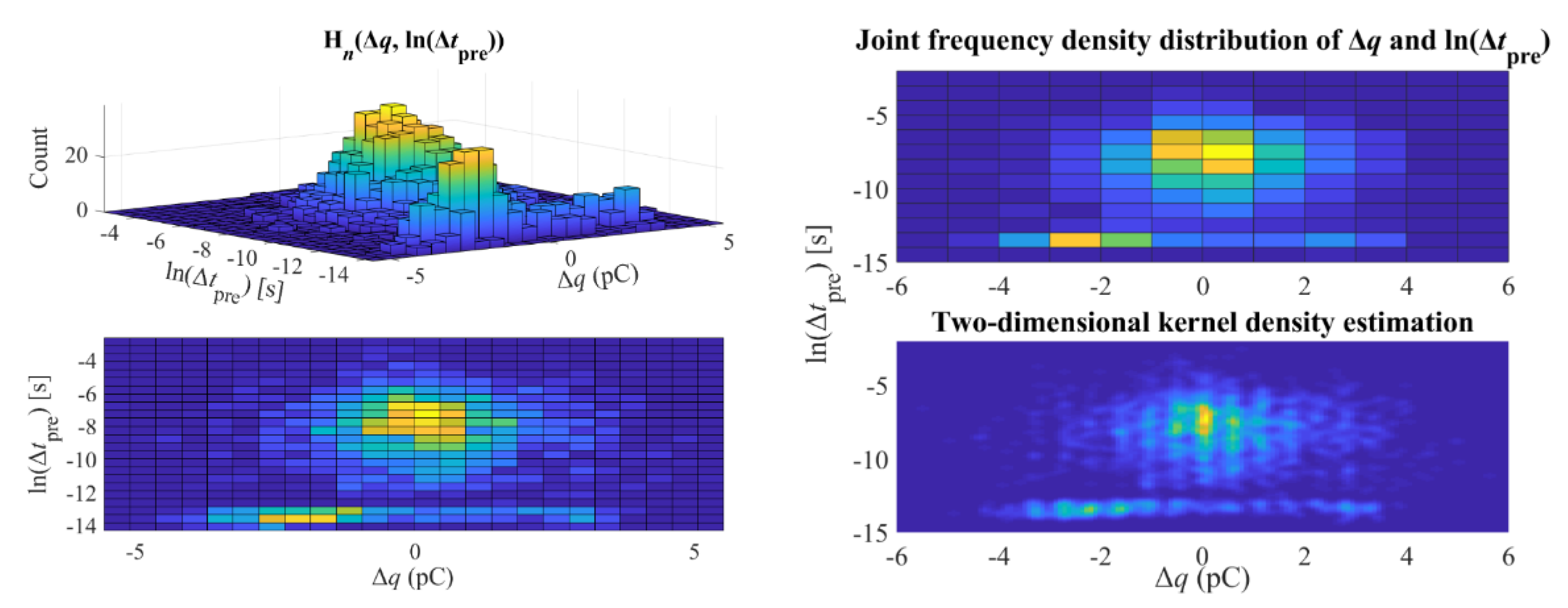
- Hn(q, ln(Δt))
- K.
- Hn(Δq,ln(Δt))
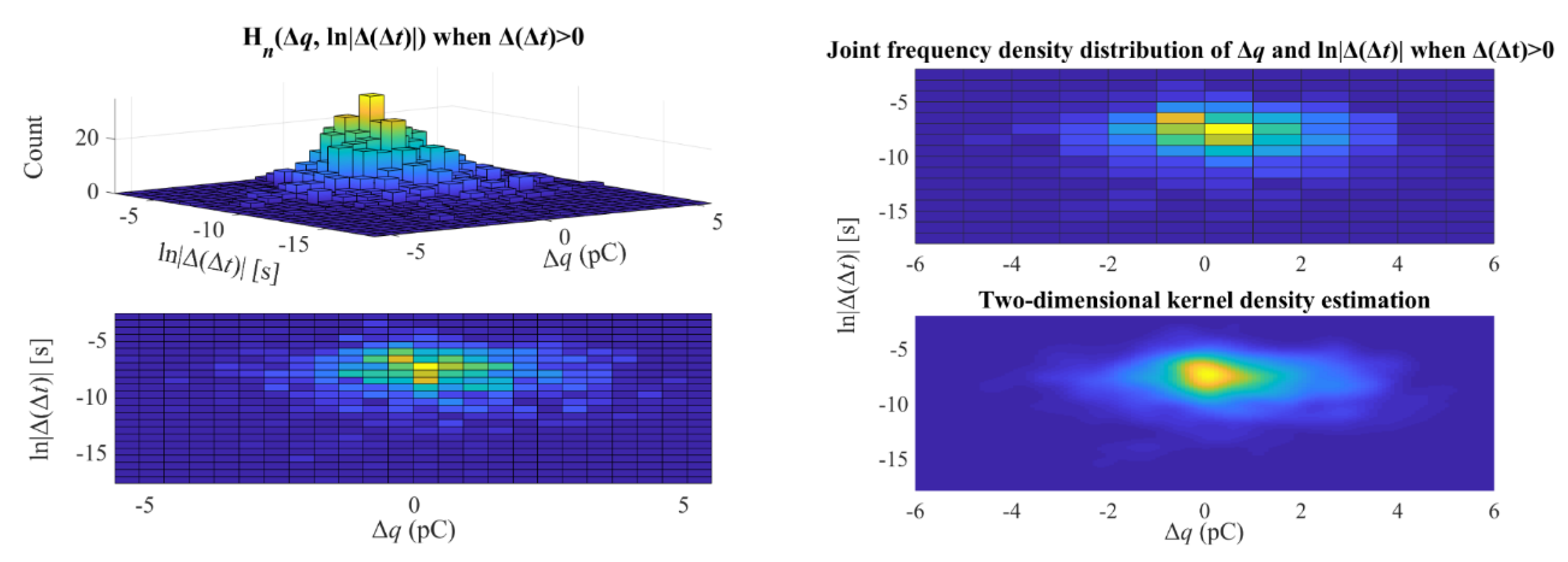
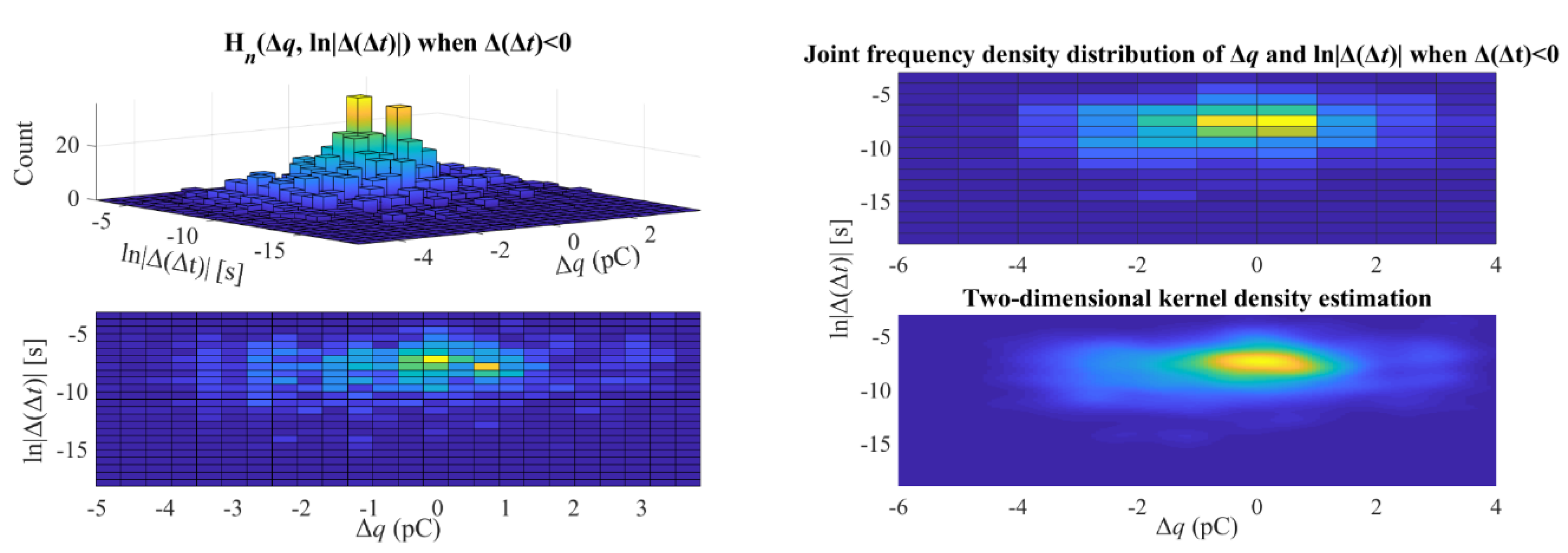
- L.
- Hn(Δq, ln|Δ(Δt)|)
4. GDCA and Its Kernelization Forms
- (0)
- Prepare Essential Parameters
- (0.1)
- Choose the projected dimensionality m;
- (0.2)
- Choose regularization parameters δ and ρ, which must satisfy the condition that δ > ρ, δ → 0+ and ρ → 0 (for simplicity, let ρ = αδ, δ → 0+ and α < 1).
- (1)
- Calculate the between-class scatter matrix SB, within-class scatter matrix SW, and center-adjusted scatter matrix SC
- (1.1)
- Use data preprocessing methods, such as standard normal density (SND) or min-max normalization (MMN), to preprocess the original recognition vectors [41];
- (1.2)
- Denote recognition vectors after preprocessing as xi∈ℝM×1 (i = 1, 2, ⋯, N), then calculate SB, SW and SC.
- (2)
- Calculate the projection matrix WGDCA
- (2.1)
- If m is not more than rank(SB), WGDCA is consisted of the eigenvectors of (SW + δI)−1(SC + ρI) corresponding to the rank(SB) larger eigenvalues arranged in descending order.
- (2.2)
- If m is larger than rank(SB), the signal-subspace projection matrix WPS is consisted of the eigenvectors of (SW + δI)−1(SC + ρI) corresponding to the rank(SB) larger eigenvalues arranged in descending order while the noise-subspace projection matrix WPN is consisted of the eigenvectors of (SW + δI)−1(SC + ρI) corresponding to the m-rank(SB) smaller eigenvalues arranged in ascending order. Finally, WGDCA = [WPS, WPN].
- (3)
- Normalize projection vectors
- (4)
- Calculate the feature sample matrix after projection
- (5)
- Whether to change the values of δ and ρ ? Return to 0.2 if yes and go to next step if no.
- (6)
- Whether to change m? Return to 0.1 if yes and output WGDCA and YGDCA if no.
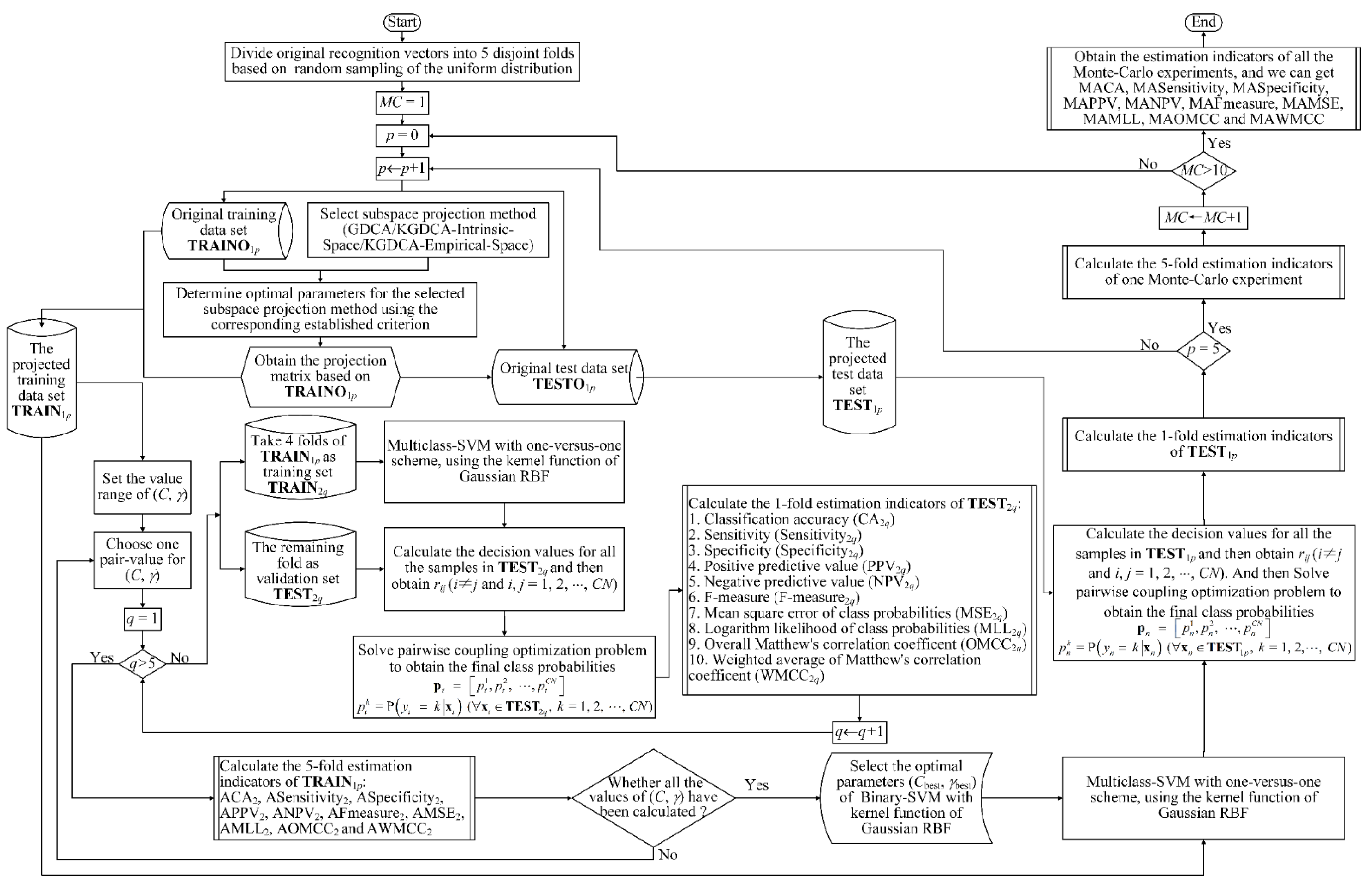
5. Results and Discussions
5.1. Test Strategy
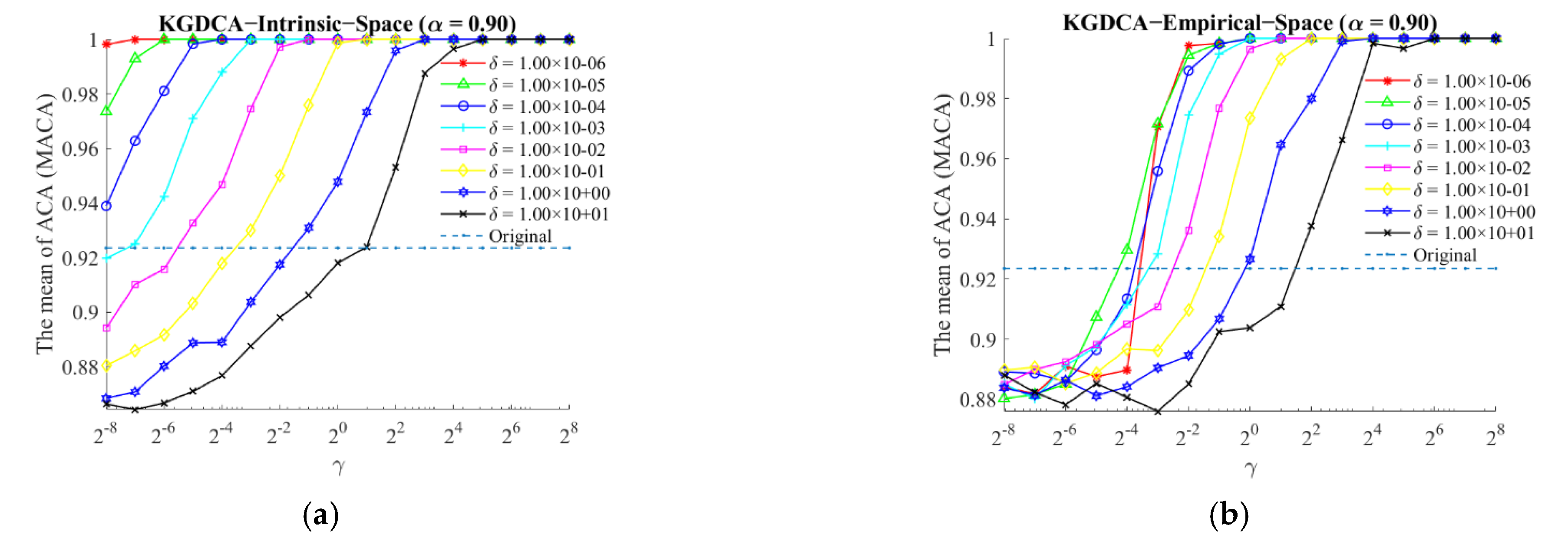
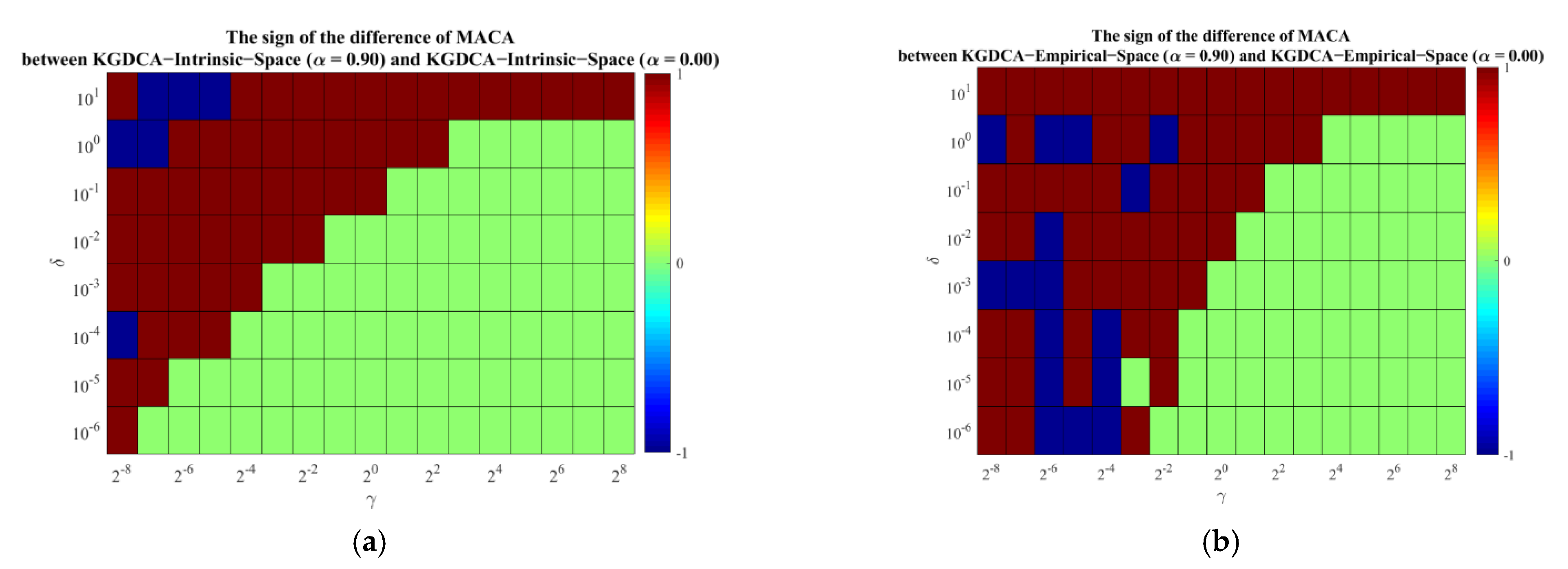
5.2. Criterion for Selecting Optimal Parameters of GDCA and Its Kernelization Forms
5.3. Recognition Effects of GDCA and Its Kernelization Forms Driven SVM
5.3.1. Recognition Effect of GDCA Driven SVM
5.3.2. Recognition Effect of GDCA’s Kernelization Forms Driven SVM
- ●
- Comparisons between KGDCA-Intrinsic-Space/KGDCA-Empirical-Space driven SVM and original SVM
- ●
- Comparisons between KGDCA-Intrinsic-Space/KGDCA-Empirical-Space driven SVM and GDCA driven SVM
- ●
- Effect of α on KGDCA-Intrinsic-Space/KGDCA-Empirical-Space driven SVM
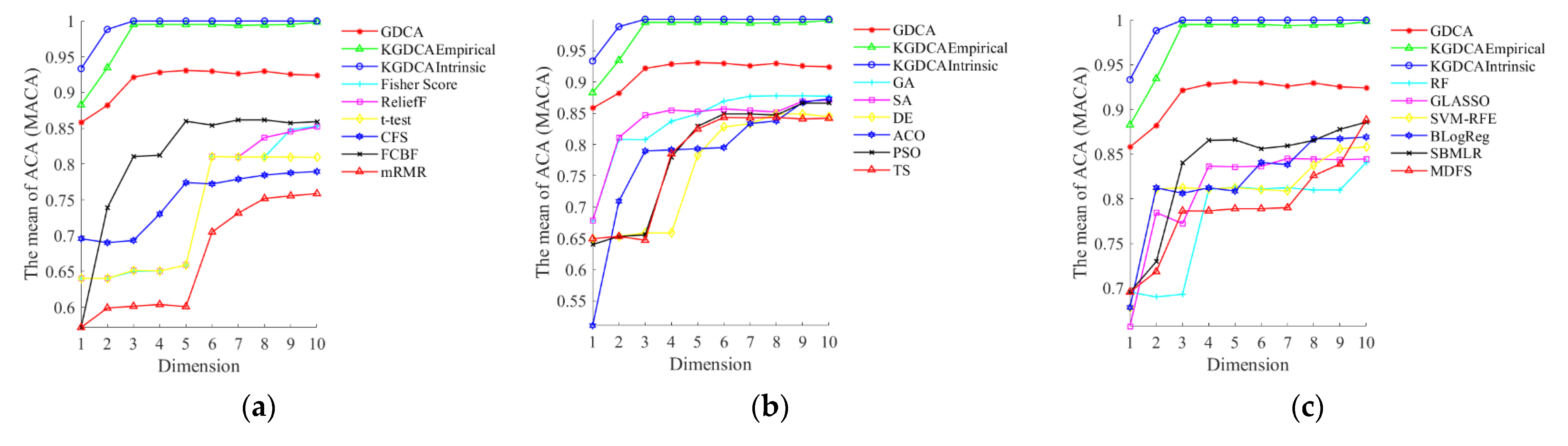
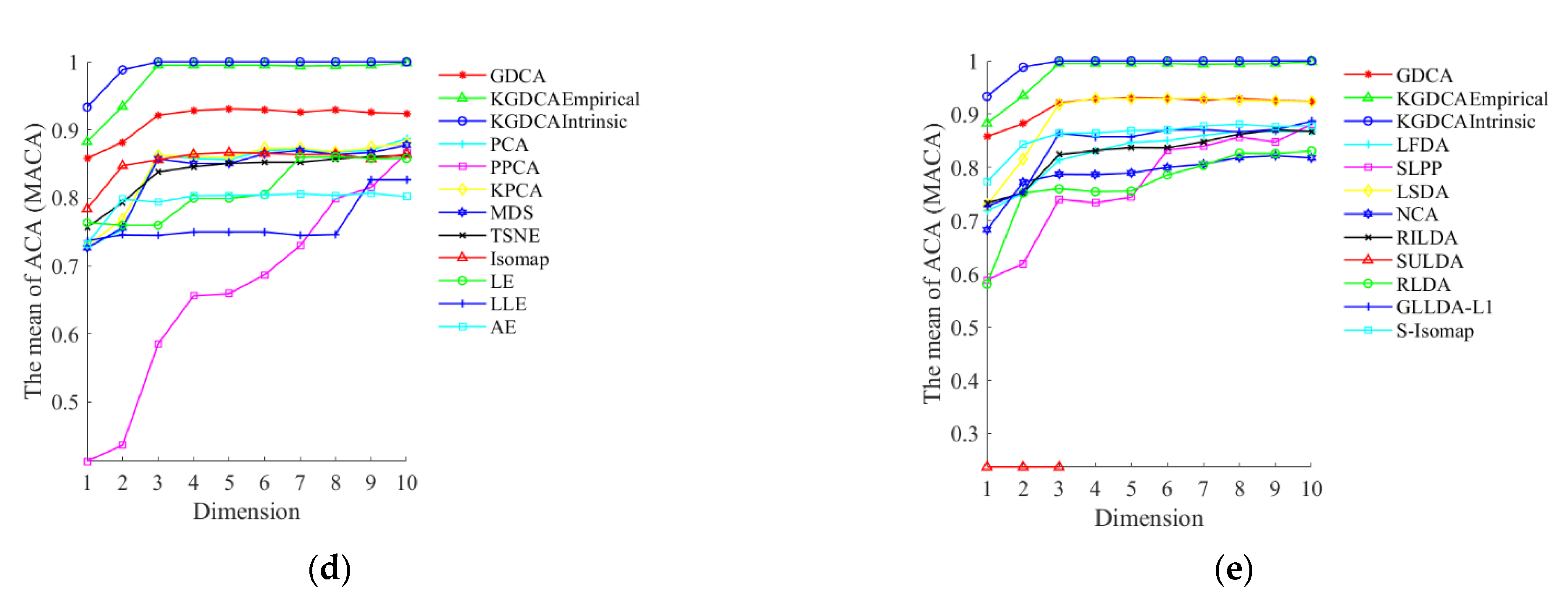
5.4. Comparisons with Other Dimensionality Reduction Algorithms
5.5. Comparisons with Other Classifiers
5.5.1. Comparisons with Ten Kinds of Neural Networks
5.5.2. Comparisons with CRS
5.5.3. Comparisons with the Remaining Classifiers
- ●
- Without attribute reduction of NRS
- ●
- with attribute reduction of NRS
6. Conclusions
- (1)
- All the problems of BDCA mentioned in Section 1 can be resolved by GDCA as well as its kernelization forms proposed in this paper. The range of δ, in which GDCA outperforms BDCA with regard to all the estimation indicators, generally expands as α expands. Especially, GDCA (0 < α < 1) is superior to BDCA in the majority span of δ. In the overwhelmingly major combinations of γ and δ under all the values of α, KGDCA-Intrinsic-Space/KGDCA-Empirical-Space outperformed GDCA.
- (2)
- By establishing an effective criterion to optimally select the parameters involved in GDCA and its kernelization forms in advance without using the evaluation indicators of classification results, the time of pattern recognition can be shortened considerably to ensure the optimal recognition effect simultaneously.
- (3)
- The newly proposed pattern recognition method greatly improved the recognition accuracy in comparison with 36 kinds of state-of-the-art dimensionality reduction algorithms and 44 kinds of state-of-the-art classifiers.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- ■
- Proof of Proposition 1
- ■
- Proof of Proposition 2
- ■
- Proof of Proposition 3
References
- Wenger, P.; Beltle, M.; Tenbohlen, S.; Riechert, U.; Behrmann, G. Combined characterization of free-moving particles in HVDC-GIS using UHF PD, high-speed imaging, and pulse-sequence analysis. IEEE Trans. Power Deliv. 2019, 34, 1540–1548. [Google Scholar] [CrossRef]
- Magier, T.; Tenzer, M.; Koch, H. Direct current gas-insulated transmission lines. IEEE Trans. Power Deliv. 2018, 33, 440–446. [Google Scholar] [CrossRef]
- Ridder, D.D.; Tax, D.M.J.; Lei, B.; Xu, G.; Feng, M.; Zou, Y.; van der Heijden, F. Classification, Parameter Estimation and State Estimation: An Engineering Approach Using MATLAB, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Kung, S.Y. Kernel Methods and Machine Learning; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Hira, Z.M.; Gillies, D.F. A review of feature selection and feature extraction methods applied on microarray data. Adv. Bioinform. 2015, 2015, 198363. [Google Scholar] [CrossRef]
- Kis, K.B.; Fodor, Á.; Büki, M.I. Adaptive, Hybrid Feature Selection (AHFS). Pattern Recognit. 2021, 116, 107932. [Google Scholar]
- Yun, L.; Tao, L.; Liu, H. Recent advances in feature selection and its applications. Knowl. Inf. Syst. 2017, 53, 551–577. [Google Scholar]
- Liu, J.; Lin, Y.; Lin, M.; Wu, S.; Zhang, J. Feature selection based on quality of information. Neurocomputing 2017, 225, 11–22. [Google Scholar] [CrossRef]
- Meenachi, L.; Ramakrishnan, S. Metaheuristic Search Based Feature Selection Methods for Classification of Cancer. Pattern Recognit. 2021, 119, 108079. [Google Scholar] [CrossRef]
- Zini, L.; Noceti, N.; Fusco, G.; Odone, F. Structured multi-class feature selection with an application to face recognition. Pattern Recognit. Lett. 2015, 55, 35–41. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.L.C. Gene selection in cancer classification using sparse logistic regression with Bayesian regularization. Bioinformatics 2006, 22, 2348–2355. [Google Scholar] [CrossRef] [Green Version]
- Bernhard, S.; John, P.; Thomas, H. Sparse Multinomial Logistic Regression via Bayesian L1 Regularization. Adv. Neural Inf. Process. Syst. 2017, 19, 209–216. [Google Scholar]
- Zhang, J.; Luo, Z.; Li, C.; Zhou, C.; Li, S. Manifold regularized discriminative feature selection for multi-label learning. Pattern Recognit. 2019, 95, 136–150. [Google Scholar] [CrossRef]
- Su, B.; Ding, X.; Wang, H.; Wu, Y. Discriminative dimensionality reduction for multi-dimensional sequences. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 77–91. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Frangi, A.F.; Yang, J.Y.; Zhang, D.; Jin, Z. KPCA plus LDA: A complete kernel Fisher discriminant framework for feature extraction and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 230–244. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tipping, M.; Bishop, C. Probabilistic principal component analysis. J. R. Stat. Soc. 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Kruskal, J.B. Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika 1964, 29, 230–244. [Google Scholar] [CrossRef]
- Wu, M.; Cao, H.; Cao, J.; Nguyen, H.L.; Gomes, J.B.; Krishnaswamy, S.P. An overview of state-of-the-art partial discharge analysis techniques for condition monitoring. IEEE Electr. Insul. Mag. 2015, 31, 22–35. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [Green Version]
- Tenenbaum, J.B.; de Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Sundaresan, A.; Chellappa, R. Model Driven Segmentation of Articulating Humans in Laplacian Eigenspace. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1771–1785. [Google Scholar] [CrossRef]
- Li, Y.; Chai, Y.; Zhou, H.; Yin, H. A novel dimension reduction and dictionary learning framework for high-dimensional data classification. Pattern Recognit. 2021, 112, 107793. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2001. [Google Scholar]
- Goldberger, J.; Hinton, G.; Roweis, S.; Salakhutdinov, R. Neighborhood Components Analysis. Adv. Neural Inf. Process. Syst. 2005, 17, 513–520. [Google Scholar]
- Masoudimansour, W.; Bouguila, N. Supervised dimensionality reduction of proportional data using mixture estimation. Pattern Recognit. 2020, 105, 107379. [Google Scholar] [CrossRef]
- Bian, W.; Tao, D. Asymptotic Generalization Bound of Fisher’s Linear Discriminant Analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2325–2337. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; McKelvey, T.; Kung, S.Y. A classification scheme for ‘high-dimensional-small-sample-size’ data using soda and ridge-SVM with microwave measurement applications. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 36–31 May 2013; pp. 3542–3546. [Google Scholar]
- Rahulamathavan, Y.; Phan, R.C.; Chambers, J.A.; Parish, D.J. Facial Expression Recognition in the Encrypted Domain Based on Local Fisher Discriminant Analysis. IEEE Trans. Affect. Comput. 2013, 4, 83–92. [Google Scholar] [CrossRef]
- Lai, Z.; Xu, Y.; Yang, J.; Shen, L.; Zhang, D. Rotational invariant dimensionality reduction algorithms. IEEE Trans. Cybern. 2016, 47, 3733–3746. [Google Scholar] [CrossRef]
- Zhang, X.; Chu, D.; Tan, R.C. Sparse uncorrelated linear discriminant analysis for undersampled problems. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1469–1485. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Z.; Nie, F. A new formulation of linear discriminant analysis for robust dimensionality reduction. IEEE Trans. Knowl. Data Eng. 2018, 31, 629–640. [Google Scholar] [CrossRef]
- Zhang, D.; Li, X.; He, J.; Du, M. A new linear discriminant analysis algorithm based on L1-norm maximization and locality preserving projection. Pattern Anal. Appl. 2018, 21, 685–701. [Google Scholar] [CrossRef]
- Peng, X.; Yang, F.; Wang, G.; Wu, Y.; Li, L.; Li, Z.; Bhatti, A.A.; Zhou, C.; Hepburn, D.M.; Reid, A.J.; et al. A convolutional neural network based deep learning methodology for recognition of partial discharge patterns from high voltage cables. IEEE Trans. Power Deliv. 2019, 34, 1460–1469. [Google Scholar] [CrossRef]
- Morshuis, P.H.F.; Smit, J.J. Partial discharges at DC voltage: Their mechanism, detection and analysis. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 328–340. [Google Scholar] [CrossRef] [Green Version]
- Seo, I.J.; Khan, U.A.; Hwang, J.S.; Lee, J.G.; Koo, J.Y. Identification of insulation defects based on chaotic analysis of partial discharge in HVDC superconducting cable. IEEE Trans. Appl. Supercond. 2015, 25, 1–5. [Google Scholar] [CrossRef]
- Pirker, A.; Schichler, U. Partial discharges at DC voltage - measurement and pattern recognition. In Proceedings of the IEEE International Conference on Condition Monitoring and Diagnosis, Xi’an, China, 25–28 September 2016. [Google Scholar]
- Yang, F.; Sheng, G.; Xu, Y.; Hou, H.; Qian, Y.; Jiang, X. Partial discharge pattern recognition of XLPE cables at DC voltage based on the compressed sensing theory. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 2977–2985. [Google Scholar] [CrossRef]
- Wenrong, S.; Junhao, L.; Peng, Y.; Yanming, L. Digital detection, grouping and classification of partial discharge signals at DC voltage. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1663–1674. [Google Scholar] [CrossRef]
- Varol, Y.; Oztop, H.F.; Avci, E. Estimation of thermal and flow fields due to natural convection using support vector machines (SVM) in a porous cavity with discrete heat sources. Int. Commun. Heat Mass Transf. 2008, 35, 928–936. [Google Scholar] [CrossRef]
- Botev, Z.I.; Grotowski, J.F.; Kroese, D.P. Kernel density estimation via diffusion. Ann. Stat. 2010, 38, 2916–2957. [Google Scholar] [CrossRef] [Green Version]
- Umbaugh, S.E. Digital Image Processing and Analysis: Applications with MATLAB and CVIPtools, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Fan, R.E.; Chen, P.H.; Lin, C.J.; Joachims, T. Working set selection using second order information for training support vector machines. J. Mach. Learn. Res. 2005, 6, 1889–1918. [Google Scholar]
- Chen, P.H.; Fan, R.E.; Lin, C.J. A study on SMO-type decomposition methods for support vector machines. IEEE Trans. Neural Netw. 2006, 17, 893–908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Platt, J.C. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. Adv. Large Margin Classif. 2000, 10, 61–74. [Google Scholar]
- Wu, T.F.; Lin, C.J.; Weng, R.C. Probability estimates for multi-class classification by pairwise coupling. J. Mach. Learn. Res. 2004, 5, 975–1005. [Google Scholar]
- Mak, M.W.; Guo, J.; Kung, S.Y. PairProSVM: Protein subcellular localization based on local pairwise profile alignment and SVM. IEEE/ACM Trans. Comput. Biol. Bioinform. 2008, 5, 416–422. [Google Scholar] [PubMed]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Pawlak, Z. Rough sets. Int. J. Parallel Program. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Hu, Q.H.; Yu, D.R.; Xie, Z.X. Neighborhood classifiers. Expert Syst. Appl. 2008, 34, 866–876. [Google Scholar] [CrossRef]
- Zhou, Z.H. Ensemble Methods Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Li, Y.; Gou, J.; Fan, Z.W. Educational data mining for students’ performance based on fuzzy C-means clustering. IET Gener. Transm. Distrib. 2019, 2019, 8245–8250. [Google Scholar] [CrossRef]
- Garcia, S.; Luengo, J.; Sáez, J.A.; Lopez, V.; Herrera, F. A Survey of Discretization Techniques: Taxonomy and Empirical Analysis in Supervised Learning. IEEE Trans. Knowl. Data Eng. 2013, 25, 734–750. [Google Scholar] [CrossRef]
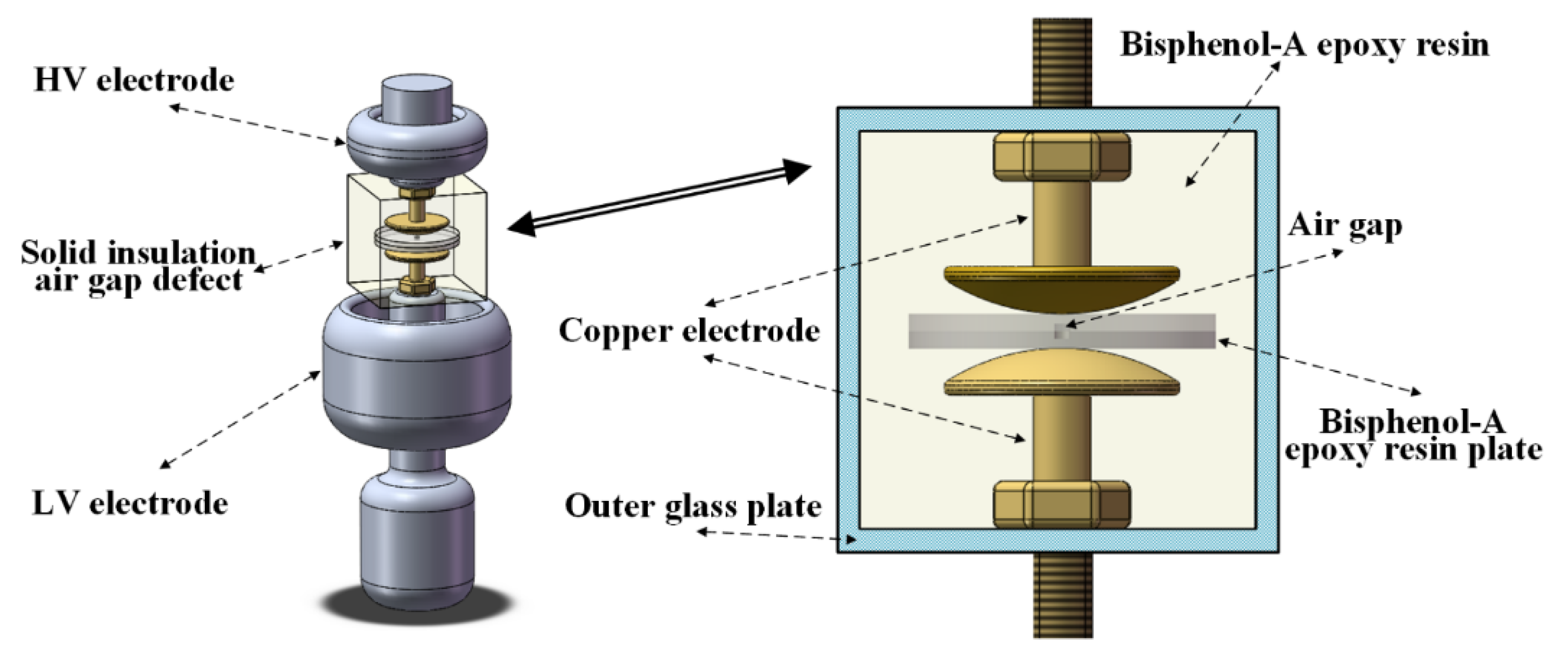






| Solid Insulation Air Gap Defect | Post Insulator Defects | Surface Defect | Floating Defect | Point Defect | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| label | 1 | 2 | 3 | label | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 1 | 2 | 3 |
| Diameter/mm | 2 | 1 | 0.5 | Diameter/mm | 1 | 0.5 | 0.5 | 0.5 | 0.6 | 2.5 | 0.6 | 0.6 | 2.5 | 0.6 |
| Height/mm | 2 | 1 | 0.5 | Length/mm | 60 | 60 | 30 | 60 | 20 | 20 | 20 | 30 | 30 | 30 |
| Distance to HV electrode/mm | 10 | 10 | 10 | 1 | 1 | 0 | 0 | |||||||
| Distance to LV electrode/mm | 10 | 1 | 0 | |||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Gao, W.; Liu, W.; Ding, D.; Zhang, B. Statistical Feature Extraction Combined with Generalized Discriminant Component Analysis Driven SVM for Fault Diagnosis of HVDC GIS. Energies 2021, 14, 7674. https://doi.org/10.3390/en14227674
Zhou R, Gao W, Liu W, Ding D, Zhang B. Statistical Feature Extraction Combined with Generalized Discriminant Component Analysis Driven SVM for Fault Diagnosis of HVDC GIS. Energies. 2021; 14(22):7674. https://doi.org/10.3390/en14227674
Chicago/Turabian StyleZhou, Ruixu, Wensheng Gao, Weidong Liu, Dengwei Ding, and Bowen Zhang. 2021. "Statistical Feature Extraction Combined with Generalized Discriminant Component Analysis Driven SVM for Fault Diagnosis of HVDC GIS" Energies 14, no. 22: 7674. https://doi.org/10.3390/en14227674
APA StyleZhou, R., Gao, W., Liu, W., Ding, D., & Zhang, B. (2021). Statistical Feature Extraction Combined with Generalized Discriminant Component Analysis Driven SVM for Fault Diagnosis of HVDC GIS. Energies, 14(22), 7674. https://doi.org/10.3390/en14227674







