Influence of the Refrigerant Charge on the Heat Transfer Performance for a Closed-Loop Spray Cooling System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental System
2.2. Spray Chamber and Heating Block
2.3. Uncertainty Analysis
2.4. Data Process
2.4.1. Data Calculation
2.4.2. Reliability Verification
3. Results and Discussion
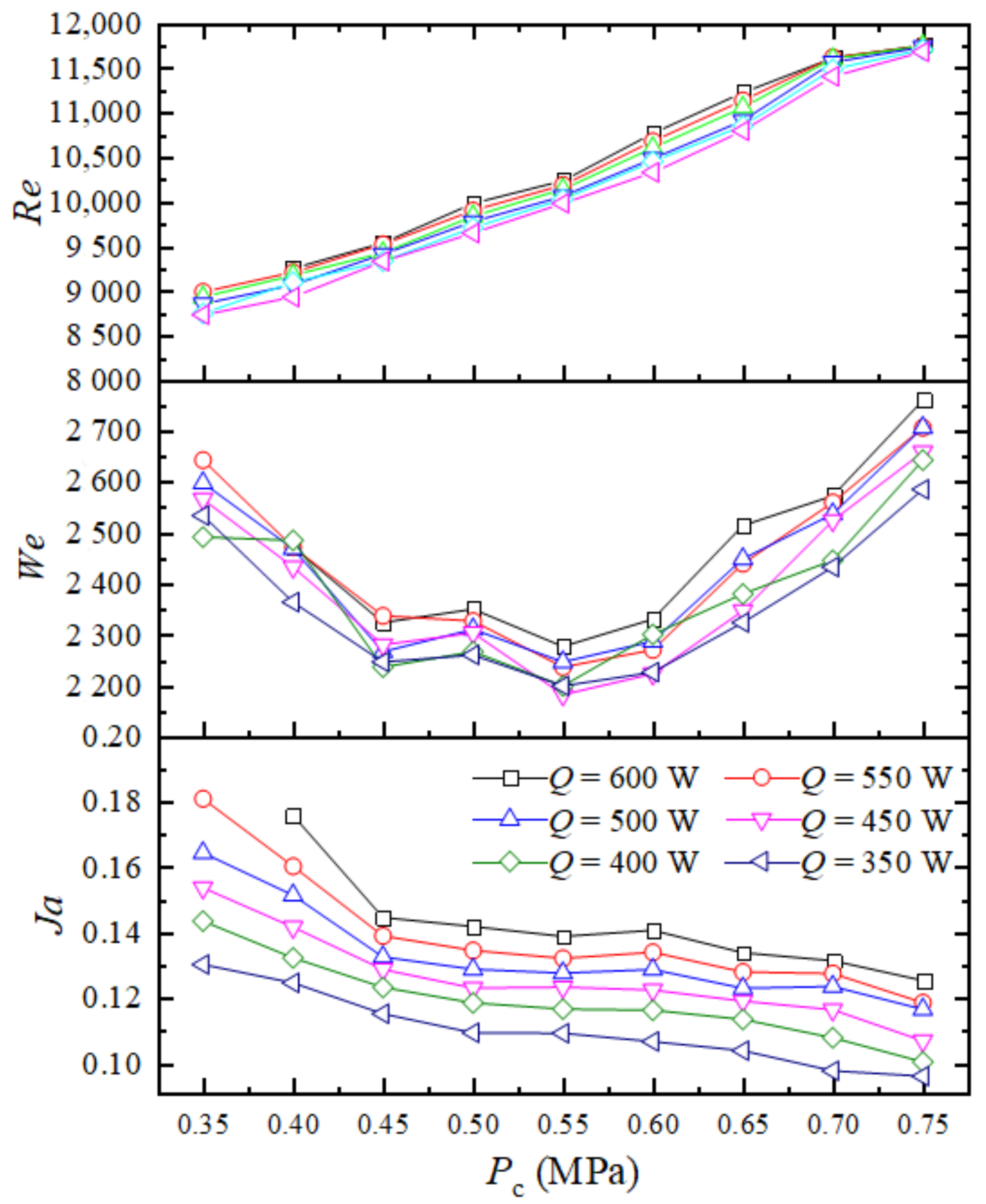
3.1. Effect of Refrigerant Charge on Spray Cooling Performance
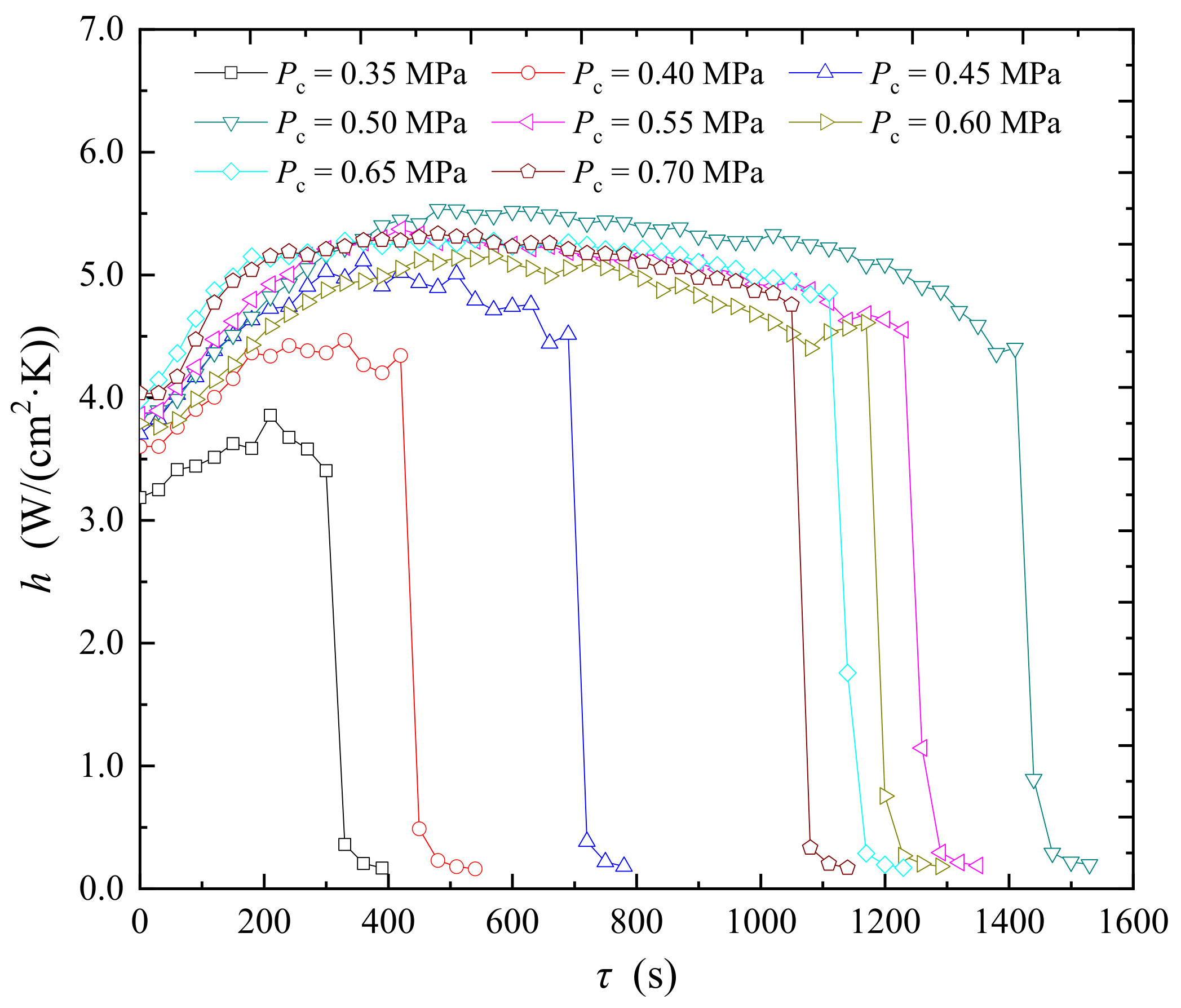
3.2. Analysis of Dynamic Heating Process under Different Refrigerant Charge
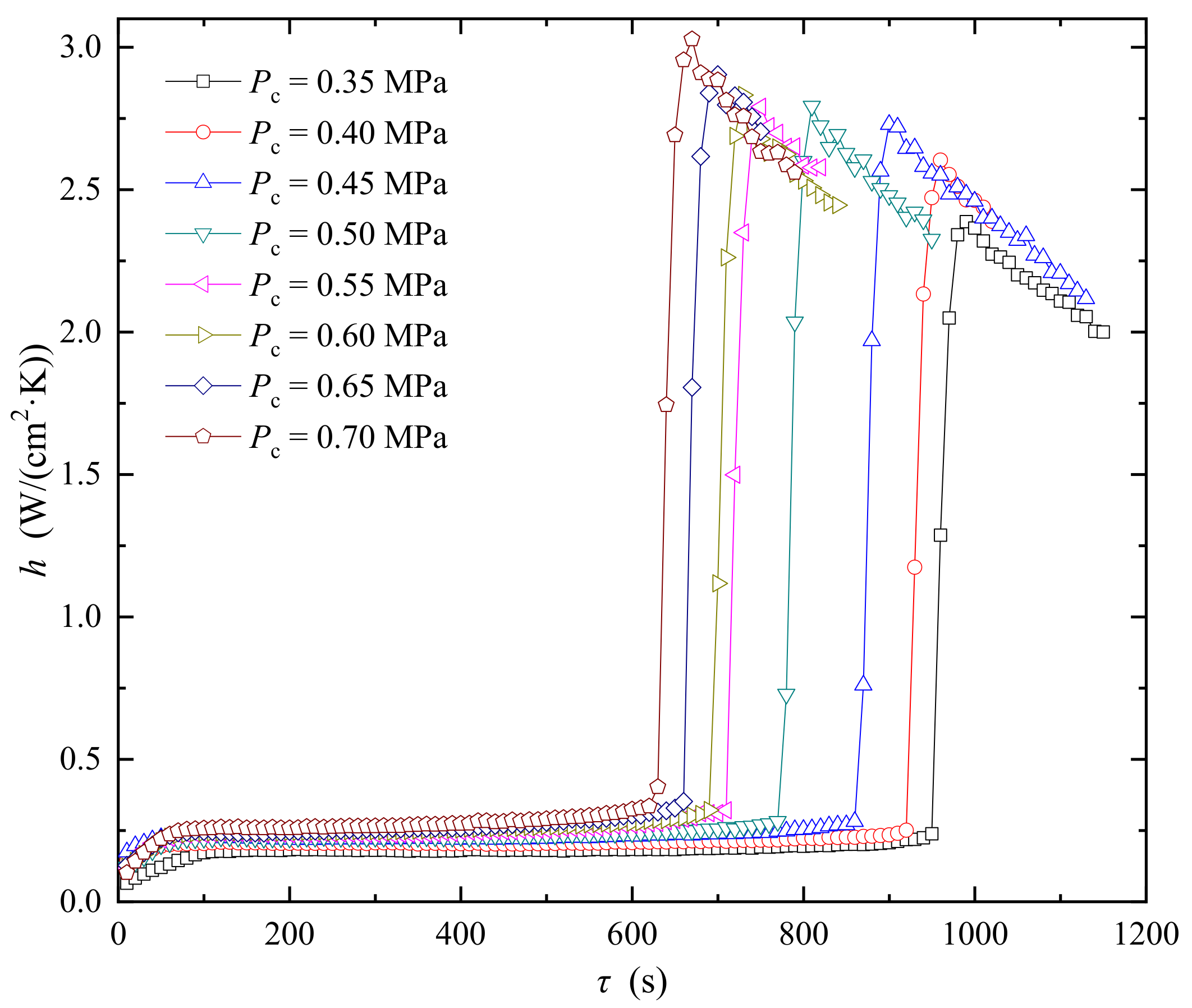
3.3. Analysis of Dynamic Dissipating Process under Different Refrigerant Charge
3.4. The Optimum Refrigerant Charge in Spray Cooling System with R22
4. Conclusions
- (1)
- In the steady-state, the heat transfer coefficient increases with the rise of the refrigerant charge.
- (2)
- In the dynamic heating process, both heat flux and heat transfer coefficient increase with a reversed rate before the critical heat flux. After critical heat flux, both would decrease rapidly.
- (3)
- In the process of dynamic dissipation, the heat transfer coefficient increases sharply when it reaches the surface temperature drop point. In addition, with the increase of refrigerant charge, the surface temperature drops point increase, and the time to the point decrease conversely.
- (4)
- When the refrigerant operating pressure was 0.5 MPa, the spray cooling process presents with a higher heat flux, heat transfer coefficient, and cooling efficiency. Meanwhile, a suitable surface temperature drop point and a more gentle heat flux curve in the nucleate boiling regime were obtained.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | surface area (m2) |
| c | specific heat capacity (J/(kg·K)) |
| d32 | Sauter mean diameter (m) |
| D | surface diameter (m) |
| G | mass flow rate (kg/s) |
| h | heat transfer coefficient (W/(m2·°C) |
| H | nozzle height (m) |
| L | latent heat (J/kg) |
| m | mass (kg) |
| P | pressure (MPa) |
| Q | heating power (W) |
| q | heat flux (W/m2) |
| T | temperature (°C) |
| u | spray velocity(m/s) |
| y | distance between thermocouples (m) |
| Greek | |
| spray cooling efficiency | |
| thermal conductivity (W/(m·K)) | |
| dynamic viscosity (Pa·s) | |
| density (kg/m3) | |
| surface tension (N/m) | |
| time (s) | |
| Subscripts | |
| c | chamber |
| in | inlet |
| Ja | Jacob number |
| m | mass |
| o | outer environment |
| Pr | Prandtl number |
| Re | Reynolds number |
| sat | saturation |
| th | thermophoresis force |
| We | Weber number |
| w | heating surface |
References
- Cheng, W.L.; Liu, Q.N.; Zhao, R.; Fan, H.L. Experimental investigation of parameters effect on heat transfer of spray cooling. Heat Mass Transf. 2010, 46, 911–921. [Google Scholar] [CrossRef]
- Zhao, R.; Cheng, W.L.; Liu, Q.N.; Fan, H.L. Study on heat transfer performance of spray cooling: Model and analysis. Heat Mass Transf. 2010, 46, 821–829. [Google Scholar] [CrossRef]
- Cheng, W.L.; Zhang, W.W.; Chen, H.; Hu, L. Spray cooling and flash evaporation cooling: The current development and application. Renew. Sustain. Energy Rev. 2016, 55, 614–628. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Liu, M.H.; Liu, D.; Wang, L.; Guo, H. Heat transfer mechanism and influencing factors in spray cooling. High Power Laser Part. Beams. 2011, 23, 2277–2281. [Google Scholar] [CrossRef]
- Grissom, W.M.; Wierum, F.A. Liquid spray cooling of a heated surface. Int. J. Heat Mass Transf. 1981, 24, 261–271. [Google Scholar] [CrossRef]
- Fabbri, M.; Jiang, S.J.; DHir, V.K. A comparative study of cooling of high power density electronics using sprays and microjets. J. Heat Transf. Trans. ASME 2005, 127, 38–48. [Google Scholar] [CrossRef]
- Hsieh, C.C.; Yao, S.C. Evaporative heat transfer characteristics of a water spray on micro-structured silicon surfaces. Int. J. Heat Mass Transf. 2006, 49, 962–974. [Google Scholar] [CrossRef]
- Pais, M.R.; Chow, L.C.; Mahefkey, E.T. Surface roughness and its effects on the heat transfer mechanism in spray cooling. J. Heat Transf. 1992, 114, 211–219. [Google Scholar] [CrossRef]
- Yang, J.R.; Wong, S.C. On the discrepancies between theoretical and experimental results for microgravity droplet evaporation. Int. J. Heat Mass Transf. 2001, 44, 4433–4443. [Google Scholar] [CrossRef]
- Yang, J.R.; Wong, S.C. An experimental and theoretical study of the effects of heat conduction through the support fiber on the evaporation of a droplet in a weakly convective flow. Int. J. Heat Mass Transf. 2002, 45, 4589–4598. [Google Scholar] [CrossRef]
- Qian, Y.; Liu, J.H.; Li, M.; Liu, X.F.; Hou, Y. Experimental Study on Heat Transfer Performance of Phase change Spray cooling with R134a. J. Xi Jiaotong Univ. 2015, 49, 97–101. [Google Scholar]
- Hou, Y.; Liu, X.F.; Liu, J.H.; Li, M.J.; Pu, L. Experimental study on phase change spray cooling. Exp. Therm. Fluid Sci. 2013, 46, 84–88. [Google Scholar] [CrossRef]
- Liu, J.H.; Sun, W.; Liu, X.F.; Hou, Y. Influences of spray chamber pressure and nozzle bore diameter on spray cooling performance. High Power Laser Part. Beams 2013, 25, 2546–2550. [Google Scholar]
- Liu, J.H.; Li, M.J.; Liu, X.F.; Hou, Y. Experiment on Phase Change Spray Cooling of Closed Cycle with R22. J. Xian Jiaotong Univ. 2013, 47, 132–136. [Google Scholar]
- Li, Q.; Tie, P.; Xuan, Y.M. Investigation on heat transfer characteristics of R134a spray cooling. Exp. Therm. Fluid Sci. 2015, 60, 182–187. [Google Scholar] [CrossRef]
- Liu, J.H.; Xue, R.; Chen, L.; Liu, X.F.; Hou, Y. Influence of chamber pressure on heat transfer characteristics of a closed loop R134-a spray cooling. Exp. Therm. Fluid Sci. 2016, 75, 89–95. [Google Scholar] [CrossRef]
- Peng, C.; Xu, X.H.; Liang, X.A. Experimental study on temperature variation patterns and deterioration of spray cooling with R21. Int. J. Heat Mass Transf. 2018, 121, 1159–1167. [Google Scholar] [CrossRef]
- Cao, L.; Chen, J.N.; Jiang, P.X.; Xu, R.N. Experimental Investigation of spray cooling system in a closed loop based on refrigeration cycle. J. Eng. Thermophys. 2018, 39, 373–378. [Google Scholar]
- Cai, C.; Liu, H.; Jia, M.; Yin, H.C.; Xie, R.; Yan, P.L. Numerical investigation on heat transfer of water spray cooling from single-phase to nucleate boiling region. Int. J. Therm. Sci. 2020, 151, 106285. [Google Scholar] [CrossRef]
- Xie, J.L.; Ranjith, K.; Wong, T.N.; Lee, H.M. Comparative study on the heat transfer characteristics of spray cooling in confined spray chambers. Appl. Therm. Eng. 2020, 164, 114463. [Google Scholar] [CrossRef]
- Zhou, Z.F.; Chen, B.; Wang, R.; Wang, G.X. Coupling effect of hypobaric pressure and spray distance on heat transfer dynamics of R134a pulsed flashing spray cooling. Exp. Therm. Fluid Sci. 2016, 70, 96–104. [Google Scholar] [CrossRef]
- Zhou, Z.F.; Wang, R.; Chen, B.; Yang, T.; Wang, G.X. Heat transfer characteristics during pulsed spray cooling with R404A at different spray distances and back pressures. Appl. Therm. Eng. 2016, 102, 813–821. [Google Scholar] [CrossRef]
- Chen, S.T.; Liu, J.H.; Liu, X.F.; Hou, Y. An experimental comparison of heat transfer characteristic between R134-a and R22 in spray cooling. Exp. Therm. Fluid Sci. 2015, 66, 206–212. [Google Scholar] [CrossRef]
- Wang, R.; Zhou, Z.F.; Chen, B.; Bai, F.L.; Wang, G.X. Surface heat transfer characteristics of R404A pulsed spray cooling with an expansion-chambered nozzle for laser dermatology. Int. J. Refrig. 2015, 60, 206–216. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Zhao, X.; Zhang, B.; Yin, Z.C. Solution of thermal boundary conditions using inverse heat conduction problem in intermittent spray cooling. J. Dalian Univ. Tech. 2019, 59, 359–365. [Google Scholar]
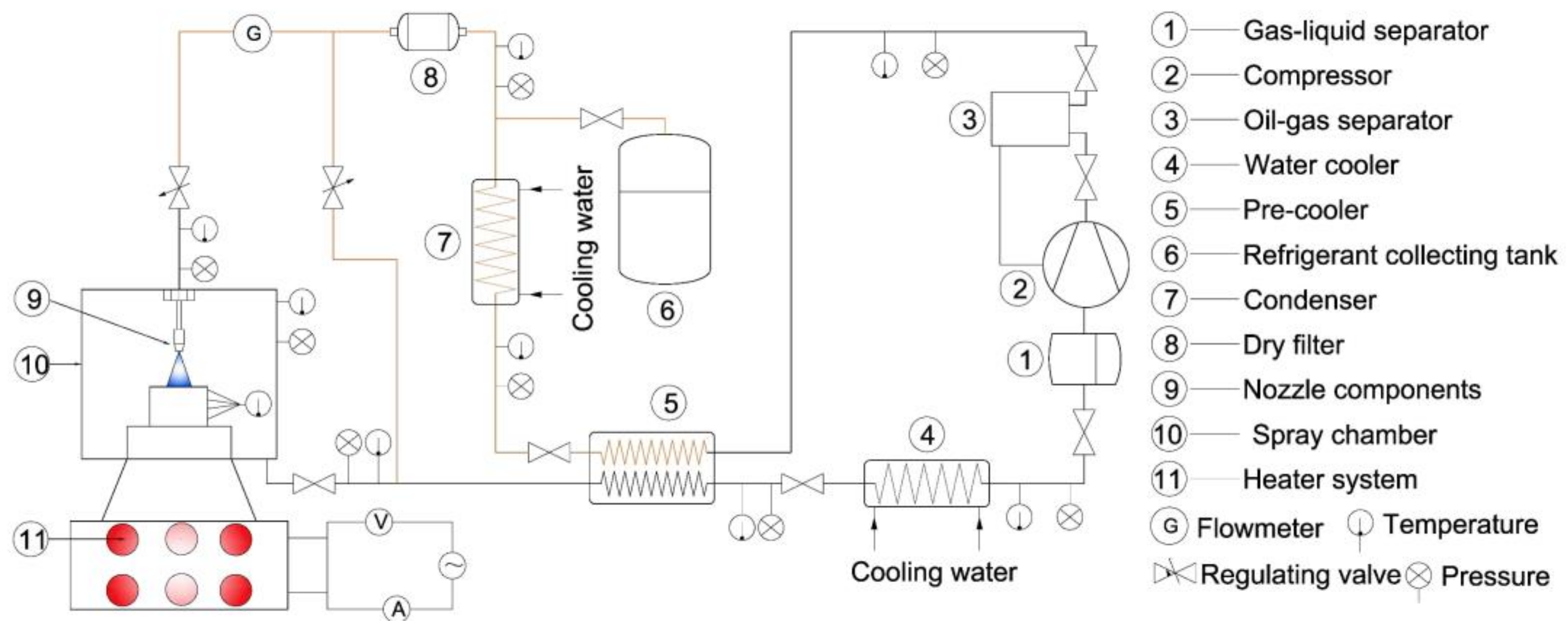

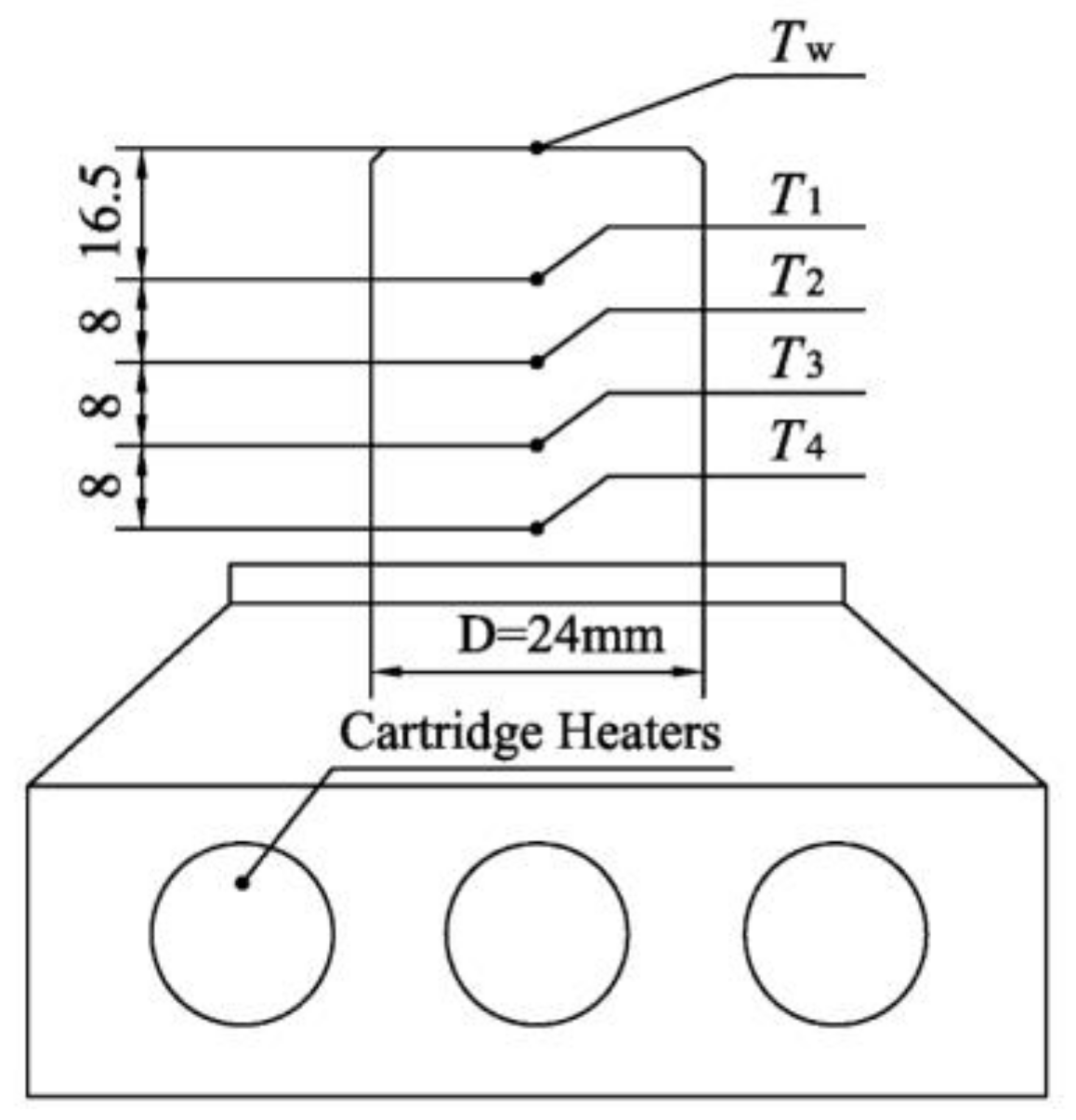


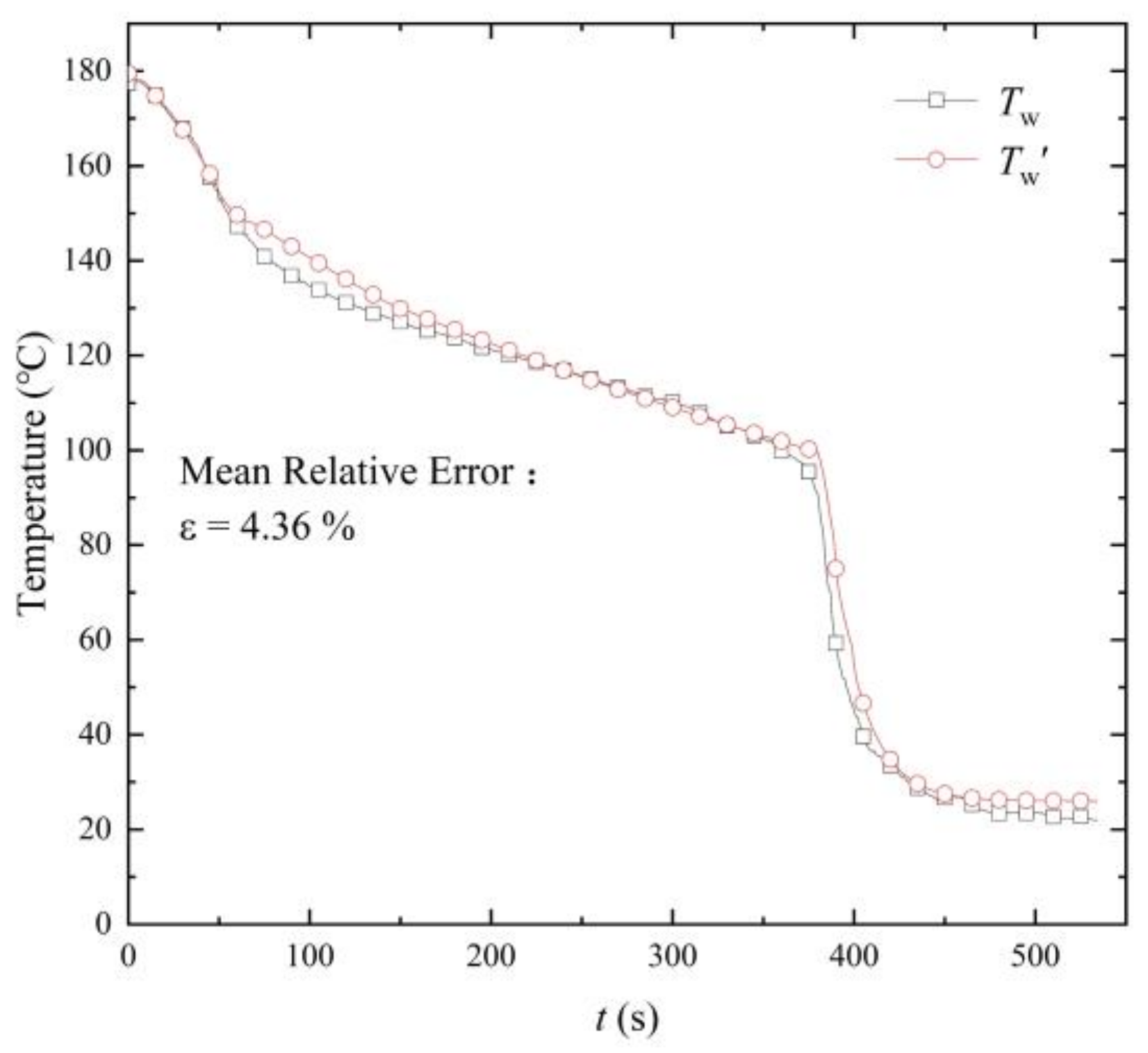
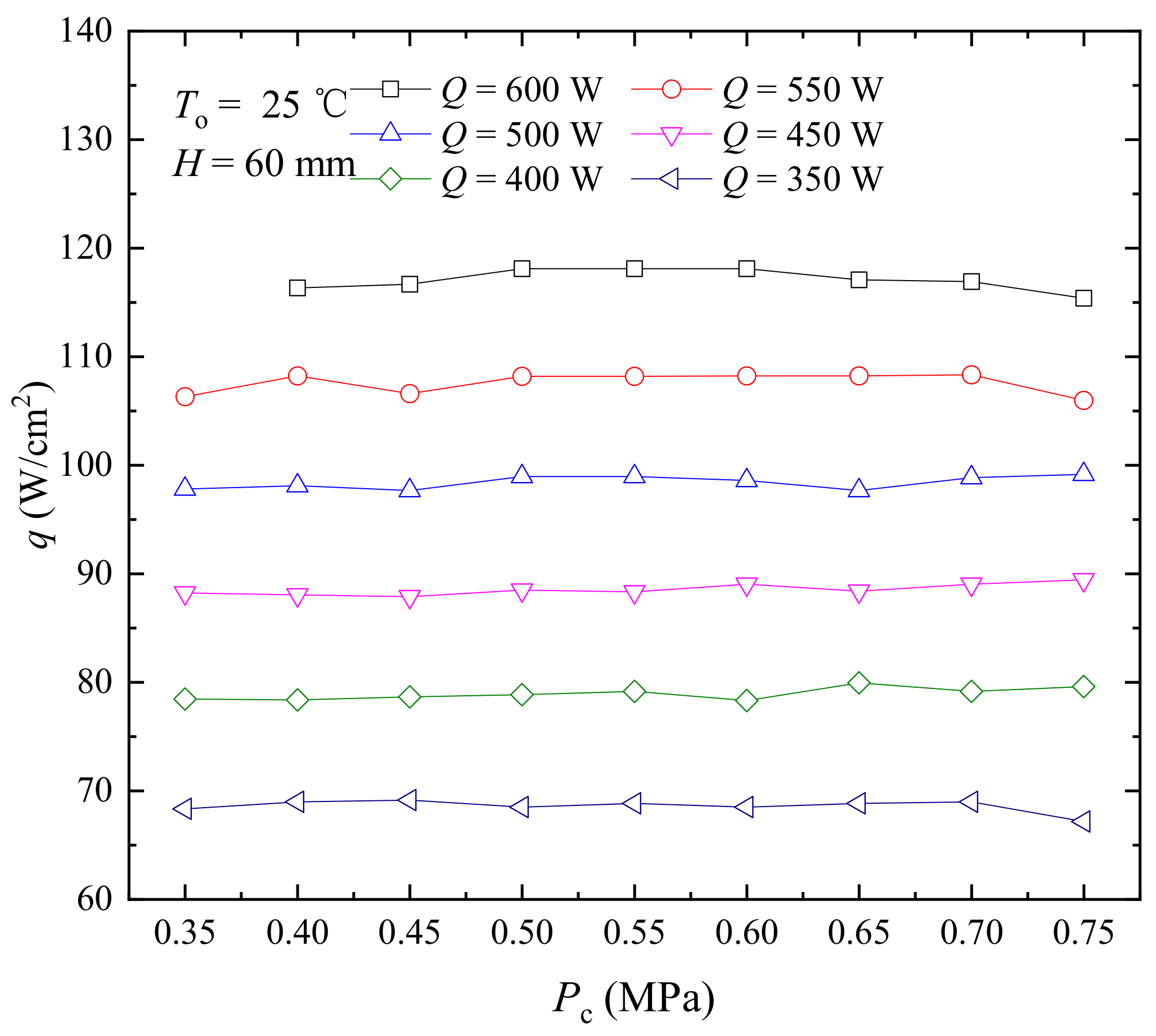



| Measured Data | Device | Range | Deviation |
|---|---|---|---|
| Pressure in chamber | Pressure sensor | 0–1.6 MPa | ±0.25% P |
| Temperature of heating block | K-type thermocouple | 0–800 °C | ±0.004 |T| |
| Temperature of chamber | PT100 | −50–150 °C | ±0.15 °C |
| Flow rate | Turbine fluid meter | 0–10 L/min | ±1% |
| Pc (MPa) | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 | 0.65 | 0.70 |
| STD (°C) | 29.84 | 32.46 | 36.82 | 45.47 | 45.84 | 46.04 | 48.42 | 49.43 |
| CHF (W/cm2) | 108.1 | 123.6 | 141.9 | 162.3 | 157.2 | 158.7 | 160.7 | 161.4 |
| hmax W/(cm2·K) | 3.86 | 4.46 | 5.11 | 5.53 | 5.37 | 5.15 | 5.29 | 5.33 |
| Time to CHF (s) | 300 | 420 | 690 | 1410 | 1230 | 1170 | 1110 | 1050 |
| Pc (MPa) | 0.35 | 0.40 | 0.45 | 0.50 | 0.55 | 0.60 | 0.65 | 0.70 |
| STD (°C) | 48.54 | 51.88 | 56.32 | 57.37 | 58.66 | 60.21 | 62.14 | 62.52 |
| hmax W/(cm2·K) | 2.39 | 2.60 | 2.73 | 2.79 | 2.79 | 2.83 | 2.90 | 3.03 |
| Time (s) | 950 | 920 | 860 | 770 | 710 | 690 | 660 | 630 |
| Pc (MPa) | Evaporating Temperature (°C) | Condensing Temperature (°C) | Sub-cooling (°C) | Superheat (°C) | Coefficient of Performance | Theoretical Refrigeration Capacity (W) | Spray Cooling Heat Exchange (W) | |
|---|---|---|---|---|---|---|---|---|
| 0.35 | −10.4 | 36.02 | 10.2 | 33.7 | 3.64 | 1580 | 488.7 | 30.93 |
| 0.40 | −6.6 | 36.88 | 11.0 | 29.5 | 4.06 | 1740 | 558.8 | 32.11 |
| 0.45 | −3.1 | 38.27 | 12.5 | 26.7 | 4.38 | 1900 | 641.4 | 33.76 |
| 0.50 | 0.1 | 40.17 | 14.7 | 23.4 | 4.64 | 1980 | 734.1 | 37.07 |
| 0.55 | 3.1 | 40.97 | 15.5 | 20.2 | 4.98 | 2150 | 710.6 | 33.05 |
| 0.60 | 5.9 | 42.01 | 16.6 | 17.1 | 5.30 | 2300 | 717.8 | 31.21 |
| 0.65 | 8.5 | 43.53 | 18.1 | 14.3 | 5.55 | 2410 | 726.7 | 30.15 |
| 0.70 | 10.9 | 44.78 | 17.9 | 11.5 | 5.75 | 2450 | 729.6 | 29.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, N.; Feng, H.; Guo, Y.; Liu, W.; Peng, H.; Lei, Y.; Deng, S.; Wang, Y. Influence of the Refrigerant Charge on the Heat Transfer Performance for a Closed-Loop Spray Cooling System. Energies 2021, 14, 7588. https://doi.org/10.3390/en14227588
Zhou N, Feng H, Guo Y, Liu W, Peng H, Lei Y, Deng S, Wang Y. Influence of the Refrigerant Charge on the Heat Transfer Performance for a Closed-Loop Spray Cooling System. Energies. 2021; 14(22):7588. https://doi.org/10.3390/en14227588
Chicago/Turabian StyleZhou, Nianyong, Hao Feng, Yixing Guo, Wenbo Liu, Haoping Peng, Yun Lei, Song Deng, and Yu Wang. 2021. "Influence of the Refrigerant Charge on the Heat Transfer Performance for a Closed-Loop Spray Cooling System" Energies 14, no. 22: 7588. https://doi.org/10.3390/en14227588
APA StyleZhou, N., Feng, H., Guo, Y., Liu, W., Peng, H., Lei, Y., Deng, S., & Wang, Y. (2021). Influence of the Refrigerant Charge on the Heat Transfer Performance for a Closed-Loop Spray Cooling System. Energies, 14(22), 7588. https://doi.org/10.3390/en14227588









